Методические указания по решению задач по разделу Кинематика

Главная

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ

3. Кинематика плоскопараллельного движения тела

3.1. Определение скоростей точек тела при плоскопараллельном движении

</ Изучение плоскопараллельного движения тела можно свести к изучению движения плоской фигуры, образованной сечением тела плоскостью, параллельной неподвижной плоскости, относительно которой движется тело.

Определение скоростей точек плоской фигуры можно выполнить одним их следующих методов:

- аналитическим;

- основанным на использовании векторного уравнения;

- основанным на использовании теоремы о проекциях скоростей точек тела на прямую, проходящую через эти точки;

- основанным на использовании мгновенного центра скоростей.

Наиболее часто применяется последний метод, ему ниже будет уделено основное внимание.

3.1.1. Аналитический метод

При использовании аналитического метода считаются известными уравнения движения плоской фигуры (тела, совершающего плоскопараллельное движение):

(54)

Тогда координаты точки М (рис. 24) будут

(55)

где b - расстояние от точки М до полюса А.

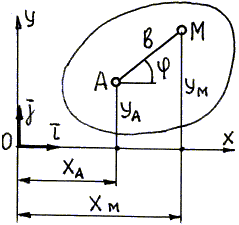
Рис. 24

Модуль скорости точки М определяется по формуле

.

Направление вектора определяется по направляющим косинусам:

Таким образом, задача по определению скоростей точек плоской фигуры сводится к известному решению соответствующей задачи кинематики точки.

Угловая скорость плоской фигуры определяется дифференцированием последнего уравнения из (54), т.е.

(56)

Аналитический метод решения задачи рекомендуется использовать в тех случаях, когда требуется определить скорости точек для большого числа положений плоской фигуры.

3.1.2. Метод, основанный на использовании векторного уравнения

Векторное уравнение для скоростей точек плоской фигуры получается из теоремы: скорость любой точки плоской фигуры равна геометрической сумме скорости полюса и скорости этой точки при вращении фигуры вокруг полюса, т.е. (рис. 25)

, (57)

где ; - скорость точки М при вращении плоской фигуры вокруг полюса А.

Скорость направлена перпендикулярно прямой АМ в сторону вращения фигуры (рис. 25) и равна по модулю

, (58)

где - угловая скорость вращения плоской фигуры.

Чтобы можно было определить скорость точки М, используя уравнение (57), необходимо знать скорость полюса А и угловую скорость вращения плоской фигуры . Для решения задачи надо построить по уравнению (57) параллелограмм скоростей (рис.25).

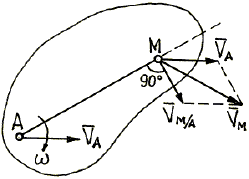
Рис. 25

Диагональ этого параллелограмма есть искомая скорость точки , ее модуль:

. (59)

Решение задачи рекомендуется начинать с изображения плоской фигуры в положении, соответствующем данному моменту времени. Затем следует выбрать полюс и для заданной точки М записать векторное уравнение (57). За полюс следует взять точку тела, скорость которой задана. Далее необходимо построить параллелограмм скоростей по уравнению (57), вычислить модуль скорости V_М/А по формуле (58), а затем модуль скорости точки V_М по формуле (59).

Пример 22. При свободном падении стержня АВ (рис. 26) его середина С движется вертикально вниз с постоянным ускорением g = 9,8 м/с², а сам стержень вращается в вертикальной плоскости вокруг центра С с постоянной угловой скоростью 1/с. Длина стержня 2 м.

В начальный момент стержень горизонтален. Найти скорость его концов А и В в момент времени t₁ = 2 с.

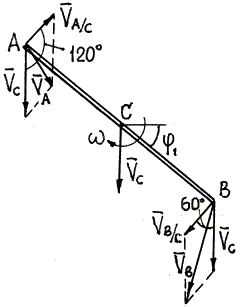
Рис. 26

Решение:

Изображаем стержень в положении, определяемом углом в момент времени t₁ = 2 сек,

рад, .

Выберем за полюс точку С, так как условием задачи определен закон ее движения: прямолинейное равноускоренное движение с ускорением .

Скорость полюса при t₁ = 2 сек:

м/с.

Запишем уравнения типа (57) для концов А и В стержня

Скорости и направлены перпендикулярно стержню АВ в сторону вращения, их модули определяются по формуле (58)

Модули скоростей точек А и В определяются по формуле (59)

3.1.3. Метод, основанный на использовании теоремы о проекциях скоростей точек тела

В п. 3.1.2 рассмотрен метод решения задачи скоростей, когда исходными данными являются скорость полюса и угловая скорость тела. Но скорость конкретной точки плоской фигуры можно найти и в том случае, если известны скорость полюса и направление искомой скорости точки. Для этого используем следующую теорему: при движении тела проекции скоростей двух точек этого тела на прямую, проходящую через точки, равны между собой(рис. 27), т.е.

. (60)

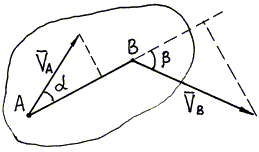
Рис. 27

Для определения скоростей точек с помощью этой теоремы рекомендуется изобразить тело в заданном положении, показать направление известной скорости и искомой скорости , затем записать уравнение (60) и определить модуль V_В.

Пример 23. Стержень АВ (рис. 28) движется в плоскости чертежа, при этом конец А скользит по вертикальной стене, а конец В - по полу. Определить скорость конца В стержня в момент, когда стержень составляет с полом угол 30⁰, если известно, что скорость конца А в этот момент 5 м/с.

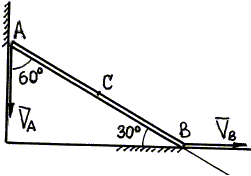
Рис. 28

Решение:

Покажем для заданного положения стержня направления скоростей точек А и В. Проектируя векторы и на линию АВ, получим

.

Откуда

Метод определения скоростей точек тела с помощью теоремы о проекциях не позволяет определить угловую скорость тела. Метод не дает общей картины (закономерности) распределения скоростей в теле для данного момента времени, в связи с чем трудно определить скорость точки, направление которой неизвестно (например, на рис. 28).

Этих недостатков нет в методе, рассмотренном в следующем подразделе.

3.1.4. Метод, основанный на использовании мгновенного центра скоростей

Мгновенный центр скоростей, или сокращенно МЦС, есть точка плоской фигуры, скорость которой в данный момент времени равна нулю. Мгновенный центр скоростей обозначается буквой Р (рис. 29). Скорости точек плоской фигуры распределены так, как если бы фигура совершала вращательное движение вокруг оси, проходящей через МЦС перпендикулярно плоскости движения. Поэтому скорость любой точки плоской фигуры перпендикулярна отрезку, соединяющему эту точку с МЦС, а модуль скорости равен произведению угловой скорости тела на расстояние точки до МЦС, т.е. (см. рис. 29).

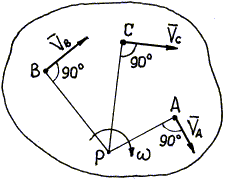
Рис. 29

и ; (61)

и ;

и и т. п.

Отсюда и т.п. (62)

Из анализа формул (61) и (62) видно, что для определения скоростей надо знать положение МЦС и скорость одной какой-нибудь точки (последнее нужно для определения ).

Рассмотрим основные способы нахождения положения МЦС.

а) В некоторых случаях удается сразу указать точку плоской фигуры, скорость которой в рассматриваемый момент времени равна нулю. Эта точка и есть МЦС. Так, в случае качения без скольжения тела по неподвижной поверхности точка соприкосновения тела с поверхностью является мгновенным центром скоростей (рис. 30). Примером служит качение колеса по рельсу.

б) Если известны направления скоростей каких-нибудь двух точек плоской фигуры в данный момент, то МЦС находится на пересечении перпендикуляров, восстановленных в этих точках к направлениям скоростей (перпендикуляры АР и ВР на рис. 31).

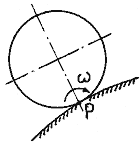
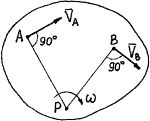
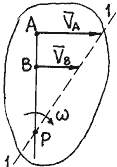
Рис. 30 Рис. 31 Рис. 32

в) Если скорости точек А и В (рис. 32) взаимно параллельны, а точки лежат на общем перпендикуляре к скоростям, то МЦС (точка Р) находится на пересечении указанного общего перпендикуляра АВ и прямой 1-1, проведенной через концы векторов скоростей этих точек. Это следует из соотношения (62).

г) Если скорости двух точек А и В (рис. 33) параллельны, а точки не лежат на общем перпендикуляре к скоростям, то МЦС находится в бесконечности. В этом случае имеем мгновенное поступательное движение плоской фигуры. Угловая скорость фигуры при таком движении равна нулю. Действительно, из формулы (62)

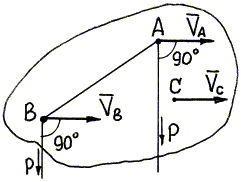
Рис. 33

Скорости всех точек фигуры в этом случае одинаковы по величине и направлению: .

Отметим, что при мгновенном поступательном движении только скорости точек одинаковы, а их ускорения в общем случае различны.

Укажем последовательность определения скоростей с использованием мгновенного центра скоростей.

1. Изобразить на чертеже тело (плоскую фигуру) в заданном положении и найти мгновенный центр скоростей одним из рассмотренных выше способов.

2. Указать направления векторов скоростей точек фигуры и записать формулы для вычисления их модулей в соответствии с (61).

3. Определить угловую скорость по формуле (62), учитывая, что скорость одной какой-либо точки задана по условию задачи.

4. Вычислить искомые модули скоростей точек по формулам (61).

Пример 24. Колесо радиусом R = 0,5 м катится без скольжения по прямому рельсу (рис. 34). Скорость центра колеса в данный момент времени V_C= 2 м/с. Определить угловую скорость колеса и скорости концов горизонтального и вертикального диаметров.

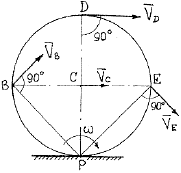
Рис. 34

Решение:

1. Мгновенным центром скоростей является точка Р касания колеса с рельсом (см. способ (а) нахождения МЦС).

2. Направления векторов скоростей точек определяются как при вращательном движении колеса вокруг Р:

Их модули:

3. Учитывая, что скорость точки С задана (V_С = 2 м/с), определим угловую скорость колеса

4. Вычислим искомые модули скоростей по написанным выше формулам (п. 2):

м/с;

м/с;

м/с.

Пример 25. Рассмотрим решение примера 23 с помощью мгновенного центра скоростей. Дополнительно определим скорость середины С стержня и его угловую скорость. Длина стержня 2 м.

Решение:

1. Так как направления скоростей точек А и В (рис. 35) стержня известны, то мгновенный центр скоростей Р определяем, проведя перпендикулярыАР и ВР к направлениям скоростей (способ (б) определения МЦС).

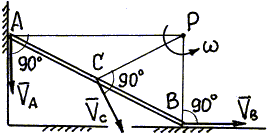
Рис. 35

2. Вектор направлен перпендикулярно СР.

Запишем формулы для модулей скоростей:

3. Определим угловую скорость стержня

4. Вычислим искомые модули скоростей по приведенным выше формулам:

м/с;

м/с.

3.1.5. Определение скоростей точек звеньев плоских механизмов

В плоских механизмах звенья могут совершать поступательное, вращательное и плоскопараллельное движения. При решении следует помнить, что в механизме, состоящем из нескольких звеньев, каждое звено, совершающее плоскопараллельное движение, имеет в данный момент времени свой мгновенный центр скоростей и свою угловую скорость.

Укажем последовательность решения задач по определению скоростей для плоских механизмов.

1. Изобразить механизм на расчетной схеме в том положении, для которого требуется решить задачу о скоростях.

2. Определить скорости точек звена, движение которого задано по условию задачи. Это звено принято называть ведущим. Может оказаться, что ведущее звено совершает не плоскопараллельное, а вращательное движение. Тогда задача о скоростях решается методом, разработанным для вращательного движения.

3. Определить скорости точек звена, присоединенного к ведущему звену, имея в виду, что скорость точки в месте соединения этих звеньев должнабыть определена ранее в п. 2.

4. Если число звеньев в механизме больше двух, то после п. 3 определяются скорости точек третьего и последующих звеньев. Скорости точек в местах соединения звеньев всегда определяются на предшествующем этапе вычислений.

Пример 26. Определить скорость точки В и угловую скорость звеньев АВ и ВО₁ четырехзвенного механизма ОАВО₁ в положении, указанном на чертеже (рис. 36), звено ОА имеет в данный момент угловую скорость 2 1/сек. Длины звеньев: ОА = 20 см, АВ = ВО₁ = 40 см.

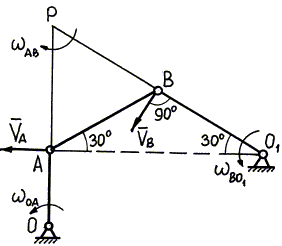
Рис. 36

Решение:

1. Механизм в заданном положении изображен на рис. 36.

2. Ведущим звеном механизма является звено ОА, совершающее вращательное движение вокруг О. Определим скорость точки А: вектор направлен перпендикулярно ОА, его модуль

см/с.

3. Определим скорости точек звена АВ, совершающего плоскопараллельное движение в последовательности, указанной в. п. 3.1.4.

4. Для определения мгновенного центра скоростей звена АВ учтем, что скорость точки В направлена перпендикулярно О₁В, как скорость при вращательном движении звена О₁В вокруг О₁. Мгновенный центр скоростей (точка Р) лежит на пересечении перпендикуляров АР и ВР к направлениям векторов и (см. способ (б) определения положения МЦС).

Угловая скорость звена

Модуль скорости точки В

см/с.

5. Рассмотрим теперь звено ВО₁, совершающее, как указывалось, вращательное движение.

Угловая скорость этого звена

.

Пример 27. Кривошип ОА (рис. 37), вращаясь с угловой скоростью = 2,5 1/с вокруг оси О неподвижной шестерни 2 радиуса R₂ = 15 см, приводит в движение насаженную на его конце шестеренку 1 радиуса R₁ = 5 см. Определить величину и направление скоростей точек А, В, С, Dподвижной шестеренки, если .

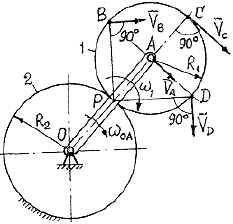
Рис. 37

Решение:

1. Механизм изображен на рис. 37. Ведущим звеном является кривошип OА, совершающий вращательное движение вокруг О. Определим скорость точки А: вектор направлен перпендикулярно ОА, его модуль

см/с.

2. Определим скорости точек шестерни 1, совершающей плоскопараллельное движение, в последовательности, указанной в п. 3.1.4.

Мгновенный центр скоростей шестеренки 1 находится в точке соприкосновения ее с неподвижной шестеренкой 2.

Направления векторов скоростей точек А, В, С, D шестеренки 1 перпендикулярны соответственно отрезкам АР, ВР, СР, DР (рис. 37). Модули скоростей

, , , .

Угловая скорость шестеренки 1

Вычисляем искомые модули скоростей:

см/с;

см/с;

см/с.

Пример 28. К ползуну В (рис. 38) кривошипно-шатунного механизма ОАВ шарнирно прикреплен стержень ВС, конец С которого скользит по направляющей, перпендикулярной линии движения ползуна В. Для момента времени, заданного углом = 90° , определить скорости точек В и С, а также угловые скорости звеньев, если кривошип ОА поворачивается с угловой скоростью = 2 1/с.

ОА = 20 см; АВ = 40 см;

см; см.

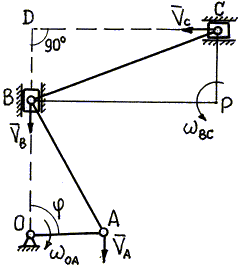
Рис. 38

Решение:

1. Механизм в заданном положении изображен на рис. 38.

2. Ведущим звеном механизма является кривошип ОА, совершающий вращательное движение. Определим скорость точки А: вектор направлен перпендикулярно ОА, его модуль

см/с.

3. Определим скорости точек звена АВ, совершающего плоскопараллельное движение в последовательности, указанной в п. 3.1.4. Мгновенный центр скоростей звена АВ для заданного положения находится в бесконечности (см. способ (г) определения МЦС). В этом случае угловая скорость звена равна нулю, а скорости всех точек звена одинаковы:

см/с.

4. Определим скорости точек звена ВС, совершающего плоскопараллельное движение, в последовательности, указанной выше. Мгновенный центр скоростей Р звена ВС лежит на пересечении перпендикуляров ВР и СР к направлениям и (см. способ (б) определения МЦС).

Угловая скорость звена

Модуль скорости точки С

Пример 29. Механизм, изображенный на рис. 39, состоит из неподвижных блоков 1, 2, подвижного блока 3 и гибкого троса, к концам которого прикреплены грузы А и В. Определить скорость центра С подвижного блока 3 радиуса R = 10 см и его угловую скорость , если груз А опускается со скоростью 8 м/с, а груз В - со скоростью 4 м/с. Считать, что трос не проскальзывает по подвижному блоку.

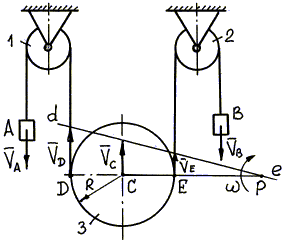
Рис. 39

Решение:

1. Механизм изображен на рис. 39.

2. Ведущими звеньями механизма являются грузы А и В, совершающие поступательное движение.

Скорости грузов заданы условием задачи.

3. Определим скорости точек подвижного блока 3, совершающего плоскопараллельное движение. Так как трос по блоку 3 не проскальзывает, то скорости точек D и Е блока равны по модулю скоростям соответствующих грузов, т.е.

м/с;

м/с.

Мгновенный центр скоростей Р блока 3 лежит на пересечении общего перпендикуляра DE к скоростям и с прямой de, проведенной через концы векторов этих скоростей (см. способ (в) определения положения МЦС).

Угловая скорость подвижного блока

Модуль скорости точки C

м/с.

3.2. Определение ускорений точек тела при плоскопараллельном движении

Определение ускорений можно выполнить одним из следующих методов:

- аналитическим;

- основанным на использовании векторного уравнения;

- основанным на использовании мгновенного центра ускорений.

3.2.1. Аналитический метод

При использовании аналитического метода уравнения движения (54) плоской фигуры считаются известными (п. 3.1.1). Дважды дифференцируя по времени выражения (55) координат точки М, получим проекции ускорения этой точки:

; .

Модуль ускорения равен

.

Направление ускорения определяется направляющими косинусами:

Таким образом, задача по определению ускорений точек сводится к соответствующей задаче кинематики точки.

Угловое ускорение тела находится дифференцированием третьего уравнения движения из (54)

.

Рекомендации по использованию аналитического метода см. п. 3.1.1.

3.2.2. Метод, основанный на использовании векторного уравнения

Векторное уравнение для ускорений получается из следующей теоремы.

Ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки при вращении фигуры вокруг полюса, т.е.

, (63)

где - ускорение полюса А (см. рис. 40); и - вращательное и осестремительное ускорение точки М при вращении плоской фигуры вокруг полюса А.

Осестремительное ускорение точки М при вращении вокруг полюса А в уравнении (63) направлено к полюсу (рис. 40), модуль его

, (64)

где - мгновенная угловая скорость плоской фигуры.

Вращательное ускорение точки М при вращении вокруг полюса А направлено перпендикулярно осестремительному в сторону дуговой стрелки углового ускорения и равно по модулю (рис. 40)

, (65)

где - мгновенное угловое ускорение плоской фигуры.

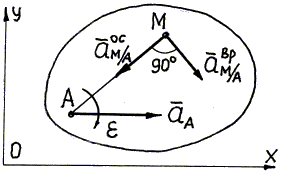
Рис. 40

Напомним, что при ускоренном вращении плоской фигуры вокруг полюса направление дуговой стрелки совпадает с направлением вращения, а при замедленном вращении - противоположно ему.

С помощью уравнения (63) задача определения ускорений чаще всего решается для заданного момента времени. При решении задачи векторное уравнение (63) проектируется на оси координат. Для этого надо изобразить на чертеже все векторы, входящие в уравнение. Проектирование начинается с векторов (или вектора), стоящих в левой части векторного уравнения. Затем ставится знак равенства и проектируются векторы правой части уравнения. В результате одно векторное уравнение (63) заменяется двумя алгебраическими уравнениями проекций. Чтобы система алгебраических уравнений была разрешима, необходимо наличие в ней не более двух неизвестных величин. В качестве неизвестных могут быть любые две из следующих трех величин: одна или две составляющие ускорения точки А и угловое ускорение плоской фигуры. Отметим, что угловая скорость определяется заранее при решении задачи о скоростях.

Все вышесказанное позволяет рекомендовать следующую последовательность решения задачи определения ускорений.

1. Изобразить на чертеже положение тела в заданный момент времени, выбрать полюс и отметить точку, ускорение которой требуется определить. За полюс выбирается точка, ускорение которой либо известно по величине и направлению, либо легко определяется по условию задачи до решения уравнения (63).

2. Записать основное векторное уравнение (63) для точки, ускорение которой надо найти.

3. Показать на чертеже все векторы, входящие в уравнение (63). Если направление искомого вектора ускорения неизвестно, то его надо представить составляющими по направлению выбранных координатных осей.

4. Провести анализ уравнения (63), то есть выявить, какие величины в нем известны, а какие неизвестны. В результате анализа и предварительных вычислений в этом уравнении должно остаться не более двух неизвестных величин.

5. Спроектировать уравнение (63) на выбранные оси координат. Следить за тем, чтобы знак равенства сохранял свое место и в уравнениях проекций.

6. Решая полученную систему уравнений проекций, определить неизвестные величины.

В зависимости от того, какие неизвестные входят в основное векторное уравнение, задачи определения ускорений могут быть разделены на три основных типа.

Тип 1 - задача, в которой неизвестными уравнения (63) являются две составляющие ускорения рассматриваемой точки М. Это значит, ускорение полюса , угловая скорость и угловое ускорение должны быть заданы или определены по исходным данным до решения векторного уравнения (см. пример 30).

Тип 2 - задача, возникающая при качении колеса без проскальзывания, когда задается скорость и ускорение центра колеса. Особенности кинематики колеса позволяют в этом случае определить угловую скорость и угловое ускорение колеса до решения векторного уравнения (см. пример 31).

Тип 3 - задача, в которой неизвестными векторного уравнения (63) являются одна из составляющих ускорений рассматриваемой точки М и угловое ускорение тела . В этих задачах, как правило, задается скорость и ускорение полюса А и траектория движения точки М (см. пример 32).

Тип задачи окончательно может быть установлен только после анализа векторного уравнения (63). Однако в наиболее простых случаях само условие задачи, весь набор данных определяют заранее тип задачи и, следовательно, особенности ее решения.

Пример 30. Равносторонний треугольник (рис. 41) со стороной 1 м движется в плоскости так, что ускорение его вершины А известно и равно = 2 м/с², угловая скорость и угловое ускорение в данный момент времени соответственно равны 1/с; 1/с². Определить ускорение вершины Втреугольника.

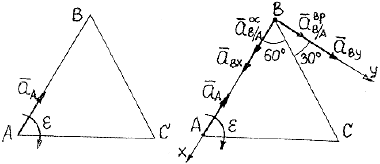
Рис. 41 Рис. 42

Решение:

1. В качестве полюса выберем точку А, ускорение которой известно.

2. Для определения ускорения точки В запишем векторное уравнение типа (63)

. (66)

3. Изобразим все векторы, входящие в уравнение (66), на рис. 42. Ускорение точки В, неизвестное по направлению, представим составляющими и ; вектор ускорения полюса А задан условием задачи; осестремительное ускорение точки В при вращении вокруг полюса А направим от точкиВ к полюсу, его модуль

м/с²;

вращательное ускорение точки В при вращении вокруг полюса А направим перпендикулярно осестремительному в сторону дуговой стрелки углового ускорения, его модуль равен

м/с².

4. Анализ векторного уравнения (66) показывает, что задача относится к типу 1, так как неизвестными здесь являются обе составляющие ускорения точки В - и .

5. Находятся они проектированием векторного уравнения (66) на координатные оси и . Отметим еще раз, что при проектировании векторного уравнения на оси, знак равенства в уравнении сохраняет свое место. В результате проектирования получим

(ось х) ;

(ось у) .

6. Отсюда находим неизвестные проекции ускорения точки В:

м/с²;

м/с2 .

Эти проекции позволяют вычислить полное ускорение точки В:

м/с².

Пример 31. Колесо радиуса R = 0,5 м катится без проскальзывания по прямолинейному рельсу (рис. 43), имея в данный момент времени скорость центра V₀ = 1 м/с и ускорение центра = 2 м/с². Определить ускорение точки А обода колеса.

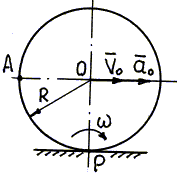
Рис. 43

Решение:

1. В качестве полюса выберем точку О - центр колеса, ускорение которого известно.

2. Составим основное векторное уравнение типа (63) для определения ускорения точки А:

. (67)

3. Изобразим все векторы, входящие в уравнение (67), на рис. 44.

Ускорение точки А, неизвестное по направлению, представим составляющими по направлению координатных осей - и . Направление ускорения полюса О задано условием задачи. Осестремительное ускорение точки А при вращении вокруг полюса О направим от точки А к полюсу. Вращательное ускорение точки А при вращении вокруг полюса направим перпендикулярно осестремительному в сторону дуговой стрелки углового ускорения, то есть вертикально вверх (колесо катится ускоренно, поэтому направления дуговых стрелок и совпадают).

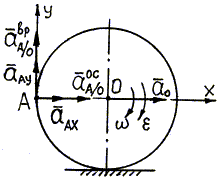
Рис. 44

4. Приступим к анализу векторного уравнения (67). Неизвестными векторного уравнения являются составляющие ускорения точки А: и , которые не могут быть найдены по условию задачи до решения уравнения (67). Следовательно, все остальные составляющие уравнения (67) должны быть найдены до решения этого уравнения. Ускорение полюса О известно. Остается найти угловую скорость колеса и угловое ускорение , чтобы потом определить модули осестремительного и вращательного ускорений точки А при вращении вокруг полюса [см. формулы (64) и (65)].

При определении скоростей было указано (см. пример 24), что мгновенный центр скоростей колеса известен, это точка касания колеса с рельсом. Зная скорость центра колеса, несложно определить угловую скорость колеса в любой момент времени (рис.43):

. (68)

В данном случае 1/сек.

При качении колеса без проскальзывания расстояние OP от центра колеса до мгновенного центра скоростей остается неизменным (оно равно радиусу колеса). Это обстоятельство дает возможность определить угловое ускорение колеса путем дифференцирования уравнения (68):

,

т.е. .

В данном случае 1/с².

Зная и , определим модули осестремительного и вращательного ускорений точки А при вращении вокруг полюса О:

м/с²;

м/с².

5. Проектируя теперь векторное уравнение (67) на оси координат, получим:

;

.

Подставляя численные значения, найдем:

м/с²;

м/с².

Полное ускорение точки А: м/с².

Пример 32. Стержень АВ (рис.45) длиной 10 м скользит концами по сторонам прямого угла. В момент времени, когда стержень составляет угол = 30° с вертикалью, скорость точки А равна м/с, ускорение точки А равно м/с². Определить ускорение точки В и угловое ускорение стержня для заданного положения.

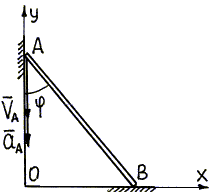
Рис. 45

Решение:

1. В качестве полюса выберем точку А, ускорение которой известно.

2. Для определения ускорения точки В составим векторное уравнение типа (63):

. (69)

3. Изобразим все векторы, входящие в состав уравнения (69), на рис. 46.

Ускорение точки В должно быть направлено по оси х, так как точка движется вдоль этой оси; примем, что направлено в положительную сторону оси х. Если в результате решения значение будет положительным, то наше предположение о направлении справедливо; если же получится отрицательным, то ускорение в действительности направлено в противоположную сторону. Ускорение полюса А известно по условию задачи. Осестремительная составляющая ускорения точки В при вращении вокруг полюса А направлена от В к полюсу.

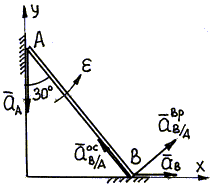
Рис. 46

Вращательную составляющую ускорения точки В при вращении вокруг полюса А направим перпендикулярно осестремительной составляющей, как показано на рис. 46, что соответствует направлению дуговой стрелки против часовой стрелки. Если в результате решения значение будет положительным, то наше предположение о направлении и дуговой стрелки справедливо; если же получится отрицательным, значит в действительности вектор и дуговая стрелка направлены в противоположную сторону.

4. Из анализа векторного уравнения (69) видим, что в левой части уравнения находится одна неизвестная величина - модуль ускорения точки В.Следовательно, в правой части уравнения должно быть не более одной неизвестной величины. Этой неизвестной является угловое ускорение .

Напомним, что угловая скорость стержня должна определяться при решении задачи о скоростях. Определение скоростей выполним с помощью мгновенного центра скоростей, который находится на пересечении перпендикуляров АР и ВР (рис. 47), проведенных к направлениям скоростей и (см. способ (б) п. 3.1.4). Угловая скорость стержня

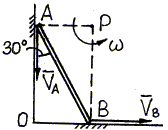
Рис. 47

Отметим, что в формуле длина отрезка АР при движении стержня изменяется, поэтому определение углового ускорения путем дифференцирования (как в примере 31) здесь не дает результата.

Модуль осестремительного ускорения точки В при вращении вокруг полюса А равен

м/с².

Таким образом в векторном уравнении (69) осталось две неизвестные величины: модуль ускорения точки В (в левой части уравнения) и угловое ускорение (в выражении в правой части уравнения). То есть задача относится к типу 3.

5. Проектируем векторное уравнение (69) на оси координат:

(на ось х) ;

(на ось у) .

Решая полученные уравнения, находим

= 60 м/с²;

м/с².

Отметим, что и получились положительными; в соответствии со сказанным выше (см. п. 3 решения задачи) заключаем, что принятые направления векторов и соответствуют их действительным направлениям.

Зная модуль вращательного ускорения , находим:

3.2.3. Метод, основанный на использовании мгновенного центра ускорений

Мгновенным центром ускорений называется точка плоской фигуры, ускорение которой в данный момент времени равно нулю, этот центр обозначается буквой Q.

Ускорения точек плоской фигуры в каждый момент времени распределены так, как если бы эта фигура поворачивалась вокруг мгновенного центра ускорений. Для точки М (рис. 48) будем иметь

; (70)

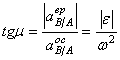. (71)

Чтобы найти положение мгновенного центра ускорений, надо знать ускорение полюса А, угловую скорость и угловое ускорение фигуры. Вектор ускорения полюса нужно повернуть в направлении дуговой стрелки (рис. 49) на угол , определяемый формулой (71); затем на полученном луче Ах надо отложить отрезок АQ, равный

(72)

Конец этого отрезка (точка Q) есть мгновенный центр ускорений.

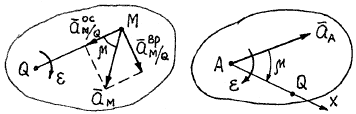
Рис. 48 Рис. 49

Если по условию задачи ускорение какой-нибудь точки тела равно нулю, то эта точка есть мгновенный центр ускорений. Например, для колеса, у которого центр движется равномерно и прямолинейно, мгновенный центр ускорений совпадает с центром колеса.

Задачу об определении ускорений рекомендуется решать в такой последовательности.

1. Определить положение мгновенного центра ускорений рассмотренным выше способом.

2. Вычислить модуль искомого ускорения по формуле (70).

3. Определить угол по формуле (71) и под этим углом к направлению MQ (рис. 48) отложить вектор искомого ускорения.

Пример 33. Квадратная пластинка (рис. 50) размером 1x1 м движется в плоскости рисунка. Ускорение вершины А в данный момент времени равно м/с², угловая скорость пластинки = 1 1/с, угловое ускорение =1 1/с². Построить мгновенный центр ускорений и определить ускорение вершины В.

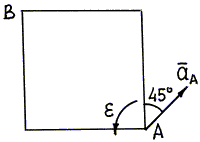
Рис. 50

Решение:

Для построения мгновенного центра ускорений определим угол по формуле (71)

.

и расстояние AQ по формуле (72)

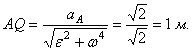
Повернем вектор в сторону дуговой стрелки на угол (рис.51) и на направлении Ах отложим отрезок AQ, равный 1 м. Получим, что мгновенный центр ускорений Q находится в правой верхней вершине квадрата.

Модуль ускорения точки В определим по формуле (70)

м/с².

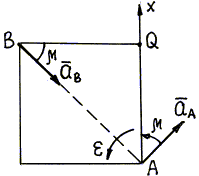
Рис. 51

Направлено ускорение точки В под углом = 45⁰ к отрезку ВQ, т.е. направлено по диагонали ВА квадрата.

Рассмотренный способ решения задачи имеет ограниченное применение из-за трудностей определения положения мгновенного центра ускорений. Чаще всего задача определения ускорений решается методом, основанным на использовании векторного уравнения (см. п. 3.2.2).

3.2.4. Определение ускорений точек звеньев плоских механизмов

Решение задачи начинается с исследования ведущего звена, то есть звена, движение которого задано. Затем рассматривается движение звена, связанного с ведущим. Далее одно за другим рассматриваются остальные звенья механизма.

При решении этих задач необходимо уметь находить связь между ускорениями точек двух соединенных между собой звеньев механизма. Рассмотрим два основных способа соединения звеньев в плоских механизмах.

1. Соединения звеньев в различного вида фрикционных и зубчатых передачах (рис. 52), а также в передачах с гибкой нерастяжимой нитью (рис. 53).

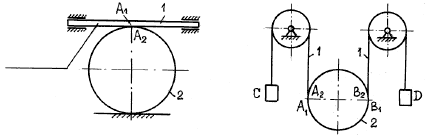
Рис. 52 Рис. 53

В соединениях этого способа происходит касание двух звеньев (касание зубчатой рейки 1 и колеса 2 на рис. 52, касание гибкой нити 1 и блока 2 на рис. 53). В месте касания совмещаются точки, принадлежащие разным звеньям. Хотя траектории совмещающихся точек различны, но у них общая касательная. При отсутствии проскальзывания звеньев указанные точки имеют одинаковые касательные ускорения (; ). Нормальные же ускорения точек не равны между собой, так как точки движутся по различным траекториям.

2. Соединения звеньев с помощью шарниров (шарнир А на рис. 54 и 55).

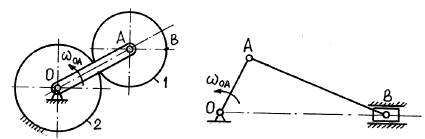
Рис. 54 Рис. 55

В шарнирных соединениях звеньев центр шарнира принадлежит одновременно двум звеньям. Вследствие этого, например, ускорение точки А на рис. 54, определенное для вращающегося кривошипа ОА, будет таким же как и ускорение точки А колеса 1, совершающего плоскопараллельное движение. Аналогичные рассуждения для точки А механизма на рис. 55.

Отметим некоторые особенности при выборе полюса. Если звено АВ механизма, совершающего плоскопараллельное движение, присоединено к ведущему звену ОА шарниром А (рис. 54, 55), то за полюс звена АВ следует взять центр шарнира А, ускорение которого можно определить при решении задачи об ускорениях звена ОА.

Звено механизма, соединенное с ведущим звеном первым способом (рис. 52, 53), является обычно колесом (или блоком). В этом случае за полюс следует выбирать центр колеса (или блока), ускорение которого можно найти до решения основного векторного уравнения типа (63). Покажем это на примере механизмов, изображенных на рис. 52 и 53.

В механизме на рис. 52 ведущим звеном является подвижная рейка 1, ее скорость и ускорение известны (рис. 56). Скорости точек А₁ и А₂одинаковы: . Учитывая, что мгновенный центр скоростей колеса 2 находится в точке P, найдем

или

.

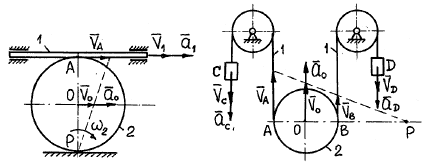
Рис. 56 Рис. 57

Эта формула справедлива для любого момента времени, поэтому дифференцируя ее по времени, будем иметь

.

Но , так как точка O движется по прямой и ее полное ускорение равно касательному ускорению.

Окончательно .

В механизме на рис. 53 и 57 ведущими звеньями являются грузы С и D, их скорости и и ускорения , известны. Согласно п. 3.1.4 мгновенный центр скоростей блока 2 находится в точке P на пересечении прямой AB и прямой, соединяющей концы векторов и . (Напомним, чтоV_A = V_C; V_B = V_D). Скорость центра O блока найдется по формуле

Полученная формула справедлива для любого момента времени. Поэтому, дифференцируя ее по времени, найдем

Рекомендуется следующая последовательность решения задачи определения ускорений плоских механизмов.

Изобразить на рисунке механизм в заданном положении.

Начиная с ведущего звена, решить задачу о скоростях, главной целью которой является определение угловых скоростей всех звеньев механизма.

Решить задачу определения ускорений точек ведущего звена механизма; найти ускорение точки ведущего звена, в которой к нему присоединяется второе звено механизма.

Решить задачу определения ускорений точек второго и затем всех последующих звеньев механизма.

Пример 34. Груз В, опускаясь, приводит в движение катушку с помощью нити, переброшенной через блок С. Считая, что катушка катится без скольжения, определить ускорение точки А, если в данный момент V_В = 80 см/с, = 160 см/с². Радиусы катушки r = 30 см; R = 50 см.

Решение:

Рассматриваемый механизм (рис. 58) состоит из груза В, совершающего поступательное движение, и катушки, совершающей плоскопараллельное движение.

Решение задачи определения скоростей. Скорость точки К касания нити с катушкой равна скорости груза, т.е. V_К = V_В. Мгновенный центр скоростей катушки находится в точке Р (рис. 59).

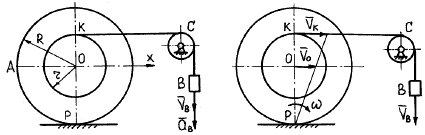
Рис. 58 Рис. 59

Угловая скорость катушки

(73)

В данном случае = 1 1/с.

Скорость центра О катушки

(74)

В данном случае V_О = 50 см/с.

3. Ведущим звеном механизма является груз В, ускорение которого задано условием задачи.

Ведущее звено и катушка связаны гибкой нитью. Точка К нити имеет, очевидно, такое же по модулю ускорение, как и груз В.

4. Решение задачи об определении ускорений точек катушки, совершающей плоскопараллельное движение. Выберем в качестве полюса центр катушки. Так как центр катушки движется прямолинейно по оси х (рис.58), его ускорение направлено по этой же оси, а модуль определится дифференцированием уравнения (74)

см/с².

Такое дифференцирование возможно, потому что при качении катушки без проскальзывания расстояния ОР и КР остаются неизменными.

Составим векторное уравнение типа (63) для точки А

. (75)

Изобразим все векторы, входящие в уравнение (75) на рис. 60.

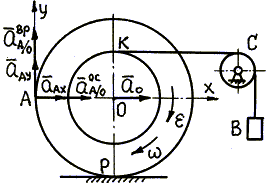
Рис. 60

Неизвестное по направлению ускорение точки А представим составляющими и . Осестремительную составляющую направим от точки А к полюсу О, вращательную составляющую направим перпендикулярно вверх, потому что катушка катится ускоренно (см. пример 31).

Приступим к анализу векторного уравнения (75). Задача об определении ускорений при качении катушки без проскальзывания относится к типу 2. Неизвестными векторного уравнения (75) являются составляющие и . Ускорение полюса О определено выше. После определения угловой скорости легко вычисляется величина осестремительной составляющей :

см/с².

Учитывая, что расстояние КР в формуле (73) остается постоянным, угловое ускорение колеса найдем дифференцированием:

В данном случае

Величина вращательной составляющей равна

см/с².

Проектируя векторное уравнение (75) на оси координат, получим:

(на ось х) см/с²,

( на ось у) см/с².

Полное ускорение точки А:

см/с².

Пример 35. Кривошип ОА шарнирного четырехзвенника ОАВО₁ (рис. 61) имеет в данный момент времени угловую скорость = 2 1/с и угловое ускорение 1/с², ОА = 10 см, АВ = ВО₁ = 20 см. Для данного положения механизма определить ускорение точек В и С, а также угловые ускорения звеньев АВ и ВО₁; АС = СВ.

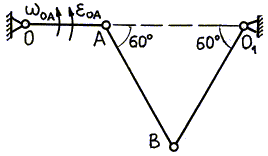
Рис. 61

Решение:

1. В рассматриваемом механизме звенья ОА и ВО₁ совершают вращательное движение, а звено АВ - плоскопараллельное движение.

2. Решение задачи определения скоростей. Найдем скорость точки А ведущего звена ОА:

см/с.

Для звена АВ вначале найдем мгновенный центр скоростей. Так как , а , то МЦС должен лежать на пересечении прямых, проведенных через ОА и ВО₁. Это значит, что МЦС звена АВ в заданном положении механизма совпадает с центром шарнира О₁ (рис. 62).

Тогда

Скорость точки В см/с.

Зная скорость точки В, найдем

3. Решение задачи об определении ускорения точки А ведущего звена - кривошипа ОА. При вращательном движении кривошипа ускорение точки Аимеет две составляющие - осестремительную и вращательную (рис. 63)

, (76)

где

см/с²;

см/с².

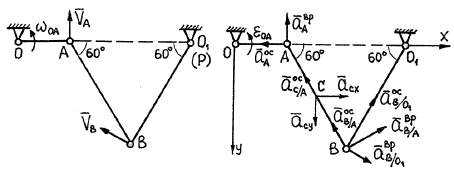
Рис. 62 Рис. 63

4. Решение задачи об определении ускорений точки В звена АВ, совершающего плоскопараллельное движение.

Звено АВ связано с ведущим кривошипом ОА шарниром А. Выберем точку А за полюс.

Составим векторное уравнение типа (63) для точки В

или с учетом (76)

. (77)

Покажем все векторы, входящие в уравнение (77), на рис. 63.

Ускорение точки В представим двумя составляющими и , так как точка В принадлежит не только стержню АВ, но и вращающемуся стержню ВО₁, т.е.

. (78)

Вектор направлен от точки В к оси вращения О₁, вектор направлен перпендикулярно ВО₁.

Осестремительное ускорение точки В при вращении стержня АВ вокруг полюса А направлено от точки В к полюсу А, вращательное ускорение - перпендикулярно АВ.

С учетом выражения (78) векторное уравнение (77) примет вид

. (79)

Приступим к анализу этого уравнения. Модуль осестремительной составляющей легко определяется

см/с².

Модуль вращательной составляющей найти до решения векторного уравнения (79) нельзя, так как в выражении

угловое ускорение - величина неизвестная. Дифференцирование выражения не дает результата, так как закон изменения V_В нам неизвестен.

Составляющие ускорения полюса и были определены выше.

Модуль осестремительной составляющей легко найти, так как определена ранее (см. п. 2 решения):

см/с².

Модуль вращательной составляющей неизвестен, так как в выражении

угловое ускорение не может быть найдено до решения векторного уравнения (79). Дифференцирование выражения здесь не дает результата, так как расстояние АР - величина переменная и закон ее изменения нам неизвестен.

Итак, в векторном уравнении (79) осталось две неизвестные величины - , в выражении (в левой части уравнения) и в выражении (в правой части уравнения). Задача относится к типу 3 (см. п. 3.2.2).

Проектируем уравнение (79) на оси х и у (см. рис.63):

,

Решая полученную систему уравнений, найдем

см/с²,

.

Знак "минус" в выражении вращательного ускорения указывает, что вектор направлен в сторону, противоположную принятому на рис. 63 направлению.

Полное ускорение точки В:

см/с²;

угловое ускорение звена АВ

У звена АВ теперь нам известны ускорение полюса А, угловая скорость и угловое ускорение звена. Это позволяет определить ускорение любой точки звена, например, точки С (задача типа 1).

Составим для точки С векторное уравнение типа (63):

. (80)

Ускорение точки С неизвестно по направлению, разложим его на составляющие по направлениям координатных осей и . Направления остальных векторов из уравнения (80) показаны на рис.63, где

см/с²,

.

Проектируя векторное уравнение (80) на оси координат, получим

;

.

Отсюда

см/с².

см/с².

Полное ускорение точки С:

см/с².

5. Решение задачи определения ускорений звена ВО₁, совершающего вращательное движение.

По модулю вращательной составляющей , найденному из решения векторного уравнения (79), определим угловое ускорение стержня ВО₁

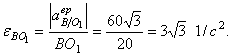
Направлено угловое ускорение звена ВО₁, в соответствии с действительным направлением вектора (см. замечание по поводу знака ), т.е. дуговую стрелку надо направить по часовой стрелке.

В рассмотренном примере основное векторное уравнение типа (63) для точки В преобразовано из обычного вида в уравнение (79), в котором неизвестными являются два угловых ускорения и . Подчеркнем, что уравнение (79) получилось в результате приравнивания двух различных выражений для ускорения точки В: первое выражение (77) записано в предположении, что точка В принадлежит звену АВ; второе (78), - что точка Впринадлежит звену ВО₁.

С уравнениями вида (79) приходится встречаться в тех случаях, когда точка В в плоском стержневом механизме является центром шарнира, соединяющего два звена, из которых одно совершает плоскопараллельное движение, а второе - вращательное движение.

Пример 36. Механизм (рис.64,а) состоит из стержней 1, 2, 3, 4 и ползуна В, cоединенных друг с другом и с неподвижными опорами O₁ и O₂шарнирами.

Дано: = 60°, = 150°, =90°, = 30°, = 30°, AD = DB, l₁= 0,4 м, l₂ = 1,2 м, l₃=1,2м, l₄= 1,4 м, = 2 с-1, = 7 с^-2 (направления и - против хода часовой стрелки).

Указания. Задача - на исследование плоскопараллельного движения твердого тела. При её решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности.

При определении ускорений точек механизма исходить из векторного равенства , где А - точка, ускорение которой или задано, или непосредственно определяется по условиям задачи (если точка А движется по дуге окружности, то ); В - точка, ускорение которой нужно определить (если точка В движется по дуге окружности радиуса l, то , где численно , входящая сюда скорость определяется так же, как и скорости других точек механизма).

Определить: , , , , .

Решение.

1. Строим положение механизма в соответствии с заданными углами (рис.64,б).

2. Определяем . Точка В принадлежит стержню АВ. Чтобы найти , надо знать скорость какой-нибудь другой точки этого стержня и направление . По данным задачи, учитывая направление , можем определить ; численно

, l₁ = 0,8 м/с; . (81)

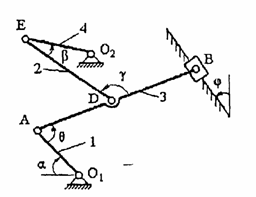
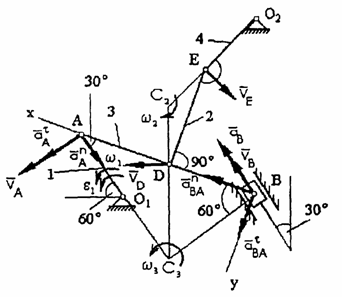
а) б)

Рис.64

Направление найдем, учитывая, что точка В принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная и направление , воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АВ) на прямую, соединяющую эти точки (прямаяАВ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим

V_Bcos 30° = V_Acos 60° и V_B = 0,46 м/с. (82)

3. Определяем . Точка Е принадлежит стержню DE. Следовательно, по аналогии с предыдущим, чтобы определить , надо сначала найти скорость точки D, принадлежащей одновременно стержню АВ. Для этого, зная и , строим мгновенный центр скоростей (МЦС) стержня АВ; это точка С₃, лежащая на пересечении перпендикуляров к и , восстановленных из точек А и В (к перпендикулярен стержень 1). По направлению вектора определяем направление поворота стержня АВ вокруг МЦС С₃. Вектор перпендикулярен отрезку C₃D, соединяющему точки D и С₃, и направлен в сторону поворота. Величину V_D найдем из пропорции

. (83)

Чтобы вычислить С₃D и C₃E, заметим, что прямоугольный, так как острые углы в нем равны 30° и 60°, и что C₃B= АВsin 30° = 0,5АВ = BD. Тогда является равносторонним и C₃B=C₃D

== 0,46 м/с; . (84)

Так как точка Е принадлежит одновременно стержню O₂E, вращающемуся вокруг O₂, то . Тогда, восстанавливая из точек Е и Dперпендикуляры к скоростям и , построим МЦС С₂ стержня DE. По направлению вектора определяем направление поворота стержня DEвокруг центра С₂. Вектор направлен в сторону поворота этого стержня. Из рис. 64,б видно, что , откуда С₂E = C₂D. Составив теперь пропорцию, найдем, что

, == 0,46 м/c. (85)

4. Определяем . Так как МЦС стержня 2 известен (точка С₂) и

, то (86)

5. Определяем . Точка В принадлежит стержню АВ. Чтобы найти , надо знать ускорение какой-нибудь другой точки стержня АВ и траекторию точки В. По данным задачи можем определить , где численно

м/с²; м/с². (87)

Вектор направлен вдоль AO₁, a - перпендикулярно AO₁; изображаем эти векторы на чертеже. Так как точка В одновременно принадлежит ползуну, то вектор параллелен направляющим ползуна. Изображаем вектор на чертеже, полагая, что он направлен в ту же сторону, что и .

Для определения воспользуемся равенством

. (88)

Изображаем на чертеже векторы (вдоль ВА от В к А) и (в любую сторону перпендикулярно ВА); численно . Найдя с помощью настроенного МЦС С₃ стержня 3, получим

и =0,61 м/с². (89)

Таким образом, у величин, входящих в равенство (88), неизвестны только числовые значения и ; их можно найти, спроецировав обе части равенства (88) на какие-нибудь две оси.

Чтобы определить , спроецируем обе части равенства (88) на направление АВ (ось х), перпендикулярное неизвестному вектору . Тогда получим

. (90)

Подставив в равенство (10) числовые значения всех величин из (87) и (89), найдем, что

= 0,72 м/с² . (91)

Так как получилось > 0, то, следовательно, вектор направлен, как показано на рис. 64,б.

6. Определяем . Чтобы найти , сначала определим . Для этого обе части равенства (88) спроецируем на направление, перпендикулярноеАВ (ось у). Тогда получим

(92)

Подставив в равенство (92) числовые значения всех величин из (91) и (87), найдем, что = -3,58 м/c². Знак указывает, что направление противоположно показанному на рис. 64,б.

Теперь из равенства получим

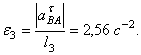
Ответ: V_B= 0,46 м/с; V_E=0,46 м/с; =0,67 c^-2; = 0,72 м/с²; = 2,56 c^-2.