Интегрированный урок литературы, математики и информатики в 10 классе

Интегрированный урок математики, литературы и информатики в 10 классе

Тема: Статистика и стихосложение

Цели:

- обобщить и систематизировать знания, полученные на уроках математики по теме "Элементы статистики", на уроках литературы по теме "Стихосложение", на уроках информатики по теме "Построение диаграмм и графиков";

- показать, что понятия и законы статистики применимы для широкого класса задач различных областей, в том числе литературы;

- продолжить развитие познавательной активности учащихся, интереса к изучению предметов.

Организация урока: урок рассчитан на 2 урока и проводится в компьютерном классе, в классе три учителя: литературы, математики и информатики. До начала урока учащиеся разбиваются на три группы.

Оборудование: проектор, компьютеры, MS PowerPoint, MS Excel, раздаточный материал со стихами А. Фета "Цветы", Н. Заболоцкого "Возвращение с работы", И. Бунина "Родине", Ф. Тютчева "Сияет солнце..."

Ход урока

Учитель литературы. Хотелось бы начать наш урок со слов Пушкина: "Вдохновение нужно в поэзии, как и в геометрии". В данном случае слово "геометрия" можно заменить на "математика", так как сегодня на уроке мы с вами узнаем, что математика и литература могут иметь точки соприкосновения.

Тема нашего урока звучит так: "Статистика и стихосложение". И прежде всего я хотел бы, чтобы в русской поэзии мы вспомнили и наиболее распространенном в русской поэзии стихотворном размере (метре) - ямбе.

Три четверти стихотворений на русском языке написаны ямбом. Четырехстопный ямб легко узнаваем. Эти размеры имеют, например, "Белеет парус одинокий" М.Лермонтова, "Няня" А.Пушкина. Ямбом А.Пушкин написал 87% поэтических произведений, а четырехстопные размеры составляют в его творчестве 68%.

Учитель математики. Математический анализ стихотворных размеров имеет давнюю традицию, идущую от русского писателя, поэта, критика, одного из ведущих деятелей символизма Андрея Белого - выпускника математического факультета Московского университета. Своему второму рождению это направление математического стихосложения обязано работам двух выдающихся ученых ХХ века - математику А.Н. Колмогорову и филологу М.Л.Гаспарову.

Интересен тот факт, что закон чередования женских и мужских окончаний был установлен французским поэтом П. Ронсаром в теоретическом труде "Алгебра французского поэтического искусства", написанном еще в 1565 г. Так что "проверять" алгеброй гармонию поэты начали задолго до Сальери!

Разницу между длиной слов или слоговой длиной слов отдельных стихотворений можно определить точными цифрами с помощью статистики. Длина слова - это количество букв, входящих в слово. Слоговая длина - это количество слогов, входящих в слово.

Учитель литературы. К сегодняшнему уроку вы должны были подготовить выразительное чтение стихотворения "Цветы" А.Фета. Давайте послушаем его.

(Ученик читает стихотворение)

С полей несется голос стада,

В кустах малиновки звенят,

И с побелевших яблонь сада

Струится сладкий аромат.

Цветы глядят с тоской влюбленной,

Безгрешно чисты, как весна,

Роняя с пылью благовонной

Плодов румяных семена.

Сестра цветов, подруга розы,

Очами в очи мне взгляни,

Навей живительные грезы

И в сердце песню зарони.

Задания по литературе

1. Определите размер этого стихотворения

Четырехстопный ямб, так как каждая строка состоит из четырех двухсложных стоп с ударением на втором слоге стопы.

2. Охарактеризуйте рифму в зависимости от расположения ударений.

Чередуется женская и мужская рифмы.

3. Определите количество строф и охарактеризуйте эти строфы.

В стихотворении три строфы; каждая состоит из четырех строк с перекрестной рифмовкой АбАб.

Задания по математике

1. Дайте определение среднего арифметического нескольких чисел.

2. Дайте определение моды набора чисел.

Модой (Мо) набора чисел называется число, которое встречается наиболее часто в этом наборе. Набор чисел может и не иметь моды.

3. Дайте определение медианы.

Медианой (Ме) набора n чисел (среди которых могут быть совпадающие) называется:

- число, стоящее посередине в упорядоченном по возрастанию наборе этих чисел, если n нечетно;

- полусумма чисел, стоящих на средних местах в упорядоченному по возрастанию ряду этих чисел, если n четно.

(На столе у каждого ученика находится раздаточный материал со стихами А.Фета "Цветы)

Учитель литературы. В стихотворении А.Фета "Цветы" подсчитайте:

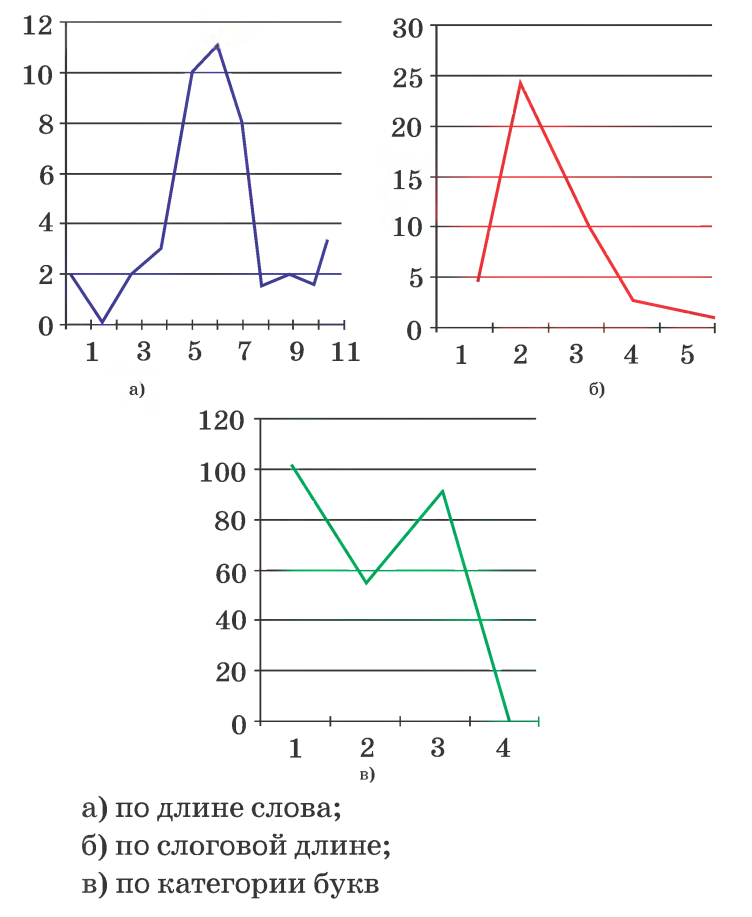
1-я группа: количество слов разной буквенной длины, при этом если предлог состоит из одной согласной буквы, то считайте его вместе со словом, к которому он относится (таблица 1)

2-я группа: количество слов разной слоговой длины, при этом если предлог не образует слога, то считайте его вместе со словом, к которому он относится (таблица 2)

3-я группа: количество сонорных согласных (Й, Л, М, Н, Р) и количество мягких знаков (таблица 3)

Учитель информатики. Вам известно, что данные для последующей обработки и построения диаграмм и графиков удобнее и эффективнее вносить в электронные таблицы. Работать с электронными таблицами мы уже умеем, поэтому можем смело ими воспользоваться. Давайте вспомним, как же работают электронные таблицы, и чем они могут нам помочь на уроке.

Вопросы по информатике

1. Что называют электронной таблицей?

2. Какие данные могут вводиться и храниться в электронной таблице?

3. Какие форматы данных, хранимых в электронных таблицах, вам известны?

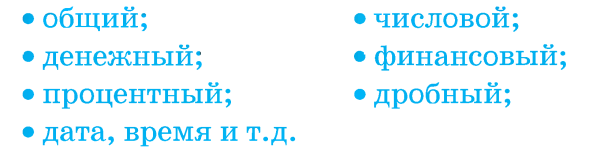
Учитель информатики. При изменении исходных данных все результаты автоматически пересчитываются и отражаются в таблице. Электронные таблицы не только автоматизируют расчеты, но и являются эффективным средством просчитывания различных вариантов и моделирования ситуаций. Меняя значения исходных данных, можно следить за изменением получаемых результатов, в том числе представленных в виде диаграмм или графиков.

(Во время выполнения задания один из членов группы вносит результаты в электронную таблицу. По мере работы на экране появляются таблицы с результатами исследования)

(Ученики сверяют свои подсчеты с результатами на экране)

Учитель математики. На основе полученных данных вам нужно построить для этого стихотворения полигоны числового ряда по длине слова, по слоговой длине и по категории букв. Подсчитаем Х, Мо, Ме. Каждая группа будет работать с полученными ей числовыми характеристиками.

Учитель информатики. Для этого необходимо вспомнить, как построить диаграмму или график по числовым данным, введенным в электронную таблицу.

Вопросы по информатике

1. Для чего предназначены диаграммы и графики?

2. Какая служебная команда позволяет вызвать Мастер диаграмм?

В результате работы учащиеся появляются полигоны частот:

Учитель математики. Итак, вы получили числовые характеристики стихотворения::

- по длине слова Х = 261/43 = 6,06, Мо = 6, Ме = 6,

- по слоговой длине: Х = 102/43 = 2,37, Мо = 2, Ме = 2.

Обратите внимание, что числовые характеристики стихотворения по длине слова одинаковы, одинаковы они и по слоговой длине; типичные по длине (ближайшие к среднему значению величины) - это шестибуквенные слова; типичные по слоговой длине - это двуслоговые слова.

Учитель литературы. Стихотворение А.Фета необыкновенно музыкально. А.Фет писал: "Поэзия и музыка не только родственны, но и нераздельны". Из исследования видно, что музыкальность стихотворения обусловлена:

1) подбором звуков (недаром во всем стихотворении 102 гласных и 53 сонорных согласных, то есть вместе их больше, чем шумных согласных - 94);

2) равномерным распределением гласных и согласных звуков (преобладание двуслоговых слов и в то же время наличие слов, в которых более 5 букв, показывает, что нет ни большого скопления согласных, ни большого скопления гласных).

А теперь самостоятельно проведите исследование стихотворений Н.Заболоцкого "Возвращение с работы", И.Бунина "Родине" и Ф. Тютчева "Сияет солнце...".

(Учитель раздает листы со стихами)

Учитель математики. Как и в предыдущем задании, постройте полигоны частот и подсчитайте числовые характеристики для длины слова и для слоговой длины.

По окончании работы учитель информатики, проверив результаты, выводит на экран подсчитанные частоты длин слов (таблица 4) и вычисленные числовые характеристики (таблица 5).

Учащиеся под руководством учителя информатики строят на компьютере:

а) полигоны частот по длине слова (диаграмм 1);

б) частоты слоговой длины (таблица 7);

в) числовые характеристики (таблица 8);

г) полигоны частот по слоговой длине (диаграмма 2);

д) частоты по категориям букв (звукобукв) (таблица 9);

е) полигоны частот по категориям букв (диаграмма 3).

Учитель математики. Обратите внимание, что в стихотворении И.Бунина числовой ряд по слоговой длине имеет две моды. Числовые характеристики стихотворений и у Н.Заболоцкого, и у И.Бунина по длине слов одинаковы. Но числовые характеристики по слоговой длине одинаковы только у Н.Заболоцкого.

Учитель литературы. Ученый-археолог историк А.П.Журавлев писал: "Мы не осознаем отдельно звука или отдельно буквы, а воспринимаем единый звукобуквенный образ. Это очень хорошо чувствуют поэты... поэты в стихах, как правило, ориентируются именно на такие звукобуквы".

Во всех рассмотренных стихотворениях количество гласных одинаковое. Это обусловлено размером стихотворений.

Соотношение между гласными вместе с сонорными согласными и остальными согласными во всех стихотворениях одинаковое, но у Н. Заболоцкого больше более длинных слов, чем у двух других поэтов. За счет этого стихотворение менее музыкальное и требует вдумчивого чтения, размышления над смыслом. Возникают задержки в чтении (останавливается внимание на отдельных словах).

Стихотворение И.Бунина делится на две части. Первая строфа более напевная, а две следующие требуют размышления над смыслом (за счет большего количества длинных слов).

Стихотворение Ф.Тютчева, как и стихотворение А.Фета, музыкально, так как равномерно распределены гласные и согласные звуки. Преобладают трехслоговые слова, в то же время наличествуют слова, в которых 4-8 букв. В стихотворении нет большого скопления согласных и гласных.

Итак, математика помогает понять строение стихотворения. Поэты интуитивно подбирают подходящее слово, они не подсчитывают количество согласных и гласных. Математико-статистический метод отнюдь не универсален, но он дает богатейший материал для филологической интерпретации и объяснения. И задача филологов найти способы проанализировать, понять и объяснить то, что описано методами математики.