ЭКОНОМИЧЕСКАЯ ТЕОРИЯ В ЗАДАЧАХ И СИТУАЦИЯХ. ЧАСТЬ 1. МИКРОЭКОНОМИКА

московский автомобильно-дорожный инститУт

(государственный технический университет)

А.А. Султыгова, В.В. БЕЗНОВСКАЯ, И. В. Кирова

ЭКОНОМИЧЕСКАЯ ТЕОРИЯ

в задачах и ситуациях

ЧАСТЬ 1

Микроэкономика

Учебное пособие

москва 2008

удк 330. 01

ббк 65. 01

Султыгова А. А., Безновская В. В., Кирова И. В. Экономическая теория в задачах и ситуациях. Часть 1: Микроэкономика: Учеб. пособие / МАДИ (ГТУ). - М., 2008. 84с.

Рецензенты:

Т. П. Минаева, заместитель директора Учебно-консультационного центра АСМАП, кандидат экономических наук, доцент.

Т. Л. Попова, вице-президент Международного фонда социальных и экономических реформ (фонд «Реформа»), кандидат экономических наук, доцент.

Данное учебное пособие знакомит читателей с основными проблемами микроэкономики. Оно состоит из пяти тем одноименного учебного курса, которые соответствуют стандарту экономического образования высших учебных заведений. Каждая тема учебного пособия содержит необходимый теоретический материал, подробный разбор типовых задач и упражнений с ответами на закрепление соответствующего материала. В конце пособия помещены тесты и ключи к ним. Для более глубокого усвоения материала приведен список литературы, предназначенный для самостоятельного изучения проблем микроэкономки и закрепления обретенных навыков.

Пособие предназначено для студентов, изучающих курс «Экономическая теория» раздел «Микроэкономика», преподавателей экономики технических вузов, техникумов, колледжей и менеджеров фирм, а также для всех, интересующихся вопросами современной экономики.

Все темы написаны авторами совместно.

© Московский автомобильно-дорожный институт

(государственный технический университет), 2008.

Введение

Уважаемые читатели!

Предлагаемое учебное пособие представляет собой разъяснение теоретических положений и практических примеров курса «Экономическая теория» (раздел «Микроэкономика»). При этом, разумеется, пособие не охватывает весь круг проблем, встречающихся как в теории микроэкономики, так и на практике. Материал учебного пособия «привязан» к определённым темам учебников и учебно-методической литературы, поэтому его следует рассматривать как дополнение к ним.

Теоретический материал учебного пособия разбит на две части: основной и дополнительный. При этом и та, и другая учебная информация является существенной, поскольку решение типовых экономических задач не возможно без опоры на неё. Знание основного материала поможет Вам в успешном усвоении экономической теории, в решении типовых задач. Умения и навыки, приобретенные при изучении дополнительного материала, позволят полученные знания представить в обобщенно-систематизированном виде, и на основании этого делать научные прогнозы.

Особое значение в пособии придаётся решению типовых экономических задач. По мнению авторов, они наглядно иллюстрируют экономические концепции и модели, позволяют усвоить материал глубже и эффективнее, развивают экономическую культуру студентов и преподавателей. В пособие включены не только задачи, придуманные его авторами, но и наиболее удачные задачи коллег из высшей школы, а также задачи, которые использовались при проведении Международных, Всероссийских и окружных олимпиад по экономике в 1997 - 2007 гг.

Идея авторов учебного пособия состоит в том, чтобы научить читателей рассматривать учебный курс на теоретическом и практическом уровне в их единстве, видеть структуру изучаемой проблемы, их логические связи, а следовательно, обеспечить более глубокое изучение учебного материала.

Авторы надеются, что пособие поможет студентам при самостоятельной работе над программным материалом, в подготовке к контрольным работам, семинарам, зачётам и экзаменам.

Желаем успеха!

Тема 1. ПРОИЗВОДСТВЕННЫЕ ВОЗМОЖНОСТИ

Основные понятия. Производственные возможности. Кривая (граница) производственных возможностей. Альтернативный товар. Альтернативные (вмененные) издержки. Закон возрастающих альтернативных издержек.

Дополнительные понятия. Предельная норма продуктовой трансформации. Парето - эффективное размещение ресурсов. Экстенсивный и интенсивный тип экономического роста.

Основные умения. Строить, анализировать и применять кривую производственных возможностей в решении задач.

Дополнительные умения. Применять принцип Парето, типы экономического роста в разъяснении задач.

Теоретический материал

Производственные возможности - это возможности производства продуктов или услуг при полном и эффективном использовании всех имеющихся ограниченных ресурсов (земли, труда, капитала) и данном уровне развития научно-технического прогресса.

Ограниченность ресурсов ставит предел возможностям производства. Так, обеспеченность человечества земельными ресурсами определяется мировым земельным фондом, в пределах 13,1 млрд. га. При этом обрабатывемые земли, которые дают необходимые человечеству продукты питания, составляют 88% от него. Что же касается производительности труда работников, станков, оборудования, то они также имеют свой верхний предел эксплуатации.

Кривая (граница) производственных возможностей (КПВ) - график, показывающий предел возможных вариантов использования имеющихся ограниченных ресурсов для производства альтернативных видов продуктов, т.е. одного продукта при фиксированном производстве другого.

Допущения модели:

• при построении КПВ прибегают к рассмотрению двухпродуктовой модели, т.к. изучение всех возможных вариантов выпуска продуктов чрезвычайно затруднено;

• полное использование ресурсов и неизменность техники рассматривается как необходимое условие их наилучшего использования (в том смысле, что при фиксированном выпуске одного продукта ресурсы используются так, чтобы максимизировать выпуск другого).

Рассмотрим экономическую ситуацию. Предположим, что общество нуждается в производстве двух продуктов - дизельного масла и газонокосилок и все имеющиеся ресурсы распределяются между ними. Пусть общее количество ресурсов (земли, труда и капитала) составляет на сумму 180 тыс. рублей. На выпуск одной тонны дизельного масла необходимо 4 тыс. рублей, а на выпуск одной газонокосилки 5 тыс. рублей. При этом совместное производство продуктов предполагает экономию ресурсов равную 10%. На основе данной ситуации:

1. составим функцию кривой производственных возможностей;

2. построим график КПВ;

3. проведем анализ данной кривой, опираясь на основные экономические положения КПВ;

4. охарактеризуем производственную программу при следующем условии совместного производства продуктов:

а) 10 т масла и 25 газонокосилок;

б) 35 т масла и 35 газонокосилок. Определим, чему равна потребность в ресурсах при данном выборе?

Решение:

1. Опираясь на вышеизложенные допущения, выразим зависимость между величинами X и Y через равенство, отражающее сбалансированность располагаемых и расходуемых ресурсов.

Пусть X и Y - необходимое для производства количество масла и газонокосилок соответственно;

Тогда тождество примет следующий вид:

4X + 5Y = 180 + 0,1 XY.

Следовательно, Y = 36 - 0,8X ∕ 1 - 0,02X

и есть функция кривой производственных возможностей.

2. Построим график кривой производственных возможностей, предварительно используя табличный метод:

X

0

10

20

30

40

45

Y

36

35

33

30

20

0

Графическое изображение кривой производственных возможностей примет следующий вид:

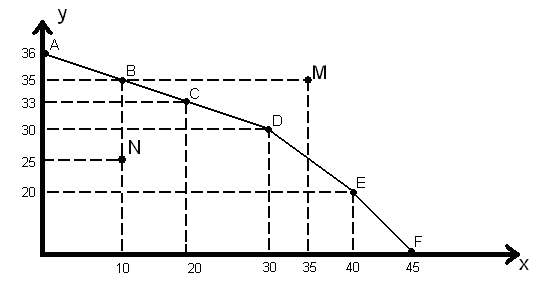
3. Проведём анализ данного графического изображения, опираясь на общеизвестные экономические положения:

а) Кривая производственных возможностей (кривая трансформации) представляет собой выпуклую форму. В чём мы и убедились, строя данную линию. Кривизна объясняется действием закона возрастающих альтернативных издержек. В случае прямой линии это означало бы, что альтернативные издержки производства любого из двух продуктов постоянны, в какую бы точку на данной прямой линии ни перемещалась экономика.

б) Минимальное количество продукта Y (газонокосилки), которым необходимо пожертвовать для увеличения производства продукта Х (масла) на единицу называется предельной нормой трансформации.

Так, первые 10 т масла стоят 1 газонокосилки (36 - 35); - точка B.

Вторые 10 т масла - уже 2 газонокосилки (35 - 33); - точка C.

Третьи 10 т - 3 газонокосилки (33 - 30); - точка D.

Четвёртые 10 т - 10 газонокосилок (30 - 20); - точка E.

Последние пять тонн - 20 газонокосилок (20 - 0); - точка F.

Таким образом, мы видим, что каждые последующие 10 т масла обходятся обществу всё дороже и дороже, а что же касается последних пяти тонн масла, то они самые дорогие.

• Точки: B, C, D, E, принадлежащие данной КПВ, отражают предельные возможности совместного производства обоих продуктов.

• Точки A и F характеризуют ситуацию, при которой производится только один из продуктов при условии полного отказа от производства другого продукта.

в) Постепенное удорожание производства масла объясняется тем, что при увеличении его выпуска приходится использовать ресурсы, приспособленные для производства газонокосилок. Поскольку производительность ресурсов в разных процессах производства различна, то переключение их из одной сферы применения в другую приводит к росту альтернативных издержек производства.

Тем самым, согласно закону возрастающих альтернативных издержек, по мере увеличения выпуска данного продукта (масла) для получения каждой следующей, т.е. дополнительной его единицы приходится отказываться от другого продукта (газонокосилок) во всё большем количестве. Следовательно, издержки производства данного продукта (масла) можно выразить в издержках другого продукта (газонокосилок), от производства которого приходится отказываться. В экономике такая стоимость или такие издержки производства называются альтернативными (вмененными) издержками. Продукт, выраженный в другом продукте, которым пришлось пожертвовать при экономическом выборе, называется альтернативным продуктом. Значит, альтернативные (вмененные) издержки - издержки одного продукта, выраженные в другом продукте, которым пришлось пожертвовать для получения первого.

г) Функционирование экономики на границе своих производственных возможностей отражает Парето-эффективное размещение ресурсов, т.е. такое размещение ресурсов, при котором нельзя увеличить выпуск одного продукта, не сократив выпуск другого. Так, двигаясь по кривой производственных возможностей, действительно, мы видим, что с увеличением производства масла выпуск газонокосилок сокращается, и наоборот.

4. Кривая производственных возможностей подвижна:

а) Она может сместиться влево или вниз. Об этом свидетельствует предлагаемый в условии задачи выбор сочетания продуктов, соответствующий координатам точки N (10; 25). Однако данный выбор неудачный (неэффективный), т.к. ресурсы используются не полностью. В данной точке потребность в ресурсах составляет 140 тыс. рублей, что меньше имеющихся 180, т.к. (4 × 10 + 5 × 25 - 0,1 × 10 × 25 = 140). Таким образом, точка N и все точки, лежащие левее или ниже границы кривой производственных возможностей, принадлежат области возможных, но неэффективных объемов производства.

б) Линия КПВ может переместиться вверх или вправо. Производство продуктов, соответствующее координатам точки M (35;35) невозможно, т.к. она лежит за границей КПВ. Об этом свидетельствует и потребность в ресурсах, которая равна 192,5 тыс. рублей (4 × 35 + 5 × 35 - 0,1 × 35 × 35 = 192,5) против исходных 180 тыс. рублей. Следовательно, точка М и все точки, лежащие правее или выше границы КПВ, принадлежат области недоступных объёмов производства в силу недостаточной обеспеченности ресурсами. Однако это совсем не означает, что в принципе производственные возможности не могут увеличиться. Можно воспользоваться двумя способами расширения производственных возможностей (экстенсивным и интенсивным):

• экстенсивный способ - предполагает вовлечение в производство дополнительных ресурсов (земли, труда, капитала);

• интенсивный способ - предполагает наилучшее использование имеющихся ресурсов (применение ресурсосберегающих технологий, повышение производительности труда, улучшение организации производства и т.п.).

Выводы:

• кривую производственных возможностей в реальной жизни не строят, а значит, она предельно абстрактна и непригодна;

• кривая производственных возможностей находит теоретическое применение при изучении теории экономического роста; при определении недогрузки мощностей; при анализе роста производительности труда и т.д.;

• кривая производственных возможностей учит нас правильной логике выбора, т.к. иллюстрирует принцип выбора в условиях ограниченности ресурсов.

Учимся решать экономические задачи

Типы задач:

• Анализ функции кривой производственных возможностей и её графическое обоснование;

• Построение кривых производственных возможностей на основании различных данных об альтернативных возможностях производителей.

• Расчёт альтернативных издержек.

• Применение закона возрастающих альтернативных издержек.

1.1. На машиностроительном предприятии в одном из цехов можно произвести 1000 двигателей или 500 агрегатов, а в другом альтернативная стоимость производства 2 агрегатов равна 8 двигателям при максимально возможном производстве двигателей равном 1600 единицам.

Постройте общую кривую производственных возможностей машиностроительного предприятия и заштрихуйте плоскость каждого цеха.

Решение:

Рассчитаем максимально возможное производство двигателей (Д.) и агрегатов (А.) в двух цехах. Если максимально возможное производство двигателей во втором цехе составляет 1600 единиц, а при этом альтернативная стоимость производства 2 А. равна 8 Д., то в данном цехе, при имеющихся ограниченных ресурсах, можно произвести 400 агрегатов. Тогда в обоих цехах можно произвести либо 2600 двигателей (1600 Д. + 1000 Д.), либо 900 агрегатов. (500 А. + 400 А.).

Приступим к построению общей КПВ машиностроительного предприятия, при условии, что в данном году руководство предприятия решило произвести только двигатели. По оси абсцисс отложим максимально возможное производство двигателей в двух цехах (2600 Д.), а по оси ординат максимально возможное производство агрегатов (900 А.).

Построение КПВ начнём со второго цеха, т.к. в данном цехе потери в виде недополученных агрегатов минимальные (альтернативная стоимость 1 Д. = ¼ А.). Линия производственных возможностей второго цеха будет соединять точку максимального производства агрегатов на предприятии (0 Д.; 900 А.) с проекцией точки наибольшего производства двигателей в данном цехе (1600 Д.; 500 А.). При таком выборе предприятие, отдавая предпочтение производству двигателей, отказалось от возможного производства агрегатов в размере 400 единиц (900 А. - 400 А.). Данная прямая линия есть частный случай общей выпуклой кривой производственных возможностей предприятия.

Точка с координатами (1600 Д.; 500 А.) - это точка перегиба КПВ.

КПВ первого цеха строится аналогично. Увеличив производство двигателей на величину возможного производства (1000 единиц), мы попадём в точку с координатами (2600 Д.; 0 А.) В данном выпуске продукции машиностроительное предприятие не сможет произвести 500 агрегатов. Линия, соединяющая точку (2600 Д.; 0 А.) с точкой перегиба, будет частным случаем кривой производственных возможностей первого цеха.

Ответ:

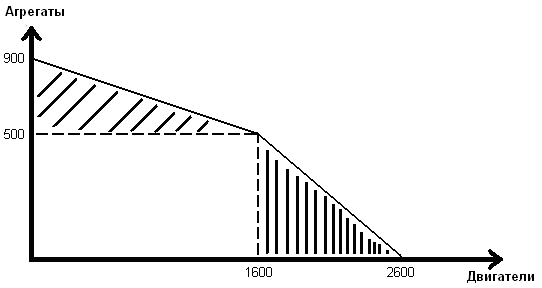
Заштрихованные области - цеха машиностроительного предприятия.

1.2. Могут ли следующие точки лежать на одной кривой производственных возможностей: А (18; 0), В (11; 16), С (16; 9), Е(8;15), М (7; 16), Р (0; 21)? Обоснуйте свое решение, не прибегая к построению графика КПВ.

Решение:

Применим закон возрастающих альтернативных издержек. Расположим заданные точки по возрастанию одной из координат (например, координаты Х): Р (0; 21), М (7; 16), Е (8; 15), В (11; 16), С (16; 9), А(18; 0). Если данные точки принадлежат одной КПВ, то значения чисел по другой координате (например, Y) должны убывать. Однако точка В с координатами (11; 16) не отвечает главному требованию нашего условия.

Ответ:

Точки А, В, С, Е, М и Р не могут принадлежать одной кривой производственных возможностей, т.к. нарушен закон возрастающих альтернативных издержек.

1.3. Ниже приведена кривая производственных возможностей машиностроительного предприятия, которое производит двигатели и агрегаты (в единицах).

Охарактеризуйте производственные возможности предприятия при условии, что в данном году оно будет производить только двигатели. Ответьте на следующие вопросы:

А) Сколько у предприятия производственных участков и чему равны альтернативные возможности производства на них?

Б) Чему равна альтернативная стоимость производства ещё одного двигателя, если их производится 60 единиц? Вычислите максимально возможное производство агрегатов.

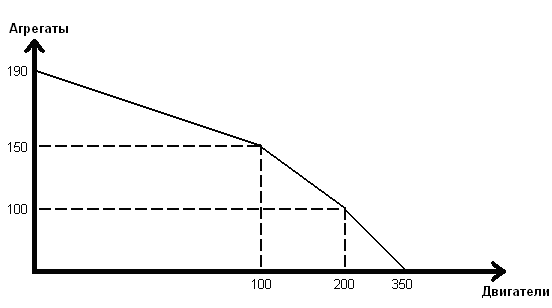
Решение:

А) На предприятии три участка с максимально возможным производством или 350 двигателей (Д.), или 190 агрегатов (А.).

На верхнем участке производственные возможности предприятия позволяют произвести или 100 Д., или 40 А. (190 А. - 150 А.). Альтернативная стоимость производства 1 Д. = 0,4 А..

На среднем участке можно будет произвести или 100 Д. (200 Д. - 100 Д.) или 50 А. (150 А. - 100 А.). Альтернативная стоимость производства 1 Д. равна 0,5 А..

На нижнем участке возможное производство составит или 150 Д. (350 Д. - 200 Д.) или 100 А. (100 А. - 0 А.) с альтернативной стоимостью производства 1 Д. = 0,7 А.

Если предположить, что в этом году на предприятии решили производить только двигатели, то процесс производства начнут с того участка, на котором потери в виде недополученных агрегатов будут минимальными, т.е. там, где альтернативная стоимость двигателей наименьшая. Следовательно, эффективное производство двигателей можно достичь на верхнем участке, где производство каждой его дополнительной единицы предполагает потерю ресурсов, предназначаемых на производство 0,4 агрегатов.

Б) Если двигателей производится 60 единиц, то это означает, что рациональный производитель будет работать на верхнем участке, т.к. на данном участке альтернативная стоимость каждой дополнительной единицы двигателя наименьшая (0,4 А.). При этом производство 60 двигателей приведёт к тому, что производитель должен будет отказаться от выпуска 24 агрегатов (60 Д. × 0,4). Увеличив производство двигателей ещё на одну единицу, производитель уже теряет 24,4 А. от максимально возможного производства. Следовательно, максимально возможное производство агрегатов, при условии, что производитель будет производить только 61 Д., составит 165,6 А. (190 А. - 61 т × 0,4).

1.4. Дана кривая производственных возможностей фермера на трех полях.

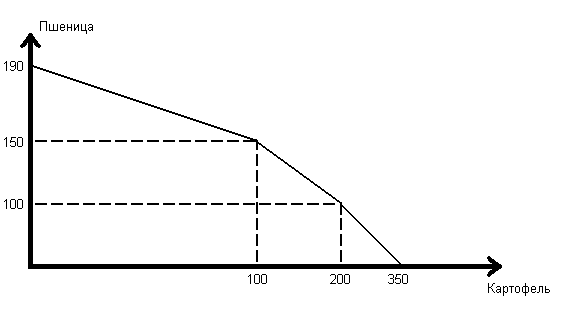
Предположим, что он решил под выращивание 130 тонн картофеля отвести нижнее поле, а два других поля не трогать. Используя графическое изображение КПВ фермера, оцените его выбор. Вычислите максимально возможное производство пшеницы, если картофеля будет произведено 130 тонн.

Решение:

В плоскости нижнего поля производство каждой тонны картофеля предполагает, что потери пшеницы на нем будут составлять ⅔ тонны от возможного выпуска. Тогда, при производстве 130 тонн картофеля, возможные потери пшеницы составят 86,6 т (130 т К. × ⅔). Отсюда следует, что максимально возможное производство пшеницы фермером будет 103,4 т (190 т П. - 86,6 т П.).

Однако следует заметить, что данный выбор фермера является не эффективным. Согласно теории КПВ эффективным считается выбор, при котором потери в виде недополученной продукции минимальны. Следовательно, фермер под выращивание 130 т К. должен отвести верхнее поле полностью и часть среднего. На данных полях потери в виде недополученной пшеницы будут минимальными (каждая тонна картофеля предполагает отказ от производства 0,4 или 0,5 тонн пшеницы соответственно). Отсюда альтернатива отказа по полям составит 55 т пшеницы (40 т П. + 30 т П. × 0,5). Тогда максимально возможное производство пшеницы фермером, при условии, что он будет производить 130 т К., составит 135 т (190 т П. - 55 т П.).

Ответ:

Эффективное производство 130 тонн картофеля возможно при возделывании верхнего поля полностью и части среднего. Потери в виде недополученной пшеницы на них будут минимальными (55 т против 86,6 т). Максимально возможное производство пшеницы составит 135 т против 103,4 т.

1.5. На одном поле фермер может произвести 1000 т картофеля или 400 т пшеницы, а на другом, альтернативная стоимость выращивания 2 т пшеницы равна 6 т картофеля при максимальном производстве картофеля равном 1500 т.

А) Постройте общую кривую производственных возможностей фермера на двух полях при условии, что фермер решил выращивать картофель. Заштрихуйте поля.

Б) Допустим, фермер всегда засевал все поля картошкой, но на этот год ему потребовалось произвести только 200 т пшеницы. На каком поле её посадить? Каково при этом максимально возможное производство картофеля (в тоннах)?

Решение:

А) Построим КПВ:

• (2500 т К.; 0 т П.) и (0 т К.; 900 т П.) - координаты максимально возможного производства картофеля и пшеницы фермером на двух полях;

• (1500 т К.; 400 т П.) - координаты точки перегиба КПВ.

• 1 т К. = 0,3 т П. - альтернативные возможности производства на верхнем поле;

• 1 т К. = 0,4 т П. - альтернативные возможности производства на нижнем поле.

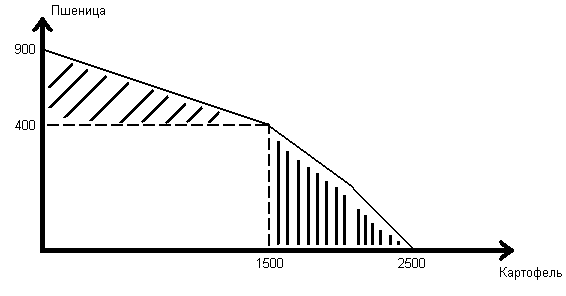
Б) Если исходить из того, что на этот год фермеру потребовалось произвести только 200 т пшеницы, то ему выгоднее всего ее посадить на том поле, где потери в виде недополученного картофеля будут минимальными, т.е. там, где альтернативная стоимость пшеницы наименьшая. В силу того что на нижнем поле альтернативная стоимость 1 т П. = 2,5 т К., а на верхнем 1 т П. = 3 т К., то фермеру выгоднее произвести 200 тонн пшеницы на том поле, где каждая тонна пшеницы предполагает отказ от производства 2,5 тонн картофеля, т.е. на нижнем.

При производстве только 200 т пшеницы потери в виде недополученного картофеля составят 500 тонн (2500 т К. - 200 т П. ×2,5). Отсюда максимально возможное производство картофеля будет 2000 тонн.

Закрепите свои умения и навыки

1.6. Кривая производственных возможностей машиностроительного предприятия по двум продуктам: двигателям и агрегатам задана тремя точками (0, 400), (400, 300), (1000, 0).

Определите:

А) сколько цехов на предприятии? Чему равны величины максимально возможного производства двигателей и агрегатов?

Б) альтернативные стоимости производства данных продуктов, при условии, что в этом году на предприятии будут производить только двигатели.

В) чему равна альтернативная стоимость производства ещё одной единицы двигателя, если общий объём производства 250 единиц?

Г) чему равно максимально возможное производство агрегатов, если двигателей будет произведено 900 единиц?

Ответ:

А) Два цеха. Максимально возможное производство двигателей и агрегатов в двух цехах составит 1000 или 400 единиц соответственно. В одном цехе можно произвести или 400 двигателей или 100 агрегатов, а в другом 600 двигателей или 300 агрегатов.

Б) В верхнем цехе альтернативная стоимость производства 1 Д. равна ¼ А., а нижнем производство каждой единицы двигателя предполагает потери в виде недополученных агрегатов в размере ½.

В) Если исходить из того, что производитель отдаёт предпочтение производству двигателей, то при общем объёме производства равном 250 Д. - альтернативная стоимость производства ещё одной его единицы составит ¼ ед. А.

Г) 50 агрегатов.

1.7. Могут ли следующие точки лежать на одной кривой производственных возможностей: А(0; 90), К(45; 55), В(30; 65), С (40; 50), D (50; 0), Е (20; 70).

Ответ: Не могут.

1.8. Фермер имеет три поля, каждое из которых однородно, хотя их продуктивность неодинакова. На первом поле он может вырастить либо 160 т картофеля, либо 60 т пшеницы, на втором 300 т и 100 т соответственно, а третьем 140 т и 50 т.

Определите:

А) максимально возможное производство картофеля и пшеницы фермером на трех полях;

Б) альтернативные стоимости производства на каждом из полей, при условии, что в данном году фермер отдаёт предпочтение производству картофеля;

В) с какого поля фермер начнет производство картофеля и почему;

Г) координаты точек перегиба КПВ;

Ответ:

А) 600 т К. и 210 т П.;

Б) альтернативные стоимости производства на каждом из полей соответственно: 1 т К. = 0.375 т П.; 1 т К. = 0,333т П.; 1 т К. = 0,357 т П.;

В) фермер начнет производство картофеля со второго поля, т.к. на нем с каждой тонны картофеля потери в виде недополученной пшеницы наименьшие (1 т К. = 0,333т П). Затем он перейдет к третьему полю, т.к. 1 т К. = 0,357 т П. Закончит производство на первом поле, поскольку здесь альтернативная стоимость 1 т К. = 0.375 т П.;

Г) (300 т К.; 110 т П.); (440 т К.; 60 т П.).

1.9. Студент МАДИ, составляя курсовой проект, рассчитал, что кривая производственных возможностей автомобильно-дорожного транспорта должна проходить по следующим населенным пунктам:

А(0, 30), В(24, 14), С(26, 0), Е(18, 20), К(14, 22), М(6, 29).

Правильно ли он произвёл расчёты?

Ответ: Да, правильно.

1.10. Даны следующие координаты точек, характеризующие деятельность фермера: (22 000 К; 0 П), (0 К; 9 900 П), (9 000; 6 900), (14 000; 4 400). Все измерения заданы в тоннах.

А) Сформулируйте экономическую задачу;

Б) Постройте кривую производственных возможностей фермера. Заштрихуйте поля;

В) Рассчитайте альтернативные стоимости производства картофеля и пшеницы, если в этом году предпочтение отдаётся производству картофеля.

Ответ:

А) Прежде чем приступить к формулировке задачи определимся в информации, которая скрыта в заданных координатах точек:

• (9 000 т К.; 6 900 т П.); (14 000 т К.; 4 400 т П.) - координаты точек перегиба КПВ. Наличие двух точек перегиба свидетельствует о том, что фермер имеет три поля;

• (22 000 т К.; 0 т П.) и (0 т К.; 9 900 т П.) - координаты точек максимально возможного производства картофеля или пшеницы фермером на трёх полях.

Задача: постройте КПВ фермера на трёх полях с учётом того, что в данном году он решил отдать предпочтение производству картофеля. При этом на одном поле он может вырастить либо 9 000 т картофеля, либо 3 000 т пшеницы, на другом 5 000 т или 2 500 т соответственно, а на третьем 8 000 т или 4 400 т.

Б) Кривая производственных возможностей фермера на трех полях: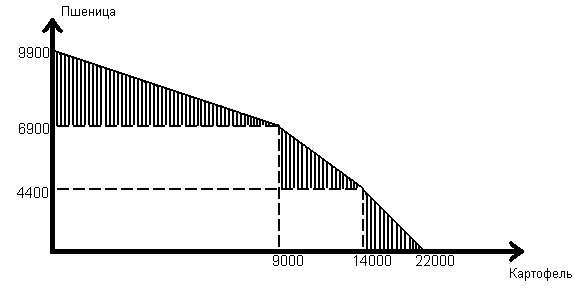

В) Альтернативные стоимости производства на каждом из полей:

• на верхнем поле - 1т К. = 0,33 т П.;

• на среднем поле - 1т К. = 0,5 т П.;

• на нижнем поле - 1т К. = 0,55 т П.

1.11. Фермер имеет пять полей, каждое из которых однородно, хотя их продуктивность неодинакова. Поля используются под кукурузу и подсолнухи. Производственные возможности фермера по полям:

• первое поле - или 150 т К. или 30 т П.;

• второе поле - или 200 т К. или 40 т П.;

• третье поле - или 50 т К. или 10 т П.;

• четвертое поле - или 250 т К. или 50 т П.;

• пятое поле - или 600 т К. или 120 т П.

Охарактеризуйте поведение (форму) кривой производственных возможностей фермера, если в данном году он будет выращивать подсолнухи.

Ответ:

«Кривизна» объясняется действием закона возрастающих альтернативных издержек. В нашем случае альтернативные издержки производства любого из двух продуктов величины постоянные и составляют 1т П. = 5 т К. Следовательно, КПВ фермера будет иметь прямую линию. Это означает, что альтернативные издержки производства любого из двух продуктов постоянны, в какую бы точку на данной линии ни перемещался фермер.

Тема 2. ТЕОРИЯ ПОЛЕЗНОСТИ И ВЫБОР ПОТРЕБИТЕЛЯ

Основные понятия. Потребность. Закон насыщения потребностей. Закон возвышения потребностей. Полезность. Функция полезности: общая и предельная. Функция полезности. Закон убывающей предельной полезности. Рациональное поведение потребителя: выбор потребителя как максимизация полезности. Первый и второй законы Госсена. Бюджетное ограничение. Уравнение бюджетной линии. Кривые безразличия. Карта кривых безразличия. Максимизация полезности: оптимум потребителя при данном бюджетном ограничении.

Дополнительные понятия. Полезность и польза. Субъективность полезности и невозможность её точного измерения. Дуговая и предельная нормы замещения.

Основные умения. Вычислять и графически анализировать общую и предельную полезность. Определять характер взаимосвязи благ (товаров и услуг) по форме кривой безразличия. Применять правило максимизации полезности. Находить потребительское равновесие по заданной кривой безразличия и бюджетному ограничению.

Дополнительные умения. Вычислять и использовать предельную норму замещения.

Теоретический материал

Потребность - это состояние неудовлетворённости, испытываемое человеком, из которого он хочет выйти, или состояние удовлетворенности, которое он желает продлить.

Свойства потребностей:

• безграничность;

• историчность (меняются во времени).

Сущность потребностей выражается двумя законами:

• законом возвышения потребности;

• законом насыщения потребности.

Объективный процесс, обусловленный тем, что в процессе удовлетворения потребностей происходит формирование новых, как в количественном, так и в качественном отношении потребностей - есть закон возвышения потребностей.

Закон насыщения потребностей предполагает, что по мере удовлетворения одновременно ряда потребностей выявляется определённый продукт или услуга, которые потребляются с максимальной интенсивностью, в силу чего наступает насыщение.

Все потребности могут быть классифицированы и объединены в отдельные группы. Границы между видами потребностей подвижны. В основании любой группировки лежат биологические потребности людей, над которыми возвышаются духовные потребности человека как социальной личности.

Средством удовлетворения потребностей служат экономические блага, т.е. товары (продукты) и услуги.

Главным фактором, определяющим выбор рационального потребителя, является полезность. При этом он стремится к её максимизации, затратив минимум средств.

Полезность - субъективное восприятие продукта или услуги потребителем, т.е. их ценность для него.

Потребительский выбор - выбор, максимизирующий функцию полезности рационального потребителя в условиях ограниченности денежного дохода.

Функция полезности:

U = f (Qx; Qy; Qz ...),

где

U - уровень полезности;

Qx; Qy; Qz - количество потребляемых продуктов или услуг за определённый период времени;

f - зависимость уровня полезности от количества потребляемых продуктов и услуг.

Различают функции:

• общей полезности (TU);

• предельной полезности (MU).

Общая полезность - сумма добавочных полезностей определенного продукта, который потребляет индивид:

TUn = MU1 + MU2 + … + Mun.

Поведение функции общей полезности изучим на основе ее графического изображения (рис. 2.1.).

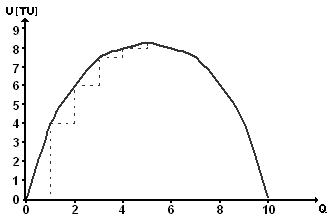
Рис. 2.1. Графическое изображение функции общей полезности:

Q - количество ( например, обувь);

U - полезность.

Как видно из графика, функция общей полезности возрастает (выпукл), а затем, достигнув своего максимального значения, убывает: TUmax = 4 + 2 + 1,5 + 0,5 + 0,2 = 8,2;

где

• ТU1 = 4;

• ТU2 = 4 + 2 = 6;

• ТU3 = 6 + 1,5 = 7,5;

• ТU4 = 7,5 + 0,5 = 8;

• ТU5 = 8 + 0,2 = 8,2;

• ТU6 = 8,2 - 0,2 = 8.

Так, две пары обуви обладают для потребителя большей полезностью, чем одна; три большей, чем две и т.д. Общая полезность растёт, хотя и медленными темпами, т.е. каждая дополнительная пара приносит все меньшую и меньшую полезность. При этом полезность шестой пары обуви отрицательна (MU6 = - 0,2), а значит, она уже приносит «вред». Отсюда можно сделать общий вывод: по мере увеличения количества потребляемого продукта (в частности обуви), общая полезность возрастает, а прирост полезности от каждой её порции (пары) убывает (суть закона возрастающей общей полезности). Тем самым потребность в них насыщается. Следовательно, полезность зависит:

• от количества потребляемого продукта (пар обуви);

• от интенсивности потребления.

Предельная полезность(MU) - добавочная полезность каждой последующей единицы продукта.

Предельная полезность определяется по формуле:

MU = ∆TU / ∆Q,

где

∆TU = TUn - TUn - 1;

∆Q = Qn - Qn - 1.

Опираясь на вышеизложенную теорию общей полезности и поведение потребителя обуви, построим график функции предельной полезности. По оси абсцисс отложим количество пар обуви, а по оси ординат значения добавочных (предельных) полезностей от потребления каждой последующей пары. Так, если:

• MU1 = TU1 - TU0 = 4;

• MU2 = TU2 - TU1 = 6 - 4 = 2;

• MU3 = TU3 - TU2 = 7,5 - 6 = 1,5;

• MU4 = TU4 - TU3 = 8 - 7,5 = 0,5;

• MU5 = TU5 - TU4 = 8,2 - 8 = 0,2;

• MU6 = TU6 - TU5 = 8 - 8,2 = - 0,2,

то график данной функциональной зависимости будет выглядеть следующим образом (см. рис. 2.2.):

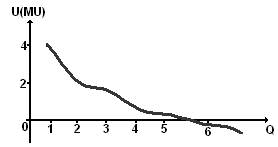
Рис. 2.2. Графическое изображение функции предельной полезности.

На основе данного графика можно заключить, что график функции предельной полезности невыпукл, а даже вогнут. По мере увеличения количества потребляемых пар обуви добавочная полезность каждой последующей пары убывает (суть закона убывающей предельной полезности (первый закон Госсена)). Минимум предельной полезности достигается в точке, когда общая полезность достигла своего максимума (ТU5 = 8,2). Дальнейшее потребление обуви принесет «вред». Об этом свительствует предельная полезность шестой пары обуви:

MU6 = TU6 - TU5 / Q6 - Q5 = 8 - 8,2 / 6 - 5 = - 0,2 / 1 = - 0,2.

Практическое применение теории общей и предельной полезности мы найдём при решении задач 2.1. и 2.2.

В микроэкономике различают две версии рационального потребительского поведения: количественную и порядковую.

Основоположники количественной теории (Менгер, Визер, Госсен) считали, что полезность конкретных продуктов можно измерить. Единица измерения полезности - ютиль (англ. «utility - полезность)». В частных случаях для измерения полезности используют денежные единицы измерения, дополнительные баллы, бонусы и т.д.

Практическое подтверждение данной теории мы найдём, решая задачи по соответствующим аспектам (см. задачи: 2.3.; 2.8).

Суть количественной теории: рациональный потребитель максимизирует общую полезность в том случае, когда денежный доход потребителя распределяется таким образом, что каждый последний рубль (доллар, евро и т.д.), затрачиваемый на приобретение продуктов или услуг, приносит одинаковую полезность (второй закон Госсена или правило максимизации полезности):

MU1 / P1 = MU2 / P2 = … Mun / Pn = λ,

где

MU1; MU2; … Mun - предельные полезности потребляемых продуктов;

P1; P2;… Pn - цены на данные продукты.

λ - предельная полезность денег

Правило максимизации полезности отражает ситуацию потребительского равновесия.

Тогда MU = P∙λ,

где

P ∙ λ - предельные издержки потребителя;

Следовательно, если MC = P∙λ, то MU = MC.

Рассмотрим экономическую ситуацию: Студент МАДИ, готовясь к сдаче экзаменационной сессии, решил улучшить свою успеваемость по трём предметам: экономической теории, математическому программированию и деталям машин. Для этого он решил воспользоваться платными услугами преподавателей. Стоимость индивидуальных занятий по всем предметам одинаковая и равна 400 рублям за один час. Количество часов, которое студент имеет возможность заниматься в день - 9. Дополнительные баллы, которые он может получить, уделяя время тому или иному предмету, следующие:

Предположим, что у студента есть средства, позволяющие ему позаниматься только 1 час. Тогда он предпочтёт занятия по экономической теории полезностью 10 баллов. Если же у него появятся деньги позаниматься второй час, то он предпочтёт занятия по математическому программированию полезностью 9 баллов, потому что полезность занятий второго часа по экономичесой теории (8 баллов) и первого часа по деталям машин (7 баллов) меньше.

При «покупке» услуг третьего часа наш студент, очевидно, предпочтёт ещё один час занятий экономической теорией полезностью 8 баллов и т.д.

Распределяя свой доход соответствующим образом, студент постепенно достигнет состояния, при котором отношения предельной полезности каждой учебной дисциплины (4 балла) к их цене (400 р за час) будут равны между собой.

Следовательно, наш студент получит максимум общей полезности, если эти часы он распределит следующим образом:

• экономическая теория - 4 часа;

• математическое программирование - 3 часа;

• детали машин - 2 часа.

Основоположники порядковой теории, в частности, Слуцкий, Хикс, Парето исходили из того, полезность отдельных продуктов измерить нельзя, но можно расставить приоритеты, т.е. построить шкалу предпочтений.

Рассмотрим экономическую ситуацию. Данные об ежемесячном потреблении двух продуктов приведены в таблице:

При этом потребителю безразлично, какой продуктовый набор выбрать. На основе табличных данных построим график, характеризующий потребительский выбор. Определим степень предпочтений потребителя.

Отложим по оси Х - киви (кг), а по оси Y - груши (кг). Отметим координаты наборов продуктов, приведенных в таблице. Построим линию, отражающую степень безразличия потребителя.

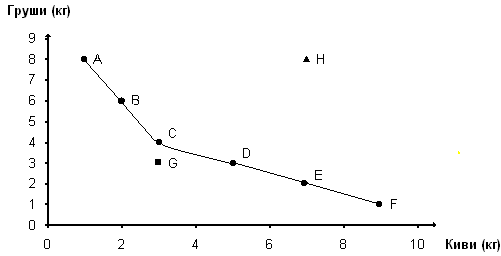
Рис. 2.3. Кривая (линия) безразличия.

Кривая безразличия (U) показывает, что в каждой её точке есть набор, состоящий из двух продуктов, который обеспечивает одинаковое удовлетворение потребностей потребителя, т.е. данные наборы продуктов одинаково безразличны потребителю.

На основе этого рисунка мы можем сделать следующие выводы:

а) наборы продуктов, соответствующие точкам A, B, C, D, E, F имеют одинаковую полезность для потребителя (т.е. потребитель безразличен к шести наборам продуктов);

б) набор продуктов, соответствующий точке G, менее предпочтителен для потребителя;

в) набор из двух продуктов, соответствующий точке Н, более предпочтителен для потребителя.

Если через точки G и H провести кривые, параллельные исходной кривой, то получим карту кривых безразличия.

Карта кривых безразличия - это вкусы и предпочтения потребителей.

Свойства кривых безразличия на карте кривых безразличия:

1. кривые безразличия не пересекаются, т.к. один набор продуктов, который предпочтительнее другого набора, не может находиться с ним на одном уровне;

2. кривые безразличия имеют отрицательный наклон, т.к. увеличение количества одного продукта сопровождается уменьшением количества другого, входящего в тот же набор продуктов;

3. кривые безразличия пологие, т.е. вогнуты. Чем менее полога кривая безразличия, тем ниже предельная норма замещения.

Нормой замещения (MRS) одного продукта другим называется такое количество продукта А, которым потребитель согласен пожертвовать, с тем чтобы приобрести дополнительную единицу продукта B, при их одинаковой общей полезности:

MRSAB = |- A / + B| = |MUВ| / |MUА|.

Если MRS >1 Высокая норма предпочтения набора В;

=1 Полная взаимозаменяемость А и В.

<1 Низкая норма предпочтения набора А.

=0 Потребитель не отказывается от набора А.

Различают:

• дуговую норму замещения;

• предельную норму замещения.

Дуговая норма замещения на отрезке АВ кривой безразличия равна: MRSух = - ∆Y / ∆X.

Разберём теорию дуговой нормы замещения, используя рис. 2.3. и данные таблицы:

Определим чему равно значение дуговой нормы замещения груш киви на отрезке АС при переходе от первого продуктового набора к третьему

Рассуждения: при переходе от первого набора продуктов А(1; 8) к третьему С(3; 4) потребитель поведёт себя следующим образом:

MRSух = - ∆Y / ∆X = - 8 + 4 / - 1 + 3 = l- 4 / 2l.

Расчёт показывает, что он ежемесячно будет отказываться от 4кг груш, замещая их 2кг киви. В конечном итоге норма замещения обеспечит одинаковый уровень полезности на единицу денежных затрат.

Таким образом, увеличивая полезность своих денежных расходов, рациональный потребитель стремится уравновесить не только взаимозаменяемые продукты, но и их цены. Для более глубокого изучения данной проблемы на практике используют формулу предельной нормы замещения (применение формулы предельной нормы замещения рассмотрим на основе разбора задачи 2.4.).

Предельная норма замещения есть производная в любой точке кривой безразличия:

MRSху = l- dY / dXl = MUx / MUy.

Формы кривых безразличия:

1. Взаимозависимые (заменяемые) блага - продукты или услуги, которые удовлетворяют потребности за счёт друг друга (например: чай и кофе, розы и гвоздики и т.д.) (Рис. 2. 4.)

2. Взаимодополняемые блага - продукты или услуги, которые удовлетворяют потребности лишь в комплексе друг с другом (например: доски и гвозди, фотоаппарат и пленка и т.д.) ( Рис. 2.5.)

3. Независимые блага - продукты или услуги, которые удовлетворяют потребности независимо друг от друга (например: чай и гвозди). (Рис. 2.6.)

4. Нежелательные блага - продукты или услуги, без которых потребитель был бы рад обойтись, но в силу каких-то причин вынужден потребить (например: горькое лекарство, услуги стоматолога и т.д.) (Рис. 2.7.)

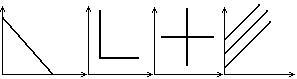
Рис. 2.4. Рис. 2.5. Рис. 2.6. Рис. 2.7.

Анализ потребительских предпочтений не показывает, какой из наборов продуктов купит покупатель. Следовательно, чтобы разобраться в этом, надо изучить покупательную способность потребителя. Для этого необходимо учитывать цены на продукты и доход потребителя.

Пусть X и Y то количество продукта, которое хотят приобрести покупатели. При этом цены на продукты равны Px и Py соответствено, а

I - номинальный доход потребителя (величина постоянная).

Тогда алгебраически бюджетное ограничение потребителя примет следующий вид: Px × X + Py × Y = I.

На основе данного тождества построим бюджетную плоскость:

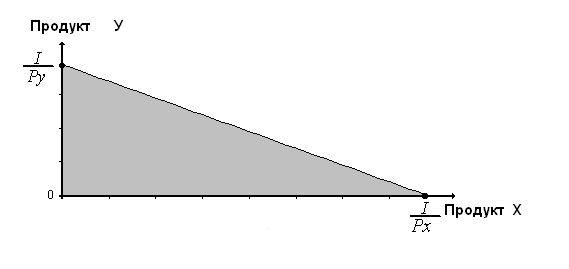
Рис. 2.8. Бюджетная плоскость.

На основе данного рисунка сделаем следующие выводы:

• заштрихованная плоскость есть бюджетное пространство (бюджетные возможности покупателя);

• все точки, лежащие внутри бюджетного пространства, показывают доступность потребителю данных продуктов (однако, приобретая их, он не полностью использует свой доход);

• наборы продуктов, лежащие за бюджетной линией предпочтительны для потребителя, но не доступны, т.к. его доход не позволяет ему их приобрести.

• Бюджетная линия - линия, которая графически отражает набор продуктов, приобретение которых требует одинаковых затрат.

• Уравнение бюджетной линии:

Поведение бюджетной линии, исходя из следующих ситуаций:

1. если цены на продукты Х и Y постоянны, а номинальный доход растет, то бюджетная линия переместится вверх параллельно первоначальной линии;

2. если номинальный доход постоянен, а цены на продукты Х и Y упали, то бюджетная линия переместится вверх параллельно первоначальной, т.к. реальный доход вырос;

3. если номинальный доход и цена на продукт Y постоянны, а цена на продукт Х падает, то спрос на продукт Y не изменится, а на продукт Х возрастёт.

Таким образом, оптимальный выбор потребителя зависит от следующих факторов:

• степени предпочтения потребителя;

• цен на продукты;

• дохода, т.е. бюджетного ограничения.

Задачи на построение бюджетной линии, анализ потребительского выбора, исходя из его дохода см.: 2.5.; 2.6; 2.9; 2.10.

Условие равновесия потребителя.

Дано:

1. Три кривых безразличия U₁-U₃.

2. Бюджетное ограничение Р_х × Х + Py × Y = I,

где

I - номинальный доход (величина постоянная).

3. Наборы продуктов, соответствующие точкам A, B, C, D, E и F.

Доказать:

что набор продуктов, соответствующий точке C (рис. 2.9.), отражает ситуацию потребительского равновесия, в которой рациональный потребитель достигает максимум общей полезности.

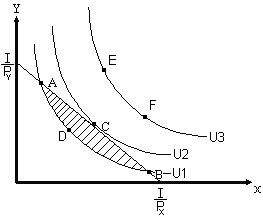
Рис. 2.9. Положение равновесия потребителя.

Доказательство:

Количественная теория поведение кривых безразличия U₁-U₃ объясняет с точки зрения убывающей предельной полезности (первый закон Госсена).

Порядковая теория поведение кривых безразличия U₁-U₃ объясняет с точки зрения снижающейся предельной нормы замещения (MRS). В любой точке кривой безразличия предельная норма замещения будет выражать следующую зависимость:

MRSxy = l- dYl / ldXl = MUx / MUy.

Рассмотрим положение бюджетной линии и кривых безразличия U1 - U3 в бюджетной плоскости:

1. для потребителя более предпочтительны наборы из двух продуктов (X,Y), соответствующие точкам E и F (кривая безразличия U3). Однако, они ему не доступны, т.к. не хватает дохода;

2. если потребитель предпочтет наборы из двух продуктов(X,Y) кривой безразличия U1 (точка A, B и D), то он поступит нерационально. При данном уровне потребления доход используется им не полностью (заштрихованная часть бюджетного пространства);

3. рациональный потребитель увеличит степень удовлетворения своих потребностей (при том же бюджетном ограничении), перейдя с кривой безразличия U1 на U2 (точка C).

Проанализируем точку C_:

• Точка C - точка касания кривой безразличия U2 и бюджетной линии. В данной точке тангенс угла наклона кривой безразличия равен тангенсу угла наклона бюджетной линии.

• Тангес угла наклона есть производная функции или отношение противолежащего катета к прилежащему катету.

• Возьмём производную в точке C:

.

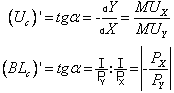Поскольку в теории потребления номинальный доход потребителя величина постоянная, то количество сэкономленных денег от недопотребления товара Y, должно соответствовать количеству денег, потраченных на приобретение товара X. Отсюда, приравняв производные:

,

получим следующее выражение:

.

Таким образом, набор из двух продуктов, соответствующий точке C отражает ситуацию потребительского равновесия, в которой рациональный потребитель достигает максимум общей полезности (второй закон Госсена). Это и требовалось доказать.

Вывод: точка C - точка потребительского равновесия. В этой точке:

• достигается максимум общей полезности;

• объединяются обе теории потребительского выбора (количественная и порядковая).

Опираясь на данное доказательство, решим следующие задачи: 2.5; 2,9 и 2.10, которые позволят нам закрепить наши умения и навыки.

Учимся решать экономические задачи

Типы задач:

• Задачи на взаимосвязь общей и предельной полезности;

• Задачи на выведение функций общей полезности по заданной предельной полезности;

• Задачи на вычисление предельной и дуговой нормы замещения;

• Задачи на применение правила максимизации полезности, составление уравнения бюджетной линии.

• Задачи на определение равновесия потребителя и максимизации полезности.

2.1. Выведите функцию предельной полезности из заданной функции общей полезности: TU = 5X - ½X².

Решение:

Из условия задачи мы видим, что функция общей полезности TU зависит от количества потребляемого продукта X . Данная функция является частным случаем функции одной переменной y = ƒ(x).

Для того чтобы вывести функцию предельной полезности, мы используем формулу MU = ∆TU / ∆Q, в которой предельная полезность равна отношению приращения функции общей полезности к приращению аргумента при ∆x → 0. Данное отношение в математике называется первой производной (y') или dy / dx. Следовательно, предельная полезность есть производная общей полезности.

Отсюда MU = (TU)' = (5X - ½X²)' = 5 - Х.

Ответ: MU(x) = 5 - Х

2.2. Какие из приведенных ниже функций соответствуют закону предельной полезности:

1) TU(x) = √x; 4) MU(x) = 1 / x;

2) MU(x) = 5 - x; 5) MU(x, y) = 45 + x - y;

3) TU(x, y) = x - y; 6) TU(x) = 2x?

Решение:

Опираясь на решение задачи 2.1, и применив к каждой функции закон убывающей предельной полезности, мы видим правильные ответы: 1, 2, 4.

Ответ: 1; 2; 4.

2.3. Цена на товар А равна 10 р. Цена товара В равна 5 р. Чему равна предельная полезность товара В, если потребитель оценивает предельную полезность товара А в 100 ютилей?

Решение:

Применим второй закон Госсена или правило максимизации полезности: 100 / 10 = MU(B) / 5. Следовательно, MU(B) = 50.

Ответ: 50.

2.4. Студент потребляет в месяц 2кг сосисок по цене 141 р за 1кг и 4 буханки хлеба по цене 12 р за одну буханку. Чему равна предельная норма замены сосисок хлебом в состоянии равновесия?

Решение:

В состоянии равновесия отношения предельных полезностей равно отношению цен товаров:

MRSс, x = | - С / + Х | = MUx / MUс = Рх / Рс,

где

с - количество сосисок;

x - количество хлеба;

MUx; MUс - предельные полезности хлеба и сосисок.

MRSc, x - предельная норма замены.

Поскольку Pc = 141, a Px = 12, то MRSc, x = 12 / 141.

Ответ: 12 / 141.

2.5. За месяц студент расходует на апельсины и бананы 100 рублей. Цена одного апельсина равна 5 р, а цена одного банана - 2 р. Какое количество апельсинов и бананов потребляет рациональный студент в месяц, если общая полезность от количества потребляемых фруктов составляет TU(х,у)=10XY, где Х и Y количество апельсинов и бананов соответственно.

Решение:

а) Выбор студента предопределён бюджетным ограничением:

100 = 5Х + 2Y;

б) В состоянии равновесия отношение предельных полезностей продуктов равно отношению цен на них: MU(x) / MU(y) = Px / Py;

в) Найдём значения предельных полезностей потребляемых товаров:

TU(x, y)'x = MU(x) =10Y;

TU(x, y)'y = MU(y) = 10X.

г) Согласно теории потребления, рациональный студент должен достичь максимума совокупной полезности от количества потребляемого продукта в точке касания кривой безразличия с линией бюджетного ограничения. Поэтому составим и решим систему уравнений:

5Х + 2Y = 100,

10Y / 10Х = 5 / 2.

Ответ:

Х = 10, а Y = 25, т.е. рациональный студент потребляет за месяц 10 апельсинов и 25 бананов.

Закрепите свои умения и навыки

2.6. Что можно сказать о полезности 11-го товара, если:

Количество товаров 6 8 10 12 14

Общая полезность 10 13 15 16 16,5

Ответ: Согласно закону предельной полезности, полезность 11-го товара будет колебаться в следующих пределах: 0,5 ≤ MU(11) ≤ 1.

2.7. Студент ежемесячно получает стипендию равную 900 р. Завтрак в столовой ему обходится в 30 р, а обед в 60 р. Как сместится бюджетная линия при росте цен на завтраки до 36 р и росте цен на обеды на 50%. Составьте уравнения обеих бюджетных линий.

Ответ:

у = 15 - 0,5х - уравнение первоначальной бюджетной линии;

у = 10 - 0,4х - уравнение бюджетной линии после изменения цен; бюджетная линия сместится влево или вниз.

2.8. Студент, работая внеурочное время, ежемесячно зарабатывает 100у.е. Функция полезности от количества потребляемых завтраков и обедов TU (x,y) = XY, где Х - количество завтраков, а Y - количество обедов.

А) Сколько завтраков и обедов потребляет рациональный студент, если цены в студенческой столовой следующие Рх = 5, Ру = 1?

Б) Как изменится потребление студента, если после вмешательства студпрофкома цены на завтраки упадут до Рх = 2?

Ответ:

А) До вмешательства студпрофкома рациональный студент потреблял: завтраков (Х) - 10; обедов (Y) - 50.

Б) После вмешательства студпрофкома: Х = 25; Y = 50.

2.9. Выведите условие равновесия потребителя с функцией полезности TU (x,y) = XY , где X и Y - количество потребляемых благ. Цены на них соответственно составляют: Px = 3 и Py = 7. Бюджетное ограничение равно 200 д.е.

Ответ: 3х = 7у.

2.10. Даны два продукта А и В. Предельная полезность первого равна 20, а второго - 60. При этом цены на продукты составляют 4 и 12 денежных единиц соответственно. Будет ли потребитель находиться в равновесии.

Ответ: Да.

2.11. Функция полезности от количества потребляемых продуктов TU (x,y) = XY, где Х и Y - количество продуктов в кг. Доход потребителя составляет 27 р.

А) Какое количество продуктов потребляет рациональный потребитель, если цены на продукты следующие: Рх = 4 р, Ру = 6 р?

Б) Как изменится потребление если цена на продукт Х возрастет до 5 р?

Ответ:

А) Х = 3, 375кг; Y = 2,25кг. Б) Х = 2,7кг; Y = 2,25кг.

Тема 3. ТЕОРИЯ СПРОСА и ПРЕДЛОЖЕНИЯ

Основные понятия. Категории спроса и предложения. Величина спроса и предложения. Функция спроса и предложения. Кривая спроса и предложения. Законы спроса и предложения. Факторы, формирующие спрос и предложение. Изменение величины спроса и предложения. Изменение спроса и предложения. Рыночное равновесие. Равновесная цена. Равновесное количество (объём продаж). Влияние изменение спроса и предложения на равновесную цену и равновесное количество. Выручка. Ценовая эластичность спроса и предложения. Точечная эластичность.

Дополнительные понятия. Шкала спроса и предложения. Дуговая эластичность. Предложение в краткосрочном и долгосрочном периодах.

Основные умения. Различать величину спроса (или предложения) и спрос (или предложение). Строить шкалы и кривые спроса (или предложения). Определять характер изменения спроса (или предложения) в зависимости от формирующих его факторов. Определять эластичность спроса (или предложения). Вычислять и использовать точечную эластичность. Находить равновесные цены и равновесный объём производства. Анализировать последствия установления предельных (фиксированных) цен.

Дополнительные умения. Различать дуговую и точечную эластичность. Вычислять и использовать дуговую эластичность, эластичность спроса (или предложения) по доходу и перекрёстную эластичность.

Теоретический материал

Спрос = потребность + возможность заплатить.

Величина спроса - это количество продукта, которое потребители хотят и могут купить по данной цене в данный период времени (день, неделя, месяц и т.п.).

Рассмотрим ситуацию: предположим, что вы имеете некоторую сумму денег и хотите купить 3кг риса. На рынке цена на рис равна 28 руб. за 1кг. Но если бы рис стоил 25 руб. за 1кг, то вы купили бы не 3, а 4кг (Q2 = 4кг). Изменение величины спроса равное Q2 есть то количество продукта, которое вы хотите и можете купить при сложившейся новой цене на данном рынке при прочих равных условиях (рис. 3.1.).

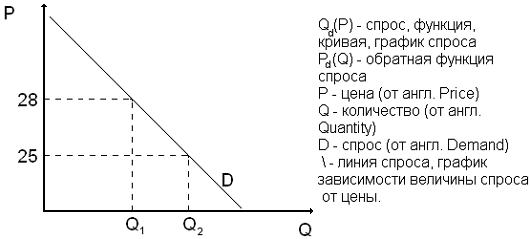
Рис. 3.1. Спрос.

Закон спроса: при прочих равных условиях, чем выше цена продукта, тем меньшее его количество люди готовы купить, или наоборот, чем ниже цена, тем большее количество продукта люди готовы купить.

Линия спроса D - функция спроса - функция, определяющая спрос в зависимости от влияющих на него различных факторов. Например: Дана функция спроса на товар: Q(D) = 7 - P. Давайте вместе с вами:

а) построим линию спроса данной функции;

б) проведём анализ рыночной ситуации, если на рынке при данном спросе предлагаются товары:

• X в количестве 3-х единиц по цене 2 р. за единицу;

• М в количестве 4-х единиц по цене 5 р. за единицу.

Рассуждения:

а) Поскольку заданная функция отражает линейную зависимость, то график данной функции построим по двум точкам: А и В (рис. 3.2.).

• Точка А - с координатами Q(D) = 0 и P = 7 - показывает, что по данной цене покупатель не может купить ни одной единицы товара. Для того, чтобы продавцу продать хотя бы одну единицу товара, надо снизить цену.

• Точка В - с координатами Р = 0, а Q(D) = 7 - показывает, что такое количество товара покупатели купят только бесплатно.

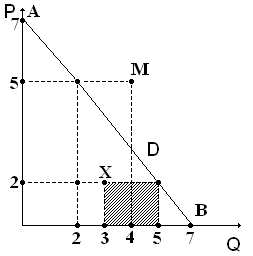
Рис. 3.2. Линия спроса функции Q(D) = 7 - P

б) На рынок выходит продавец с двумя товарами Х и М:

• в точке Х - при цене P = 2 продавец предлагает количество товара Q = 3. Однако по этой цене покупатель хочет купить 5 единиц товара (Q(D) = 7 - 2). Возникает дефицит в размере 2-х единиц товара (5 - 3). Данные 2 единицы товара и все точки левее линии спроса отражают ситуацию дефицита на рынке;

• в точке М - товар в количестве 4 единиц предлагают по цене Р = 5 ден.ед. Однако по данной цене покупатели предъявят спрос только на 2 ед. (Q(D)) = 7 - 5). Cледовательно, предложение товара превышает спрос на 2 единицы (4 - 2). Эти 2 единицы и все точки правее линии спроса отражают ситуацию излишка товара на рынке.

Факторы, влияющие на спрос, бывают ценовые и неценовые:

Q(D) = ƒ(P, I, Z, W, Psub, Pcom, N),

где

P - цена на данный продукт (ценовой фактор отражает суть закона спроса).

Неценовые факторы:

I - доходы покупателей;

Z - вкусы и предпочтения;

W - ожидания будущего изменения цен и доходов;

Psub - цена на товары-субституты, т.е. цены на товары-заменители (например, такие, как рис и гречка);

Pcom - цена на комплиментарные блага, т.е. на взаимодополняемые товары, (например, зелёный салат и свежие помидоры к нему);

N - число покупателей на рынке.

Рассмотрим влияние неценовых факторов на спрос:

• доходы покупателей (I). Увеличение денежных доходов покупателей (при отсутствии инфляции) означает повышение спроса, т.е. сдвиг линии спроса вправо, уменьшение доходов - сдвиг линии спроса влево. По мере роста доходов потребители увеличивают спрос на мясные продукты, фрукты, технику, модную одежду и т.д. При снижении дохода спрос на такие продукты падает.

Продукты, спрос на которые возрастает в прямой зависимости по мере увеличения денежного дохода, называются продуктами роскоши.

Продукты, спрос на которые возрастает при снижении доходов, называются низшими продуктами (например, маргарин вместо сливочного масла).

Продукты, которые потребляются в одних и тех же количествах, независимо от величины дохода называются нормальными (например, хлеб, спички, соль и т.д.)

• вкусы и предпочтения покупателей (Z). Увеличение спроса на продукт, вошедший в моду, сдвигает линию спроса вправо. Сокращение спроса на продукт, в связи с выходом его из моды, сдвигает линию спроса влево.

• oжидания будущего изменения цен и доходов (W). Например, если в скором будущем ожидается увеличение цен на крупы, то покупатель увеличит спрос на них. В данном случае линия спроса сместится вправо или вверх. Если ожидается снижение цен, то линия спроса сместится влево или вниз.

• цены на товары-субституты (Psub) (например, рис и гречка). При увеличении цены на гречку и неизменной цене риса, потребители увеличивают спрос на рис. Следовательно, линия спроса на рис сместится вправо. Если цена на гречку упадёт, тогда линия спроса на рис сместится влево.

• цены на комплементарные блага (Pcom) (например, зеленый салат и свежие помидоры). Снижение цены на помидоры ведёт к увеличению спроса на зелёный салат, следовательно, линия спроса сместится вправо. Повышение цены на помидоры приведёт к сокращению спроса на салат, линия спроса сместится влево.

• число покупателей на рынке(N). Рост населения или любое другое увеличение покупателей на рынке приведёт к повышению спроса и сдвинет линию спроса вправо. Сокращение населения приведёт к уменьшению спроса и сдвинет линию спроса влево.

Таким образом, сдвиг линии спроса в результате влияния какого-либо неценового фактора показывает изменение спроса. Смещение линии спроса вправо и вверх - увеличение спроса (рис. 3.3.); влево и вниз - уменьшение спроса (рис 3.4.).

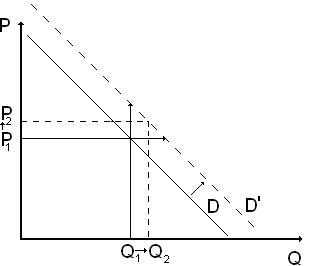
Рис. 3.3. Увеличение спроса (объёма продаж и цены) с ростом: доходов потребителей; числа покупателей; ожиданий в будущем и т.п.

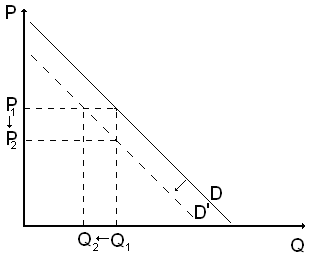
Рис. 3.4. Сокращение спроса (объёма продаж и цены) с уменьшением: доходов потребителей; количества покупателей и т.п.

То, как реагирует объём продаж на изменение таких факторов как:

• цена на данный продукт;

• доход потребителя;

• цены на взаимозаменяемые или взаимодополняемые продукты, называют эластичностью спроса.

1. Эластичность спроса по цене (ценовая эластичность) - это относительное изменение объёма продаж под влиянием изменения цены на один процент:

|Ed | = - ∆Q / Q1 : ∆ P / P1 (3.1.1),

где

Ed - эластичность спроса (в данном случае по цене);

∆Q =Q2 - Q1 - изменение объёма продаж;

∆P = (P2 - P1) - изменение величины цены.

Наличие знака «минус» отражает суть закона спроса, в основе которого лежит обратная зависимость между ценой и объёмом продаж. Поэтому для удобства расчёта данного коэффициента мы пользуемся «математическим модулем».

Коэффициент эластичности предложения рассчитывается по аналогичным формулам, но поскольку он является величиной безразмерной и положительной, то мы обходимся без «модуля».

Точечная эластичность спроса по цене находится через производную, т.е. вычисляется в конкретной точке (например, P1; Q1). Ее рассчитывают при небольшой разнице между величинами P2 и P1, а также Q2 и Q1.

|Ed| = - dQ / dP : Q1 / P1 или |Ed| = - dQ / dP × P1 / Q1 (3.1.2),

где

dQ / dP - производная функции спроса в этой точке.

При значительных колебаниях факторов, влияющих на спрос, применяют дуговую эластичность.

Коэффициент дуговой эластичности рассчитывается по формуле:

|Ed| = - ∆Q / ½(Q1+ Q2) : ∆P / ½(P1 + P2) (3.1.3),

где

Ed - эластичность спроса (в данном случае по цене);

∆Q =Q2 - Q1 - изменение величины спроса на отрезке;

½ (Q1 + Q2) - усредненная величина спроса на данном отрезке;

∆P = (P2 - P1) - изменение величины цен;

½ (P1 + P2) - усредненное значение цен на данном отрезке.

Например: Пусть линейная функция спроса задана уравнением: Q(D) = 1800 - 3P. Выведим формулу эластичности спроса по цене.

Рассуждения:

А) Для того, что бы вывести формулу ценовой эластичности заданной функции: Q(D) = 1800 - 3P, достаточно воспользоваться формулой точечной эластичности: | Ed| = - dQ / dP × P0 / Q0,

где Р - зависимая переменная.

Тогда:

• dQ = (1800 - 3P)' = 0 - 3 × 1 = -3;

• dP = (P)' = 1.

Подставим данные значения в формулу точечной эластичности:

• lEdl = l-3 / 1 × P / Ql = l-3P / Ql, где Q = 1800 - 3P.

Следовательно:

• |Ed| = l-3P / (1800 - 3P)l.

На основе решения данной задачи:

а) построим график линейной функции спроса Q(D)=1800 - 3P (рис.3.5).

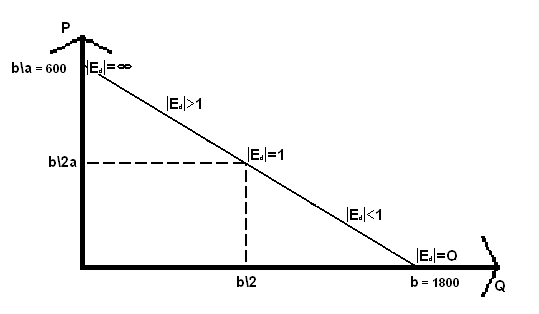
Рис. 3.5. Линейная функция спроса Q(D)=1800 - 3P.

б) сформулируем общетеоретические выводы, которые в последующем используем при решении задач (см. 3.9.; 3.10.; 3.11.; 3.13.):

• эластичность спроса по цене линейной функции спроса будет рассчитываться по формуле: Ed = - aP / (b - аР) (3.1.4.);

• Эластичность спроса растёт от нуля при P = 0 до бесконечности при P = b/а.

• Если | Ed | > 1, то спрос будет эластичным;

• если | Ed | < 1, то спрос будет неэластичным;

• если | Ed | = 1, то спрос обладает единичной эластичностью;

• если|Ed|=0 спрос совершенно (абсолютно) неэластичный;

• если |Ed| → ∞,то спрос называют совершенно (абсолютно) эластичным.

2. Эластичность спроса по доходу и перекрёстная эластичность рассчитываются аналогично.

Эластичность спроса по доходу показывает, насколько изменение объёма продаж зависит от изменения дохода. Данный вид эластичности имеет дело со смещением кривой спроса (вверх или вниз).

Ei = ∆Q / Q1 : ∆ I / I1, (3.2.1.)

где I - величина дохода;

Тип товара взависимости от значения коэффициента эластичности спроса по доходу:

• Ei < 0 - низшие продукты;

• 0 < Ei < 1 - предметы первой необходимости;

• Ei >1 - предметы роскоши.

3. Перекрёстная эластичность (Eig) показывает, насколько объём продаж подвержен изменениям в зависимости от колебания цен на другие продукты. Данный коэффициент оценивает степень взаимозависимости рынков:

• Eig > 0 - взаимозаменяющие продукты;

• Eig < 0 - взаимодополняющие продукты;

• Eig = 0 - независимые продукты.

Предложение - это вся представленная на рынке для продажи масса продукции. Цена предложения - это цена, назначаемая производителем на свою продукцию. В ней он учитывает все затраты, т.е. то, что затрачено на его производство, и величину желательной прибыли (избыток над затратами). Например: затраты на производство 1 чебурека (тесто, мясо, жир, зарплата пекарям и т.д.) составляют 12 р. Предположим, что продают чебурек по 16 р. Тогда прибыль с одного чебурека составит 4 р. (16 - 12).

Величина предложения - это количество продукции, которое будет предложено для продажи при данной цене в данный период (рис.3.6).

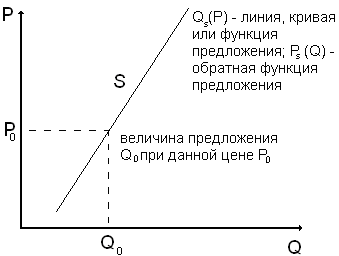
Рис. 3.6. Предложение.

Закон предложения: при прочих равных условиях производитель готов произвести больше продукции, если за неё больше платят. Цена - главный фактор, влияющий на изменение величины предложения.

Функция предложения определяет предложение в зависимости от влияющих на него различных факторов.

Факторы бывают ценовые и неценовые.

Q(s) = ƒ(P, Pr, K, T, N, B),

где

P - цена на данный продукт (ценовой фактор).

Неценовые факторы:

Pr - цены на ресурсы (рабочую силу, сырьё, машины и т.д.);

K - технологии (методы производства товаров);

Т - налоги государства (акцизы, налог на добавленную стоимость и т.д.)

N - число продавцов на рынке (конкуренция со стороны производителей аналогичной продукции);

В - ожидания в экономике.

Влияние ценового фактора (изменение величины предложения) означает движение по линии предложения. Влияние неценовых факторов (изменение предложения) приводит к сдвигу линии предложения. Увеличение предложения сдвигает линию предложения вправо или вниз, уменьшение предложения - влево или вверх.

Рассмотрим влияние неценовых факторов на предложение:

1. цены на ресурсы, технология производства товаров (Pr; К). Например: затяжные дожди требуют дополнительных затрат на производство риса. Следовательно, нужно изменить технологию производства, построить хранилище, купить технику, чтобы сушить рис, нанять больше работников и т.д. Расходы увеличатся, поэтому линия предложения сдвинется влево или вверх (рис. 3.7.)

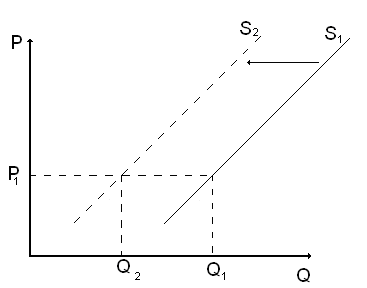
Рис. 3.7. Сдвиг линии предложения влево.

• налоги государства (Т). Снижение налогов приводит к снижению затрат на производство единицы продукции и увеличивает её предложение, т.к. при сохранении той же самой цены на рынке производство становится более прибыльным. Линия предложения сместится вправо или вниз.

• число продавцов на рынке(N). Увеличение на рынке числа продавцов аналогичной продукции приводит к снижению цены на данную продукцию, а значит, к сокращению прибыли отдельного производителя. Следовательно, в данной ситуации производителям будет выгодно сокращать предложение. Линия предложения сместится влево или вверх.

• ожидания в экономике (В). Например, если производители ожидают роста цен на свою продукцию в будущем, то они могут задержать ее доставку на рынок по сегодняшним более низким ценам, и это сократит предложение. Линия предложения сместится влево или вверх.

Рассмотрим следующую экономическую ситуацию: Функция спроса на продукцию имеет вид: Q(D) = 6 - P, функция предложения: Q(s) = 3P - 3, где P - цена в рублях, а Q - количество в штуках. Государство установило фиксированную цену в размере 2 р за шт.

1. Определим величину:

А) предложения;

Б) дефицита или излишка, объём продаж;

В) выручки продавца.

2. Предположим, государство решило ввести дотации производителю в размере 1 р. на единицу проданной продукции. Как это отразится на рыночной ситуации, если спрос постоянен?

Рассуждения:

1. А) Подставим значение фиксированной цены (2 р.) в уравнение предложения: Q(s) = 3Р - 3 = 3 × 2 - 3 = 3. Величина предложения составит 3 шт.

Б) Подставим значение фиксированной цены (2 р.) в уравнение спроса: Q(D) = 6 - P = 6 - 2 = 4. Величина спроса составит 4 шт. Поскольку величина предложения равна 3 шт., а спрос предъявляют на 4 шт., то на рынке возникает ситуация дефицита в размере 1 шт. (3 - 4). Объём продаж при данном спросе есть 3 шт.

В) Величина выручки продавца (TR = P × Q) равна произведению количества проданной продукции на цену продажи. Отсюда выручка продавца (TR = 3 × 2 = 6) составит 6 р.

2. При введении дотации призводителю в размере 1 р. на единицу проданного товара, функция предложения примет следующий вид: Q(s) = 3(P + 1) - 3 или Q(s) = 3P. Тогда величина предложения при цене 2р. за шт. будет равна 6 (3 × 2). Поскольку спрос предъявляют на 4 шт., то после введения дотации, на рынке возникнет излишек в 2 шт. (6 - 4). В данной рыночной ситуации объём продаж составит 4 шт., следовательно, выручка от продажи будет равна 8 р. (4 × 2).

Изменение предложения во многом зависит от периода времени.

Рассмотрим ситуацию: рыбаки приморской деревни привезли на местный рынок свежевыловленную рыбу. При этом учтите, что свежая рыба, если она хранится, быстро теряет свои качества. Цена на рыбу высокая, но, несмотря на это, рыбаки не смогут увеличить предложение, т.к. в тот же день не успеют выйти в море. Данный период времени называют кратчайшим (мгновенным), а линия (кривая) предложения будет вертикальной.

Если рассматриваемый период составляет более одного дня, то рыбаки смогут при высокой цене увеличить предложение, например, наняв дополнительное число работников. Данный период времени называется кратковременным. На основе данного примера мы сами можем сформулировать определение кратковременного периода. Получается, что кратковременный период - период, когда рост производства достигается за счёт дополнительного труда при неизменном капитале. Кривая предложения в данном случае будет возрастающей.

Долговременный период времени позволит рыбакам не только нанять дополнительное число работников, но и докупить дополнительные лодки, организовать доставку свежевыловленной рыбы до рынка, открыть свои павильоны для продажи ит.п. Следовательно, в долговременном периоде все факторы производства переменные. Кривая предложения будет возрастающей, но менее пологой. (Обретенные навыки и умения закрепим, решая задачу 3.8)

Мы уже знаем, что покупатель по более высокой цене хочет и может купить как можно меньше продукции. Однако производитель, при более высокой цене, готов продать её как можно дороже. Когда цена, по которой продаёт продавец свою продукцию, равна цене, по которой покупает её покупатель, тогда на рынке наступает равновесие спроса и предложения (рис. 3.8).

Графически равновесию спроса и предложения соответствует точка пересечения соответствующих линий (кривых).

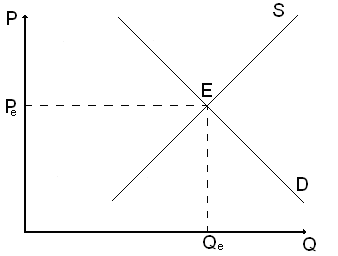
Рис. 5.7. Равновесие на рынке.

Точка E(с координатами Pe,Qe) называется точкой равновесия, а соотвествующие цена (Pe) и объём продаж(Qe) - равновесными.

Рассмотрим экономическую ситуацию:

Функция спроса и предложения на продукцию составляют:

Q(D) = 7 - P, a Q(s) = 2P - 5. Найдем:

А) равновесную цену;

Б) равновесный объём продаж;

В) что случится, если правительство страны установит цену на уровне 6 рублей за единицу?

Рассуждения:

А) По теории рыночного равновесия равновесная цена устанавливается в точке пересечения линии спроса и предложения. Следовательно, для того, чтобы определить равновесную цену, приравняем уравнения функции спроса и предложения: 7 - Р = 2Р - 5. Отсюда Ре = 4 (равновесная цена).

Б) Чтобы определить равновесный объём продаж подставим равновесную цену в любое из уравнений (спроса или предложения): Qe = Q(D) = Q(s) =7 - 4 = 2 × 4 - 5 = 3;

Qe = 3 (равновесный объём продаж).

В) Подставим новое значение цены в функцию спроса и предложения: Q(D) = 7 - 6 = 1; Q(s) = 2 × 6 - 5 = 7.

При цене 6 рублей за единицу равновесие на рынке не будет достигнуто, т.к. количество предлагаемого товара составляет 7 единиц, тогда как количество спрашиваемого товара - всего лишь 1 единицу. Следовательно, на рынке возникает излишек товара, который равен 6 единицам (7 - 1 = 6).

Учимся решать экономические задачи

Типы задач:

• Задачи на вычисление равновесной цены и равновесного объёма;

• Задачи на вычисление и использование эластичности спроса и предложения по цене;

• Задачи на определение максимальной выручки производителя;

• Задачи на определение цены и выручки от продаж после введения косвенных налогов;

• Анализ параметров, влияющих на процесс производства.

3.1. Предположим, что рыночное предложение инвалидных колясок составляет Q(S) = 7P - 2100, где Р - цена коляски в условных единицах. Правительство решило стимулировать производство и доплачивать производителям 100 условных единиц. Какой вид примет новая функция предложения?

Решение:

Дотации представляют собой адресные выплаты производителям. Потоварные дотации можно рассматривать как потоварный налог. Следовательно, 100 условных единиц можно рассматривать как потоварный налог, устанавливаемый правительством на отдельные товары и услуги по тем или иным причинам.

Отсюда новая функция предложения примет следующий вид:

Q(S) = 7(Р + 100) - 2100 = 7Р + 700 - 2100 = 7Р - 1400.

Ответ: Q(S) = 7P - 1400.

3.2. Допустим, функции спроса и предложения представлены уравнениями: Q(D) = 2 - 3P и Q(s) = 2P - 1, где P - это цена в рублях, а величины спроса Qd и предложения Qs - в килограммах. Найдите равновесную цену и равновесное количество.

Решение:

Для того чтобы определить равновеную цену и равновесное количество приравняем уравнения спроса и предложения:

2 - 3Р = 2Р - 1; ==> Pe = 0,6.

Равновесной цене соответствует и равновесное количество:

Qe = Qd = Qs; => 2 - 3 ∙ 0,6 = 2 ∙ 0,6 - 1 = 0,2; ==> Qe = 0,2.

Ответ: Pe = 0,6; Qe = 0,2.

3.3. На рынке некоторого товара присутстуют два покупателя. Рыночное предложение задано следующей функционнальной зависимостью: Qs = 10P - 83. Определите равновесную цену, если покупатели имеют две разные шкалы спроса:

Qd(1)

130

110

90

85

83

80

Qd(2)

100

85

77

75

70

60

P(р)

20

22

25

28

30

36

Решение:

Табличное представление функции спроса называют шкалой спроса. В нашей задаче шкала спроса представлена спросом двух индивидуальных покупателей. Рыночный спрос есть сумма индивидуальных спросов при каждой данной цене.

Рассчитаем рыночный спрос обоих покупателей и величину рыночного предложения при каждой данной цене. Заполним таблицу:

Р (руб)

20

22

25

28

30

36

Qd (1+2)

230

195

167

160

153

140

Qs

117

137

167

197

217

277

Ответ: Pe = 25 руб., т.к. Qd(1 + 2) = Qs = 167 единиц.

3.4. Известно, что товар Х приобретается двумя потребителями. При этом спрос обоих потребителей задается соответствующими функциями: Q(1) = 90 - P и Q(2) = 240 - 2P. Определите значение цены при величине равновесного спроса, равного 42.

Решение:

Равенство величин спроса и предложения говорит о достижении в данный момент равновесной цены и равновесного объёма. Поскольку рыночный спрос есть сумма индивидуальных спросов, то мы получим: Q(1) + Q(2) = (90 - Р) + (240 - 2Р) = 330 - 3Р. Приравняем функцию рыночного спроса с его равновесным значением: 330 - 3Р = 42. Тогда значение цены при величине равновесного объёма составит: Р = 96.

Ответ: 96.

3.5. Проанализируем следующую экономическую ситуацию. на рынке сельхозпродукции функция предложения фермера задана следующим уравнением: Q(S) = - 200 + 10P, спрос не превышает 850кг и падает на 75кг при увеличении цены на 3 руб. за 1кг, где Q(D), Q(S) - объём продукции в кг, P - цена в руб. за 1кг.

1. Выведим новое уравнение функции предложения, если будут установлены одновременно следующие налоги:

а) акцизный налог, равный 1руб., взимаемый с каждой проданной единицы продукции;

б) налог с продаж в размере 7% к цене проданной продукции.

2. Как изменится объём продаж, рыночная цена и выручка от реализации продукции после введения налогов?

Решение:

1. Выведим уравнение функции предложения после введения:

а) акцизного налога.

По условию задачи акцизный налог, равный 1 р., будет взиматься с каждой проданной единицы продукции. Тогда функция предложения Q(S) = - 200 + 10P после введения данного налога примет следующий вид: Q(S) = - 200 + 10 (P - 1).

б) налога с продаж.

Налог с продаж в России отменён, но в США, как правило, он составляет 7%. Рассмотрим механизм действия данного налога, опираясь на налоговую ставку, указанную в условии задачи. Из новой цены (а именно она и будет рыночной ценой при прочих равных условиях) у продавца остаётся 100 частей и, кроме того, 7 частей он должен будет заплатить государству в виде налога с продаж. Значит, вся рыночная цена, которую платит потребитель за товар, составит 107 частей от цены продавца.

Следовательно, при налоге с продаж, равном 7%, цена примет следующий вид: Р×(100 / 100+Т), где Т= 7%. Отсюда уравнение новой функции предложения после введения налога с продаж примет следующий вид: Q(S) = - 200 + 10P / 1,07.

Тогда функция предложения после введения обоих налогов (акцизного налога и налога с продаж) примет вид:

Q(S) = - 200 + 10 × (P / 1,07 - 1).

2. Рассмотрим, как повлияет налоговая политика на объём продаж, рыночную цену и выручку от продаж.

а) Найдем рыночную цену, объём продаж и выручку от продаж до введения налогов:

• Составим уравнение функции спроса: Q(D) = 850 - 75 / 3P или Q(D) = 850 - 25Р.

• Найдём равновесную цену: 850 - 25Р = - 200 + 10Р.

• Тогда равновесная цена (Р) будет равна 30 р за кг.

• Равновесный объём продаж Q(D) = Q(S) составит:

850 - 25 × 30 = - 200 + 10 × 30 = 100(кг).

• Отсюда выручка от продаж (TR) до введения налогов будет равна 3000 р (PQ = 30 × 100).

б) Найдем рыночную цену, объём продаж и выручку после введения налогов:

• Приравняем функцию предложения после введения обоих налогов (акцизного налога и налога с продаж) и функцию спроса:

-200 + 10(Р / 1,07 - 1) = 850 - 25Р. Тогда новая цена с учётом налогов будет Р = 30,86р;

• Величина нового предложения составит:

Q(S) = -200 + 10 × (30,86 : 1,07 - 1) = 78,4кг; а

величина нового спроса: Q(D) = 850 - 25 × 30,86 = 78,5кг.

Таким образом, мы видим, что на рынке образовался незначительный дефицит. При этом объём продаж после введения налогов составил 78,4кг. Выручка производителя при новой цене и новом объёме продаж будет составила TR = 2419, 42 р.

Ответ:

1. функция предложения после введения обоих налогов (акцизного налога и налога с продаж) станет следующим:

Q(S) = - 200 + 10 × (P / 1,07 - 1).

2. После введения косвенных налогов:

• цена на сельхозпродукцию фермера выросла с 30 до 30,86 р;

• предложение сократилось на 21,6кг (100 - 78,4);

• спрос упал на 21,5кг (100 -78,5);

• выручка производителя сократилась (TR = PQ = 30,86 × 78,4) и составила 2419,42 рубля против 3000 рублей.

Закрепите свои умения и навыки

3.6. Спрос на бананы индивидуального покупателя задан функцией: Q(D) = 9 - 3P, где Q(D) - количество килограммов бананов; P - цена 1кг бананов в рублях.

А) Определите, по какой цене, покупатель не сможет купить бананы.

Б) Какое количество бананов покупатель купит, но бесплатно?

Ответ:

А) при Р = 3 р. за 1кг.

Б) Q = 9кг.

3.7. Рыночный спрос на товар задан функцией:

Q(D) = 9 - 3P. Количество товара, которое выставлено на продажу, равно 6ед.

А) Определите, при какой цене покупатели полностью скупят весь товар?

Б) Что произойдёт, если цена на товар составит 2 р., при условии неизменности количества выставленного на продажу товара?

Ответ:

А) при Р = 1 р.

Б) на рынке появится излишек товара в 3 ед. (6 - (9 - 3 × 2)).

3.8. Даны три уравнения кривой предложения компъютеров на внутреннем рынке за год в тысячах штук при цене Р в рублях:

a) Q(S) = 5000; б) Q(S) = 5P - 10000; в) Q(S) = P - 7500.

Какая из этих функций описывает предложение в кратчайшем, кратковременном и долговременном периоде?

Ответ:

а) в кратчайшем периоде;

б) в долговременном периоде;

в) в кратковременном периоде.

3.9. Цена на товар выросла с 30 до 33 руб. Точечная эластичность спроса на него при цене 30 руб. равна (-2). Каков был первоначальный объём рыночного спроса, если после повышения цены он составил 1200 единиц.

Ответ: 1000.

3.10. Функция предложения задана уравнением: Q(S) = 5P - 2500.

А) Выведите формулу точечной эластичности этой функции предложения.

Б) При какой цене эластичность предложения по цене составит 2.

Ответ:

А) Es = 5P / 5P - 2500;

Б) При P = 1000 эластичность Es = 2.

3.11. Функция спроса на товар имеет следующий вид:

Q(D) = 50 - 2P. При каком значении цены точечная эластичность спроса по цене составит - 4?

Ответ: при Р = 20.

3.12. Функция спроса задана как: Q(D) = 360 - 8P, а функция предложения: Q(S) = 2P - 40. Государство установило на данном рынке некоторую фиксированную цену товара. В результате этого вмешательства, на рынке возник дефицит в размере: Q(D) - Q(S) = 240. Какую цену установило государство?

Варианты ответа:

1) 40. 2) 20. 3) 36. 4) Нет правильного ответа.

Ответ: 4) Нет правильного ответа.

Тема 4. ТЕОРИЯ ПРОИЗВОДСТВА:

ИЗДЕРЖКИ, ВЫРУЧКА И МАКСИМУМ ПРИБЫЛИ.

Основные понятия. Издержки производства: общие, средние, предельные. Кривые издержек производства в краткосрочном периоде. Характерные точки минимума средних переменных и средних общих издержек производства. Эффект масштаба производства. Закон убывающей предельной производительности переменного фактора производства. Доходы и прибыль. Бухгалтерская, экономичекая и нормальная прибыль. Маржинальный, или предельный, анализ прибыли.

Дополнительные понятия. Периоды производства. Масштаб производства. Общий, средний и предельный продукт переменного фактора производства. Затраты в долговременном периоде.

Основные умения. Различать и вычислять все виды издержек на условных примерах. Вычислять объём выпуска, при котором фирмой достигается производственный оптимум. Определять эффект масштаба. Вычислять бухгалтерскую, экономическую прибыль на условных примерах. Рассчитывать выручку.

Дополнительные умения. Применять на практике закон убывающей предельной производительности переменного фактора производства.

Теоретический материал

Функция издержек производства отражает зависимость между объемом произведенной продукции и минимально необходимыми затратами на данное производство.

Различают три периода производства: мгновенный, кратковременный и долговременный.

В мгновенном периоде все издержки производства считаются постоянными, т.е. не зависящими от объёма производства.

В кратковременном периоде хотя бы один из факторов производства является постоянным.

В долговременном периоде все факторы производства имеют переменный характер.

В кратковременном периоде общие или валовые издержки (TC) состоят из постоянных (FC) и переменных(VC).

TC(Q)= FC + VC,

где

FC - постоянные издержки, величина которых не зависит от объёма производства. К ним относятся:

• заработная плата повременных работников;

• банковский процент за кредит;

• плата за коммунальные услуги;

• арендные платежи;

• амортизационные отчисления.

VC - переменные издержки, величина которых растёт по мере увеличения объёма производства. К ним относят расходы на:

• сырьё,

• материалы,

• топливо,

• заработную плату сдельщиков.

Допустим, что функция общих издержек фирмы на выпуск Q единиц продукции представлена следующим образом:

TC = Q² + 16Q + 400.

Выведим уравнения функций всех видов издержек, используемых в экономической теории для описания поведения фирмы.

Отсюда, согласно теории:

• FC = 400 - это постоянные издержки, т.к. они не зависят от выпуска продукции (Q);

• VC = Q² + 16Q - переменные издержки - зависят от выпуска продукции (Q).

Для экономического анализа деятельности фирм, предприятий особый интерес представляют средние и предельные издержки.

Средние общие издержки (AC или ATC) - это общие расходы на единицу выпуска продукции:

AТC = TC / Q = (FC / Q + VC / Q),

где

• FC / Q = AFC есть средние постоянные издержки;

• VC / Q = AVC - средние переменные издержки.

Средние переменные издержки (AVC) - это переменные издержки на единицу выпуска продукции:

AVC = VC / Q = Q + 16.

Средние постоянные издержки (AFC) - это постоянные издержки на единицу выпуска продукции:

AFC = FC / Q = 400 / Q.

Применительно к анализируемой нами функции общих издержек, уравнение функции средних общих издержек примет вид:

AТC = (Q + 16) + 400 / Q.

Предельные (маржинальные) издержки (MC) - это прирост издержек на выпуск дополнительной единицы продукции:

MC = ∆TC / ∆Q или MC = dTC / dQ, т.е. производная общих издержек.

Тогда уравнение функции предельных издержек, анализируемой нами функции общих издержек, будет иметь следующий вид:

MC = 2Q + 16.

Характер изменения кратковременных издержек производства графически можно представить следующим образом:

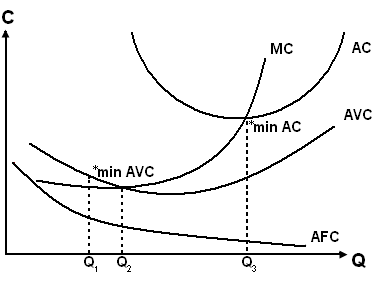
Рис. 4.1. Издержки производства в кратковременном периоде.

Проведем анализ данного графического изображения, опираясь на общеизвестные теоретические положения:

1 участок: от 0 до Q1 характеризует снижение всех видов издержек (предельных и средних);

2 участок: от Q1 до Q2 - снижение средних переменных, постоянных и общих средних издержек при повышении предельных.

3 участок: от Q2 до Q3 отражает повышение предельных и средних переменных издержек при соответствующем снижении средних общих издержек. При объёме выпуска продукции Q3 достигается минимум средних общих издержек, т.е. производственный оптимум (AТC = MC).

Производственный оптимум предполагает достижение такого объёма выпуска, при котором все производственные мощности, задействованы полностью, работники работают без прогулов и перенапряжения. Применительно к анализируемой нами функции общих издержек фирмы: TC = Q² + 16Q + 400 можно заключить, что оптимальный выпуск продукции достигнут при объеме выпуска продукции Q3 = 20 (AТC = MC или Q + 16 + 400 / Q = 2Q + 16). Следовательно, точка Q3 = 20 - точка производственного оптимума.

4 участок: от Q3 и выше - одновременное повышение всех видов издержек. Значит, дальнейшее увеличение выпуска продукции будет невыгодным.

На величину издержек производства в кратковременном периоде влияют следующие факторы:

• общий выпуск продукции;

• закон убывающей предельной производительности;

• эффект масштаба.

Проведем факторный анализ издержек производства на основе данных, приведеных в следующей таблице:

Из таблицы мы видим, что в определённый период времени:

1. труд L является единственным переменным фактором производства (при условии постоянства величины ставки заработной платы);

2. дневная ставка заработной платы одного рабочего фиксирована и равна 120 рублям;

3. другие факторы производства постоянные;

4. объем выпуска продукции зависит от количества привлекаемых в производство рабочих.

Рассуждения:

Для того чтобы проследить влияние переменного фактора производства L на объем выпуска продукции, введем понятия среднего и предельного продукта (рис. 4.2.). Так, средний продукт АPL (awerage product) - это количество продукта, приходящееся на единицу переменного фактора производства. Предельный продукт MPL (";"> АPL = Q / L и MPL = ∆Q / ∆L соответственно.

Поскольку труд является единственным переменным фактором производства, то общие издержки будут расти вместе с выпуском продукции. Рост переменных издержек приведет к изменению средних переменных и предельных издержек. Расчёт переменных издержек произведём по формуле:

VC = w × L.

Скорость увеличения издержек зависит от производительности труда. Теоретически между средними переменными издержками и средней производительностью труда (средним продуктом) существует прямая связь, т.к. средний продукт равен объему выпуска на единицу используемого фактора. Но так как в нашей ситуации ставка заработной платы фиксирована, то между средними переменными издержками (предельными издержками) и средним продуктом (предельным продуктом) соответственно существует обратная зависимость.

Заполним соответствующие графы следующей таблицы:

Количество

рабочих

в день

L, чел.

Объем

выпуска продук

ции

Q, шт.

Днев-ная

ставка зар-

платы

W, р.

Перемен-

ные

издержки,

VC = w ∙ L,

Р.

Средние общие издержки ATC =

AVC = VC / Q

Средний продукт труда,

АPL =

Q / L

Преде-

льные

издер-

жки,

MC =

∆VC/∆Q

Преде-льный

продукт,

MPL =

∆Q / ∆L

0

0

120

0

-

-

-

-

1

5

120

120

24

5

24

5

2

15

120

240

16

7,5

12

10

3

30

120

З60

12

10

8

15

4

50

120

480

9,6

12,5

6

20

5

75

120

600

8

15

4,8

25

6

95

120

720

7,58

15,83

6

20

7

110

120

840

7,64

15,71

8

15

8

110

120

960

8,73

13,75

0

На основе анализа данных таблицы можно заключить следующее:

• наем первых пяти работников привёл к повышению их предельной производительности труда (MPL1- 5 = 5; 10; 15; 20; 25) и к снижению величины предельных издержек (МС1-5 = 24; 12; 8; 6; 4,8);

• при найме шестого и последующих работников их предельная производительность труда падает (MPL6-8 = 20; 15; 0), а предельные издержки начинают расти (МС6-8 = 6; 8; и т.д.), т.е. с момента найма шестого работника производство каждой дополнительной единицы продукции обходится все дороже. Налицо действие эакона убывающей предельной производительности труда: с ростом использования какого-либо переменного фактора производства (при неизменности остальных), рано или поздно наступает такой момент, когда, дополнительное привлечение данного фактора даёт всё уменьшающийся предельный продукт (предельная производительность труда работников снижается) (рис. 4.2);

• оптимальный выпуск продукции Q = 95 достигается при числе работников L = 6 ( ATC(6) ≈ 7,58; МС(6) ≈ 6, а АPL(6) ≈ 15,83; MPL(6) ≈ 20).

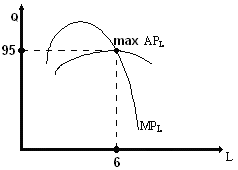
Рис. 4.2. Средний АPL и предельный продукт MPL переменного фактора производства. Закон убывающей предельной производительности труда.

Эффект масштаба производства - реакция объёма выпуска на изменение масштаба производства.

Масштаб производства определяется размером используемых ресурсов (см. рис. 4.3).

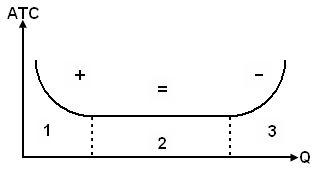
Рис. 4.3. Реакция объёма выпуска продукции на изменение масштаба производства.

1 участок - если с ростом выпуска продукции средние издержки снижаются, то говорят, что наблюдается положительный эффект масштаба (растущая отдача);

2 участок - если издержки не зависят от масштаба производства, то это нулевой эффект (постоянная отдача);

3 участок - если с ростом выпуска растут средние издержки, то это отрицательный эффект (убывающая отдача).

Определим эффект масштаба производства на основе анализа функции общих издержек производства: TC = Q² + 16Q + 400.

Вычислим значение выпуска Q, при котором средние общие издержки минимальны. Для этого необходимо найти первую производную общих средних издержек и приравнять её к нулю:

(ATC)' = (Q + 16 + 400 / Q)' = 1 - 400 / Q² = 0.

Отсюда получим, что при Q = 20 средние общие издержки будут минимальны. Значит, до объёма выпуска Q = 20 наблюдается положительный эффект масштаба производства, а начиная с Q = 20, имеет место отрицательный эффект масштаба.

Следовательно, если:

• (ATC)' < 0 - положительный эффект масштаба производства;

• (ATC)' > 0 - отрицательный эффект масштаба производства;

• (ATC)' = 0 - постоянный эффект масштаба производства.

Функционирование фирм в долговременном периоде теоретически предполагает ряд допущений:

1. все факторы производства и труд, и капитал и НТП, являются переменными;

2. цены на факторы производства неизменны;

3. средние постоянные издержки исчезают в силу большого объема выпуска продукции, а значит АFC = 0;

4. средние переменные издержки равны средним общим AVC= AТC (в долговременном периоде используется только понятие кратковременные средние издержки - SRAC);

5. между предприятиями, к примеру П_1-4, входящими в состав фирмы, возможен перелив капитала;

6. А, В, С, D - точки минимума кратковременых средних издержек, т.е. точки оптимального выпуска продукции;

7. LRAC - долговременные средние издержки;

8. принцип минимизации издержек определяется по предельному продукту труда в расчете на единицу стоимости данного фактора.

Графическое изображение долговременных средних затрат (см. рис. 4.4.)

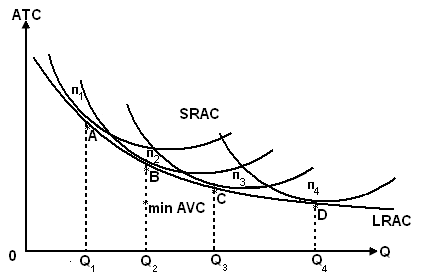
Рис. 4.4. Долговременные средние затраты.

• на участке [OD] прослеживается растущая отдача или положительный эффект масштаба производства;

• выше этого участка идет повышение долговременных средних издержек;

Прибыль (PR) - это разница между доходами фирмы от продажи продукции (TR) и ее издержками:

PR = TR - TC,

где

TR - общий доход или выручка от реализации продукции;

TC - общие издержки.

Доходы бывают:

1. Общий доход: TR = P × Q или выручка от продаж;

2. Средний доход: AR = TR / Q или доход, приходящийся на единицу продукции (равен цене данной единицы продукции);

3. Предельный доход: MR = ∆TR / ∆Q или приращение дохода, которое возникает за счёт бесконечно малого увеличения выпуска продукции.

Разберём хрестоматийную задачу: Преподаватель экономики маленького провинциального городка, получавший в конце года после всех вычетов (в том числе и подоходного налога) 18 тыс. р. в год, в новом году решил открыть собственный магазин. Его стартовый капитал составляет 25 тыс. р. Он рассчитывает получить выручку, равную 170 тыс. р. Для реализации этого проекта ему нужно в начале года:

• оплатить арендную плату в размере 40 тыс. р. за помещение магазина за год вперёд;

• выполнить ремонтные работы в арендуемом помещении стоимостью 20 тыс. р.;

• нанять трёх работников с оплатой по 15 тыс. р. в год каждому, причём 5 тыс. р. выплатить в начале года в качестве аванса, а 10 тыс. р. заплатить в конце года из выручки;

• занять в банке недостающую для покрытия расходов сумму денег сроком на год;

• оставить труд преподавателя и сосредоточиться на предпринимательской деятельности.

Иных затрат у него нет. Банковский процент по депозитам (вкладам) равен 40%, а по кредитам - 50%.

Определим величину бухгалтерской и экономической прибыли за год без учета налога на прибыль.

1. Рассчитаем бухгалтерскую прибыль.

Бухгалтерская прибыль - определяется как разница между общим доходом (TR) и явными (внешними) издержками фирмы:

PR_б. = TR - ТC_я,

где

• PR_б - прибыль бухгалтерская;

• TR - общая выручка;

• ТC_я - внешние (явные) издержки.

Внешние (явные) издержки или бухгалтерские издержки - реально произведённые платежи внешним поставщикам (издержки на сырьё, материалы, зарплата рабочим и т.д.) или условно начисленные расходы (проценты на заёмные средства, амортизация).

А) Из условия задачи следует, что величина первоначальных средств, необходимых бывшему преподавателю для начала предпринимательской деятельности, составит 75 тыс. р.:

• оплата аренды - 40 тыс. р.

• ремонтные работы - 20 тыс. р.

• аванс трём работникам - 15 тыс. р.

Б) Из них он располагает стартовым капиталом - 25 тыс. р. Следовательно, недостающая для покрытия расходов сумма денег, которую он возьмёт в банке сроком на один год, составит 50 тыс. р. (75 - 25).

В) В конце года состаявшийся предприниматель должен вернуть банку 75 тыс. р. Данная сумма включает:

• 50 тыс. р. - это величина банковского кредита;

• 25 тыс. р. - это проценты за пользование кредитом.

Г) Внешние (явные) издержки предпринимателя составят:

• 50 тыс. р. - банковский кредит;

• 25 тыс. р. - проценты за банковский кредит;

• 25 тыс. р. - стартовый капитал, который он должен возместить;

• 30 тыс. р. - зарплата рабочим, которую он должен выплатить в конце года.

Следовательно: TCя = 50 + 25 + 25 + 30 = 130 тыс. руб.

Д) Тогда величина бухгалтерской прибыли составит:

PRб = 170 - 130 = 40 тыс. р.

Таким образом , бухгалтерская прибыль включает:

• экономическую прибыль;

• нормальную прибыль;

• внутренние (неявные) издержки;

• издержки на ресурсы, принадлежащие предпринимателю.

2. Рассчитаем экономическую прибыль.

Экономическая прибыль - доход, который можно было бы получить при наиболее выгодном из альтернативных вариантов вложения собственных средств и использования своего рабочего времени.

Существует два способа расчёта экономической прибыли:

PRэ = TR - ТСэ.

• PRэ - экономическая прибыль;

• TR - общая выручка;

• ТCэ (экономические издержки) = ТCя + ТCн ;

• ТСя - внешние (явные) издержки.

• ТCн - внутренние (неявные) издержки.

Экономические издержки включают в себя внутренние (неявные) и внешние (явные) издержки предпринимателя.

Внутренние (неявные) издержки - издержки внутренних ресурсов, принадлежащих предпринимателю и не включенных в бухгалтерский баланс. К ним относят:

• издержки собственных материалов предпринимателя;

• издержки его капитальных ресурсов;

• издержки труда собственников бизнеса, измеряемые возможной заработной платой или прибылью (нормальной прибылью);

• издержки принадлежащих ему финансовых ресурсов.

Из условия нашей задачи следует, что учитель экономики, приняв решение открыть своё дело, лишается:

• заработной платы преподавателя, которую он потерял, занявшись предпринимательской деятельностью, 18 тыс. рублей;

• дохода, который он смог бы заработать, если бы положил бы свой собственный капитал (25 тыс. р) в банк на депозитный счёт под 40% (25 × 0,4) - 10 тыс. р.

Данные 28 тыс. р. (18 + 10) - это внутренние (неявные) издержки нашего предпринимателя.

Если к величине внутренних издержек мы прибавим внешние издержки, то мы получим экономические издержки - 158 тыс. рублей (130 + 28). Тогда экономическая прибыль составит:

PRэ = 170 - 158 = 12 тыс. р.

3. Экономическую прибыль можно исчислить и другим способом:

PRэ = PRб - ТСн.

Из величины бухгалтерской прибыли, составляющей 40 тыс. р., вычтем неявные (внутренние) издержки 28 тыс. р,(т.е. величину того дохода, который потерял учитель, занявшись предпринимательской деятельностью). Тогда величина экономической прибыли составит:

PRэ = 40 - 28 = 12 тыс. р.

Выводы:

• предприниматель заработает экономическую прибыль только в том случае, если он, выбрав данный вариант вложения средств, использует их более эффективно, чем при любом другом варианте их вложения;

• если PR_э = 0, то это означает, что предприниматель получает только нормальную прибыль, которая позволяет удержаться ему в данном бизнесе.

Условие максимизации прибыли.

Маржинальный, или предельный, анализ предполагает принятие решения о том, стоит ли производить дополнительную единицу продукции. При наилучшем соотношении выгод и издержек предельный доход должен быть равен предельным издержкам. Следовательно, максимум прибыли достигается при условии:

MR = MC.

Характеристики условия максимизации прибыли:

• До тех пор пока с ростом объёма выпуска выполняется неравенство MR > MC, для увеличения массы прибыли следует наращивать производство. При условии равенства MR = MC можно выбирать любое количество выпуска продукции, которое обеспечивает данное равенство. В данном конкретном случае будет достигаться локальный максимум.

• Данное равенство MR=MC задаёт необходимое, но недостаточное условие максимума прибыли, т.е. оно позволяет найти локальный максимум, но не гарантирует, что данный объём продукции задает глобальный максимум.

• При данном условии MR = MC максимизируется масса прибыли, а не её норма.

Учимся решать экономические задачи

Типы задач:

• Задачи на выведение формул всех видов издержек, используемых в экономической теории;

• Задачи на взаимосвязь общих, средних, предельных издержек;

• Задачи на расчёт выручки от продаж;

• Задачи на расчёт амортизационных отчислений.

• Задачи на определение эффекта масштаба производства.

4.1. Допустим, общие издержки фирмы на выпуск Q единиц продукции составляют: TC = 2Q² + 10Q + 162.

А) Выведите функции всех видов издержек, используемых в экономической теории для описания поведения фирмы;

Б) При каких значениях Q средние общие издержки достигают своего минимума?

Решение:

А)

• FC = 162, постоянные издержки;

• VC = 2Q² + 10Q, переменные издержки;

• AFC = FC / Q = 162 / Q, средние постоянные издержки;

• AVC = VC / Q = 2Q + 10, средние переменные издержи;

• ATC = TC / Q = (FC / Q + VC / Q) = (2Q + 10) + 162 / Q, средние общие издержки;

• MC = dTC / dQ = 4Q + 10, предельные издержки.

Б) Минимум средних общих издержек приходится на пересечение графиков AТC с MC, следовательно, мы приравняем эти функции:

2Q + 10 + 162 / Q = 4Q + 10;

2Q² + 10Q + 162 = 4Q² + 10Q;

- 2Q² = - 162;

Q = 9.

Min ATC достигается при выпуске (Q) = 9; при данном объёме производства достигнут производственный оптимум.

4.2. Функция общих издержек имеет вид:

TC = 36 + 12Q + Q². Определить, чему равны средние постоянные издержки при объёме производства, равном 10.

Решение:

AFC = FC / Q где FC = 36, т.к. постоянные издержки не зависят от объёма производимой продукции.

Следовательно: AFC = 36/10 = 3,6.

Ответ: 3,6.

4.3. Определите максимальную выручку, если спрос вплоть до пересечения с осями описывается линейной функцией: Q(D) = b - aР, где Р - цена товара, выпускаемого предпринимателем; b и a - коэффициенты функции спроса.

Решение:

Первый вариант:

а) Согласно экономической теории, предприниматель достигает максимума выручки (дохода) при продаже товара:

• по цене, равной половине запретительной цены (А/2);

• при объёме продаж, равном половине массы насыщения (В/2) (см. рис. 4.5).

Формула максимальной выручки имеет следующий вид:

TR max = A/2 × B/2.

б) Найдём значения запретительной цены и массы насыщения:

• при Q(D) = 0 значение цены P = А = b/a (величина запретительной цены);

• при P = 0 значение Q(D) = В = b (величина массы насыщения).

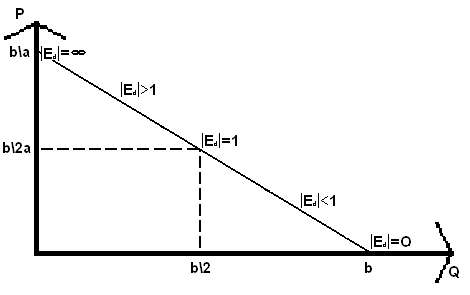
Рис. 4.5. График линейной функции спроса Q(D) = b - a Р.

в) Тогда:

• A/2 = (b/a):2 = b/2a;

• B/2 = b/2;

г) Отсюда значение максимума выручки составит:

TR = b/2a × b/2 = b²/4a.

Второй вариант:

По условию задачи величина спроса составляет: Q(D) = b - aP. Определим цену, при которой предприниматель получает максимальную выручку: TR = P × Q = P × (b - aP).

а) Для этого производную по цене функции выручки приравняем к нулю: (P × (b - aP))' = 0. Мы получим цену: P = b / 2a.

б) Определим объём производства, при котором предприниматель получит максимум выручки. Подставим значение цены в функцию спроса: Q(D) = b - a × b / 2a = b / 2; ==> Q(D) = b / 2.

в) Следовательно, максимальная выручка предпринимателя составит: TRmax = Q × P = b / 2 × b / 2a = b² / 4a.

Ответ: b²/4a.

4.4. Объём выпуска фирмы в условиях совершенной конкуренции -1000 ед. продукции, цена продукции - 80 у.е., общие средние издержки (АТС) при выпуске 1000 ед. товара - 30. Определите величину бухгалтерской прибыли.

Решение:

а) бухгалтерскую прибыль рассчитаем по формуле: PR = TR - TC. Тогда выручка фирмы составит TR = 80 × 1000 = 80 000.

б) Используя формулу средних общих издержек:

• вычислим величину общих издержек по формуле: AC = TC / Q и

• выразим общие издержки: 30 = ТС / 1000; ТС = 30 000.

в) Тогда прибыль PR = 80 000 - 30 000 = 50 000

Ответ: 50 000.

4.5. Грузовик стоимостью 100 тыс. руб. пройдёт до списания 250 тыс. км. Чему равна величина амортизационных отчислений?

Решение:

Амортизация - это уменьшение бухгалтерской стоимости капитальных ресурсов и постепенное перенесение их стоимости на стоимость произведенного продукта по мере износа.

Существуют различные способы начисления амортизации:

• прямолинейный способ,

• ускоренный способ,

• способ единицы услуг.

Воспользуемся способом единицы услуг т.к. физический нормативный износ связан с оказанием услуг. Следовательно, амортизационные отчисления на 1км составят 0,4 р. независимо от срока службы.

Ответ: 0,4 р. на 1км.

4.6. Даны функции спроса Q(D) = 220 - 4Р и предельных издержек MC = 10 + 4Q. Максимальная прибыль составляет 125 денежных единиц. Определите величину постоянных издержек.

Решение:

Чтобы определить величину постоянных издержек, выведим уравнение функции общих издержек: TC = FC + VC. Для этого найдем первообразную функции предельных издержек MC = 10 + 4Q. Уравнение функции общих издержек примет вид: TC = 10Q + 2Q² + FС.

1. Определим объем производства, максимизирующий прибыль, применив правило максимизации прибыли MC = MR.

2. Выведим уравнение функции предельного дохода. Если применить формулу предельного дохода: MR = (TR)' = (Р × Q)', то мы получим,что MR = ((55 - 0,25Q) × Q)' (где Р = 55 - 0,25Q является обратной функцией для функции спроса Q(D) = 220 - 4Р). Отсюда уравнение функции предельного дохода будет следующим: MR = 55 - 0,5Q. Следовательно, объем производства Qopt, максимизирующий прибыль, составит 10единиц.

3. Вычислим значение общей выручки TR(Qopt 10) = 55Q - 0,25Q² = 525.

4. Найдем значение общих издержек, используя формулу прибыли:

PR = TR - TC,

где

PR =125, а TR = 525. Величина общих издержек TC составит 400.

Приравняем уравнение функции общих издержек с величиной общих издержек: 400 = 10Q + 2Q² + FC, где Qopt= 10.

Следовательно, FC= 100.

Ответ: FC = 100.

Закрепите свои умения и навыки

4.7. Допустим, предельные издержки на выпуск Q единиц продукции выглядят следующим образом:

МС(Q) = 2Q - 18; FC = 100.

А) Выведите функции всех видов издержек;

Б) Найдите выпуск, при котором достигается производственный оптимум.

Ответ:

А) TC = Q²- 18Q + 100;

FC = 100;

VC = Q² - 18Q;

ATC = Q - 18 + 100 / Q;

AFC = 100 / Q;

AVC = Q - 18.

Б) при Q = 10.

4.8. Даны функции предельных издержек: МС(Q) = 2Q - 18 и величина постоянных издержек FC = 100. Определите эффект масштаба производства.

Ответ: Q = 10 (средние общие издержки будут минимальны). До объёма выпуска Q = 10 наблюдается положительный эффект масштаба производства, а начиная с Q = 10, имеет место отрицательный эффект масштаба.

4.9. Вычислить остаточную стоимость оборудования, купленного 4,5 года назад за 20 млн. р., при норме амортизации, равной 20%, и нулевой ликвидационной стоимости.

Ответ: 2 млн.р.

4.10.Дана функция общих издержек: TC= Q²- 18Q + 100.

Сравните выпуск, обеспечивающий минимум средних общих издержек, с оптимальным выпуском при Р = 30. На сколько изменится прибыль?

Ответ: При выпуске продукции Q = 10, обеспечивающем минимум средних общих издержек, недополучено прибыли 196 денежных единиц:

• PR(Q=10) = TR - TC = 30 × 10 - (10²- 18 × 10 + 100) = 280;

• MC = P; => Qopt (2Q - 18 = 30) = 24

• Отсюда следует, что PR(Q=24) = TR - TC = 30 × 24 - (24² - 18 × 24 + 100) = 476.

4.11. Определите характер эффекта масштаба производства при МС(Q) = 23,5 + Q.

Ответ: эффект масштаба отрицательный.

4.12. Определите характер эффекта масштаба производства, если

TC = 20Q - Q².

Ответ: эффект масштаба положительный.

Тема 5.КОНКУРЕНЦИЯ И МОНОПОЛИЯ.

Основные понятия. Конкуренция. Совершенные и несовершенные конкуренты. Рыночная власть. Рынок совершенной конкуренции. Прибыль (экономическая прибыль, сверхприбыль) конкурентной фирмы и ее максимизация в краткосрочном периоде. Нулевая экономическая прибыль конкурентной фирмы в долгосрочном периоде. Поведение конкурентной фирмы в краткосрочном и долгосрочном периоде. Монополия. Максимизация прибыли монополиста. Максимизация выручки монополиста. Соотношение предельной выручки и цены на рынке несовершенной конкуренции. Монопольное производство на разных предприятиях. Ценовая война. Ценовая дискриминация.

Дополнительные понятия. Масса и норма прибыли. Предложение конкурентной фирмы. Монополистическая конкуренция и олигополия. Монопсония.

Основные умения. Определять тип рыночной структуры. Определять объём продаж и цену, максимизирующую прибыль фирмы на рынках совершенной и несовершенной конкуренции в краткосрочном и долгосрочном периоде; анализировать поведение данных фирм. Вычислять оптимум монополии в услових ценовой дискриминации и производства на разных предприятиях.

Дополнительные умения. Вычислять при известном рыночном спросе точку равновесия и число фирм. Доказывать основные соотношения и выводить основные формулы на рынках несвершенной конкуренции.

Теоретический материал

Конкуренция - это экономическая борьба, соперничество за рынок сбыта, за сферу вложения капитала.

Методы конкуренции бывают: ценовые и неценовые.

Рыночная власть - это способность продавца или покупателя влиять на цену продукции и объём продаж.

Коэффициент Лернера (L), отражающий рыночную власть:

(P - MC) / P = |1 / Ed|.

Различают два вида конкуренции: совершенную и несовершенную.

Рассмотрим рынок совершенной конкуренции на конкретном примере. Цена единицы продукции задана и равна 4 д.е. Данные об объёме выпуска продукции фирмы и издержках производства приведены в таблице:

Количество единиц продукции Q, шт.

Общие

издержки TC

Постоянные издержки FC

Переменные

издержки VC

0

150

0

5

20

15

40

30

60

50

80

75

100

95

120

110

140

120

160

125

180

125

200

1. Рассчитаем значения всех видов издержек производства фирмы, используемых в экономической теории для описания ее поведения.

2. Начертим график, отражающий поведение фирмы на рынке совершенной конкуренции.

3. На основе рассчетов и графика, обоснуем:

а) характерные черты фирмы на рынке совершенной конкуренции,

б) стратегию фирмы на данном рынке.

Решение:

1. Рассчетные значения всех видов издержек, используемых в экономической теории для описания поведения фирмы, сведем в следующую таблицу:

Q

TR

FC

VC

TC

AFC

AVC

ATC

AR

MC

MR

PR

0

-

150

0

150

-

-

-

-

-

-

- 150

5

20

20

170

30

4

34

4

4

4

- 150

15

60

40

190

10

2,66

12,66

4

2

4

- 130

30

120

60

210

5

2,0

7,0

4

1,33

4

- 90

50

200

80

230

3

1,6

4,6

4

1

4

- 30

75

300

100

250

2

1,33

3,33

4

0,8

4

50

95

380

120

270

1,58

1,26

2,84

4

1

4

110

110

440

140

290

1,36

1,27

2,64

4

1,33

4

150

120

480

160

310

1,25

1,33

2,58

4

2

4

170

125

500

180

330

1,20

1,44

2,64

4

4

4

170

125

500

200

350

1,20

1,6

2,8

4

-

-

1502. На основе данных рассчетов начертим график, отражающий поведение фирмы на рынке совершенной конкуренции (рис.5.1).

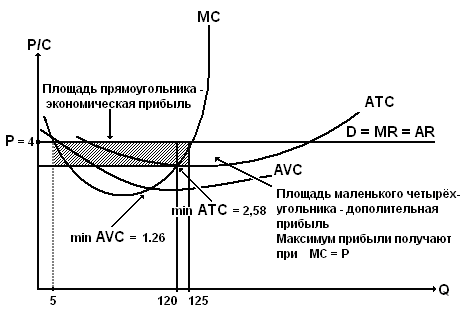
Рис. 5.1. Фирма на рынке совершенной конкуренции.

3. а) Характерные черты фирмы на рынке совершенной конкуренции.

• Период производства кратковременный, поскольку именно он характеризуется невозможностью изменения постоянных издержек (величина FC = 150 д.е. неизменна при любом объме выпуска продукции).

• Фирма - ценополучатель (цена единицы продукции задана и равна 4 д.е.)

• Коэффициент Лернера ((P - MC) / P = |1 / Ed|) равен нулю, данная рыночная структура не имеет рыночной власти.

• Предельный и средний доходы при любом объеме производства величины постоянные и равны цене:

P = 4 = MR = AR.

• Согласно закону спроса: чем выше цена, тем ниже спрос или наоборот. Однако спрос на данном рынке является совершенно (абсолютно) эластичным. D = MR = AR. Поэтому линия спроса на продукцию фирмы данного рыночного пространства горизонтальна и совпадает с линией предельного и среднего дохода.

б) Стратегия фирмы на рынке совершенной конкуренции.

Для определения объёма производства, максимизирующего прибыль, воспользуемся правилом максимизации прибыли:

MC = MR = Р.

Правило максимизации прибыли выдерживается при объёме выпуска продукции: Q = 5 и Q = 125 единиц. При Q = 5 фирма несёт убытки равные 150 д.е., а при Q = 125 ед. прибыль фирмы максимальная (PR = 170 д.е.). Следовательно, оптимальным объёмом производства будет Q = 125 единиц. При данном выпуске продукции MC = P = 4 = MR = AR.

• Условие максимума прибыли для фирмы рынка совершенной конкуренции будет выглядеть следующим образом:

MC = P = MR = AR.

Несмотря на то, что в интервале от Q= 5 ед. продукции до Q = 75 ед. фирма несёт убытки, ей не стоит уходить с рынка. В случае ухода с рынка убытки фирмы будут равны расходам, связанным с приобретением постоянных факторов производства (FC = 150 д.е.) Если фирма останется в отрасли, то убытки будут меньше на величину постоянных издержек: (FC + VC - PQ) < FC (при этом AVC < P, а VC < PQ). Отсюда стратегия конкурентой фирмы в кратковременном периоде должна состоять в следующем:

• фирма продолжает производство, если min AVC ≤ P < min ATC. В экономической теории такая ситуация называется минимизирующей убытки фирмы.

• AVC ≥ P, то фирме стоит уйти с рынка, т.к. каждая выпускаемая единица продукции приносит дополнительные убытки.

• При увеличении производства продукции с 75 единиц фирма получает экономическую прибыль т.к. AТC < P.

Общетеоретические выводы:

• Линия предложения в кратковременном периоде совпадает с линией предельных издержек на отрезке: minAVC ≤ P < minATC.

• Линия предложения в долговременном периоде совпадает с линией предельных издержек, начиная с выпуска продукции, при котором цена P ≥ min AТC. Экономическая прибыль фирмы в долговременном периоде равна нулю, если выдерживается условие:

MR = AR = MC = AC = P.

Причиной этого является тот факт, что в данном периоде возможен перелив капитала из менее прибыльных отраслей в более прибыльные. Перелив капитала способствует увеличению предложения продукции отрасли и соответственно снижению равновесной цены при неизменном рыночном спросе. Тогда новая цена будет равна величине средних общих и предельных издержек традиционной фирмы: P = AC = MC.

Чистая монополия - единственный производитель уникального продукта (рис. 5.2).

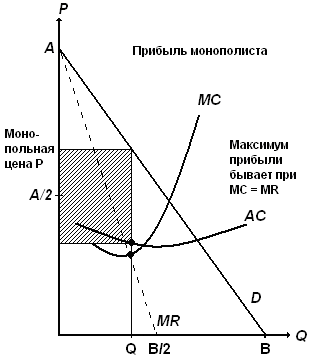
5.2. Чистая монополия.

Характерные черты чистой монополии:

• Монополист обладает рыночной властью. Коэффициент Лернера ((P - MC) / P = |1 / Ed|) больше нуля.

• Производство продукции фирмы - монополиста ограничено рыночным спросом (D = AR).

• Цена на продукцию фирмы - монополиста выше, чем половина запретительной цены (А/2).

• Объем производства продукции ниже, чем половина массы насыщения (В/2).

• Правило максимизации прибыли предполагает равенство MC и MR. Монопольная прибыль определяется разницей между TR и TC.

Рассмотрим поведение фирмы - монополиста на следующем примере. Даны функция издержек производства фирмы - монополиста и функции спроса на продукцию этой монополии на двух рынках:

TC = ¼ Q² + 10Q + 300;

Q(1) = 400 - 2P(1);

Q(2) = 600 - 4P(2).

А) Найдём объёмы продаж и цены на каждом из двух рынков, максимизирующие прибыль, при условии, что ценовая дискриминация незапрещена государством?

Б) Определим прибыль монополиста при ценовой дискриминации.

В) Как изменятся объём продаж, цены и прибыль, если ценовая дискриминация запрещена государством?

Рассуждения:

Из курса экономической теории мы знаем, что монополист, может производить любой объем продук­ции и продавать ее по цене, какой захочет. Главная цель монополиста - получить максимум прибыли при имеющихся возможностях.

Ценовая дискриминация - это продажа товара разным покупателям по разным ценам. Согласно закону спросу: чем выше цена, тем меньше реализуемый объем производства, или наоборот. Между тем от монополиста не зависит существующий на рынке спрос и уровень его издержек в данный момент времени.

Попробуем найти тот объем производства и соот­ветственно уровень цен на каждом из двух рынков, максимизирующие прибыль монополи­ста при условии, что ценовая дискриминация незапрещена государством.

Решение:

А) Воспользуемся правилом максимизации прибыли монополиста при ценовой дискриминации:

MC = MR(1) =MR(2),

где 1, 2 - число разных групп покупателей, приобретающих монопольный товар по разным ценам.

Данное правило основано на принципе выравнивания предельных доходов, получаемых на каждом из двух рынков. Поскольку достигнутый при этом уровень доходов может быть выше или ниже предельных издержек, то для получения наибольшей массы прибыли необходимо или сокращать объём выпуска, или наращивать.

Первая производная общих издержек есть предельные издержки:

(TC)' = MC = ½Q + 10.

Поскольку монополист функционирует на двух рынках, то функция предельных издержек примет следующий вид:

MC = ½ (Q(1) + Q(2)) + 10.

Выведим функции предельного дохода (MR(1) и MR(2)) монополиста на двух рынках. Функция предельного дохода есть первая производная общего дохода: MR =(TR)' = (P × Q)'.

Поскольку спрос на первом рынке составляет Q(1) = 400 - 2P(1), а спрос на втором рынке равен Q(2) = 600 - 4P(2), то обратные функции спроса, отражающие зависимость цены спроса от величины спроса соответственно примут соответствующий вид:

P(1) = 200 - ½ Q(1) и

P(2) = 150 - ¼ Q(2).

Отсюда функции предельного дохода на двух рынках составят:

MR(1) =(TR)' =((200 - ½ Q) × Q)' = (200Q - ½ Q²)' = 200 - Q(1);

MR(2) =(TR)' =((150 - ¼ Q) × Q)' = (150Q - ¼ Q²)' = 150 - ½Q(2).

Составим и решим систему уравнений:

Решим выражение(2) и подставим в первое (1). Получим:

Q(2) = 2 Q(1) - 100.

Подставляем Q(2) в первое выражение и находим Q(1):

½ (Q(1) + 2Q(1) - 100) + 10 = 200 - Q(1).

Следовательно, объем производства на каждом из двух рынков, максимизирующие прибыль монополи­ста составят:

• Q(1) = 96 штук;

• Q(2) = 92 штук.

Вычислим уровень цен на каждом из двух рынков, максимизирующий прибыль монополи­ста:

• P(1) = 200 - ½ × 96 = 152 д.е.

• P(2) = 150 - ¼ × 92 = 127 д.е.

Б) Подсчитаем прибыль монополиста при ценовой дискриминации по формуле: PR = TR - TC.

• TR = (Q(1) × P(1) + Q(2) × P(2)) = (96 × 152 + 92 × 127) = 26 276 д.е.

• TC = ¼ (Q(1) + Q(2))² + 10(Q(1) + Q(2)) + 300 = (¼ × 188² + 10 × 188 + 300) = 11 016 д.е.

• PR = 15 260 д.е.

В) Как изменятся объём продаж, цены и прибыль, если ценовая дискриминация запрещена государством?

Во всех экономически развитых странах существует антимонополь­ное законодательство. Данные законы объявляют незаконными действия лиц, которые осуществляют дискриминацию в ценах между различными покупателями товаров одного и того же сорта, качества, когда результатами такой дискриминации является существенное ограничение конкуренции. Данный закон не налагает уголовной ответственности (т.е. является актом гражданского кодекса).

Если ценовая дискриминация будет запрещена государством, то товар на обоих рынках будет продаваться по одной и той же цене. Отсюда общий рыночный спрос составит:

Q(D) = (400 - 2P(1)) + (600 - 4P(2))= 1 000 - 6P.

Тогда обратная функция спроса примет следующий вид:

P = 167 - 1/6Q.

Определим объём производства, максимизирующий прибыль. Найдём Q, исходя из условия максимизации прибыли MC = MR.

MC = ½Q + 10; а

MR = (TR)' = (( 167 - 1/6 Q) × Q)' = (167 Q - 1/6 Q²)' = 167 - 1/3 Q.

Приравняем значения MC и MR:

0,5Q + 10 = 167 - 1/3Q.

Следовательно, Q ≈ 188 шт., а Р ≈ 167 - 1/6 × 188 ≈ 136 д.е.

Найдем максимальное значение прибыли: PR = TR - TC.

PR = 188 × 136 - (¼ × 188² + 10 × 188 + 300) = 14 552 д.е.

Прирост прибыли монополиста при ценовой дискриминации составил: 708 д.е. (15260 - 14552).

Модели антимонопольного регулирования.

Основу американской модели представляют три нормативно-правовых акта США:

1. Закон Шермана ("Закон, направленный на защиту торговли и промышленности от незаконных ограничений и монополий" 1890г.) признает незаконным всякий договор, либо сговор, направленный на ограничение развития промышленности или свободы торговли. Лицо, признанное виновным в соответствующем нарушении подвергается штрафу или тюремному заключению.

2. Закон "О Федеральной торговой комиссии" (1914г.) позволяет фирмам, ведущим хозяйственную деятельность на рынках США, приобретать не менее 15% голосующих акций предприятий США при соблюдении следующих ограничительных условий:

• обязательна межштатная торговля;

• один из участников сделки должен иметь активы или объемы продаж на $ 100 млн. или более, а второй участник  не менее чем $ 10 млн.;

• предметом сделки должен быть пакет акции с правом голоса в размере не менее 15%, либо цена сделки должна быть не менее 15 млн. долларов;

• Федеральная торговая комиссия США должна быть уведомлена о совершении сделок по пакетам акций с правом голоса от 5% до 15%.

3. Закон Клейтона объявляет незаконными действия лица, которое осуществляет дискриминацию в ценах между различными покупателями товаров одного и того же сорта, качества, когда результатами такой дискриминации явится существенное ограничение конкуренции или же тенденция к образованию монополий в любой сфере деятельности. Данный закон является актом гражданского кодекса.

Европейская модель, в отличие от американской модели, предполагает контроль за монополиями в целях недопущения ими злоупотреблений своим господствующим положением на рынке. Такой подход требует создания специальной системы административных органов, призванных регистрировать определенные виды соглашений о создании монополий или существенном ограничении конкуренции. В случае необходимости эти органы используют корректирующие, регулирующие и запретительные меры преимущественно административного характера.

Вывод:

• американская модель построена на принципе запрещения монополии как структурной единицы независимо от социально-экономических последствий ее деятельности;

• европейская модель построена на принципе регулирования монополистической практики путем устранения его отрицательных социально-экономических последствий.

Российская антимонопольная практика больше всего тяготеет к европейской модели. Основу антимонопольного законодательства России составляют: Конституция РФ, Закон РСФСР "О конкуренции и ограничении монополистической деятельности на товарных рынках" 1991г. (значительно переработан в 1995г.), а также изданные в соответствии с ними федеральные законы, указы Президента, постановления и распоряжения правительства.

Специфика антимонопольной политики России состоит в том, чтобы:

• использовать выгоды крупномасштабной экономики;

• нейтрализовать возможные негативные последствия, связанные с ослаблением конкуренции.

• сохранить некоторые виды монополий, обеспечивая их государственное регулирование (в частности, денежно-эмиссионную деятельность; экспорт, импорт отдельных товаров; производство и сбыт алкогольной продукции и др.)

• контролировать деятельность естественных монополий, используя следующие методы:

  1. ценовое регулирование, осуществляемое посредством определения цен (тарифов) или их предельного уровня;

  2. определение потребителей, подлежащих обязательному обслуживанию;

  3. установление минимального уровня обеспечения потребности товаром, в случае, если невозможно удовлетворенить данную потребность в полном объеме.

Учимся решать экономические задачи

Типы задач:

• Задачи на определие типа рыночной структуры: совершенная или несовершенная конкуренция;

• Задачи на нахождение объёма производства, максимизирующего прибыль в условиях совершенной или несовершенной конкуренции;

• Задачи на анализ ситуации с ценовой дискриминацией;

• Задачи на определение эластичности рыночного спроса в точке максимальной прибыли монополиста.

• Задачи на определение объёма производства монополиста на нескольких предприятиях с разными издержками;

5.1. Продаваемая продукция приносит выручку производителям в размере:

А) TR = 9Q;

Б) MR = 3;

В) TR = 8Q - ¼ Q²;

Г) MR = 7 - 0,5Q.

Определим тип рыночной структуры.

Решение:

Из всего многообразия признаков, отличающих один тип рыночной структуры от другого, воспользуемся главным признаком - ценовым. По ценовому признаку мы можем судить, в какой мере продавец обладает рыночной властью. В частности, в условиях совершенной конкуренции цена не зависит от объёма продаж, а при несовершенной конкуренции - зависит.

В микроэкономике, если прямая функция спроса описывает зависимость величины спроса от цены (Q(D) = b - aP), то обратная функция цены спроса от величины спроса будет выглядеть следующим образом: (P=b / а - Q / a).

Применительно к условию нашей задачи мы имеем следующее:

А) TR = 9×Q; => P×Q = 9×Q; а P=9.

Б) MR = 3; тогда TR = 3×Q или P×Q = 3Q; => P=3.

В) TR = 8Q - ¼Q²; тогда P×Q = 8Q - ¼Q²; => P = 8 - ¼Q.

Г) MR = 7 - ½Q; тогда TR = 7Q - ¼Q² или P×Q = 7Q - ¼Q²; =>

P = 7- ¼Q.

Ответ: А); Б) - случай совершенной конкуренции, т.к. цена не зависит от объёма продаж; В); Г) - случай несовершенной конкуренции, т.к. цена зависит от объема продаж.

5.2. Монополия на рынке сталкивается с предельным доходом, определенным функцией MR = 60 - 2Q. Предельные издержки имеют следующий вид: MC= -15 + 3Q.

Определим рыночную цену монополиста.

Рассуждения. Линия спроса монополиста имеет отрицательный наклон, т.к. чем больше фирма предлагает товаров на рынок, тем по меньшей цене она сможет их продать.

Рыночная цена монополиста соответствует среднему доходу:

P = AR = TR / Q,

где Q - объем продукции монополиста, максимизирующий прибыль.

Следовательно, для того чтобы рассчитать рыночную цену монополиста необходиомо определить величину объёма продукции, максимизирующий его прибыль и величину общего дохода.

Решение:

Согласно правилу максимизации прибыли (MR = MC) приравняем значения соответствующих функций: 60 - 2Q = - 15 + 3Q. Тогда объем продукции, максимизирующий прибыль (Q) будет равен 15.

Поскольку предельный доход (MR) есть первая производная общего дохода, то функция последнего примет следующий вид: TR = 60Q - Q². Подставив значения объема продукции, при котором фирма получает максимум прибыли, в формулу общего дохода, определим величину общего дохода: TR = 60 × 15 - 15² = 675.

Отсюда, рыночная цена монополиста P = AR = TR/Q = 675 : 15 = 45.

Ответ: P = 45.

5.3. Найдем ценовую эластичность рыночного спроса монополиста в точке максимальной прибыли, если он, действуя наилучшим для себя образом и обладая полной информацией, назначает цену на уровне:

P = 52 - 2Q. При этом общие издержки на произвоство продукции составляют: TC = 120 - 8Q + Q².

Решение:

Для определения ценовой эластичности рыночного спроса монополиста воспользуемся коэффициентом Лернера (L):

(P - MC) / P = 1 / |Ed|.

По условию задачи мы располагаем функциями цены и общих издержек фирмы. Следовательно, определив объём производства, при котором фирма - монополист получает максимум прибыли, мы сможем найти соответствующее значение цены и рассчитать ценовую эластичность рыночного спроса.

Первый способ:

а) Определим объём производства, максимизирующий прибыль, используя правило максимизации MR = MC.

MR = (TR)' = (P×Q)'=((52 - 2Q) × Q)' = (52Q - 2Q²)' = 52 - 4Q;

MC = (TC)' = (120 - 8Q + Q²)' = 2Q - 8.

Приравняем значения соответствующих выражений MR и MC. Мы получим следующее выражение: 52 - 4Q = 2Q - 8. Отсюда, объём продукции, максимизирующий прибыль монополиста, составит 10 ед.

б) Монопольная цена фирмы в точке, максимизирующей прибыль, должна быть равна величине среднего дохода (AR).

Рассчитаем величину среднего дохода по формуле: AR = TR / Q, где TR = 52Q - 2Q², а Q = 10.

Отсюда, величина среднего дохода составит:

AR = 32 д.е. (52Q - 2 Q²) / Q = 52 - 2Q = 52 - 2 × 10).

Тогда монопольная цена фирмы (P) будет 32 (т.к. AR = 32).

в) Определим величину предельных издержек MC = 2Q - 8 в точке, максимизирующей прибыль. Мы получим: MC = 2 × 10 - 8 = 12.

г) Для определения ценовой эластичности рыночного спроса монополиста воспользуемся индексом Лернера (L):

(P - MC) / P = 1 / |Ed|.

• (32 - 12) / 32 = 1 / |Ed|

• 1,6 = 1 / |Ed| ==>

• Ed = 1,6.

Второй способ:

По условию задачи, мы располагаем функциями монопольной цены и общих издержек монополиста. Для того, чтобы найти ценовую эластичность рыночного спроса в точке максимальной прибыли, мы должны знать величину монопольной цены и предельных издержек.

а) Вычислим величину монопольной цены P = 52 - 2Q. Из формулы цены мы видим, что нам не хватает значения объёма производства (Q), максимизирующего прибыль. Для его исчисления воспользуемся формулой прибыли PR = TR - TC, где TR = P × Q. Если мы приравняем производную функции прибыли к нулю, то сможем определить объём производства, максимизирующий прибыль.

• Запишем формулу прибыли:

PR = (52 - 2Q) × Q - (120 - 8Q + Q²) = 52Q - 2 Q² - (120 - 8Q + Q²) =>

PR = 60Q - 3Q² - 120.

• Приравняем производную функции прибыли к нулю и определим объём производства, максимизирующий прибыль:

(PR)' = (60Q - 3Q² - 120)' = 60 - 6Q.

60 - 6Q = 0;

Q = 10ед.

Отсюда, величина монопольной цены P = 52 - 2 ×10 = 32 д.е.

б) Найдем значение предельных издержек.

Функция предельных издержек есть первая производная общих издержек: MC = (TC)' = (120 - 8Q + Q²)' = 2Q - 8. Если мы подставим значение объема производства, максимизирующего прибыль, в формулу функции предельных издержек, тополучим соответствующее значение MC = 2Q - 8 = 2×10 - 8 = 12.

в) Ценовую эластичность рыночного спроса Ed рассчитаем по формуле: (P - MC) / P = 1 / |Ed|.

• (32 - 12) / 32 = 1 / |Ed|;

• 20 / 32 = 1/ |Ed|;

• Ed = 1,6.

Ответ: Ed = 1,6. Чем более эластичен спрос, тем меньшей рыночной властью обладает фирма.

5.4. Даны значения цены и объёма выпуска продукции, при которых монополист получает максимальную выручку P = 25 и Q = 100.

Выведим формулу линейной функции спроса на продукцию монополиста.

Решение:

Согласно теории, монополист заработает максимум выручки при линейной функции спроса Q(D) = b - aP, если продавать продукцию:

• по цене (P), равной половине запретительной цены (А/2) и

• при объёме продаж, равном половине массы насыщения (В/2) (см. задачу 4.3 и рис. 4.5).

а) Найдём значения запретительной цены и массы насыщения, если спрос на продукцию монополиста задан линейной функцией:

Q(D) = b - aP.

• При P = 0 значение Q(D) = В = b (величина массы насыщения). Объём производства, при котором монополист получит максимум выручки, определим по формуле Q = B/2 = b / 2. Тогда, если вместо величины, соответствующей половине массы насыщения мы подставим ее значение, то получим следующее выражение: 100 = b / 2. Отсюда коэффициент b = 200.

• При Q(D) = 0 цена P = A = b/a (величина запретительной цены). Цену, при которой монополист получает максимальную выручку, определим по формуле P = A / 2 = b / 2a. Если вместо величины, соответствующей половине запретительной цены мы подставим ее значение, то получим следующее выражение: 25 = 200 / 2a. Отсюда, значение коэффициента а = 4.

б) Подставим полученные значения коэффициентов в линейную функцию спроса: Q(D) = b - aP. Формула линейной функции спроса на продукцию монополиста примет вид: Q(D) = 200 - 4P.

Ответ: Q(D) = 200 - 4P.

5.5. Кривая рыночного спроса на продукцию монополии задана следующей функцией P(Q) = 40 - bQ. Предельные затраты составляют: МС = 20. Найдите цену, при которой достигается максимум прибыли.

Решение:

• Цена монополиста, в точке максимизирующей его прибыль определим по формуле P = AR = TR / Q. Величина общего дохода TR = (40 - bQ) × Q = 40Q - bQ². Тогда P = (40Q - bQ²) / Q = 40 - bQ .

• Объем производства, максимизирующий прибыль монополиста, достигается в точке MC = MR. Значение МС нам известно. Найдем значение MR, взяв первую производную общих издержек. Тогда MR = (TR)' = (40Q - bQ²)' = 40 - 2 bQ.

• Приравняв MC и MR, мы можем определить объем производства, максимизирующий прибыль монополиста. Так, если 40 - 2bQ = 20, то Q = 10 / b.

• Подставим в формулу цены: P = 40 - bQ значение Q = 10 / b. Отсюда цена монополиста P = 30.

Ответ: 30.

Закрепите свои умения и навыки

5.6. Даны функция издержек монополиста и функции спроса на продукцию этой монополии на двух рынках:

TC = ½ Q² - 10Q + 15; Q(1) = 100 - 4P(1); Q(2) = 100 - 2P(2).

А) Найдите объёмы продаж и цены на каждом из двух рынков, при которых прибыль монополии будет максимальной (ценовая дискриминация).

Б) Как изменятся объём продаж и цена, если ценовая дискриминация будет запрещена государством?

Ответ:

А) Q(1) = 5; P(1) = 23,75;

Q(2) = 27,5; P(2) = 36,25.

Б) Q = 32,5; P = 27,88.

5.7. Издержки производства и общая выручка монополиста заданы следующими формулами ТС = 4Q + 6 и TR = 10Q - Q² соответственно.

Найдите оптимум производителя-монополиста.

Ответ: Q = 3; P = 7.

5.8. Определите формулу линейной функции спроса на продукцию фирмы - монополиста, если известно, что он получает максимальную выручку в точках P = 150 и Q = 450.

Ответ: Q(D) = 900 - 3P.

9. Даны функции общих издержек и выручки монополиста:

ТС = ½Q² + 20Q + 90;

TR = 140Q - 3/2 Q².

Определите ценовую эластичность рыночного спроса в точке максимальной прибыли.

Ответ: 2,1.

5.10. Дана функция издержек монополиста TC = ¼ Q² + 10Q + 300 и

функции спроса на продукцию этой монополии на двух рынках:

Q(1) = 400 - 2P(1) и Q(2) = 600 - 4P(2). Известно, что максимум прибыли монополиста равен 14 552 д.е. Найдите величину постоянных издержек.

Ответ: 300.

ТЕСТЫ ПО МИКРОЭКОНОМИКЕ

Выберите единственно правильный из четырех вариантов ответ.

1. Какое утверждение о кривой производственных возможностей (КПВ) является верным?

а) КПВ всегда имеет форму выпуклой кривой;

б) любое совершенствование производственных технологий приводит к параллельному сдвигу КПВ влево;

в) по КПВ можно определить, какое соотношение производимых товаров является наиболее эффективным с точки зрения использования ограниченных ресурсов;

г) при построении КПВ предполагается, что количество и качество производственных ресурсов является неизменным.

2. Кривая трансформации имеет выпуклый вид в силу того, что:

а) отказ от производства одного товара сопровождается ростом затрат на производство другого товара;

б) в обществе происходят изменения в технологии производства, растёт производительность труда;

в) альтернативные издержки производства любого из двух товаров постоянны, в какую бы точку на данной линии мы не перемещались;

г) будущий экономический рост достигается ценой отказа от текущего потребления.

3. Молодой человек покупает подарок своей девушке на 8 Марта. Что из следующих утверждений описывает проблему его рационального выбора:

а) он не обращает внимания на цену и руководствуется только своими предпочтениями;

б) его бюджет ограничен и поэтому он обращает внимание только на цену;

в) прежде, чем купить подарок он соизмеряет предельную полезность подарка с ценой;

г) молодой человек очень любит свою девушку, поэтому он не руководствуется принципами рационального потребителя.

4. Рациональный покупатель будет покупать разные наборы продуктов тогда, когда:

а) изменение общей полезности товара для покупателя будет связано строгой пропорциональной зависимостью с динамикой предельной полезности;

б) когда точки, лежащие на кривой производственных возможностей, могут дать для потребителя более эффективную комбинацию товаров, чем точки на кривой безразличия;

в) предельные полезности всех потребляемых им продуктов равны;

г) отношение предельных полезностей товаров равно отношению их цен.

5. Рациональный студент предпочтёт купить компъютер, а не мопед, если:

а) цена на компъютер ниже, чем цена на мопед;

б) предельная полезность компъютера выше, чем предельная полезность мопеда;

в) предельные полезности компъютера и мопеда так соотносятся друг с другом, как цены на них;

г) предельные полезности равны между собой.

6. Бюджетное ограничение для потребителя представляет собой:

а) линию предельной полезности;

б) линию максимального удовлетворения потребителя;

в) ограничение, налагаемое на рациональный выбор потребителя;

г) линию спроса.

7. Повышение цены на продукт Х приводит к смещению равновесия потребителя на карте кривых безразличия (при прочих равных условиях):

а) вправо (вверх);

б) влево (вниз);

в) или влево, или вправо;

г) движение вдоль той же самой кривой безразличия.

8. Кривая рыночного спроса показывает:

а) как будет снижаться потребление блага при снижении доходов покупателей;

б) по какой цене будет осуществляться подавляющая часть сделок;

в) что потребители склоны покупать больше продуктов по более высокой цене;

г) какое количество продукта потребители желают и могут покупать в данных условиях по данной цене.

9. Что случится с кривой рыночного спроса, если цена на товар возрастёт на 20% при прочих равных условиях:

а) кривая спроса сместится вправо;

б) кривая спроса сместится влево;

в) кривая спроса не изменит своего положения;

г) ничто не подходит.

10. Сдвиг линии спроса вправо для товаров низшей категории может быть связан:

а) с увеличением цен на дополняющие товары;

б) с уменьшением цен на заменяющие товары;

в) с ростом цен на данный товар;

г) с уменьшением доходов потребителей.

11. Когда увеличивается величина спроса на тетради, растёт спрос на авторучки. Когда уменьшается величина спроса на тетради, сокращается и спрос на авторучки. Студенты, изучающие экономику, сказали бы, что это:

а) несопряжённые товары;

б) взаимозаменяемые товары;

в) взаимодополняющие товары;

г) эластичные товары.

12. Рыночное равновесие достигается тогда:

а) когда цена, по которой продаёт продавец свой товар, равна цене, по которой покупает его покупатель.

б) когда на рынке устанавливается цена предложения.

в) когда на рынке устанавливается цена покупателя.

г) когда ни цена покупателя, ни цена продавца не влияет на рыночную ситуацию.

13. Если при прочих равных условиях спрос на товар Х уменьшается при увеличении цены на товар У, то мы можем утверждать, что товары Х и У:

а) заменяют друг друга в потреблении;

б) дополняют друг друга в потреблении;

в) не связаны друг с другом в потреблении;

г) являются товарами низшей категории.

14. 10%-ое снижение цены, которое приводит к 15%-ому увеличению объёма спроса, свидетельствует о том, что:

а) спрос неэластичен по цене;

б) спрос эластичен по цене;

в) имеет спрос с единичной эластичностью;

г) общие расходы покупателей уменьшились.

15. В теории производства кратковременным периодом называется:

а) период, на протяжении которого хотя бы один фактор производства остается неизменным по объёму;

б) время, необходимое для того, чтобы изменить выпуск продукции;

в) период времени, в течение которого все факторы производства являются переменными;

г) любой промежуток времени меньше одного года.

16. Неценовыми факторами предложения являются:

а) изменения в технологии;

б) изменения в ценах ресурсов;

в) изменения в налогообложении фирм;

г) все вышеперечисленные факторы.

17. При прочих равных условиях сдвиг кривой предложения вправо приводит:

а) к росту равновесной цены и равновесного объёма;

б) к снижению равновесной цены и равновесного объёма;

в) к росту равновесной цены и снижению равновесного количества;

г) к снижению равновесной цены и росту равновесного количества.

18. Если величина предложения превысит величину спроса, то на рынке наступит:

а) дефицит;

б) излишек;

в) возрастёт спрос со стороны покупателей;

г) производители сократят предложение.

19. Увеличение спроса и предложения одновременно:

а) приведёт к росту цены равновесия;

б) оставит цену равновесия без изменения;

в) снизит цену равновесия;

г) может привести к любому из выше перечисленных последствий.

20. Конкуренция со стороны производителей аналогичного товара может привести:

а) к снижению цены равновесия;

б) к увеличению спроса;

в) к увеличению цены равновесия;

г) к любому из вышеперечисленных последствий.

21. Можно с полной уверенностью утверждать, что спрос на товар эластичен, если:

а) общая выручка продавцов увеличивается с уменьшением цены продукта;

б) общая выручка продавцов уменьшается с уменьшением цены товара;

в) изменение цены товара не влияет на величину общей выручки продавцов;

г) кривая спроса имеет положительный наклон.

22. Линия предложения в кратчайшем периоде может быть:

а) вертикальной;

б) горизонтальной;

в) пологой;

г) вогнутой.

23. Коэффициент ценовой эластичности предложения является:

а) положительной величиной и безразмерной;

б) отрицательной величиной;

в) неотрицательной величиной;

г) как отрицательной, так и положительной величиной.

24. Коэффициент перекрёстной эластичности спроса для взаимодополняющих благ:

а) положительная величина;

б) отрицательная величина;

в) равен нулю;

г) г) как положительная, так и отрицательная величина.

25. Государство, защищая интересы покупателей, установило на рынке совершенной конкуренции минимальную цену, ниже цены равновесия. При прочих равных условиях, по сравнению с ситуацией невмешательства в экономику, объём продаж:

а) должен сократиться;

б) не изменится;

в) должен увеличиться;

г) ничто из выше перечисленного не подходит.

26. В кратковременном периоде к переменным издержкам относят:

а) амортизационные отчисления;

б) плату за арендуемое конторское имущество;

в) зарплату рабочих;

г) плату за банковский кредит.

27. В кратковременном периоде к постоянным издержкам относят:

а) затраты на топливо;

б) амортизационные отчисления;

в) зарплата рабочих;

г) затраты на сырье.

28. К неявным (внутренним) издержкам фирмы относят:

а) издержки на приобретение факторов производства;

б) издержки собственных ресурсов фирмы;

в) издержки на единицу продукции;

г) общие издержки (постоянные и переменные).

29. Кривые средних переменых и предельных издержек

пересекаются в точке:

а) минимума средних общих издержек;

б) минимума средних переменных издержек;

в) максимума предельных издержек;

г) максимума средних переменных издержек.

30. Введение налога на единицу продукции означает, что тяжесть налогового бремени несут:

а) производители;

б) потребители;

в) и производители, и потребители;

г) чиновники, которые собирают налоги.

31. Бухгалтерская прибыль включает:

а) как экономичекую, так и нормальную прибыль;

б) только нормальную прибыль;

в) только экономическую прибыль;

г) нет правильного ответа.

32. Понятие экономических издержек означает, что:

а) нужно учитывать альтернативную стоимость всех используемых фирмой ограниченных ресурсов;

б) они, в отличие от бухгалтерских издержек, не учитывают внутренние (неявные) издержки;

в) величина собственых ресурсов фирмы не учитывается при их подсчёте;

г) они меньше бухгалтерских издержек на величину амортизационных отчислений.

33. Если общая выручка машиностроительного предприятия снизится, то:

а) цены на отечественные автомобили снизились, а спрос на рынке эластичный;

б) цены на отечественные автомобили увеличились, а спрос неэластичный;

в) снизились цены на автомобили;

г) из-за введения новых налогов на российской таможне сократился ввоз импортных автомобилей.

34. Как изменится общая выручка продавцов при росте цен, если ценовая эластичность спроса меньше 1:

а) уменьшится;

б) останется без изменений;

в) увеличится;

г) изменение выручки не связано с эластичностью спроса.

35. Рынок совершенной конкуренции:

а) включает монополию,олигополию, монополистическую конкуренцию;

б) характеризуется множеством покупателей и продавцов;

в) это место, где присутствует несколько продавцов;

г) регулируется государством.

36. Какой из признаков не характеризует рынок монополистической конкуренции:

а) на рынке продается дифференцированный товар;

б) на рынке отсутствует монопольная власть;

в) на рынке много продавцов и покупателей;

г) на рынке монополистической конкуренции по сравнению с совершенной конкуренцией цены на продукцию выше, а объём продаж ниже.

37. Олигополистический рынок схож с рынком монополистической конкуренции в том, что:

а) обладает рыночной властью;

б) отсутствуют любые барьеры для входа;

в) существуют труднопреодолимые барьеры;

г) вход и выход свободный.

38. Если фирмы, действующие на рынке, не получают экономической прибыли в долговременном периоде, то их называют:

а) монопсонией;

б) олигополией;

в) совершенной конкуренцией;

г) монополией.

39. В качестве барьера для проникновения в отрасль новых производителей могут служить:

а) законодательное оформление исключительных прав;

б) патенты и лицензии;

в) низкие издержки производства;

г) всё вышеперечисленное.

40. В некоторых европейских высших учебных заведениях плата за обучение для иностранных студентов выше, чем для тех, кто проживает в данной стране. Чем это объяснить:

а) отсутствием контроля со стороны государства иностранных студентов над процессом образования в чужой стране;

б) ценовой дискриминацией в европейских странах;

в) монополией в высшем образовании данных стран;

г) ничто из вышеперечисленного не подходит.

КЛЮЧ к ТЕСТАМ по МИКРОЭКОНОМИКЕ

ЛИТЕРАТУРА

1. Арутюнова Г.И. Экономическая теория: Учебник. - М.: Междунар. отношения, 2003.

2. Курс экономики: Учебник. - 3-е изд., доп. / Под ред. Б.А. Райзберга. - М.: ИНФРА. - М, 2001.

3. Курс экономической теории: учебник для студентов высших учебных заведений. / Под об. ред. проф. Чепурина М.Н., Киселевой Е.А. - 5-е изд. - Киров: «АССА», 2006.

4. Лемешевская Л.В. Экономическая теория: тесты, ситуации, задачи: Учебное пособие. - Мн.: Книжный дом; Мисанта, 2005.

5. Мицкевич А.А. Сборник заданий по экономике: - М.: «Вита-Пресс», 1998.

6. Мицкевич А.А. Сборник заданий по экономике: - М.: Вита-Пресс, 2001.

7. Микроэкономика: Учеб. пособие/ М.И. Плотницкий, А.К. Корольчук, Л.В. Лемешевская, М.К. Радько; Под об. Ред. М.И. Плотницкого. - 2-е изд. - Минск.: Новое знание, 2003.

8. Нуреев Р.М. Курс микроэкономики: Учебник для вузов. - 2-е изд., изм. - М.: Норма, 2005.

9. Савицкая Е.В, Серёгина С.Ф. Рабочая тетрадь по экономике: - В 2-х частях. - М.: Вита-Пресс, 2004.

10. Черняк В.З. Экономика: задачи и тесты: Пособие для студ. высш. и сред. спец. учеб. заведений. - М.: Гумманит. изд. центр ВЛАДОС, 2001.

Содержание

Введение………………………………………………………………………...3

тема 1. Производственные возможности……………………………….4

Теоретический материал………………………………………………4

Учимся решать экономические задачи………………………...........8

Закрепите свои умения и навыки……………………………………14

тема 2. Теория полезности и выбор потребителя…..………………17

Теоретический материал…………………………………………..…17

Учимся решать экономические задачи……………..………….......28

Закрепите свои умения и навыки……………………………..…….30

тема 3. Теория спроса и предложения………….……………...………31

Теоретический материал……………………………………………..31

Учимся решать экономические задачи……………..………….......42

Закрепите свои умения и навыки……………………………..…….45

тема 4. Теория производства: издержки, выручка и максимум

прибыли ……………………………………………………………………….47

Теоретический материал……………………………………………..47

Учимся решать экономические задачи…………………………….57

Закрепите свои умения и навыки……………………………………61

тема 5. Конкуренция и монополия.…….………………………………..62

Теоретический материал…………………………………………….62

Учимся решать экономические задачи…………………………….70

Закрепите свои умения и навыки……………………….…………..74

Тесты по микроэкономике………………………………..……................76

Ключ к тестам по микроэкономике…………………….........................82

Литература……….……………………………………………………………83

Айнаа Ахмедовна Султыгова,

Вера Викторовна Безновская,

Ирина Владимировна Кирова.

ЭКОНОМИЧЕСКАЯ ТЕОРИЯ В ЗАДАЧАХ И СИТУАЦИЯХ

Учебное пособие

Часть 1

Микроэкономика

Редактор И. А. Короткова

Технический редактор И. А. Короткова

Тем. План 2008 г., п. 18

Подписано в печать Формат 60 × 84/16

Печать офсетная Усл. печ. л. 5,3 Уч-изд. л. 4,2

Тираж 300. экз. Заказ Цена 40 р.

Ротапринт МАДИ (ГТУ). 125319, Москва, Ленинградский проспект. 64