Конспект урока математики на тему Задачи на движение вдогонку

План-конспект урока по математике по теме: «Движение вдогонку»

Урок по образовательной системе «Школа 2100»

Цели урока:

1. Образовательные:

• научить решать задачи на движение вдогонку;

• научить составлять задачи на движение вдогонку.

2. Развивающие:

• Развивать логическое мышление, память, внимание, навыки устных и письменных вычислений, самоанализа и самоконтроля;

• Развивать познавательный интерес, умение переносить знания в новые условия.

3. Воспитательные:

• Создать условия для воспитания коммуникативной культуры, умение выслушивать и уважать мнения других;

• Воспитывать ответственность, любознательность, усидчивость, познавательную активность, доброе отношение к своим одноклассникам;

• Формировать потребность в здоровом образе жизни.

Формирование УУД:

• Личностные действия: (самоопределение, смыслообразование, нравственно-этическая ориентация);

• Регулятивные действия: (целеполагание, планирование, прогнозирование, контроль, коррекция, оценка, саморегуляция);

• Познавательные действия: (общеучебные, логические, постановка и решение проблемы);

• Коммуникативные действия: (планирование учебного сотрудничества, постановка вопросов, разрешение конфликтов, управление поведением партнера, умение с достаточной точностью и полнотой выражать свои мысли в соответствии с задачами и условиями коммуникации).

Оборудование:

• Карточки для работы на разных этапах урока;

• Презентация;

• Учебник и рабочая тетрадь.

ХОД УРОКА

1. Самоопределение к деятельности.

Первое - предлог,

Второе - летний дом,

А целое порой

Решается с трудом.

• Что это?

• Задача.

• Значит, чем мы будем заниматься на уроке?

• Решать задачи.

• Да, сегодня мы с вами продолжаем знакомиться с темой движения, и будем решать задачи нового типа.

• Но для начала нам надо подкрепить наш вычислительный аппарат.

2. Актуализация знаний.

• Представьте, что вы кругосветные путешественники. «Почему?» - спросите вы. Да, потому, что каждый из вас успел в своей жизни, сам того не подозревая, пройти пешком путь, равный окружности земного шара. Не верите? Давайте вместе и проверим.

t = 5 ч 1 день - 25 км V = 8000 км/год

V = 5 км/ч 360 дней - ? км S = 40000 км

S - ? км t - ? лет

• В течение дня вы проводите на ногах не менее 5 часов. При средней ходьбе человек проходит 5 км/ч. Сколько километров проходит человек за день?

• 25 км.

• Определите, какой путь проходит каждый из нас в течение года.

• 25 * 360 = 9000 (км)

• Какое правило используем для вычисления?

• Умножение суммы на число.

• Человек, никогда не покидавший родного города, ежегодно проходит пешком 8000 - 9000 километров. Окружность Земного шара имеет длину 40000 километров. Вычислите, во сколько лет совершаем мы пешеходное путешествие, равное кругосветному?

• 40000 : 8000 = 5 (лет)

• Будем считать, что человек начинает ходить с 2-х летнего возраста. Во сколько лет вы совершите 2 таких кругосветных путешествия?

• В 12 лет.

• Дожив до 60 лет, мы 10 раз обойдем вокруг Земного шара, т.е. пройдем путь, более длинный, чем расстояние от Земли до Луны.

• Какими понятиями мы пользовались?

• Скорость, время, расстояние.

• Как найти скорость?

• V = S : t

• Как найти время?

• t = S : v

• Как найти расстояние?

• S = v * t

• Сегодня, эти понятия помогут нам в решении задач.

• Внимание на доску:

• Что можете сказать об этих схемах?

• Два объекта движутся навстречу друг другу и в противоположных направлениях.

• Какие понятия помогут нам решить задачи по этим схемам?

• Внимание на доску:

Скорость сближения

V_сбл. = V₁ + V₂

Скорость удаления

V_удал. = V₁ - V₂

• Что такое скорость сближения?

• (Ответы детей)

• Что такое скорость удаления?

• (Ответы детей)

• Составьте выражение и найдите его значение:

Из пунктов А и В, удаленных друг от друга на 200 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 10 км/ч, а автобус догоняет его со скоростью 60 км/ч. Как изменяется расстояние между ними за 4 часа? Когда произойдет встреча?

3. Постановка учебной задачи.

• Какое задание выполняли?

• Находили расстояние между велосипедистом и автобусом через 4 часа после их выхода.

• Как они двигались?

• Одновременно вдогонку.

• Почему вы не смогли найти это расстояние?

• У нас нет алгоритма его выполнения.

• Что же нам сделать, чтобы решить задачу - поставьте перед собой цель.

• Нам надо построить алгоритм нахождения расстояния между объектами при движении вдогонку.

• Сформулируйте тему урока.

• Движение вдогонку.

4. «Открытие нового знания».

№1, стр.97.

• Прочитайте задачу.

1. Из пунктов А и В, удаленных друг от друга на 200 км, одновременно в одном направлении выехали автобус и велосипедист. Скорость велосипедиста 10 км/ч, а автобус догоняет его со скоростью 60 км/ч. Как изменяется расстояние между ними за 1 час? Чему оно будет равно через 1 ч, 2 ч, 3 ч, t ч? Когда произойдет встреча?

Закончи построения на координатном луче и обозначь место встречи флажком. Заполни таблицу и запиши формулу зависимости расстояния d между автобусом и велосипедистом от времени движения t.

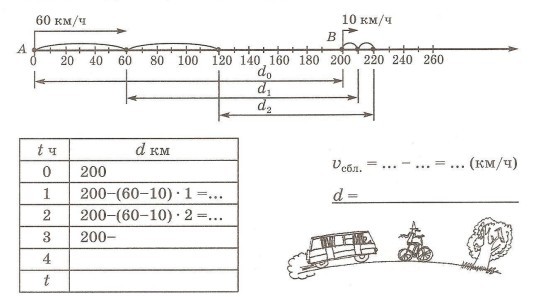
2. Как найти время до встречи с помощью вычислений? Докажи.

3. Запиши формулу зависимости между величинам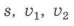и и

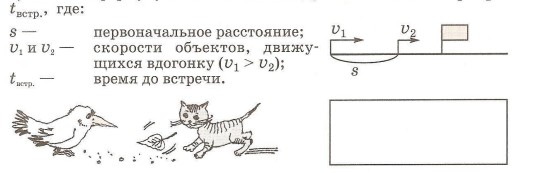
• Какое расстояние было между велосипедистом и автобусом в самом начале?

• 200 км.

• Какова их скорость сближения? Заполните в учебнике.

• V_сбл. = 60 - 10 = 50 (км/ч)

• Что показывает скорость сближения 50 км/ч?

• Она показывает, что велосипедист и автобус за каждый час сближаются на 50 км.

• Как же узнать, каким оно стало через 1 час?

• Надо 50 км вычесть из 200 км, получим 150 км.

• Что же будет происходить дальше?

• Потом они сблизятся еще на 50 км, потом еще на 50 км и т.д.

• Как же определить расстояние через 2 ч, 3 ч?

• Надо из 200 вычесть 50 * 2, 50 * 3.

• Закончите заполнение таблицы.

• 200 - (60 - 10) * 2 = 100

• 200 - (60 - 10) * 3 = 50

• 200 - (60 - 10) * 4 = 0

• 200 - (60 - 10) * t = …

• Запишите формулу расстояния d между велосипедистом и автобусом в момент времени t.

• d = 200 - (60 - 10) * t, или d = 200 - 50 * t.

• Что произошло через 4 часа?

• Велосипедист и автобус встретились.

• Как это вычислить по формуле, не используя построений?

• Расстояние в момент встречи равно 0, значит, t_встр. = 200 : (60 - 10).

• Запишите это равенство, используя знак умножения.

• 200 - (60 - 10) * t_встр.

Полученные равенства фиксируются на доске:

d = 200 - (60 - 10) * t 200 = (60 - 10) * t_встр.

• Обозначьте первоначальное расстояние (200 км) буквой s, а скорости велосипедиста и автобуса (10 км/ч и 60 км/ч) - v₁ и v₂ и запишите полученные равенства в обобщенном виде.

Число 200 закрывается в равенствах на доске буквой s, а числа 10 и 60 - буквами v₁ и v₂. Получаются формулы, которые на данном уроке можно использовать как опорные конспекты:

d = s - (v₁ - v₂) * t s = (v₁ - v₂) * t_встр.

• Эти формулы можно перевести с математического языка на русский в форме правил:

1. Чтобы при одновременном движении вдогонку найти расстояние между двумя объектами в данный момент времени, можно из первоначального расстояния вычесть скорость сближения, умноженную на время в пути.

2. При одновременном движении вдогонку первоначальное расстояние равно скорости сближения, умноженной на время до встречи.

Данные правила не должны заучиваться формально - это малопродуктивно, а должны воспроизводиться как выражение в речи смысла построенных формул. При этом каждая из формул хранит в себе богатейшую информацию о том, как найти значение любой из входящих в нее величин. Например, из второй формулы следует, что время до встречи равно первоначальному расстоянию, деленному на скорость сближения, а скорость сближения, наоборот, - первоначальному расстоянию, деленному на время до встречи. Таким образом, построенные формулы помогают решить практически любую задачу на одновременное движение вдогонку, поскольку в них показана связь между всеми существенными его характеристиками.

5. Первичное закрепление.

Организуется комментированное решение задач на использование введенных алгоритмов: сначала фронтально, затем в группах или парах.

№2, стр. 98.

• Решите задачу.
  
  
  
  Миша начал догонять Борю, когда расстояние между ними было 100 м. Миша идет со скоростью 80 м/мин, а Боря - со скоростью 60 м/мин. Через сколько времени Миша догонит Борю?

1. 80 - 60 = 20 (м/мин) - скорость сближения мальчиков;

2. 100 : 20 = 5 (мин).

100 : (80 - 60) = 5 (мин).

Ответ: Миша догонит Борю через 5 мин.

№4, стр. 98.

• Составьте по схемам взаимно обратные задачи и решите их:

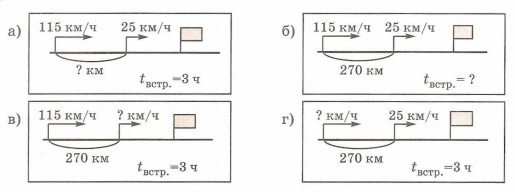
1 и 2 выполняются фронтально.

3 и 4 выполняются в группах или парах.

1. (115 - 25) * 3 = 270 (км);

2. 115 - 270 : 3 = 25 (км/ч);

3. 270 : (115 - 25) = 3 (ч);

4. 270 : 3 + 25 = 115 (км/ч).

6. Самостоятельная работа.

Учащиеся проводят самоконтроль и самооценку усвоения ими построенного алгоритма. Они самостоятельно решают задачу на новый вид движения, проверяют и оценивают правильность своего решения и убеждаются в том, что новый способ действий ими освоен. В случае необходимости ошибки корректируются.

№3, стр. 98.

• Решите задачу.

Из пунктов А и В одновременно в одном направлении выехали 2 поезда. Скорость</</u> первого поезда равна 80 км/ч, а скорость второго поезда, идущего вдогонку первому поезду, равна 110 км/ч. Встреча произошла через 4 ч после выезда поездов. На каком расстоянии друг от друга находятся пункты А и В?

1. 110 - 80 = 30 (км/ч) - скорость сближения поездов;

2. 30 * 4 = 120 (км).

(110 - 80) * 4 = 120 (км).

Ответ: пункты А и В находятся на расстоянии 120 км друг от друга.

7. Включение в систему знаний и повторение.

Выполняются задания на закрепление ранее изученного материала.

№6, стр. 98.

• Решите задачу.

В бочку с водой проведен шланг, через который в нее вливается 9 ведер воды в час. Через другой шланг водой из бочки поливают огород, расходуя при этом 16 ведер воды в час. Через сколько времени опустошится полная бочка, вмещающая 21 ведро воды, если оба шланга начнут использоваться одновременно?

1. 16 - 9 = 7 (в./ч) - скорость уменьшения воды в бочке;

2. 21 : 7 = 3 (ч).

21 : (16 - 9) = 3 (ч).

Ответ: полная бочка опустошится через 3 часа.

8. Домашняя работа.

• Дома по новой теме нужно выучить опорные конспекты - то есть новую формулу и придумать и решить свою задачу на новый вид движения - движение вдогонку, аналогичную №2.

• Дополнительно по желанию можно выполнить задачу №7.

№7, стр. 99

В кухне у Вовочки было 18 мух. Вовочка бьет мухобойкой 5 мух в минуту, и в кухню в то же время влетают 2 новые мухи. Через сколько времени в кухне не останется мух?

18 : (5 - 2) = 6 (мин).