Системно-деятельностный подход на уроке математике тема «Сочетательное свойство умножения» (УМК «Перспективная начальная школа», 3 класс)

Муниципальное автономное образовательное учреждение

дополнительного профессионального образования

«Институт повышения квалификации»

(МАОУ ДПО ИПК)

ТВОРЧЕСКАЯ РАЗРАБОТКА

Системно-деятельностный подход на уроке математике

тема «Сочетательное свойство умножения»

(УМК «Перспективная начальная школа», 3 класс)

Выполнил: Осина Т.Г. гр.18/4

должность: учитель начальных классов

МБОУ «СОШ №77»

Новокузнецк 2016

СОДЕРЖАНИЕ

1. Введение…………………………………………………………….3стр

2. Разработка урока по математике………………………………….5 стр

3. Заключение………………………………………………………….9 стр

4. Список используемой литература……………............................10 стр

5. </ Приложение………………………………………………………..11 стр

1. Введение

В основе ФГОС лежит системно-деятельностный подход.

Системно-деятельностный подход - это организация учебного процесса, в котором главное место отводится активной и разносторонней, в максимальной степени самостоятельной познавательной деятельности школьника. Ключевыми моментами деятельностного подхода является постепенный уход от информационного репродуктивного знания к знанию действия,· воспитание и развитие качеств личности, отвечающих требованиям информационного общества;

Основная идея его состоит в том, что новые знания не даются в готовом виде. Дети «открывают» их сами в процессе самостоятельной исследовательской деятельности. Они становятся маленькими учеными, делающими свое собственное открытие. Задача учителя при введении нового материала заключается не в том, чтобы все наглядно и доступно объяснить, показать и рассказать. Учитель должен организовать исследовательскую работу детей, чтобы они сами додумались до решения проблемы урока и сами объяснили, как надо действовать в новых условиях.

Системно-деятельностный подход, лежащий в основе Стандарта нового поколения, основной результат применения которого - развитие личности ребенка на основе универсальных учебных действий, предполагает:

1.​ воспитание и развитие качеств личности, отвечающих требованиям информационного общества;

2.​ переход к стратегии социального проектирования и конструирования в системе образования на основе разработки содержания и технологий образования;

3.​ ориентацию на результаты образования (развитие личности обучающегося на основе УУД);

4.​ признание решающей роли содержания образования, способов организации образовательной деятельности и взаимодействия участников образовательного процесса;

5.​ учет возрастных, психологических и физиологических особенностей учащихся, роли и значения видов деятельности и форм общения с детьми;

6.​ обеспечение преемственности дошкольного, начального общего, основного и среднего (полного) общего образования;

7.​ разнообразие организационных форм, обеспечивающих рост творческого потенциала, познавательных мотивов обучающихся;

Курс математике в начальной школе направлен на следующие цели: уметь

• ​использовать математические представления для описания окружающего мира (предметов, процессов, явлений) в количественном и пространственном отношении;

• ​ производить вычисления для принятия решений в различных жизненных ситуациях;

• читать и записывать сведения об окружающем мире на языке математики;

• ​ формировать основы рационального мышления, математической речи и аргументации;

• ​ работать в соответствии с заданными алгоритмами;

• ​ узнавать в объектах окружающего мира известные геометрические формы и работать с ними;

• ​ вести поиск информации (фактов, закономерностей, оснований для упорядочивания), преобразовать её в удобные для изучения и применения формы.

В результате освоения предметного содержания предлагаемого курса математики у учащихся предполагается формирование универсальных учебных действий (познавательных, регулятивных, коммуникативных) позволяющих достигать предметных, метапредметных и личностных результатов.

2. Разработка урока по математике

Тема: «Сочетательное свойство умножения»

Цели:

1. Обучающая: Способствовать овладению способом сочетательного свойства умножения, формировать представление о возможности использовать изученное свойство для вычисления.

2. Развивающая: Развивать умения контролировать самого себя, находить свои ошибки и исправлять их.

3. Воспитательная: Воспитывать умения работать в парах, оценивать самого себя и свою деятельность.

Средства обучения: учебник, тетрадь на печатной основе, раздаточный материал.

Ход урока:

1. Организационный момент

Проверка готовности к уроку.

2. Актуализация опорных знаний и умений.

   1. Устный счет. Графический диктант

- Я диктую вам примеры, если пример правильный рисуем _, если неправильный ^.

3*8=24

5*3=15

16:2=7

2*9=19

4*4=16

7*8=54

9*9=81

8*3=27

24:4=6

21:7=4

Ответы: _ _ ^ ^ _ ^ _ ^ _ ^ (Ответы записаны на доске)

- А сейчас обменяйтесь с соседом по парте тетрадями и проверьте правильность выполнения задания. Правильные ответы записаны на доске.

- Встаньте те, кто выполнил без ошибок.

- А теперь у кого 1-2 ошибки.

- У кого более 2 ошибок?

-----Почему вы допустили ошибки?

-Плохо знали таблицу умножения;

-Были невнимательны.

-----Что нужно сделать в следующий раз, чтобы не было ошибок?

-Повторить знание табличного умножения и деления;

-Быть более внимательными при выполнении задания

(Хорошо, молодцы! Дома ещё раз повторите таблицу и, в следующий раз будете внимательнее и выполните работу без ошибок.)

3. Изучение нового материала.

Проблемная ситуация

- Устно найдите наиболее удобным способом значения выражений

(Примеры записаны на доске)

(9+5)+5=

(7+6)+4=

(28+6)+2=

(17+9)+3=

(7*2)*5=

25*2*7=

- Каким свойством сложения, вы пользовались при вычислении выражений? (Сочетательным свойством сложения)

-----Как применяли? Прокоментировать 2-3 примера.

- Для чего нужен этот способ сложения? (Для более удобного сложения слагаемых) (Молодцы, правильно, с заданием справились.)

----- В каком выражении известный вам способ не работает? Почему?

(7*2)*5=

25*2*7=

• Выражения записать на доске

- Чем эти выражения отличаются от остальных? (Здесь умножение, а в остальных сложение)

---- Чего мы не знаем? (Мы не знаем способа умножения двузначного числа на однозначное)

Постановка учебной задачи.

-----Для этого нам нужен другой способ.

А такой способ есть? Давайте попробуем его найти

• Чтение темы урока в учебнике (читает ученик)

«Сочетательное свойство умножения»

Значит, есть другой способ? (Да, есть другой способ, как и при сложении)

- Правильно в математике есть не только сочетательное свойство сложения, но и сочетательное свойство умножения.

--- Зная сочетательное свойство умножения, вы можете найти значения выражений (обратить внимание на выражения в рамочке) - рационално.

--- Вот сегодня на уроке, вы попытаетесь сформулировать это свойство и применять его на практике.

4. Первичное закрепление знаний.

1. Комментированно, с объяснением, используя новый способ

25*4*3=

45*2*5=

15*10*2=

Вывод: удобнее и быстрее находить значения таких выражений.

В учебнике, прочитать вывод правила на странице, 87.

2. Работа в парах

I- вариант II-вариант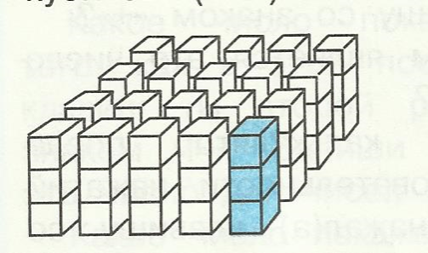

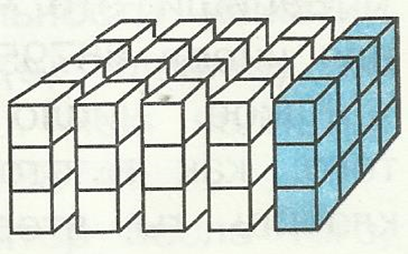
- У каждого варианта на партах лежит рисунок конструкции, составленные из кубиков.

- Вам нужно рассмотреть рисунки, вычислить, сколько кубиков в этой конструкции и составить выражение.

-Какое выражение получилось у I- варианта? (3*(4*5)=60)

-Какое выражение получилось у II- варианта? ((3*4)*5=60)

- Хорошо, а теперь с соседом по парте сравните значения этих выражений.

- Сделайте вывод. (Значения выражений равны, число кубиков в конструкции одинаково 3*(4*5)=(3*4)*5)

- Можете ли вы теперь сформулировать правило сочетательного свойства умножения?

- Сравните свои высказывания с выводом в учебнике.

- А теперь вместе с соседом по парте составьте буквенное выражение сочетательного свойства умножения, пользуясь прочитанным правилом.

- Какое выражение получилось? ((а*b)*с=а*(b*с))

- Какое свойство мы сформулировали? (Сочетательное свойство умножения)

- А теперь вернемся к нашим выражениям, где мы не смогли найти ответ и попробуем решить их, используя новый способ вычисления.

(7*2)*5=

25*2*7=

• Итог: 1.Прочитать ещё раз правило.

2.Записать выражение: ((а*b)*с=а*(b*с) -- в свои таблички- помощники

3. Самостоятельная работа. Задание с «ловушкой»

- В данных выражениях расставь скобки так, чтобы упростить вычисление значений этих выражений. Вычислите значения данных выражений. Проверка- объяснить как выполнили, где затруднились , почему?

(Примеры записаны на доске)

7*2*5 3*4*5 2*5*9 8*2*35 45*2*7 2*3*10*4

5. Контроль и оценка

Самостоятельная работа с последующей проверкой

- У каждого из вас есть на партах карточки. Не вычисляя значений произведений составь из них верные равенства, используя буквенное выражения сочетательного свойства умножения (а*b)*с=а*(b*с).

15*(10*6) (20*5)*3

( Самопроверка, открыть запись выполнения задания на доске )

- Встаньте те, кто выполнил без ошибок.

- А теперь у кого 1 ошибка. (Почему вы допустили ошибки?)

--- не поняли, не применили новый способ---

• Что нужно сделать в следующий раз, чтобы не было ошибок?

6. Домашнее задание по выбору

   1. Тетрадь на печатной основе страница 57, упражнение 121.

   2. Учебник страница 87, упражнение 285.

VII . Рефлексия

- Вы могли в начале урока вычислить значения этих выражений?(7*2)*5=

25*2*7=

- Почему не могли? (не знали способа решения таких выражений)

-А теперь сможете вычислить значения этих выражений? Почему?

(Узнали новый способ решения)

-Какой способ?( «Сочетательное свойство умножения»)

Молодцы! Спасибо. Все свободны.

3. Заключение

Данный урок по математике на тему «Сочетательное свойство умножения» попыталась выстроить в системно-деятельностном подходе. При разработки урока придерживалась структурой современного урока ФГОС.

Тип урока открытие нового знания. На уроке были учтены возрастные и психологические особенности учащихся. На всех этапах урока ученики были вовлечены в практическую, мыслительную деятельность, детям надо было найти новый способ вычисления уже известного им действия. Каждый этап имел свою завершённость и имел свой логический переход к другому этапу. Для ребят был предложен материал с разным уровнем сложности. Всё это способствовало развитию творческо-поисковой активности детей. На уроке прослеживалась активность учащихся благодаря использованию разнообразных видов деятельности, которые вызвали у детей интерес, желание выполнять задания.

Для активной деятельности учащихся использовала парную, самостоятельную работу. При проведении парной работы я ставила перед собой цель сплотить ребят, учить их работать вместе, сообща, выслушивая мнение других, предлагать свои идеи и делать общий вывод. Упражнения использовались по нарастающей сложности. Прорабатывала вопросы, которые помогали детям делать выводы, обобщать, сформулировать новое правило.

Учебная информация была привлекательна для детей. За счёт привлекательности содержания заданий и подачи учебного материала, повысились возможности учеников в достижении поставленных целей на уроке.

На уроке побуждала учащихся к самопроверке, самоанализу. Домашнее задание предлагается на основе выбора и носит дифференцированный характер.

Этап Контроль и оценка показал, что урок цели достиг

Понимаю и осознаю значение организации и последовательности всех этапов урока для формирования у детей учебной самостоятельности.

3. Список используемой литературы

1. Математика [Текст]: 3 кл.:Учебник: В 2 ч. / А.Л Чекин; под ред. Р.Г, Чураковой. - 3-е изд. , испр.- М.: Академкнига/Учебник, 2013. - 112 с.

2. Математика в вопросах и заданиях [Текст]: 3 кл.:Тетрадь для самостоятельной работы №1/О.А.Захарова, Е.П.Юдина;под ред. Р.Г, Чураковой. - 3-е изд. , испр.- М.: Академкнига/Учебник, 2013. - Ч.1:96 с.

3. Урок в современной начальной школе: лучшие педагогические практики: пособие для учителей /под рад. Т.О. Автайкиной - Новокузнецк: МАО ДПО ИПК, 2013. - 45 с. - (Мастер-класс)

4. Примерная основная образовательная программа начального общего образования [Текст] / сост. Е.С. Савинов.- М.: Просвещение, 2010. 204 с.

5. Федеральный государственный образовательный стандарт начального общего образования [Текст] - М.: Просвещение, 2009. 41 с.

5. Приложение

   1. Страница учебника

2. Раздаточный материал

Не вычисляя значений произведений составь из них верные равенства, используя буквенное выражения сочетательного свойства умножения (а*b)*с=а*(b*с).

15*(10*6)

18*(5*8)

(20*5)*3

1. 12