Муниципальное казённое общеобразовательное учреждение средняя общеобразовательная школа п.Красноярка

СОГЛАСОВАНО:

Зам. директора по УВР

___________________ Н.Е.Есаулкова

УТВЕРЖДАЮ:

Директор МКОУ СОШ п.Красноярка

Филиппов А.Н._________________

Приказ №______________________

От «___» ________________2016 г.

РАБОЧАЯ ПРОГРАММА

ВНЕУРОЧНОЙ ДЕЯТЕЛЬНОСТИ

«Клуб юных математиков»

4 КЛАСС

Учитель-составитель:

Новокрещенова В. В.

2016г.

«...Только то обучение является хорошим,

которое забегает вперед развития»

Л.С.Выготский

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Актуальность программы определена тем, что младшие школьники должны иметь мотивацию к обучению математики, стремиться развивать свои интеллектуальные возможности. Данная программа позволяет учащимся ознакомиться со многими интересными вопросами математики на данном этапе обучения, выходящими за рамки школьной программы, расширить целостное представление о проблеме данной науки. Решение математических задач, связанных с логическим мышлением закрепит интерес детей к познавательной деятельности, будет способствовать развитию мыслительных операций и общему интеллектуальному развитию. Не менее важным фактором реализации данной программы является и стремление развить у учащихся умений самостоятельно работать, думать, решать творческие задачи, а также совершенствовать навыки аргументации собственной позиции по определенному вопросу.

Содержание программы соответствует познавательным возможностям младших школьников и предоставляет им возможность работать на уровне повышенных требований, развивая учебную мотивацию.

Содержание занятий кружка представляет собой введение в мир элементарной математики, а также расширенный углубленный вариант наиболее актуальных вопросов базового предмета - математика. Занятия математического кружка должны содействовать развитию у детей математического образа мышления: краткости речи, умелому использованию символики, правильному применению математической терминологии и т.д.

Творческие работы, проектная деятельность и другие технологии, используемые в системе работы кружка, должны быть основаны на любознательности детей, которую и следует поддерживать и направлять. Данная практика поможет ему успешно овладеть не только общеучебными умениями и навыками, но и осваивать более сложный уровень знаний по предмету, достойно выступать на олимпиадах и участвовать в различных конкурсах. Все вопросы и задания рассчитаны на работу учащихся на занятии. Для эффективности работы кружка желательно, чтобы работа проводилась в малых группах с опорой на индивидуальную деятельность, с последующим общим обсуждением полученных результатов. Кружок создается на добровольных началах с учетом склонностей ребят, их возможностей и интересов. Следует помнить, что помочь ученикам найти себя как можно раньше - одна из важнейших задач учителя начальных классов.

Программа занятий рассчитана на 1 год. Занятия 1 раз в 2 недели. Продолжительность каждого занятия не должна превышать 30 - 40 минут.

Цель: развивать математический образ мышления

Задачи:

• расширять кругозор учащихся в различных областях элементарной математики;

• расширять математические знания в области многозначных чисел;

• содействовать умелому использованию символики;

• учить правильно применять математическую терминологию;

• развивать умения отвлекаться от всех качественных сторон и явлений, сосредоточивая внимание на количественных сторонах;

• уметь делать доступные выводы и обобщения, обосновывать собственные мысли.

Гипотеза. Предположение об эффективности задач логического, поискового, познавательного характера обосновывается следующими доводами:

• развитие личности ученика, его творческого потенциала;

• развитие интеллекта, исследовательского начала, развитие познавательных действий и операций, начиная от действий, связанных с восприятием, припоминанием уже знакомого, запоминанием посредством мнемонических действий, умений классифицировать посредством осмысления и сознательности и кончая оперированием логического и творческого мышления.

Принципы программы:

• Актуальность. Создание условий для повышения мотивации к обучению математики, стремление развивать интеллектуальные возможности учащихся.

• Научность. Математика - учебная дисциплина, развивающая умения логически мыслить, видеть количественную сторону предметов и явлений, делать выводы, обобщения.

• Системность. Курс строится от частных примеров (особенности решения отдельных примеров) к общим (решение математических задач).

• Практическая направленность. Содержание занятий кружка направлено на освоение математической терминологии, которая пригодится в дальнейшей работе, на решение занимательных задач, которые впоследствии помогут ребятам принимать участие в школьных и городских олимпиадах и других математических играх и конкурсах.

• Обеспечение мотивации. Во-первых, развитие интереса к математике как науке физико-математического направления, во-вторых, успешное усвоение учебного материала на уроках и выступление на олимпиадах по математике.

• Реалистичность. С точки зрения возможности усвоения основного содержания программы - возможно усвоение за 34 занятия.

• Курс ориентационный. Он осуществляет учебно-практическое знакомство со многими разделами математики, удовлетворяет познавательный интерес школьников к проблемам данной точной науки, расширяет кругозор, углубляет знания в данной учебной дисциплине.

Предполагаемые результаты. Занятия в кружке должны помочь учащимся:

• усвоить основные базовые знания по математике; её ключевые понятия;

• помочь учащимся овладеть способами исследовательской деятельности;

• формировать творческое мышление;

• способствовать улучшению качества решения задач различного уровня сложности учащимися; успешному выступлению на олимпиадах , играх, конкурсах.

Основные виды деятельности учащихся:

• решение занимательных задач

• оформление математических газет

• участие в математической олимпиаде, международной игре «Кенгуру»

• знакомство с научно-популярной литературой, связанной с математикой

• проектная деятельность

• самостоятельная работа

• работа в парах, в группах

• творческие работы

• экскурсия

КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

п/п

Темы занятий

Дата

проведения

1

Что дала математика людям? Зачем ее изучать? Когда она родилась, и что явилось причиной ее возникновения?

2

Старинные системы записи чисел. Упражнения, игры, задачи.

3

Иероглифическая система древних египтян. Упражнения, игры, задачи.

4

Римские цифры. Упражнения, игры, задачи.

5

Римские цифры. Как читать римские цифры?

6

Решение задач из стенгазеты № 1.

7

Пифагор и его школа. Упражнения, игры, задачи.

8

Бесконечный ряд загадок. Упражнения, игры, задачи.

9

Архимед. Упражнения, игры, задачи.

10

Умножение. Упражнения, игры, задачи.

11

Конкурс знатоков. Математические горки. Задача в стихах. Логические задачи. Загадки.

12

Деление. Упражнения, игры, задачи.

13

Делится или не делится.

14

Решение задач

15

Игра «Веришь или нет».

16

Математический КВН. Решение ребусов и логических задач.

17

Решение олимпиадных задач, счёт. Загадки-смекалки.

Занятие 1.

ТЕМА. ЧТО ДАЛА МАТЕМАТИКА ЛЮДЯМ? ЗАЧЕМ ЕЁ ИЗУЧАТЬ?

КОГДА ОНА РОДИЛАСЬ, И ЧТО ЯВИЛОСЬ ПРИЧИНОЙ ЕЁ ВОЗНИКНОВЕНИЯ?

Цель: показать практическую значимость математики, познакомить с историей развития.

Ход занятия

I. Актуализации опорных знаний. (Знаю.)

Задания. Разделить учащихся на три группы и предложить ответить на вопросы:

- Что дала людям математика?

- Зачем ее изучать?

- Когда она родилась и, что явилось причиной её возникновения? (Дети рассказывают друг другу, записывают главные мысли, выбирают консультанта, и он выступает от данной группы с выводами по этим вопросам.)

II. Стадия осмысления содержания.

Рассказ учителя.

По поводу древности математики никто не спорит, а вот о том, что же побудило людей заниматься ею, существует много мнений. Одно из них: математика, так же как поэзия, живопись, музыка, театр и вообще - искусство, была вызвана к жизни духовными потребностями человека, его, быть может, не до конца осознанным еще стремлением к познанию и красоте.

В истории науки принято называть первым математиком Фалеса - греческого купца, путешественника и философа (он родился в VII веке до н. э.). Конечно, существуют более ранние египетские и вавилонские источники, содержащие разнообразные арифметические и геометрические сведения, но в них нет ещё намека на доказательства.

Фалесу же приписывают первые математические теоремы. Кстати, Фалес не был только «чистым» математиком, он решал и прикладные задачи.

Изменив тень от египетской пирамиды и тень от шеста, и применив свои теоремы о подобии, он вычислил высоту пирамиды. Так, по легенде, родилась наша наука - математика.

В прежние времена, вплоть до конца XIX столетия, математикой занимались немногие. Сейчас ей посвящают жизнь десятки, а возможно, и сотни тысяч людей. Одних вдохновляет прикладной аспект науки, других - её внутренняя красота и гармония, а третьих привлекает и то и другое.

«Красота? Какая еще красота, - с недоумением спросит ученик, не полюбивший ещё этот предмет. - Искусство - совсем другое дело!» Мы не удивляемся, когда волшебная сила искусства заставляет рыдать человека. Но математика?

Послушайте рассказ одного человека, современника Шекспира, об истории своего открытия.

«Восемь месяцев тому назад передо мной блеснул луч света, за три месяца увидел я день, и наконец, совсем недавно я смог увидеть лучезарное солнце ... я похитил золотые сосуды египтян, чтобы создать храм моему божеству вдали от пределов Египта ... Жребий брошен, я пишу книгу. Прочтется ли она моими современниками или потомством - мне все равно - она найдет своего читателя. Разве господь Бог не ожидал шесть тысяч лет созерцателя Своего творения?» Кто пишет это восторженное послание? И что произошло?

Но математика - это не только вдохновение и восхищение тех, кто способен оценить ее достижения. Её история переполнена и драматическими событиями. Нередко первооткрыватели опережали свое время и не встречали понимания у современников. Так было с открытием в XIX в. неевклидовой геометрии - одним из фундаментальных достижений науки, которое стало основой для всей современной физики; выдающийся русский ученый Николай Иванович Лобачевский умер непризнанным и неоцененным.

На вопрос: «Для чего изучают математику?» - замечательно ответил ещё в XIII веке английский философ и естествоиспытатель Роджер Бэкон:

«Тот, кто не знает математики, не может узнать никакой другой науки и даже не может обнаружить своего невежества».

Не правда ли, хорошо сказано!

1. Разминка «Думаем!».

1. На что похожа половинка яблока?

2. Можно ли в решете принести воды?

3. Что находится между городом и селом?

4. Что можно увидеть с закрытыми глазами?

5. У семерых братьев по сестре. Сколько всего сестер?

6. Сын моего отца, а мне не брат. Кто это?

7. Почему часто ходят и никогда не ездят?

8. Как далеко в лес может забежать заяц?

9. Как можно прочесть слово «загадка»?

10 Что летит быстрее стрелы?

Ответы: 1. На вторую половину; 2. Можно, когда она замерзает; 3. Союз и, 4. Сон;. 5. Одна. 6. Я сам; 7. По лестнице; 8. До середины леса, дальше он уже выбегает из леса; 9. Только слева направо; 10. Мысль.

2. Засеките время, за которое время вы справитесь с этим заданием.

Допишите недостающее число:

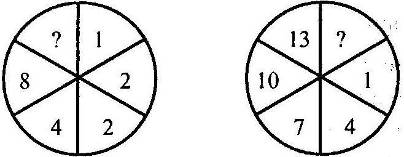
3.Задачи и задание

Задача 1.

В первый день путешественники проехали 40 километров, а во второй - 45 километров. Но из-за ремонта дороги им пришлось на 15 километров вернуться назад. Сколько всего километров они проехали за два дня?

Решение

Малыши-коротыши проехали 100 километров за два дня (40 + 45 + +15=100).

Задача 2.

В школе-интернате 800 учащихся. Пятая часть всех учеников отправится путешествовать, половина из них едет по «Золотому кольцу». Сколько детей едет по «Золотому кольцу»?

Решение

(800:5):2 = 80 уч. - едет по « Золотому кольцу».

Это интересно!

Задание.

Проведите на этих четырех геометрических фигурах всего по одной линии, чтобы из них образовались буквы. Они составят название одного из видов спорта.

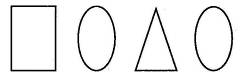
Решение

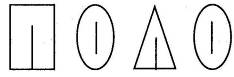
Ребусы

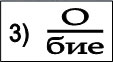
Ответы на математические ребусы

1. Показатель

2. Наклонная

3. Подобие

4. Стереометрия

III. Стадия рефлексии.

- Какое задание вам показалось трудное?

- Почему вам было трудно?

- А что вам было интересно?

- Кто был первым математиком?

- Почему именно Фалес?

- Как он вычислил высоту египетской пирамиды

- Кто замечательно ответил на вопрос: «Для чего изучают математику?» Что он сказал по этому поводу.

Занятие 2.

ТЕМА. СТАРИННЫЕ СИСТЕМЫ ЗAПИСИ ЧИСЕЛ. УПPАЖНЕНИЯ, ИГРЫ, ЗАДАЧИ.

Цели: расширить познания об истории; развивать внимание, память, воображение, логику мышления.

Ход занятия

I. Стадия вызова.

- Когда появилась единичная система счисления?

- Для чего она была нужна? Какой вы знаете счет?

( Выслушать все ответы детей . Сделать вывод из сказанного детьми. )

II. Стадия осмысления содержания.

1. Рассказ учителя.

Память человечества не сохранила, не донесла до нас имя изобретателя колеса или гончарного круга. Это и неудивительно: более 10 тысяч лет прошло с тех пор, как люди всерьез занялись земледелием, скотоводством и производством простейших товаров. Назвать же имя гения, впервые задавшегося вопросом « сколько?», тем более невозможно.

В каменном веке, когда люди собирали плоды, ловили рыбу и охотились на животных, потребность в счете возникла так же естественно, как и потребность в добывании огня. Об этом свидетельствуют находки археологов на стоянках первобытных людей. Например, в 1937 году в Вестонице (Моравия) на месте одной из таких стоянок была найдена кость с 55 глубокими зарубками. Позже и в других местах находили столь же древние каменные предметы с точками и черточками , сгруппированными по три или по пять. Такая система записи чисел называется единичной, так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Группировки и вспомогательные значки используются лишь для облегчения восприятия больших чисел.

Единичная система счисления первобытных людей, рисовавших палочки на стенах пещеры или делавших зарубки на костях животных и ветках деревьев, не забыта и по сей день. Как узнать, на каком курсе учится курсант военного училища? Сосчитайте, сколько полосок нашито на рукаве мундира. На Кубе на форме девочек на юбке, нашито столько полос, на каком курсе она учится. О количестве самолетов противника, сбитых асом в воздушных боях, говорит число звездочек, нарисованных на фюзеляже его самолета.

Поштучно считать предметы удобно тогда, когда их не очень много. Пересчитывать же таким образом большие совокупности скучно и утомительно, поэтому возникла идея объединять единицы в группы. Появился счет пятерками, десятками, двадцатками - по количеству пальцев рук и ног «счетовода».

2. Разминка.

1) 4 крыла, а не бабочка. Крыльями машет, а ни с места. Что это такое?

2) Имеет 4 зуба. Каждый день появляется за столом, а ничего не ест. Что это?

3) Для пяти мальчиков пятеро чуланчиков, а выход один. Что это?

4. 1 ствол, много ветвей, а на веточках много гостей.

5. Что становится легче, когда его надувают?

6. 3 брата по одной дорожке бегут. 1 впереди, а 2 - позади: эти 2 бегут, но никак переднего догнать не могут.

7) Всегда шагаем мы вдвоем, похожие, как братья. Мы за обедом - под столом, а ночью - под кроватью.

8) У него 4 лапки, лапки-цап-царапки, пара чутких ушей, он гроза для мышей.

9) На четырех ногах стою, ходить же вовсе не могу.

10) Возле елок из иголок летним днем построен дом. За травой не виден он, а жильцов в нем миллион.

Ответы. 1. Ветряная мельница; 2. Вилка; 3. Перчатка; 4. Дерево; 5. Резиновый шарик; 6. Колесо детского велосипеда; 7. Ботинки; 8. Кот; 9. Стол; 10. Муравейник.

3. Вставьте пропущенное число.

16 (93) 15

14 (...) 12

Ответ: 78.

3. Вставьте пропущенную букву.

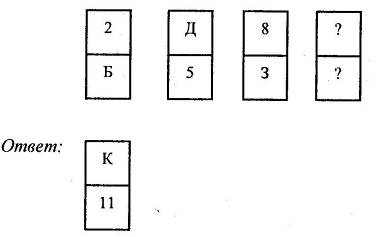
3. Расставьте в пустые клетки квадрата числа 11,15,19,25,29, 33, 39, 43 так, чтобы значения сумм во всех вертикальных и горизонтальных строчках были равны 87.

3. Решите задачу.

Для семьи дачница на зиму засаливает 86 кг огурцов. Сначала она засолила 42 кг огурцов, разложив их в три банки. Затем засолила еще три такие же банки. Хватит ли засоленных огурцов для семьи?

Решите задачу разными способами.

1-й способ.

Решение:

1) 42 : 3 = 14( кг) - в одной банке огурцов.

2. 14 х 3 = 42 (кг) - в трех банках.

3. 42 + 42 = 84 ( кг) - засолила дачница огурцов.

4. 86 - 84 = 2 ( кг) - осталось огурцов.

Ответ: останется 2 кг огурцов, так как 84 < 86.

2-й способ.

Решение:

1) 42 + 42 =84 (кг) - засолила дачница огурцов, так как «затем засолила три такие же банки».

2) 86 - 84 = 2 (кг) - осталось огурцов у дачницы.

Ответ: останется 2 кг огурцов.

3-й с п о с о б .

86 - (42 +42) = 2 (кг) - останется огурцов у дачницы.

7. Учимся думать.

Найдите три одинаковых рисунка.

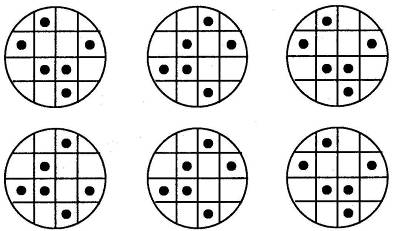
8. Задача-сказка

Дубы для царя

Однажды поехал царь посмотреть на свое царство. Проезжает через лес, видит стоит на поляне двадцать дубов, один другого краше. Обомлел царь от удивленья. А потом и говорит слугам: "Хочу, чтобы эти дубы у моего дворца росли". Да разве столетние дубы пересадишь? Но приказ есть приказ. Дни и ночи думали царские мастеровые, а толку никакого. Как веленье царя исполнить? Дались ему эти дубы...

Подсказка.

Дубы переносить затруднительно... Но уж если царь приказал, чтобы у царского дворца дубы росли - придется выполнить. Как? Может, посадить маленькие дубки, а царь подождет лет сто?

Ответ.

Один мастеровой посоветовал не дубы пересадить, а на поляне дворец построить. Так и сделали. Царь остался доволен. И дубы при дворце , и дворец при царе.

III. Стадия рефлексии.

- Какое задание вам показалось легким?

- Какие задания вас заставляют думать, развивают вашу па-

мять, мышление?

- Почему возникла у людей потребность в счете?

- На чем они делали отметки?

- Какая система называется единичной?

- Где, в каких случаях сейчас пользуются этой системой?

- Как удобно считать большие совокупности?

- Какой появился счет?

Домашнее задание: найдите в энциклопедии сведения о старинной системе древних египтян; приготовьте сообщение.

Занятие 3

ТЕМА. ИЕРОГЛИФИЧЕСКАЯ СИСТЕМА ДРЕВНИХ ЕГИПТЯН.

УПРАЖНЕНИЯ, ИГРЫ, ЗАДАНИЯ

Цели: познакомить с иероглифической системой; учить логически мыслить; управлять своим мышлением.

Ход занятия

I. Стадия вызова.

- Что вы знаете о иероглифической системе древних египтян?

- Какие записи чисел они употребляли?

- Откуда мы узнали о тайне древнеегипетского счета?

II. Стадия осмысления.

Сообщения учителя.

Около 3-2,5 тысяч лет до новой эры древние египтяне придумали свою числовую систему. В ней ключевые числа: 1, 1О, 100 и т. д. - изображались специальными значками-иероглифами. Египтяне высекали их на стенах погребальных камер, писали тростниковым пером на свитках папируса.

Для записи чисел они употребляли следующие иероглифы:

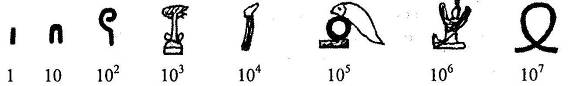
Все остальные числа составлялись из этих ключевых при помощи операции сложения. Например, запись:

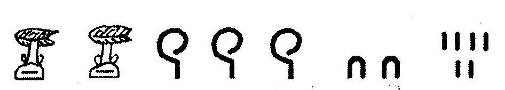
расшифровывалась так: две тысячи, три сотни, два десятка и шесть единиц.

Величина числа, записанного в иероглифической системе, не зависит от того, в каком порядке расположены составляющие его знаки. Даже если записать их справа налево, один под другим или вперемешку - число от этого не изменится.

В результате упрощений и стилизаций от иероглифов позднее произошли условные знаки, облегчающие письмо от руки. Они легли в основу так называемого иератического письма (от греческого «иератикос» - «священный»). Эту систему записи чисел можно обнаружить в более поздних египетских папирусах.

Уцелели два математических папируса, раскрывающие тайну древнеегипетского счета. Один из них назван « папирусом Райнда», другой - «Московским».

III Стадия закрепления содержания.

1. Разминка.

1) Три сестры собирали грибы. Первая нашла 9 подберезовиков, вторая - 6 подберезовиков. Сколько нашла третья сестра, если всего они собрали 20 грибов?

2. Какое число следует за числами: 6; 8; 11.

3. Какие числа на 3 больше чисел: 8,9; 14.

4. Увеличьте числа на 5: 12; 14; 16; 18.

5. Задумано число, прибавили к нему число 3 и получили число 9. Какое число задумали?

6) Задумано число. Увеличили его на 11 и получили число 16.

Какое число задумали?

7. Назовите самое наименьшее двузначное число?

8. Какой отрезок меньше: 4 см или 2 см 1 мм?

9. Какое число больше двадцати девяти на 17?

10. Задумайте однозначное число, прибавьте к нему 17, из полученной суммы вычтите 9, из остатка вычтите задуманное число. В результате получится 8. Проверьте.

2. Учимся думать.

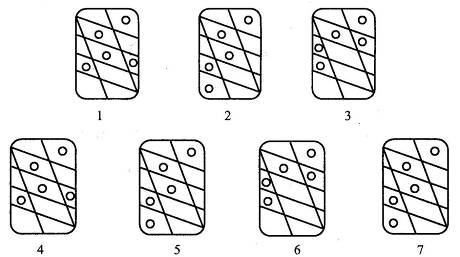
3. Задачи сказочного характера.

Красная Шапочка несла бабушке 14 пирожков: с мясом, с грибами и с капустой, которых было наибольшее количество. Причем пирожков с капустой было вдвое больше, чем пирожков с мясом. Сколько пирожков с грибами?

Решение

Пусть пирожков с мясом 2, тогда с капустой 2 х 2=4 (п.) Следовательно, с грибами 14 - (2+4)) = 8 (п.)

Но в этом случае пирожков с капустой не наибольшее количество.

Пусть пирожков с мясом 3, тогда с капустой 3 х 2=6 (п.)

Этот результат соответствует условию задачи.

Ответ: Красная Шапочка несла 5 пирожков с грибами.

4. Сколько лет каждому сыну?

Некто имеет 6 сыновей, один другого старше 4 годами, а самый старший сын втрое старше младшего. Каков возраст сыновей?

Ответ: Так как каждый из сыновей на 4 года старше последующего, то старший брат на 20 лет старше младшего. Значит, удвоенный возраст младшего сына равен 20 годам. Поэтому младшему сыну 1О лет. А возраста остальных братьев равны 14, 18, 22, 26 и 30 годам.

IV. Стадия рефлексии.

- Как вы считаете величина, записанного в иероглифической системе зависит от того, в каком порядке расположены составляющие его знаки?

- Как названы найденные египетские папирусы?

V. Итог занятия.

- Что было трудно на этом занятии?

- Какое из заданий было более интересно для вас?

- Как вы считаете, на уроках математики вам пригодятся те знания, которые вы получили на внеклассных занятиях?

Домашнее задание: подберите несколько занимательных задач.

3анятие 4.

ТЕМА. РИМСКИЕ ЦИФРЫ

(игры, упражнения, занимательные задачи)

Цели: учить решать занимательные задачи; учить рассуждать; развивать мышление.

Ход занятия

I. Проверка домашнего задания.

- Какие вы нашли задачи занимательного характера? Работа по группам.

1-я группа дает занимательные задания второй группе.

2-я группа - третьей группе.

3-я группа - первой группе.

Консультанты рассказывают, как они решили задачи. Подводится итог.

II Стадия вызова.

- Какая из множества иероглифических систем счисления используется до сих пор?

- Изменился ли облик римских цифр?

- Какие вы знаете обозначения римских цифр. Запишите их.

Сообщение учителя.

Среди множества иероглифических систем счисления, которые существовали в разные времена у разных народов, только одна используется до сих пор. Её цифры знакомы всем, хотя им уже около 2,5 тысячелетий. Эти цифры встречаются на циферблатах часов, фронтонах старинных и современных зданий, памятниках, страницах книг. Ну конечно же, речь идет о римской системе счисления.

Нельзя сказать, что время совсем не коснулось облика римских цифр. Если бы житель Древнего Рима захотел прочитать число, обозначающее дату открытия станции метро «Римская» в Москве, то он оказался бы в неимоверном затруднении. Причина в том, что только знаки I, V, Х с течением времени не претерпели каких-либо изменений. Другие же цифры в древности изображались иначе.

Ученые предполагают, что первоначально иероглиф для числа 100 имел вид пучка из трех палочек наподобие русской буквы Ж, а для числа 50 - вид верхней половинки этой буквы: W. В дальнейшем последний иероглиф постепенно трансформировался в знак L. А число 100 стали обозначать буквой С (от начальной буквы латинского слова сеntur - «сто»).

Символы для чисел 500 и 1000 также прошли длительную эволюцию. Вначале для числа 1000 применялись значки Ф. Например, на титульном листе книги «Рассуждение о методе» известного французского математика и философа Рене Декарта, изданной в 1637 г., указана дата ФРСХХХVII. В этой записи наряду с уже известными нам цифрами I, V, Х, С использованы старинные римские иероглифы: Ф = 1000, D = 500 Пришедшие им на смену знаки М и D произошли от начальных букв латинских слов mille «тысяча» и demimillle - «половина тысячи», «пятьсот».

Древние римляне могли выразить одним знаком и числа больше тысячи.

Цифра, помещалась в рамку, умножалась на100000.

III. Стадия осмысления содержания.

1. Разминка.

1. На четырех ногах стою, ходить же вовсе не могу.

2. Один сторож, много веток: все по горнице гуляют, сор повсюду подбирают,

3) Рядышком двое стоят, направо, налево глядят. Только друг

друга не видят, это, должно быть, им очень обидно.

4. Спинка, доска и 4 ноги - что я задумал, скорей назови!

5. Вверху зелено, внизу красно, в землю вросло.

6. 5 братьев: годами равные, ростом разные.

7. У двух матерей по 5 сыновей.

8. Как только с места тронусь я, так четверо начнут кружиться.

9. Восемь ног, как восемь рук, вышивают шелком круг. Мастер в шелке знает толк. Покупайте, мухи, шелк!

10) 5 братьев у всех одно имя.

Ответы: 1. Стол. 2. Веник. 3. Глаза. 4. Стул. 5. Морковь. 6. Пальцы. 7. Пальцы. 8. Телега. 9. Паук. 10. Пальцы.

2. Подумайте, как следует разделить эту фигуру на четыре равные и одинаковые по форме части, чтобы сумма чисел в каждой из них равнялась 20.

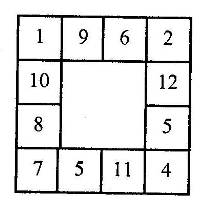
3. Выберите правильный ответ.

- Выберите нужную фигуру из 6 пронумерованных , чтобы завершить картинку.

4. Вычислите!

На соревнованиях леопард прыгнул в длину на 7 метров. Это на 1 м дальше, чем собака. Антилопа прыгнула на 4 м дальше, чем собака, и на 7 м дальше, чем лягушка. На сколько метров прыгнули антилопа, лягушка, собака?

Ответ: Леопард - на 7 метров, собака - на 6 метров; антилопа- на 10 м (6 + 4); лягушка - на 3 м (10 - 7).

5. Порассуждайте!

Летела стая гусей, а навстречу им гусак:

- Здравствуйте, десять гусей!

- Нет. Нас не десять. Если бы ты был с нами да еще двое гусей, то тогда бы было десять.

Сколько в стае гусей? (1 0- 3 = 7.)

6. «Геометрический»

- Сколько треугольников на чертеже?

3. Решите задачу.

Помидоры укладывали в одинаковые ящики. В 7 ящиках помещается на 32 кг больше, чем в 3 ящиках. На базе 120 ящиков. Хватит ли их для укладки 872 кг помидоров?

Решение:

1) 7 - 3 = 4 ( ящ.)

2. 32: 4 = 8 (кг) - помещается помидоров в 1 ящик.

3. 872 : 8 = 109 - необходимо ящиков.

Ответ: хватит, так 120> 109.

8. Подумайте!

Двое ели сливы. Один сказал другому: «Дай мне свои две сливы, тогда будет у нас слив поровну», - на что другой ответил: «Нет, лучше ты мне дай свои две сливы - тогда у меня будет в два раза больше, чем у тебя». Сколько слив у каждого?

Ответ: так как передача двух слив уравнивает число слив у собеседников, то у одного из них на четыре сливы больше, чем у другого. Если же человек, у которого слив меньше, две сливы, отдаст человеку, у которого их больше, то разница увеличится до 8 слив. Поскольку второй человек тогда будет иметь слив в два раза больше, то ясно, что у одного из них после передачи будет 8 слив, а у другого 1 6 слив. Следовательно, до передачи двух слив у одного было 10 слив, а у другого было 14 слив.

IV. Стадия рефлексии.

- Какая из задач показалась вам трудной? В чем?

- Вам интересно узнавать новое о математике? Например,

о римской системе счисления?

- Какой иероглиф был для числа 100?

- Как стали обозначать число 100?

Домашнее задание: найдите в литературе ( в энциклопедии или «Я познаю мир» или любой другой записи римских чисел.

Занятие 5.

ТЕМА. РИМСКИЕ ЦИФРЫ. КАК ЧИТАТЬ РИМСКИЕ ЦИФРЫ?

Цели: познакомить с римскими цифрами; учить решать задачи логического характера; делать анализ и синтез задач.

Ход занятия

I. Стадия вызова.

- Какой значок у древних римлян мог выразить числа больше

тысячи?

. II Стадия осмысления содержания.

1. Сообщение учителя.

Как читать римские цифры? Одно из правил записи римских чисел гласит: «Если большая цифра стоит перед меньшей , то они складываются, если же меньшая стоит перед большей (в этом случае меньшая цифра не может повторяться), то меньшая вычитается из большей». К примеру, VII = 5 + 1 + 1 = 7; IX = 10 - 1 = 9. Пользуясь этим правилом можно рассчитать, в каком году открылась станция метро «Римская»:

МСМХСУ = 1000 + (1000 - 100) + (100 - 10) +5 = 1995.

В наши дни любую из римских цифр запрещается записывать в одном числе более трех раз подряд. В связи с этим выражения VIIII, ХХХХ и т. п. считаются некорректными. Однако древние римляне о подобном ограничении ничего не ведали, и число 1995 скорее всего записали бы так: MDCCCCLXXXXV.

Только что мы столкнулись С любопытным феноменом в «обществе» римских чисел: разрешив цифрам-кирпичикам при «сборке» новых чисел не только складываться, но и вычитаться, мы тем самым лишили римские числа одного из важных математиче­ских свойств - единственности представления. Что теперь мешает, например, записать дату открытия станции метро «Римская» как МVМ, или как М DVD, или еще несколькими другими способами?

Если вы хотите записывать римские числа так, чтобы они полностью соответствовали пока ещё не утвержденному международному стандарту, то в этом поможет приведенная таблица.

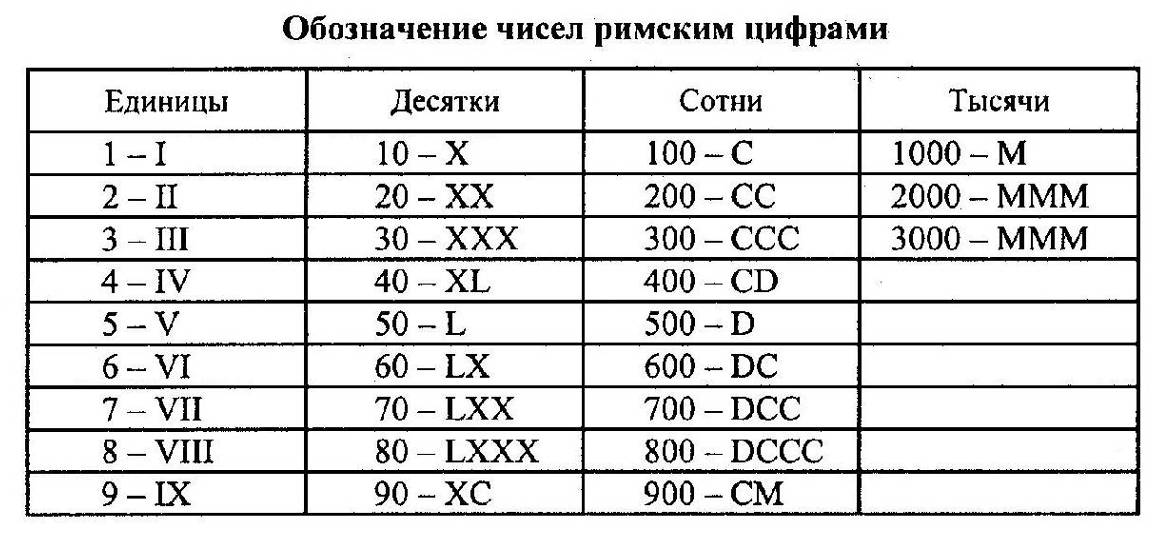
Она позволяет обозначить любое число от 1 до 3999. Сначала запишите число как обычно, в десятичной системе. Затем для цифр, стоящих в разрядах тысяч, сотен, десятков и единиц, по таблице подберите соответствующую кодовую группу. Например, вот как будет выглядеть число 3999: MMMCMXCIX.

2. Разминка.

1. На сколько число 59 больше числа 32?

2. На сколько число 72 больше числа 17?

3. На сколько число 79 меньше 90?

4. На сколько число 93 больше 31?

5. К числу 31 прибавил и задуманное число и получили число

96. Какое число задумали?

6. Из числа 76 вычли 28, Какое число получилось?

7. Из числа 84 вычли 37. Какое число получилось?

8. Дополните число 93 до 100.

9. Дополните число 69 до следующего десятка.

10. Задумайте однозначное число, прибавьте к нему 17, из полученной суммы вычтите 9. Из остатка вычтите задуманное число. В результате получится число 8. Проверьте.

3. Добавьте крючочки и палочки к овалам, чтобы получилось слово:

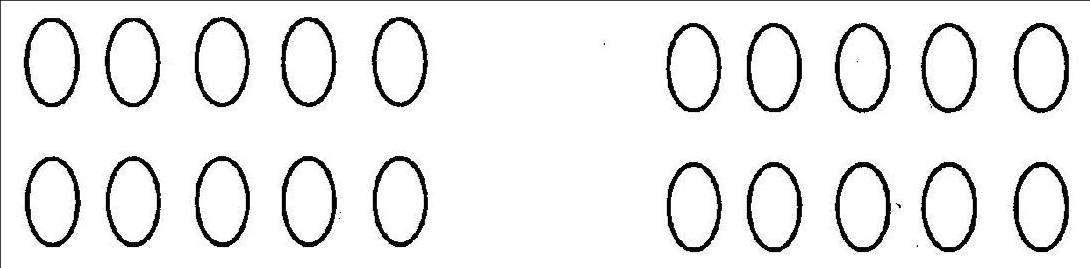
4. Нестандартные задачи

5.Решите задачу.

Лиса Алиса и кот Базилио привели на пустырь Буратино.

- Это поле чудес: если закопаешь золотые монеты, то наутро вырастет дерево, на котором в 3 раза больше золотых монет. Затем полученные монеты снова можно закопать в землю, и снова вырастет дерево с монетами. Так можно снять несколько урожаев. Мы можем посторожить ночью эти монеты.

В награду за услуги лиса и кот потребовали отдавать после каждого урожая 9 монет. Подумав немного, Буратино не согласился с их требованиями. он заявил, что после двух урожаев у него совсем не останется денег. Уж лучше он сам посторожит.

Сколько золотых монет было у Буратино?

Решение

Второй урожай даст 9 монет. Значит, во второй раз Буратино посадит 9 : 3 = 3 ( монеты). Первый урожай даст 3 + 9 = 12 (монет). Следовательно, в первый раз Буратино посадит 12 : 3 = 4 (монеты).

Ответ: У Буратино было 4 золотые монеты.

6. Найдите первый множитель,

**

х

..8

96

Решение

Так как при умножении двузначного числа ** на число 8 мы получаем двузначное число, то число десятков множимого должно быть равно 1.

При умножении числа единиц множимого на число 8 мы получаем число, в числе единиц которого стоит цифра 6. Это возможно в двух случаях: или число единиц множимого равно 2, или оно равно 7. Но в последнем случае имеем произведение 17 х 8 = 136, то есть число трехзначное, а по условию задачи оно должно быть двузначным. Значит, число единиц множимого равно 2, и пример расшифровывается так:

12 8=96

7. Забавные истории.

Смекалистый слуга

Постоялец гостиницы обвинил слугу в краже всех его денег.

Смекалистый слуга сказал так: «Это правда, я украл все, что он имел». Тогда слугу спросили о сумме украденных денег, и он отвечал: «Если к украденной мною сумме прибавить еще 10 рублей, то получится мое годовое жалованье. А если к сумме его денег прибавить 20 рублей получится вдвое больше моего жалованья».

Сколько денег имел постоялец, и сколько рублей в год получал слуга?

Решение

Из условия задачи следует, что удвоенное жалованье слуги на 10 рублей превышает его жалованье. Значит, годовое жалованье слуги составляет 10 рублей, а постоялец, заявивший, что его обокрали, вообще не имел денег.

8. Решите задачу.

Школьники посадили за 3 дня 390 деревьев. В первый день они посадили 120 деревьев, во второй - на 50 деревьев больше, чем в первый, а в третий - все остальные деревья. Сколько деревьев посадили школьники в третий день?

Решение

1. 120 + 50 = 170 (д.) - посадили 130 второй день.

2. 120 + 170 = 290 (д.) - посадили в первый и второй день вместе.

3. 390 - 290 =100 (д.) - посадили в третий день.

Ответ: 100 деревьев.

9. Найдите правило изменения фигур (закономерность).

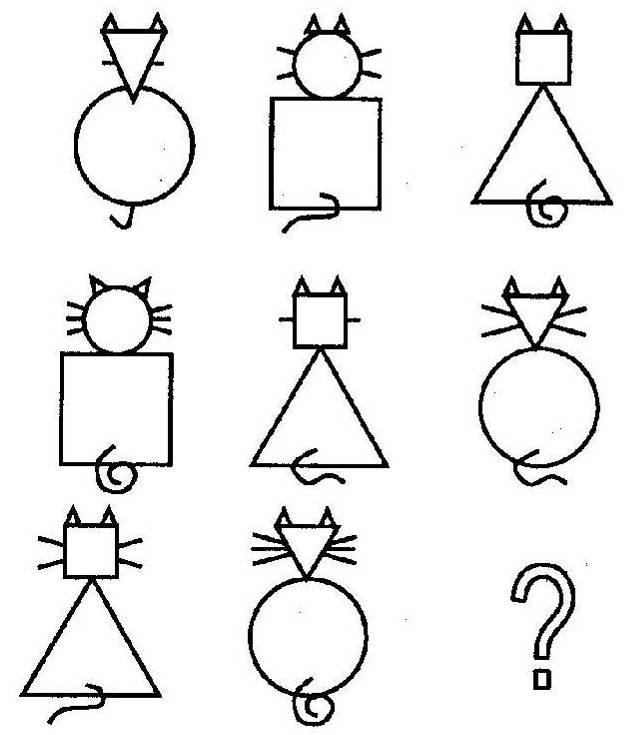
Ответ: На этом рисунке представлены схематичные изображения кошек. Уши кошек всегда одинаковые.

Их туловища в первом и во втором ряду представлены в виде треугольника, прямоугольника и круга.

В третьем ряду туловища двух первых кошек - круг и треугольник, следовательно, туловище третьей кошки в третьем ряду прямоугольник.

Головы кошек также представлены геометрическими фигура­ми, причем у треугольного туловища голова всегда квадрат, у прямоугольного - круг. Следовательно, голова у недостающей кошки должна быть в виде круга.

В первом и втором ряду кошки имеют по одной, две и три пары усов.

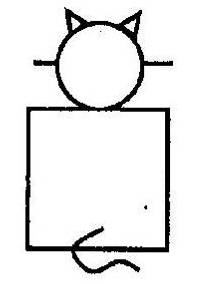
В последнем не хватает кошки с одной парой усов. В каждом ряду есть три разные формы хвостов.

В последнем ряду не хватает хвоста, обращенного вправо. Значит, недостающая кошка выглядит так:

III Стадия рефлексии.

- Как будут выглядеть числа 2898; 1865, обозначенные римскими цифрами?

- Так как читать римские цифры?

- Какое вы знаете правило?

IV. Итог занятии.

- Какие задания вызвали у вас затруднения?

- Что было легко?

- Что вам дал этот урок?

- Пригодится ли вам такая «разминочка» на уроках?

Домашнее задание: какие вы знаете другие иероглифические системы; найдите материал в энциклопедии и подготовьте к следующему занятию,

Занятие 6.

ТЕМА. ДРУГИЕ ИЕРОГЛИФИЧЕСКИЕ СИСТЕМЫ. УПРАЖНЕНИЯ, ИГРЫ, ЗАДАНИЯ.

Цели: познакомить с другими иероглифическими системами; развивать память, мышление, умение решать логические задачи; умение рассуждать.

Ход занятия

I. Стадия вызова.

- Какие вы знаете иероглифические системы?

Запишите число как обычно, в десятичной системе, например, 1287. А сейчас запишите его же римскими цифрами, для этого по таблице, которую мы с вами записали, подберите соответствующую кодовую группу.

II. Стадия осмысления содержания.

1.Сообщение учителя.

Кроме египетской и римской к иероглифической системам чисел относятся финикийская, пальмирская, критская, сирийская, греческая аттическая, или Геродианова ( именно из сообщения грамматика Геродиана, жившего во II- III веках, западноевропейские историки впервые узнали о её существовании ). Известны также старокитайская, староиндийская , ацтекская иероглифические системы. В них, как и в египетской и римской системах, вводятся ключевые числа, для обозначения которых применяются специальные иероглифы. Все остальные числа образуются приписыванием с той или иной стороны ключевого числа других ключевых чисел, возможно, с некоторыми повторениями.

Любопытно отметить, что у многих народов для обозначения числа 1 применялся один и тот же символ - вертикальная черточка. Это самое древнее число в истории человечества. Оно возникло из простой черты на земле, из зарубки на дереве или кости.

2 Разминка.

1 Два отца и два сына съели 3 апельсина, причем каждый съел по апельсину. Как это возможно?

2 Петя утверждает, что позавчера ему было 10 лет, а в будущем году исполнится 13. Возможно ли это ?

3 Какие цифры скрыты в каждой клеточке:

□□□ - □□ = 1

4 Три зайчонка: Прыг, Скок, Трусь - учились в разных классах лесной школы. Прыг был не старше Труся, а Скок не старше Прыга. Назови имя старшего, среднего и младшего зайчонка.

5 Какими способами можно разложить 15 карандашей в две коробки?

6 Задумайте число больше 10, к нему прибавьте 28, из полученной суммы вычтите 16, из остатка вычтите задуманное число. В результате получится число 12 . Проверьте.

7 Первое слагаемое 39, второе слагаемое на 17 больше. Чему равно второе слагаемое?

8 Какое число надо прибавить к числу 29, чтобы получить 65?

9 Дополните число 93 до 100.

Ответы: 1. Апельсин ели дед, отец, сын. 2. Свое заявление Петя делает 1 января, 31 декабря у него был день рождения, и ему исполнилось 11 лет, а 30 (позавчера) было 10, тогда на будущий год исполнится 13, поскольку в этом году ему исполнится 12.

3 Задача

Возраст старика Хоттабыча записывается числом с различными цифрами. Об этом числе известно следующее:

если первую и последнюю цифры зачеркнуть, то получится двузначное число, которое в сумме цифр, равной 13, является наибольшим;

первая цифра больше последней в 4 раза.

Сколько лет Хоттабычу?

Решение

Наибольшим двузначным числом с суммой цифр, равной 13, является 94.

Пусть последняя цифра 1, тогда первая цифра 1x4 =4. Но такая цифра в числе уже есть - ведь все цифры различные.

Пусть последняя цифра 2, тогда первая цифра 2 х 4 = 8. В этом случае все цифры различные.

Ответ: Старику Хоттабычу 8942 г.

4. Решите задачи.

1) Один из пяти братьев разбил окно.

Андрей сказал: «Это или Витя, или Толя».

Витя сказал: «Это сделал не я и не Юра».

Дима сказал: «Нет, один из них сказал правду, а другой неправ­ду».

Юра сказал: «Нет, Дима, ты не прав».

Их отец, которому, конечно, можно доверять, уверен, что не менее трех братьев сказали правду. Кто разбил стекло?

Решение

Установим имена братьев, сказавших правду.

Предположим, что Толя сказал правду. Тогда сказали неправду Андрей, Витя (про них Толя сказал, что они говорят неправду) и Дима, который возражает Толе.

Таким образом, сказавших неправду будет больше двух, а это противоречит условию задачи. Следовательно, Толя говорит неправду.

Предположим, что Дима говорит правду. Тогда неправду сказали Толя, один из первых двух братьев (это утверждает Дима) и Юра, который возражает Диме.

Вновь приходим к противоречию. Следовательно, Дима сказал неправду.

Значит, правду сказали Андрей, Витя и Юра. Но из высказываний Андрея и Вити следует, что окно разбил Толя.

2) В школу-интернат привезли 3 мешка муки и расходовали в течение четырех дней, каждый день по 28 кг. После этого осталось 32 кг муки. Сколько весил один мешок муки?

</ Решение

1. 28 х 4 = 112 (кг) - израсходовали за 4 дня.

1. 112 + 32= 144 (кг) - было всего муки.

2. 144 : 3 = 48 (кг) - было муки в одном мешке.

Ответ: 48 кг.

5. Ребусы.

Ответы на ребусы

1. Теорема Пифагора

2. Теорема

3. Отрезок

4. Задача

6. Геометрическая задача.

III. Стадия рефлексии.

1. Какое вы знаете самое древнее число в истории человечества?

2. Кроме египетской и римской системы, какие иероглифические системы вы знаете?

3анятие. 7.

ТЕМА. ПИФАГОР И ЕГО ШКОЛА

Цели: познакомить с Пифагором и его школой; развивать математическую любознательность и инициативу, умение рассуждать.

Ход занятия

I. Стадия вызова.

- Какой союз обосновал Пифагор, что входило в сферу интересов союза?

- Почему от пифагорейцев не осталось никаких текстов?

- Как называли пифагорейцы собственные исследования?

II. Стадия осмысления содержания.

1. Слово учителя.

Великий древнегреческий ученый Пифагор родился на острове Самос в VI в. до н. э. В молодости побывал в Египте, где учился у жрецов. Говорят, что он был допущен в сокровенные святилища Египта, посетил халдейских мудрецов

и персидских магов. Около 530 г. до н. э. Пифагор переехал в Кротон - греческую колонию в Южной Италии, где основал так называемый пифагорейский союз. В сферу интересов членов союза входили научные исследования, религиозно-философские искания, политическая деятельность. Они вели суровый образ жизни, превыше всего ценили самообладание, смелость и коллективную дисциплину. Пифагорейцы жили вместе, у них было совместное имущество, и даже свои открытия они считали общим достоянием.

Деятельность союза была окружена тайной, поэтому никаких текстов от ранних пифагорейцев не осталось. Кроме того, по традиции, они все открытия приписывали Пифагору, о котором уже при жизни ходили легенды. Кто на самом деле является автором того или иного результата, неизвестно.

Пифагорейцы называли собственные исследования «математа», что означает «науки», и делили их на четыре части: арифметику, геометрию, астрономию и гармонию (учение о музыке). Главной

считалась арифметика - наука о числах. Именно она лежала в основе и геометрии, и астрономии, и гармонии.

2.Разминка.

1) Представьте в виде сотен, десятков и единиц числа 8б; 807;

б04; 310.

2. Запишите число, которое при счете предшествует числу 600.

Какое число при счете следует за числом 599?

2. Задумали число, увеличили в 15 раз, получили число 525.

Какое число задумали?

4) Какое число состоит из 35 десятков и 7 единиц? б) Разность чисел 750 и 450 увеличить в 3 раза.

5)Произведение чисел 75 и 20 увеличить в 3 раза и уменьшить на 200.

6)Длина прямоугольника 17 см, ширина 3 см. Вычислите пери-

метр прямоугольника. Найдите площадь этого прямоугольника. 9)Увеличьте число в 10 раз и уменьшите на 10 единиц.

7) Какое число состоит из 6 сотен и 3 десятков?

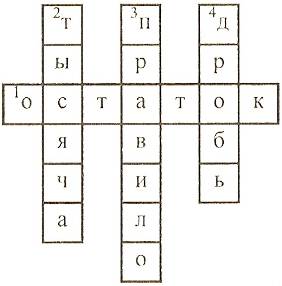
3. Разгадайте кроссворд.

1. Название числа, которое иногда получается при делении.

2. Наименьшее четырехзначное число.

3. Вывод, который ученик заучивает наизусть.

4. Особое число, которое записывается с помощью двух цифр.

4. Задача-шутка.

Разделите поровну 5 пряников между шестью мальчиками, не разрезая ни одного пряника, на 6 равных частей.

Решение

Если мы из 5 данных пряников 3 разрежем пополам, то получим 6 равных кусков, каждый из которых и отдадим мальчикам.

Затем разрежем 2 оставшихся пряника каждый на 3 равных части и получим опять 6 равных кусков, которые и отдадим мальчикам. Таким образом, задача решена, причем ни одного пряника не пришлось разрезать на 6 равных частей.

5. Какие оценки?

Когда Аня, Женя и Нина спросили какие им поставили оценки за контрольную работу по математике, учительница ответила: «Попробуйте догадаться сами, если я скажу, что в вашем классе двоек нет, а у вас троих оценки разные: причем у Ани - не 3, у Нины - не 3 и не 5. Какую оценку получила каждая из учениц?»

Ответ: у Нины - 4, у Ани - 5, У Жени - 3.

6.Задачи с девятками.

l) Представьте число 18 двумя девятками.

2) Выразите число 27 тремя девятками.

3) Напишите число 90 тремя цифрами 9.

4) Выразите число 0 четырьмя девятками и только одним мате-

матическим знаком.

5) Запишите число 36 четырьмя цифрами 9.

6) Представьте число 81 четырьмя девятками.

Ответы:

1. 18 = 9 + 9;

2. 27 = 9 + 9 + 9

3. 90 = 99 - 9

4. 0 = 99 - 99

5. 36 = 9 + 9 + 9 + 9

6. 81 = 99 - 9 - 9

7.Задача-шутка.

Двое пошли-

3 гвоздя нашли.

Следом четверо пойдут Много ли гвоздей найдут?

Ответ: Скорее всего, ничего не найдут.

8.Нестандартная задача.

IV. Стадия рефлексии.

- На какие части пифагорейцы делили «математа»?

- Какая часть считалась главной?

- В основе каких наук лежала арифметика.

3АНЯТИЕ 8.

ТЕМА. БЕСКОНЕЧНЫЙ РЯД ЗАГАДОК

Цели: познакомить с историей натурального числа; развивать творчество и инициативу детей; развивать математическое мышление.

Ход занятия

I. Стадия вызова.

- Кто назовет самое большое число?

- Существует ли самое большое число?

- Какое название для чисел, которые записываются с помощью

восьмидесяти миллионов миллиардов нулей, придумал Архимед?

- Какая самая большая, самая смелая «выдумка» за всю человеческую историю была высказана Архимедом?

II. Стадия осмысливания содержания.

1. Рассказ учителя.

«Кто назовет самое большое число?» в эту игру играли не только дети, но давным-давно и взрослые были озадачены этим вопросом.

Существует такая легенда: «И сказал Висвамитра:

- Перейдем к числам. Считай , повторяя за мной, пока не дойдем до ста тысяч: один, два, три, четыре ... затем десятки , сотни и тысячи.

И назвал отрок вслед за наставником единицы, десятки, сотни, но не остановился на сотне тысяч; нет, он шептал дальше до тех чисел, которыми можно считать все, начиная от зерен в поле ... Потом он перешел к счету звезд ночных, капель в море, и далее к счету песчинок великой реки Ганг, и к счету песчинок в миллионах таких рек ... Затем пошли еще более громадные числа ... и, наконец,

число, при помощи которого боги вычисляют свое прошедшее и будущее ... »

В этой прекрасной легенде есть очень важное слово «наконец»!

Как бы ни был искусен в счете Будда, он все-таки считал, что самое большое число существует! Правда, число это и по нашим сегодняшним меркам очень большое: в другой легенде о Будде говорится, что оно изображается единицей с 54-мя нулями. Как видите, фантазии у Будды эватало.

И все-таки его намного превзошел дневнегреческий ученый Архимед. Он написал книгу, которая называется: «Исчисление песчинок». Посвящена эта книга царю, который правил тогда в Сиракузах, городе, где жил Архимед. Вот как начинается книга Архимеда:

«Многие думают, государь, что число песчинок бесконечно. Я говорю не только о песке кругом Сиракуз и во всей Сицилии, но о леске на всей суше, как обитаемой, так и необитаемой. Другие не считают это число бесконечным, но думают, что назвать такое число невозможно.

Я же постараюсь по казать тебе, что можно назвать числа, намного превосходящие не только число песчинок в песчаной куче размером со всю Землю, но даже число песчинок, которое нужно для того, чтобы наполнить песком всю Вселенную ... »

Архимед считал Вселенную не бесконечной, но все-таки довольно большой: в сто миллионов раз больше Земли. И вот, по расчетам Архимеда, в такой Вселенной уместил ось бы количество песчинок, равное числу с 63-мя цифрами. Казалось бы, это почти то же самое что и «число Будды», но на самом деле оно в миллиард раз больше!

Однако Архимед не остановился на этом числе: он придумал названия для чисел, которые записываются с помощью восьмидесяти миллионов миллиардов нулей! Тут уж не только само число, но даже запись числа представить трудно. И все же попробуем. Предположим, что это число записано цифрами размером в один сантиметр, вот так: 10000000000

Если бы Архимед, назвав свое число, сразу же сел в космический корабль и полетел на нем вдоль записи этого числа, то до конца записи он долетел бы как раз к нашему времени - лететь ему пришлось бы больше двух тысяч лет!

Однако Архимед не мог бы даже начать записывать это число: ведь он не знал индийских (арабских) цифр. Но он смог такое число назвать! Вот это название: мириада мириад мириадо-мириадных чисел мириадомириадного периода. Название, конечно, длинновато, но во сколько раз оно короче записи!

Так выглядят «квадратные» числа. Мы сейчас называем их «квадратными» - например, мы говорим: четыре в квадрате - шестнадцать. Какие следующие «квадратные» числа?

Но самое главное даже не в том, что Архимед смог назвать число, которое намного превосходит потребности даже современной науки. Главное в том, что он впервые ясно высказал идею о бесконечности натурального ряда - это, может быть, самая смелая «выдумка» за всю человеческую историю!

Поразив воображение древних греков, идея бесконечности стала с тех пор одной из главных во всей математике. Вот что пишут об этом самые крупные математики двадцатого столетия - немецкий ученый Гильберт и французский ученый Пуанкаре.

Гильберт: «Ни одна проблема не волновала так глубоко человеческую душу, как проблема бесконечности».

Пуанкаре: «Если кто-нибудь захочет кратким и выразительным словом определить само существо математики, тот должен сказать, что математика - это наука о бесконечности».

Первыми начали изучать свойства натуральных чисел индийцы и греки - они заметили, что каждое натуральное число чем-то замечательно и не похоже на другие числа. Изменение всего-навсего на единицу меняет многие свойства числа - например, соседние числа никогда не делятся на одно и то же число. В древности были открыты и признаки делимости чисел (кстати, семь - единственное число из первого десятка, для которого нет удобного признака делимости).

То, что в воображаемом мире чисел существуют свои законы (например, сумма двух нечетных чисел - всегда четное число!), навело ученых на мысль, что законы чисел могут быть связаны с закономерностями в окружающем мире. И действительно, древнегреческий ученый Пифагор, который жил в VI веке до нашей эры, открыл удивительную связь между законами чисел и законами музыки: например, если уменьшить длину струны или флейты вдвое, тон звука повышается точно на одну октаву. Это произвело на Пифагора такое впечатление, что он провозгласил: «число есть начало всех вещей».

Пифагор установил и первую связь между числами и фигурами:

он ввел «треугольные» и «квадратные» числа.

Пифагор обнаружил интересную связь между нечетными числами и «квадратными»: сумма последовательных нечетных чисел, начиная с единицы, обязательно будет «квадратным» числом! Например, 1 + 3 = 4; 1 + 3 + 5 + 9; 1 + 3 + 5 + 7 + 16 и так далее.

Прошло две тысячи лет после того, как Пифагор открыл связь между нечетными и «квадратными: числами, и это открытие помогло Галилею открыть один из важнейших законов природы. Когда Галилей изучал падение тел, он заметил, что путь, пройденный падающим телом за вторую секунду, втрое больше, чем за первую секунду, а путь, пройденный за третью секунду, в пять раз больше, чем за первую, и так далее. Отсюда Галилей сделал вывод, что путь прямо пропорционален квадрату времени движения - так и был открыт закон падения тел.

2. Задача.

В портфеле лежат 15 тетрадей разной разлиновки: в одну линейку, в две линейки и в клеточку. Тетрадей в одну линейку в 7 раз больше, чем тетрадей в две линейки. Не раскрывая портфеля, узнайте, сколько в нем лежит тетрадей каждой разлиновки.

Ответ: допустим, что тетрадей в две линейки было 2. Тогда тетрадей в одну линейку было бы 14. И вместе тетрадей в одну линейку и две линейки было 16. Но в портфеле всего 15 тетрадей. Значит, тетрадей в две линейки было не 2, а 1. Тогда тетрадей в одну линейку - 7, а остальные 7 тетрадей - в клетку.

3. Задача «За грибами».

Дедушка пошел с четырьмя внучатами в лес по грибы. В лесу разошлись в разные стороны и стали искать грибы. Через полчаса дедушка сел под дерево отдохнуть и пересчитал все грибы: их оказалось 45штук. Тут прибежали к нему внучата, все с пустыми руками, ни один ничего не нашел.

- Дедушка! - просит один внук, - дай мне своих грибов, чтобы кузовок не был пустой. Авось, с твоей легкой руки много грибов наберу.

- И мне, дедушка!

- И мне дай!

Дед дал каждому и раздал, таким образом, детям все свои грибы. Все снова разбрелись в разные стороны, и случилось следующее. Один мальчик нашел еще 2 гриба, другой 2 потерял, третий нашел еще столько, сколько получил от деда, а четвертый потерял половину полученных от деда. Когда дети пришли домой и подсчитали свои грибы, то оказалось у всех поровну.

Сколько каждый получил от дедушки грибов, и сколько было у каждого, когда они пришли домой?

Решение

Нетрудно видеть, что третьему внуку дед дал грибов меньше всего, потому что третий внук должен был набрать еще столько же грибов, чтобы сравняться с братьями. Для простоты скажем, что третьему внуку дед дал грибов одну горсть.

Сколько же он дал четвертому горстей?

Третий внук принес домой 2 горсти, потому что сам еще нашел столько же грибов, сколько дал ему дед. Четвертый внук принес домой ровно столько же грибов, сколько и третий, т. е. тоже 2 горсти; но он половину своих грибов растерял по дороге, значит, дед дал ему 4 горсти.

Первый внук принес домой 2 горсти, но из них два гриба он сам нашел, значит, ему дед дал 2 горсти без двух грибов. Второй внук принес домой 2 горсти, да по дороге он потерял два гриба; значит , дед ему дал 2 горсти да еще 2 гриба.

Итак, раздал внукам 1 горсть, да 4 горсти, да 2 горсти без двух грибов, да 2 горсти с двумя грибами, итого 9 полных горстей (в двух горстях не хватало по два гриба, зато в двух других горстях было по два лишних гриба) В 9 равных горстях было 45 грибов; значит, в каждой горсти 45 : 9 = 5 грибов.

Третьему внуку дед дал 1 горсть , т. е. 5 грибов ; четвертому - 4 горсти, т. е. 5 х 4 = 20 грибов; первому - 2 горсти без двух грибов, т. е. (5 х 2) - 2 = 8 грибов; второму - 2 горсти с двумя грибами, т. е. (5 х 2) + 2 = 12 грибов.

4.Какая величина «лишняя» в каждой строчке?

а) 7 м 5 см, 750 см, 75 дм, 7 м 50 см;

б) 2741 км, 3047 дм, 7408 Ц, 1800 м;

в) 1000 см, 10000 см, 100 дм, 1 м.

Ответ: в первой строчке 7 м 5 см; во второй строчке 7408 ц; в

третьей строчке 1000 см.

IV. Стадия рефлексии.

- Как древние греки любили изображать числа?

- Как выглядят «квадратные» числа?

- Какое открытие помогло Галилею открыть один из важнейших законов природы?

- Как был открыт закон падения тел?

Занятие 9

ТЕМА. АРХИМЕД

Цели: познакомить с открытиями гениального ученого; воспитывать познавательный интерес к математике.

Ход занятия

I. Стадия вызова.

- Чему посвящены труды Архимеда?

- Какая идея осенила Архимеда?

- Какой закон открыл Архимед?

- Как своими знаниями помогал Архимед воинам?

II. Стадия осмысления содержания,

1. Слово учителя.

Несомненно, Архимед - самый гениальный ученый Древней Греции. Он стоит в одном ряду с Ньютоном, Гауссом, Эйлером, Лобачевским и другими величайшими матема-

тиками всех времен. Его труды посвящены не только математике. Он сделал замечательные открытия в механике, хорошо знал астрономию, оптику, гидравлику и был поистине легендарной личностью.

Сын астронома Фидия, написавшего сочинение о диаметрах Солнца и Луны, Архимед родился и жил в греческом городе Сиракузы на Сицилии. Он был приближен ко двору царя Гиерона II и его сына-наследника.

Хорошо известен рассказ о жертвенном венце Гиерона. Архимеду поручили проверить честность ювелира и определить, сделан венец из чистого золота или с примесями других металлов и нет ли внутри него пустот. Однажды, размышляя об этом, Архимед погрузился в ванну и заметил, что вытесненная его телом вода пролилась через край. Гениального ученого тут же осенила яркая идея, и с криком: «Эврика. Эврика!» (т. е. «Нашел , нашел!») он , как был нагой, бросился проводить эксперимент.

Идея Архимеда очень проста. Тело, погруженное в воду, вытесняет столько жидкости, каков объем самого тела. Поместив венец в цилиндрический сосуд с водой, можно определить, какое количество жидкости он вытеснит, т. е. узнать его объем. А зная объем и взвесив венец, легко вычислить удельную массу. Это даст возможность установить истину: ведь золото - очень тяжелый металл, а более легкие примеси, и тем более пустоты, уменьшают удельную массу изделия.

Но Архимед на этом не остановился. В труде «О плавающих телах» он сформулировал закон, который гласит: «Тело, погруженное в жидкость, теряет в своем весе столько, каков вес вытесненной жидкости». Закон Архимеда является (наряду с другими, позже открытыми фактами) основой гидравлики - науки, изучающей законы движения и равновесия жидкостей. Именно этот закон объясняет, почему стальной шар (без пустот) тонет в воде, тогда как деревянное тело всплывает. В первом случае вес вытесненной воды меньше веса самого шара, т. е. архимедова «выталкивающая» сила недостаточна для того, чтобы удержать его на поверхности. А тяжело груженый корабль , корпус которого сделан из металла, не тонет, погружаясь только до так называемой ватерлинии. Поскольку внутри корпуса корабля много пространства, заполненного воздухом, средняя удельная масса судна меньше плотности воды и выталкивающая сила удерживает его на плаву. Закон Архимеда объясняет также, почему воздушный шар, заполненный теплым воздухом или газом, который легче воздуха (водородом или гелием), улетает ввысь.

Знание гидравлики позволило изобрести винтовой насос для выкачивания воды. Такой насос (кохля) до недавнего времени применялся на испанских и мексиканских серебряных рудниках.

Малому и старому знакомо Архимедово правило рычага. Согласно преданию ученый произнес крылатую фразу: «Дайте мне точку опоры, и я подниму Землю!» Конечно, Архимед имел в виду применение рычага, но, прямо скажем, он был несколько самоуверен: кроме точки опоры и рычага понадобился бы совершенно фантастический - невероятно длинный и при этом несгибаемый стержень.

Достоверные факты и многочисленные легенды говорят о том, что Архимед изобрел немало интересных машин и приспособлений,

Царь Гирон приказал построить огромный корабль «Сиракосия». Но он был так тяжел, что множество воинов не могли сдвинуть его с места. Тогда Архимед сконструировал механизм, который позволил сделать это одному человеку. Царь сам спустил корабль на воду и в восторге закричал: «Отныне, что бы ни сказал Архимед, мы все будем считать истинным!»

Архимед был семидесятилетним стариком, когда римляне осадили его родной город Сиракузы. Чтобы помочь жителям в обороне, он изобретал военные машины. Мощные катапульты метали тяжелые камни на римские легионы. А более легкие обрушивали на врага целый град ядер. Специальные береговые краны, возвышавшиеся над крепостными стенами, поднимали крюками корабли римлян и опрокидывали их. Римский военачальник Марцелл, недовольный своими военными инженерами, восхищался Архимедом, который «черпал» море римскими кораблями». А легионеры в панике разбегались, когда из-за городской стены показывалась какая-нибудь веревка или бревно: «Архимед придумал новую машину на нашу погибель!»

Чтобы отразить нападение большого римского корабля, Архимед заставил греческих воинов до блеска отполировать металлические щиты, а затем выстроиться вдоль берега. По его указанию воины сфокусировали солнечные лучи от щитов в одной точке на борту корабля. Деревянная обшивка судна нагрелась до высокой температуры и вспыхнула - на корабле начался пожар.

Но для самого ученого все эти военные изобретения были лишь незначительными практическими приложениями его научных открытий. Кроме правила рычага и закона о выталкивающей силе,

заставляющей тела плавать, Архимед создал учение о центрах тяжести тел и с его помощью доказал теорему о медианах треугольника, которую теперь называют его именем.

2. Разминка.

1) Первое число 15, а другое число на 12 больше. Чему равна сумма этих чисел?

2) Первое слагаемое 39, второе слагаемое на 17 больше. Чему равно второе слагаемое?

3) Первое слагаемое 52, второе слагаемое на 33 меньше. Чему

равно второе слагаемое?

4. Первое слагаемое 27, второе слагаемое 19. Чему равна сумма?

5. Уменьшаемое 37 вычитаемое 19. Чему равна разность?

6. 6)Уменьшаемое 29, вычитаемое 16. Чему равна разность?

7. Какое число надо прибавить к числу 29. чтобы получилось

число 50?

8. Какое число надо прибавить, чтобы получилось 90?

9. Какое число надо вычесть из числа 74, чтобы получить число 68?

10) Если к числу 18 прибавить задуманное число, то получится

число 59~ Какое число задумано?

3. Старинная задача.

За какое время окупятся куры?

Один человек купил 3 курицы и заплатил за них 46 копеек.

Первая курица несла по 3 яйца через 4 дня, вторая по 2 яйца через 3 дня, а третья - по 1 яйцу через 2 дня.

Продавал он' яйца по 5 штук за полкопейки. За какое время окупятся куры?

Решение

Три курицы стоят 46 копеек. Для того чтобы возместить эту сумму, необходимо продать (46: 1/2) х5 = 400 яиц.

За 12 дней первая курица снесла 9 яиц, вторая - 8 яиц, а третья- 6 яиц. Вместе же они снесли 23 яйца. Так как 460 = 23 х 20, то за 12 х 20 = 240 дней курицы снесут 23 х 20 = 460 яиц. Значит, куры окупятся за 240 дней.

4.Решите задачу.

На стоянке стояли 17 машин « Жигули», «Москвичей» на 14 машин больше , а машин « Нива» стояло столько сколько «Жигулей» и «Москвичей» вместе. Сколько машин стояло на стоянке?

Решение

17 + 14 = 31 (м.) - стояло «Москвичей».

31 + 17 = 48 (м) - стояло машин «Нива».

17 + 31 + 48 = 96 машин стояло на стоянке.

Ответ: 96 машин.

5. Номера телефонов.

Участвуя в военизированной игре, первая из команд решила напасть на штаб второй команды. Штаб находился в одном из домов большого города, поэтому первой команде надо было узнать адрес этого дома. Разведчики первой команды смогли выведать только номера двух телефонов, по которым штаб второй команды условным кодом передавал своим отрядам приказы и распоряжения. Номера телефонов были зашифрованы так, как показало под рисунками.

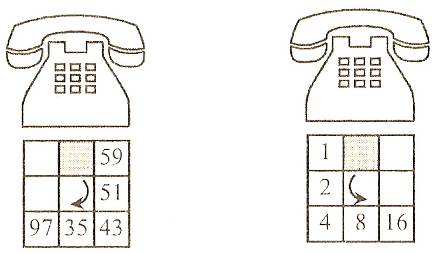
Известно, что по номерам телефонов, пользуясь городской телефонной книгой, можно узнать и адрес самого штаба. Итак, стоит только узнать номера телефонов - и адрес штаба будет известен.

Ребята, помогите разведчикам узнать эти номера.

Ответ: 19-11 и 32-64.

6 3адача.

Фермер, имевший трех сыновей, распорядился, чтобы они поделили между собой стадо коров так, чтобы старший взял половину всех коров, средний - треть и младший - девятую часть всех коров. В стаде было 17 коров. Сыновья начали дележ, но оказалось, что число 17 не делится ни на 2, ни на 3, ни на 9. В недоумении, как им быть, братья обратились к ветеринару. Тот приехал к ним с собственной коровой и разделил стадо так, как повелел отец.

Решение

Ветеринар пустился на уловку. Он прибавил к стаду на время свою корову, тогда их стало 18. Разделив это число на 1/2 - старший сын получил 9 коров, средний 18 : 3 = 6 (коров), младший от 18 получил 1/9, ветеринар взял обратно свою корову (9 + 6 + 2 + 1 = 18). Секрет решения этой задачи в том, что сыновья должны были делить стадо, в котором части не составляют - 1.

Действительно:

1/2 + 1/3 + 1/9 = 17/18.

IV. Стадия рефлексии.

- Почему легионеры при осаде Сиракуз панике разбегались, когда видели в стане врага поднимающуюся веревку или бревно?

- Какую теорему сейчас называют именем Архимеда?

- При каких обстоятельствах Архимед с криком: «Эврика! Эврика!» - бросился проводить эксперимент?

- Какую крылатую фразу произнес Архимед, согласно преданию, когда открыл правило рычага? И мог ли он это сделать на самом деле?

3анятие 10.

ТЕМА. УМНОЖЕНИЕ

Цели: познакомить с умножением в средние века; учить детей мыслить логически; развивать математическую любознательность и инициативу.

Ход занятия

I. Стадия вызова.

- Что означает «решетчатое умножение»?

- Что означает «маленький замок?

II. Стадия осмыслении содержания.

1. Сообщение учителя.

Умножение чисел сейчас изучают во втором классе школы. А вот в средние века совсем немногие владели искусством умножения. Редкий аристократ мог похвастаться знанием таблицы умножения, даже если он окончил европейский университет.

За тысячелетия развития математики было придумано множество способов умножения чисел. Итальянский математик Лука Пачоли в своем трактате «Сумма знаний по арифметике, отношениям и пропорциональности» (1494 г.) приводит восемь различных методов умножения. Один из них носит название «Ревность, или решетчатое умножение».

Сначала рисуется прямоугольник, разделенный на квадраты, причем размеры сторон прямоугольника соответствуют числу десятичных знаков у множимого и множителя. Затем квадратные клетки делятся по диагонали, и « ... получается картинка, похожая на решетчатые ставни-жалюзи, - пишет Пачоли. - Такие ставни вешались на окна венецианских ломов, мешая уличным прохожим видеть сидящих у окон дам и монахинь».

Перемножим этим способом числа 1998 и 987. Для этого запишем вверху таблицы число 987, а слева 1998, как показано на рисунке:

Теперь в каждый квадратик впишем произведение цифр-сомножителей, расположенных в одной строке и в одном столбце с этим квадратиком. Десятки располагаются в нижнем треугольнике, а единицы - в верхнем. После того как все треугольники заполнены, цифры в них складываются вдоль каждой диагонали. Результаты записываются справа и снизу от таблицы - получается 1 972 026.

Этот способ ничуть не хуже, чем общепринятый. Он даже проще, поскольку в клетки таблицы заносятся числа прямо из таблицы умножения без одновременного сложения, присутствующего в стандартном методе. Затем остается только произвести сложение.

Другой способ называется « маленький замок ). Сначала, как мы привыкли, одно число записывается под другим, но затем цифры верхнего числа поочередно умножаются на нижнее число, причем начинают с цифры старшего разряда и каждый раз добавляют нужное число нулей.

Его преимущество в том, что уже с самого начала определяются цифры старших разрядов, а это бывает важно, если требуется быстро оценить величину. Остальные шесть приемов, описанных Пачоли, также опираются на знание таблицы умножения.

Однако в России среди крестьян некоторых губерний был распространен способ, который не требовал знания всей таблицы умножения. Он получил название «русский крестьянский способ умножения». Здесь необходимо было лишь умение умножать и делить числа на 2. Перемножим еще раз числа 987 и 1998 этим способом.

Напишем одно из чисел слева, а второе - справа на одной строчке. Левое число будем делить на 2, а правое - умножать на 2 и результаты записывать в столбик.

Если при делении возникнет остаток (то есть делимое окажется нечетным числом), то он отбрасывается. Умножение и деление на 2 продолжаем до тех пор, пока слева не останется 1. Затем вычеркнем те строчки столбиков, в которых слева стоят четные числа. Теперь сложим оставшиеся числа в правом столбике - получим 1972026. Это и есть произведение перемножаемых чисел.

«Крестьянский способ» может понравиться тем, кто не в ладах с таблицей умножения, правда, здесь приходится производить больше сложений. Однако таблицу умножения все-таки стоит выучить! Ну не хвататься же за карандаш и бумагу, чтобы выяснить, сколько будут стоить 7 пирожков по 80 копеек за штуку!

2. Разминка.

«Крылатые слова». Объясните их значения.

l) За семью печатями. (Это выражение означает что-то непонятное, скрытое, недоступное пониманию, разумению.)

2) Семи пядей во лбу. (Очень умный, мудрый, выдающийся, талантливый человек.)

3) Семимильными шагами. ( Очень быстро . Так говорят о развитии чего-либо .)

4. Седьмая вода на киселе. (Очень дальний родственник.)

5. До седьмого пота. (Работать , трудиться до крайнего утомления, полного изнеможения.)

6. Семь верст до небес. (Очень много наобещать , наговорить.)

7. Семь смертных грехов. ( Библейское выражение . Со временем получило значение каких-либо плохих , непростительных поступков.)

8) Семь бед - один ответ. ( Рискнем еще раз , и если придется отвечать - так за все сразу, одновременно. Говорится в решимости сделать еще что-нибудь рискованное , опасное в добавление уже к сделанному.)

9) Семь раз примерь (отмерь), один раз отрежь. ( Перед тем как сделать что-нибудь серьезное , тщательно все обдумай, все предусмотри. Говорится в качестве совета обдумать все возможные варианты действий перед началом какого-нибудь дела .)

10) У семи нянек дитя без глазу. (Без глазу (устар.) - без nрисмотра, без надзора. Дело выполняется плохо, неудовлетворительно, когда за него отвечают сразу несколько человек.

Говорится, когда несколько человек (или даже организаций), ответственных за дело, надеются друг на друга и каждый в отдельности относится к своим обязанностям недобросовестно.)

3. Задача - шутка.

В саду у дачника был выкопан пруд, и по углам его росли яблони.

Дачнику очень хочется увеличить пруд. У него два условия:

1. Пруд должен иметь квадратную форму.

2. Нельзя трогать яблони - это хорошие сорта. Помогите дачнику, соблюдая его условия.

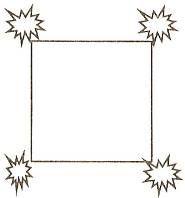
Решение

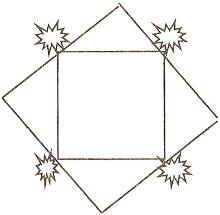
4. Задача.

Лена купила 5 метров красной ленты по 9 рублей и тесьмы 3 метра по той же цене за метр. Сколько стоила вся покупка?

Решение

1. 9 х 5 = 45 (руб.) - Лена заплатила за ленту.

2. 9 х 3 = 27 (руб.) - заплатила за тесьму.

3. 45 + 27 = 72 (руб.) - всего заплатила за покупку.

Ответ: 72 рубля.

5. Задача-шутка.

На зеленом лугу паслись два совершенно одинаковых ослика, хозяйки их отличали по хвостам. У одного был раза в два длиннее хвост. В течение 2 часов в невероятно жаркую погоду, они щипали зеленую травку. Какой из осликов съел больше травы, если они закончили есть одновременно?

Ответ: Ослик с длинным хвостом съел больше травы, так как он имел большую возможность отгонять оводов и мух, мешающих осликам утолять голод.

6.Решите задачу.

2 кг рисовой крупы нужно развесить в пакеты по 200 г. Имеются весы. Гиря весом 500 г и молоток массой 900 г. Как развесить рисовую крупу с помощью гири, весов и молотка?

Решение

1. 900 - 500 - разница между массой молотка и массой гири.

2. Разделим эту массу на два пакета поровну и уравновесим на чашках весов, получим два пакета по 200 г.

3) Продолжим дальше: 2000 - 400= 1600 (г) - развешивание до 8 раз.

IV. Стадия рефлексии.

- Расскажите и покажите «русский крестьянский способ умножения».

- Сделайте умножение «маленьким замком».

3анятие 11.

ТЕМА. ДЕЛЕНИЕ

Цели: познакомить с историей возникновения методов деления; учить мыслить последовательно, доказательно; отстаивать свою точку зрения.

Ход занятия

I. Стадия вызова .

- Почему в старое время людей, умеющих выполнять действие деления, называли «магистрами деления».

- Какие методы деления в своих сочинениях привел монах-

математик Герберт?

- Что это за метод - «золотое деление»?

II. Стадия осмысления содержания.

1. Сообщение учителя.

Хотя умножение в старину и считалось нелегким делом, однако деление было еще сложнее. В Италии до сих пор сохранилась поговорка: «Трудное дело - деление». Так обычно говорят. Когда оказываются перед почти неразрешимой проблемой. В Средние века людей, умевших производить действие деление, можно было пересчитать чуть ли не по пальцам. Их уважительно называли «магистрами деления». Они переезжали из города в город по приглашениям купцов, желавших привести в порядок свои счета.

Методов деления было придумано немало. Монах-математик Герберт, будущий Папа Римский Сильвестр II, привел в своих сочинениях несколько способов деления на абаке. При этом он придерживался таких принципов:

- как можно меньше применять таблицу умножения, в частности не использовать умножение в уме двузначных чисел па однозначные;

- избегать вычитаний, заменяя их сложениями;

- работа должна выполняться автоматически, без проверок, при которых тоже могут появиться ошибки.

Такие строгие ограничения он ввел, учитывая, сколь неграмотны были монахи, производившие вычисления. Почти никто из них не знал таблицы умножения. Но в итоге правила Герберта оказались настолько сложными, что не были понятны даже самым прилежным счетчикам - абацистам. Когда в Европе появился арабский способ деления, основанный на принятой сейчас позиционной десятичной системе счисления, он получил название «золотое деление». Им мы пользуемся и по сей день. А метод Герберта стали называть «железным делением». Кроме этих способов были и другие. Например, раскладывали делитель на множители, а затем последовательно делили делимое на эти числа. При этом для деления на однозначные числа существовал специальный метод.

Долгое время в Европе конкурировали два способа деления: «золотое деление» и «галера». Прежде всего напомним правила «золотого деления». Разделим 987654 на 345:

Сначала находим наибольшее целое число, которое, будучи умноженным на 346, окажется меньше, чем 987. Такое число - 2, оно и будет первой цифрой частного. Затем в уме умножаем 346 на 2, результат записываем под первыми тремя цифрами делимого и производим вычитание.Потом к полученному числу приписываем следующую цифру делимого и продолжаем процесс, повторяя те же действия.

Второй способ итальянцы называли «галера», из-за того что после окончания вычислений цифры располагаются 13 виде фигуры, напоминающей это гребное судно. У англичан он известен как «метод зачеркиваний», поскольку здесь постоянно приходится зачеркивать цифры. Лука Пачоли считал этот способ самым быстрым.

Метод «галера» отличается от «золотого деления» тем, что в нем нет умножения в уме многозначного числа на однозначное.

Оно заменяется несколькими умножениями однозначных чисел на однозначные и вычитаниями полученных результатов по очереди.

Этот метод родился в Индии, оттуда через арабские страны он и проник в Европу. Правда, у индийцев в результате деления никаких корабликов не получалось. Ведь в то время они не пользовались для вычислений бумагой, а писали на дощечках, которые были покрыты пылью или песком. Вместо того чтобы зачеркивать цифры, они их просто стирали.

2. Разминка.

1) Когда котенку исполнится 2 года, что будет дальше? (Пойдет третий.)

2) При постройке забора плодники поставили по прямой 5 столбов , расстояние между которыми было по 2 метра. Какова длина забора? (6 м.)

3) Который час, если оставшаяся часть суток вдвое больше прошедшей? (8 часов. Всего в сутках 24 часа. Одна третья часть суток - это 8 часов , 16 часов вдвое больше восьми.)

4) Два брата договорились сесть в четвертый вагон поезда. Но один из братьев сел в четвертый вагон от начала поезда, а другой в четвертый от конца. В одном ли вагоне едут братья. Если всего 8 вагонов.

(Нет . Второй брат едет в вагоне , который является пятым от начала.)

5) В коробке было три желтых и три красных шарика. Мальчик взял четыре шарика. Сколько шариков каждого цвета могло быть у мальчика? Найдите три ответа. Сколько шариков осталось в коробке? (Два желтых и два красных; три желтых и один красный,' три красных и один желтый; в коробке осталось 2 шарика.)

6) Кто из какого класса?

В математическом кружке учитель дал задание ученикам составить логическую задачу.

На вопрос: «Из какого кто класса?» - каждый должен дать два ответа: один - правильный, а другой - неправильный, но чтобы по их ответам можно было определить, кто в каком классе учится.

Мальчики дали ответы:

Арасов. Я из класса «А», а Волин - из «В».

Билецкий. я из класса «Б», а Волин из «Г»

Волин. Я из класса «В», а Арасов из «Б».

Горин. Я из «А», а Арасов из «В».

Определите, в каком из параллельных классов учится каждый ученик.

(Арасов - «Г», Билецкий - «Б», Волин - «В», Горин - «А».)

7) Чтобы попасть в кино, двум отцам и двум сыновьям понадобится только три входных билета. Как такое может быть? ( Их всего было трое: сын отец, дедушка . Поэтому трех билетов было достаточно. )

8) Три девочки - Валя, Наташа и Катя пришли в театр в платьях разного цвета: одна в белом, другая в сером, третья в черном. В каком платье была каждая , если известно, что Валя - не в черном и не в сером, Катя - не в черном? (Валя - в белом, Катя - в сером, Наташа - в черном.)

9) В соревнованиях по теннису Анастасия, Валя, Геля и Настя заняли первые четыре места. Определите, кто какое место занял, если известно, что Геля вторая , Настя хотя и не была победителем, но в призеры попала, а Валя проиграла Анастасии.

(Анастасия заняла 1-е место, Геля -2-е, Настя - З-е, Валя - 4-е место.)

10) Шесть ног, две головы, один хвост. Кто это? (Всадник на осле.)

3.Найдите верные утверждения и подчеркните.

1) Чтобы найти периметр прямоугольника, надо сложить длины всех его сторон и умножить на 2.

2) Чтобы найти периметр квадрата, надо длину его стороны умножить на 4.

3) Чтобы найти периметр прямоугольника, надо сложить значения его длины и ширины и полученную сумму увеличить в 2 раза.

4) Чтобы найти длину стороны квадрата, надо его периметр разделить на 4.

5) Р = (а + Ь) х 2.

Ответ: 2) Чтобы найти периметр квадрата, надо длину его стороны умножить на 4.

3) Чтобы найти периметр прямоугольника, надо сложить значения его длины и ширины и полученную сумму увеличить в 2 раза.

4) Чтобы найти длину стороны квадрата, надо его периметр разделить на 4.

5) Р = (а + Ь) х 2.

4. Задача

Ученики второго класса учились действию сложения, выходили к доске «цепочкой» и заполнили цифрами 9 числовых дорожек. В каждой строке сумма двух соседних чисел должна была равняться последующему числу. Но дети сделали много ошибок. На скольких числовых дорожках дети сделали вычисления правильно?

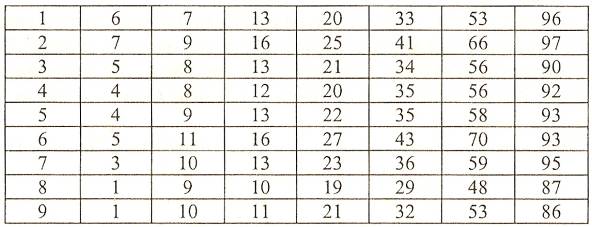
Ответ: только на одной. На седьмой.

5. Докажите.

В 4 классе «Б» учатся 34 ученика. Докажите, что в этом классе найдутся, по крайней мере, два ученика, у которых фамилии начинаются с одной и той же буквы.

Ответ: В русском алфавите 33 буквы, и есть среди них такие, с которых фамилии не начинаются. Так как учеников в классе больше, чем букв в русском алфавите, то в нем обязательно встретится несколько фамилий, начинающихся с одной и той же буквы.

6.Во сколько раз быстрее?

Самолет расстояние от Петербурга до Владивостока пролетит за 9 часов. А скорому поезду удается преодолеть это расстояние лишь за 9 суток. Во сколько раз быстрее можно добраться от Петербурга до Владивостока на самолете, чем на скором поезде?

Ответ: в 24 раза.

7. Задача.

За три дня в музее побывало 670 человек. В первый день пришло 7 групп по 15 человек, во второй - 375 человек. Сколько человек побывало в музее в третий день?

Решение

1. 15 х7 = 105 (ч.) - в первый день человек побывало в музее.

2. 375 + 105 = 480 (ч.) - побывало за два дня.

3. 670 - 480 = 190 (ч.) - побывало в музее в третий день.

Ответ: 190 человек побывало в музее в третий день.

IV. Стадия рефлексии.

- Почему способ деления итальянцы назвали «галера»?

- Чем метод «галера» отличается от метода «золотого деления»?

3анятие 12 .

ТЕМА. ДЕЛИТСЯ ИЛИ НЕ ДЕЛИТСЯ

Цели: познакомить с признаками делимости на 2, на 4, на 5, на 8; развивать математическую любознательность и инициативу.

Ход занятия

I. Стадия вызова.

- Как узнать, делится ли одно число на другое, не прибегая к традиционному делению «уголком»?

- В каком случае число делится на 2, на 4, на 8, на 5?

II. Стадия осмысления содержания.

1. Сообщение учителя.

Иногда возникает ситуация, когда нужно быстро определить, делится одно число на другое или нет. Предположим, вы купили в магазине 3 ластика, 6 карандашей и 9 одинаковых тетрадей, а продавец говорит: «С вас за покупку 10 рублей». Даже не зная точной цены покупки, можно сразу понять, что продавец ошибся. Ведь итоговая стоимость обязательно должна делиться на 3, но ни 10 рублей. Ни 1000 копеек на 3 не делится.

Как узнать, делится ли одно число на другое, не прибегая к традиционному делению «уголком»? Для небольших делителей существуют простые, легко запоминающиеся признаки.

Признак делимости на 2. Число 11 делится на 2 в том и только в том случае, если его последняя цифра делится на 2.

Признак делимости на 4. Число 11 делится на 4 в том случае, если на 4 делится число, образованное из двух последних цифр числа п.

Признак делимости на 8. Число п делится на 8 в том и только в том случае, если на 8 делится трехзначное число, образованное на трех последних цифр числа п,

Приведем пример: делимость числа 199619 971 998 на 2 определяется лишь по одной его последней цифре 8 (на 2 делится) ; на 4 по двум последним цифрам (98 не делится на 4); на 8 - по числу 998 (на 8 не делится; впрочем, это уже следует из того факта, что число 199 619 971 998 не делится на 4).

Признак делимости на 5. Число п делится на 5 в том и только

в том случае, если его последним цифра 0 или 5.

2. Разминка.

1) Летела стая гусей, одного убили. Сколько осталось? (Один.)

2)Муж с женой, отец с сыном, да мать с ребенком. Сколько всех? (Трое.)

3. После семи лет что будет корове? (Восьмой пойдет.)

4. Чего кругом избы не обнесешь? (Воду в решете.)

5. Что милее ста рублей? (Двести.)

6. Что родится без костей? (Язык.)

7. Чего языком не достанешь? (Своего лба.)

8. Сидят три кошки; против каждой кошки - две кошки. Много ль всех? (Три кошки.)

9) Чего нельзя купить ни за какие сокровища? (Потерянного времени.)

10) Что дальше хвоста не уйдет? (Лошадь.)

3. Задача-шутка.

Что сказал старик?

Два молодых казака, оба лихие наездники, часто бились между собой об заклад, кто кого пере гонит. Не раз то тот, то другой был победителем, наконец, это им надоело.

- Вот что, - сказал Григорий, - давай спорить наоборот. Пусть заклад достанется тому, чей конь придет в назначенное место вторым, а не первым.

- Ладно! - ответил Михаил.

Казаки выехали на своих конях в степь. Зрителей собралось множество: всем хотелось посмотреть на такую диковинку. Один старый казак начал считать, хлопая в ладоши:

- Раз! .. Два! .. Три! ..

Спорщики, конечно, ни с места. Зрители стали смеяться, судить да рядить и порешили , что такой спор невозможен и что спорщики простоят на месте, как говорится, до скончания века. Тут к толпе подошел седой старик, видавший на своем веку разные виды.

- В чем дело? - спрашивает он. Ему сказали.

- Эге ж! - говорит старик, - вот я им сейчас шепну такое слово, что поскачут, как ошпаренные ... и действительно ... подошел старик к казакам, сказал им что-то, и через полминуты казаки уже неслись по степи во всю прыть, стараясь непременно обогнать друг друга, но заклад все же выиграл тот, чья лошадь пришла второй.

Что сказал старик?

Решение

Старик шепнул казакам: «Пересядьте», Те поняли, мигом пересели каждый на лошадь своего противника, и каждый погнал теперь во всю прыть чужую лошадь, на которой он сидел, чтобы собственная его лошадь пришла второй.

4.Возможна ли солнечная погода?

Если поздней осенью в 11 ч вечера идет дождь, то возможна ли через 48 ч солнечная погода?

Ответ: нет. так как будет ночь.

5. Нестандартные задачи.

1.

2.

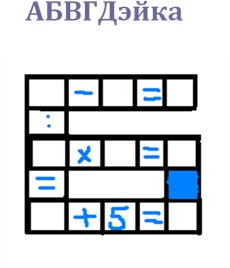
6. Есть ли такие ученики?

В нашем доме живут 12 учеников из одной и той же школы. В этой школе имеются 3 первых, 3 вторых и 3 третьих класса.

Подумайте и ответьте, есть ли среди учеников, живущих в нашем доме, хотя бы два человека, которые учатся у одной и той же учительницы. Объясните свой ответ.

Ответ: в школе всего 3 + 3 +3 = 9 классов, а число учеников, живущих в нашем доме, больше, чем число классов в школе. Поэтому среди учеников, проживающих в нашем доме, найдутся такие, которые учатся у одной и той же учительницы.

IV. Стадия рефлексии.

- Какие вы знаете признаки делимости?

- Какие примечательные особенности есть при делении на 3 и на 9? (Число n делится на 3 в том и только в том случае , если сумма его цифр делится на 3. У признаков делимости на 3 и на 9 есть примечательные особенности. Они могут применяться многократно: сначала к самому числу, потом к сумме его цифр, затем к сумме цифр полученного числа и т. д., пока начальное, сколь бы огромное, оно ни было число постепенно не «свернется» в одну единственную цифру. Пусть, например, нужно узнать, делится ли на число 9 число, составленное из 1998 единиц: 11 ... 11. Сумма его цифр равна 1998. Последнее число делится на 9, поскольку сумма его цифр (1 + 9 + 9 + + 8 = 27) делится на 9. Значит , и исходное число также делится на 9.)

Занятие 13.

ТЕМА. ИНТЕЛЛЕКТУАЛЬНЫЙ МАРАФОН

Цели: проверить знания, умения, навыки детей.

1. Знаете ли вы?

1. Когда появилась единичная система счисления?

2. Какие две великие цивилизации древности оставили самые ранние математические тексты?

3. Как умножали, делили, складывали и вычитали древние?

4.Когда возникли Олимпийские игры?

5.Какой союз обосновал Пифагор, что входило в сферу интересов союза?

6.Что толкнуло человека к счету предметов?

7.Существует ли самое большое число?

8.Чему посвящены труды Архимеда?

9.Какие вычислительные приборы существовали, и какими

пользуемся сейчас?

10.Что означает «решетчатое умножение»?

11.На что похожа половинка груши?

12.Что находится между дорогой и лесом?

13.Можно ли принести в решете воды?

14.Как можно прочесть слово «занавес»?

2. «Разминочка».

В нашем классе два Ивана

Две Татьяны, два Степана,

Три Катюши, три Галины,

Пять Андреев, три Полины,

Восемь Львов, четыре Саши,

Шесть Ирин и две Наташи,

И всего один Виталий.

Сколько всех вы насчитали?

Повезло опять Егорке

У реки сидит не зря.

Два карасика в ведерке

И четыре пескаря.

Но смотрите - у ведерка

Появился хитрый кот ..

Сколько рыб домой Егорка

На уху нам принесет?

Посчитай и посмотри

Хорошенько -

Раз, два, три.

Три у клевера листка,

Три у дыма завитка.

Три зубца у старой вилки,

«Три» в тетради у Данилки,

Он урок недоучил,

Вот и тройку получил.

Мать игрушки принесла

И ребятам раздала.

Подарила Маше шар.

А Танюше - самовар.

Сыну Ване - барабан,

Дочке Милочке - диван.

3. «Набери себе балл!»

Игра проводится по группам. Выбираются капитан, консультанты. В конце подводится итог. Победители награждаются.

1. На скачках тройка лошадей пробежала 30 км. По сколько километров пробежала каждая лошадь?

(l балл.)

2. На крыше сидело 5 голубей, к ним прилетели еще 3 голубя.

Кот подкрался и схватил одного голубя. Сколько осталось на крыше голубей?

(2 балла.)

1. Фермер заготовил сена 21 т 840 кг. С первого и второго участков накосили поровну, а с третьего участка на 2 т 910 кг больше, чем с каждого из первых двух. Сколько сена накосили с каждого участка?

2. балла.)

4. Как пятью семерками выразить число 7?

2. балла.)

4. В вазе лежат 3 груши. Можно ли эти груши поделить поровну между тремя подругами так, чтобы в вазе осталась одна груша? Резать груши нельзя.

(4 балла.)

4. В семье четверо детей: 5, 8, 13 и 15 лет, а зовут их Катя, Дима, Даша и Юля. Сколько лет каждому из них, если одна девочка ходит в детский сад, Катя старше, чем Дима, а сумма лет Даши и Кати делится на 3?

(5 баллов.)

4. Отгадай загадку:

Что за шустрый старичок,

Восемьдесят восемь ног,

Все по полю шаркают

За работой жаркою.

(2 балла.)

4. На дворе ходят гуси и лошади, у всех вместе 10 голов и 26 ног. Сколько гусей и сколько лошадей?

(2 балла.)

4. Дачница вырастила 7 тыкв, массы которых 1 кг, 2 кг, 3 кг, 4 кг, 5 кг, 6 кг, 7 кг. Эти тыквы она разложила в 4 сетки так, что в каждой сетке масса тыкв была одинакова. Как это она сделала?

(4 балла.)

4. Кирилл ехал в школу на велосипеде. Занятия в школе начинаются в 9 ч. В 8 ч 40 мин, он уже проехал половину пути. Если Кирилл будет продолжать ехать с такой же скоростью, то он приедет в школу за 10 мин до начала занятий. Сколько минут он ехал в школу?

(3 балла.)

4. В детском садике одинаковое количество мальчиков и девочек. Для праздника купили 234 воздушных шара. Каждому мальчику досталось 5 шаров, а каждой девочке по 4 шара. Но так как девочки расплакались от такой несправедливости, пришлось докупить шары. Тогда всем, и девочкам и мальчикам досталось поровну по 6 шаров. Сколько шаров докупили?

(5 баллов.)

4. Покажи порядок действий:

78000-(64000:128-3280:164х15)х70+192000:800

(2 балла.)

4. Можно ли семью тройками выразить число 48?

(4 балла.)

4. В портфеле лежат 15 тетрадей разной разлиновки: в одну линейку, в две линейки и в клеточку. Тетрадей в одну линейку в 7 раз больше, чем тетрадей в две линейки. Не раскрывая портфеля, узнай, сколько в нем лежит тетрадей каждой разлиновки.

(5 баллов.)

4. Который круг лишний? Проследи за изменениями чисел и найди круг, в котором это изменение не такое, как в других.

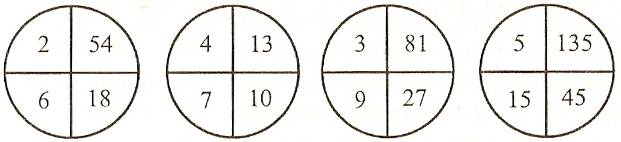
(4 балла.)

4. В квартирах № 1,2,3 жили Катя, Маня, Петя. В квартирах № 1 и № 2 не жила Маша. Катя не жила в квартире № 1. В какой квартире жили Катя, Маня и Петя.

(3 балла.)

4. Как, имея три сосуда ёмкостью 8л, 5л и 3 л, налить в котел 7 литров воды?

(5 баллов.)

4. У хозяйки есть рычажные весы и гиря в 100 г. Как за три взвешивания она может отвесить 700 г крупы?

(2 балла.)

4. Найди закономерность и более легкий способ вычисления.

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9.

(4 балла.)

4. Если Маша купит 3 пиона, то у неё останется 14 руб., а если 5 таких же пионов, то у неё останется 1 10 руб. Найди цену одного пиона.

(2 балла.)

4. Одна из сторон прямоугольника 24 см, а другая - в 3 раза больше. Найди периметр и площадь прямоугольника.

(5 баллов.)

22. «Магический квадрат».

Заполнить все клеточки таблицы цифрами от 1 до 25 так, чтобы сумма чисел по всем направлениям равнялась 65. Числа не должны повторяться (для всех команд одинаковые квадраты)

2. баллов.)

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. Агаркова Н. В. Нескучная математика. 1 - 4 классы. Занимательная математика. Волгоград: «Учитель», 2007

2. Агафонова И. Учимся думать. Занимательные логические задачи, тесты и упражнения для детей 8 - 11 лет. С. - Пб,1996

3. Асарина Е. Ю., Фрид М. Е. Секреты квадрата и кубика. М.: «Контекст», 1995

4. Белякова О. И. Занятия математического кружка. 3 - 4 классы. - Волгоград: Учитель, 2008.

5. Лавриненко Т. А. Задания развивающего характера по математике. Саратов: «Лицей», 2002

6. Симановский А. Э. Развитие творческого мышления детей. М.: Академкнига/Учебник, 2002

7. Сухин И.Г. Занимательные материалы. М.: «Вако», 2004

8. Шкляров Т.В. Как научить вашего ребёнка решать задачи. М.: «Грамотей», 2004

9. Сахаров И.П., Аменицын Н.Н. Забавная арифметика. С.- Пб.: «Лань», 1995

10. Узорова О.В., Нефёдова Е. А. «Вся математика с контрольными вопросами и великолепными игровыми задачами. 1 - 4 классы. М., 2004

11. Занимательные задачи для маленьких. Москва 1994

12. Математика. Внеклассные занятия в начальной школе. Г.Т.Дьячкова. Волгоград 2007