Урок математики 1 класс Уравнения. Решение уравнений вида х + а = б»

УРОК МАТЕМАТИКИ

Предмет: математика

Класс: первый

Тип урока: открытие новых знаний

Тема: Уравнения. Решение уравнений вида х + а = б

Технологии: технология деятельностного метода обучения, технология сотрудничества и ИКТ-технология работы с мультимедийной доской.

Формы организации деятельности детей: коллективная, парная, групповая.

Методы: частично-поисковый метод, проблемный метод, словесной и наглядной передачи информации, самостоятельная работа, методы стимулирования мотивов интереса к учению.

Практическая реализация:

Урок построен на основе технологии деятельностного метода обучения.

Содержание подобрано в соответствии с программными требованиями и поставленными задачами, с учётом психолого-педагогических особенностей детей младшего школьного возраста.

Использовались принципы технологии развивающего обучения: обучение на высоком уровне трудности с соблюдением меры трудности, ведущая роль теоретических знаний, осознание процесса учения, работа над развитием каждого ребёнка.

Методы, используемые на уроке: методы стимулирования мотивов интереса к учению; частично-поисковый метод, проблемный метод, методы словесной и наглядной передачи информации, самостоятельная работа.

Методическая разработка урока математики

Тема: «Уравнение. Решение уравнений вида х + а = б»

Цель: -познакомить с понятием «уравнение»;

- формировать умения решать уравнения с опорой на знания о взаимосвязи между

частью и целым;

- закреплять умения решать составные задачи на сложение и вычитание, отрабатывать навыки счёта в пределах 10;

- развивать речь, логическое мышление, память, внимание, расширять словарный запас.

(Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, аналогия, обобщение.)

Планируемый результат:

учащиеся научатся:

- решать уравнения с опорой на знания о взаимосвязи между частью и целым, употреблять в речи понятие «уравнение», работать по алгоритму;

- анализировать задачу, устанавливать зависимость между величинами, взаимосвязь между условием и вопросом задачи, определять количество и порядок действий для решения задачи, выбирать и объяснять выбор действий;

- умение выполнять устно сложение, вычитание, однозначных чисел в пределах 10.

Задачи:

-активизировать умение решать простые задачи на сложение и вычитание;

-тренировать автоматизированный навык счета в пределах 9.

-развивать мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, синтез, обобщение.

-создавать мотивацию к учебной деятельности на уроке посредством создания проблемной ситуации.

-привитие умения работать в группе, паре, воспитание чувства товарищества, взаимопомощи.

В результате формируются УУД:

Личностные УУД:

- учебно-познавательный интерес к новому учебному материалу и способам решения новой задачи;

- уметь проводить самооценку успешной учебной деятельности.

Метапредметные:

Регулятивные УУД:

- определять и формулировать цель деятельности на уроке с помощью учителя;

- учиться работать по предложенному учителем плану;

- проговаривать алгоритм действий на уроке;

- планировать свои действия в соответствии с поставленной задачей;

- уметь проверять правильность решения уравнений на основе алгоритма.

Познавательные УУД:

- осуществлять синтез как составление целого из частей;

- делать выводы в результате совместной работы класса и учителя;

- уметь составлять алгоритм на основе знаний;

- учиться отличать уравнения от других математических записей;

- самостоятельно решать уравнения на основе коллективно составленного алгоритма;

- уметь проверять правильность решения уравнений методом подбора на основе знаний о составе чисел в пределах 10.

Коммуникативные УУД:

- учиться формулировать связный ответ на поставленный вопрос;

- учиться умению договариваться и приходить к общему решению в совместной деятельности в паре, в группе.

Средства обучения: мультимедиапроектор

Демонстрационный материал:

1) изображение 2 шагов учебной деятельности:

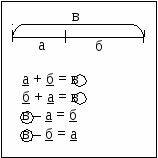
2) эталон «Отрезок и его части»:

Раздаточный материал:

1) индивидуальные листы;

2) карточка с заданием на пробное действие:

3) карточка для групповой работы (такая же, как и для пробного действия, но размер А-4)

4) эталон к уроку: х + а = б

х = б - а

Литература

1. Петерсон Л. Г. Математика: 1 класс. Часть 3. - М.: Издательство «Ювента», 2009. - 96с.

2. Петерсон Л. Г. Методические рекомендации к учебнику для 1 кл. М.: «Ювента», 2009.

3. Шушковская А.И. (АПК и ППРО РФ, ЦСДП «Школа 2000…»), 2008.

Ход урока:

Название этапа

Цель

Организация учебного процесса

№ слайда

Формирование УУД

1. Мотивация к учебной деятельности

1) создать мотивацию к учебной деятельности на уроке путём обращения к внутреннему состоянию каждого;

2) определить содержательные рамки урока: сложение двузначных чисел.

В школу мы пришли учиться

В жизни это пригодится

Тот, кто хочет много знать

Должен сам все постигать.

- Ребята, согласны ли Вы с содержанием девиза урока?

-Как Вы понимаете, что учение пригодится в жизни? (Без знаний ничего не сделаешь)

- Выделите главное слово в последних двух строчках и объясните свой выбор.

(Слово "сам", т.к. мы учимся тогда, когда сами понимаем, чего мы не знаем и сами открываем новые знания.)

- Когда человек сможет обладать знаниями? (Если он сам их добывает.)

- Каким образом? (сделать 2 шага)

На доске вывешены картинки с изображением шагов учебной деятельности

- Вы готовы добывать знания?

- Я вижу, что вы готовы к работе. Пожелайте друг другу успехов и примемся за работу.

- самоопределение в учебной деятельности, предполагающее осознанное подчинение себя системе нормативных требований учебной деятельности и выработке внутренней готовности к их реализации (Л)

2. Актуализация знаний и фиксация затруднения в пробном учебном действии

1) актуализировать правила нахождения части и целого, при решении примеров с «окошками» способом подбора;

2) сформировать представление о понятиях «уравнение», «корень уравнения», решение уравнения способом подбора;

3) тренировать вариативность мышления, мыслительные операции: сравнение, анализ, обобщение;

4) мотивировать к пробному действию и его самостоятельному выполнению и обоснованию;

5) организовать фиксацию образовательной цели и темы урока;

6) организовать выполнение пробного действия и фиксацию затруднения;

7) организовать анализ полученных ответов и зафиксировать индивидуальные затруднения в выполнении пробного действия или его обосновании.

На 1 слайде дан ряд чисел: 4 5 9.

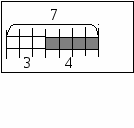Чтобы и сегодня открыть новые знания, нам нужно повторить ранее изученное. Готовы?

1) Начнем урок с устного счета.

Дан ряд чисел 4 5 9

-Назовите самое большое и самое маленькое число в этом ряду.

-Назовите число, которое является суммой двух других чисел

-На сколько 9 больше 4? На сколько 4 меньше 9?

-Как узнать, на сколько одно число больше или меньше другого?

-Назовите числа, которые можно заменить суммой одинаковых слагаемых?

-Расскажите все, что знаете о числе 9.

-С каким числом будет связан устный счет?

2) Работа с диском «Уроки Кирилла и Мефодия» часть 3, урок 24

Задание 2 -состав числа 9

Задание 9 -компоненты суммы

Задание 13 -собрать пазлы (решить примеры)

3) Актуализация правила нахождения «части и целого».

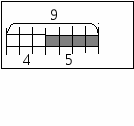
К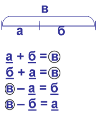акое задание вы можете придумать по этому отрезку. Дети составляют все возможные равенства (работа в парах , составление всех возможных пар)

- Проверяем ваши результаты.

Проводится фронтальная проверка.

У детей должно получиться:

4 + 5 = 9; 5 + 4= 9; 9 - 4 = 5; 9 - 5 = 4

- Каким правилом вы пользовались? (Правилами нахождения «части и целого».) Сравните с эталоном и с учебником.

Учитель открывает эталон на слайде.

4)Предлагаю каждой группе решить примеры на карточке.

Н 2+4 Р 4-2 И 5+4

У 6-5 Я 2+8 А 9-6

Н 5+3 Е 10-3 В 0+5

- Распределите (устно) примеры на 2 группы и объясните.

(1 группа - примеры на сложение, находим целое.)

(2 группа - примеры на вычитание, находим часть.)

5) Формирование представления о понятиях «уравнение», «корень уравнения».

А теперь посмотрите на эту запись.

-Вставьте в окошко пропущенное число

…+3=9

(9 - это 6 и 3, поэтому вставим 6, получаем 6+3 = 9).

-Это равенство с "окошком" или с неизвестным числом. Хотите узнать, как называется такое равенство?

Запишите в таблицу ответы примеров в порядке возрастания и прочтите полученное слово.

УРАВНЕНИЕ

- Знакомо ли вам такое слово? Встречалось ли оно вам раньше?

- Какая же будет тема урока? (Уравнение).

- Какую цель поставим перед собой? (Узнать, что такое уравнения и научиться их решать.)

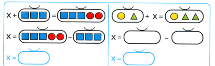
-Действительно, в математике называют такие равенства уравнениями. Неизвестный компонент чаще всего в математике обозначают латинской буквой Х (икс).

-Поставим его в "окошко" и получим равенство. Прочтем запись.

- х+3=9 - это уравнение.

х=6 - корень уравнения.

-Мы решили уравнения с помощью подбора.

-Что значит решили? (Подобрали такое число Х, при котором равенство верно.)

- Чем вы пользовались, когда подбирали число? (Составом чисел 1-9.)

Учитель открывает тему урока.

- Давайте потренируемся решать уравнения, находить корень уравнения.

Дети выполняют № 1 на стр.20 Задание решается фронтально у доски (слайд 4) способом подбора.

-Как вы думаете, что нужно сделать в этом задании? (Надо подобрать предметы в мешок - часть, так, чтобы получилось верное равенство.)

- Как называются такие равенства? (Уравнения).

- Верно ли решено первое уравнение? Докажите.

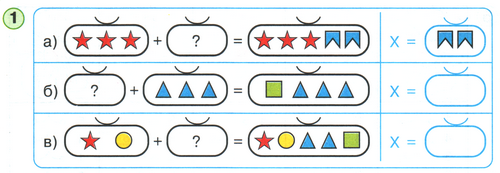
Образец комментирования:

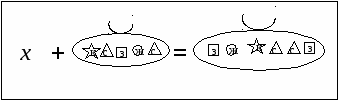
- Во втором уравнении неизвестный мешок (корень уравнения) состоит из зеленого квадрата, так как он есть в «целом» и нет в известной «части»

3.3. - Молодцы, вы все справились с заданием и теперь решите самостоятельно уравнение на карточке.(групповая работа)

6) Пробное действие.

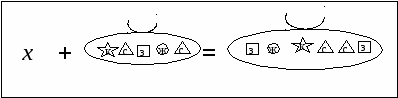
- Какое задание выполняли? (Решали уравнения, в котором неизвестна часть).

-Чему равен х? (Появляются разные ответы.) Учитель фиксирует на доске полученные учащимися варианты ответов. Затруднения.

1

2

3

4

- анализ, сравнение, аналогия, обобщение (П);

- использование знаково-символических средств (П);

- осознанное и произвольное речевое высказывание (П);

- подведение под понятие (П);

- выполнение пробного учебного действия (Р);

- фиксирование индивидуального затруднения в пробном действии (Р);

- волевая саморегуляция в ситуации затруднения (Р);

- выражение своих мыслей с достаточной и полнотой и точностью (К);

- учёт разных мнений (К);

- использование критериев для обоснования своего суждения (К)

3. Выявление места и причины затруднения

1) выявить и зафиксировать место и причину затруднения

- Чем это задание отличается от предыдущего? (Много фигур, они разной формы и цвета.)

- А в чем возникло затруднение? (Мы путаемся).

- Если фигур становится больше - легче или труднее будет подбирать решение? (Труднее).

- Каким способом вы пытались найти решение? (Способом подбора.)

- Чем же это уравнение отличается от предыдущих? (Неудобно подбирать неизвестный компонент.)

- Почему же будут возникать подобные затруднения? (Известный способ не удобен, а другого способа нет.)

- постановка и формулирование проблемы (П);

- волевая саморегуляция в ситуации затруднения (Р);

4. Построение проекта выхода из затруднения

1) построить проект выхода из затруднения

- Сформулируйте цель вашей деятельности? (Открыть способ решения уравнений.)

- Какой компонент неизвестен в этом уравнении? (Неизвестно слагаемое, часть.)

- Какие правила о взаимосвязи частей и целого, помогают нам в самых разных ситуациях?

Правило1: Целое равно сумме частей.

Правило 2: Чтобы найти часть, надо из целого вычесть часть.

- А теперь каждый из вас должен догадаться какое из этих правил подойдет? (дети предлагают способ).

- Вычтите из обеих частей равенства поровну - фигурки из первого мешка. Обозначьте вычитание зачеркиванием.

- Удобно так искать неизвестное слагаемое? (Да)

- Какое правило нам помогло. (Нахождение части.)

- Составим алгоритм наших действий. (работа в парах)

Какой будет первый шаг? (Определим компоненты действия, подберем правило.)

- Какой будет следующий шаг? (Решим уравнение.)

- Какой будет третий шаг? (Сформулируем способ.)

Учитель записывает план действий на доске

- смыслообразование (Л);

- выделение и формулирование познавательной цели (П);

- поиск и выделение необходимой информации (П);

- планирование (П);

5. Реализация построенного проекта

1) организовать коммутативное взаимодействие с целью реализации построенного проекта, направленного на приобретение недостающих знаний;

2) организовать фиксацию построенного способа действия в речи и знаково (с помощью эталона);

3) организовать уточнение общего характера нового знания.

- Я предлагаю поработать вам в группах. (с.20 №2) Назовите правила работы. (Каждый имеет право высказать свое мнение, остальные должны его выслушать. В каждой группе должен быть ответственный. Он отвечает за работу всей группы, за результат. Работать в группе нужно так, чтобы не мешать другим группам.)

- Выполните в группах первый и второй пункты плана.

Группы в течение 3 минут работают самостоятельно

- Какие результаты у вас получились?

На доске выставляются результаты работы групп.

- Каким правилом вы воспользовались? Чему равна неизвестная часть?

- В какой группе были допущены ошибки?

- Какой шаг осталось выполнить? (Проанализировать наши действия и сформулировать способ.)

- Какое уравнение вы решали? (Уравнение, в котором неизвестна часть.)

- Что необходимо выполнить сначала? (Определить, какой компонент неизвестен.)

- Чтобы было удобно, я предлагаю прямо в уравнении выделять «части» и «целое».

Учитель на доске пишет уравнение в общем виде, выделяет на нем «части» и «целое».

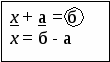- Что в данном виде уравнения неизвестно? (Неизвестна «часть».) Что необходимо сделать? Эталон:

- Как проверить, верно, ли вы рассуждали? (По эталонам, в учебнике посмотреть.)

- Что вам позволяет «открытый» способ? (Решать уравнения данного вида.)

5

- планирование учебного сотрудничества с учителем и сверстниками (К);

- выдвижение гипотез и их обоснование (П);

- волевая саморегуляция, познавательная инициатива (Р);

- моделирование (П);

- установление причинно-следственных связей (П);

- осознание ответственности за общее дело (Л);

- выражение своих мыслей с достаточной и полнотой и точностью (К);

- учёт разных мнений (К);

- использование критериев для обоснования своего суждения (К)

6. Первичное закрепление во внешней речи

1) создать условия для фиксации изученного способа действия во внешней речи.

- Что теперь нам надо сделать? (Потренироваться в решении уравнений.)

Открывается 6 слайд

№ 3 стр. 20. с комментированием у доски

- Далее я вам предлагаю потренировать при решении уравнений с числами.

Открывается 7 слайд

№ 5, стр. 21. С комментированием первое уравнение- объяснение, анализ, применяя полученные знания.

- Вы поработали все вместе, как вы будете сейчас работать? (В парах.)

- Выполните два других уравнения в парах.

Проводится проверка по образцу на 7 слайде.

- Кто допустил ошибку? В чем она? Исправьте допущенные ошибки. Вы молодцы, что поняли причину ошибки.

- Кто выполнил все верно? Сделайте вывод. (Мы умеем решать уравнения.)

- Как в этом убедиться? (Нужно выполнить самостоятельную работу.)

6

7

- выполнение действий по алгоритму (П);

- выражение своих мыслей с достаточной и полнотой и точностью (К)

7. Самостоятельная работа с самопроверкой по эталону

1) организовать самопроверку и самооценку учащимися умения решать уравнения на сложение с неизвестным слагаемым.

- . Самостоятельная работа с самопроверкой по эталону с.21 №5 б), в)

Самооценивание.

-У кого есть ошибки? В чем они.

-Сделайте вывод. Проверьте по эталонам.

- Проверьте по эталону самопроверки на 8 слайде.

- - Где вы можете потренироваться? (При выполнении дополнительного задания дома.)

- У кого нет ошибок? Сделайте вывод? (Мы умеем применять новый способ.)

8

- выполнение действий по алгоритму (П);

- контроль, самооценка (Р);

8. Включение в систему знаний и повторение

1) организовать работу по совершенствованию вычислительных навыков;

2) организовать повторение составных задач на нахождение целого.

- Какие умения необходимо развивать, чтобы правильно решать уравнения? (Необходимо уметь размышлять, правильно считать.)

- Верно, с этой целью я вам предлагаю выполнить

1) № 9, стр. 21 самостоятельно с проверкой по образцу

2) № 6, стр. 21.

- Что вам может помочь решить задачу? (Эталон с прошлого урока.)

- Проанализируйте задачу. (В задаче известно, что на катке катались 2 мальчика, а девочек на 4 больше. Необходимо узнать все количество ребят. Чтобы узнать все количество ребят, необходимо сложить количество мальчиков и девочек. Мы это сделать не можем, так как не знаем количество девочек.)

- Расскажите план решения задачи. (Первым действием мы узнаем, сколько девочек каталось на катке, вторым действием ответим на вопрос задачи.)

В случае затруднения детей при анализе задачи, учитель помогает вопросами.

- Что известно в задаче? Что надо узнать? Как ответить на вопрос задачи?

- Можете ли сразу ответить на вопрос? Почему? А это можем узнать? Как?

Самопроверка по эталону на 10 слайде.

9

10

- установление причинно-следственных связей (П);

- контроль, коррекция, самооценка (Р);

- выражение своих мыслей с достаточной и полнотой и точностью (К)

9. Рефлексия учебной деятельности на уроке

1) зафиксировать в речи новый способ действий, изученный на уроке: решение уравнений с неизвестным слагаемым;

2) зафиксировать затруднения, которые остались, и способы их преодоления;

3) оценить собственную деятельность на уроке.

- -Вот и все! Напоследок только оглянемся назад. Какую цель перед собой ставили. (Узнать, что такое уравнение и научиться их решать)

- Достигли своей цели? (Да)

- Докажите. (Уравнение - это равенство с неизвестным числом и чтобы его решить надо следовать плану. Чтобы найти неизвестную часть надо из целого вычесть известную часть)

- Что дает нам новое знание? (Научились сами и теперь можем научить других.)

Кто может сказать, что сумел сам сделать «открытие»? Докажите.

- Кому не удалось, почему?

-Просмотрите еще раз свою работу на уроке и оцените свою деятельность. (Понятно, интересно, работал) Что оцениваете на 1 шкале? (Как было понятно.) На второй? (Насколько было интересно на уроке.) На третьей? (Как я работал на уроке.)

Учащиеся в группах на специальных листах заполняют шкалы.

11

- рефлексия способов и условий действия (П);

- контроль и оценка процесса результатов деятельности (П);

- самооценка на основе критерия успешности (Л);

- адекватное понимание причин успеха/неуспеха в учебной деятельности (Л);

- формулирование своего мнения, учёт разных мнений (К)