Формирование вычислительных умений и навыков.

Тема по самообразованию:

«Формирование вычислительных умений и навыков у первоклассников».

Тюмень, 2016

В результате изучения курса математики учащиеся на уровне начального общего образования:

-научатся использовать начальные математические знания для описания окружающих предметов, процессов, явлений, оценки количественных и пространственных отношений;

-овладеют основами логического и алгоритмического мышления, пространственного воображения и математической речи, приобретут необходимые вычислительные навыки;

-научатся применять математические знания и представления для решения учебных задач, приобретут начальный опыт применения математических знаний в повседневных ситуациях;

-получат представление о числе как результате счета и измерения, о десятичном принципе записи чисел; научатся выполнять устно и письменно арифметические действия с числами; находить неизвестный компонент арифметического действия; составлять числовое выражение и находить его значение; накопят опыт решения текстовых задач;

-познакомятся с простейшими геометрическими формами, научатся распознавать, называть и изображать геометрические фигуры, овладеют способами измерения длин и площадей;

-приобретут в ходе работы с таблицами и диаграммами важные для практикоориентированной математической деятельности умения, связанные с представлением, анализом и интерпретацией данных; смогут научиться извлекать необходимые данные из таблиц и диаграмм, заполнять готовые формы, объяснять, сравнивать и обобщать информацию, делать выводы и прогнозы [1].

Формирование вычислительных умений и навыков в первом классе играет особо важную роль и является одной из главных задач обучения математике, поскольку вычислительные навыки необходимы как в дальнейшем обучении, так и в практической жизни человека. Практика современной школы показывает, что в основе формирования навыка вычислений должно лежать осмысление тех конкретных действий, от которых зависят правильность и скорость выполнения вычислений. Ученик, прежде всего, должен осознать цель, ради которой он формирует тот или иной навык. А учитель должен помочь ему в осознании этой цели. [3] Под вычислительным умением понимается знание конкретного вычислительного приёма и его использование для определённого вида выражений. Вычислительные навыки, в отличие от умений, характеризуются свёрнутостью операций, действием, доведённым до автоматизма. При этом следует заметить, что вычислительные умения и навыки тесно связаны между собой. С одной стороны, навыки составляют основу вычислительного умения, с другой стороны, вычислительные умения являются основой создания прочного вычислительного навыка.

Вычислительные навыки успешно формируются у учащихся при создании в учебном процессе определённых условий. Процесс овладения вычислительными навыками довольно сложен: сначала ученики должны усвоить тот или иной вычислительный приём, а затем в результате тренировки, научиться достаточно быстро выполнять вычисления, а в отношении табличных случаев - запомнить результат наизусть.

Приём вычислений складывается из ряда последовательных операций, а число операций определяется прежде выбором теоретической основы вычислительного приёма.

Формирование любого вычислительного приема проходит ряд этапов.

1. Подготовительный этап.

2. Этап ознакомления с новым вычислительным приемом.

3. Этап усвоения вычислительного приема и формирования вычислительного навыка.

Рассмотрим подготовительный этап. Одной из задач этого тапа является актуализация определенного круга знаний, умений, навыков через серию специально подобранных заданий. Этап ознакомления с новым вычислительным приемом представляет собой графическую классификационную схему, исходным элементом которой является вычислительный прием. На этапе актуализации необходимо убедиться в полной готовности учащихся к усвоению нового вычислительного приема. С этой целью детям предлагается серия заданий. Перед их составлением учителю необходимо ответить на следующие вопросы:

• Какие задания предложить учащимся на уроке по ознакомлению с новым вычислительным приемом на этапе актуализации?

• Каким требованиям должны удовлетворять эти задания?

Для ответа на поставленные вопросы обратимся к той части вычислительной деятельности ученика, где действие носит развернутый характер. На этом этапе учащиеся выполняют с комментированием все операции, входящие в вычислительный прием. Убедимся в этом на конкретном примере.

9+4=13

9+1+3=13

Комментарий ученика может быть таким: «у 9 прибавить 4. К 9 прибавлю 1, чтобы получить десяток. Надо было прибавить 4, прибавили 1, осталось прибавить 3. К 10 прибавить 3, получиться 13».

Анализируя деятельность ученика на этом этапе, приходим к выводу: теоретическая основа данного вычислительного приема - конкретный смысл действия сложения (сложение по частям).Значит, умение ученика выполнять сложение по частям является необходимым для усвоения нового вычислительного приема 9+4.

Операции, входящие в данный вычислительный прием:

- дополнение числа 9 до 10;

- разбиение второго слагаемого (4) на части (1 и 3);

- сложение чисел 10 и 3.

Каждая из названных операций может быть успешно выполнена учеником лишь в том случае, если он:

- умеет дополнить однозначное число до 10;

- знает состав чисел от 1 до 10;

- умеет выполнять сложение вида 10 + .

Вычислительный навык - это высокая степень овладения вычислительными приёмами. Приобрести вычислительные навыки - значит, для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия и выполнять эти операции достаточно быстро.

Полноценный вычислительный навык характеризуется правильностью, осознанностью, рациональностью, обобщённостью, автоматизмом, прочностью.

Правильность - ученик правильно находит результат арифметического действия, то есть правильно выбирает и выполняет операции, составляющие приём.

Осознанность - ученик осознаёт, на основе каких знаний выбраны операции и установлен порядок их выполнения, в любой момент может объяснить, как он решал и почему так может решать.

Рациональность - ученик выбирает для данного случая более рациональный приём, то есть выбирает те из возможных операций, выполнение которых легче других и быстрее приводит к результату.

Обобщённость - ученик может применить приём вычисления к большому числу случаев, то есть способен перенести приём вычисления на новые случаи.

Автоматизм - ученик выполняет и выделяет операции быстро и в свёрнутом виде, но всегда может вернуться к объяснению выбора системы операций. Высокая степень автоматизации должна быть достигнута по отношению к табличным случаям сложения и вычитания, умножения и деления.

Прочность - ученик сохраняет сформированные вычислительные навыки на длительное время.

Согласно действующей программе по математике до уровня навыка доводятся: таблица сложения и соответствующая ей таблица вычитания в пределах 10, табличное умножение и соответствующие случаи деления, умножение на 10, 100 и т.д. и соответствующие случаи деления чисел, оканчивающихся нулями. Сложение и вычитание чисел в пределах 100, деление и умножение двузначных чисел на однозначное, деление двузначного на двузначное, деление с остатком должны быть усвоены учащимися на уровне умения.

Наряду с усвоением умений и навыков устных вычислений младшие школьники овладевают алгоритмами письменных вычислений. В начальном курсе математики рассматриваются различные случаи сложения, вычитания, умножения и деления многозначных чисел в тех случаях, когда выполнение устных приёмов становится сложным для учащихся. Навыки письменных вычислений доводятся до автоматизма.

Упражнения в устных вычислениях должны пронизывать весь урок .

Их можно соединять с проверкой домашних заданий, закреплением изученного материала, предлагать учащимся при опросе.

Наряду с этим в практике учителей утвердилась хорошая традиция: на каждом уроке специально отводить 5-7 минут для устных вычислений, проводить так называемый устный счет. Материал для этого этапа урока учитель подбирает из учебников, а также из специальных сборников устных задач и упражнений. Устные упражнения должны соответствовать теме и цели урока и помогать усвоению изучаемого на данном уроке или ранее пройденного материала. В зависимости от этого учитель определяем место устного счета на уроке.

Задания для устного счета предлагают детям так, чтобы они воспринимали их либо зрительно, либо на слух, либо и зрительно, и на слух.

Устные вычисления в сочетании с иными видами упражнений активизируют мыслительную деятельность, развивают логическое мышление, сообразительность, память, наблюдательность и математическую зоркость, способствуют развитию речи учащихся. Практическое значение устных вычислений состоит в том, что быстрота и правильность вычислений необходимы в жизни, особенно в тех случаях, когда письменно выполнить действия не представляется возможным.

Необходимо отметить, что уровень трудности упражнений должен постепенно увеличиваться.

В 1-м классе в течение года на уроках математики проводится работа над формированием вычислительных навыков в пределах десяти. Перед учителями встаёт вопрос, как сделать привычную и, казалось бы, однообразную работу интересной и увлекательной. Присутствие в вычислительных упражнениях элемента занимательности, игры, догадки, сообразительности, использование интересного наглядного материала - вот те основные приёмы активизации познавательной деятельности, реализация которых позволит решить в практике обучения и задачу формирования прочных вычислительных навыков, и задачу развития познавательных способностей учащихся.

Вот некоторые игровые упражнения.

1. Домики. Нужно заселить домик.

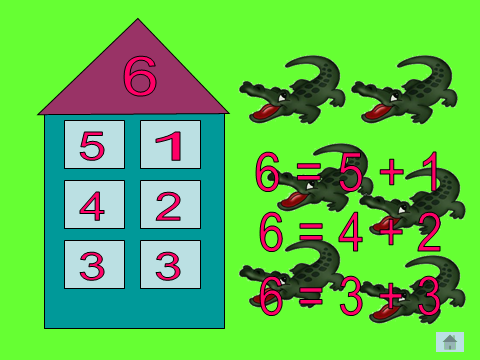
В 1 классе при изучении темы "Нумерация чисел от 1 до 10" дети усваивают все случаи состава чисел в пределах 10. Например, состав числа 6. Число 6 вставляют на крышу домика, в окошечках числа 5, 1, 4, 2 и т.д. Дети отвечают: 6 - это 5 и 1, 4 и 2 и т.д.

2. Выполните задание по образцу, комментируя следующим образом: «Надо было прибавить 7, прибавили 2, осталось прибавить 5».

7 7

2 5 ? ?

3. Вставь пропущенные числа. Заполни окошечки.

6 + = 8 9 = 2 +

4. Заполните таблицы.

7

6

5

4

3

2

1

5. Числовой веер. Игра «Молчанка».

Его хорошо использовать при проведении математического диктанта в 1-2 классах. Сам же диктант активизирует внимание и мышление детей, способствует формированию вычислительных навыков.

6. Разного вида ромашка:

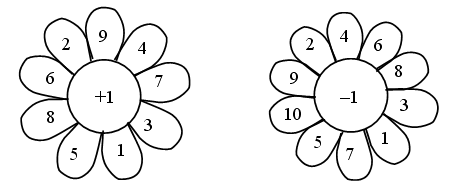
7. Традиционные перфокарты можно связать с известными детям литературными персонажами, героями мультфильмов, весёлыми человечками.

8. Задания вычислительного характера сопровождаю игровыми сюжетами и рисунками. Например:

• Буратино в недоумении, он не знает, как выполнить задание. Помогите ему!

• Пятачок собрался в гости к Пуху, но ему надо успеть решить примеры. Помогите ему!

• Незнайка с этим заданием уже справился, а вы справитесь? Объясни ему ход его выполнения.

Разнообразие форм кроссвордов, разных уровней сложности позволяет длительное время поддерживать интерес к выполнению данного вида работы.

Элементы занимательности и новизны, игры, встречи с любимыми героями, несложные, но интересные наглядные пособия вызывают у детей интерес к работе.

9. При организации фронтальной работы с классом можно включать такие упражнения как «цепочки». Они могут быть различного вида.

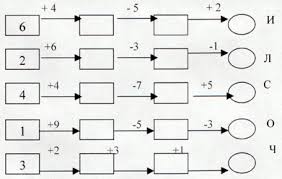
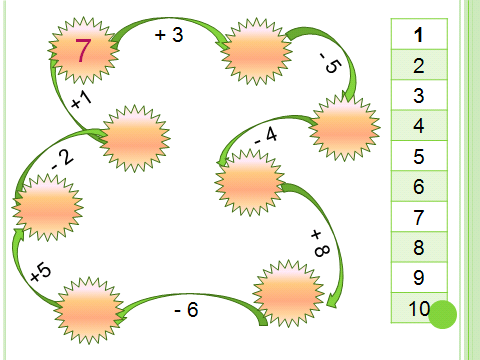
10. Работа с магическими квадратами ведётся на протяжении всего обучения в начальной школе.

• Проверь, магический ли это квадрат. Суммы по строкам, по столбцам и из угла в угол - равны.

5

30

15

25

35

20

45

10

По мере прохождения материала задания связанные с магическими квадратами, усложняются:

• Заполни магический квадрат:

106

112

122

• Дан магический квадрат. Докажите, что в клетке со звёздочкой не может стоять число 32.

6

*

16

2

Опыт использования магических квадратов показывает, что выполнение заданий с ними вызывает интерес у учащихся. А это способствует не только формированию вычислительных навыков, но и развивает мышление, умение планировать и контролировать свою деятельность.

11. Составление круговых примеров.

• Учитель пишет на доске примеры, у которых задан первый компонент. Учащиеся составляют примеры с ответом, равным первому компоненту следующего примера. Например:

17-5=12, 12+6=18 и т.д.

12. Задачи в стихотворной форме так же идут на отработку навыков устного счёта в пределах 20.

• Два опенка, пять маслят,

Пара рыжиков румяных,

Сколько всех грибов, ребята? ( 2+5+2=9)

• 10. Дружно муравьи живут

И без дела не снуют.

Два несут травинку,

Три несут былинку,

Пять несут иголки.

Сколько муравьев под елкой? ( 2+3+5=10)

15. Математические диктанты.

Учитель читает задания, дети записывают только ответы.

1.К 5 прибавь 6

2.Увеличь 7 на 8.

3.Из 11 вычти 8.

4.Запиши число, которое меньше 9 на 3.

5. Запиши число, которое больше 6 на 5.

6.Уменьши 16 на 9.

7.На сколько 14 больше 8?

8. На сколько 7 меньше 10?

9.Найди сумму чисел 3 и 8.

10. Найди разность чисел 17 и 9.

В процессе правильно организованной игры учащиеся незаметно для себя выполняют большое количество тренировочных упражнений в быстром темпе, что играет важную роль в формировании навыка вычислений.

1. "Кто быстрее".

Напротив каждого ряда прикрепляется картинка, под которой записаны примеры.Такие задания не только формируют вычислительные умения и навыки, но и развивают устойчивость внимания, увеличивают его объем, учат распределять и переключать его.

С целью оптимальной занятости учащихся на уроке необходимо постоянно использовать индивидуальные формы работы. В последние годы значительное место в преподавании математики в начальной школе занимает самостоятельная деятельность учащихся. Для большей эффективности самостоятельная деятельность в учебном процессе должна носить творческий характер. Тогда она способствует сознательному усвоению и переносу знаний, умений и навыков в новые ситуации, что ведёт к развитию познавательной самостоятельности и активности. В связи с этим необходимо на уроке использовать задания для самостоятельной деятельности творческого характера, которые нацелены на формирование у младших школьников вычислительных навыков. При этом каждый ученик получает свое задание, которое он выполняет независимо от других. Чаще всего это задания-карточки, где учитель имеет возможность их дифференцировать, что позволяет обеспечивать индивидуальную работу в зависимости от уровня подготовленности учащихся. Индивидуальные задания особенно важны для школьников с негативным отношением к учебе. Определяя индивидуальные учебные работы для учащихся, потерявших веру в свои силы, учитель исходит из того, что для них посильно. Такого рода задания требуют выполнения различных преобразований и обобщений с опорой на ранее приобретённые знания и умения. Учащиеся должны воспроизвести не только отдельные функциональные характеристики знаний, но и структуру этих знаний в целом, т.е. научиться применять эти знания в новых ситуациях. Тем самым знания углубляются, становятся более совершенными, а мышление учащихся достигает уровня продуктивной деятельности .

Получив карточку с разноуровневым заданием, ученик выбирает задание по уровню своих умственных способностей. Справившись со своим заданием, школьник может перейти к следующему заданию.

На этапе закрепления знания приёма и выработки вычислительного навыка внетабличного умножения и деления можно использовать задания для самостоятельной деятельности творческого характера.

Использование таких заданий способствует эффективной организации самостоятельной деятельности младших школьников, а также повышает эффективность процесса формирования соответствующего вычислительного навыка.

Развитию вычислительной культуры у младших школьников на уроках математики способствуют тесты. Тесты обладают целым рядом положительных характеристик:

• Быстрота проверки выполненной работы,

• Оценка достаточно большого количества учащихся,

• Возможности проверки усвоения теоретического материала,

• Проверка большого объёма материала,

• Объективность оценки результатов выполненной работы.

</ Из всего многообразия видов тестов в начальных классах целесообразно использовать тестовые задания с выбором одного верного ответа, так как они наиболее доступны младшим школьникам. Огромный интерес у учащихся вызывает работа с электронными тренажёрами. Такие формы работы не только отрабатывают вычислительные навыки, но и формируют познавательную самостоятельность учащихся, развивают интерес к предмету [2].

Список литературы

1. Примерная основная общеобразовательная программа начального общего образования.

2. Шубина В.П. Первое сентября. Формирование вычислительных навыков у младших школьников.

3. Холлохова З.Г. Первое сентября. Формирование вычислительных навыков у младших школьников.