Конспект урока на тему: Оценка разности

Урок 7

Тема: «Оценка разности».

Тип урока: ОНЗ.

Авторы: Т.В. Зайцева (№ 1159, г. Москва), Н.Н. Бирюкова (Православная гимназия, г. Рязань).

Основные цели:

1) сформировать способность к оценке разности;

2) тренировать способность к оценке суммы, повторить взаимосвязь между компонентами и результатом действия вычитания;

3) тренировать навык вычисления значений выражений с переменной, решения уравнений с комментированием по компонентам действий.

Мыслительные операции, необходимые на этапе проектирования: сравнение, аналогия.

Демонстрационные материалы:

1) смайлики:

В

се смайлики прошлых уроков;

2) задания для актуализации знаний:

а) список литературы из задания Стивенса:

Художественная литература: Между:

Про животных - 491шт. а) 900 и 1000

Фантастика - 784 шт. б) 1100 и 1300

в) 1200 и 1500

Учебники:

«Математика» - 84 шт. а) 380 и 500

«Русский язык» - 342 шт. б) 300 и 600

в) 480 и 700

Словари:

Толковые - 642 шт. а) 1000 и 1200

Орфографические - 500 шт. б) 1200 и 1300

в) 1100 и 1200

б) сравнение разностей:

558 - 302 * 598 - 302

973 - 456 * 973 - 452

684 - 325 * 690 - 315

372 - 123 * 172 - 123

851 - 467 * 851 - 479

938 - 680 * 920 - 690

3) опорные конспекты «Взаимосвязь между компонентами и результатом действия вычитания»:

а↑ - b = c↑

а - b↓ = c↑

a↑ - b↓ = c↑

а↓ - b = c↓

а - b↑ = c↓

a↓ - b↑ = c↓

4) гирлянда флажков из белой бумаги (по количеству детей в классе):

5) рисунок острова Рокфор;

6) «портрет» Стивенса;

7) конверт;

8) опорный конспект «Оценка суммы» (урок № 6, Д-8);

9) блоки для конструирования алгоритма оценки разности:

1

м б б м

- < a - b < - 0) опорный конспект по алгоритму оценки разности:

11) образец выполнения задания при работе в парах на этапе первичного закрепления:

в) 4000 - 2000 < 4611 - 1315 < 5000 - 1000

2000 < 4611 - 1315 < 4000

г) 9000 - 4000 < 9568 - 3419 < 10000 - 3000

5000 < 9568 - 3419 < 7000

12) карточка с условием задачи для этапа включения знаний:

контейнер с грузом - 3219 кг,

пустой контейнер - 237 кг

Раздаточные материалы:

1) блоки (по числу групп) для конструирования алгоритма оценки разности (такие же, как Д-9);

2) эталон для самопроверки самостоятельной работы (№ 2, стр. 19):а)

90 - 30 < 94 - 27 < 100 - 20

60 < 94 - 27 < 80

м б б м

- < a - b < -

1) заменяю уменьшаемое меньшим круглым числом 90, а вычитаемое - большим круглым числом 30;

2) заменяю уменьшаемое большим круглым числом 100, а вычитаемое - меньшим круглым числом 20;

3) нахожу значения полученных выражений (60, 80) и записываю двойное неравенство.

б)

900 - 700 < 975 - 639 < 1000 - 600

200 < 975 - 639 < 400

м б б м

- < a - b < -

1) заменяю уменьшаемое меньшим круглым числом 900, а вычитаемое - большим круглым числом 700;

2) заменяю уменьшаемое большим круглым числом 1000, а вычитаемое - меньшим круглым числом 600;

3) нахожу значения полученных выражений (200, 400) и записываю двойное неравенство.

Ход урока:

1. Мотивация к учебной деятельности

Цель:

1) включение учащихся в учебную деятельность - тренировать в понимании значения уметь учиться, рассмотреть смайлики пятого этапа;

2) определить содержательные рамки урока: оценка результатов арифметических действий;

3) мотивация учащихся к учебной деятельности посредством включения их в игру-путешествие.

Организация учебного процесса на этапе 1:

На доске смайлики с прошлых уроков, гирлянда из белых флажков, на дополнительной доске - рисунок острова Рокфор и «портрет» Стивенса. Учитель держит в руках конверт.

- Ребята, сегодня у вас не совсем обычный урок. Вы получили приглашение совершить путешествие на загадочный остров Рокфор. Путешествие ваше будет математическим и к нему надо хорошо подготовиться. Как вы будем готовиться? (Повторим материал прошлых уроков, материал, который нам пригодится в путешествии.)

- Какие знания, полученные на прошлых уроках, вам могут пригодиться? (…)

- Всем приплывающим чужеземцам островитяне загадывают математические загадки. Мудрейший житель острова Стивенс сам встречает и оценивает всех гостей. Какой математический термин вы услышали в моих словах? (Оценивать.)

- Готовясь к путешествию, вы продолжите заниматься оценкой результатов арифметических действий.

2. Актуализация знаний и фиксация затруднения в пробном действии.

Цель:

1) повторить алгоритм оценки суммы, взаимосвязь между компонентами и результатом действия вычитания;

2) активизировать мыслительные операции: сравнение, аналогия;

3) мотивировать к пробному действию и его самостоятельному выполнению и обоснованию;

4) предъявить индивидуальное задание для пробного действия (оценка разности);

5) организовать фиксацию образовательной цели и темы урока;

6) организовать выполнение пробного действия и фиксацию затруднения, демонстрирующего недостаточность имеющихся знаний, для оценки разности;

7) организовать анализ полученных ответов и зафиксировать индивидуальные затруднения в выполнении пробного действия или его обосновании.

Организация учебного процесса на этапе 2:

1) Повторение и знаковая фиксация алгоритма оценки суммы.

- Стивенс всех чужеземцев просил оставлять ему книги, учебники и словари. Со временем их скопилась так много, что, расставляя их на полки своей библиотеки, Стивенс затруднился с оценкой их количества.

Учитель открывает запись на доске:

Художественная литература: Между:

Про животных - 491шт. а) 900 и 1000

Фантастика - 784 шт. б) 1100 и 1300

в) 1200 и 1500

Учебники:

«Математика» - 84 шт. а) 380 и 500

«Русский язык» - 342 шт. б) 300 и 600

в) 480 и 700

Словари:

Толковые - 642 шт. а) 1000 и 1200

Орфографические - 500 шт. б) 1200 и 1300

в) 1100 и 1200

- Какая оценка подойдет? Докажите.

Учащиеся работают на планшетках, выбирают правильный вариант ответа, показывают учителю. Учитель одного из учеников просит обосновать свой выбор. Если, кто-то из учащихся допускает ошибку, то обосновывает свой выбор именно этого ученика.

- Каким алгоритмом вы пользовались, выполняя задания? (Алгоритмом оценки суммы.)

Учитель помещает на дополнительную доску опорный конспект по алгоритму оценки суммы (Д-8). При необходимости можно попросить учащихся проговорить шаги соответствующего алгоритма.

2) Повторение взаимосвязи между компонентами и результатом действия вычитания.

- Стивенс все время придумывает головоломки. Попробуйте решить одну из них, чтобы лучше подготовиться к встрече с жителями острова.

Учитель открывает записи на доске:

558 - 302 * 598 - 302

973 - 456 * 973 - 452

684 - 325 * 690 - 315

372 - 123 * 172 - 123

851 - 467 * 851 - 479

938 - 680 * 920 - 690

- Сравните значения данных выражений, не вычисляя.

Учащиеся работают фронтально, обосновывая выбор знака сравнения взаимосвязью между компонентами и результатом действия вычитания. По ходу выполнения задания учитель записывает на доске выбранные знаки сравнения и соответствующие опорные схемы:

558 - 302 < 598 - 302 а↑ - b = c↑

973 - 456 < 973 - 452 а - b↓ = c↑

684 - 325 < 690 - 315 a↑ - b↓ = c↑

372 - 123 > 172 - 123 а↓ - b = c↓

851 - 467 > 851 - 479 а - b↑ = c↓

938 - 680 > 920 - 690 a↓ - b↑ = c↓

После этого учитель еще раз уточняет сам или просит обобщение сделать учащихся по взаимосвязи между компонентами и результатом действия вычитания:

- Перечислите все случаи, когда разность уменьшается. (Уменьшаемое уменьшается, вычитаемое не изменяется; вычитаемое увеличивается, уменьшаемое не изменяется; уменьшаемое уменьшается, вычитаемое увеличивается.)

- Перечислите все случаи, когда разность увеличивается. (Уменьшаемое увеличивается, вычитаемое не изменяется; уменьшаемое не изменяется, вычитаемое уменьшается; уменьшаемое увеличивается, вычитаемое уменьшается.)

Походу беседы сначала на доску вместо первых трех строчек записей помещается первый из опорных сигналов Д-6, а затем - второй:

- Что вы сейчас повторили? (Оценку суммы и как зависит разность от изменения уменьшаемого и вычитаемого.)

- Какое следующее задание я вам предложу? (Задание для пробного действия.)

- С какой целью вам предлагается пробное задание? (Чтобы понять, что мы ещё не знаем, что нового сегодня будет на уроке.)

- Может быть так, что оно не получится? (Да.)

3) Индивидуальное задание.

- Приготовьте свои планшетки. Составьте выражение по тексту задачи; «В этом году гости острова Рокфор из 915 головоломок, которые придумал Стивенс, отгадали только 346. Как много головоломок остались неразгаданными?».

- Это задание является пробным? (Нет, мы умеем составлять выражения по тексту задачи.)

- Выполните задание.

Ученики работают на планшетках. Они должны записать выражение 915 - 346.

- Покажите, что у вас получилось.

Учитель фиксирует на доске получившиеся выражения. Если возникнет необходимость, проводится их коррекция. В результате на доске остается согласованный вариант 915 - 346.

- А теперь оцените значение получившегося выражения.

- Что нового в этом задании? (Надо оценить разность.)

- Сформулируйте цель урока. (Оценить разность.)

- Сформулируйте тему урока. (Оценка разности.)

Тема записывается на доске.

- Выполните задание в течение 1 минуты.

Дети работают самостоятельно.

- Стоп! Закончили работу.

- У кого нет результата? (…)

- Что вы не смогли сделать? (Мы не смогли оценить разность чисел.)

- У кого есть ответ, покажите, что у вас получилось.

Вероятно, многие учащиеся воспользуются уже известным алгоритмом оценки суммы, что приведет к неверному числовому неравенству 600 < 915 - 346 < 600. Другие, опираясь на подготовительные задания, могут выполнить задание верно и т.д. Как и в предыдущем задании, учитель организует фиксацию на доске всех имеющихся вариантов, предлагая каждому учащемуся выбрать свою позицию (например, при помощи поднятия руки), и подводит их к осознанию недостаточности имеющихся знаний.

- Проанализируйте, что у вас получилось? (Разные ответы, некоторые не выполнили задание.)

У тех ребят, кто выполнили задание попросить назвать, какой алгоритм использовали при выполнении задания. (Такого алгоритма нет.)

- Что же делать? (Надо подумать, почему так получилось.)

- Что вы должны теперь сделать? (Определить, каких знаний у нас не хватает, чтобы выполнить задание.)

3. Выявление места и причины затруднения.

Цель:

1) организовать восстановление выполненных операций и фиксацию (вербальную и знаковую) места - шага, операции, где возникло затруднение;

2) организовать соотнесение действий учащихся с используемым способом (алгоритмом, понятием и т.д.) и на этой основе организовать выявление и фиксирование во внешней речи причины затруднения - тех конкретных знаний, умений или способностей, которых недостаёт для решения исходной задачи такого класса или типа.

Организация учебного процесса на этапе 3:

- Какое задание выполняли? (Оценивали разность 915 и 346.)

- Что вы использовали при выполнении задания? (…)

Если учащиеся использовали алгоритм оценки разности обратить их внимание на то, что в задании надо было оценить разность, если кто-то использовал взаимосвязи между компонентами и результатом действия вычитания, то зафиксировать это предложение, как интересный вариант, но пока этот выбор необоснован.

- В каком месте возникло затруднение? (При определении нижней и верхней границы.)

- Почему возникло затруднение? (У нас нет алгоритма оценивания разности.)

4. Построение проекта выхода из затруднения.

Цель:

в коммуникативной форме о

Этап 4рганизовать построение учащимися проекта будущих учебных действий:

1. уточнение цели проекта (построить алгоритм оценки разности);

2. определение средств (алгоритмы, модели, учебник и т.д.);

3. построение плана достижения цели.

Организация учебного процесса на этапе 4:

- Что надо теперь сделать? (Надо поставить цель, составить план работы.)

- Уточните цель своей деятельности. (Построить алгоритм оценки разности.)

- Что вы сможете из повторенного использовать при построении нового алгоритма? (Правила изменения разности при изменении уменьшаемого и вычитаемого.)

- Вспомните, как мы строили алгоритм оценки суммы и предложите, по какому плану вы будете действовать? (Найдём верхнюю границу разности, найдём нижнюю границу разности, составить алгоритм.)

План может быть зафиксирован на доске.

5. Построение проекта выхода из затруднения.

Цель:

1) организовать коммуникативное взаимодействие с целью реализации построенного проекта, направленного на приобретение недостающих знаний: алгоритм оценки разности;

2) создать условия для построения учащимися алгоритма оценки разности; зафиксировать его в речи, графической и знаковой форме (с помощью эталона);

3) организовать уточнение общего характера нового знания.

Организация учебного процесса на этапе 5:

- Вы составили план действий, а что дальше надо делать? (Этот план выполнить.)

На доску вывешивается смайлик:

- Какими числами удобно заменить оба компонента действия, чтобы было удобно вычислять? (Круглыми.)

- Что будет являться нижней границей разности? (Меньшая разность.)

Учитель обращает внимание детей на опорный конспект, фиксирующий все случаи уменьшения разности в зависимости от изменения компонентов действия вычитания:

- Какое равенство поможет вам найти нижнюю границу разности? (Равенство, в котором изменяются оба компонента действия: уменьшаемое уменьшается, а вычитаемое увеличивается.)

- Какими числами следует заменить уменьшаемое и вычитаемое, чтобы определить нижнюю границу? (Уменьшаемое надо заменить меньшим круглым числом, а вычитаемое - большим круглым числом.)

- Запишите выражение для нахождения нижней границы составленной разности.

Один из учащихся работает на доске с комментированием, остальные дети - в тетрадях:

900 - 400 < 915 - 346

- Что будет являться верхней границей разности? (Большая разность.)

- Когда разность увеличивается? (Если уменьшаемое увеличивается, а вычитаемое - уменьшается.)

- Как же найдем верхнюю границу разности? (Надо заменить уменьшаемое большим круглым числом, а вычитаемое - меньшим круглым числом.)

- Запишите выражение для нахождения верхней границы разности чисел 915 и 346.

Другой учащийся выполняет записи на доске, комментируя свои действия, остальные - продолжают работать в тетрадях:

900 - 400 < 915 - 346 < 1000 - 300

- Самостоятельно выполните вычисления и определите, в каких границах заключена разность.

Учащиеся выполняют задание самостоятельно. Правильность его выполнения проверяется фронтально. После проверки учитель завершает на доске запись выполнения оценки разности:

900 - 400 < 915 - 346 < 1000 - 300

500 < 915 - 346 < 700

- Вы справились с заданием Стивенса. Что теперь надо сделать? (Составить алгоритм.)

На доску вывешивается смайлик:

Шаги алгоритма оценки суммы можно предложить детям вывести самостоятельно в парах или группах, затем проверить получившиеся алгоритмы фронтально. Перед работой в группах вспомнить правила работы в группах.

В менее подготовленном классе можно дать готовые блоки и попросить учащихся расположить их в нужном порядке. Можно также использовать подводящий диалог:

- С чего следует начать оценку разности? (Заменить уменьшаемое меньшим круглым числом, а вычитаемое - большим круглым числом, и найти нижнюю границу.)

- Что надо сделать дальше? (Найти верхнюю границу, для этого заменить уменьшаемое большим круглым числом, а вычитаемое - меньшим круглым числом.)

- И последнее, что остается сделать? (Найти значения составленных выражений и записать двойное неравенство.)

В ходе беседы учитель последовательно помещает на доску карточки с шагами алгоритма (Д-9) оценки разности. В результате данный алгоритм фиксируется на доске:

Заменить уменьшаемое а меньшим круглым числом, а вычитаемое b - большим круглым числом (нижняя граница)

Заменить уменьшаемое а большим круглым числом, а вычитаемое b - меньшим круглым числом (верхняя граница)

Найти значения полученных выражений и записать

двойное неравенство

- Придумайте опорный конспект по этому алгоритму.

Данное задание можно предложить выполнить по группам, в парах или индивидуально. После проверки согласованный вариант опорного конспекта помещается на доску (Д-10):

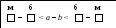
- Что теперь необходимо сделать? (Надо потренироваться использовать построенный алгоритм.)

6. Первичное закрепление во внешней речи.

Цель:

зафиксировать в речи изученное учебное содержание: алгоритм оценки разности, тренироваться в применении, построенного алгоритма при выполнении задания.

Организация учебного процесса на этапе 6:

№ 3, стр. 20

а) 700 - 300 < 711 - 284 < 800 - 200 б) 800 - 400 < 856 - 397 < 900 - 300

400 < 711 - 284 < 600 400 < 856 - 397 < 600

Учащиеся работают на печатной основе. Задания а) и б) выполняются по цепочке с комментированием. Задания в) и г) - в парах, и после выполнения проверяют по образцу (Д-11).

7. Самостоятельная работа с самопроверкой по эталону.

Цель:

1) организовать самостоятельное выполнение учащимися заданий на новый способ действий: проверить свое умение производить оценку разности.

2) организовать самооценку детьми правильность выполнения задания (при необходимости - коррекцию возможных ошибок).

Организация учебного процесса на этапе 7:

- Молодцы! Вы, действительно, команда! Все вместе с заданиями справились и к путешествию готовы. А теперь проверьте каждый себя и выполните самостоятельно задание № 2, стр. 19.

№ 2, стр. 19.

Учащиеся работают самостоятельно на печатной основе. На самостоятельную работу отводится 2-3 минуты.

- Закончили работу. Как вы думаете, как определить правильно вы выполнили задание или нет? (Надо проверить себя по эталону.)

Проверка проводится по эталонам для самопроверки, проговаривается каждый шаг алгоритма.

- Зафиксируйте результаты проверки соответствующими знаками «+» или «?».

- Какие возникли затруднения? (Не смогли воспользоваться нужным алгоритмом, не смогли подобрать круглые числа и т.п.)

- Скажите, в чем причина ошибок? (Допустили ошибки в вычислениях границ, взяли не те круглые числа для определения границ и т.п.)

- Кто допустил ошибки, исправьте их. Вы молодцы!

- Кто не допустил ошибок в самостоятельной работе? Молодцы!

8. Включение в систему знаний и повторение.

Цель:

1) тренировать способность к оценке разности;

2) тренировать навык вычисления значений выражений с переменной, решения уравнений с комментированием по компонентам действий.

Организация учебного процесса на этапе 8:

1) № 6, стр. 20

- Собираясь в путь на далекий остров, мы весь груз положим в контейнер. Контейнер с грузом весит 3219 кг, а пустой контейнер - 237 кг. Докажите, что наш груз весит больше 2700 кг, но меньше, чем 3800 кг.

Учитель читает задание и открывает на доске запись с данными этой задачи:

контейнер с грузом - 3219 кг,

пустой контейнер - 237 кг

Один из учащихся выполняет задание на доске, остальные дети работают в тетрадях:

3000 - 300 < 3219 - 237 < 4000 - 200

2700 < 3219 - 237 < 3800

- Хитроумный Стивенс придумывает для гостей острова разные задания. Чтобы не попасть впросак, повторим действия с многозначными числами.

2) № 10, стр. 21

а) 642 ∙ х

Если х = 407, то 642 ∙ 407 = 261 294; 6 4 2

если х = 4070, то 642 ∙ 4070 = 2 612 940; 4 0 7

если х = 40 700, то 642 ∙ 40 700 = 26 129 400. 4 4 9 4

2 5 6 8

2 6 1 2 9 4

б) у : 5.

Если у = 1030, то 1030 : 5 = 206; 1 0 3 0 5

если у = 10 300, то 10 300 : 5 = 2060; 1 0 2 0 6

если у = 103 000, то 103 000 : 5 = 20 600. 3 0

3 0

0

Двое учащихся работают на доске (по очереди), а остальные - в тетрадях. При выполнении задания дети должны заметить, что в случае (а) первый множитель остается без изменения, а второй - каждый раз увеличивается в 10 раз, поэтому и произведение будет увеличиваться в 10 раз. Аналогично, в случае (б): делитель не меняется, а делимое увеличивается в 10 раз, поэтому частное каждый раз будет увеличиваться во столько же раз.

3) № 11 (а), стр. 21

- Теперь повторим решение уравнений.

Решение уравнения с комментированием выполняется на доске одним из учащихся, остальные дети работают в тетрадях. Можно организовать работу с уравнением по цепочке с места.

9. Рефлексия учебной деятельности на уроке.

Цели:

1) зафиксировать новое содержание, изученное на уроке;

2) организовать рефлексивный анализ учебной деятельности с точки зрения выполнения требований, известных учащимся;

3) оценить собственную деятельность на уроке;

4) зафиксировать неразрешенные на уроке затруднения, если они есть, как направления будущей учебной деятельности;

5) обсудить и записать домашнее задание.

Организация учебного процесса на этапе 9:

- Какими новыми знаниями вы овладели? (Мы научились проводить оценку разности.)

- Какую цель вы ставили перед собой? (Построить алгоритм для оценки разности)

- Вы достигли цели? (…)

- Как вы думаете, готовы ли вы к дальнейшему путешествию? (…)

- На следующем уроке вы отправитесь в путь на остров Рокфор. Давайте украсим корабль флажками. Приготовьте фломастеры или цветные карандаши. Подойдите к доске и раскрасьте каждый свой флажок. Если вы считаете, что разобрались в новой теме, выберите зеленый цвет, а если нет - желтый.

Каждый учащийся раскрашивает свой флажок в выбранный цвет. После того, как получится гирлянда из раскрашенных флажков, учитель может еще раз поговорить с детьми об их готовности или неготовности к путешествию и предложить домашнее задание, прокомментировав его.

Домашнее задание:

Конспект текста учебника, стр. 19

№ 4, стр. 20, № 13 (а или б), стр. 21;

J № 7, стр. 20.