Факультативное занятие по математике Магические квадраты

Факультативное занятие по математике

3 класс

Тема: Магические квадраты.

Цель: Продолжить обучение заполнению магических квадратов на основе исследовательской деятельности закономерности. Развивать умение наблюдать, исследовать, анализировать полученные знания, умение обобщать. Прививать стремление к познанию нового, интерес к математике.

Оборудование: компьютер, интерактивное оборудование, флипчарт, презентация PowerPoint, оценочный лист.

Ход занятия:

1. Орг. момент.

Прозвенел уже звонок

Начинается урок

Но сначала повернитесь

И друг другу улыбнитесь

Улыбнитесь мне, гостям

И садитесь по местам!

- Добрый день, юные математики!

- Приглашаю всех на очередное увлекательное занятие. Не забудьте взять с собой

быстроту мысли, находчивость, смекалку и сообразительность.

- А начать наше занятие предлагаю с разминки.

2. Разминка «Поиск закономерностей». (флипчарт 1, 2)

   1. Найдите закономерность, впишите номер нужной фигуры. Посмотрите на рисунок. В нем две части: левая - в прямоугольнике и правая. Вы должны внимательно рассмотреть все рисунки в левой части, нарисованные по определенному плану, и подумать, какой рисунок из правой части надо поместить в пустой прямоугольник. (ответ: №4)

   2. Найди закономерность, впиши номер нужной фигуры. Проверка: на какие элементы рисунка вы обращали внимания? (на форму сумки и на форму ручки). Какая же сумка подходит? (ответ: №6)

   3. Вставь недостающее число. (ответ: 61)

21 7 ?

36 17 24 11 72

15

4. Закончи ряд чисел

10 17 24 (прибавляем каждый раз 7)

40 35 30 (вычитаем по 5)

Используя закономерность, придумай свой ряд чисел.

5. Вставь пропущенное число

3 ?

6

12 2 9 3 10 2

Ответ: 5

6. Найди недостающее число.

Ответ: 5

Самопроверка. Оценивание.

- Что помогло вам справиться со всеми заданиями?

- Что такое закономерность? (Закономерность - это последовательное проявление действия какого нибудь закона. Закономерность явлений).

3. Определение темы занятия.

- У вас на партах лежат разноцветные листы. Что на них изображено?

- Какие это квадраты?

- Сформулируйте тему нашего занятия.

- А, как и где появились первые «магические квадраты»?

(выступление подготовленных учеников) (презентация)

«В давние времена, научившись считать и выполнять арифметические действия, люди с удивление обнаружили, что числа имеют самостоятельную жизнь, удивительную и таинственную. Складывая различные числа, располагая их друг за другом или одно под другим, они иногда получали одинаковую сумму. Наконец, разделив числа линиями так, чтобы каждое оказалось в отдельной клетке, увидели квадрат, любое из чисел которого принимало участие в двух суммах, а те, что расположены вдоль диагоналей - даже в трех, и все суммы равны между собой! Недаром древние китайцы, индусы, а вслед за ними и арабы приписывали таким конструкциям таинственные и магические свойства. Магические квадраты появились на Древнем Востоке очень давно. Одна из сохранившихся легенд повествует о том, что когда император Ю из династии Шан стоял на берегу Ло, притоке Желтой реки, вдруг появилась огромная черепаха, у которой на спине был рисунок из двух мистических символов - черных и белых кружочков, который был осознан затем как изображение магического квадрата порядка. Магические квадраты были воплощены в амулетах, заклинаниях. Они использовались в качестве талисманов по всей Индии. Их рисовали на кувшинах удачи, медицинских кружках. До сих пор они используются у некоторых восточных народов как талисман. Их можно встретить на палубах больших пассажирских судов как площадку для игры.»

- Что нового вы узнали про магические квадраты? Где они появились впервые?

На спине, какого животного был рисунок? Что это были за символы?

В качестве чего использовались квадраты?

- Итак, сегодня мы продолжим работу с магическими квадратами, и выявим новые закономерности при заполнении этих квадратов.

- Под магическими будем понимать квадраты, в которых суммы чисел, стоящих в

любом столбце или в любой строке, а также по диагоналям, одинаковы.

4. Решение задач.

(работа в группах)

Задача 1. Даны числа 1, 2, 3, 4, 5, 6, 7, 8, 9. Часть из них расставлена по клеткам. Требуется расставить остальные числа так, чтобы в любом направлении в сумме получалось 15. (флипчарт 3)

- Объясните, как вы заполнили магический квадрат?

(В данном квадрате есть закономерность, надо из 15 вычесть сумму двух известных чисел, стоящих в одном столбце. Получаем следующий квадрат).

Задача 2. Даны числа: 2, 3, 4, 5, 6, 7, 8, 9, 10. Требуется вписать их в клетки квадрата так, чтобы в любом направлении в сумме получилось одно и то же число. Часть чисел уже вписана в квадрат. (флипчарт 4)

- Получается, заполнить квадрат? Почему?

(Мы не знаем сумму чисел, которая должна получиться в строках, столбцах и по диагонали)

- Подумайте, как это можно сделать?

- В каждом магическом квадрате есть еще закономерность. Самый простой способ

найти число, это умножить число 6 на 3, получим 18. А теперь впишите числа.

Получаем следующий квадрат:

Задача 3. Даны числа 5, 6, 7, 8, 9, 10, 11, 12, 13. Два их них вписаны в клетки квадрата. Впишите остальные так, чтобы в любом направлении получилось в сумме одно и то же число. (флипчарт 5) - Посмотрим на все три заполненных квадрата и попробуем найти еще ряд

закономерностей, которые помогут заполнить квадрат еще с меньшим кол-вом чисел,

вписанных в квадрат. (флипчарт 6)

1, 2, 3, 4, 5, 6, 7, 8, 9 2, 3, 4, 5, 6, 7, 8, 9, 10

5, 6, 7, 8, 9, 10, 11, 12, 13

- Посмотрите, какое число стоит в центре квадрата?

- Как оно расположено в ряду данных чисел?

(В центре квадрата всегда записывается число, стоящее на пятом месте нашей

последовательности, т. е. одинаково удаленное с левого и правого ее краев.)

- Можно заметить еще ряд закономерностей:

в квадрате по разные стороны от центрального числа стоят числа, одинаково

удаленные от левого и правого краев последовательности. Покажем пары

соответствующих чисел на примере заполнения квадрата числами от 1 до 9.

(флипчарт 7)

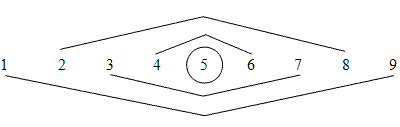
- Зная это, можно заполнить квадрат, почти не считая.

- Посмотрите, как расположены в квадрате числа, стоящие рядом с центральным, а

также числа, записанные от них через одно число. Они соединены линиями сверху.

(Они расположены по диагоналям квадрата.)

- А где расположены остальные числа, которые соединены линиями снизу?

(Они расположены по вертикали и по горизонтали.)

- Давайте проверим, выполняются ли эти закономерности.

Задача 5. Даны числа: 3, 4, 5, 6, 7, 8, 9, 10, 11. Впишите их в клетки квадрата так, чтобы в любом направлении получилось одно и то же число. (флипчарт 8)

(Найдем, какая сумма должна получаться в каждом направлении. Для этого умножим центральное число 7 на 3. В результате получим 21. В центр квадрата поставим число 7, по одной диагонали числа 6 и 8, по другой - 4 и 10. Осталось расставить недостающие числа: сумма записанных в первой строке чисел равна 10, до 21 недостает 11, значит, в пустой клетке верхней строки запишем число 11 (первое справа). Тогда в нижней строке запишем число 3 (первое слева). В левый столбик запишем число 5 (21 - (6 + 10)), тогда в правом столбике останется записать число 9. Таким образом, мы расставили все 9 чисел в клетки магического квадрата, при этом ни одно число по условию задачи в квадрате не было поставлено.)

- Итак, какие закономерности мы использовали для решения магического квадрата? (флипчарт 9)

1) Чтобы найти сумму чисел в каждом столбце или строке, можно центральное число умножить на 3.

2) В центре квадрата стоит число, записанное в ряду пятым.

3) В квадрате по разные стороны от центрального числа стоят числа, одинаково удаленные от левого и правого краев последовательности.

4) Числа, стоящие рядом с центральным и через одно от него, расположены по диагоналям квадрата. Числа, стоящие с краю и через одно от него, расположены в квадрате по вертикали и по горизонтали.

- Оцените свою работу в оценочном листе.

5. Индивидуальная работа.

- Используя алгоритм, заполните квадраты.

(для каждого ученика раздаются задания)

- Оцените свою работу в оценочном листе.

VI. Итог

- Чему мы сегодня научились на нашем занятии?

- Что нужно знать, чтобы разгадать магический квадрат?

7. Рефлексия.

«Лесенка успеха»