Урок математики в 3 классе.

Тип урока: ОНЗ.

Тема: «Свойства пересечения множеств».

Основные цели:

1) формировать представление о переместительном и сочетательном свойствах операции пересечения множеств;

2) повторить переместительное и сочетательное свойства сложения и умножения, закрепить понятие пресечения множеств;

3) тренировать навыки решения уравнений и задач на приведение к единице.

Познавательные УУД:

• использование имеющихся знаний;

• исследование учебной задачи;

• установление логических, причинно-следственных связей, построение логической цепи рассуждений,

• применение знаково-символической схемы.

Регулятивные УУД:

• оценивать уровень успешности;

• производить контроль своих действий;

• определять цель учебной задачи;

• планировать свою деятельность, определяемую результатом,

• контроль в форме сличения способа действия и его результата с заданным эталоном.

Коммуникативные УУД:

• умение слушать и вступать в диалог;

• умение правильно выражать свои мысли;

• умение контролировать и корректировать действия других;

• оформление своей мысли в устной речи;

• обоснование своего ответа;

• умение ориентироваться в своей системе знаний;

Личностные УУД:

• самооценка своих возможностей;

• формирование положительного отношения к учению.

Мыслительные операции, необходимые на этапе проектирования: сравнение, обобщение, аналогия.

Демонстрационный материал:

1) карточки с высказываниями:

«Новое умение - везде найдёт применение».

«Торопись - да не ошибись».

«Повторение - мать учения».

2) карточки с записями:

3) карточки с записью свойств чисел:

а + b = b + а (а + b) + с = а + (b + с)

а · b = b · а (а · b) · с = а · (b · с)

4) карточки для составления эталона:

А ∩ В = В ∩ А

(А ∩ В) ∩ С = А ∩ (В ∩ С)

(А ∩ В) ∩ С = А ∩ (В ∩ С)

Пересечение множеств не зависит

от порядка множеств …

…и от изменения порядка действий.

5) алгоритм рассуждений для вычислений:

Читаю выражение

Определяю свойство, которое можно использовать для упрощения вычислений

Вычисляю

6) эталон для самопроверки к этапу 7:

М ∩ К = К ∩ М Пересечение множеств не зависит

от порядка множеств и порядка

(М ∩ К) ∩ Т = М ∩ (К ∩ Т) действий.

7) «лесенка успеха» Я УЗНАЛ НАУЧИЛСЯ ЗАПОМНИЛ УДИВИЛСЯ

Раздаточный материал:

1. Листы для выполнения заданий для пробного действия.

2. Самопроверка к заданиям по выбору (задача)

4 под. - n кв.

6 под. - ? кв.

1 под. - ? кв.

Ответ: 96 квартир в 6 подъездах.

3. Самопроверка к заданиям по выбору (уравнения)

а

б) 604 - х = 286; 604

х = 604 - 286; 286

х = 318. 318

604 - 286 = 318

318 =318

) х - 394 = 286; 286

х = 286 + 394; 394

х = 670 670

286 + 394 = 670

670 = 670

4. Самопроверка к заданиям по выбору (примеры)

а) (13 + 8 · 4 ) : 5 - (27 : 3 - 0 · 6) = 9 - 9 = 0

9. 0

9

32

45 9

б) 40 : (24 : 6) + 7 · (12 - 2 · 2) - 5 · 5 = 10+ 56 - 25 = 10 + 56 - 25 = 41

4 4 25

10 56 8

Ход урока:

1. Мотивация к учебной деятельности.

Цель:

1) создать условия для возникновения у учащихся внутренней потребности включения в учебную деятельность («хочу») через создание ситуации, вызывающей интерес;

2) организовать деятельность учащихся по установке тематических рамок урока («могу»): пересечение множеств.

3) организовать актуализацию требований к ученику со стороны учебной деятельности («надо»).

Организация учебного процесса на этапе 1:

1)- Ребята к нам сегодня пришли гости. Давайте поздороваемся.

- Вы любите тайны? (Да)

• Сегодня на уроке мы с вами будем раскрывать математические тайны.

• Давайте подумаем каким образом вы будите это делать? (С повторения того, что нам пригодится для открытия нового.)

  - Пожелайте друг другу удачи и поднимаясь по нашей математической лестнице вы сможете узнать новую тайну.

  Организация учебного процесса на этапе 2:

К нам в гости на урок пришла буква Я, которая вместе с нами будет раскрывать математические тайны.(На доску вывешивается буква Я).

Предлагаю вам до повторения необходимого потренироваться в устном счёте. (Под первой ступенькой появляется слово повторение).

Кто сегодня подготовил математический диктант? Кто? (Сафронова А.)

33 больше задуманного числа на 8. Какое число задумано?

Задуманное число меньше 42 на 10. Какое число задумано?

Какое число надо прибавить к 17, чтобы получить 56?

Какое число надо вычесть из 61, чтобы получить 15?

70 больше неизвестного числа на 17. Чему равно неизвестное число?

44 меньше неизвестного числа на 16. Чему равно неизвестное число?

- Проверим. (25; 32; 39; 46; 53, 60; ).

- Посмотрите закономерность и скажите следующие три числа в данном ряду чисел. (Числа увеличиваются на 7. Следующее число 67;74; 81.)

• Соотнесите числа с буквами в порядке убывания и вы узнаете какому разделу математики будет посвящён урок.

• 25 32 39 46 53 60 67 74 81(СЛАЙД)

О В Т С Е Ж О Н М

- Какое слово получилось?

- Раскрываем следующую тайну.

• Посмотрите на множества.(На проекторе диаграмма пересекающихся множеств А и В.)(СЛАЙД)

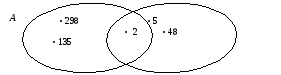В

Перечислите элементы множества А и множества В.

Что значит «общие элементы» множеств? (В множестве А есть такие же элементы, как и в множестве В.)

Где находится точка 2? (На пересечении этих двух множеств.)

Что называют «пересечением» множеств? (Правило). На доске появляется стебель (цветка) со словом ПЕРЕСЕЧЕНИЕ).

На слайде - математические выражения:

(5  48)  2

2) Актуализация представлений о переместительном и сочетательном свойствах сложения и умножения.

• Назовите эту запись математическим термином. (Выражение.)

• Какие свойства операций умножения вы знаете? (Переместительное, сочетательное и распределительное.)

• Для чего используют эти свойства? (Для удобства вычислений.)

• Найдите значение этого выражения, пользуясь свойствами. Каким свойством вы воспользуетесь? (Сочетательным. От изменения порядка действий произведение не изменяется.) Назовите сочетательное свойство.

Учитель вывешивает эталон с лепестком:

(a · b) · c = a · (b · c)

-Примените сочетательное свойство умножения при решении этого выражения.

(Дети делают самостоятельно)

- Скажите, какие множители вы сгруппировали.(5и2)

- Проверьте свою запись.(Слайд)

(5 · 48) · 2 = (5 · 2) · 48 = 10 · 48 = 480.

- Каким свойством мы сейчас пользовались?(Сочетательным)

- А если знак умножения заменить на знак плюс, что мы получим?

(Сочетательное свойство сложения)

- Давайте хором его назовём.((a + b) + c = a + (b + c)

(Вывешиваю лепесток на доску)

- Какие свойства мы повторили?(сочетательное свойство умножения и сочетательное свойство сложения)(Слайд)

- На проекторе новое выражение(СЛАЙД)

259 + 648…648 + 259

Посмотрите на следующее выражение. Какой знак надо поставить между выражениями?(=)

- Почему?(Они равны)

• Каким свойством вы воспользуетесь? (Переместительным. От перестановки слагаемых сумма не изменяется.)

a + b = b + a (вывешиваю свойство)

Какое ещё переместительное свойство вы знаете?(Переместительное свойство умножения)

- Назовите его.( a · b = b · a )

(Вывешиваю на доску лепесток)

• Давайте назовём, что мы с вами сейчас повторили? ( Показываю на цветке и повторяю с детьми (Множество, пересечение, переместительное и сочетательные свойства умножения и сложения, сравнивали выражения).

• Давайте произнесём какие главные слова были у нас на этом этапе повторения? (Множество, пересечение, свойство)

• Кто может используя эти слова сформулировать тему нашего урока? («Свойства пересечения множеств».)

(Учитель вывешивает кружок в середину цветка с названием темы на доску и буква Я переходит на лестницу НОВОЕ).

• Значит, какую цель поставим перед собой? (Выяснить, обладает ли пересечение множеств переместительным и сочетательным свойствами, записать и сформулировать его.)

• 3. Выявление места и причины затруднения.

• Цель:

• 1) организовать восстановление выполненных операций и фиксацию (вербальную и знаковую) места - шага, операции, где возникло затруднение;

• 2) организовать соотнесение действий учащихся с используемым способом (алгоритмом, понятием и т.д.) и на этой основе организовать выявление и фиксирование во внешней речи причины затруднения - тех конкретных знаний, умений или способностей, которых недостаёт для решения исходной задачи такого класса или типа.

На проекторе появляется.(CЛАЙД)

А ∩ В … В ∩ А

(А ∩ В) ∩ С …..А ∩ (В ∩С)

- Что нового в этом задании? (Надо определить, верны равенства с пересечениями или нет, а мы такого никогда не делали).

- Попробуйте выполнить задание на маркерных досках.

- Проверим выполнение. Кто не справился с заданием? Почему возникла у вас проблема? (Мы не можем определить, равны эти пересечения или нет.)

- Кто определил, верны или нет эти равенства?

Какое задание вы выполняли? (Мы должны были определить, верно ли то, что пересечения множеств равны.)

Как вы выполняли задания? (…)

Где у вас возникло проблема?

Почему она возникло? (У нас нет правила, эталона, чтобы определить, верны ли эти равенства.)

- Давайте вернёмся к числовым выражениям.

Что помогло нам сравнить числовые выражения? (Свойства сложения и умножения.)

Посмотрите на эталоны, которые висят на доске. На какие из них похожи данные равенства? (Первая - на переместительное свойство умножения и сложения, вторая - на сочетательное…)

А, может быть, данными свойствами обладают и пересечения множеств? И именно эти знания помогут нам.

- Вспомните ещё раз, что мы повторяли. Подумайте, что поможет вам доказать, что пересечения множеств обладают свойствами сочетательным и переместительным.

Проверим, обладает операция пересечения множеств переместительным и сочетательным свойствами или нет. Сейчас мы будем работать в группе. Не забывайте как надо работать в группе.

• - Умеем мы задавать множества? Умеем обозначать их на диаграммах?

• Проверим, обладает операция пересечения множеств переместительным и сочетательным свойствами или нет.

Форма работы: групповая на планшетах.

- Перед вами задание №1. Прочитайте внимательно задание и выполните его на маркерных досках.

• 1. Задайте множества А и В пересечением.

  - Изобразите с помощью диаграммы Венна множество А, множество В. Что заметили? Сделайте вывод. (Они имеют общие элементы, их пересечение равно…)

• Изобразим множество В, множество А. Что заметили?

• Сделайте вывод. (Получился такой же результат.)

• Какой вывод вы можете сделать? (Пересечение множеств обладает переместительным свойством.)

  - 2. Задайте множества А , В и С пересечением.

  - Изобразите с помощью диаграммы Венна множество А, множество В и множество С. Что заметили? (Они имеют общие элементы, их пересечение равно…)

  - Какой вывод можете сделать? (Пересечение множеств обладает сочетательным свойством).

- Где можем проверить наш вывод? (В учебнике.)

Обращаются к учебнику стр. 27, проверяют себя.

- Что мы доказали? (Что пересечение множеств обладает переместительным и сочетательным свойствами, а стало быть, предложенные нам равенства верны.)

Справились с проблемой? (Да.)

Молодцы! Вы открыли ещё одну математическую тайну. Учитель вывешивает на доску два лепестка со свойствами пересечения множеств.

4.ФИЗКУЛЬТМИНУТКА

5. Первичное закрепление.

Цель:

• зафиксировать изученные свойства множеств в записи.

1) На проекторе появилось выражение: (СЛАЙД)

«НОВОЕ УМЕНИЕ ВЕЗДЕ НАЙДЁТ ПРИМЕНЕНИЕ».

• Как вы думаете, чем займёмся? (Будем применять новое умение в заданиях.)

• Н

  Задание:

  А = {1; 2; 3; 4}, В = {3; 4; 5}. Запиши с помощью фигурных скобок множества

  А ∩ В и В ∩ А. Отметь элементы этих множеств на диаграмме Венна. Сделай вывод.ачнём с № 2 стр. 27. Прочитайте задание.(Работает у доски Шнурков Даниил), остальные учащиеся работают в учебнике)

Перечислите элементы множества А. (А = {1; 2; 3; 4}.)

Перечислите элементы множества В. (В = {3; 4; 5}.)

Какие элементы являются общей частью множеств А и В, В и А? (Элементы 3 и 4.)

Запишите элементы множеств А и В и отметьте их на диаграмме. (А ∩ В = {3; 4},

В ∩ А = {3;4}.)

Докажите. (Пересечение множеств не зависит от порядка множеств.)

2) № 3, стр. 27

• Прочитайте задание. (Работает у доски Курашов Андрей, остальные учащиеся работают в учебнике)

• Чем отличаются записи (А ∩ В) ∩ С = А ∩ (В ∩ С)? (В первом случае сначала находится пересечение множеств А и В, затем его пересечение с множеством С. Во втором случае, наоборот, сначала находится В ∩ С, а затем его пересечение с А.)

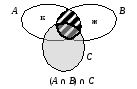
- Какой вы сделайте вывод. (Пересечение множеств не зависит от порядка действий.)

6.Работа в парах с самопроверкой по эталону.

Цель:

1) организовать самостоятельное выполнение учащимися заданий на новые понятия;

2) организовать самооценку детьми правильность выполнения задания (при необходимости - коррекцию возможных ошибок).

На проекторе выражением: « ТОРОПИСЬ - ДА НЕ ОШИБИСЬ!»(СЛАЙД)

• Как вы думаете, к какому виду деятельности подходит это выражение? (самостоятельная работа).

• С какой целью мы выполняем эту работу? (Чтобы выяснить, как усвоили новые знания.)

  - Перед вами задание №2.

  Прочитайте внимательно задание и выполните его на листочках.

  Задание:

  Допишите равенства, выражающие переместительное и сочетательное свойства операции пересечения множеств:

  М ∩ К =

  (М ∩ К) ∩ Т =

  (Слад)

М ∩ К = К ∩ М Пересечение множеств не зависит

от порядка множеств и порядка

(М ∩ К) ∩ Т = М ∩ (К ∩ Т) действий.

Проверка:

• Поставьте знак «+», если вы выполнили так же «?» если по-другому.

• Какие были затруднения? (…)

• Исправьте ошибки.

7. Физкультминутка для глаз и дыхания .

8.Включение в систему знаний и повторение.

Цель:

1) тренировать вычислительные навыки через решение примеров с использованием свойств для сложения и умножения;

2) повторить решение задач на приведение к единице, составление и решение уравнений, порядок действий в выражениях со скобками;

3) проверить у детей способность к оценке собственных достижений.

Организация учебного процесса на этапе 8:

- Новые знания помогут нам в дальнейшем при решении задач, но мы с ними встретимся на других уроках.

На проекторе выражение: «ПОВТОРЕНИЕ - МАТЬ УЧЕНИЯ».(СЛАЙД)

• Прочитайте выражение и подумайте, чем мы продолжим заниматься? (Повторим те знания, которые изучили раньше.)

Форма работы: индивидуальная.

Решение задания по выбору.

Учащиеся, по желанию выбирают одно из заданий № 7(а), 9(а), 11(а) стр. 28.

Перед выбором учитель даёт установку к заданиям.

• Если вы выберите № 7(а) стр. 28, то проверите своё умение решать задачи.

• Если у вас трудности в решении уравнений, полезно будет выполнить № 9(а) стр. 28.

• Выполнение № 11(а) стр. 28 повысит ваши вычислительные навыки.

• Но вы можете выбрать и то задание, которое вам больше понравилось.

На слайде учитель фиксирует:

№ 7 (а) стр. 28 - задача;

№ 9 (а) стр. 28 - уравнение;

№ 11 стр. 28 - вычисления.

После выполнения заданий самопроверка по образцам который лежит у учителя на столе.

№7(а)

4 под. - n кв.

6 под. - ? кв.

1 под. - ? кв.

Ответ: 96 квартир в 6 подъездах.

№

9(а)

а) х - 394 = 286; 286

х = 286 + 394; 394

х = 670 670

286 + 394 = 670

670 = 670

№11(а)

а) (13 + 8 · 4 ) : 5 - (27 : 3 - 0 · 6) = 9 - 9 = 0

9. 0

32

45 9

1) № 6 стр. 28.

Ученик с места читает задание.

На слайде алгоритм рассуждений для вычислений.

Читаю выражение

Определяю свойство, которое можно использовать для упрощения вычислений

Вычисляю

• Следуя шагам алгоритма, выполните действия.

Образец рассуждения:

• Читаю выражение: (298 + 386) + 102.

• Определяю свойство: переместительное и сочетательное свойства сложения.

• Вычисляю: (298 + 386) + 102 = (386 + 298) + 102 = 386 + (298 + 102) = 386 + 400 = 786.

• Какая ещё операция обладает переместительным и сочетательным свойствами? (Операции умножения, пересечения множеств.)

- Молодцы! Как считаете раскрыли вы сегодня на уроке новую математическую тайну?(Да)

10. Рефлексия учебной деятельности на уроке.

Цель:

1) зафиксировать новое содержание, изученное на уроке;

2) организовать рефлексивный анализ учебной деятельности с точки зрения выполнения требований, известных учащимся;

3) оценить собственную деятельность;

4)зафиксировать неразрешенные на уроке затруднения, если они есть, как направления будущей учебной деятельности;

5) обсудить домашнее задание.

Организация учебного процесса на этапе 11:

- Что нового узнали на уроке? (Операция пересечения множеств обладает переместительным и сочетательным свойствами.)

- Какую цель вы поставили сегодня на уроке? (Выяснить, обладает ли пересечение множеств переместительным и сочетательным свойствами, записать и сформулировать его.)

Справились вы с поставленной целью?(Да)

Что нам доказывает?

Ребята у которых возникла проблема в выполнение самостоятельной работы, ещё раз дома её сделайте.

- Наша буква Я переходит к следующим словам.

- Я УЗНАЛ?

-Я НАУЧИЛСЯ?

- Я ЗАПОМНИЛ?

- Я УВИДИЛ?

Первая ступенька - многое не понял и остались вопросы; вторая ступенька - многое понял, но были ошибки; третья ступенька - трудности преодолены.

Домашнее задание:

 № 5 стр. 28, № 8 стр. 28;

10