Конспект урока по математике на тему'Нахождение части числа' (4 класс)

Тип урока: ОНЗ.

Тема: «Нахождение части числа».

Автор: Т.В. Григоренко (МБОУ СОШ №38, г. Сургут).

Основные цели:

1) сформировать умение решать задачи на нахождение части числа, выраженной дробью.

2) актуализировать алгоритм решения задач на нахождение доли числа.

3) тренировать навыки решения составных уравнений и текстовых задач.

Мыслительные операции, необходимые на этапе проектирования: анализ, синтез, обобщение, аналогия.

Демонстрационный материал:

1) «Дом дробей» для этапа самоопределения:

2) опорный конспект «Нахождение доли числа» (урок № 23, Д-4);

3) опорный конспект, опорный сигнал и правило «Нахождение части числа, выраженной дробью»:

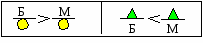
Нахождение части числа,

выраженной дробью

1 - а

·

: - ?

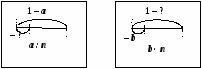
Чтобы найти часть числа, выраженную дробью, надо это число разделить на знаменатель и умножить на числитель дроби.

4

а)

б)) заготовки схем для решения задач а) № 3, стр.86 (этап 6) и б) № 5, стр.87 (этап 8):

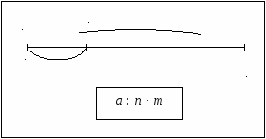
5) образец выполнения задания самостоятельной работы в парах на этапе 6 (№ 4 (в, г), стр. 86:

в) 400 : 100 · 4 = 16 (м); г) 2 000 : 100 · 15 = 300 (руб.).

6) карточки с числами для этапа актуализации знаний:

105

25

7) карточка с задачей этапа актуализации знаний:

Пятачок ко дню рождения приготовил 42 кг меда. Винни-Пух, зайдя проведать друга, съел этих запасов. Сколько меда съел Винни-Пух?

8) карточка с решением задачи на этапе актуализации знаний:

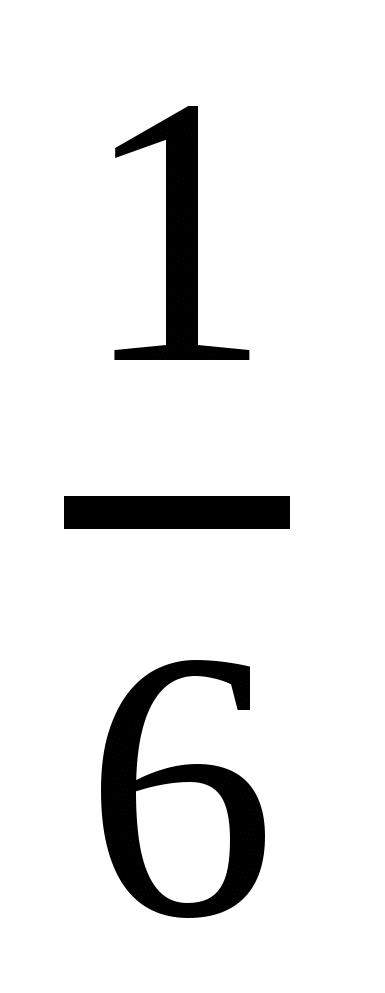
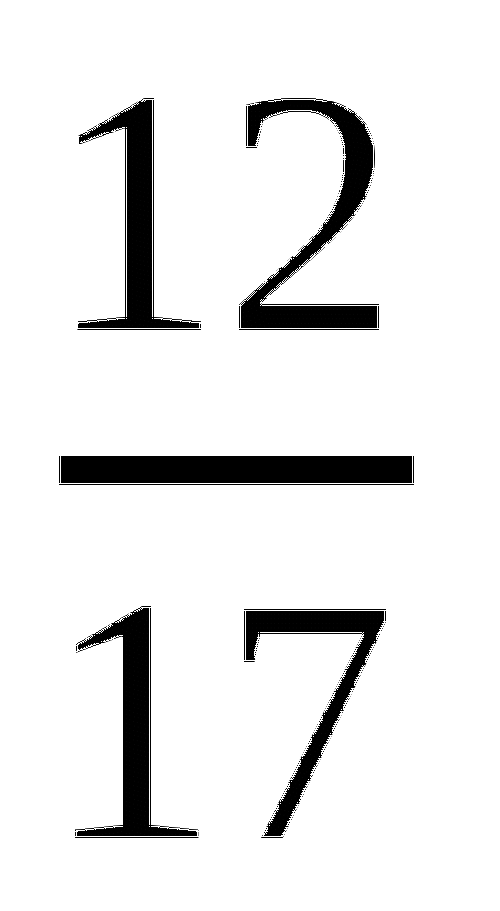1 - 42 кг

- ?

42 : 7 = 6 (кг)

9) к

Пятачок ко дню рождения приготовил 42 кг меда. Винни-Пух, зайдя проведать друга, съел этих запасов. Сколько меда съел Винни-Пух?арточка для пробного задания:

10) карточка с заданием для групп:

Задание группам:

1. Заполнить вторую схему по тексту задачи пробного задания.

2. Проанализировать обе схемы: найти сходство и различие.

3. Записать выражение для решения второй задачи.

4. Записать её решение в общем виде.

5. Составить эталон для нахождения части числа (схема, выражение).

11) правила работы в группах (из урока № 1, Д-9.)

Раздаточный материал:

1) планшетки;

2) карточка с заданием для работы в группах на этапе 5:

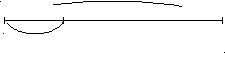
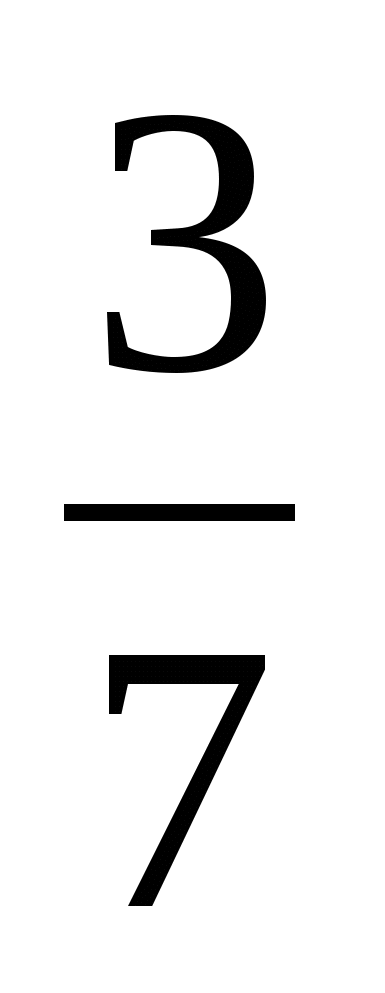
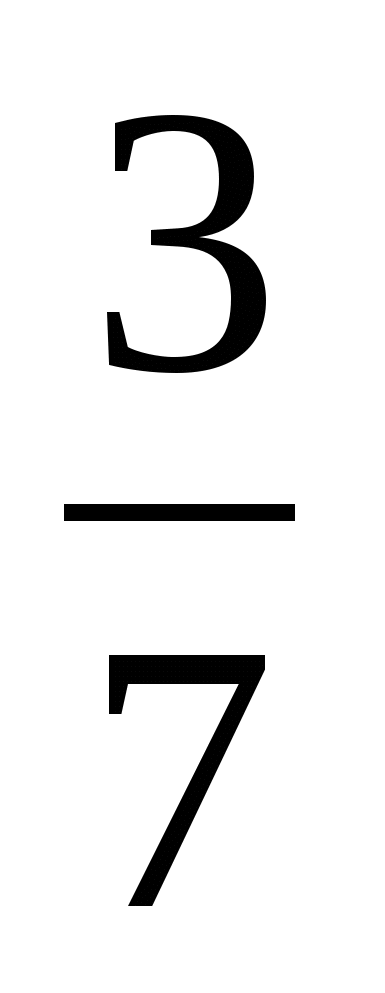
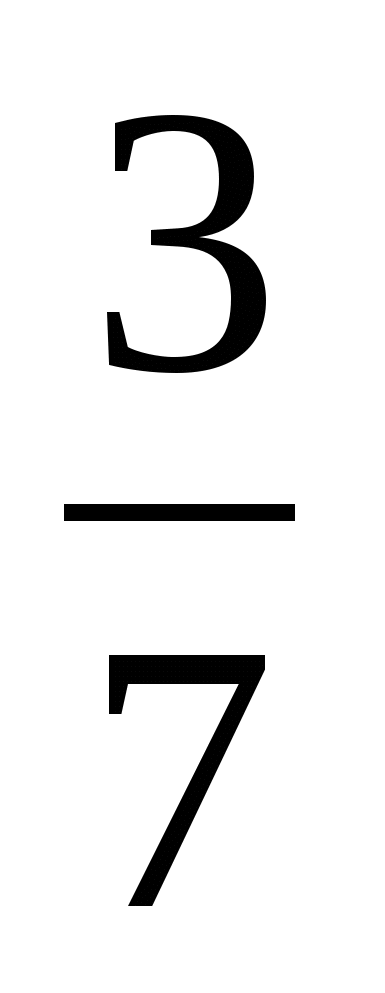
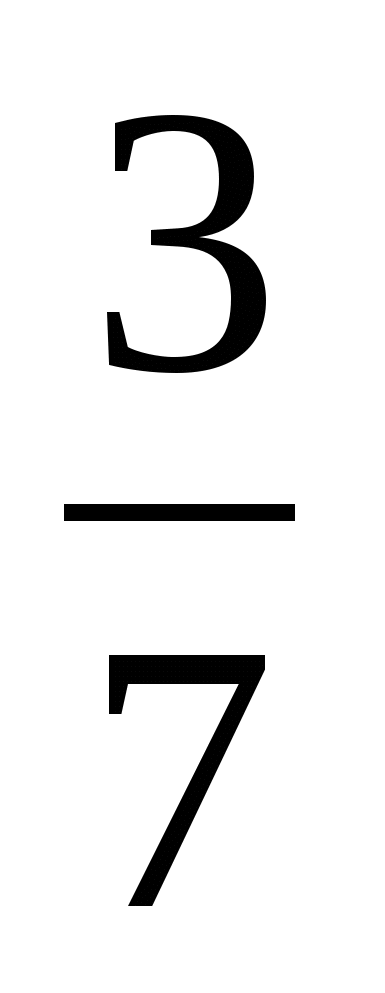
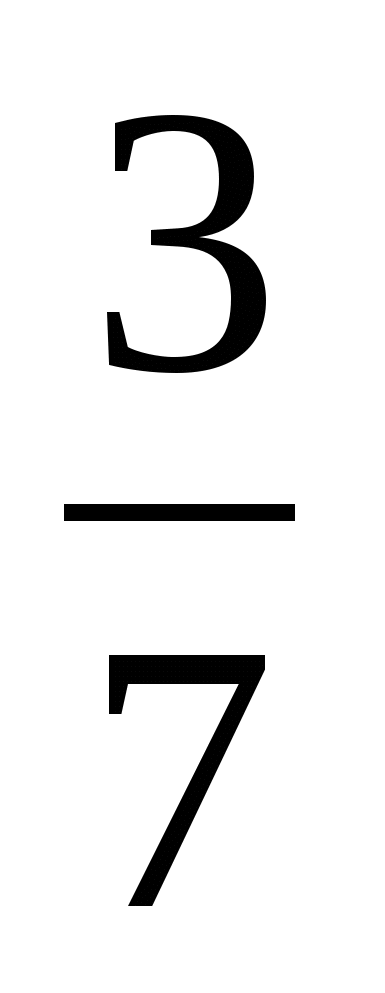
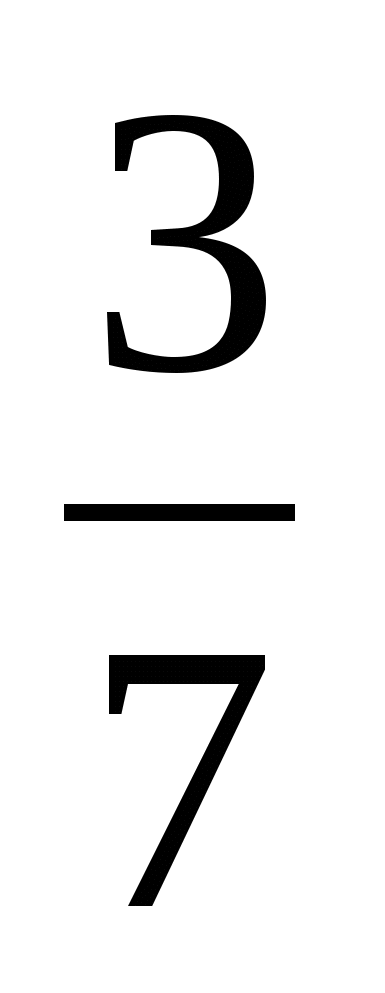
1 - 42 кг

- ? кг

Решение задачи Решение задачи

42 : 7 = 6 (кг)

Решение задачи в общем виде Решение задачи в общем виде

Способ нахождения части числа

Схема:

Выражение:

3) карточка с самостоятельной работой на этапе 7:

1) Реши задачу:

Корова Мурка дает 10 л молока. Матроскин выпивает этого молока сам, а остальное достается Шарику. Сколько молока выпивает Матроскин?

Ответ: ____ л молока выпивает Матроскин.

2) Найди и запиши выражение:

а) от числа а б) от числа b в) от числа c

4) эталон для самопроверки самостоятельной работы на этапе 7:

1)

1 - 10 л 1 - а

- ? л - ?

10 : 5 ∙ 3 = 6 (л)

Ответ: 6 л молока выпивает Матроскин.

2)

а) от числа а а : 3 · 2

б) от числа b b : 7 ∙ 3

в) от числа c c : 5 ∙ 4

а : п · m

Нахождение части числа,

выраженной дробью

·

:

Ход урока:

1. Мотивация к учебной деятельности

Цель:

1) включение учащихся в учебную деятельность - тренировать в понимании значения уметь учиться;

2) определить содержательные рамки урока: дроби;

3) мотивация учащихся к учебной деятельности посредством игровой ситуации.

Организация учебного процесса на этапе 1:

- Над какой темой вы работаете? (Дроби.)

Рядом с доской прикрепляется «Дом дробей» (Д - 1).

- Рассмотрите «Дом», который выстроился в процессе изучения темы. Что интересного вы замечаете? (В нем все, что мы изучили в этой теме.)

- Изучая дроби, вы поднимались по этажам. Давайте вспомним, что вы умеем делать с дробями. (Изображать дроби на моделях, сравнивать их, решать задачи на нахождение доли числа, числа по доле.)

- На этом уроке вы продолжите работу над темой «Дроби». Как вы думаете, почему некоторые окошки этажом выше закрыты? (Наверное, что-то еще не знаем в этой теме.)

- Хотите подняться на следующий этаж и узнать что-то новое о дробях? (Да.)

- Тогда в путь!

- По какому плану вы будете открывать новые знания? (…)

2. Актуализация знаний и фиксация затруднения в пробном действии.

Цель:

1) актуализировать знания о нахождении доли числа и числа по доле;

2) тренировать мыслительные операции, необходимые на этапе проектирования;

3) мотивировать к пробному действию и его самостоятельному выполнению и обоснованию;

4) предъявить индивидуальное задание для пробного действия (решить задачу по нахождению части числа выраженную дробью);

5) организовать фиксирование цели и темы урока;

6) организовать выполнение пробного действия и фиксацию затруднение в учебной деятельности (невозможность решить или обосновать решение задачи на нахождение части числа выраженную дробью);

7) организовать анализ полученных ответов и зафиксировать индивидуальные затруднения в выполнении пробного действия или его обосновании.

Организация учебного процесса на этапе 2:

Учащиеся работают на планшетках.

На доске запись: , 105, , , , 25.

- На какие две группы можно разбить числа ряда? (Дроби и натуральные.)

- Выпишите дроби. (,,,.)

На доске выделяются карточки с дробями.

- Что показывает дробь? (Дробь показывает, что число разделили на равные части и взяли сколь то таких частей.)

- Какую особую группу можно выделить из множества этих дробей? (Доли.)

- Выпишите их. (, .)

На доске выделяются карточки с долями.

- Почему вы определили, что это доли? (Доля это одна из равных частей, на которые разделили целое.)

- Определите, какую из доле, от какого натурального числа из нашего ряда можно найти? ( от 105.)

На доске:

от 105.

- Обоснуйте ваш ответ. (Чтобы найти долю от числа на число разделить на количество частей.)

Учитель вывешивает на доску эталон Д-2.

- Найдите от числа 105 и запишите ответ. (3.)

- Осталось два числа и 25, какое задание можно придумать с этими числами? (Найдите число, если его доля составляет 25.)

- Как найти число по доле? (Чтобы найти неизвестное число по доле, нужно его долю умножить на количество равных частей.)

Учитель вывешивает на доску эталон Д-3.

- Найдите число по доле. (105.)

- Что интересного вы заметили? (Что найденное число, равно числу, от которого находили .)

- Где используются повторенные эталоны? (При решении задач.)

На доске текст задачи Д-7.

- Прочтите задачу, определите, какой эталон надо применить для решения задачи? (Эталон нахождения доли от числа.)

- Составьте схему к задаче и запишите её решение на планшетках.

Р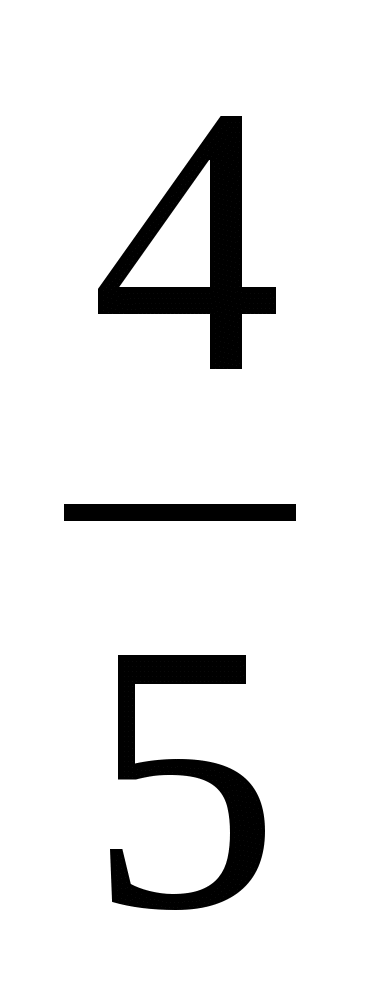езультат фиксируется на доске (Д-8):

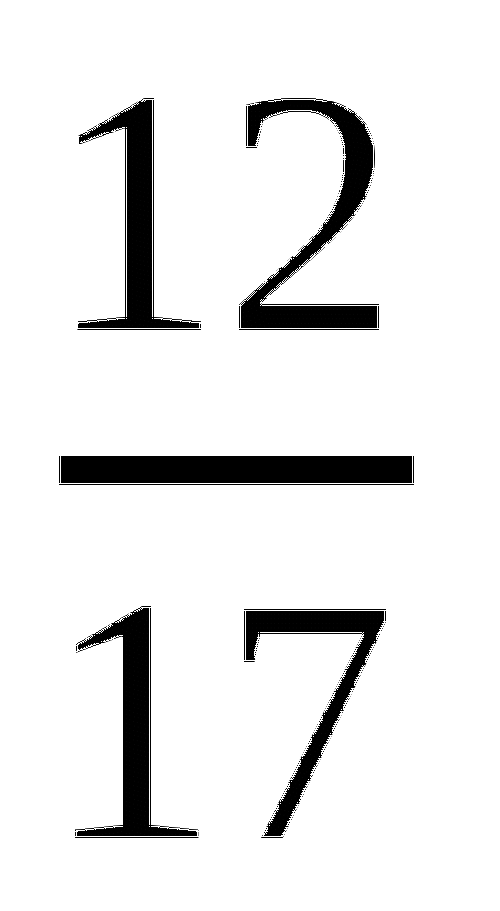1 - 42 кг

- ?

42 : 7 = 6 (кг)

- Что вы сейчас повторили? (Понятие дроби, доли, решение задач на доли.)

- Почему надо было повторить именно этот материал? (Он нам пригодиться при открытии новых знаний.)

- Какое следующее задание я вам предложу? (Пробное задание, задание в котором будет что-то новое, задание по которому мы поймём, что нового будет сегодня на уроке, задание по которому мы поймём, чего мы не знаем.)

На доске текст задачи Д-9.

- Прочтите задачу. Что в этой задаче нового? (Винни-Пух съел запаса мёда, часть выражена не долей, а дробью.)

- Сформулируйте цель. (Решить задачу по нахождению части числа, выраженную дробью.)

- Сформулируйте тему урока. (Нахождение части числа, выраженную дробью.)

- Что вы сейчас будете делать? (Попробуем решить задачу.)

Учащиеся самостоятельно работают в течении 1 минуты.

- У кого нет ответа?

Учащиеся поднимают руки.

- В чём у вас затруднение?

- Какие ответы получились?

Дети показывают свои записи, могут быть разные варианты, например:

42 : 7 · 3 = 18 (кг), 42 : 7 : 3 = 2 (кг), 42 : и т.д.

Учитель просит нескольких детей с различными вариантами записи выставить свои планшетки на доске, и предлагает остальным детям определить свою позицию, например, при помощи поднятия руки.

- Проанализируйте результаты выполнения пробного задания. (Некоторые не смогли дать ответ, у остальных получились разные ответы.)

- Обоснуйте своё решение. (Нет эталона, с помощью которого мы могли бы обосновать своё решение.)

3. Выявление места и причины затруднения.

Цель:

1) организовать восстановление выполненных операций и фиксацию (вербальную и знаковую) места - шага, операции, где возникло затруднение;

2) организовать соотнесение действий учащихся с используемым способом (алгоритмом, понятием и т.д.) и на этой основе организовать выявление и фиксирование во внешней речи причины затруднения - тех конкретных знаний, умений или способностей, которых недостаёт для решения исходной задачи такого класса или типа.

Организация учебного процесса на этапе 3:

- Давайте разберемся, какой эталон нужен. Уточните, какое задание вы выполняли? (Решали задачи на нахождение части числа.)

- Это задание похоже на предыдущее, с которым вы легко справились? (Да, в обоих случаях надо найти часть числа.)

- Почему же возникло затруднение? (В первом случае мы искали долю числа, а здесь - надо найти часть, выраженную дробью.)

- Почему вы не справились с заданием или не смогли обосновать своё решение? (У нас нет способа нахождения части числа, которая выражена дробью.)

4. Построение проекта выхода из затруднения.

Цель:

в коммуникативной форме о

Этап 4рганизовать построение учащимися проекта будущих учебных действий:

1. уточнение цели проекта (найти способ нахождения части числа, выраженной дробью);

2. определение средств (алгоритмы, модели, учебник и т.д.);

3. построение плана достижения цели.

Организация учебного процесса на этапе 4:

- Уточните цель своей деятельности. (Построить алгоритм нахождения части числа, выраженной дробью.)

- Чем удобно воспользоваться, чтобы найти способ решения новых задач? (Можно составить схему, алгоритмом нахождения доли числа, т.к. доля и тоже часть числа, доля это дробь.)

- По какому плану вы будете действовать? (Мы построим схему к задаче, решим задачу, запишем решение в общем виде, составим алгоритм для решения таких задач.)

5. Построение проекта выхода из затруднения.

Цель:

1) организовать коммуникативное взаимодействие с целью реализации построенного проекта, направленного на приобретение недостающих знаний: способа нахождения части числа;

2) создать условия для построения учащимися алгоритма нахождения части числа и зафиксировать его в речи, графической и знаковой форме (с помощью эталона, опорной схемы), сформировать способность к его практическому использованию;

3) организовать уточнение общего характера нового знания.

Организация учебного процесса на этапе 5:

Дальше работу можно организовать по группам. Группам раздаются листы Р-2. На доску вывешивается задание группам (Д-10).

Задание группам:

1. Заполнить вторую схему по тексту задачи пробного задания.

2. Проанализировать обе схемы: найти сходство и различие.

3. Записать выражение для решения второй задачи.

4. Записать её решение в общем виде.

5. Составить эталон для нахождения части числа (схема, выражение).

Перед началом работы вспомнить правила работы в группах (Д-11).

Группы работают в течение 5 минут. По окончании работы одна из групп представляет свою работу, комментирует её, остальные работают на дополнение и коррекцию.

В результате работы на доске фиксируется опорный конспект, опорный сигнал и правило (Д-3).

Можно работу провести фронтально.

- Начертите в тетради рядом друг с другом обе схемы.

Дети строят схемы в тетради. Один ученик работает у доски.

- Что заметили? (В первой задаче находят одну из семи частей целого, а во второй - три таких части. Значит, надо значение одной части умножить на 3.)

- Запишите решение второй задачи.

42 : 7 · 3 = 18 (кг)

Ответ: Винни-Пух съел 18 кг меда.

- Проанализируем ваши действия. Что обозначено числом «семь» в дроби? (Знаменатель.)

- Что обозначено числом «три» в дроби? (Числитель.)

- На основании выполненных действий, сформулируйте правило нахождения части числа, выраженной дробью. (Чтобы найти часть числа, выраженную дробью, надо это число разделить на знаменатель и умножить на числитель дроби.)

Можно предложить детям заменить буквами числа на второй схеме и самостоятельно записать выражение для нахождения части числа, выраженной дробью. После обсуждения вариантов, которые предложат дети, на доску вывешивается опорный конспект, опорный сигнал Д-3.

- Подведите итог своей работы. (Мы сами вывели правило нахождения части числа, выраженной дробью.)

Учитель помещает опорный конспект в пустую клетку верхнего этажа «Дома».

- Вы достигли своей цели? (Мы только построили способ, но ещё не можем сказать, что научились решать такие задачи.)

- А что для этого надо сделать? (Потренироваться в решении задач на нахождение части числа.)

6. Первичное закрепление во внешней речи.

Цель:

зафиксировать новый способ действий во внешней речи, тренироваться в применении, новых правил при выполнении задания.

Организация учебного процесса на этапе 6:

1). Работа с текстом учебника.

Работа проводится фронтально.

- К чему вы можем обратиться для доказательства, что вы сделали всё правильно? (К тексту учебника.)

- Откройте учебник на стр. 85 и прочитайте текст, выделенный в рамке.

Учащиеся работают с текстом учебника.

2) № 1, стр. 85.

Задание выполняется на печатной основе, дети комментируют решение с места «по цепочке».

Комментарии: а разделить на знаменатель 4 и умножить на числитель 3.

Решение:

а) а : 4 · 3; б) b : 7 · 5; в) с : 100 · 2; г) d : 100 · 16; д) 60 : n · m.

3) № 3, стр. 86.

- Заполните схему к задаче на печатной основе. Решение запишите в рабочей тетради.

Дети дополняют схему и записывают решение. Один ученик работает на доске с заготовкой схемы Д-4 (а).

- Проанализируйте задачу. (Известно, что урок длился 45 минут. Из них длился диктант. Надо узнать сколько времени длился диктант. 45 минут - это целое, единица. Его разделили на пять равных частей и взяли три из них. Для ответа на вопрос задачи нужно длительность урока - 45 мин - разделить на знаменатель 5 и умножить на числитель 3.)

1 - 45 мин

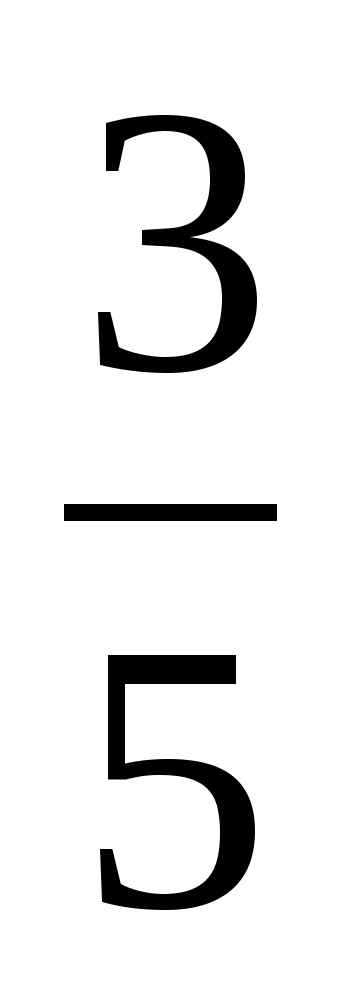
45 : 5 · 3 = 27 (мин)

- ? мин Ответ: диктант длился 27 минут.

4) № 4, стр. 86.

З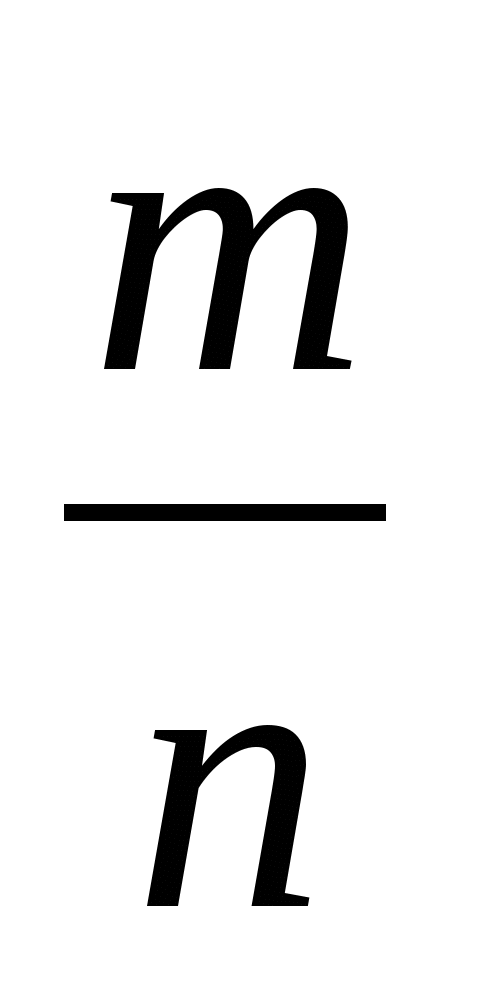адания (а) и (б) выполняются в рабочей тетради, комментирование учащимися ведется с места.

а) 18 : 9 · 2 = 4 (кг); б) 300 : 5 · 3 = 180 (руб.)

Задания (в) и (г) комментируется в парах. Проверка проводится по образцу Д-5.

7. Самостоятельная работа с самопроверкой по эталону.

Цель:

1) организовать самостоятельное выполнение учащимися заданий на новые понятия;

2) организовать самооценку детьми правильность выполнения задания (при необходимости - коррекцию возможных ошибок).

Организация учебного процесса на этапе 7:

- Вы поработали вместе, в парах, что теперь? (Надо поработать самостоятельно.)

- Почему это необходимо? (Только работая самостоятельно можно понять разобрался ты в теме или есть затруднение.)

- Прочитайте задание на карточке.

Используется карточка Р-3. Учащиеся читают задание про себя.

- Выполните задания самостоятельно.

Учащиеся выполняют самостоятельную работу, по окончании которой проверяют себя по эталону для самопроверки Р-4.

- Что теперь вы должны сделать? (Проверить свои работы по эталону для самопроверки.)

- Как вы это будете делать? (Мы проверим решение и сопоставим решение с эталоном.)

- А если обнаружатся ошибки, что будете делать? (Определим в каком месте допустили ошибку и постараемся почему эта ошибка произошла.)

- Проверьте себя по эталону для самопроверки и зафиксируйте результат проверки при помощи знаков «+» или «?».

- Кто допустил ошибки при выполнении задания? (…)

- Где вы допустили ошибку и в чем её причина?

- Что вам поможет исправить ошибки? (Эталон.)

- Поднимите руки, у кого все верно. Вы молодцы!

- Где вы ещё сможете потренироваться в решении задач? (При выполнении домашнего задания.)

8. Включение в систему знаний и повторение.

Цель:

1) использовать способ нахождения части числа, выраженной дробью, для решения составных задач;

2) тренировать навык решения и комментирования составных уравнений.

Организация учебного процесса на этапе 8:

1) № 5, стр. 86.

- Прочтите задачу. Что вы можете сказать о задаче? (Это составная задача, в ней надо будет найти часть числа, выраженной дробью.)

- Дополните схему к задаче.

Дети чертят схему Д-4 (б) в тетради и дополняют ее данными задачи. Один ученик работает у доски.

-
Проанализируйте задачу. (Известно, что у Кати было 28 рублей, этого она истратила на завтрак. Требуется узнать, сколько стоил завтрак, и сколько денег у нее сталось. Для ответа на первый вопрос нужно целое - 28 руб. - разделить на знаменатель 7 и умножить на числитель 3 (по правилу нахождения части числа, выраженной дробью). Затем ответим на второй вопрос, вычитая полученное число из целого (чтобы найти часть целого, можно из целого вычесть другую часть.)

1 - 28 руб.

завтрак

осталось

- ? руб.

? руб.

1) 28 : 7 · 3 = 12 (руб.) - стоил завтрак;

2) 8 - 12 = 16 (руб.)

Ответ: 12 руб. стоил завтрак, 16 руб. осталось у Кати.

- Какие задания на стр. 86 - 87 вы отнесли к заданиям на повторение? (…)

- Повторим способы решения уравнений.

2) № 11, стр. 87.

По одному ученику работают у доски, а остальные - в рабочих тетрадях.

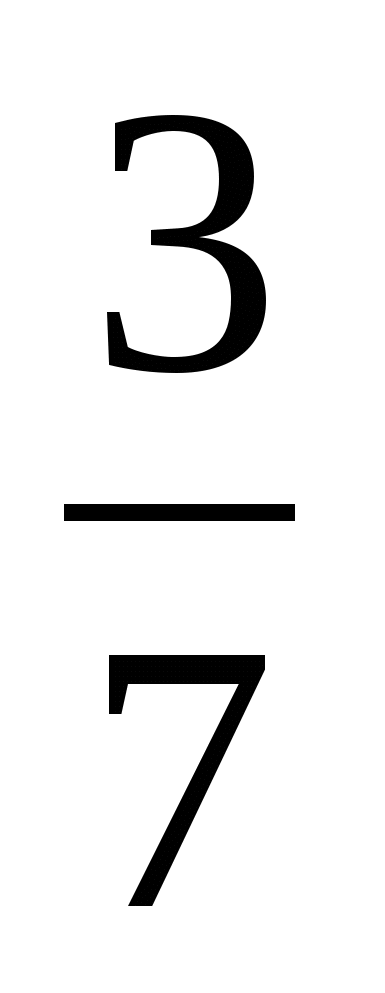
90 · х + 17 = 800 - 423 240 : (у : 15)= 42 + 18

90 · х + 17 = 377 240 : (у : 15)= 60

90 · х = 377 - 17 у : 15 = 240 : 60

90 · х = 360 у : 15 = 4

х =360 : 90 у = 15 · 4

х = 4 у = 60

90 · 4 + 17 = 800 - 423 240 : (60 : 15) - 18 = 42

377 = 377 42 = 42

9. Рефлексия учебной деятельности на уроке.

Цели:

1) зафиксировать новое содержание, изученное на уроке;

2) организовать рефлексивный анализ учебной деятельности с точки зрения выполнения

требований, известных учащимся;

3) оценить собственную деятельность на уроке;

4) зафиксировать неразрешенные на уроке затруднения, если они есть, как направления будущей учебной деятельности;

5) обсудить и записать домашнее задание.

Организация учебного процесса на этапе 9:

- Подошла к концу работа, что необходимо сделать? (Подвести итог.)

- В каком задании было общее затруднение? (В решении задач на нахождение части числа.)

- Почему возникло затруднение? (Не было способа нахождения части числа, выраженной дробью.)

- Что помогло выйти из затруднения? (Работа со схемами задач, алгоритм нахождения доли числа.)

- Как найти значение части числа, выраженной дробью? (Чтобы найти часть числа, выраженную дробью, надо это число разделить на знаменатель и умножить на числитель дроби.)

- Достигли ли вы цели урока? (Да.)

- В нашем «Доме» открылось еще одно окошко, но некоторые все еще закрыты. Как вы думаете, почему? (Наверное, что-то еще не знаем в этой теме.)

- Это темы наших будущих уроков. Но чтобы справиться с ними, нужно закрепить изученный материал дома.

Д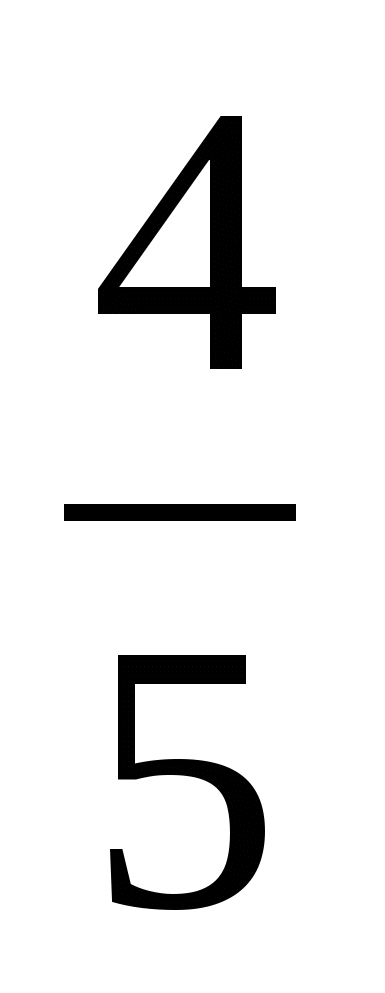омашнее задание:

Т правило на стр. 85;

 № 2, стр. 85, № 6, стр. 86;

 № 12, стр. 87.