Урок математики в 3 классе на тему: «Решение составных уравнений».

Тип урока: ОНЗ.

Тема: «Решение составных уравнений».

Основные цели: - Познакомить с составными уравнениями, сводящимися к цепочке простых, и построить алгоритм их решения.

- Формировать на автоматизированном уровне способность к нахождению неизвестных компонентов действий и умение комментировать выполняемые операции, называя компоненты действий.

- Отрабатывать навыки устных и письменных вычислений, повторить и закрепить понятие переменной и предложения с переменной, правило порядка действий в выражениях, решать задачи, содержащие переменную.

Планируемые результаты:

Предметные:

∙ решать составные уравнения, сводящиеся к цепочке простых (2 шага), и комментировать ход решения по компонентам действий

∙ читать и записывать числовые и буквенные выражения, содержащие действия сложения, вычитания, умножения и деления (со скобками и без скобок);

∙ анализировать текстовые задачи в 2−4 действия с многозначными числа-

ми всех изученных видов, строить графические модели и таблицы, планировать и реализовывать решения, пояснять ход решения, искать разные способы решения, соотносить полученный результат с условием задачи и оценивать его правдоподобие;

ЛИЧНОСТНЫЕ РЕЗУЛЬТАТЫ

∙ проявление самостоятельности и личной ответственности за свой результат, в исполнительской деятельности, собственный опыт творческой деятельности;

∙ умение выполнять самоконтроль по образцу, подробному образцу и эталону;

∙опыт рефлексивной самооценки собственных учебных действий;

∙проявление целеустремленности в учебной деятельности на основе согласованных эталонов;

∙ проявление интереса к занятиям математикой и учебной деятельности в целом ∙ уважительное, позитивное отношение к себе и другим, нацеленность на

максимальный личный вклад в общий результат, стремление к общему успеху;

МЕТАПРЕДМЕТНЫЕ РЕЗУЛЬТАТЫ

Регулятивные

Учащийся научится:

∙ называть и фиксировать прохождение двух основных этапов и шагов учебной деятельности (12 шагов);

∙фиксировать индивидуальное затруднение в учебной деятельности в различных типовых ситуациях;

∙ определять на основе применения эталона место и причину индивидуального затруднения в учебной деятельности;

∙ составлять план своей учебной деятельности при открытии нового знания на основе применения алгоритма;

∙фиксировать результат своей учебной деятельности на уроке открытия нового знания в форме согласованного эталона;

∙использовать эталон для обоснования правильности выполнения учебного задания;

∙ использовать правило закрепления нового знания;

Познавательные

∙применять алгоритмы обобщения и классификации множества объектов по заданному свойству;

∙применять простейшие приёмы развития своей памяти;

∙умение определять виды моделей (предметные, графические, знаковые, блок- схемы алгоритмов и др.), использовать в учебной деятельности в простейших случаях метод моделирования как метод познания;

Коммуникативные:

∙в совместной работе предлагать свои варианты решения поставленной задачи, оценивать различные варианты, исходя из общей цели;

∙ в процессе ведения диалога применять простейшие приемы ораторского искусства, чтобы понятно для других выражать свою мысль;

∙применять правила ведения диалога при работе в паре, в группе;

∙осуществлять взаимоконтроль, при необходимости оказывать помощь и

поддержку одноклассникам

Учебные материалы : Учебник « Математика» ( 3 кл., 2 ч.,- авт. Л.Г. Петерсон), компьютер, презентация, блок - схема алгоритма решения составных уравнений, карточки для пробного действия, эталоны для самопроверки, изображение 2 шагов учебной деятельности; лестница «успеха» для этапа №9.

Ход урока:

1. Мотивация к учебной деятельности:

Организация учебного процесса на этапе 1:

На доске вывешены картинки с изображением шагов учебной деятельности .

- Ребята, что вы видите на доске? (На доске расположены 2 шага учебной деятельности.) ( Слайд 1.)

- Чему будет посвящен сегодняшний урок? (Будем открывать что-то новое.)

- Сегодня вы продолжите работать с уравнениями. Как вы думаете, зачем на доске зафиксированы эти два шага? (Мы должны постараться сами «открыть» новое знание.)

- Я вижу, что вы готовы к работе. Пожелайте друг другу успехов и примемся за работу.

2. Актуализация знаний и фиксация затруднения в пробном учебном действии.

1Актуализация буквенных выражений и уравнений.

На доске записи

а + в × с х+7 =7 23 - у= 18 (х - у) : 3 к× 3 = 54 +36 4× d + ( m - n) 60 : n = 4 ( Слайд 2.)

- На какие группы можно разделить эти записи. ( Выражения и уравнения)

а + в × с 23 - у= 18

(х - у) : 3 х +7 =7

4× d + ( m - n) 60 : n = 4

( Слайд 3 )

Как называются записи в 1 группе? ( выражения)

- Прочитайте их, называя последнее действие. (Сумма чисел а и произведение чисел в и с; частное разности и числа 3; сумма удвоенного числа d и разности чисел m и n )

- Найдите лишнее выражение.

( Например : а + в × с - в записи этого выражения нет чисел и скобок, а в остальных выражениях есть; 4× d + ( m - n) - содержит 3 действия, а остальные по 2) ( Слайд 4)

- Устно вычислите корни уравнений. ( Слайд 5.)

- Что вы заметили? ( 0, 5, 15, 30. Числа увеличиваются сначала на 5, потом на 10, потом на 15) ( Слайд 6.)

- Какое число должно быть следующим? Обоснуйте свой ответ. ( 50, так как число 30 должно увеличиться на 20, а 20 + 30 = 50) ( Слайд 7.)

2) Пробное действие.

- Сейчас я вам предложу новое задание, как вы его называете? (Пробное задание.)

- Почему оно так называется?

- Достаньте карточку для пробного действия.

Учащиеся достают карточку с заданием для пробного действия

( у - 4) × 3 = 15

- Является ли эта запись уравнением? ( Да)

- Почему? ( Это равенство, содержащее переменную)

- Найдите корень этого уравнения. (?!)

Для выполнения этого задания учитель ограничивает время. Это делается для того, чтобы учащиеся не смогли правильно подобрать ответ.

- У кого нет ответа?

Учащиеся поднимаю руки.

- О чём говорит ваш результат? (Мы не смогли решить уравнение.)

• Покажите ответы, у кого они есть.

Учитель фиксирует на доске полученные учащимися варианты ответов.

• Я вижу, что среди вариантов нет правильного. О чём говорит такой результат? (Мы не смогли решить уравнение правильно.)

3. Выявление места и причины затруднения.

Организация учебного процесса на этапе 3:

- Что надо сделать? (Остановиться и подумать.)

- А как вы будете это делать? (Мы разберёмся, почему возникло затруднение.)

- Подходит ли для решения этого уравнения известный нам алгоритм. ( Нет)

- Почему? (Неизвестный компонент является выражением, а мы такие уравнения ещё не решали).

4. Построение проекта выхода из затруднения.

Цель:

построить проект выхода из затруднения;

Организация учебного процесса на этапе 4:

- Сформулируйте цель вашей деятельности? (Открыть способ решения уравнений. Научиться решать уравнения, в которых неизвестный компонент действия является выражением)

- Составим план наших действий. Какой будет первый шаг? (Определим компоненты действия, подберем правило.)

- Какой будет следующий шаг? (Решим уравнение.)

- Какой будет третий шаг? (Проанализируем наши действия, сформулируем способ.)

5. Реализация построенного проекта.

Организация учебного процесса на этапе 5:

- Как вы думаете, по какому пути пойти?

- А может быть нам помогут уже изученные виды уравнений?( Слайд)

-На какое из известных нам уравнений похоже наше уравнение ?

-Чем является выражение в левой части - суммой, разностью, произведением или частным? Почему?

В результате обсуждения обучающиеся устанавливают, что выражение в левой части уравнения является произведением, так как последнее действие - умножение

Учитель накладывает на выражение у - 4 карточку х, и получается уравнение , которое они легко решат

х × 3 = 15

х = 15: 3

х = 5 ( Слайд 8.)

Затем карточка с переменной переворачивается, вместо нее восстанавливается запись

у - 4 и решение доводится до конца:

( у - 4 ) × 3 = 15

у - 4 = 15 : 3

у - 4 = 5 ( Слайд 9.)

Проверка показывает, что корень уравнения найден верно: ( 9 - 4 ) × 3 = 5

(Слайд 10)

- Решение составных уравнений напоминает, как зайчик ест капусту: сначала он съедает последний листочек, потом следующий, пока не доберётся до кочерыжки. Последний листочек определяется по последнему действию, а кочерыжка - это корень уравнения.

- А что вам напоминает решение составных уравнений?

- Составное уравнение может содержать несколько листочков. Это зависит от того, сколько действий в выражении с переменной. Поэтому в решении составного уравнения может быть большее число шагов.

- Давайте составим блок-схему решения таких уравнений.

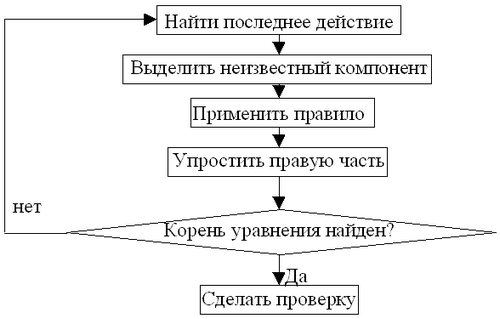
( Слайд 11)

Физкультминутка ( Слайд 12)

6. Первичное закрепление во внешней речи.

Цель:

создать условия для фиксации изученного способа действия во внешней речи.

Организация учебного процесса на этапе 6:

- Что теперь нам надо сделать? (Потренироваться в решении уравнений.)

№ 1, стр. 83

- Откройте в учебнике № 1 на стр.83.

№1 (а, б),с.83 - проговаривание в громкой речи.

а) (у-5) · 4=28, - неизвестен 1 множитель (у-5)

у-5=28:4, - чтобы его найти, надо произведение разделить на 2 множитель

у-5=7, - теперь неизвестно уменьшаемое

у=5+7, - чтобы его найти, надо к разности прибавить вычитаемое

у=12. - корень уравнения равен 12

(12-5) · 4=28, - проверка: подставим в уравнение вместо у число12 и сосчитаем

28=28.(и) - получили верное равенство

уравнение решено правильно

б) 3· а - 7=14 - подробное комментирование

Второе уравнение один ученик решает комментированием у доски. Учитель заранее переносит это уравнение на доску.

- Кто допустил ошибку? В чем она? (Неправильно применил правило, ошибся в вычислениях.)

- Исправьте допущенные ошибки. Вы молодцы, что поняли причину ошибки.

- Кто выполнил все верно? Сделайте вывод. (Мы умеем решать уравнения.)

- Как в этом убедиться? (Нужно выполнить самостоятельную работу.)

7. Самостоятельная работа с самопроверкой по эталону.

Организация учебного процесса на этапе 7:

- Вы поработали все вместе, как вы будете сейчас работать? (В парах.)

- Выполните два других уравнения в парах.

. №1 (в, г), с.83 - работа в парах (с проговариванием)

- Какая пара быстрее справилась с заданием?

- Проверка по эталону. У кого так?

№1 (д, е), с 83 - по вариантам

Проверка по эталону. Учитель открывает на доске эталон для самопроверки . Проводиться вербальная поэтапная проверка. Учащиеся по шагам вместе с учителем проверяют правильность своего хода решения и вычислений. ( Слайды 13, 14)

- Кто выполнил без ошибок?

- Кто допустил ошибки? С чем это связано?

- Чему мы научились? (Научились решать уравнения нового вида)

- Зачем нужен алгоритм? (Чтобы правильно решать задачи и уравнения)

- Проговорите ещё раз алгоритм решения составных уравнений.

- Для тех, кто хочет проверить свои силы - №2,с.83.

- Решите столько уравнений, сколько сможете.

- У кого есть ошибки? В чем они? (Учащиеся называют свои ошибки.)

- Сделайте вывод. (Нам необходимо потренироваться в решении уравнений, в вычислениях.)

- Где вы можете это сделать? (При выполнении домашнего задания.)

- У кого нет ошибок? Сделайте вывод? (Мы умеем применять новый способ.)

8. Включение в систему знаний и повторение.

Организация учебного процесса на этапе 8:

- Какие умения необходимо развивать, чтобы правильно решать уравнения? (Необходимо уметь размышлять, правильно считать.)

- Верно, с этой целью я вам предлагаю выполнить № 6, стр. 84

№ 6, стр. 84.

- Откройте в учебнике № 6 на стр. 21. Прочитайте задачу.

-

- Проанализируйте задачу.

- Расскажите план решения задачи. (Первым действием мы узнаем, сколько марок о космосе, вторым действием узнаем сколько марок о спорте и о космосе вместе, третьим действием узнаем сколько марок о животных, четвертым ответим на вопрос задачи.)

Один из учеников выходит к доске и записывает решение с наименованием и пояснением.

1. 129 × 2 =258 ( м)- о космосе

2. 129 + 258 = 387 ( м.) - о спорте и космосе вместе

3. 512 - 387 = 125 (м.) - о животных

4. 129 >125, 129 - 125 = 4 (м.)

Ответ: о спорте у Димы на 4 марки больше, чем о животных

9. Рефлексия учебной деятельности на уроке.

Организация учебного процесса на этапе 9:

- Что необходимо сделать в конце урока? (Анализируем свою работу.)

- Какова была цель сегодняшнего урока? (Построить способ решения уравнений, в которых выражение является неизвестным компонентом.)

- Достигли ли цели? Докажите.

- Давайте вернемся к шагам учебной деятельности. Кто может сказать, что сумел сам сделать «открытие». Докажите.

- Кому не удалось, почему?

- Оцените свою деятельность на лестнице «успеха».( Слайд 15.)

Учитель проводит рефлексию оценивания учащихся.

- Посмотрите, сколько ребят поставили себя на среднюю ступень. О чем это говорит?

- Какие же трудности у вас еще встречаются?

- Где можно над ними поработать?

9. Домашнее задание.

Повторить алгоритм решения составных уравнений.

№2, с.83 - для тех, кто хочет проверить свои силы