Тема урока: Решение уравнений 6 класс

Тема урока: Решение уравнений 6 класс

На этом уроке вы узнаете, какие свойства уравнений можно применять при их решении. Вы познакомитесь с определением линейного уравнения и уравнения, сводящегося к линейному. Разобранные примеры и упражнения проиллюстрируют применение рассмотренных правил и позволят связать новый и ранее изученный материал в единое целое.

Первое свойство уравнений. Иллюстрирующий пример. Формулировка

Рассмотрим решение уравнения:

Уравнение (2) можно получить из уравнения (1), разделив обе части уравнения на 5.

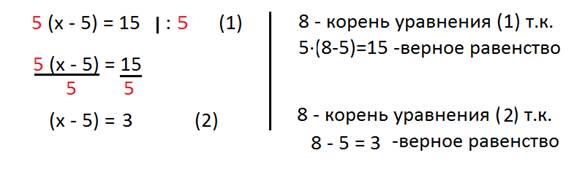Число 8 - это корень уравнения (1) и корень уравнения (2).

Сформулируем первое свойство уравнения.

Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю, и корни уравнения не изменятся.

Применение первого свойства уравнений. Упражнения

Пример 1.Умножим обе части уравнения на 9. Тогда коэффициент перед станет целым.

Ответ:

Пример 2.Умножим обе части уравнения на 10. Тогда коэффициенты перед станут целыми.

Ответ:

Пример 3. Разделим обе части уравнения на 20.

Ответ:

Пример 4. Разделим обе части уравнения на 2,1.

Ответ:

Второе свойство уравнений. Иллюстрирующие примеры. Формулировки

Рассмотрим решение уравнения:

Число 4 - это корень уравнения (1) и корень уравнения (2).

Заметим, что уравнение (2) можно было получить, перенеся число +5 из левой части в правую с противоположным знаком:

Сформулируем второе свойство уравнения:

Любое слагаемое можно перенести из одной части уравнения в другую, изменив при этом его знак на противоположный.

Рассмотрим решение еще одного уравнения: .Вычтем из левой и правой части уравнения . Тогда останется только в левой части.

Число 4 - это корень уравнения (3) и корень уравнения (4).

Второе свойство уравнений можно сформулировать иначе.

Если к обеим частям уравнения прибавить одно и то же число, то корни уравнения не изменятся. Если из левой и правой части уравнения вычесть одно и то же число, то корни уравнения не изменятся.

Применение второго свойства уравнений. Упражнения

Пример 1. Воспользуемся вторым свойством уравнений. Принято слагаемые, которые содержат неизвестное, собирать в левой части уравнения, а остальные в правой.

Пример 2. Перенесем слагаемые, которые содержат неизвестное, в левую часть, а известные слагаемые в правую часть.

Примеры решения более сложных уравнений

Пример 1.

Сначала раскроем скобки.

Перенесем слагаемые, которые содержат неизвестное, в левую часть, а известные слагаемые в правую часть.

Пример 2.

Воспользуемся основным свойством пропорции. Произведение средних равно произведению крайних.

Раскроем скобки в левой и в правой части уравнения.

Перенесем неизвестное влево, а известное вправо.

Линейные уравнения. Определение

Во всех рассмотренных примерах мы приводили уравнение к виду

Уравнения такого вида называют линейными уравнениями с одним неизвестным. Уравнения, которые можно с помощью преобразований привести к такому виду, называют сводящимися к линейным.

Упражнение

При каких значениях переменной значение выражения равно значению выражения ?

Составим уравнение и решим уравнение.

Перенесем неизвестное влево, а известное вправо.

Ответ: при

Текстовая задача</</p>

Условие. Рост мальчика - 75 см и еще половина его роста. Найдите рост мальчика.

Решение.1. Пусть (см) - половина роста.Тогда весь рост равен (см),

с другой стороны, весь рост - (см).

Составим уравнение:

75 см - половина роста

2. - весь рост мальчика

Ответ: 150 см.