- Учителю
- Итоговое повторение по математике 7-9 класс
Итоговое повторение по математике 7-9 класс











 Итоговое повторение курса алгебры 7-9-х классов - 21 час
Итоговое повторение курса алгебры 7-9-х классов - 21 час
Пояснительная записка
Цели:
подготовить учащихся к сдаче ГИА в соответствии с требованиями, предъявляемыми новыми образовательными стандартами.
Структура курса.
Курс рассчитан на 21 занятие. Включенный в программу материал предполагает повторение и углубление следующих разделов алгебры:
-
Числа и вычисления.
-
Алгебраические выражения.
-
Уравнения и системы уравнений.
-
Неравенства и системы неравенств.
-
Последовательности и прогрессии.
-
Функции.
-
Реальная математика. Теория вероятностей.
Примерное планирование итогового повторения курса алгебры 7-9-х классов.
№
Тема
Количество часов
Форма контроля
1
Числа и вычисления.
3
тест
2
Алгебраические выражения.
3
тест
3
Уравнения, системы уравнений.
3
тест
4
Неравенства, системы неравенств.
3
тест
5
Последовательности и прогрессии.
3
тест
6
Функции.
3
тест
7
Реальная математика. Теория вероятностей.
3
тест
Итого:
21
Тест «Числа и вычисления»
-
Расположите в порядке возрастания числа:
 ;
;  ; 0,7; 0,3
; 0,7; 0,3
1) ;
;  ; 0,3; 0,7 2) 0,3;
; 0,3; 0,7 2) 0,3;  ;
; ; 0,7 3) 0,3;
; 0,7 3) 0,3; ;
;  ; 0,7 4)
; 0,7 4)  ;
;  ; 0,7; 0,3.
; 0,7; 0,3.
-
Какому из данных промежутков принадлежит число
 ?
?
1) [0,4; 0,5] 2) [0,5; 0,6] 3) [0,6; 0,7] 4) [0,7; 0,8]
3. Какое из чисел  ,
, 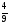 ,
, 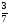 является иррациональным?
является иррациональным?
1)  2)
2) 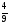 3)
3) 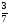 4) все эти числа
4) все эти числа
4. На координатной прямой отмечены числа а и b. Какое из следующих утверждений является верным?
![]()
-
ab › 0; 2) a + b ‹ 0; 3) b(a + b) ‹ 0; 4) a(a + b) ‹ 0
5. Известно, что х и у - нечётные числа. Какое из следующих чисел также является нечётным?
1) х + у; 2) 4х + у; 3) 4(х + у +1); 4) (х + 2)(у + 1)
6. На коробке с тортом имеется надпись, гарантирующая, что масса торта равна 500 ± 15 г. Какую массу при этом условии не может иметь торт?
1) 505г 2) 483г 3) 515г 4) 495г
7. Найдите десятичную дробь, равную 56,48 * 10-6.
-
0,05648 2) 0,005648 3) 0,00005648 4) 0,0000005648
8. Две трубы наполняют бассейн за 5,3 часа. За какое время наполнят бассейн 5 таких труб (в ч)?
1) 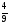 ; 2) 13,25; 3) 2,12 4) 0,53
; 2) 13,25; 3) 2,12 4) 0,53
9. Вычислите 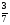
1) 120; 2)30; 3)20; 4)60.
10. Вычислить ( 5,5 - 2 ) : 4 -1.
) : 4 -1.
-
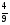 2) -
2) - 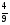 3)
3)  4) 9
4) 9 .
.
Тест «Алгебраические выражения»
-
Найти значение выражения
 при а = 0,64; в = 0,08.
при а = 0,64; в = 0,08.
Ответ: _____________________________
-
При каком значении переменной x выражение
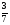 не имеет смысла?
не имеет смысла?
1)1; 2)-3; 3)5; 4)0.
-
Соотнесите каждое выражение с его областью определения.
А) 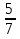 Б)
Б) 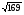 В)
В) 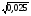 Г)
Г) 
-
с ≠ -3 2) с ≠ -1 3) с ≠ -3 и с ≠ -1 4) с - любое число
-
При каком из указанных значений х выражение
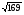 имеет смысл?
имеет смысл?
1) х = -2 2) х = -5 3) х = 5 4) х = 1
-
За 45 минут человек прошел 4 км. Какое расстояние он пройдет за t минут, если будет идти с той же скоростью?
-
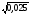 2)
2)  3)
3) 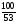 4)
4) 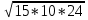
6. Из формулы s = s0 + vt выразите переменную v.
1) v = 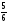 ; 2) v =
; 2) v = 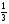
Ответ: _____________________________
7. Представьте выражение 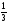 в виде степени.
в виде степени.
-
a2 2) a-4 3) a8 4) a-2
8. Найдите значение выражения (3,4 • 10-3)*(2•10-2).
-
6800000 2) 0,00068 3) 0,000068 4) 0,0000068
9. Упростите выражение (а + 2)2 - (4 - а2).
-
0 2) 2а2 3) 4а 4) 2а2 + 4а
10. Сократите дробь 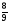 .
.
-
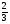 2)
2) 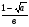 3)
3) 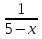 4)
4) 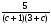
11. Упростите выражение 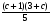 :
: 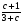 .
.
-
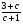 2) -
2) -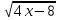 3) -
3) - 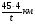 4)
4) 
Тест «Уравнения, системы уравнений»
-
Решите уравнение 4х2 - 13х - 12 =0.
1)0,75; 4 2) -0,75; 4 3) 0,75; -4 4) -0,75; - 4
-
Найдите корни уравнения (2х - 5)(х + 3) = 0
1) 3;2,5 2) -3;2,5 3) 3; -2,5 4) -3;-2,5
-
Найдите сумму корней уравнения 4х2 - 12х + 5 = 0.
-
12 2) - 3 3) 3 4) 1,25
-
Соотнесите каждое квадратное уравнение и его корни:
А) х2 - 9 = 0 Б) х2 + 2х = 0 В) х2 + 4 = 0
-
0; -2 2) -2; 2 3) -3; 3 4) нет корней
5. Решите уравнение  .
.
Ответ: ___________________________
6. Найдите решение системы уравнений 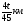
-
(-2; 1) 2) нет решений 3) (-2; -1) 4) (1; -2)
7. Найдите координаты точки пересечения параболы у = х2 -5х и прямой у = 16 + х.
Ответ: _____________________________
8. Расстояние между пристанями на реке 12 км. Катер проплыл от одной пристани до другой и вернулся обратно, затратив на весь путь 2 ч 30 мин. Какова скорость течения реки (в км/ч ), если собственная скорость катера равна 10 км/ч?
Выберите уравнение, соответствующее условию задачи, если буквой х обозначена скорость течения реки (в км/ч).
-
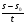 2) х =
2) х = 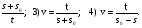
3) 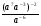 4)
4) 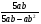
9. Решите уравнение х4 - 3х3 + 4х2 - 12х = 0 Ответ: ____________
Тест «Неравенства и системы неравенств»
1. Одна из точек, отмеченных на координатной прямой, соответствует числу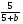 . Какая это точка?
. Какая это точка?
![]()
1) М 2)Р 3) N 4)Q
2. О числах a и b известно, что a>b. Среди приведенных ниже неравенств выберите верные:
1) a - b > - 17 2) b - a >2 3) b - a <10 4) a - b > 17
3. Решите неравенство 6 - х 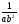 2х .
2х .
1) (-∞; -0,5] 2) [-0,5; +∞) 3) (-∞; 2] 4) [-2; +∞)
4. Решите неравенство 8х + 12 > 4 - 3(4 - х).
1) х > -4 2) х < -4 3) х > -5,6 4) х < -5,6
5. Для каждой системы неравенств укажите номер рисунка, на котором изображено множество её решений.
А) 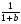 1)
1) ![]()
2) ![]()
Б) 
3) ![]()
В) 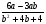 4)
4) ![]()
6. Решите неравенство х2 - 9> 0
1) решений нет 2) (-∞;-3) U (3; +∞) 3) (-3; 3) 4) (-∞; 3)
7. Решите неравенство х2 -2 х +1< 0
Ответ: ______________________________
8. Укажите неравенство, которое не имеет решений.
1) 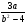 + 5 ≥ 0 2)
+ 5 ≥ 0 2)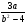 + 5 ≤ 0
+ 5 ≤ 0
3)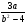 - 5 ≤ 0 4)
- 5 ≤ 0 4) 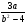 - 5 ≥ 0
- 5 ≥ 0
Тест «Последовательности и прогрессии»
-
Последовательность чисел
 задана равенствами
задана равенствами  и
и 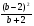 при всех
при всех
n ≥ 2. Какое из указанных ниже чисел является членом этой последовательности?
1) 152 2) 55 3) 35 4) 25
2. Числовая последовательность задана следующими условиями:
а1 = 2; аn+1 = 3аn - 2. Найдите пятый член этой последовательности.
1) 64 2) 71 3) 81 4) 82
3. Укажите какая из нижеперечисленных последовательностей является арифметической прогрессией.
1) 2; 7; 11; 16;… 2) 5; 8; 11; 13;… 3) 7; 9; 10; 12;… 4) 10; 20; 30; 40;….
4. Каждой последовательности поставьте в соответствие формулу n-го члена.
А) 6; 12; 24… Б) 8; 6; 4… В) 2; 8; 18…
1) 10 - 2n 2) аn = 2n2 3) аn = 2n + 6 4) аn = 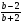
5. Найдите неизвестный член геометрической прогрессии
…; 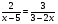 ; х;
; х; 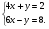 ; …, если
; …, если 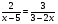 ; х;
; х; 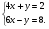 - последовательные члены и х > 0.
- последовательные члены и х > 0.
1) 1 2)  3)
3)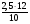 4) другой ответ
4) другой ответ
6. В первом ряду стоят 23 спортсмена, а в каждом последующем на два спортсмена больше. Сколько спортсменов в ряду с номером n?
1) 23 + 2n 2) 2n 3) 21 + 2n 4) 25 + n
7. Геометрическая прогрессия (bn) задана условиями: b1, и bn+1 = bn·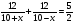 . Определите формулу n-го члена этой прогрессии.
. Определите формулу n-го члена этой прогрессии.
1) bn = 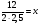 2) bn =
2) bn = 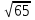 3) bn =
3) bn = 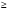 4) bn =
4) bn = 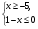
8. В геометрической прогрессии b1 = -81 , q = 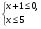 . В каком случае при сравнении членов этой прогрессии знак неравенства поставлен неверно?
. В каком случае при сравнении членов этой прогрессии знак неравенства поставлен неверно?
1) b1< b2 2) b1 < b3 3) b2 > b4 4) b3 > b5
9. Найдите сумму первых шести членов арифметической прогрессии, если а1 = 12, d =3.
1) 117 2) 81 3) 78 4) 39
10. Сколько положительных членов в последовательности (сn), заданной формулой
Сn = 34 - 4n?
1) 4 2) 8 3) 9 4) 17
Тест « Функции»
1. На рисунке изображён график функции y = f(x), областью определения, которой является промежуток [-4;4]. Используя рисунок, выясните, какое из утверждений неверно.