Урок +презентация по геометрии для 11 класса «Решение задач на вычисление объемов и площадей поверхностей тел»

Подготовка к ЕГЭ по математике

Открытый урок

по теме: «Решение задач на вычисление

объемов и площадей поверхностей тел».

(задачи В10, В13)

Учитель: Мартыненко П. А.

г. Зеленокумск

февраль 2014 г.

Цель урока: Закрепление навыков у учащихся на решение задач на нахождение

объемов и площадей поверхностей тел. Умение решать задачи на

комбинацию различных тел.

Ход урока

1. Организационный момент.

2. Проверка домашнего задания:

№ 667 решение:

;

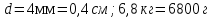
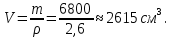
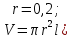
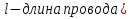
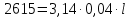Получим, что

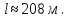
№ 690 решение:

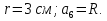
Получим: 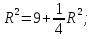из уравнения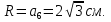

Высота боковой грани:

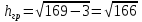
Площадь боковой грани:

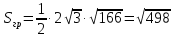
Т. О.

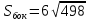
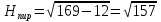
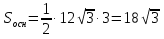
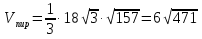
3. Опрос учащихся:

I

Устная работа по готовым чертежам:

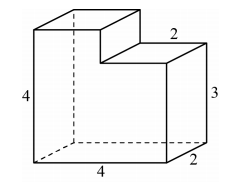
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

Ответ: 28

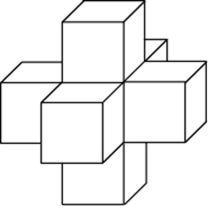
Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

Ответ: 7

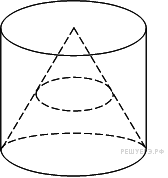
Конус вписан в цилиндр. Объем конуса равен 5. Найдите объем цилиндра.

Ответ: 15

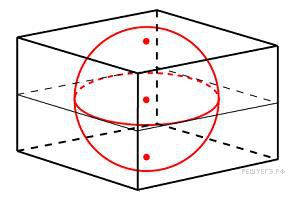
Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.

Ответ: 3

II

Опрос учащихся у доски (решение задач по карточкам)

III

Записать формулы объемов многогранников и тел вращения на доске

4. Письменная работа с учащимися на доске и в тетрадях (решение

задач на закрепление изученной темы)

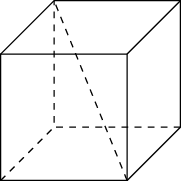
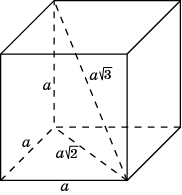
1. Диагональ куба равна 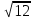. Найдите его объем

Решение: Если ребро куба равно a, то его диагональ равна 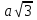.Отсюда следует, что если диагональ куба равна 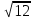, то его ребро равно 2 и, значит, объем этого куба равен 8

Ответ: 8

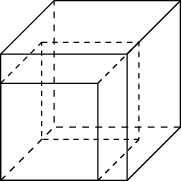
2. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 30. Найдите ребро куба и его объем.

Решение: Если ребро куба равно x, то площадь его поверхности равна 6x². Если ребро куба увеличить на 1, то его площадь поверхности будет равна 6(x+1)². Учитывая, что площадь поверхности куба при этом увеличивается на 30, получаем уравнение 6(x+1)² = 6x² + 30, решая которое, находим x = 2.

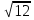
Ответ: 2; 8

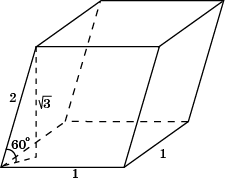
3. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60^о. Одно из ребер параллелепипеда составляет с этой гранью угол в 60^о и равно 2. Найдите объем параллелепипеда

Решение: Площадь грани параллелепипеда, являющейся ромбом со стороной 1 и острым углом 60^о, равна 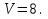. Высота, опущенная на эту грань, равна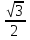. Объем параллелепипеда равен 1,5.

Ответ: 1,5

4. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы

Решение: Площадь основания отсеченной призмы равна четверти площади основания исходной призмы. Высота отсеченной призмы равна высоте исходной призмы. Следовательно, объем отсеченной призмы равен четверти объема исходной призмы, т.е. равен 8

Ответ: 8

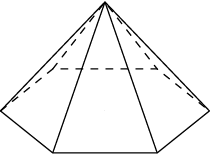
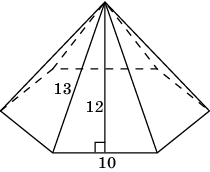
5. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности пирамиды.

Решение: Высота боковой грани пирамиды равна 12. Площадь боковой грани равна 60. Площадь боковой поверхности этой пирамиды равна 360.

Ответ: 360

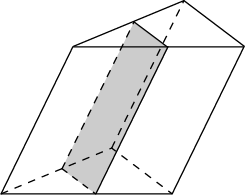
6. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3

Решение: Площадь основания пирамиды равна 27, высота равна 3. Следовательно, объем пирамиды равен 27.

Ответ: 27

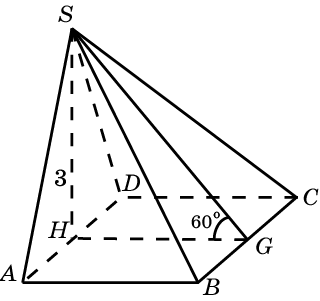
7. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60⁰. Высота пирамиды равна 3 см. Найдите объем пирамиды.

Решение: Треугольник SAD равносторонний со стороной ,

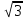AB = GH =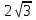Площадь прямоугольника ABCD равна 6. Следовательно, объем пирамиды равен 6.

Ответ: 6

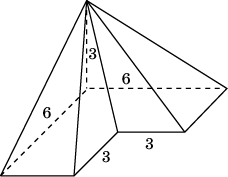
8. От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

Решение: 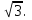= 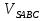коэффициентом подобия, равным 2. Значит 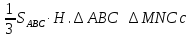. Так как пирамиды имеют одинаковые высоты, а площадь основания отсеченной пирамиды в 4 раза меньше площади основания данной пирамиды, то и ее объем будет в 4 раза меньше объема данной.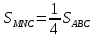

Ответ: 3

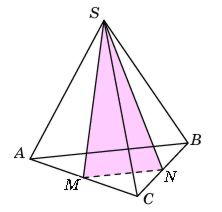
9. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Решение: Радиус основания вписанного конуса будет равен половине стороны основания пирамиды, т.е. 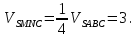тогда 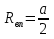Радиус основания описанного конуса будет равен половине диагонали пирамиды, т.е. 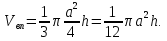тогда 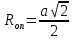Таким образом,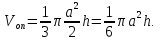

Ответ: 2

5. Подведение итогов урока

Вопросы учащимся

• Какова была тема и цель урока;

• Задачи какого типа решались на уроке

(задачи на нахождение объемов);

• Каково практическое применение данного типа задач;

• Имеют ли место данные задачи в материалах ЕГЭ.

6. Домашнее задание: (домашняя самостоятельная работа по карточкам).