Конспект урока на тему Противоположные числа

Урок математики в 6 классе

Тема: «Сравнение десятичных дробей»

Учитель: Лапина Е.А.

Класс: 6Д

Предмет: математика

Цель: формировать представление о противоположных числах, научить применять его на практике.

Задачи:

образовательная:

• закрепить понятие координатной прямой, ввести понятие числа противоположного данному, научить распознавать, записывать и откладывать на координатной прямой;

развивающая:

• развивать коммуникабельность, умение анализировать, сравнивать, выделять главное;

воспитательная:

• воспитывать познавательный интерес к предмету и уверенность в своих силах, ответственность и аккуратность

Вид урока: урок «открытия» нового знания

Формы работы: командная, индивидуальная, фронтальная

Планируемый результат: формировать представление о противоположных числах, научить применять его на практике

Личностные УУД: самоопределение, смыслообразование

Познавательные УУД: формулирование проблемы, самостоятельное выделение и формулирование познавательной цели, осознанное и произвольное построение речевого высказывания в устной и письменной форме

Регулятивные УУД: учитывать правило в планировании и контроле способа решения

Коммуникативные УУД: уметь договариваться и приходить к общему решению в совместной деятельности, уметь контролировать действия партнера, строить монологическое высказывание, владеть диалогической формой речи

Обучающие структуры: Тэйк Оф - Тач Даун, Финк-Райт-Райд Робин, Микс Пэа Шэа, Релли Робин, Раунд Тэйбл

ТСО: мультимедийное оборудование, карточки с заданиями

Ход урока

1. Организационный момент

2. Актуализация знаний

3. Постановка учебной задачи и открытие нового знания

4. Первичное закрепление

5. Самостоятельная работа с самопроверкой

6. Домашнее задание

</<font face="Times New Roman, serif">7. Этап рефлексии учебной деятельности

1. Орг. момент

Очень восхитительные

Числа положительные!

А числа отрицательные?

Тоже замечательные!

Только ноль, как постовой,

Охраняет их покой.

Если точка вам нужна -

Выходите вы с нуля.

Ну а противоположные

Вообще не очень сложные!

Мы тоже сегодня постараемся внести элемент занимательности в урок и узнаем много нового и интересного.

Итак, отправляемся в путь за новыми знаниями.

Откройте, пожалуйста, тетради и запишите дату, классная работа, а для темы урока оставьте строчку, вы сами ее сформулируете позже.

Создать благоприятный психологический настрой на работу

Прогнозирование своей деятельности

Планирование учебного сотрудничества с учителем и сверстниками

Умение выделять нравственный аспект поведения

мотивация учения

2. Актуали-зация знаний

Прежде чем узнавать новое, нужно повторить уже изученное, поэтому поработаем устно, используя ОС Тэйк Оф - Тач Даун - если утверждение верное встаем, иначе сидим на месте

1. Отрицательные числа расположены правее нуля (нет)

2. Ноль, не является ни отрицательным, ни положительным числом (да)

3. На координатной прямой положительные числа расположены левее нуля (нет)

4. Точка с координатой -17 расположена левее нуля (да)

5. Точка, расположенная правее от нуля на 100 единичных отрезков имеет координату 100 (да)

6. Точка, с координатой -18 расположена левее от нуля на

-18 единичных отрезков (нет)

Мы с вами повторили, какая прямая называется координатной прямой, понятия положительных и отрицательных чисел.

Структурирова-ние собственных знаний

Контроль и оценка процесса и результатов деятельности

Организовывать и планировать учебное сотрудничество с учителем и сверстниками

Определение границы собственного знания и «незнания»

3. Постанов-ка учебной задачи и открытие нового знания

Смотрим на экран. Я начну фразу, а вы продолжайте, смело хором отвечайте.

Мужчина высокий и….

Рисунок черный и …

Собака большая и …

Вода горячая и ….

Как в русском языке называются такие слова?

Что такое антонимы? Стол №1, участник №3

-Мир, окружающий нас, интересен, но противоречив. Вы читаете сказки, в которых уживаются добро и…(зло), вы учитесь в школе и получаете оценки: хорошие и…(плохие).

И в математике есть противоположности. Давай узнаем, какие противоположности бывают в математике. Проведем интересный эксперимент.

Мне нужны 2 помощника. Встали спиной друг к другу. Сделали по 3 шага.

- На каком расстоянии в шагах они находятся от меня.

- Если рассматривать на координатной прямой, то каким координатам соответствуют мои помощники?

- Ещё раз напомните, в каком направлении двигались помощники?

- Значит числа 3 и -3 называются какими? Посмотрите на доску, кому соответствуют числа с противоположными координатами? Стол №1, участник №3

- Так какая же тема нашего урока? Какие цели будут стоять перед нами? Подумайте 5 секунд Стол №1, участник №3

Запишите тему урока в рабочих тетрадях.

Мы уже познакомились с противоположными числами, а теперь я вам предлагаю выполнить задание, с помощью которого вы сформулируете определение противоположных чисел. Работать будем при помощи ОС Финк-Райт-Райд Робин.

Начертите координатную прямую, приняв за единичный отрезок длину одной клетки тетради. Отметьте на этой прямой точки:

А(5), Р(-6), М(6), В(8), К(-3).

Запишите в тетрадях ответы на следующие вопросы

- Чему равно расстояние (в единичных отрезках) от точки О до К?

- Чему равно расстояние (в единичных отрезках) от точки О до Р?

- Чему равно расстояние(в единичных отрезках) от точки О до М?

- Какие точки одинаково удалены от начала отсчёта?

- Пусть нам надо выйти из точки и пройти путь в 6км (1км = 1 ед.отрезку). В какую точку мы попадём?

- Как надо двигаться, чтобы попасть в эти точки?

- Значит, числа 6 и -6 будут противоположными. Попробуйте сформулировать определение, какие же числа называются противоположными. Подумайте 3-5 сек. Обсудите в команде, у каждого участника 30 сек., начинает участник №1. Стол №1, участник №3

Опр: Два числа, отличающиеся друг от друга только знаками, называются противоположными.

Хорошо, молодцы! Знак «-» означает число, противоположное данному, тогда, как, используя знак «-», мы можем записать число, противоположное -2? -(-2) = 2

А сейчас, аналогично данному примеру запишите в тетрадях число:

- противоположное числу -1,6?

- противоположное числу -11?

- противоположное числу -х?

- чему равно число - (-(-(-5))) ? Почему?

- чему равно число - (-(-(-(-10,32)))) ? Почему?

Давайте сделаем выводы, заполнив пропуски в предложениях. Подумайте 3-5 сек., какие слова пропущены.

а) Если перед числом стоит чётное количество минусов, то получится … число.

б) Если перед числом стоит нечётное количество минусов, то получится … число.

Поиск и выделение необходимой информации, сравнение и опознание объектов. Учащиеся собирают и выделяют информацию, существенную для решения проблемы

Целеполагание

Высказывают свою точку зрения.

Умение вступать в диалог, участвовать в коллективном обсуждении вопроса.

Самоопределение

4. Первичное закрепление нового материала

А сейчас мы с вами закрепим понятие противоположных чисел при помощи ОС Микс Пэа Шэа. Пожалуйста, встаньте, задвиньте стулья и смешайтесь под музыку, после моей команды необходимо образовать пару с ближайшим к вам учеником. На слайде даны числа, а вы назовите им противоположные. Но называть числа в паре будем при помощи ОС Релли Робин, т.е. один за другим. Первый начнет тот, у кого мизинец длиннее.

-9

12

144

-8

-74

256

21

-36

-1

5

Микс! Первым начнет тот, кто выше.

11

7

16

-12

-41

52

143

-15

18

-66

Микс! Первым начнет тот, кто старше.

-12

-10

520

76

-94

65

31

-33

89

100

Какой можно сделать вывод: если даны числа положительные, то им противоположные….

Если отрицательные, то им противоположные…. Стол №1, участник №3

На столах у вас карточка №1 с зашифрованной фамилией учёного математика, который ввёл в математический язык символы «+» и «-». Участники №3, раздайте карточки №1 всем участникам команды.

Задание - выберите числа, противоположные данным и расшифруйте фамилию чешского математика, который в XYвеке предложил применять эти символы.

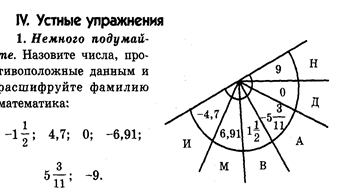
Я. Видман.

История говорит о том, что люди долго не могли привыкнуть к отрицательным числам. Отрицательные числа казались им непонятными, ими не пользовались, просто не видели особого смысла.

Современные знаки «+» и «-» появились в Германии в последнее десятилетие 15 века в книге Видмана, которая была руководством по счету для купцов. Купцы, на пустых бочках ставили «-», означавший «убыль». Если бочку заполняли то знак «-» перечёркивали и получался «+», означавший «прибыль».

Следующее задание выполним при помощи ОС Раунд Тэйбл. Все участники команды, запишите в тетрадь уравнения, которые Вы видите на слайде в тетрадь и решите их

1. - х=32

2. - х= - 32

3. х= - (-32)

4. х= - (- (-32))

На выполнение задания у вас 3 минуты.

Передайте свою тетрадь в команде по часовой стрелке следующему участнику и проверьте правильность выполнения задания со слайдом.

Формирование интереса к данной теме.

Контроль и оценка процесса и результатов деятельности

Планирование своей деятельности для решения поставленной задачи и контроль полученного результата

Умение оформлять свои мысли в устной форме; слушать и понимать речь других

Умение адекватно и осознанно строить речевое высказывание в устной речи

Формирование готовности к самообразо-ванию

5. Самостоя-тельная работа

А сейчас выполним небольшую самостоятельную работу, по результатам которой вы получите оценки за сегодняшний урок.

Участник №3, раздайте карточки №3 с заданиями. На выполнение работы 5 минут.

Вариант 1

1.Какие их чисел являются противоположными?

а) 3 и ;

б) 3 и ;

в) 3 и -3;

г) 3 и 0,3.

2. Расположите числа 2,3; - -2,5; 0; -2,3 по убыванию.

3.Найдите длину отрезка, соединяющего точки 2а и -2а.

Вариант 2

1.Какие их чисел являются противоположными?

а) 6 и ;

б) 6 и ;

в) 6 и -6;

г) 6 и 0,6.

2. Расположите числа 2,3; - -2,5; 0; -2,3 по возрастанию.

3.Найдите длину отрезка, соединяющего точки а и -2а.

6. Домашнее задание

п. 27, выучить определение, 943, 945, по желанию 935

7. Рефлексия

Участники команды №4, раздайте всем членам команды координатную прямую. Предлагаю Вам порефлексировать о нашем уроке. Прикрепите человечка на точку с той координатой, как вы оцениваете свою работу.

В точечном царстве, в координатном государстве, на берегу нулевой реки жили-были числа-близнецы. Их домики стояли на одинаковом расстоянии от нулевой реки. Только одни из них поселились на левом берегу, а другие - на правом, противоположном, поэтому числа 1 и -1, 2 и -2, 3 и -3, противоположными стали называть

Но случилась беда: стали теряться пары противоположных чисел. Сыщики выяснили, что они исчезают в нулевой реке. Почему исчезали пары чисел? Это мы узнаем на следующем уроке

Оценивание собственной деятельности на уроке