Урок геометрии 9 класс Аксиомы стереометрии и простейшие следствия из них

АКСИОМЫ СТЕРЕОМЕТРИИ. ПРОСТЕЙШИЕ СЛЕДСТВИЯ ИЗ АКСИОМ.

Автор: Злавдинова Гульмира Муталимовна, учитель математики КГУ ОШ № 155

Цель урока: Организация деятельности учащихся по восприятию, осмыслению и первичному запоминанию новых знаний и способов деятельности

Задачи :

Образовательные: - к концу урока учащиеся познакомятся с историей возникновения геометрии:

• будут знать, что изучает стереометрия; ее основные понятия;

• изучат группу аксиом и следствия из них, выражающие основные свойства плоскостей в пространстве;

• научатся распознавать, изображать и обозначать расположение точек, прямых и плоскостей.

сформируют новые понятия, правила и построенные на их основе алгоритмы деятельности;

Развивающие:развивать творческую и мыслительную деятельность учащихся на уроке с помощью решения задач исследовательского характера, интеллектуальные качества личности школьников такие, как самостоятельность, способность к оценочным действиям, обобщению, быстрому переключению; способствовать формированию навыков самостоятельной работы; формировать умение четко и ясно излагать свои мысли.

Воспитывающие:прививать учащимся интерес к предмету с помощью изучения истории и развития науки, применения информационных технологий (с использованием компьютера); использовать текст учебника и справочный материал при изучении новой темы.формировать умение аккуратно и грамотно выполнять математические записи.

Тип урока: Изучение и первичное запоминание новых знаний и способов деятельности

Оборудование урока: запись на доске, алгоритмы, презентация на интерактивной доске .

Методы: словесные, наглядные, практические

Формы: фронтально-коллективные, работа в паре, индивидуальные.

ХОД УРОКА

1.Организационный момент. ( подготовка учащихся к общению, обеспечить нормальную обстановку для работы на уроке.)

2 . Актуализация ( сообщение темы урока, постановка перед учащимися учебной проблемы, совместное с учащимися планирование работы на уроке.)

Напомнить учащимся, что до данного урока ими изучались темы из раздела геометрии под названием «Планиметрия». По стратегии перепутанные логические цепочки - закончить предложение. ( групповая работа)

1.Геометрия - наука о свойствах геометрических фигур.

2.Геометрия - в переводе с греческого означает землемерие.

3.Планиметрия - раздел геометрии, в котором изучаются свойства фигур на плоскости.

4.К основным фигурам на плоскости относятся точка и прямая.

5. Основные разделы геометрии - планиметрия и стереометрия.

6. Аксиома - исходное положение научной теории, принимаемое без доказательства.

3. Формирование новых понятий и способов действий

I повторение( парная работа)

Какие из этих утверждений являются аксиомами планиметрии?

1. Через любую точку плоскости можно провести бесчисленное множество различных прямых.

2. Через любые две точки проходит прямая и притом только одна.

3. Для каждой прямой существуют точки, принадлежащие ей, и точки, не принадлежащие ей.

4. Из трех точек прямой одна и только одна лежит между двумя другими.

5. Две прямые пересекаются, если имеют одну общую точку.

II Изучение новой темы

1. Показать учащимся фигуры (тела), которые нельзя отнести к плоским. Для изучения свойств этих фигур сведения, полученные в разделе «Планиметрия» недостаточны. Такие фигуры относятся к пространственным. В связи с этим вводится новый раздел геометрии - «Стереометрия». Рассмотреть понятие плоскости в пространстве, ее изображение и обозначение на рисунке

2. Изучение новой темы учащимися по учебнику( дневник двойной записи)

Глава VI §1.2-1.3 стр 145-147:

Основная часть ребят заполняют таблицу:(индивидуальная работа)Аксиомы стереометрии

Рисунок

Математическая запись

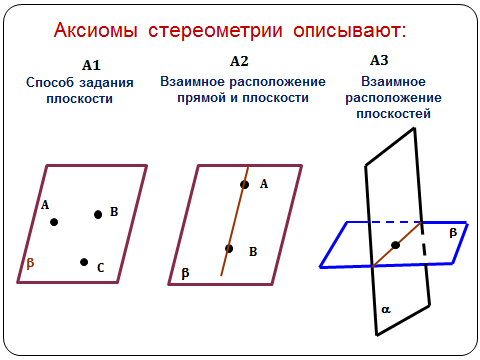
А₁

</<font face="Times New Roman, serif">Какова бы ни была плоскость, существуют _____________ ______________________________,

А₂

Через любые три точки, __________________

плоскость, и притом ____________________

А₃

Если две точки прямой лежат в плоскости, то

_______________________________________

в этой плоскости.

А₄

Если две плоскости имеют общую точку, то эти __________________________________,

____________________________________эту общую точку.

выборочно несколько учащихся рассматривают доказательства следствий из аксиом (Теоремы 1-2)

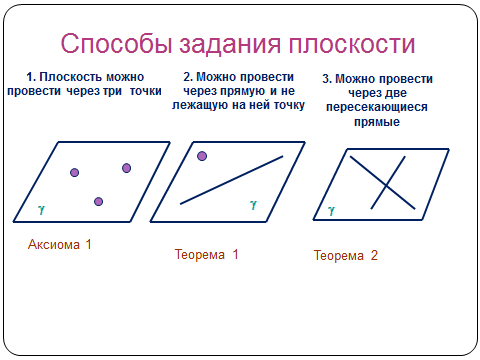
Теорема 1- (через две пересекающие прямые…)

Теорема 2

IIIсовместное обсуждение темы + подведение итогов по слайдам

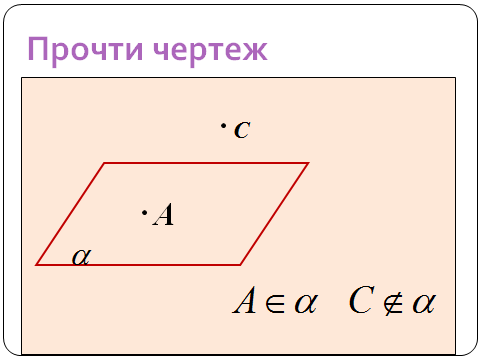
4. Применение. Формирование умений и навыков

1 устная работа в группах

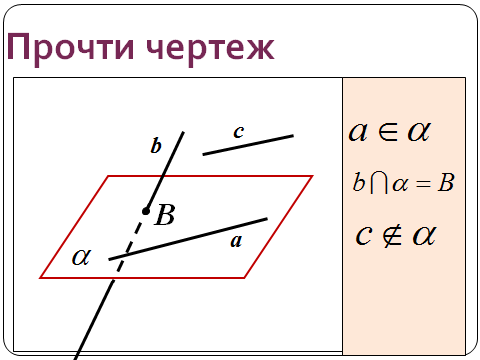
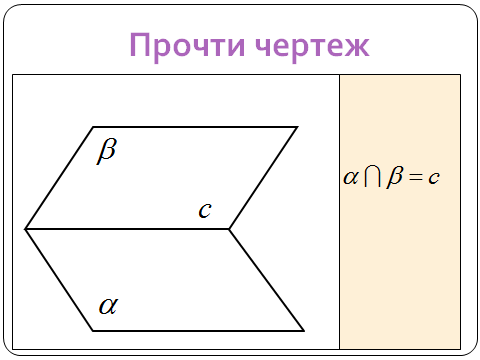
3. Решение задач в группах (3-4 мин)

1 группа

1. Какое минимальное число точек определяет прямую? (чертеж)

2. Какое минимальное число точек определяет плоскость? ( чертеж)

2 группа

1. Сколько плоскостей проходит через три точки лежащие на прямой?

( продемонстрировать на примере)

2. Сколько плоскостей проходит через три точки не лежащие на прямой?

( продемонстрировать на примере)

3группа

Верно ли что все точки окружности принадлежат плоскости, если эта окружность имеет с плоскостью:

а )две общие точки

б) три общие точки(продемонстрируйте)

4 группа

В плоскости даны три точки А, В,С, не принадлежащие одной прямой. Как расположены стороны треугольника АВС относительно плоскости α? (чертеж)

5 группа

Определите по рисунку. Как расположены плоскости α и β?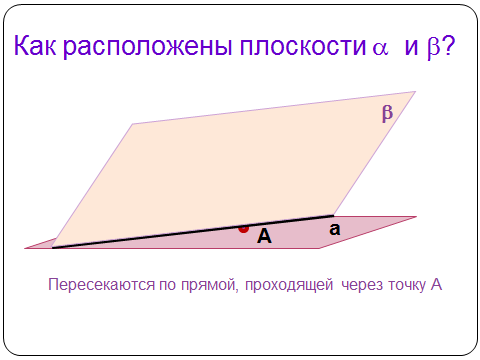

6 группа

Сколько различных плоскостей можно провести через данную точку пространства? (продемонстрируйте)

4. Тест

Первый вариант

1. Назовите основные фигуры на плоскости

а)отрезок и прямая m) точка и отрезок p)точка и прямая

2. Сколько плоскостей можно провести через прямую и точку не лежащую на ней

а) двеl) однуp) бесконечно

3. Сколько общих точек может быть у прямой и плоскости?

a)ни одной, одна или много l) одна, две или ни однойp) одна или две

4. Могут ли прямая и плоскость иметь только две общие точки?

m) да n) нет p) недостаточно условий

5. Какое минимальное число точек определяет плоскость?

u)триm) две n) четыре

6. Даны три прямые попарно пересекающиеся в различных точках. Сколько плоскостей через них можно провести?

u) триm) одну n) бесконечно

Второй вариант

1. Назовите основные фигуры в пространстве

а) точка, отрезок и плоскостьe) точка, отрезок и луч m)точка , прямая и плоскость.

2. Сколько плоскостей можно провести через четыре точки лежащие на одной прямой?

а) две e) бесконечно m) одну

3. Сколько прямых можно провести через две точки?

m) двеn) бесконечно много t)одну

4. Могут ли прямая и плоскость иметь только одну общую точку?

e) недостаточно условий r) нет t) да

5. Какое минимальное число точек определяет прямую?

e)две r) одна t) три

6. Даны плоскость α и точки А и В, такие, что А принадлежит α, В не принадлежит α .

Лежит ли в плоскости α середина отрезка АВ?

a) даe) невозможно определить o) нет

5. Этап информации о домашнем задании _

§1.2-1.3 (знать аксиомы и уметь отвечать на вопросы стр148).

Решить задачи уровень А№630; уровень В№635 уровень С ПЗ стр 148

6. Подведение итогов урока, выставление оценок

7. Этап рефлексии

Закончить предложения с практическим применением или выразить свое отношение :

1. Стереометрия - раздел геометрии, …

2. Основные фигуры в пространстве: …

3. К геометрическим телам относятся …