- Учителю
- Инструктивно-методические материалы к выполнению практических работ
Инструктивно-методические материалы к выполнению практических работ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ДОНЕЦКОЙ НАРОДНОЙ РЕСПУБЛИКИ
ГПОУ «ГОРЛОВСКИЙ КОЛЛЕДЖ ПРОМЫШЛЕННЫХ ТЕХНОЛОГИЙ И ЭКОНОМИКИ»
УТВЕРЖДАЮ:
Зам. директора
_________О.Ю.Цыба
__.__.2015
ИНСТРУКТИВНО-МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ
к выполнению практических работ
по дисциплине «Математика»
Специальность: 38.02.01 Экономика и бухгалтерский учет (по отраслям)
Рассмотрено на заседании цикловой комиссии математической и
общей естественнонаучной подготовки и рекомендовано к утверждению
Протокол № от « » г.
Зав.методическим кабинетом _________________Т.В.Кучеренко
Подготовил преподаватель
Е.В.Мудрецкая
г.Горловка, 2015
Инструктивно-методические материалы к выполнению практических работ по дисциплине «Математика». Подготовил преподаватель высшей квалификационной категории Е.В.Мудрецкая - Горловка: ГПОУ «Горловский колледж промышленных технологий и экономики», 2015.-
81 с.
Представлен: перечень тематических практических работ по дисциплине «Математика», предусмотренных рабочей программой учебной дисциплины для студентов 2 курса дневной формы обучения специальности 38.02.01 Экономика и бухгалтерский учет (по отраслям), непосредственно практические задания и методические рекомендации к их выполнению, задания для формирования знаний и умений, задания для закрепления знаний.
Предназначены для организации практических занятий по дисциплине, используется как методическое обеспечение занятий.
Для преподавателей и студентов
Рецензенты:
1. Арчаков А.В., преподаватель Енакиевского металлургического техникума,
специалист высшей категории.
2. Свириденко М.Н., преподаватель Горловского колледжа промышленных технологий и экономики, специалист высшей категории.
СОДЕРЖАНИЕ
практ.
зан.
Номер и тема практической работы
с
1
Практическая работа 1
по теме «Действия над матрицами»
5
2
Практическая работа 2
по теме «Вычисление определителей второго и третьего порядка»
11
3
Практическая работа 3
по теме «Нахождение обратной матрицы. Решение систем линейных уравнений методом обратной матрицы»
14
4
Практическая работа 4
по теме «Решение систем линейных уравнений: задачи с профессиональной направленностью»
18
6
Практическая работа 5
По теме «Вычисление первого и второго замечательных пределов»
23
7
Практическая работа 6
по теме «Вычисление производных сложных функций. Дифференцирование сложной функции.»
26
8
Практическая работа 7
по теме «Решение заданий экономического смысла методом дифференциального исчисления»
30
9
Практическая работа 8
по теме «Вычисление неопределенных интегралов методом замены переменной и по частям»
37
10
Практическая работа 9
по теме «Вычисление определенного интеграла методом замены переменной и интегрированием по частям»
40
11
Практическая работа 10
по теме «Решение заданий экономического смысла методом интегрального исчисления»
44
13
Практическая работа 11
по теме «Действия над комплексными числами»
49
15
Практическая работа 12
по теме «Выполнение операций над множествами»
56
16
Практическая работа 13
по теме «Нахождение вероятности при повторении испытаний»
60
практ.
зан.
Номер и тема практической работы
с
17
Практическая работа 14
по теме «Составление и анализ случайных величин»
68
18,19
Практические работы 15,16
по теме «Составление и анализ случайных величин. Нахождение числовых характеристик.»
74
20
Практическая работа 17
по теме «Решение задач математической статистики»
78
Литература
81
Практическое занятие 1
Практическая работа 1
по теме «Действия над матрицами»
Цель работы: сформировать необходимые умения и навыки по выполнению элементарных операций на матричном множестве.
Актуализация знаний
Фронтальный опрос
1. Матрицы, виды матриц.
2. Действия над матрицами.
Краткие теоретические и учебно-методические материалы по теме практической работы
Матрицей называется множество чисел, которые образуют прямоугольную таблицу и содержат m строк и n столбцов
Действия над матрицами:
-умножение матрицы на число:
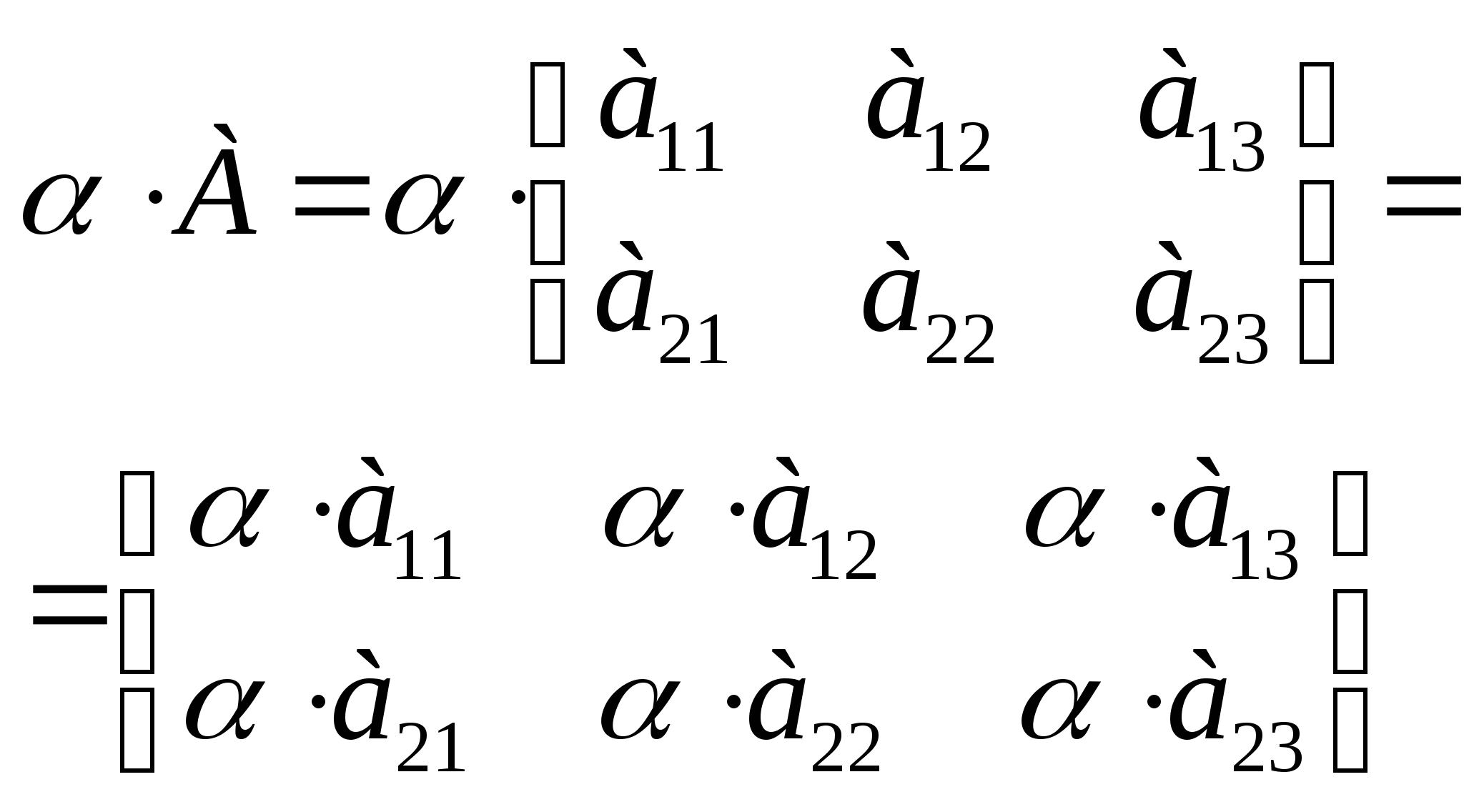
- сумма и разность матрицы
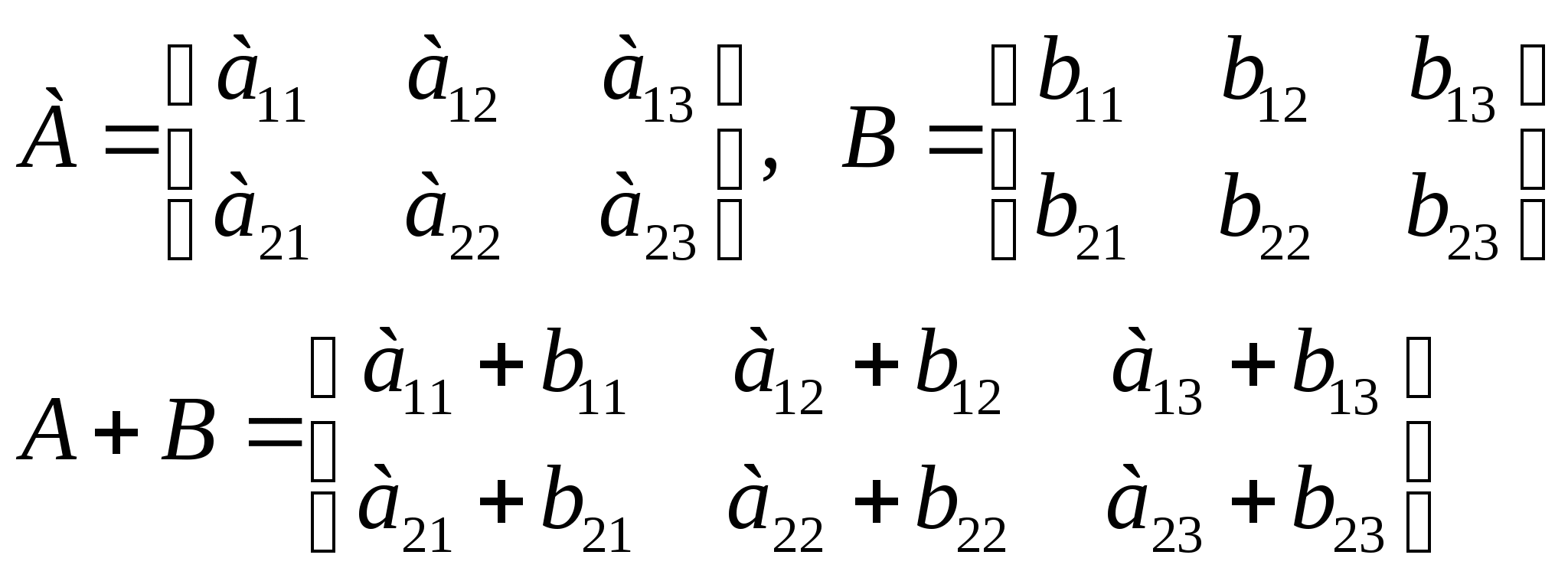
- транспонирование
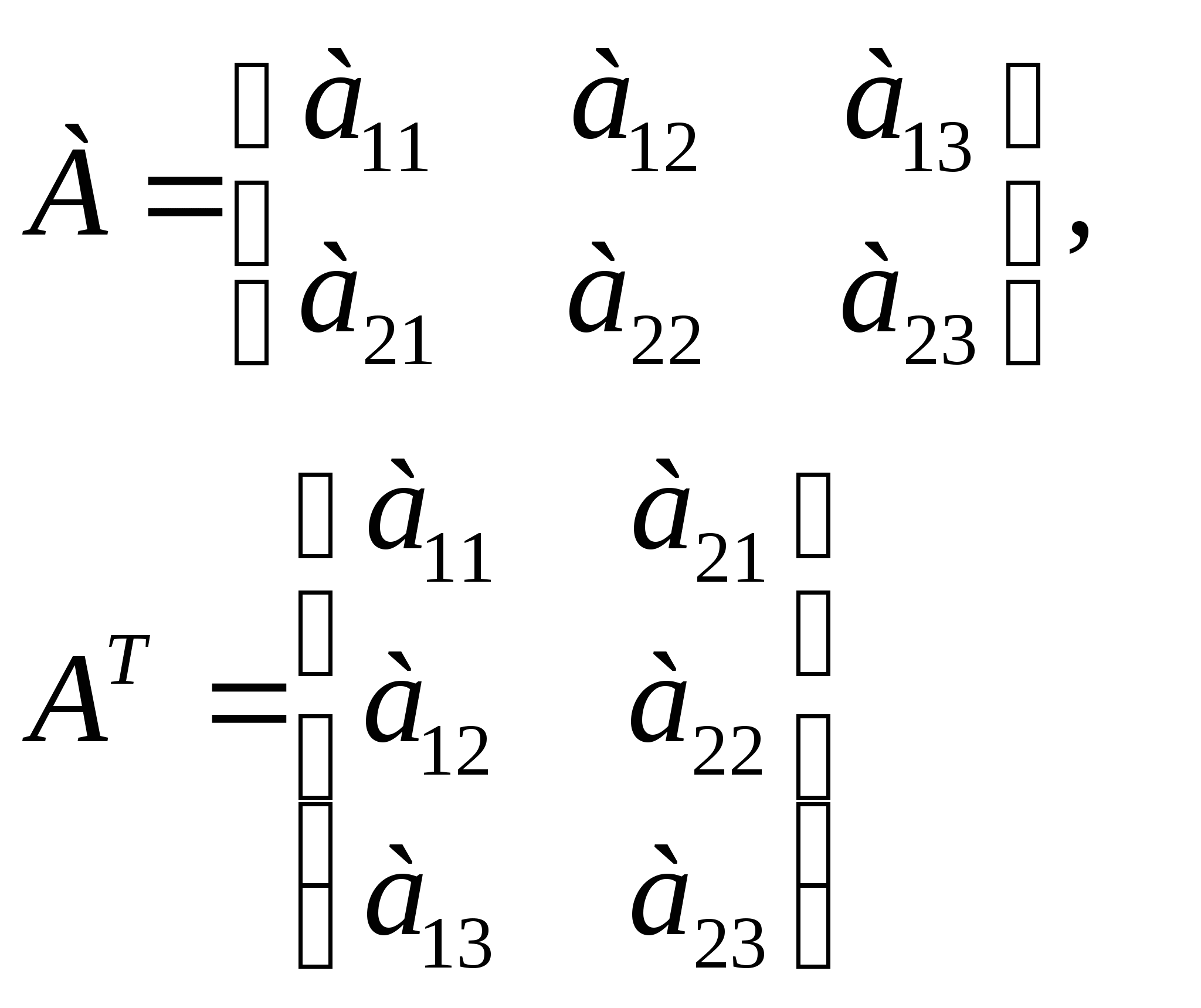
- умножение матриц
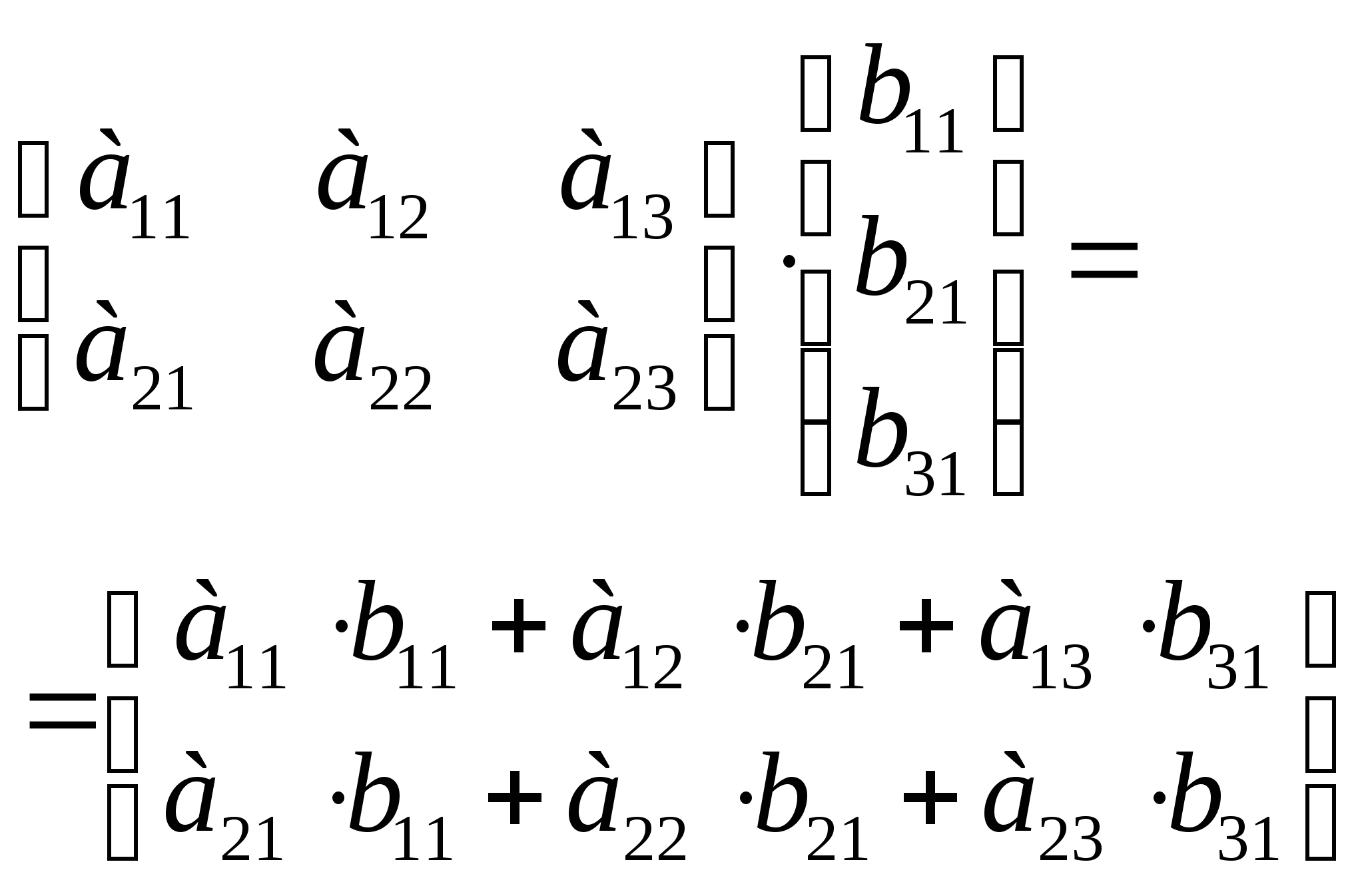
Формирование необходимых знаний и умений
Коллективное решение и обсуждение предложенных задач
Пример 1
Даны матрицы А и В. Найти матрицы А+В и 5А, если
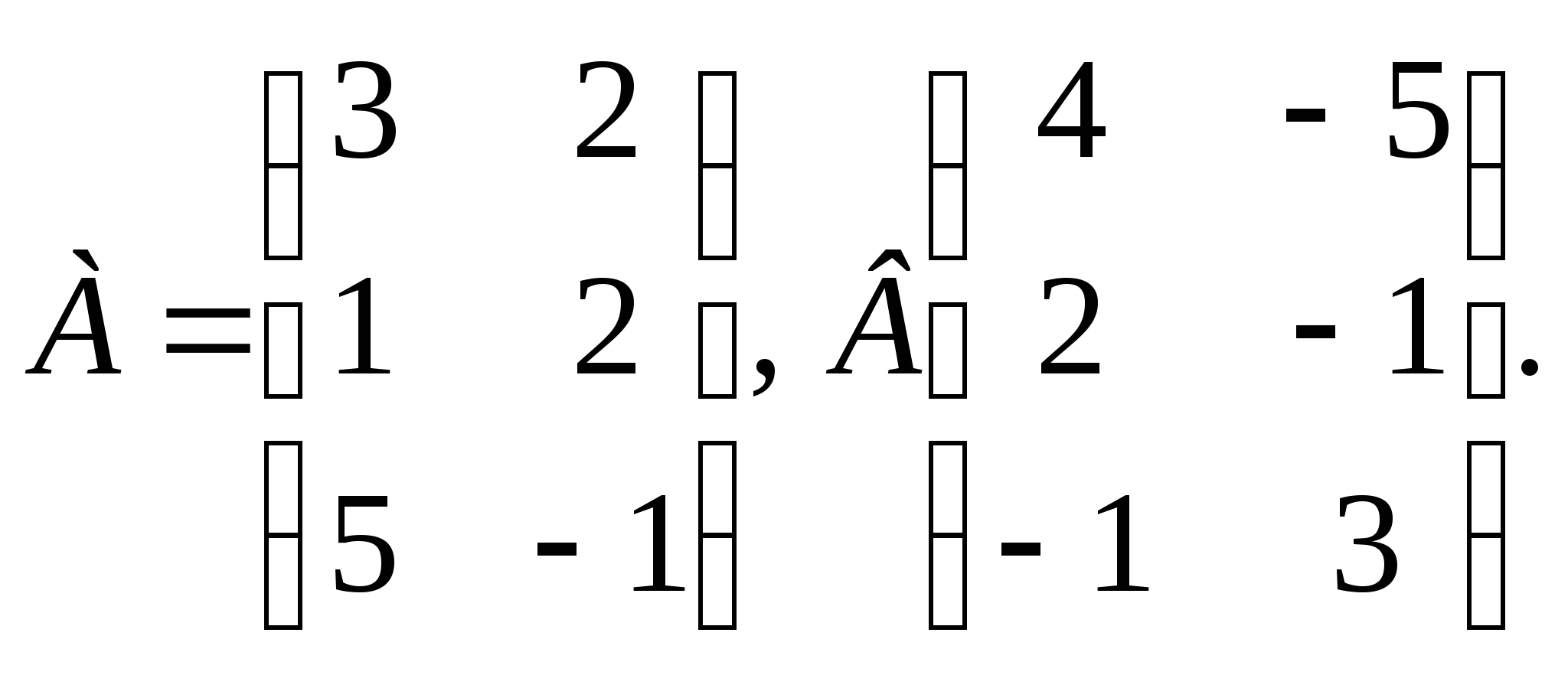
Решение:
По формуле получим:
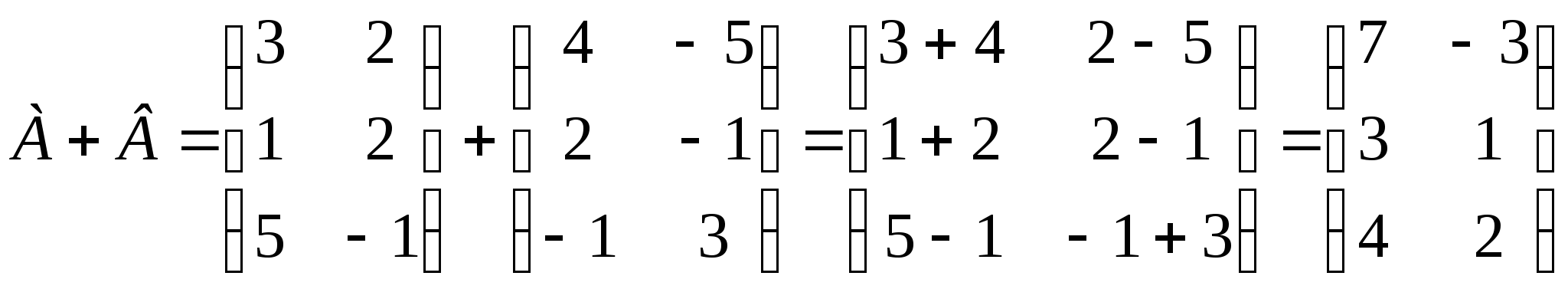
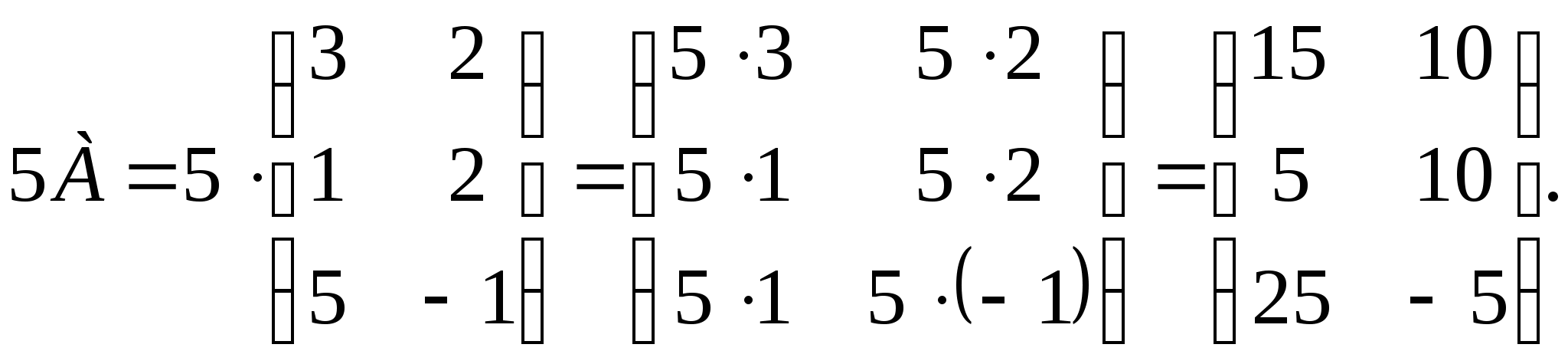
Пример 2
Вычислить произведение матриц А и В, если
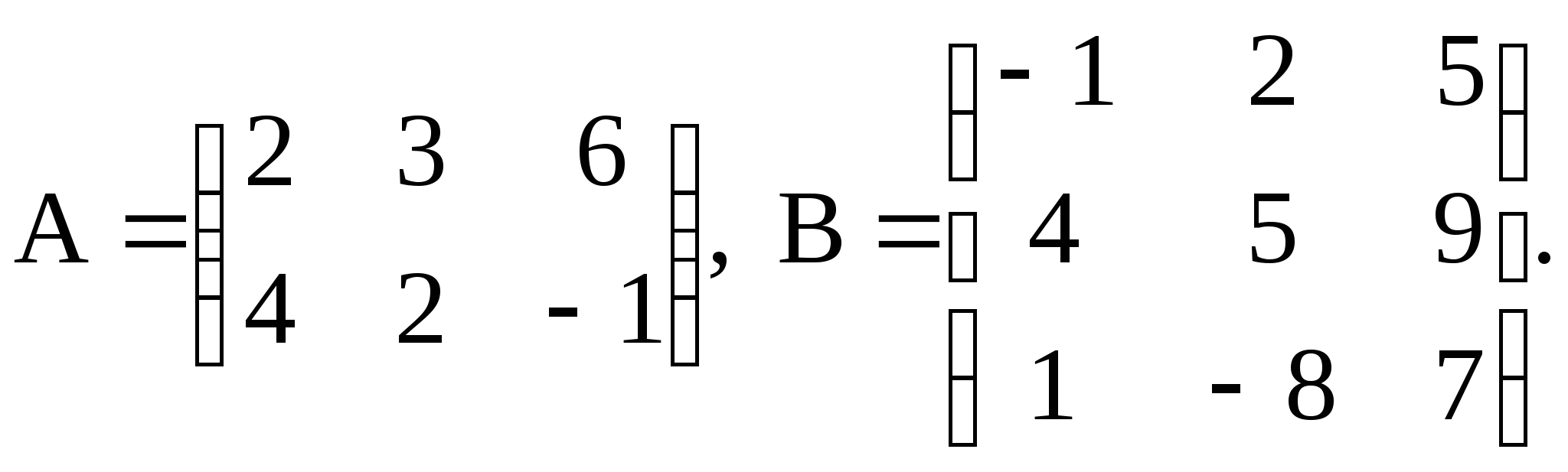
Решение:
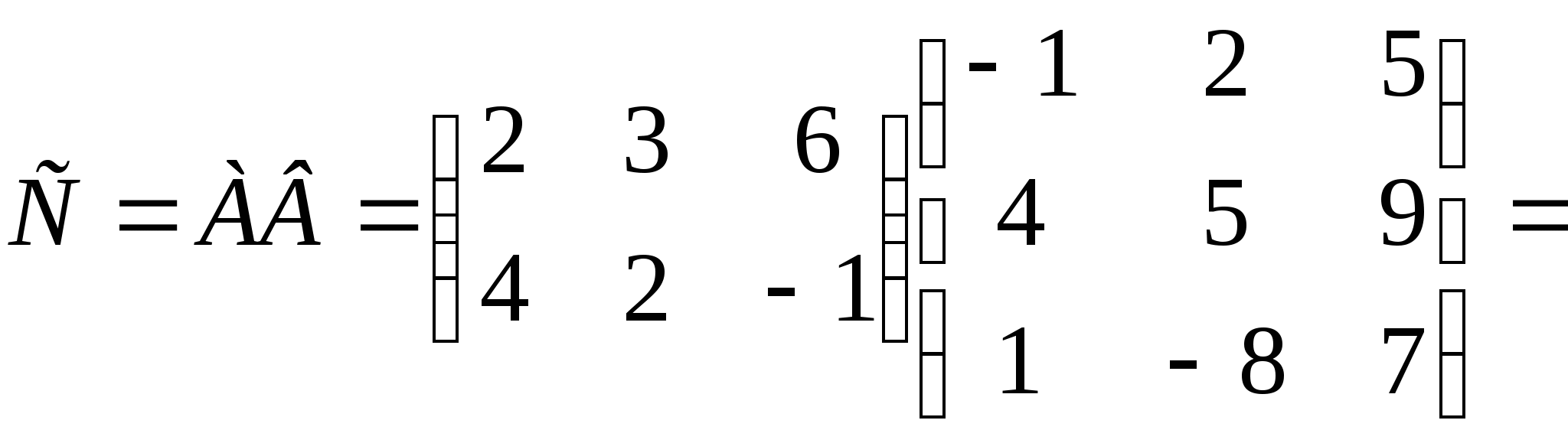
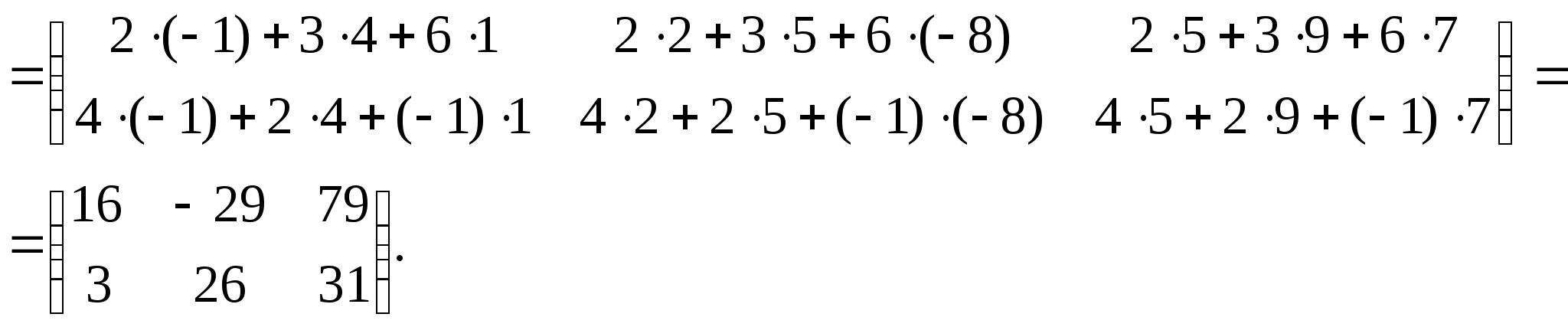
Пример 3
В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины М1, М2 и М3, причем доставка единицы продукции с каждого молокозавода в магазин М1 стоит 50 ден. ед., в магазин М2 - 70, а в М3 - 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.
Магазин
М1
М2
М3
1
20
35
10
2
15
27
8
Решение. Обозначим через А матрицу,
данную нам в условии, а через
В - матрицу, характеризующую стоимость доставки единицы продукции в
магазины, т.е.,
А =![]() ,
В = (50, 70, 130).
,
В = (50, 70, 130).
Тогда матрица затрат на перевозки будет иметь вид:
АВT = ![]()
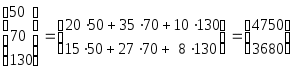 .
.
Итак, первый завод ежедневно тратит на перевозки 4750 ден. ед., второй - 3680 ден.ед.
Пример 4
Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется вектором X = (10, 15, 23). Используются ткани четырех типов Т1, Т2, Т3, Т4. В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Вектор С = (40, 35, 24, 16) задает стоимость метра ткани каждого типа, а вектор P = (5, 3, 2, 2) - стоимость перевозки метра ткани каждого вида.
Расход ткани
Т1
Т2
Т3
Т4
Зимнее пальто
5
1
0
3
Демисезонное пальто
3
2
0
2
Плащ
0
0
4
3
1. Сколько метров ткани каждого типа потребуется для выполнения плана ?
2. Найти стоимость ткани, расходуемой на пошив изделия каждого вида.
3. Определить стоимость всей ткани, необходимой для выполнения плана.
4. Подсчитать стоимость всей ткани с учетом ее транспортировки.
Решение. Обозначим через А матрицу, данную нам в условии, т. е.,
A = 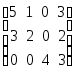 ,
,
тогда для нахождения количества метров ткани, необходимой для выполнения плана, нужно вектор X умножить на матрицу А:
X А = (10,15, 23) 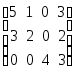 =
= ![]() =
=
= (95, 40, 92, 129).
Стоимость ткани, расходуемой на пошив изделия каждого вида, найдем, перемножив матрицу А и вектор CT:
А CT = 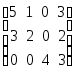
![]() =
=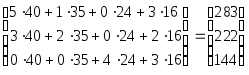 .
.
Стоимость всей ткани, необходимой для выполнения плана, определится по формуле:
X А C T =
(10,15,23)![]() =
=![]() .
.
Наконец, с учетом транспортных расходов вся сумма будет равна стоимости ткани, т. е. 9472 ден. ед., плюс величина
X А P T = (95, 40, 92,
129)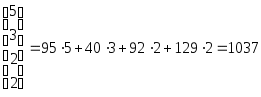 .
.
Итак, X А C T + X А P T = 9472 + 1037 = 10509 (ден. ед).
Примеры
Известны матрицы А = 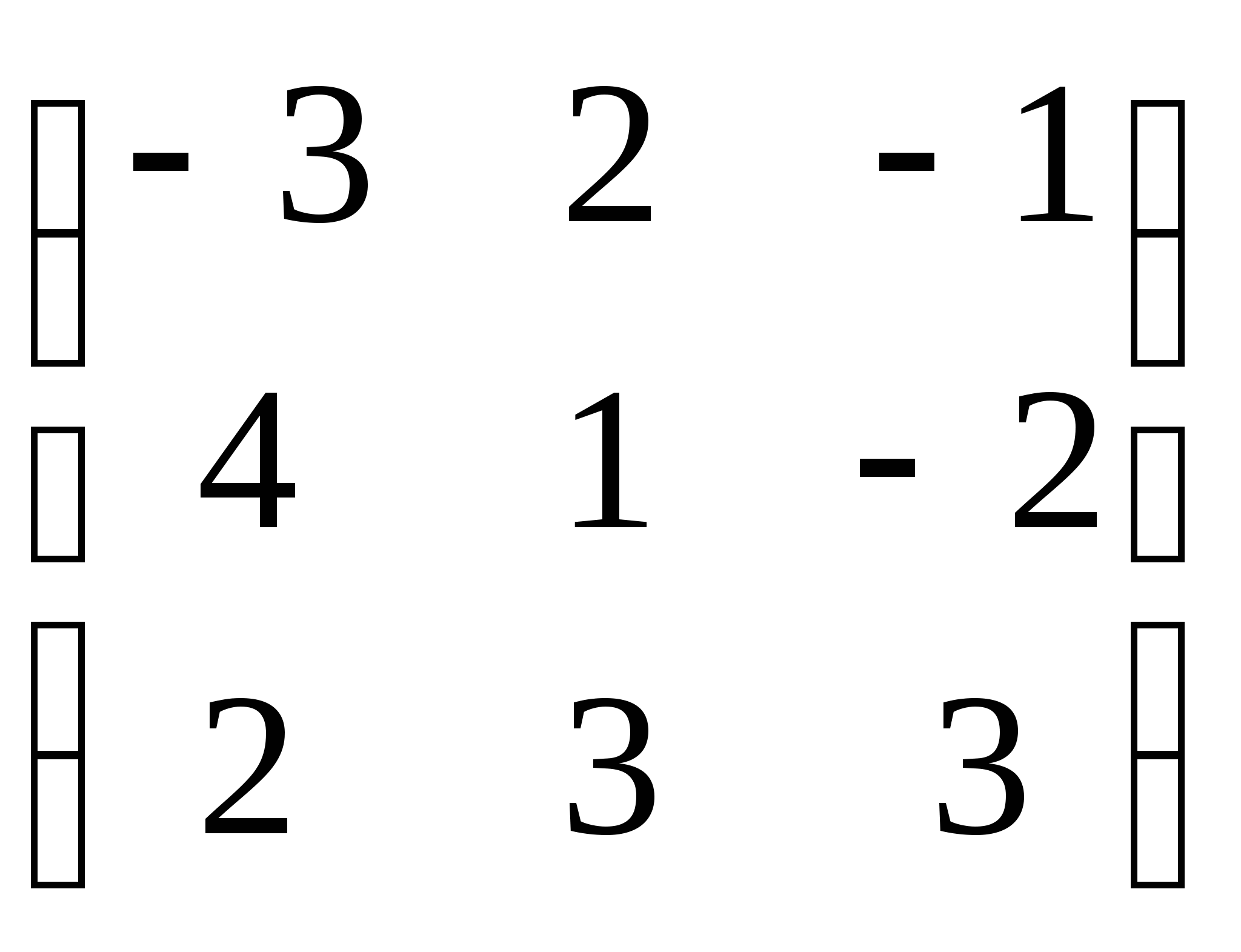 и В =
и В = 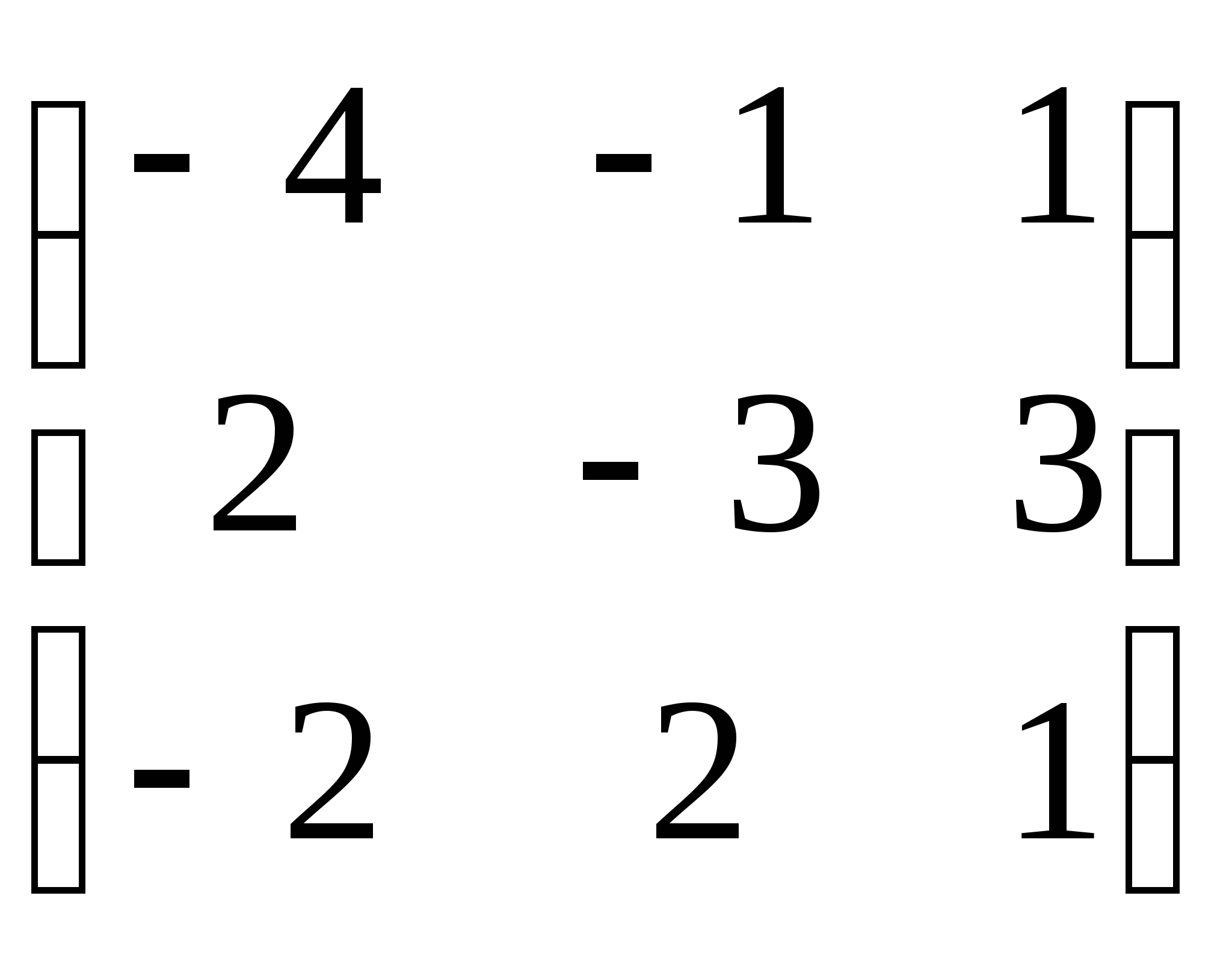 . Найти Ст , если "C" является результатом указанных
действий над матрицами А и В.
. Найти Ст , если "C" является результатом указанных
действий над матрицами А и В.
Закрепление сформированных знаний и учений:
Закрепление полученных знаний по данной теме проводится во время самостоятельного решения заданий
Известны матрицы А = 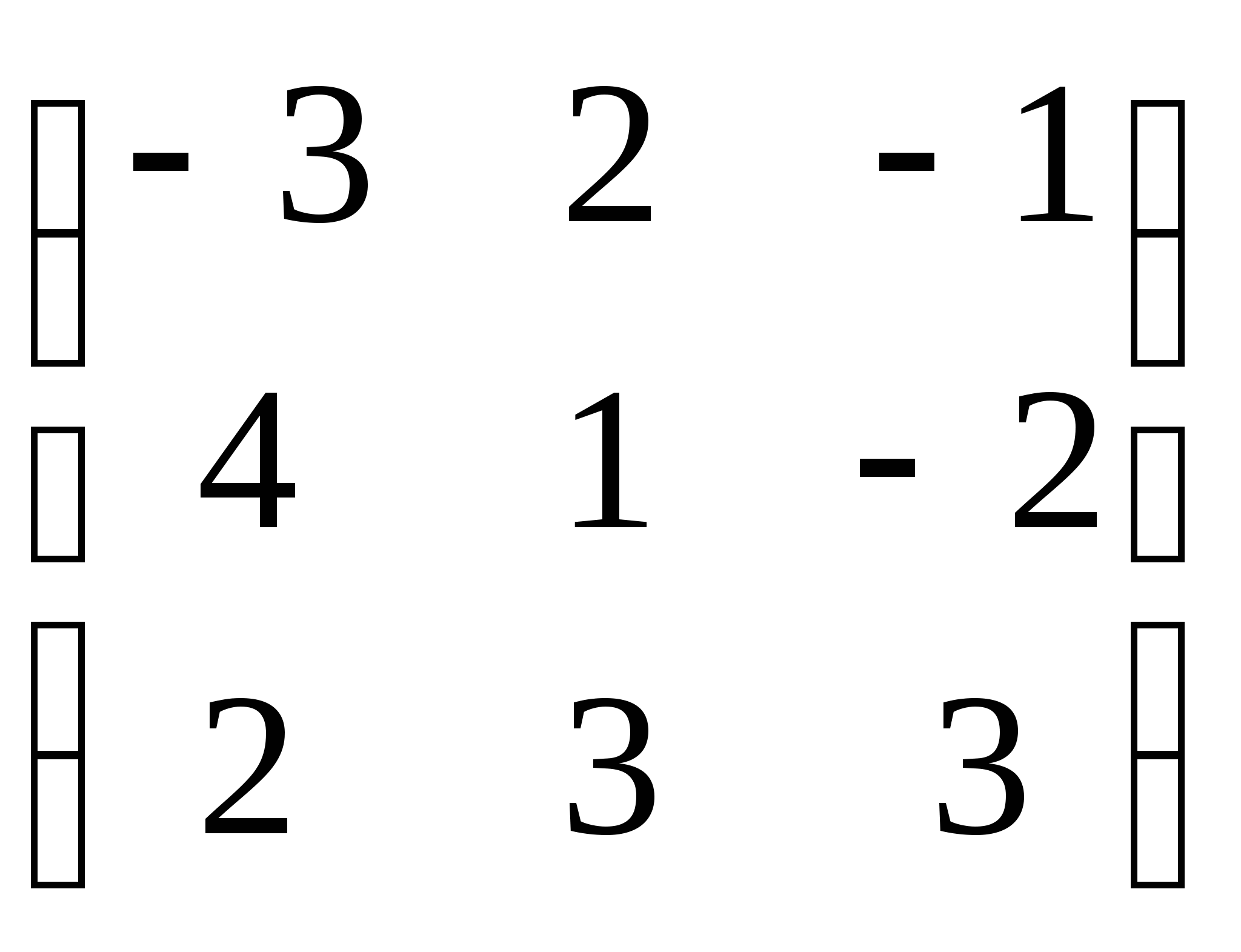 и В =
и В = 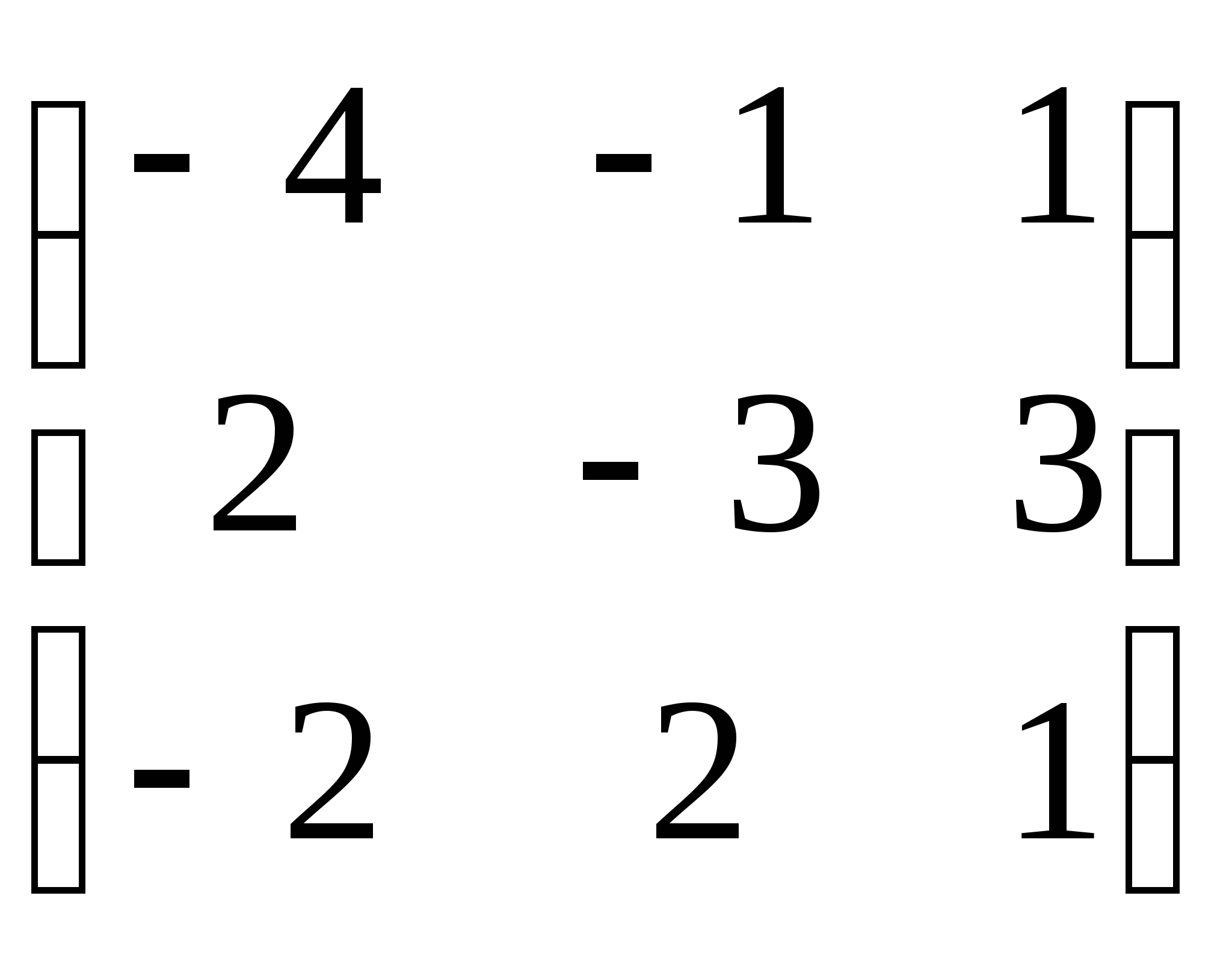 . Найти Ст , если "C" является результатом указанных
действий над матрицами А и В.
. Найти Ст , если "C" является результатом указанных
действий над матрицами А и В.
Задачи для домашнего решения
1.Найти матрицы: 1) 2А+5В; 2)3В-2А; 3) АТ-В; 4)
2АТ+5ВТ, если ![]()
2. Найти матрицы: 1) 3А+4В; 2)7В-2А; 3)
АТ-3В; 4) АТ+2ВТ, если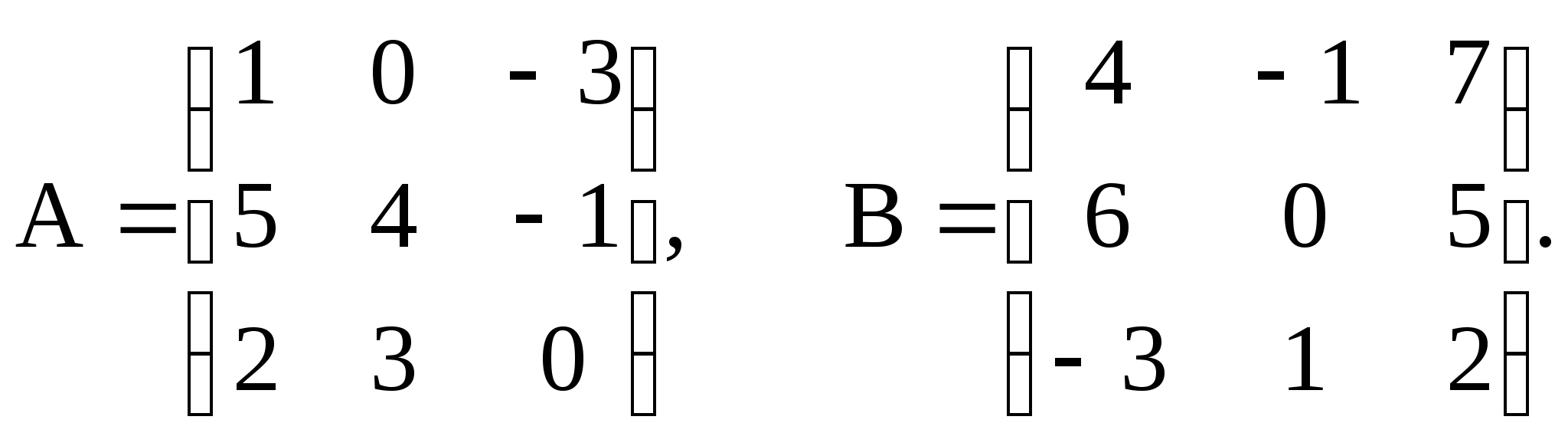
3. Найти произведение АВ и ВА матриц А и В, если
1) 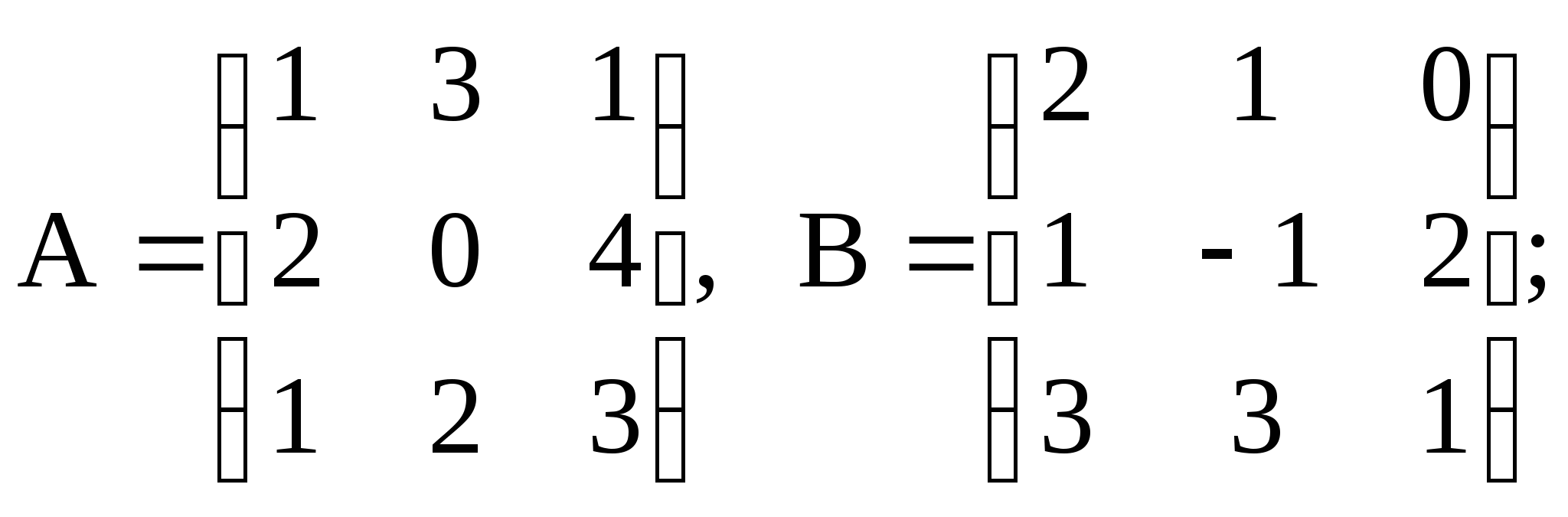 2)
2) 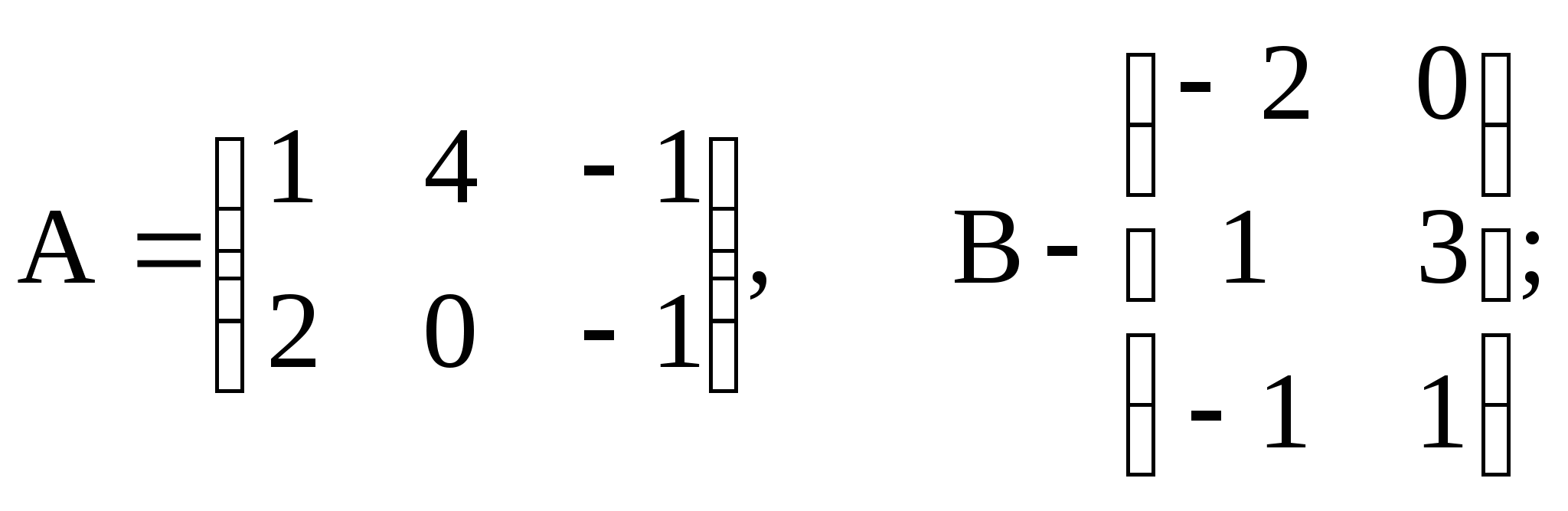
3) 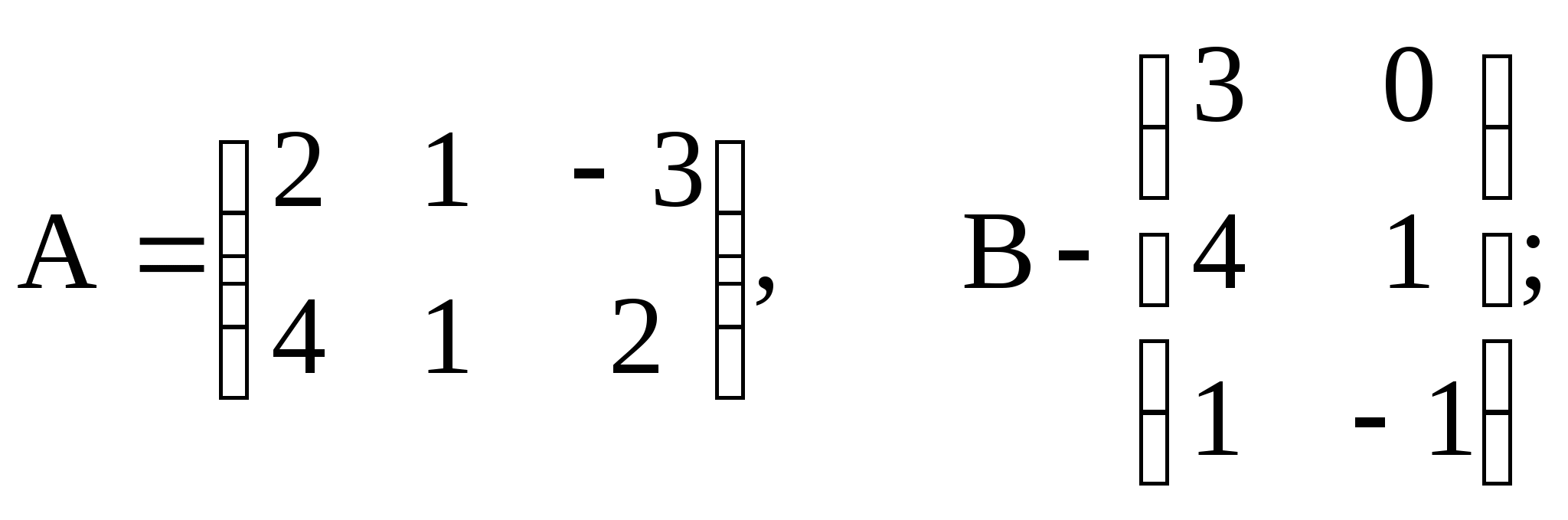 4)
4) 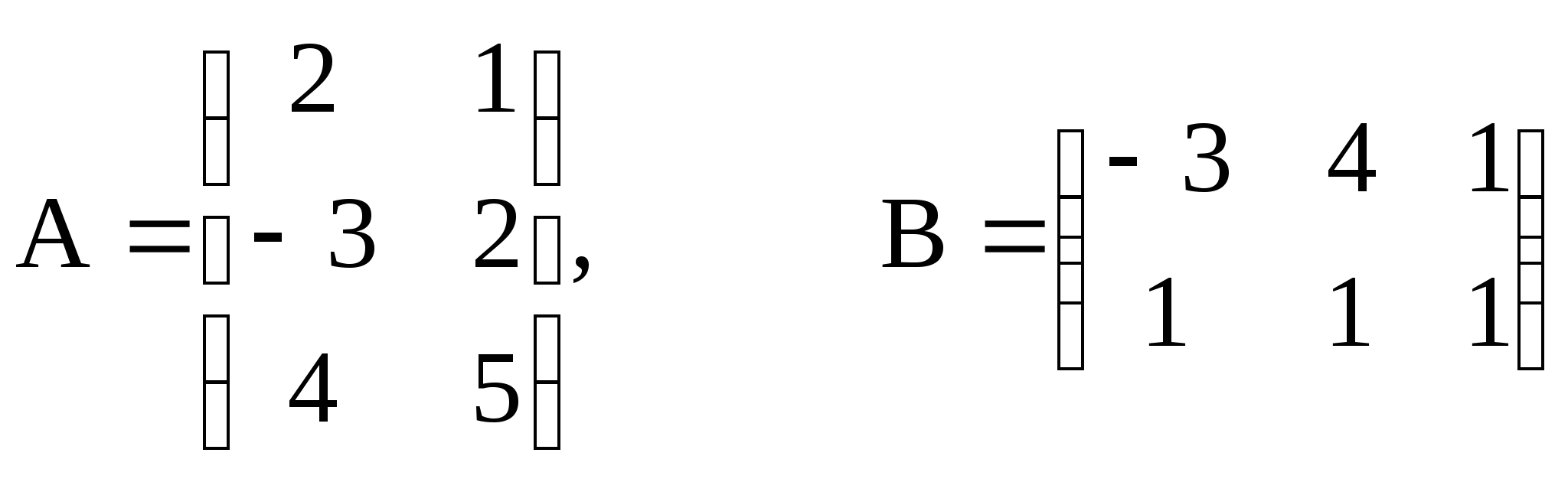
Практическое занятие 2
Практическая работа 2
по теме «Вычисление определителей второго и третьего порядка»
Цель работы: сформировать необходимые умения и навыки вычисления определителей второго и третьего порядков.
Актуализация знаний
Фронтальный опрос
1. Понятие определителя, его свойства.
2. Вычисление определителей второго порядка.
3. Вычисление определителей третьего порядка.
Краткие теоретические и учебно-методические материалы по теме практической работы
Определитель второго порядка равен разности произведений элементов главной и вспомогательной диагоналей:
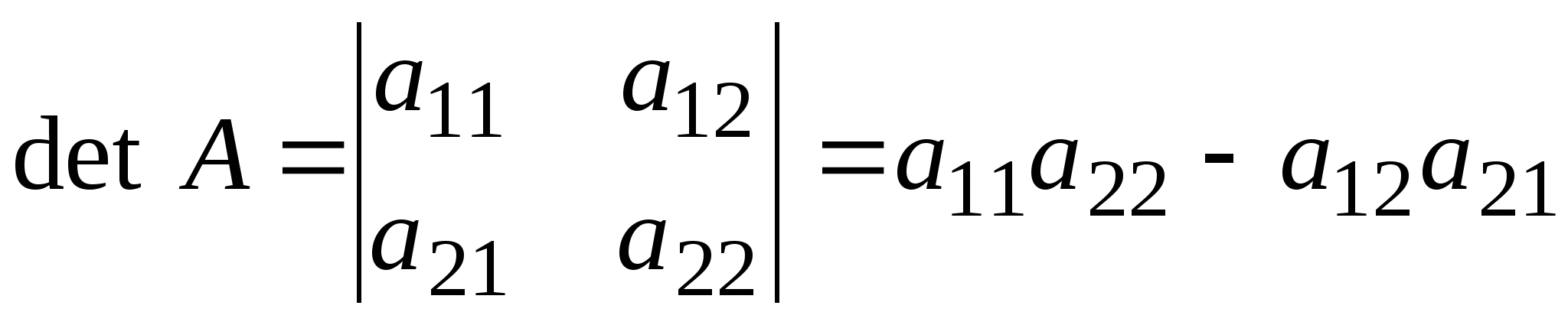
Определитель третьего порядка вычисляется по формуле:
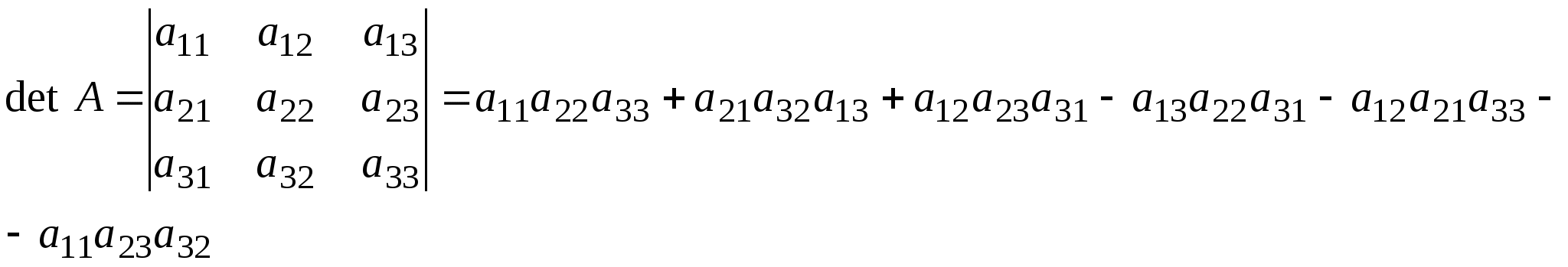 При вычислении определителей третьего порядка удобно пользоваться
правилом треугольников (правилом Сарруса)
При вычислении определителей третьего порядка удобно пользоваться
правилом треугольников (правилом Сарруса)
Формирование необходимых знаний и умений
Коллективное решение и обсуждение предложенных задач
Пример 1
Вычислить определитель:
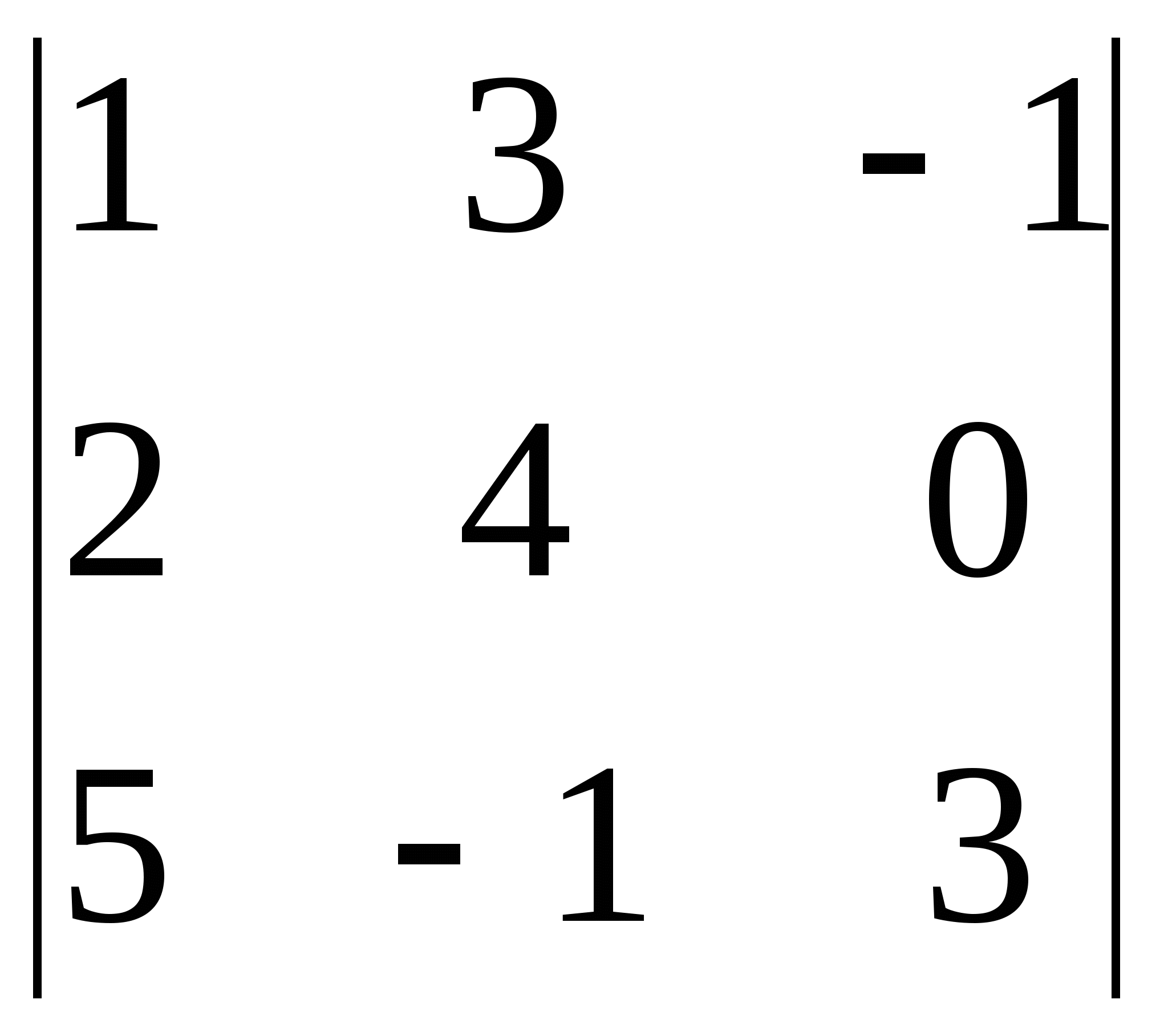 .
.
Решение:
Вычислим определитель по правилу треугольников:
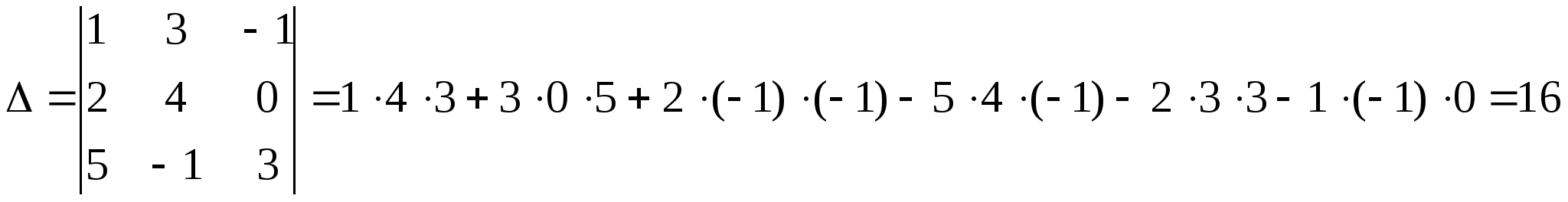
Примеры:
Вычислить определители::
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) 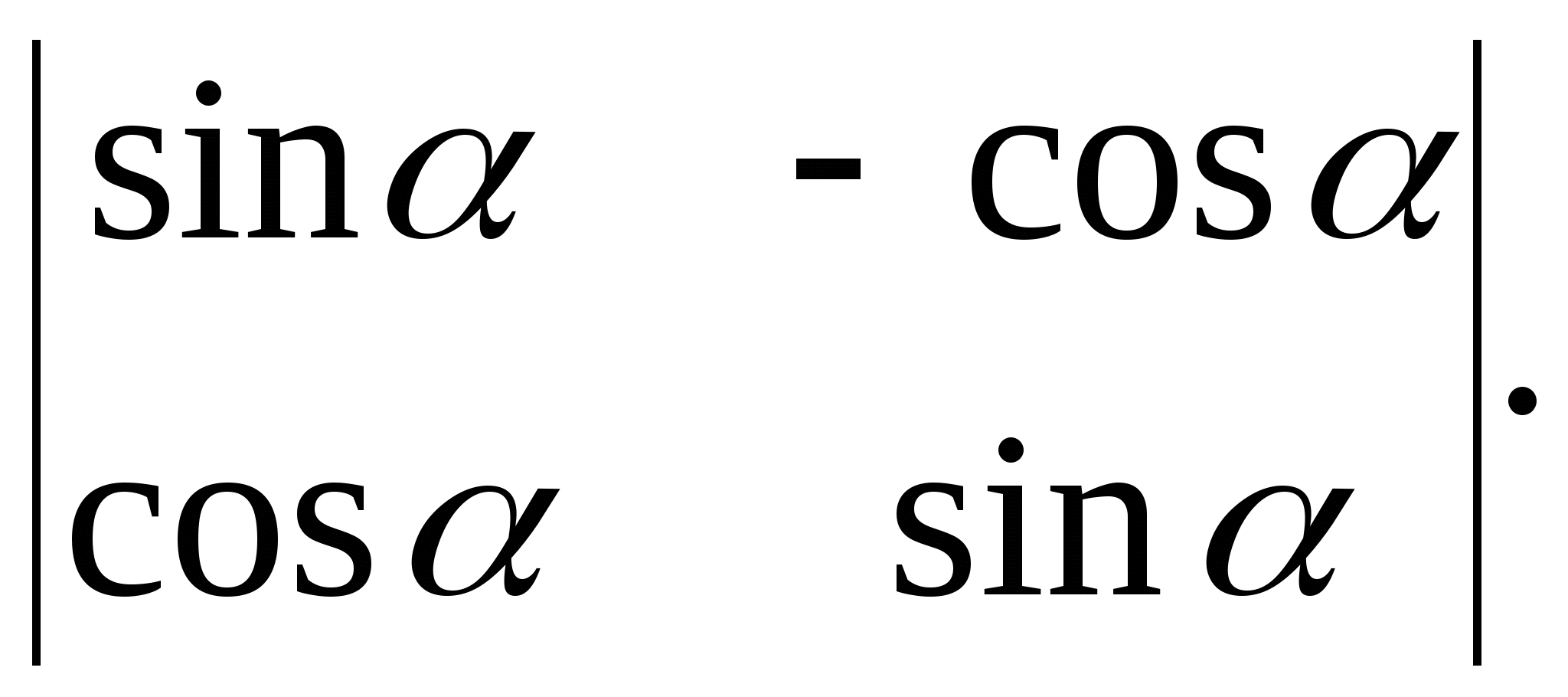
6)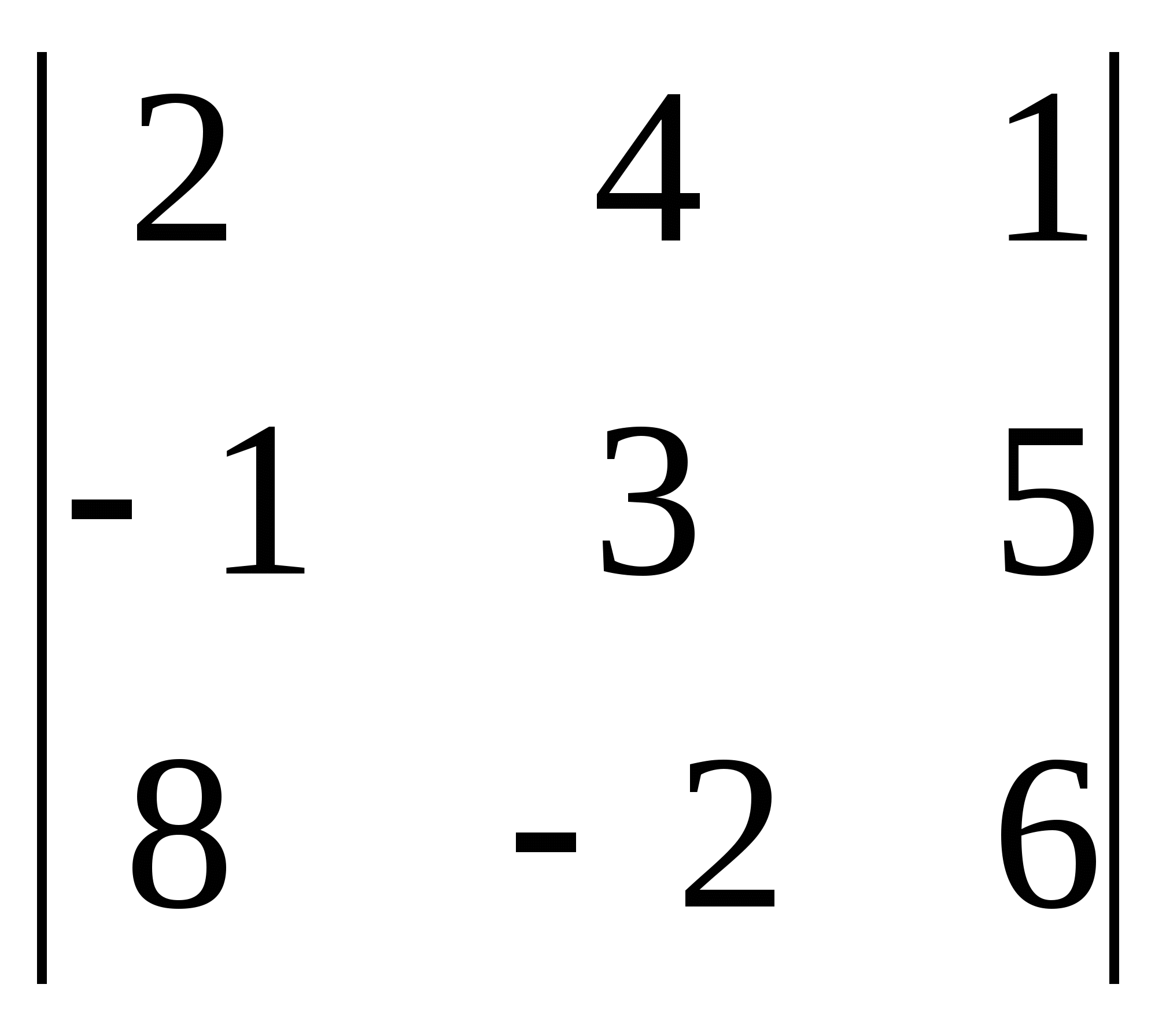 ; 7)
; 7) 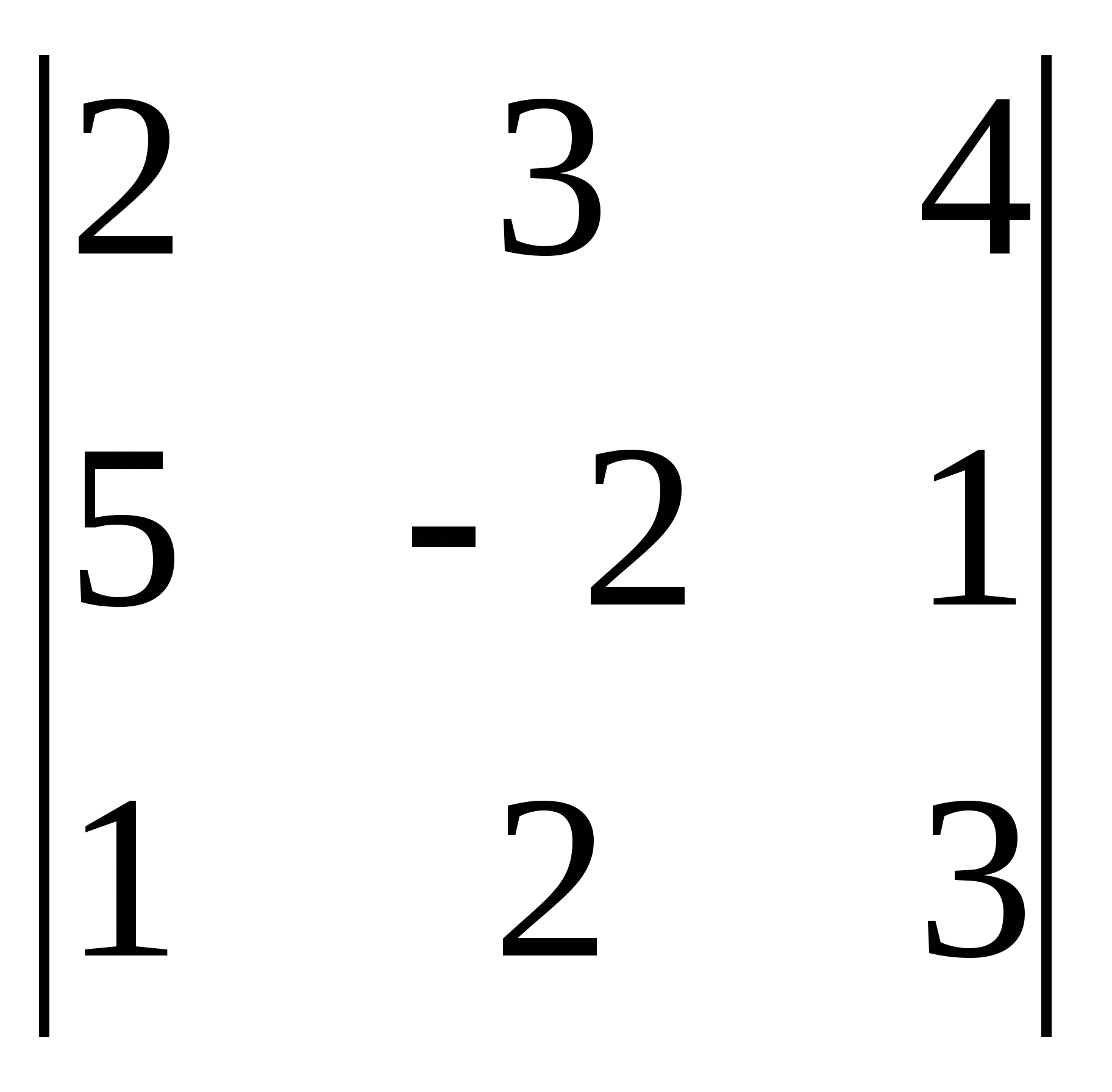 ; 8)
; 8) 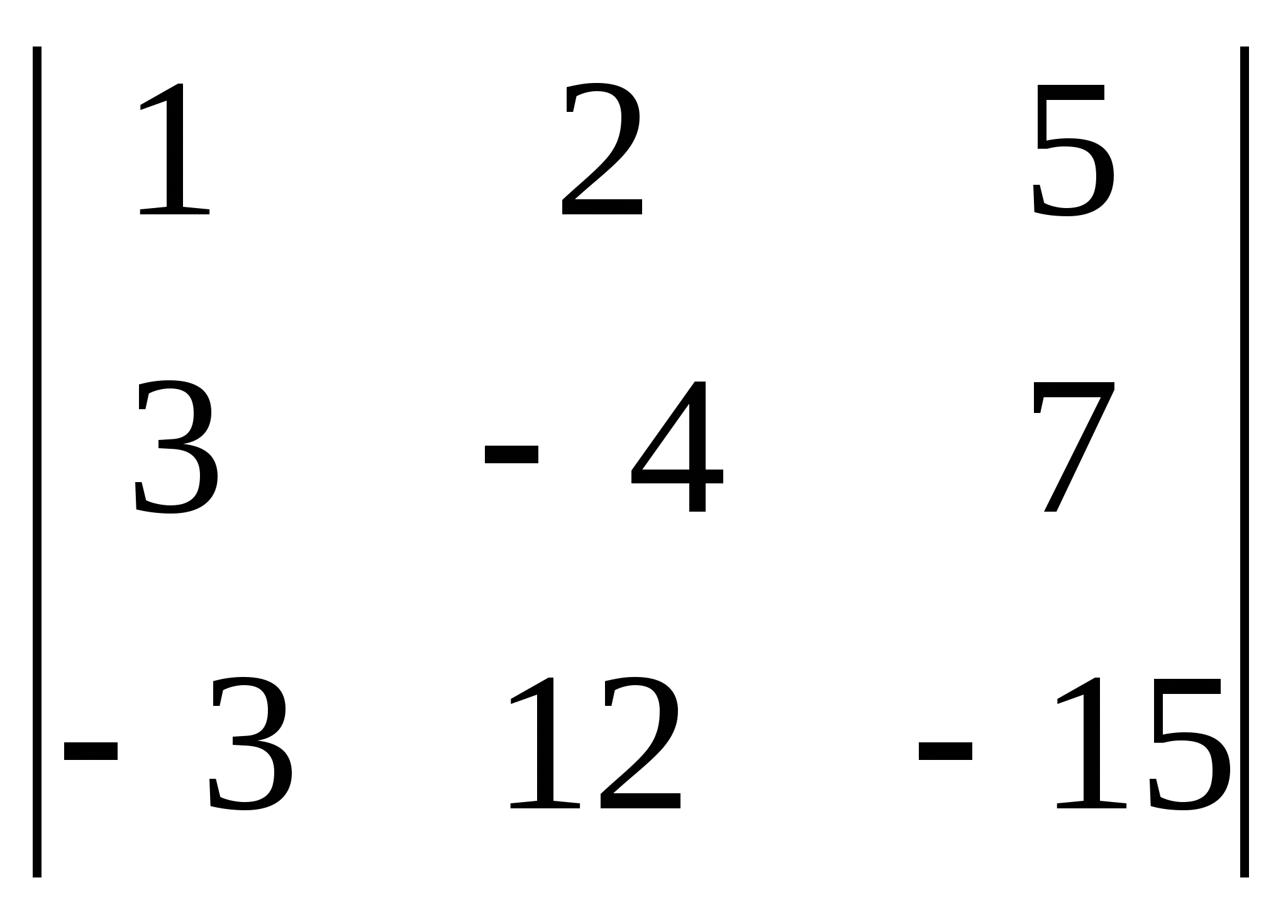 ; 9)
; 9) 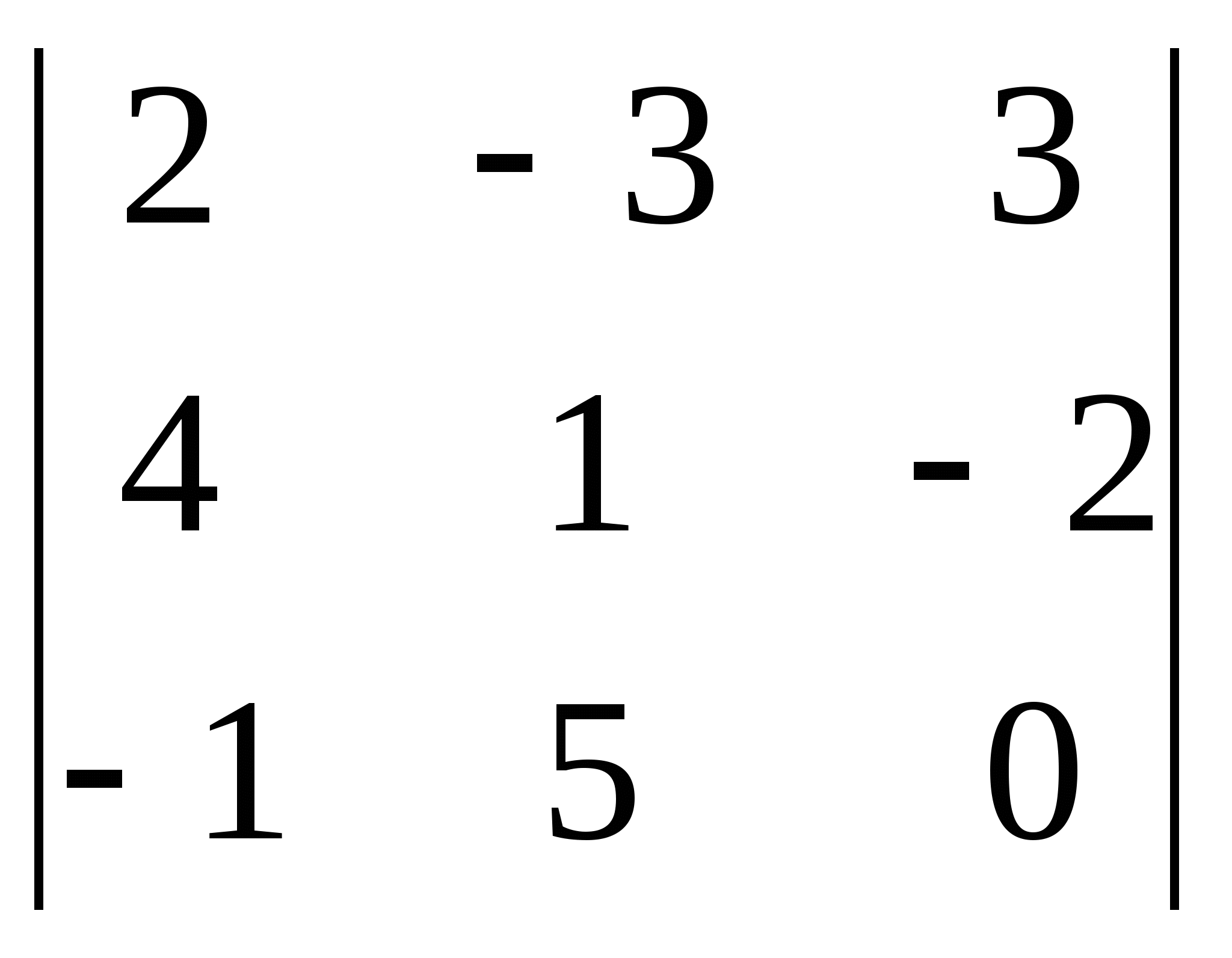 ;
;
10) 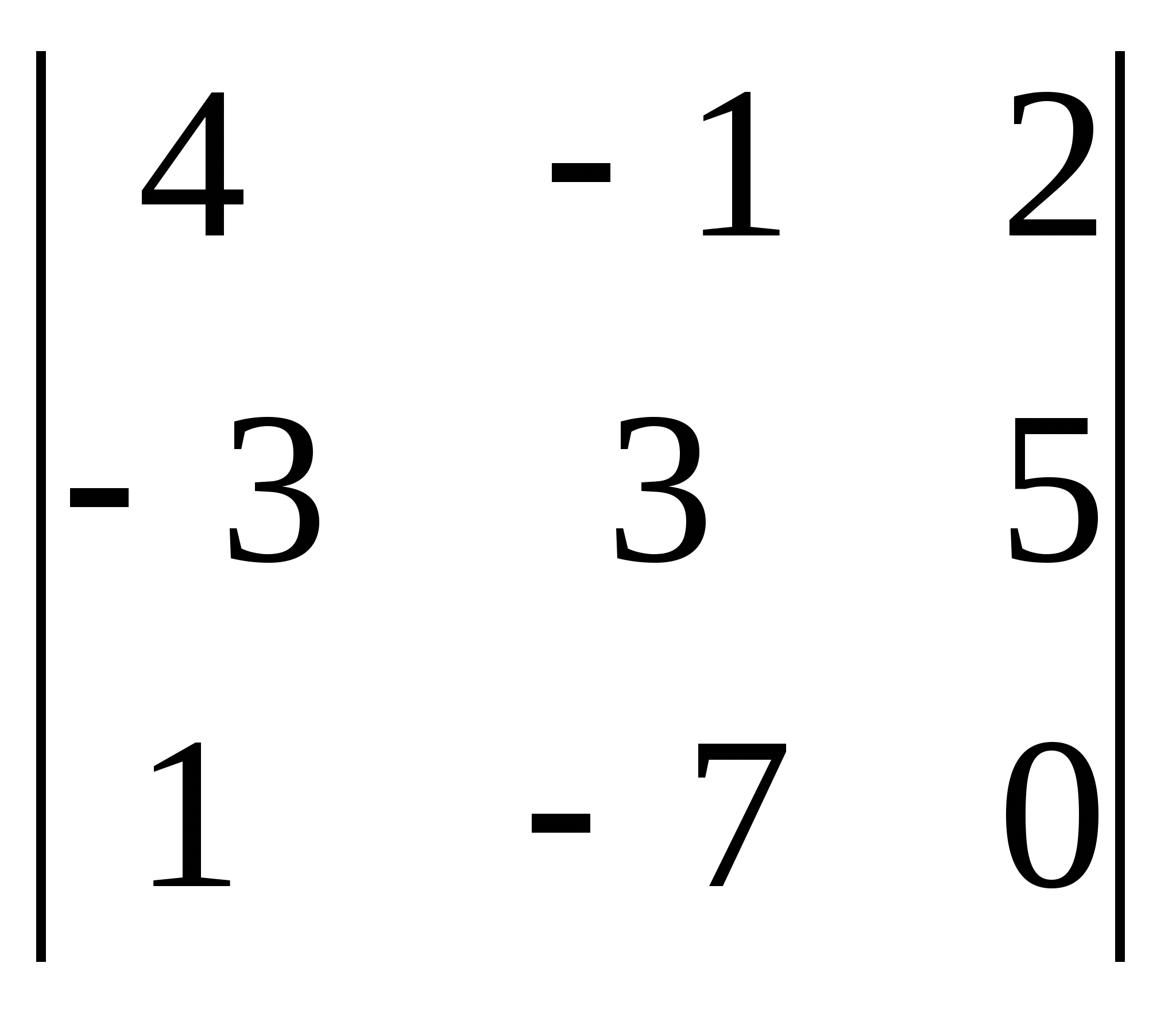 ; 11)
; 11) 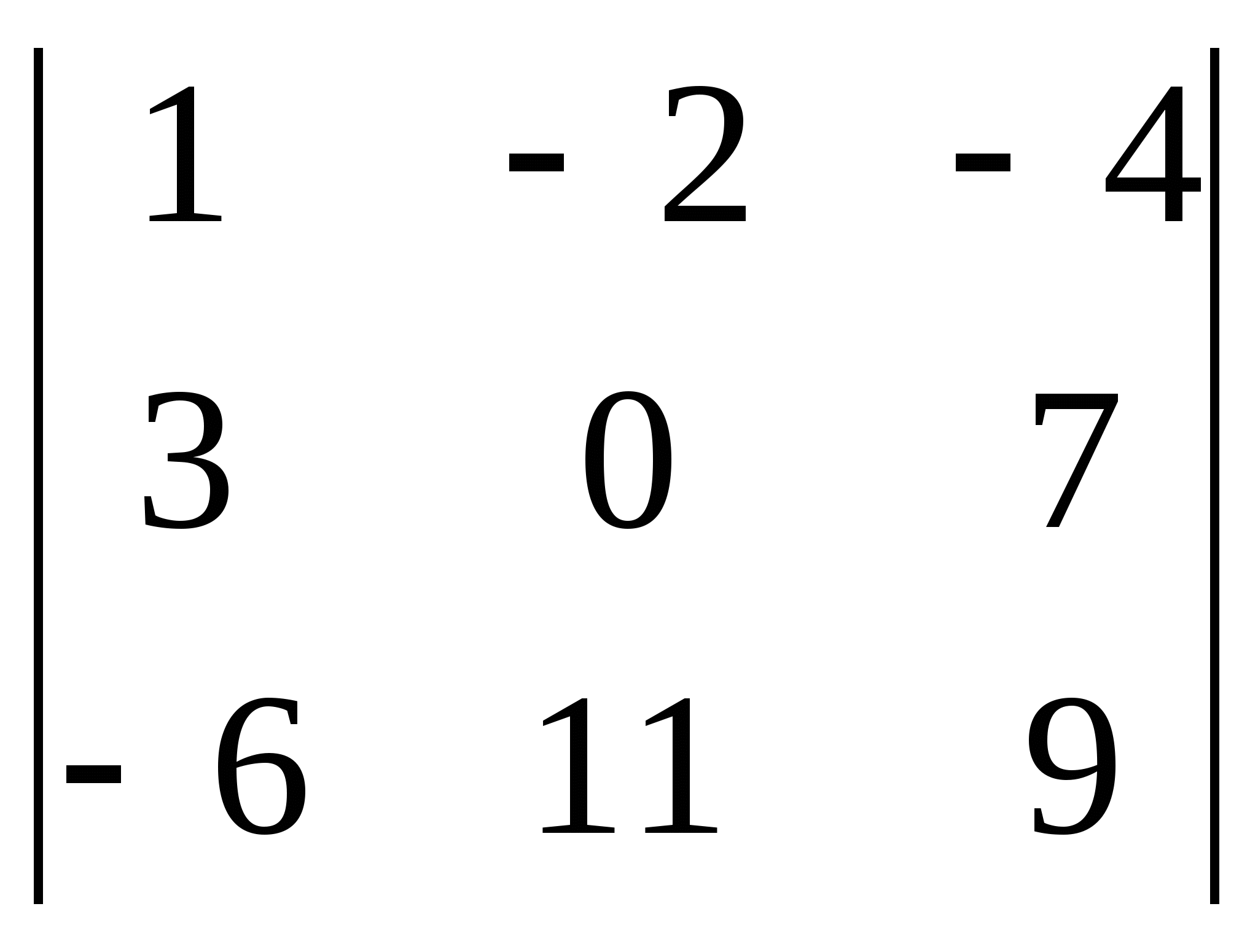 ; 12)
; 12) 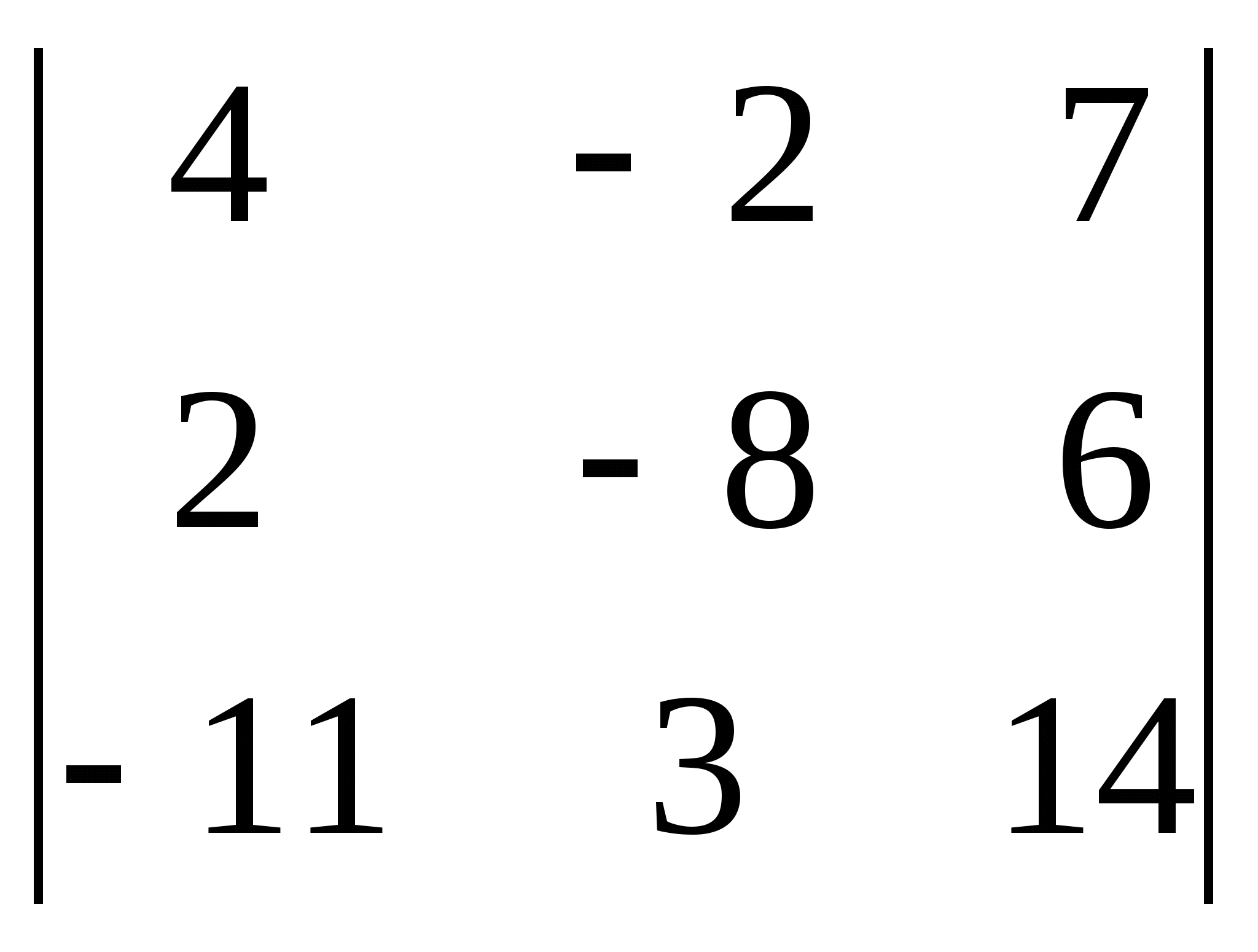 ; 13)
; 13) 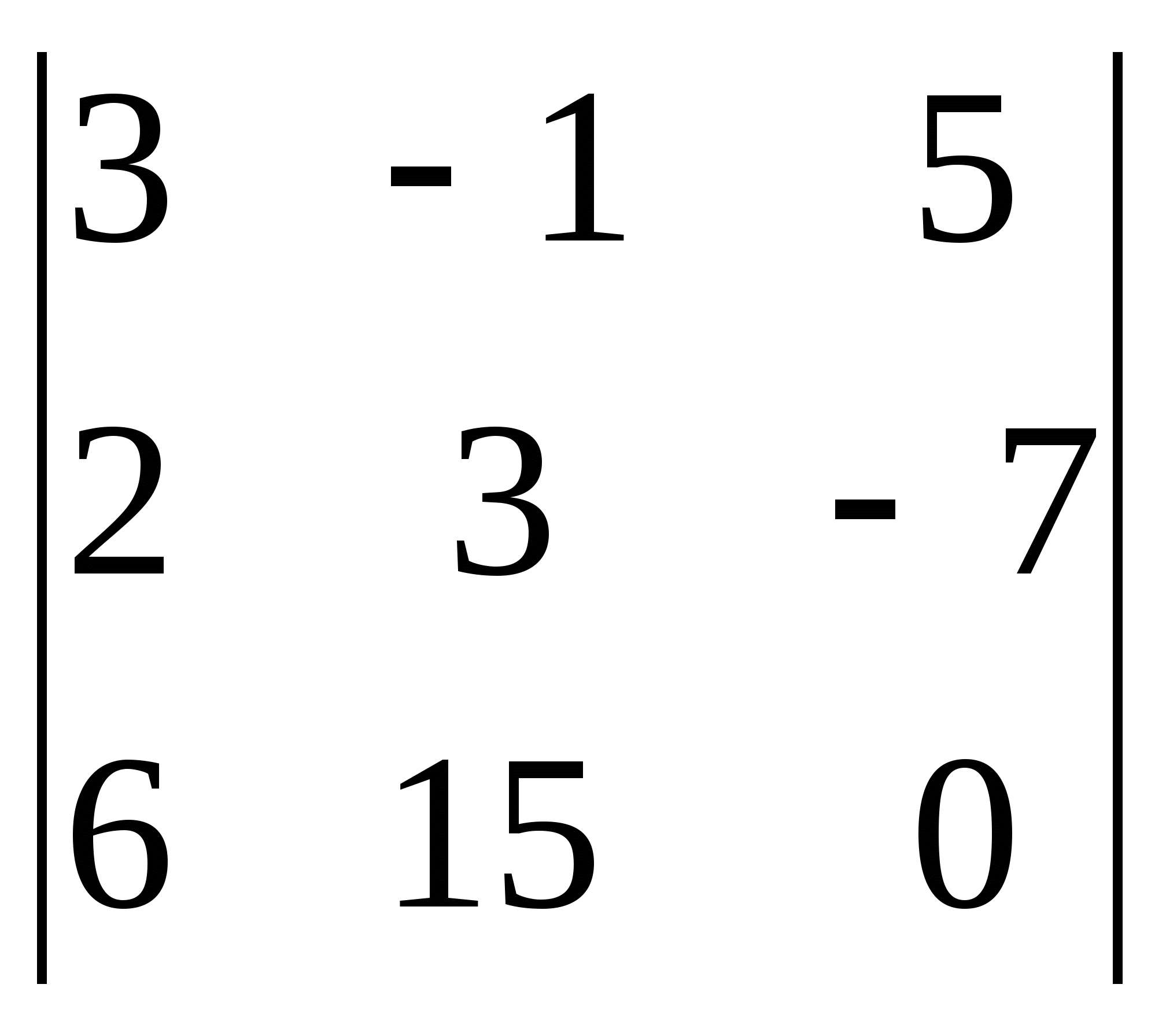 .
.
Закрепление сформированных знаний и учений:
Закрепление полученных знаний по данной теме проводится во время самостоятельного решения заданий
Вычислить определители:
1) 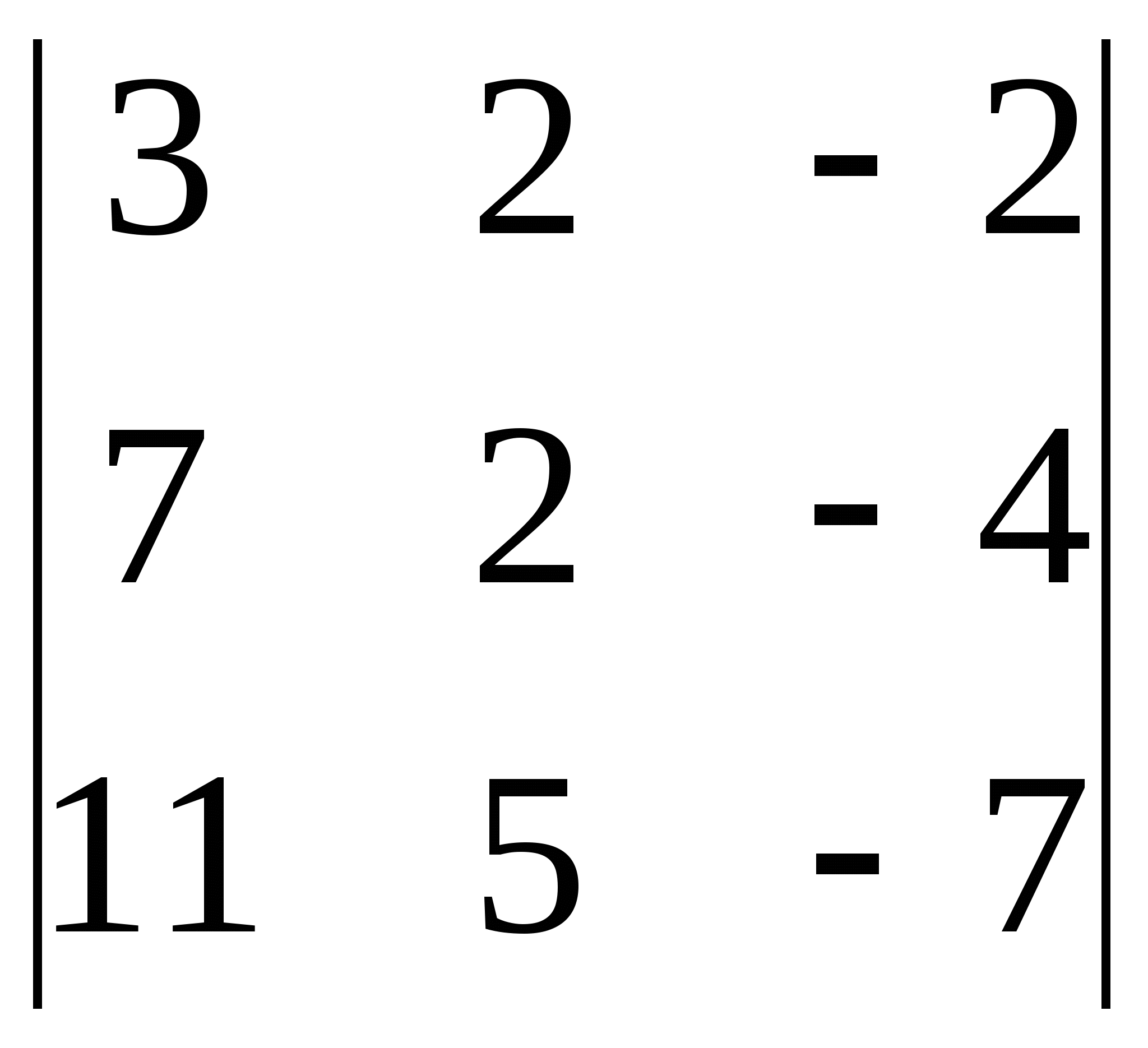 2)
2)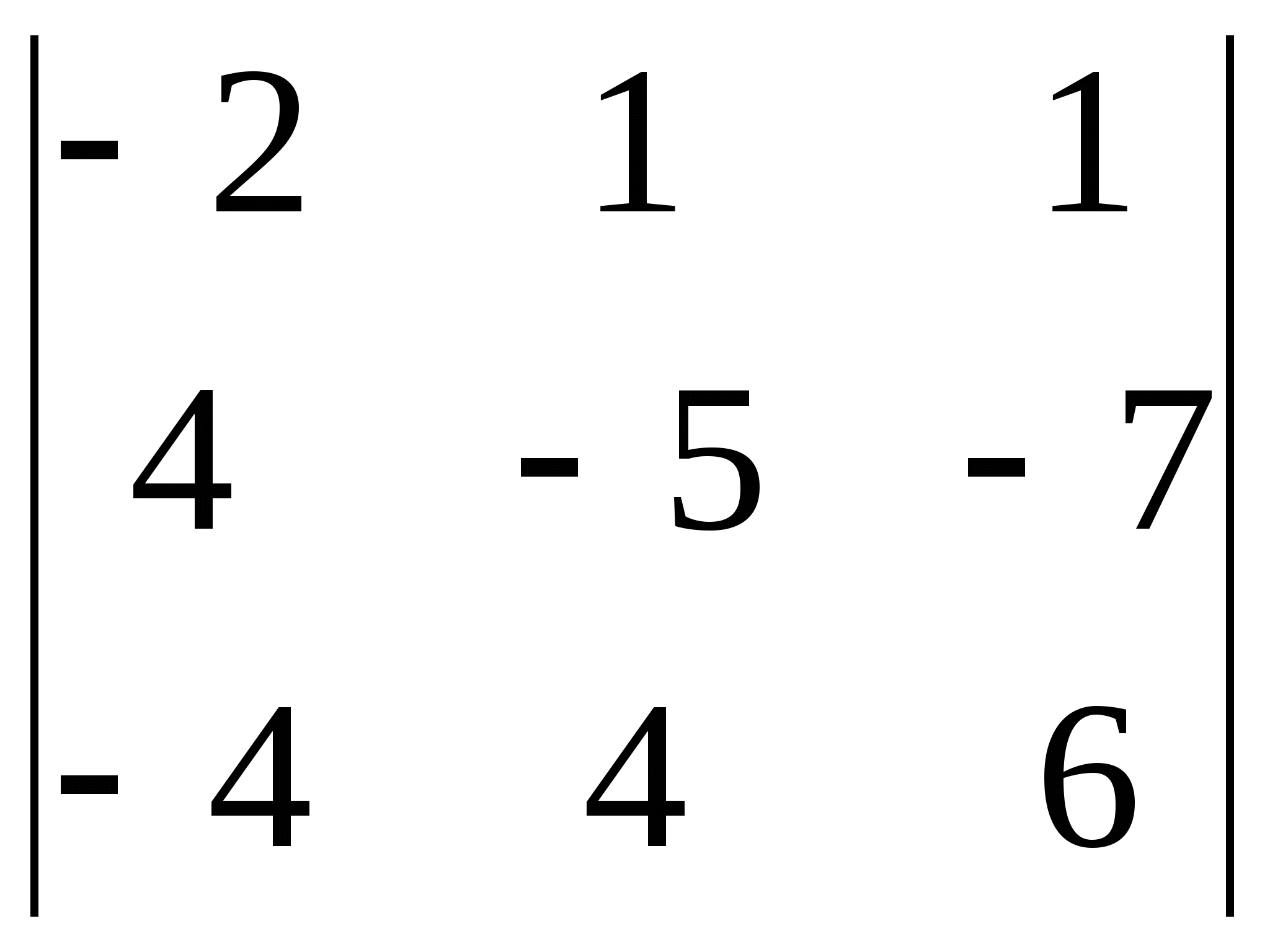
3) 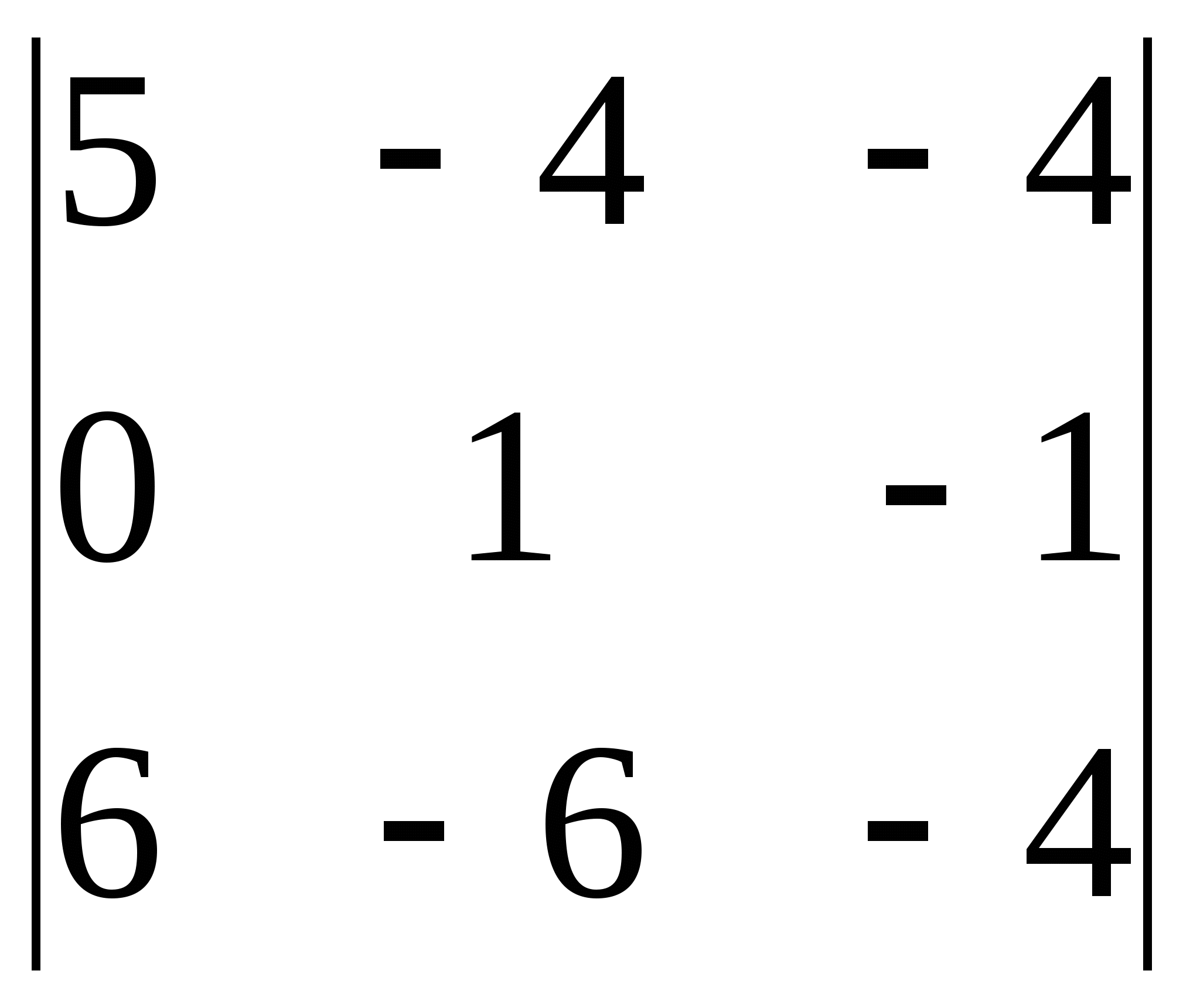 4)
4)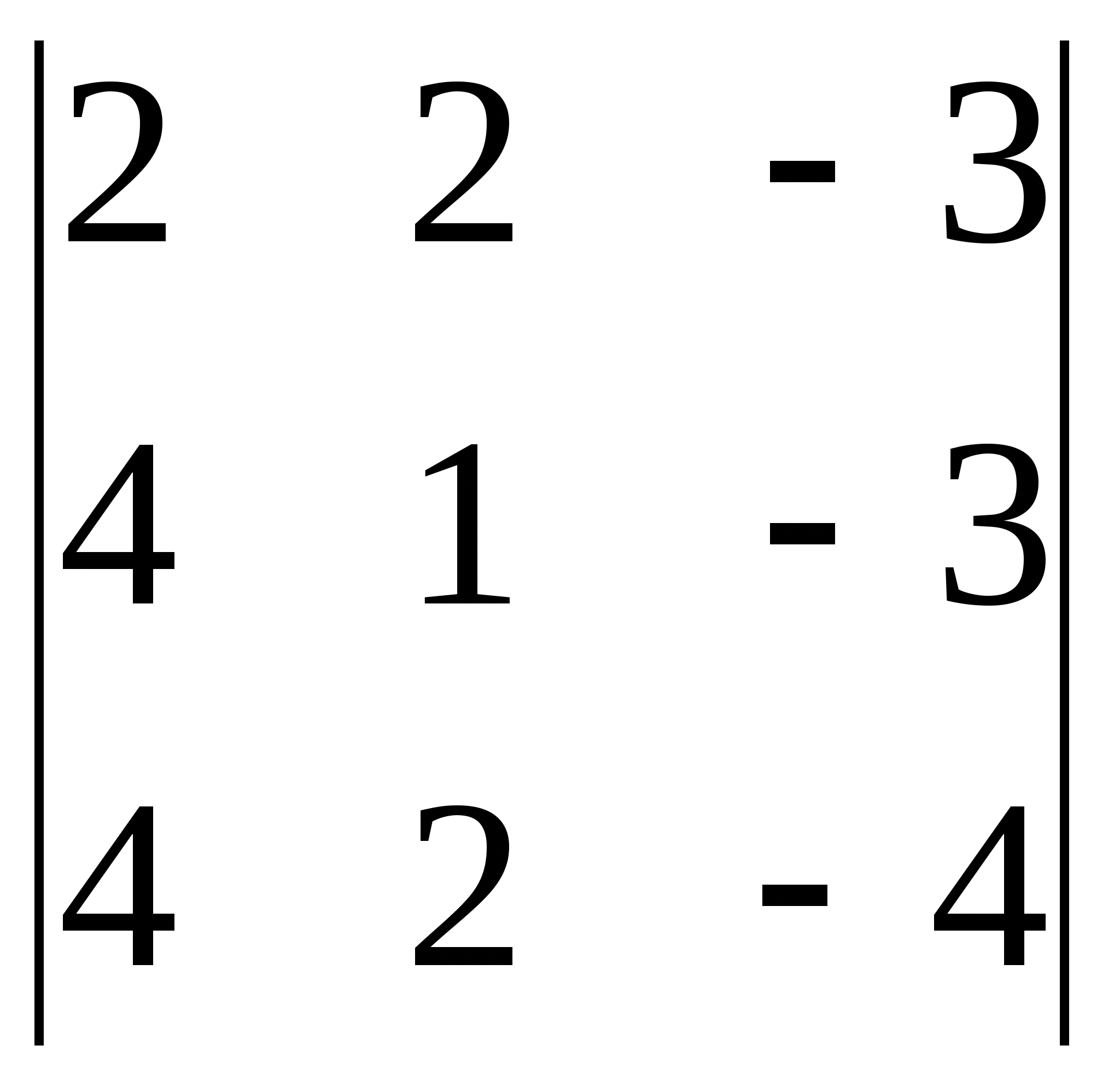
5) 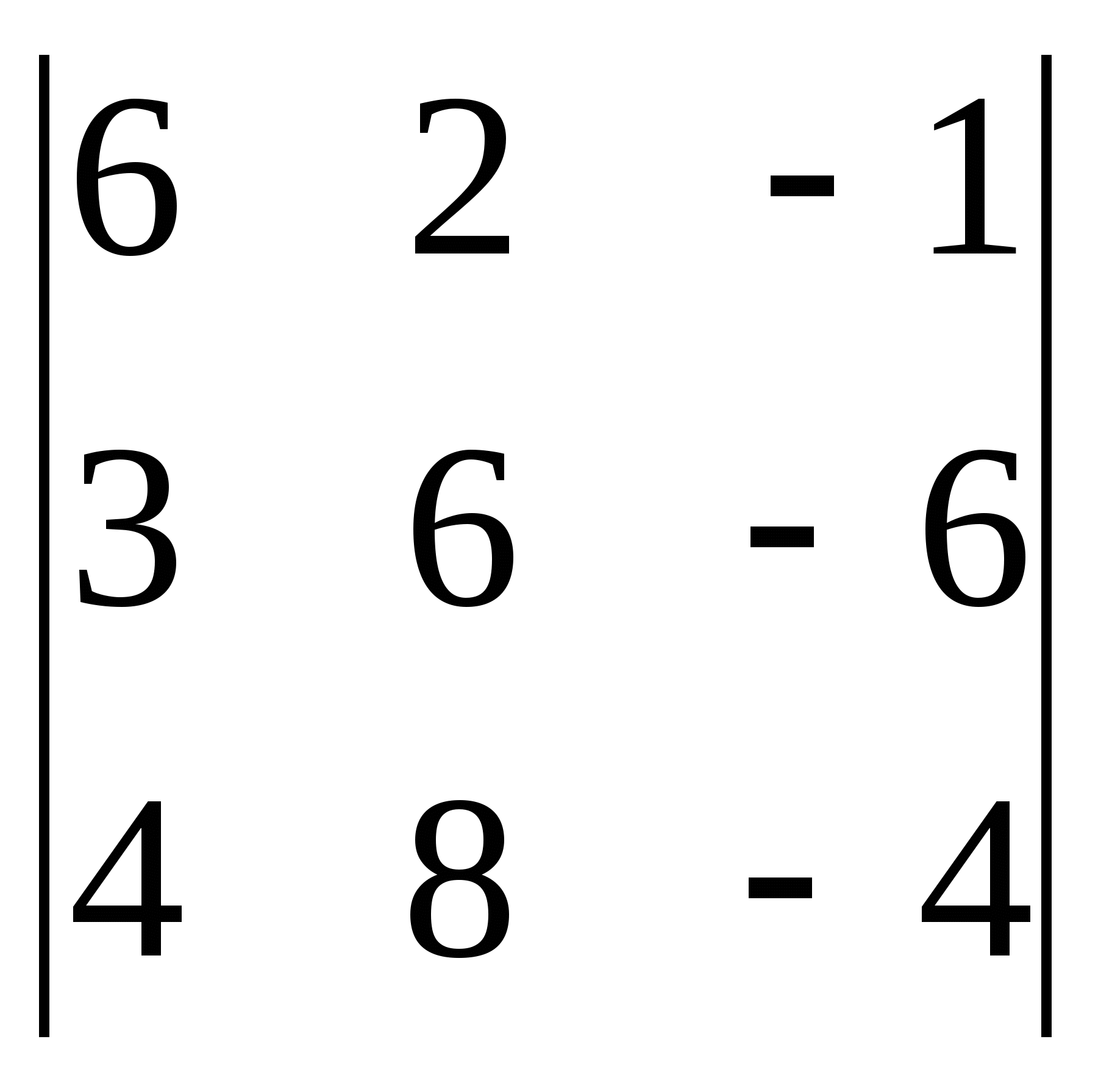 6)
6) 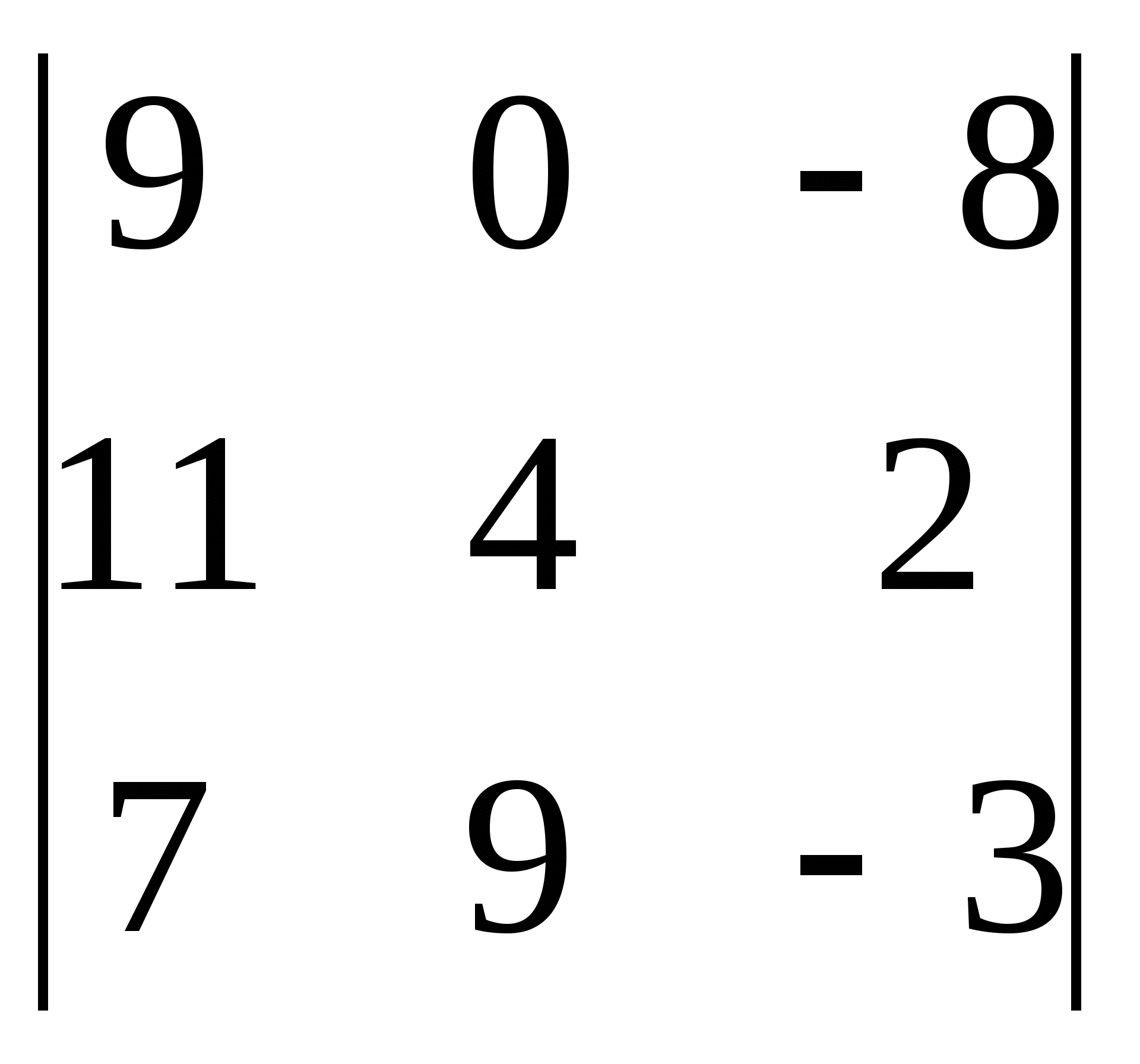
7) 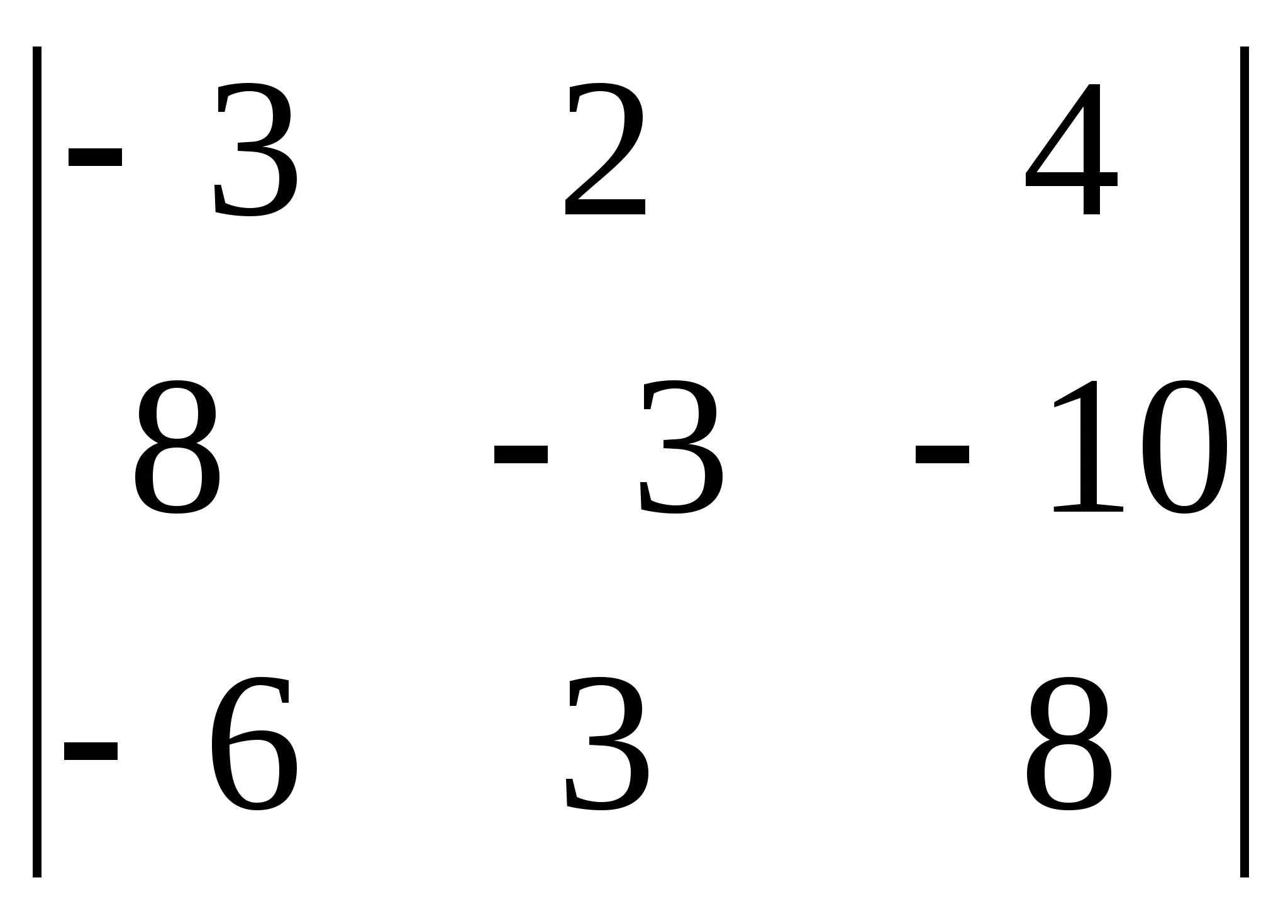 8)
8) 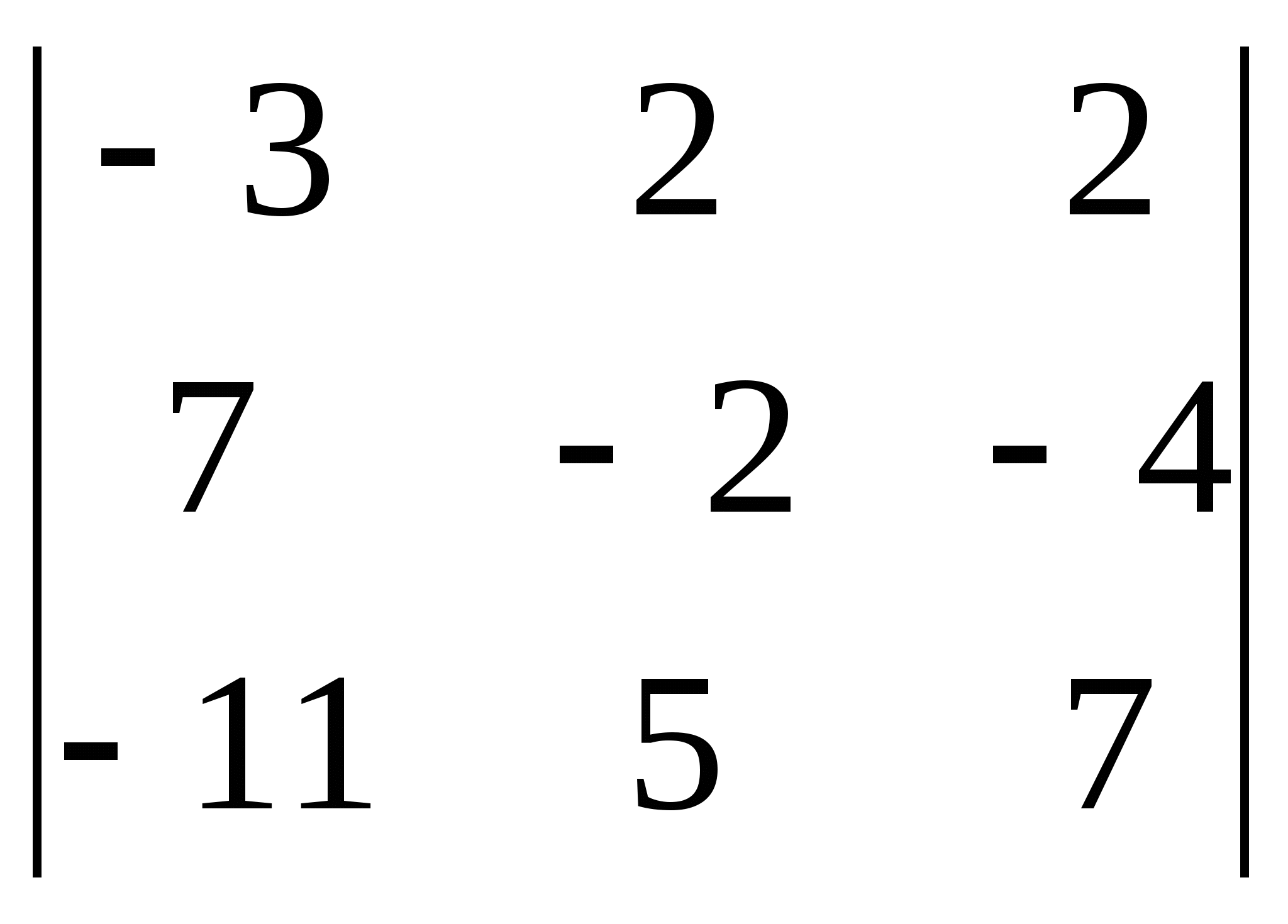
Задачи для домашнего решения
Вычислить определители:
1) 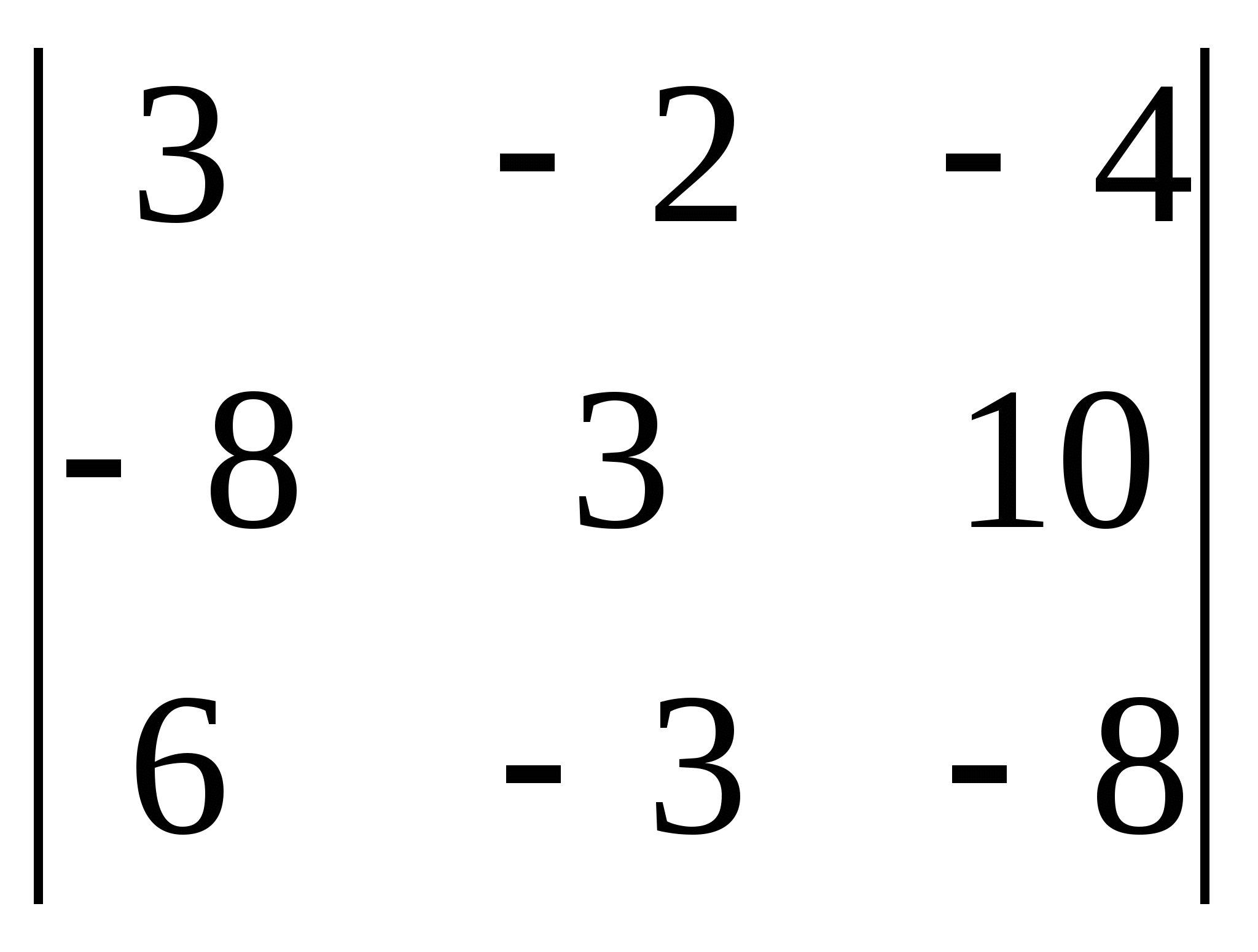 2)
2)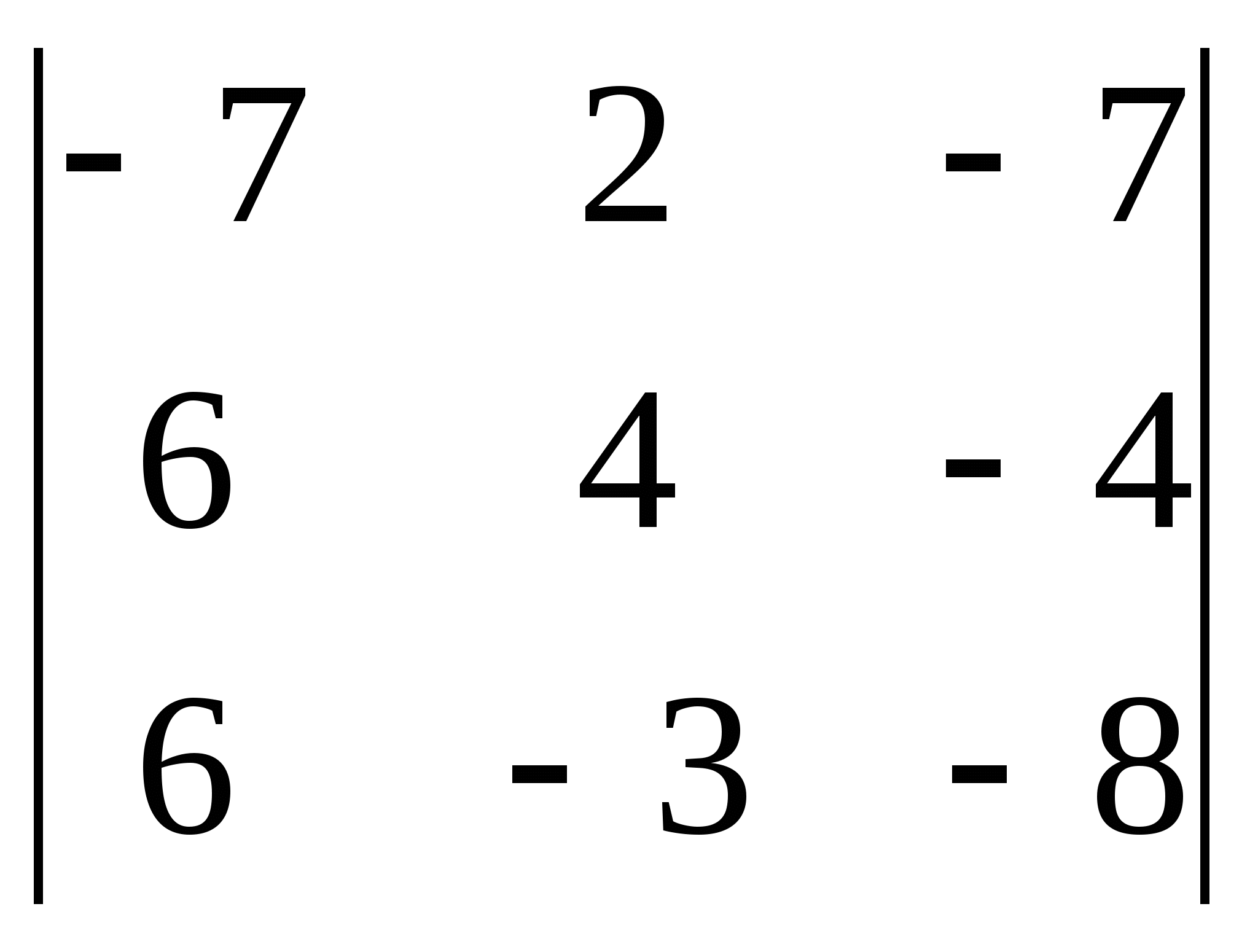
3) 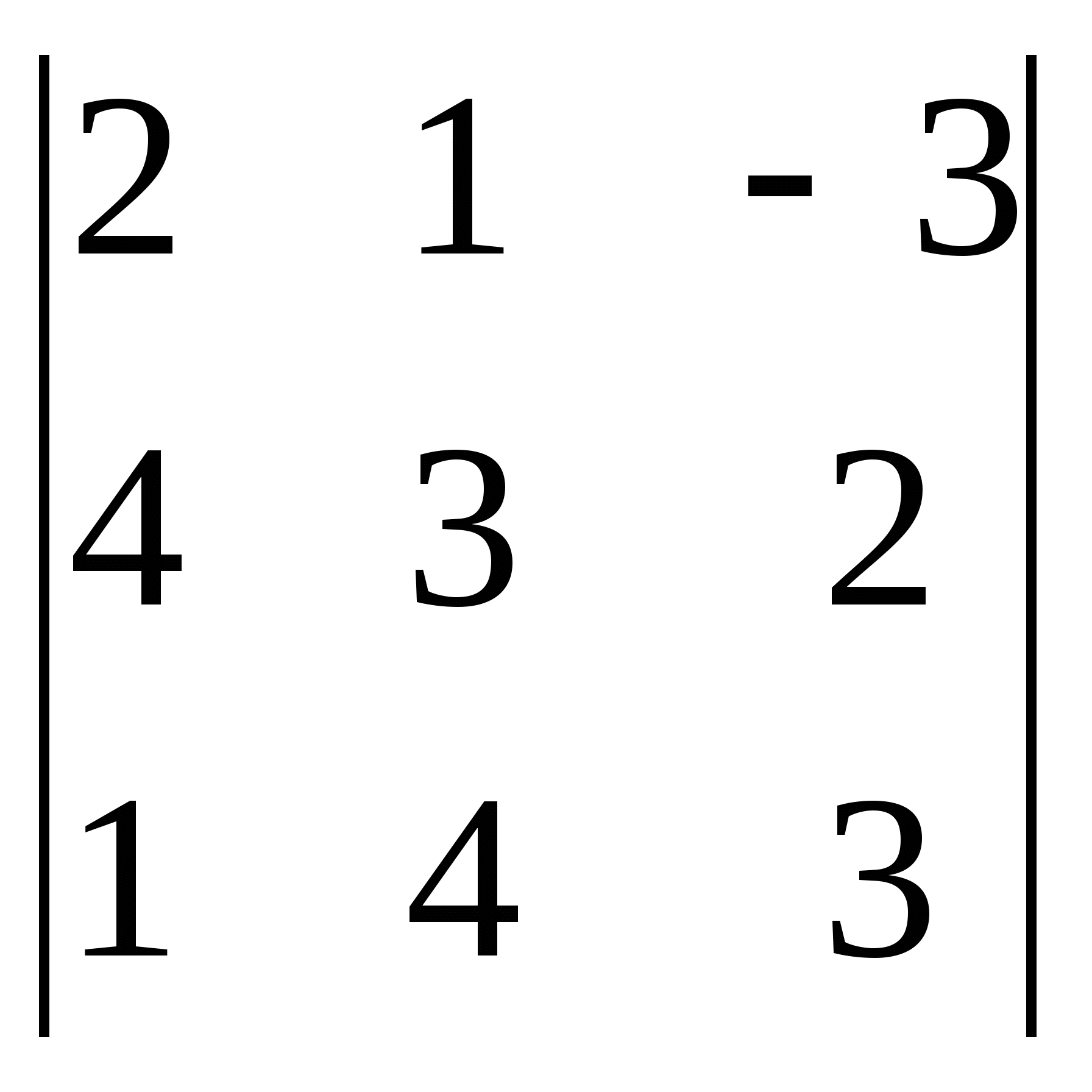 4)
4) 
Практическое занятие 3
Практическая работа 3
по теме «Нахождение обратной матрицы. Решение систем линейных уравнений методом обратной матрицы»
Цель работы: сформировать необходимые умения и навыки нахождения обратной матрицы, навыки решения систем линейных уравнений методом обратной матрицы.
Актуализация знаний
Фронтальный опрос
1. Понятие определителя, его свойства.
2. Вычисление определителей второго порядка.
3. Вычисление определителей третьего и высшего порядка.
4. Миноры и алгебраические дополнения.
5. Теорема о разложении определителя по элементам строки или столбца.
6. Алгоритм нахождения обратной матрицы.
7. Решение систем линейных уравнений методом обратной матрицы.
Краткие теоретические и учебно-методические материалы по теме практической работы
Пусть имеется квадратная матрица n-го порядка
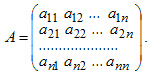
Матрица А-1 называется обратной матрицей по отношению к матрице А, если А*А-1 = Е, где Е - единичная матрица n-го порядка.
Теорема условия существования обратной матрицы
Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
Матрица называется
невырожденной, если векторы-столбцы являются
линейно независимыми. Число линейно независимых векторов-столбцов
матрицы называется рангом матрицы ![]() . Поэтому можно сказать, что для того, чтобы существовала обратная
матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее
размерности, т.е. r = n.
. Поэтому можно сказать, что для того, чтобы существовала обратная
матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее
размерности, т.е. r = n.
Алгоритм нахождения обратной матрицы:
-
Находят определитель матрицы А:
-
Находят алгебраические дополнения всех элементов
 матрицы А и
матрицы А и
Записывают новую матрицу из алгебраических дополнений:
![]()
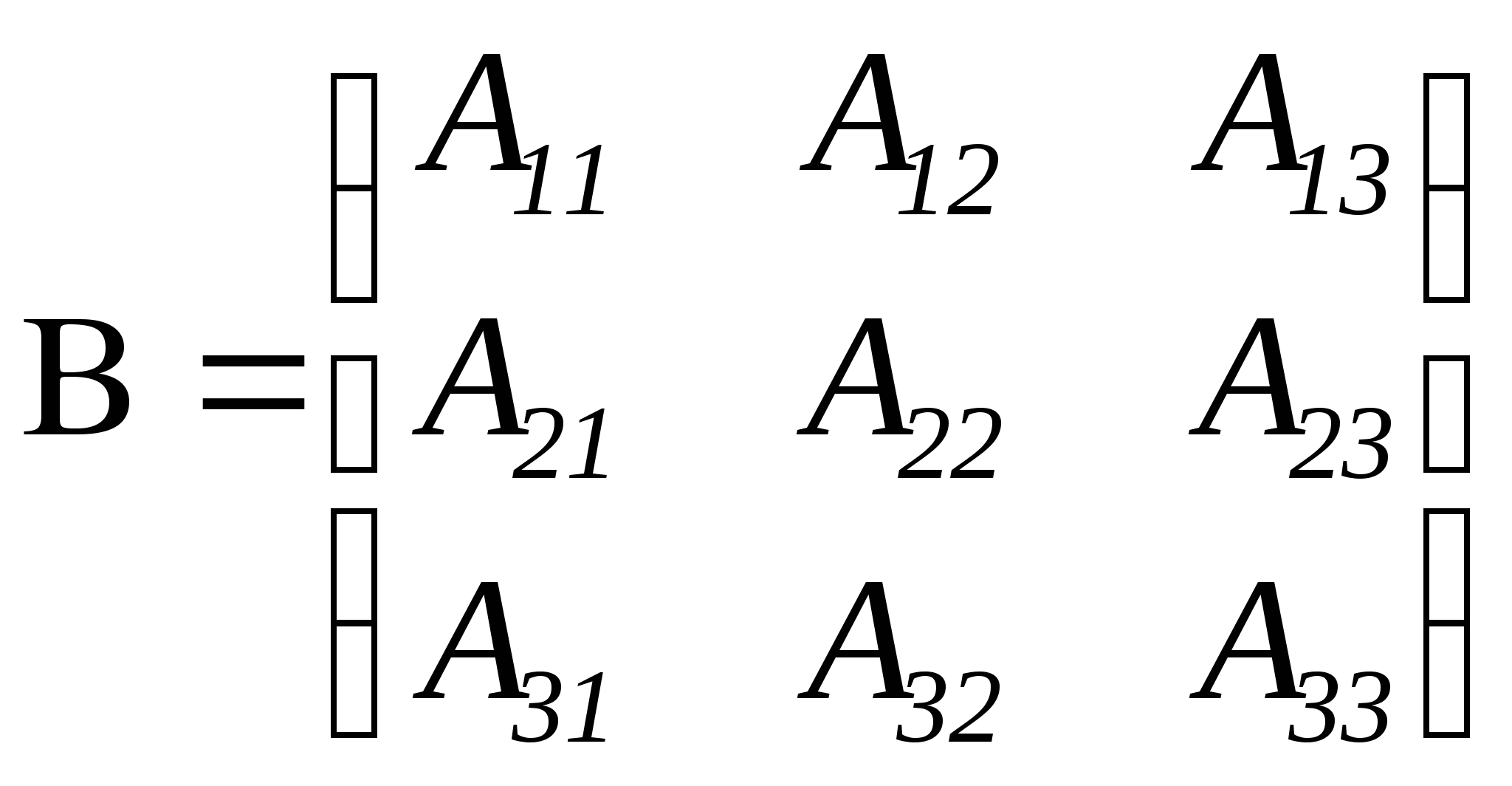
3. Транспонируют матрицу В.
![]() =
=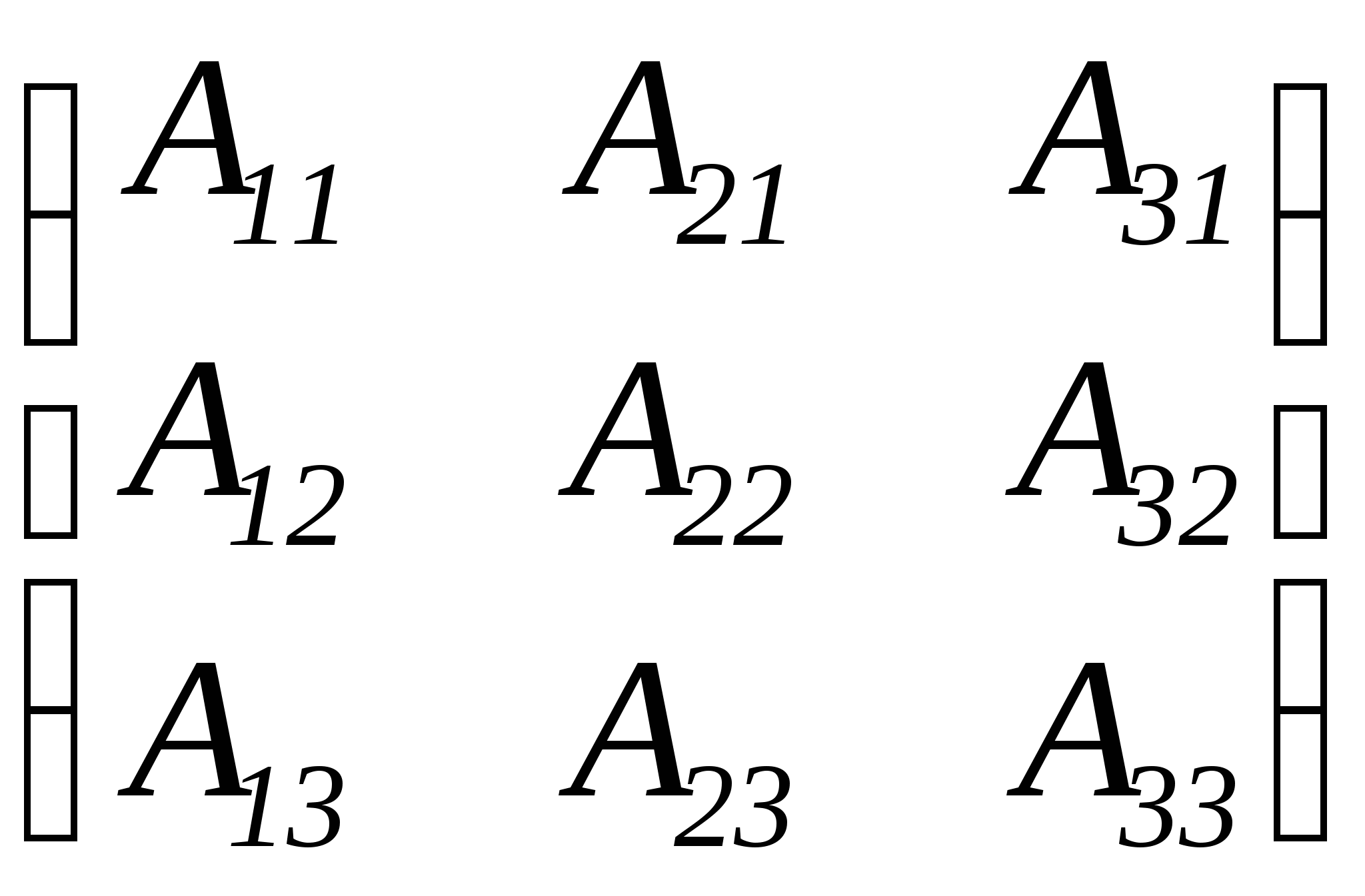
-
Умножить транспонированную матрицу на обратный определитель, т.е.
![]()
Простейшее матричное уравнение:
Х=В*А-1
Схема решения:
-
Найти обратную матрицу А-1.
-
Найти произведение обратной матрицы А-1 на столбец свободных членов , т.е.
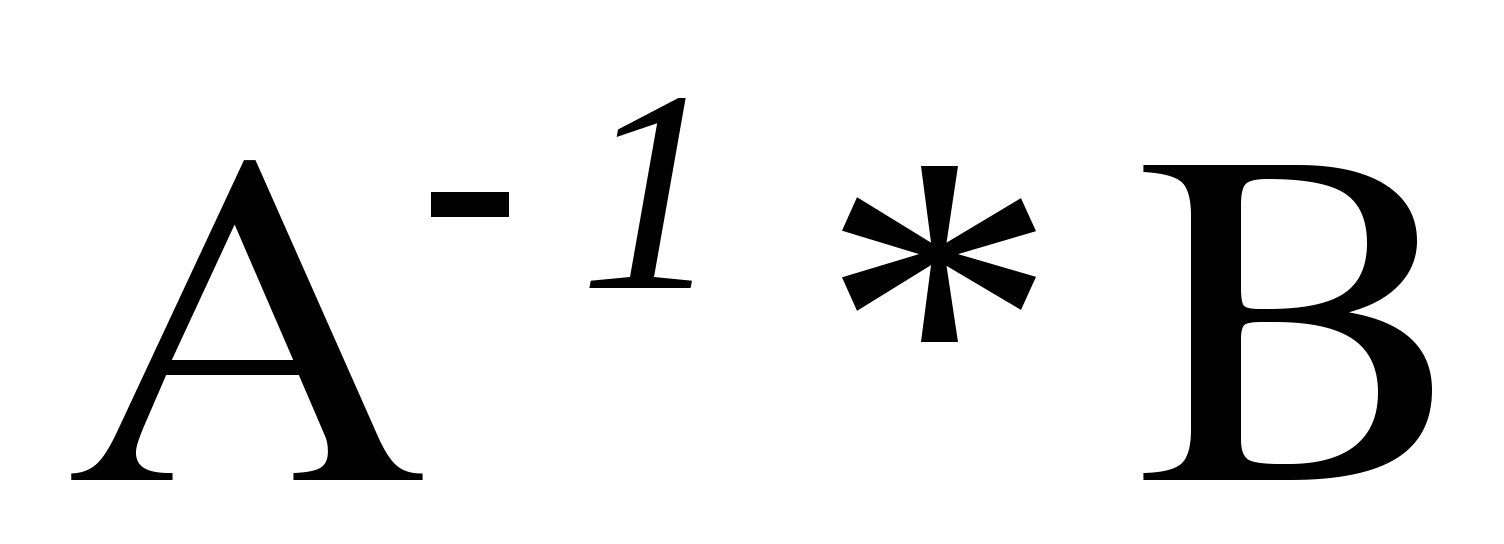 .
.
3. Пользуясь определением равных матриц, записать ответ.
Так как, систему линейных уравнений можно записать в виде матричного уравнения, то эту систему можно решить как матричное уравнение.
Формирование необходимых знаний и умений
Коллективное решение и обсуждение предложенных задач
Пример 1
Найти обратную матрицу для матрицы А, сделать проверку, если
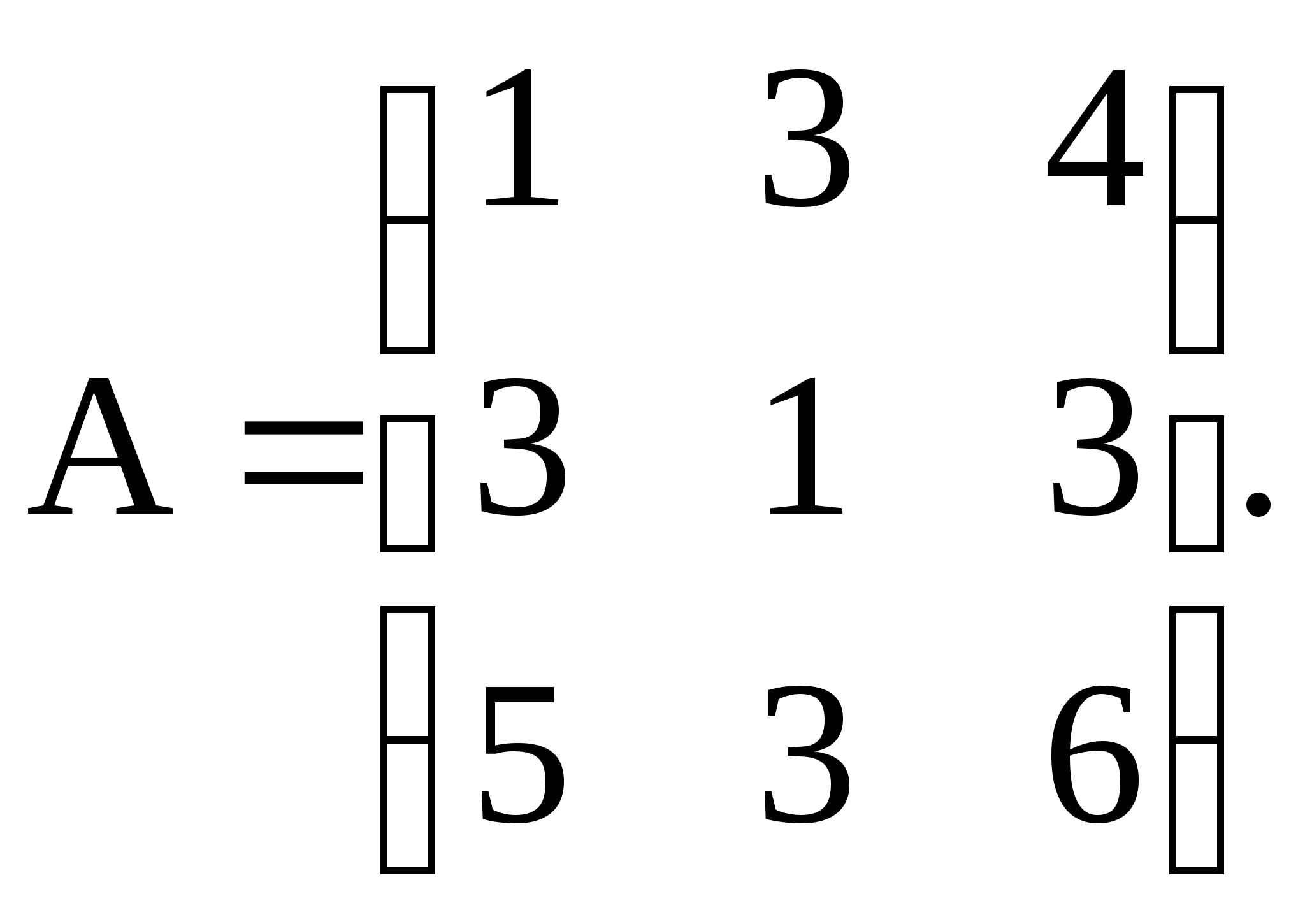
Решение. Вычислим определитель матрицы А:
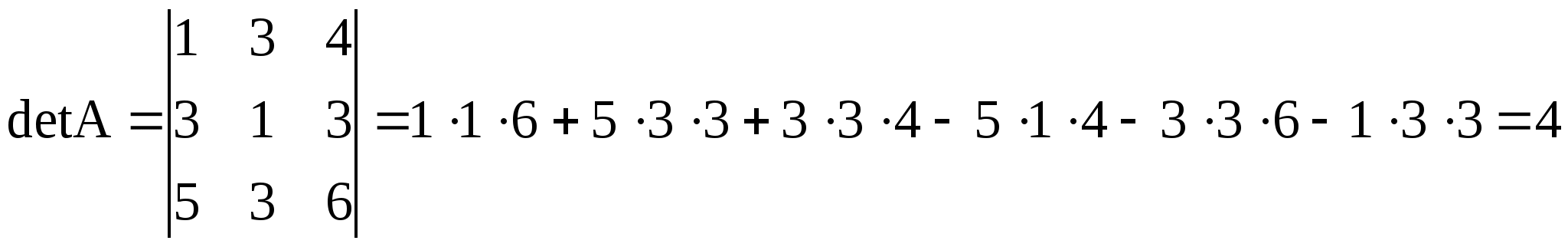 .
.
Поскольку detА≠0, то существует обратная матрица А-1. Найдем алгебраическое дополнение для каждого элемента матрицы А.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Тогда
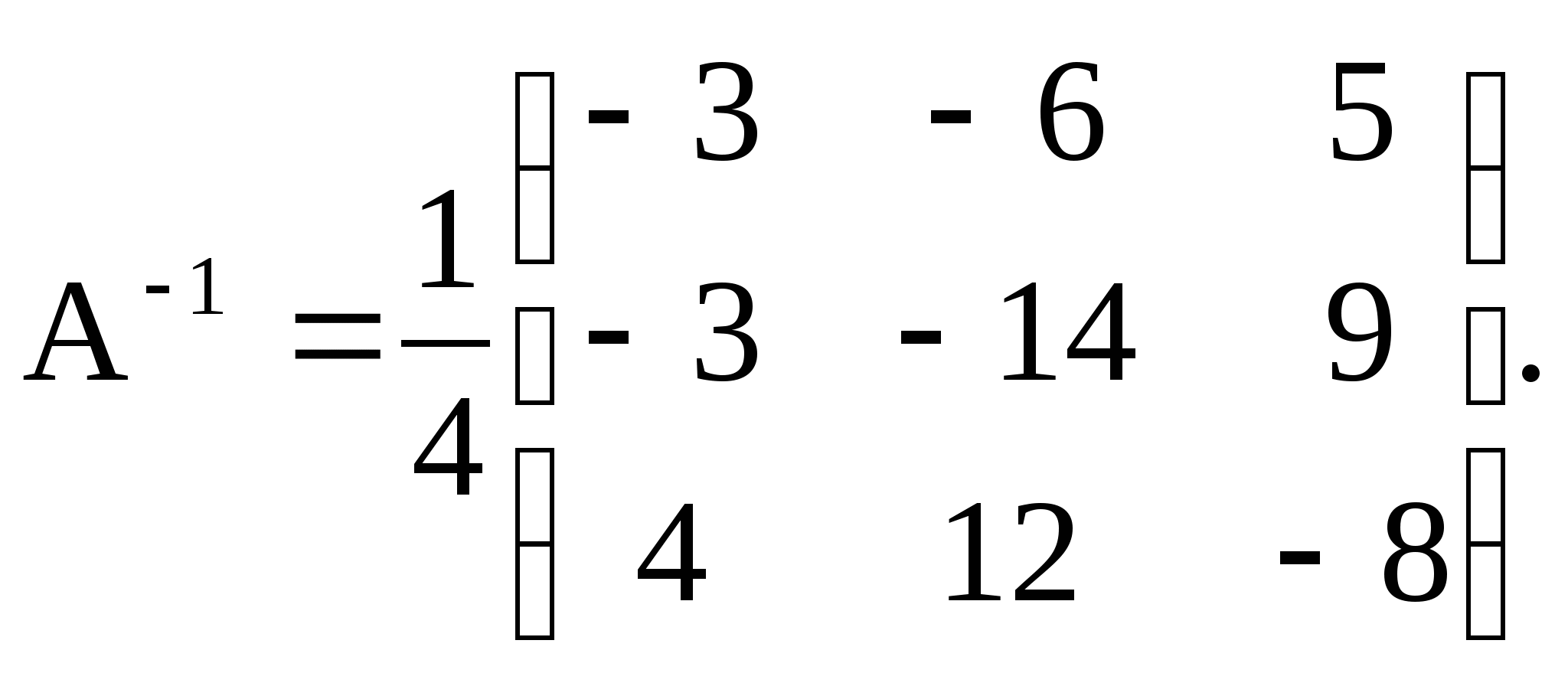
Сделаем проверку:
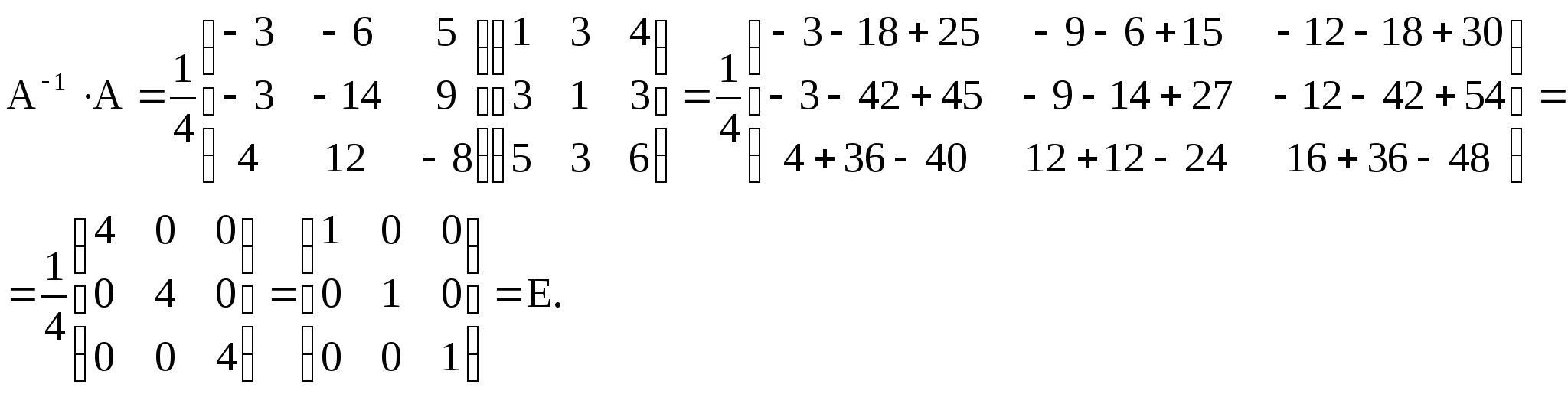
Примеры:
1. Дана матрица А. Найти обратную матрицу. Выполнить проверку
1) 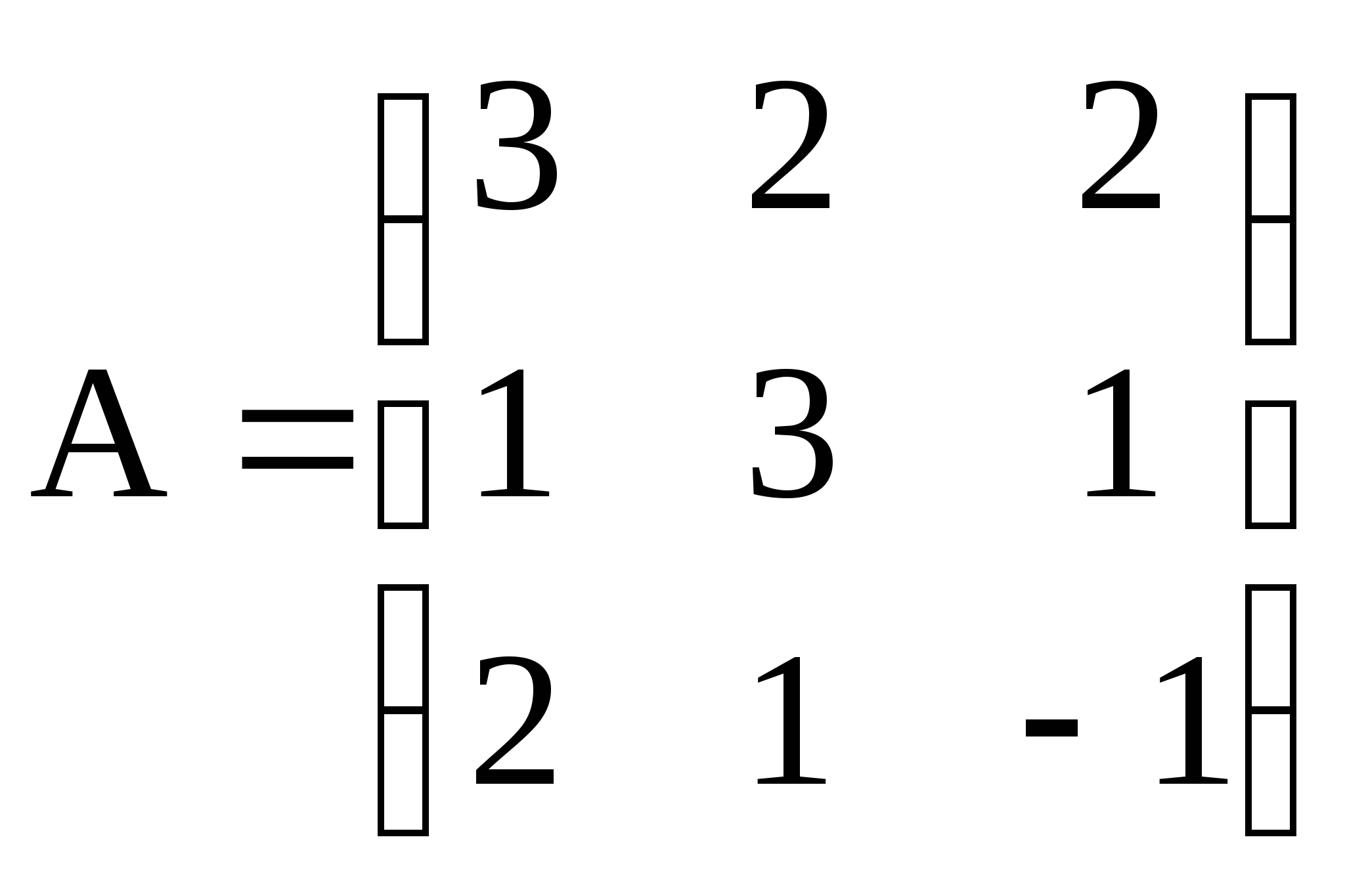 ; 2)
; 2) 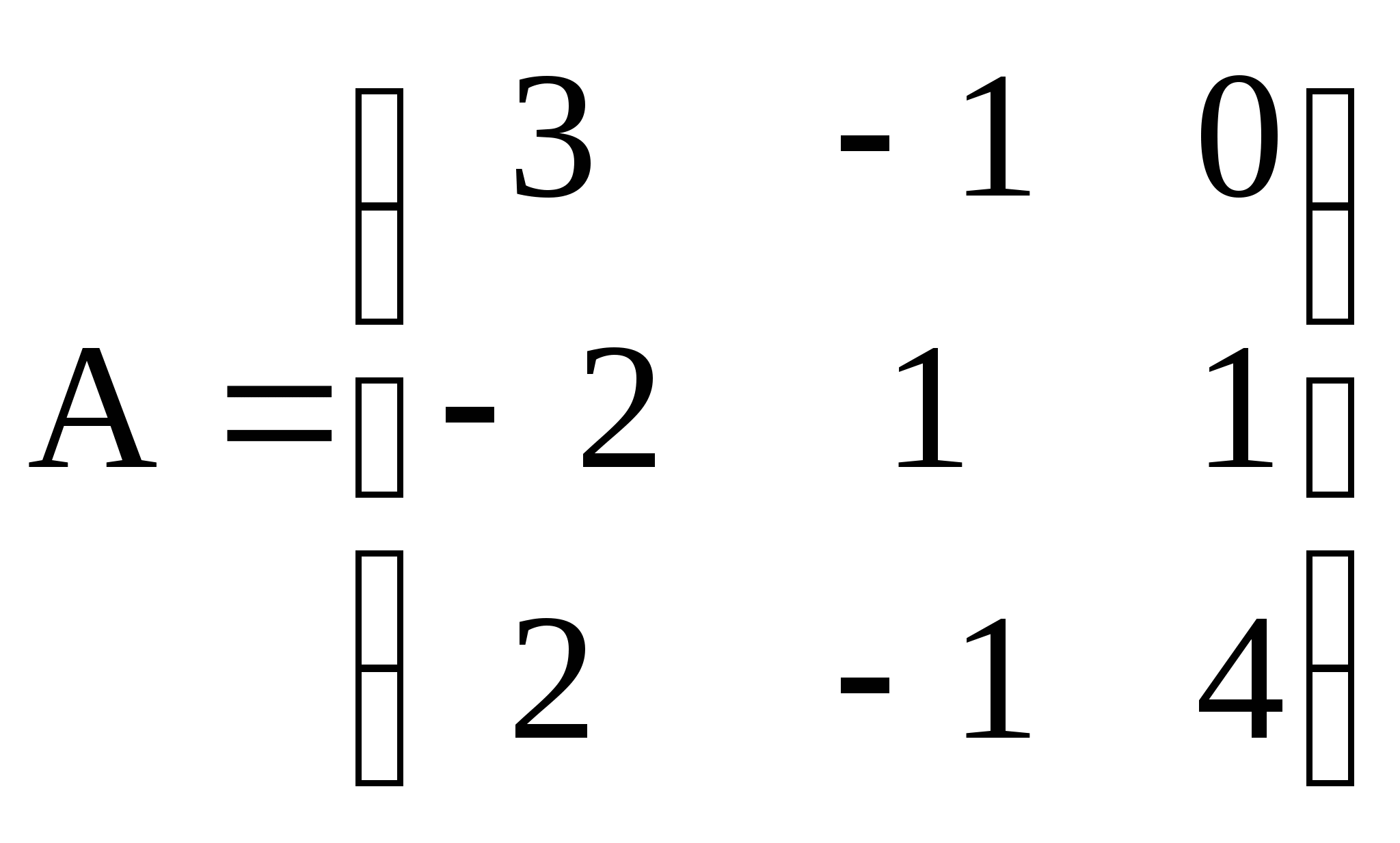 ; 3)
; 3) 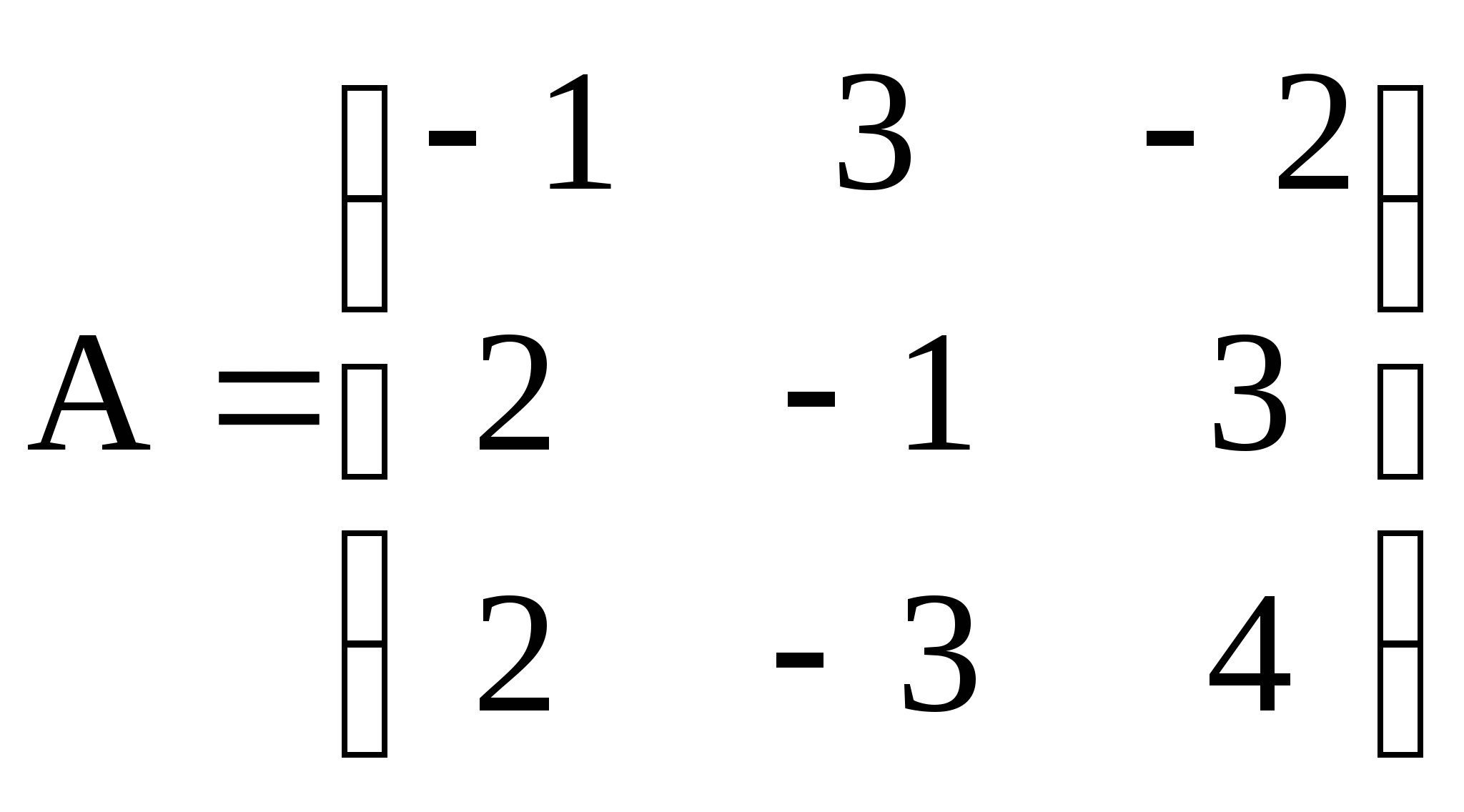 ;
;
2. Решить систему линейных уравнений методом обратной матрицы:
1) 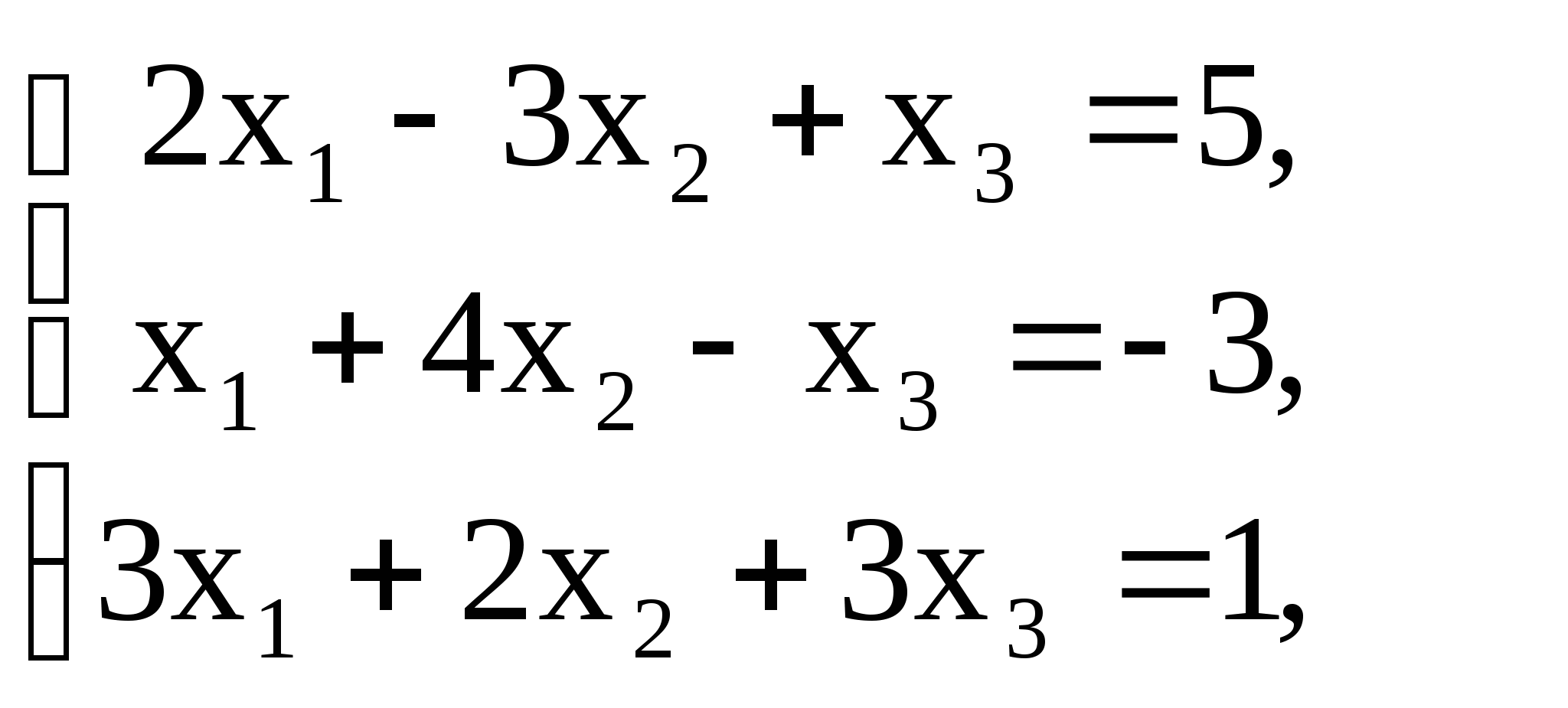 2)
2) 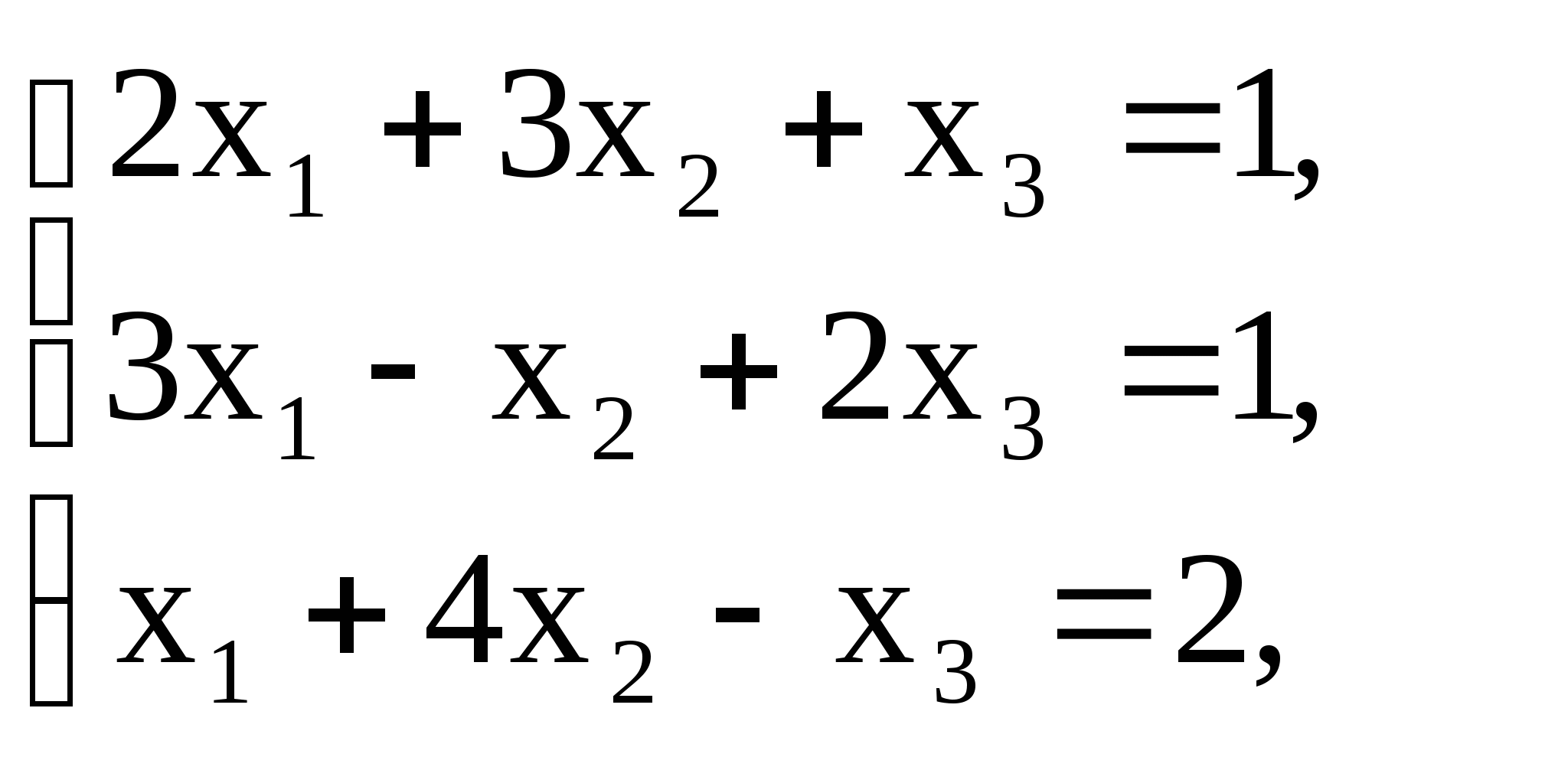
Закрепление сформированных знаний и учений:
Закрепление полученных знаний по данной теме проводится во время самостоятельного решения заданий
1. Дана матрица А. Найти обратную матрицу. Выполнить проверку
1) 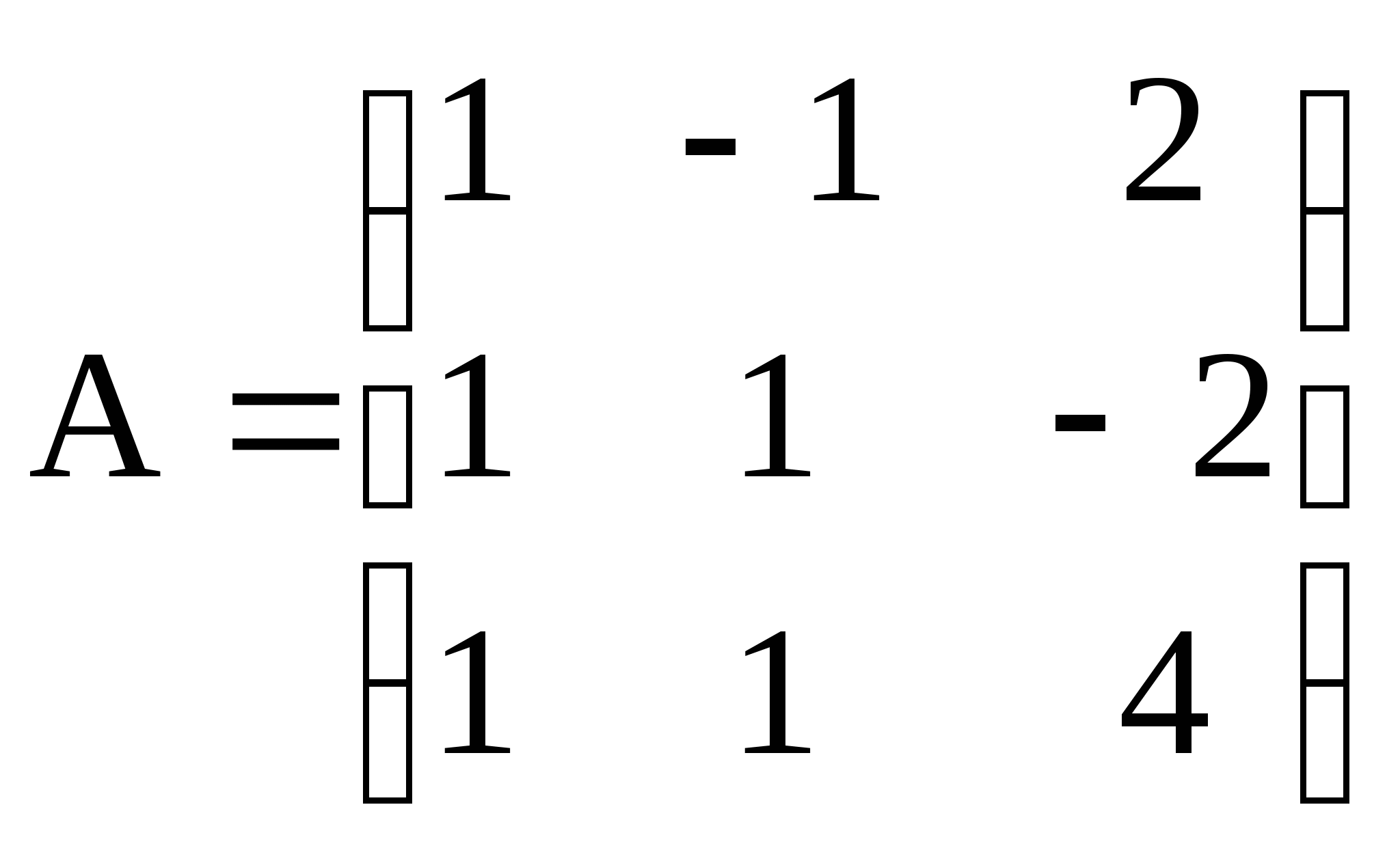 ; 2)
; 2) 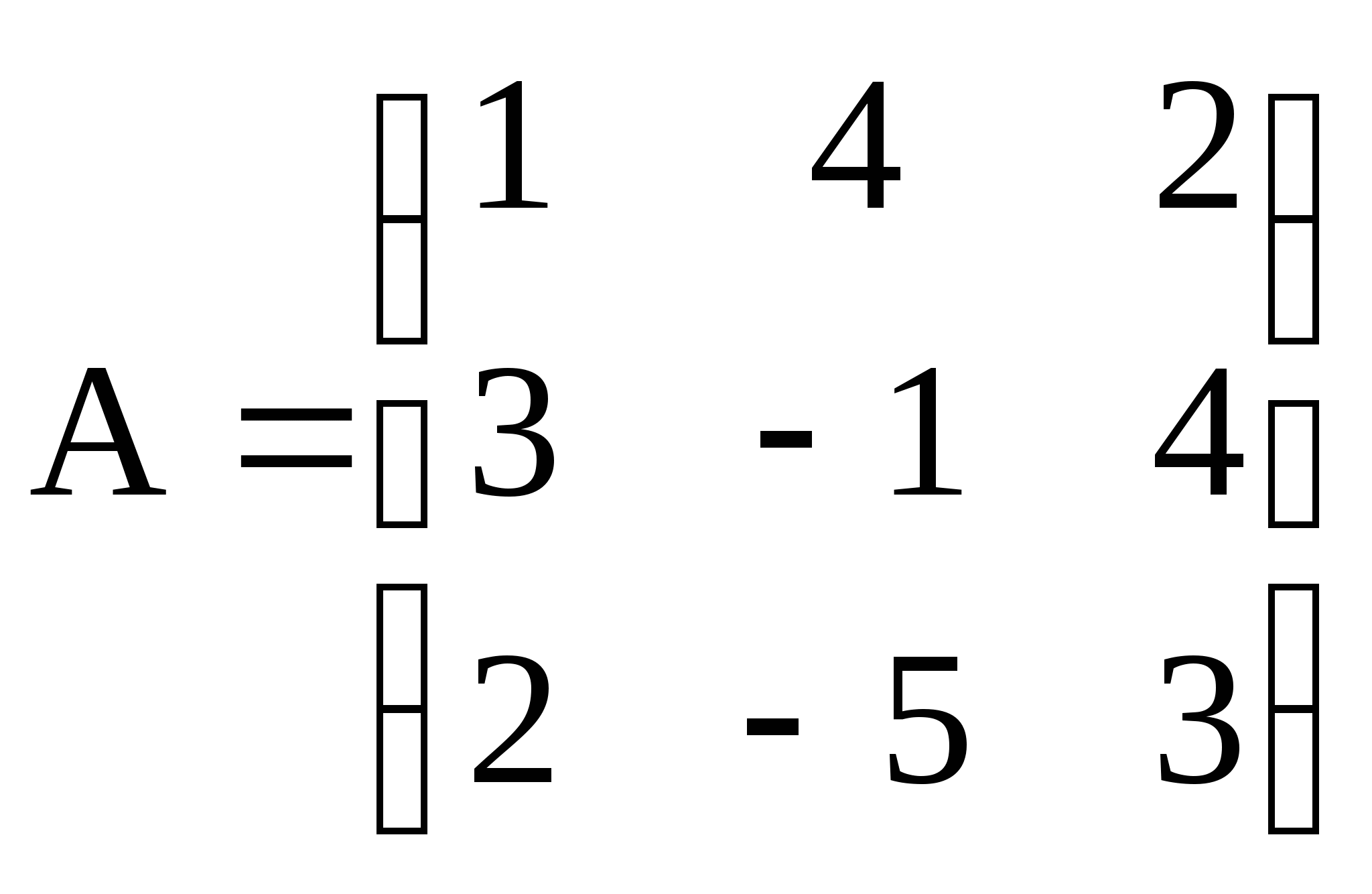 ; 3)
; 3) 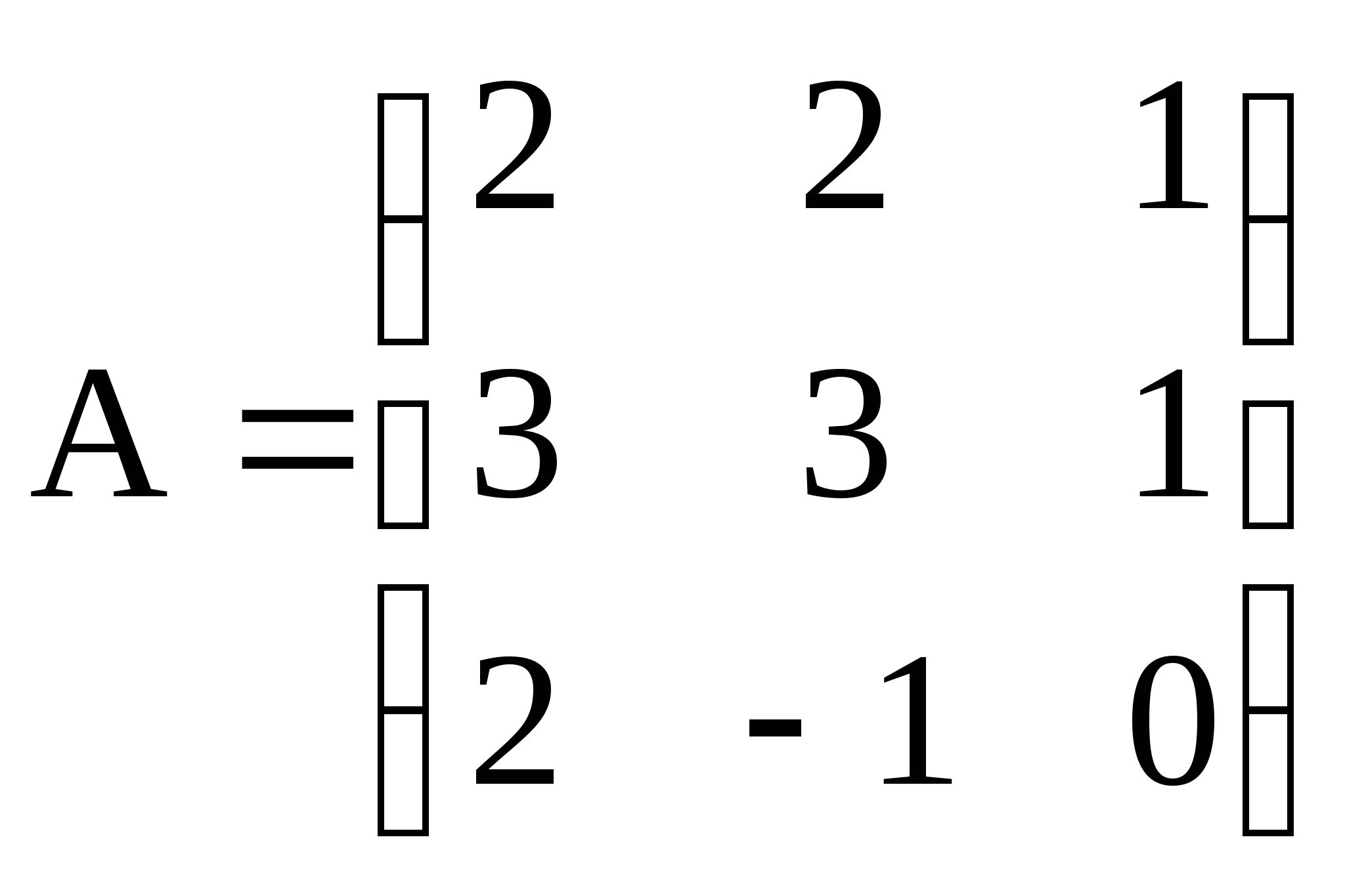 ;
;
4) 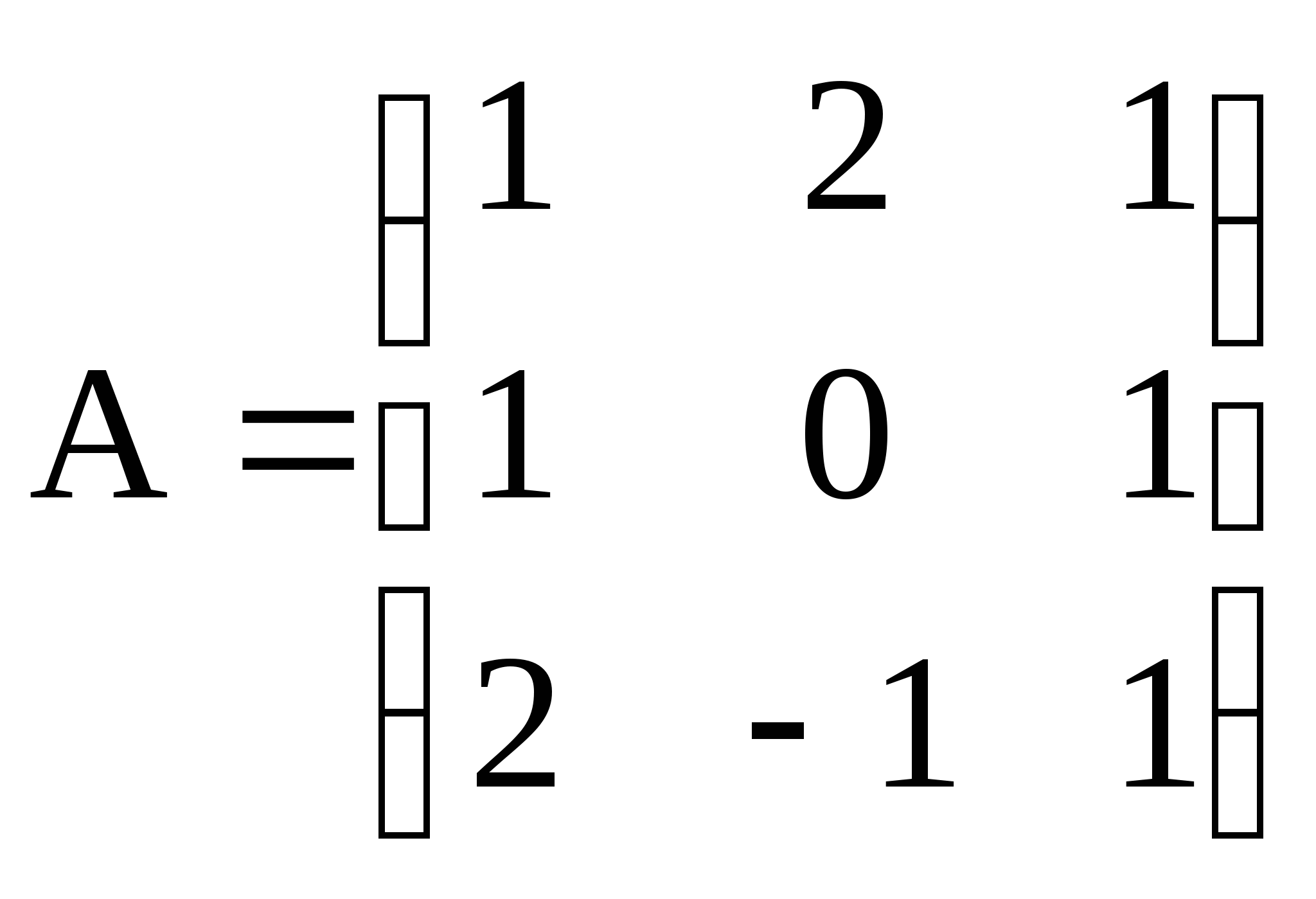 ; 5)
; 5) 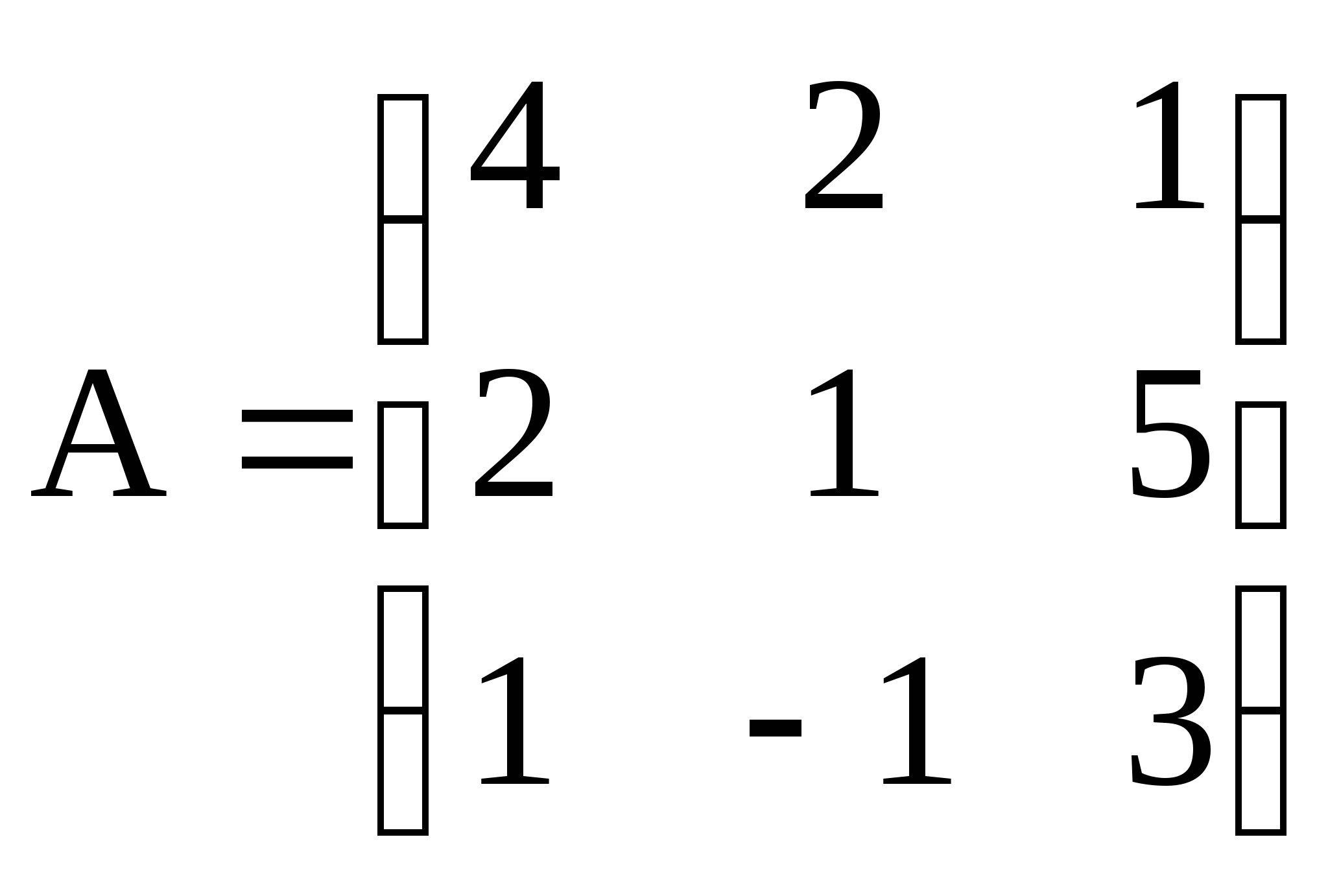
2. Решить систему линейных уравнений методом обратной матрицы:
1) 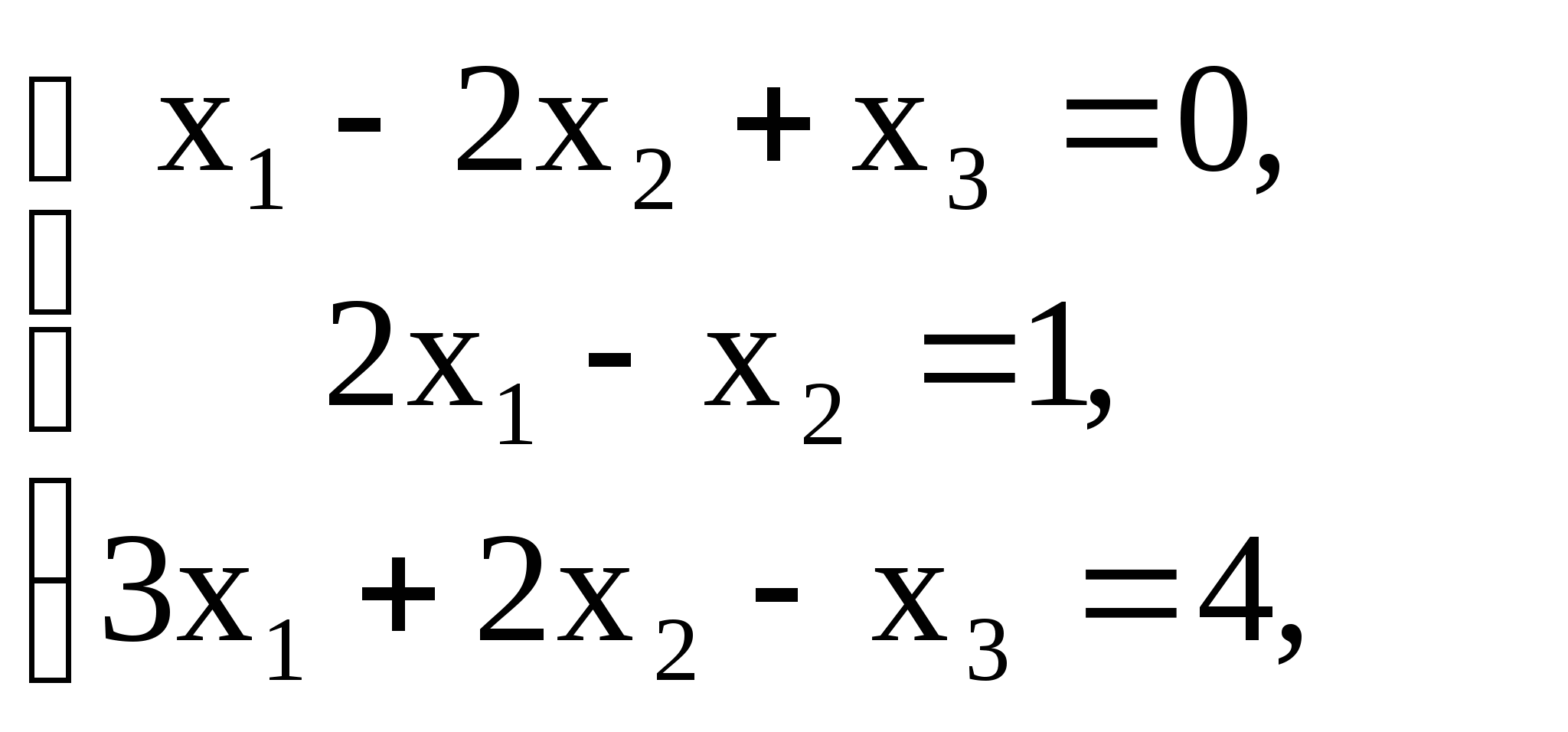 2)
2) 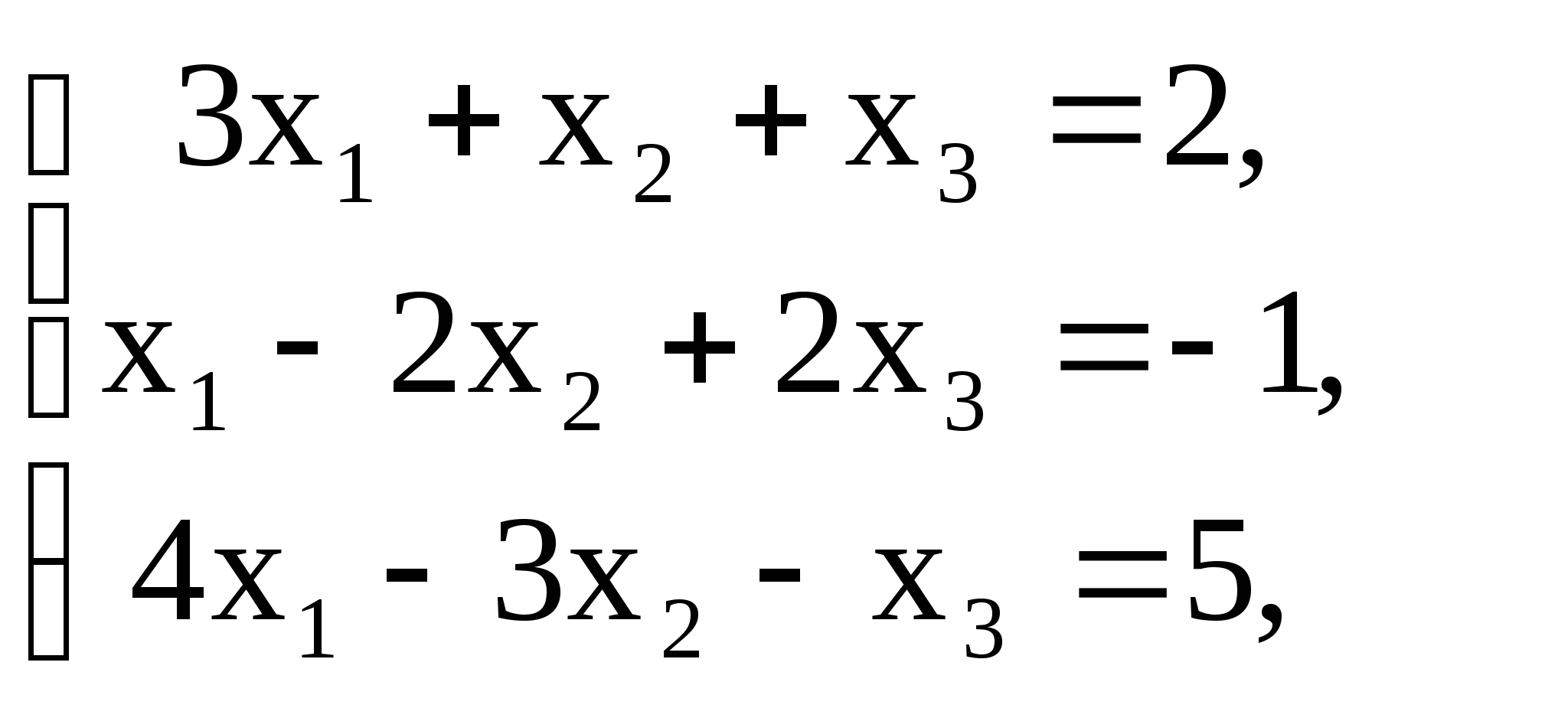
Задачи для домашнего решения
Решить систему линейных уравнений методом обратной матрицы:
1) 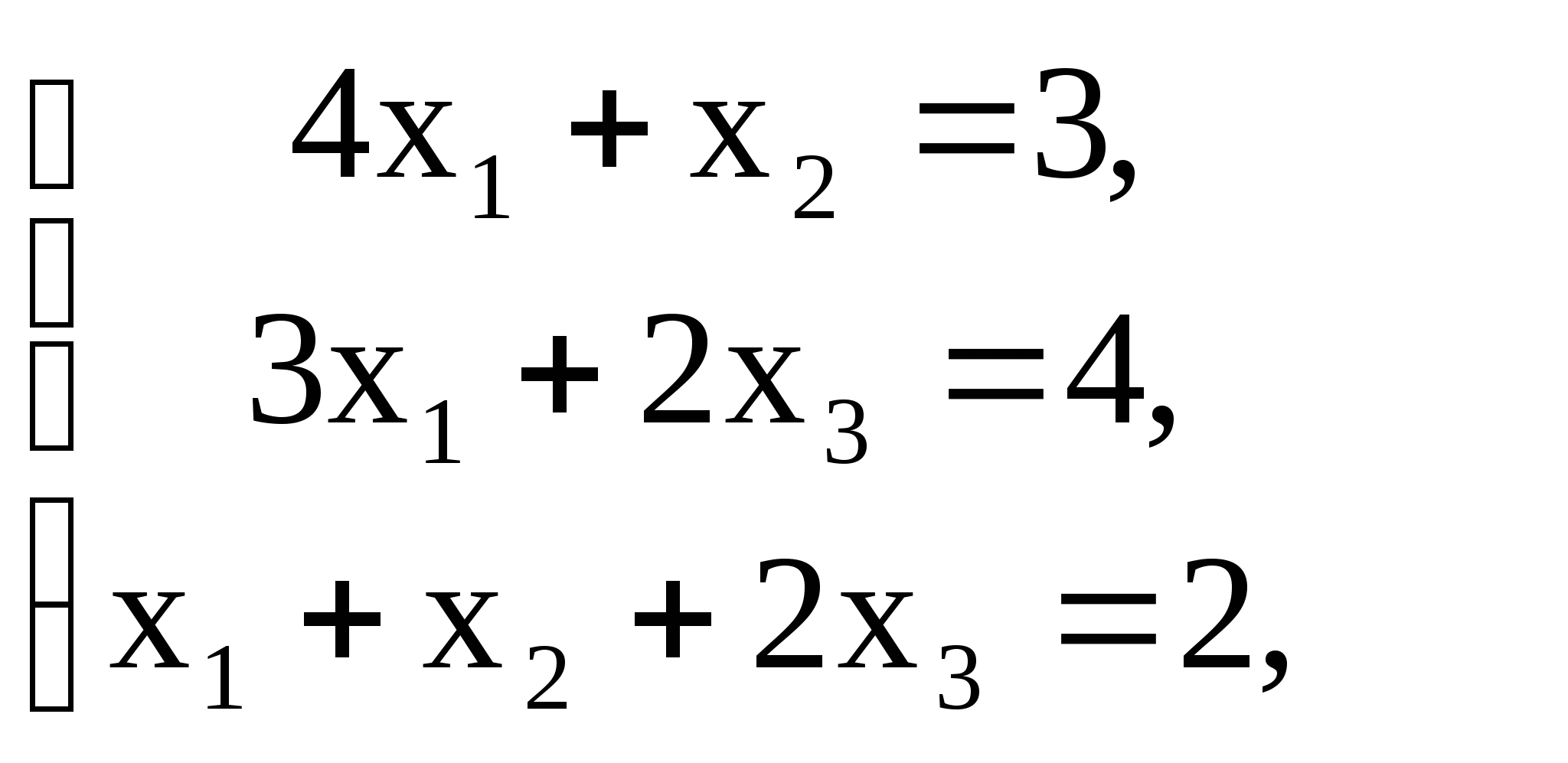 2)
2) 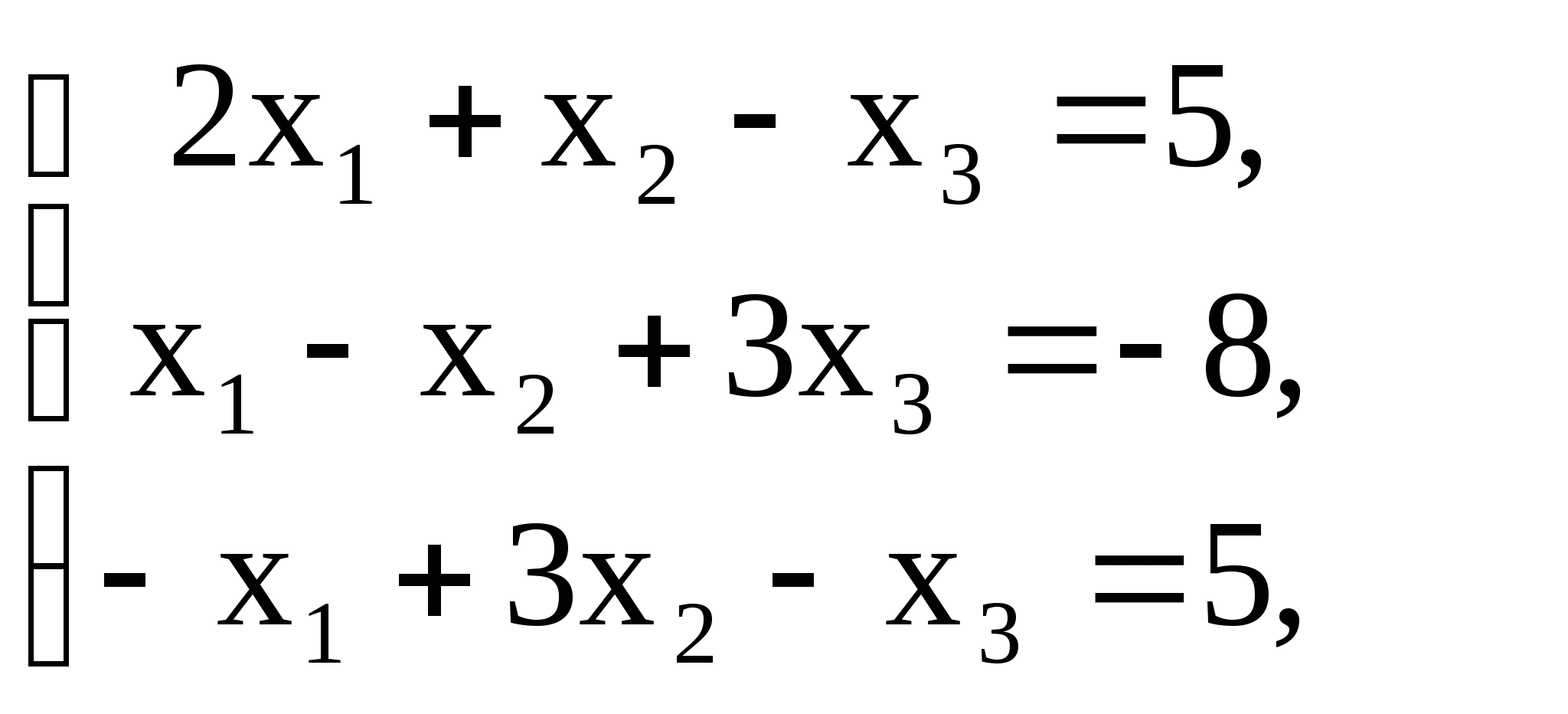
Практическое занятие 4
Практическая работа 4
по теме «Решение систем линейных уравнений: задачи с профессиональной направленностью»
Цель работы: сформировать необходимые умения и навыки решения систем линейных уравнений методами Крамера и Гаусса для решения задач с профессиональной направленностью.
Актуализация знаний
Фронтальный опрос
1. Понятие определителя, его свойства.
2. Вычисление определителей второго порядка.
3. Вычисление определителей третьего и высшего порядка.
4. Миноры и алгебраические дополнения.
5. Теорема о разложении определителя по элементам строки или столбца.
6. Алгоритм нахождения обратной матрицы.
7. Решение систем линейных уравнений методом обратной матрицы, Крамера и Гаусса.
Краткие теоретические и учебно-методические материалы по теме практической работы
Метод Гаусса:
1. Систему уравнений приводят к эквивалентной ей системе с треугольной
матрицей. (Системы называются эквивалентными, если множества их решений совпадают.) Эти действия называют прямым ходом.
2. Из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход):
- умножение или деление коэффициентов свободных членов на одно и то же число
- сложение и вычитание уравнений
- перестановку уравнений системы
- исключение системы уравнений, в которых все коэффициенты при
неизвестных и свободные члены равны нулю.
Метод Крамера:
Формулы Крамера для решения системы n линейных уравнений с n неизвестными, записываются так:
![]()
![]() или
или
![]()
![]()
![]()
Если ![]() , то система имеет единственное решение
, то система имеет единственное решение
Если ![]() , множество решений
, множество решений
Если ![]() , то нет решений
, то нет решений
Матричный способ
Х=В*А-1
Схема решения:
-
Найти обратную матрицу А-1.
-
Найти произведение обратной матрицы А-1 на столбец свободных членов , т.е.
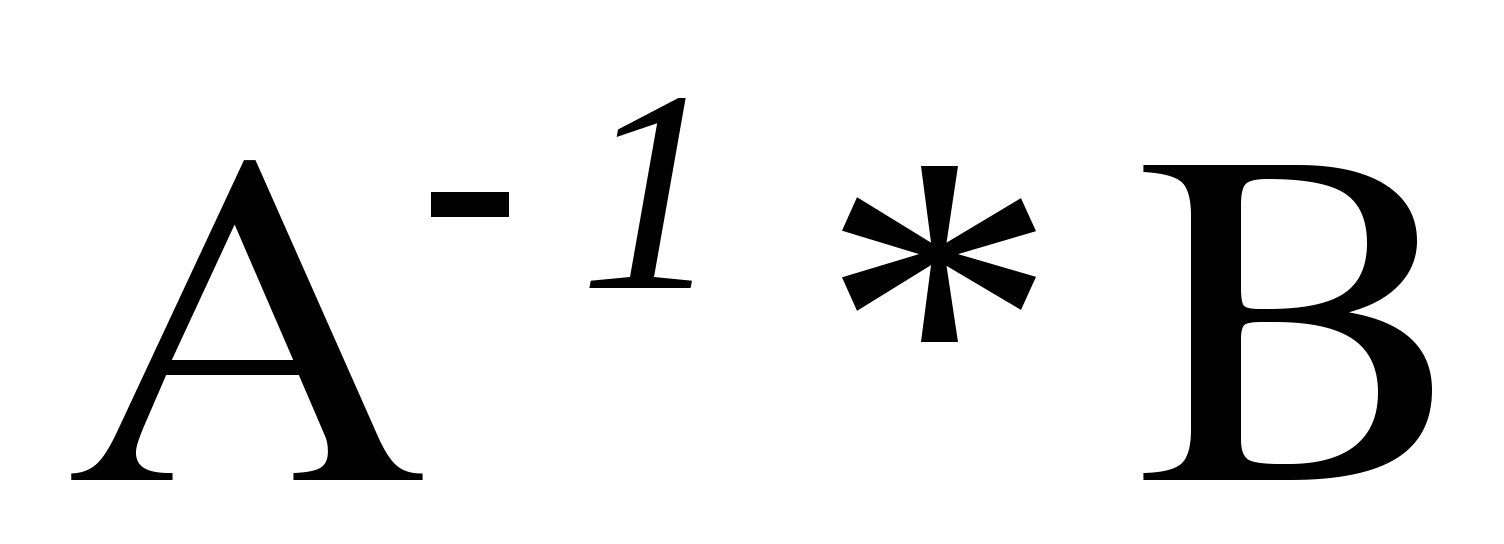 .
.
3. Пользуясь определением равных матриц, записать ответ.
Так как, систему линейных уравнений можно записать в виде матричного уравнения, то эту систему можно решить как матричное уравнение.
Формирование необходимых знаний и умений
Коллективное решение и обсуждение предложенных задач
Пример 1
Составить план изготовления продукции трех видов
с трех видов сырья с целью полной реализации запасов этого сырья.
Известны технология затрат каждого вида сырья на изготовление
единицы продукции определенного вида А =  и объемы запасов сырья В =
и объемы запасов сырья В = ![]() .
.
Решение:
Пусть ожидаемый план изготовления предусматривает производство:
-
І вид продукции - "х" условных единиц,
-
ІІ вид продукции - "у" условных единиц,
-
ІІІ вид продукции - "z" условных единиц.
Таким образом, для находжения нужного плана
необходимо решить матричное уравнение  *
*![]() =
=![]() ,
например по схеме Гаусса, тождественно преобразовывая расширенную
матрицу следующим образом:
,
например по схеме Гаусса, тождественно преобразовывая расширенную
матрицу следующим образом:
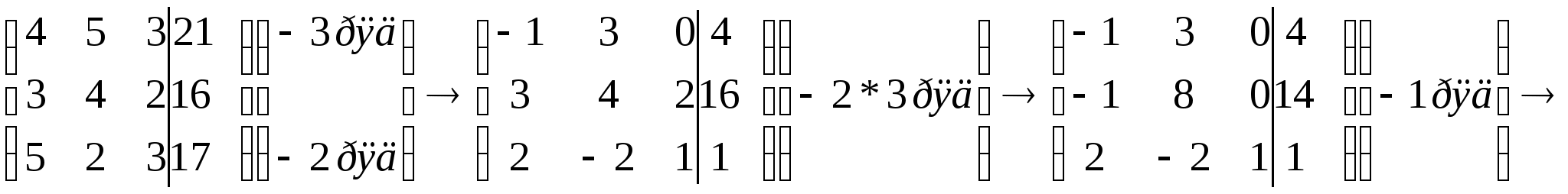
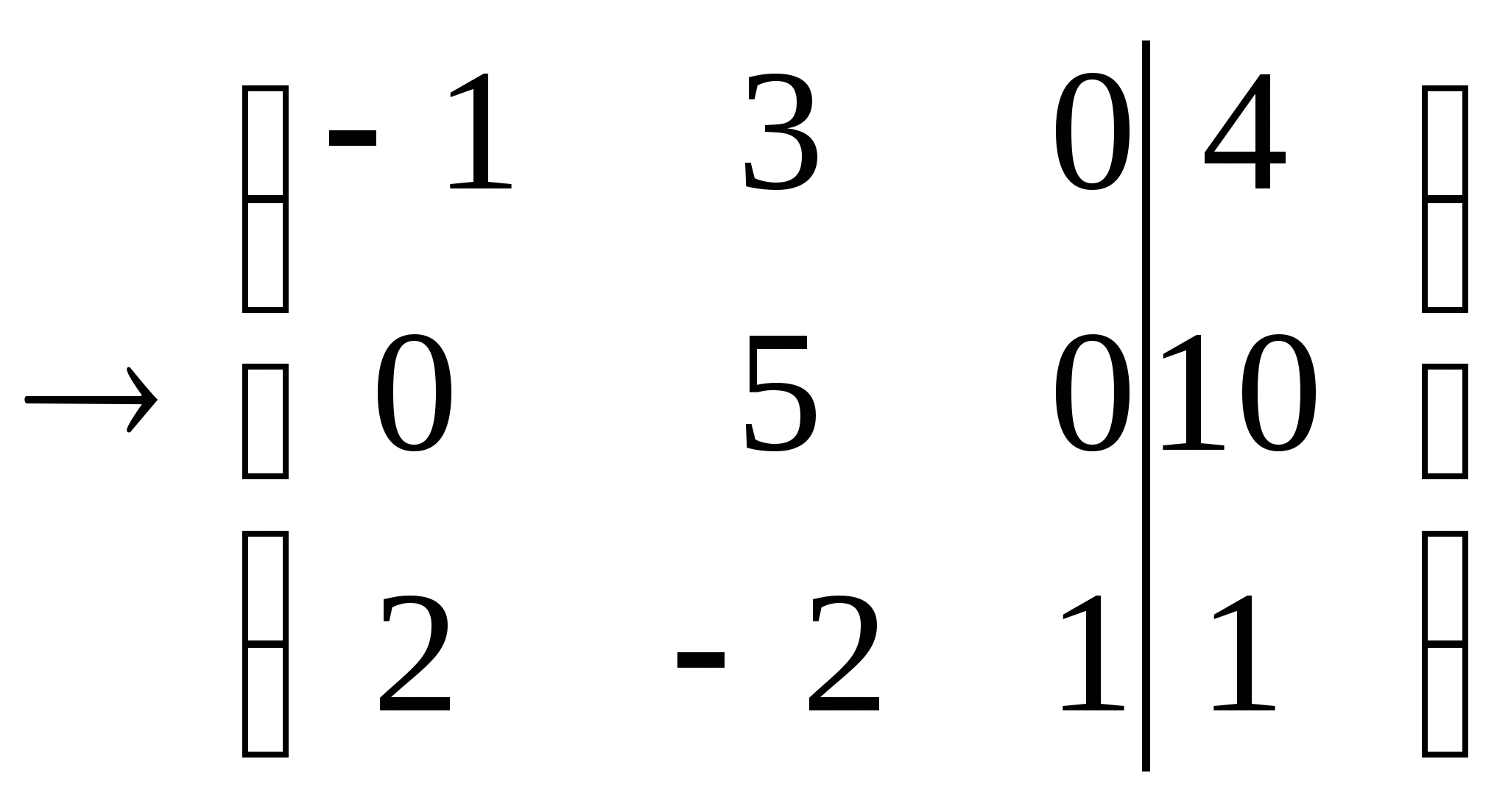
Полученная расширенная матрица задает систему линейных уравнений :
-
х
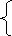 + 3у = 4,
+ 3у = 4,
5у = 10,
2х - 2у + z = 1.
Последовательное решение системы, начиная с уравнения, которое содержит только одну переменную , т.е.:
-
5у = 10
 у = 2,
у = 2,
-
- х + 3у = 4
 -х + 3*2 = 4
-х + 3*2 = 4  х = 6 - 4 = 2,
х = 6 - 4 = 2,
-
2х - 2у + z = 1
 2*2 - 2*2 + z = 1
2*2 - 2*2 + z = 1  z = 1.
z = 1.
Таким образом, необходимый план предусматривает изготовление:
-
І вид продукции - 2 у.е.,
-
ІІ вид продукции - 2 у.е.,
-
ІІІ вид продукции - 1 у.е.
Проверка:
Запишем систему, которая соответствует составленному матричному уравнению, и проверим ее на тождественность :
4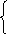 х
+ 5у + 3z = 21,
х
+ 5у + 3z = 21,
3х + 4у + 2z = 16,
5х + 2у + 3z = 17.
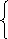
4*2 + 5*2 + 3*1 = 21,
3*2 + 4*2 + 2*1 = 16,
5*2 + 2*2 + 3*1 = 17.
Таким образом, система уравнений превратилась в тождества, то есть решение задания найдено верно.
Ответ: (2;2;1).
Примеры:
1. Составить план изготовления продукции трех видов с трех видов сырья с целью полной реализации запасов этого сырья. Известны технология затрат каждого вида сырья на изготовления единицы продукции определенного вида (матрица А) и объемы запасов сырья (матрица В).3 2
2 4
4 3 3
12
14
17
2
-
2 3
-
2 1
3 3 2
15
15
14
2.7 9
2 3
4 5 8
44
25
31
Закрепление сформированных знаний и учений:
Закрепление полученных знаний по данной теме проводится во время самостоятельного решения заданий
1. Для изготовления детских игрушек используются отходы матерчатых материалов (М1, М2, М2) различных размеров. Вычислить количество материала, который расходуется при раскрое, если количество необходимых заготовок представлена таблицей:
2. Самостоятельная работа. Предлагаются 8 вариантов
Составить план изготовления продукции трех видов с трех видов сырья с целью полной реализации запасов этого сырья. Известны технология затрат каждого вида сырья на изготовления единицы продукции определенного вида (матрица А) и объемы запасов сырья (матрица В).
Задачи для домашнего решения
Составить план оптимальной загрузки участка на последовательную обработку продукции трёх видов с целью отсутствия простоев трёх станков во время, которое предусмотрено нормативами для их безостановочной работы. Сведения о сроке обработки каждого вида продукции на соответствующем станке заданы в условных единицах времени матрицей А, время безостановочной работы станков - матрицей В.
1) 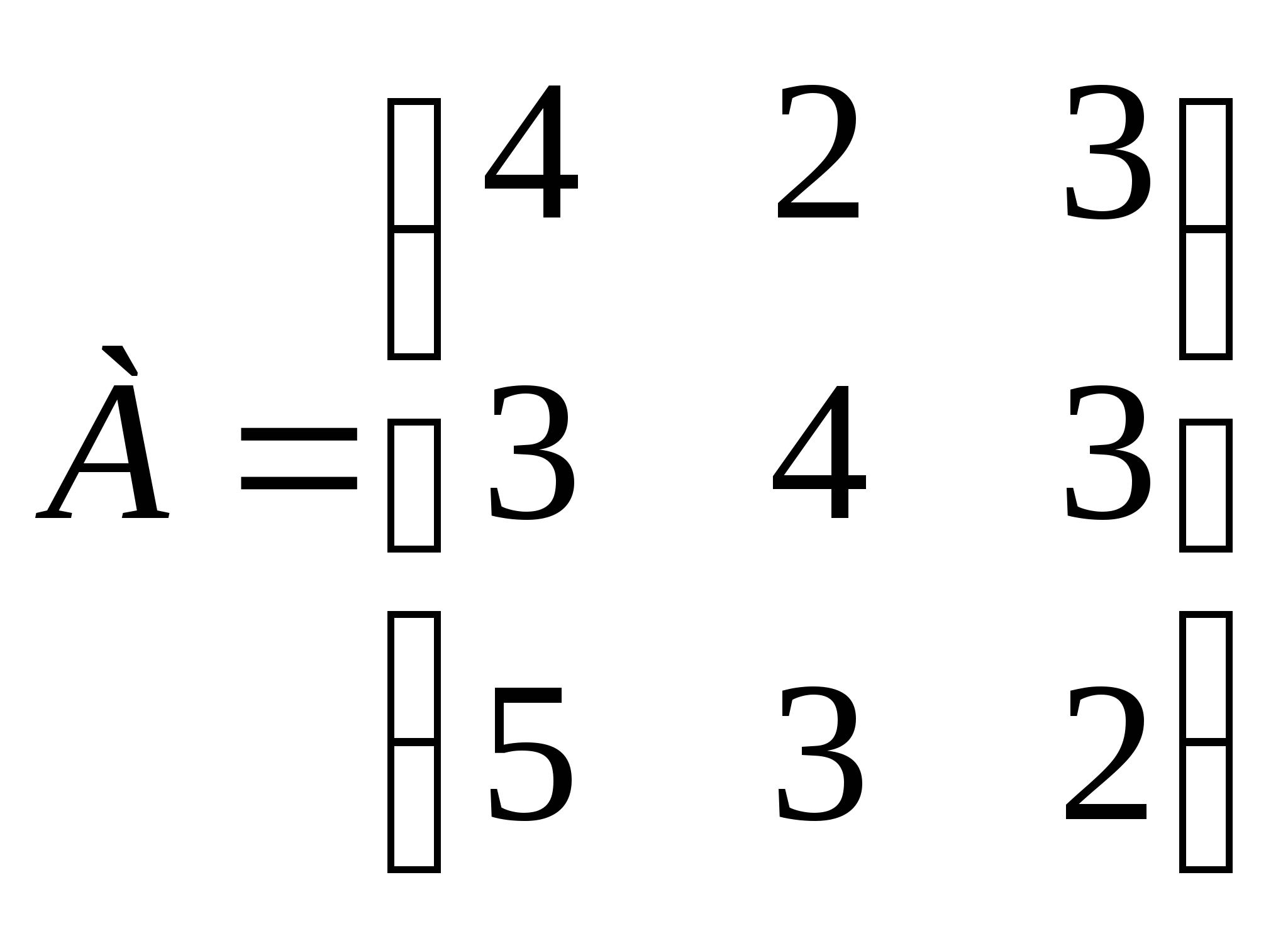 ,
, 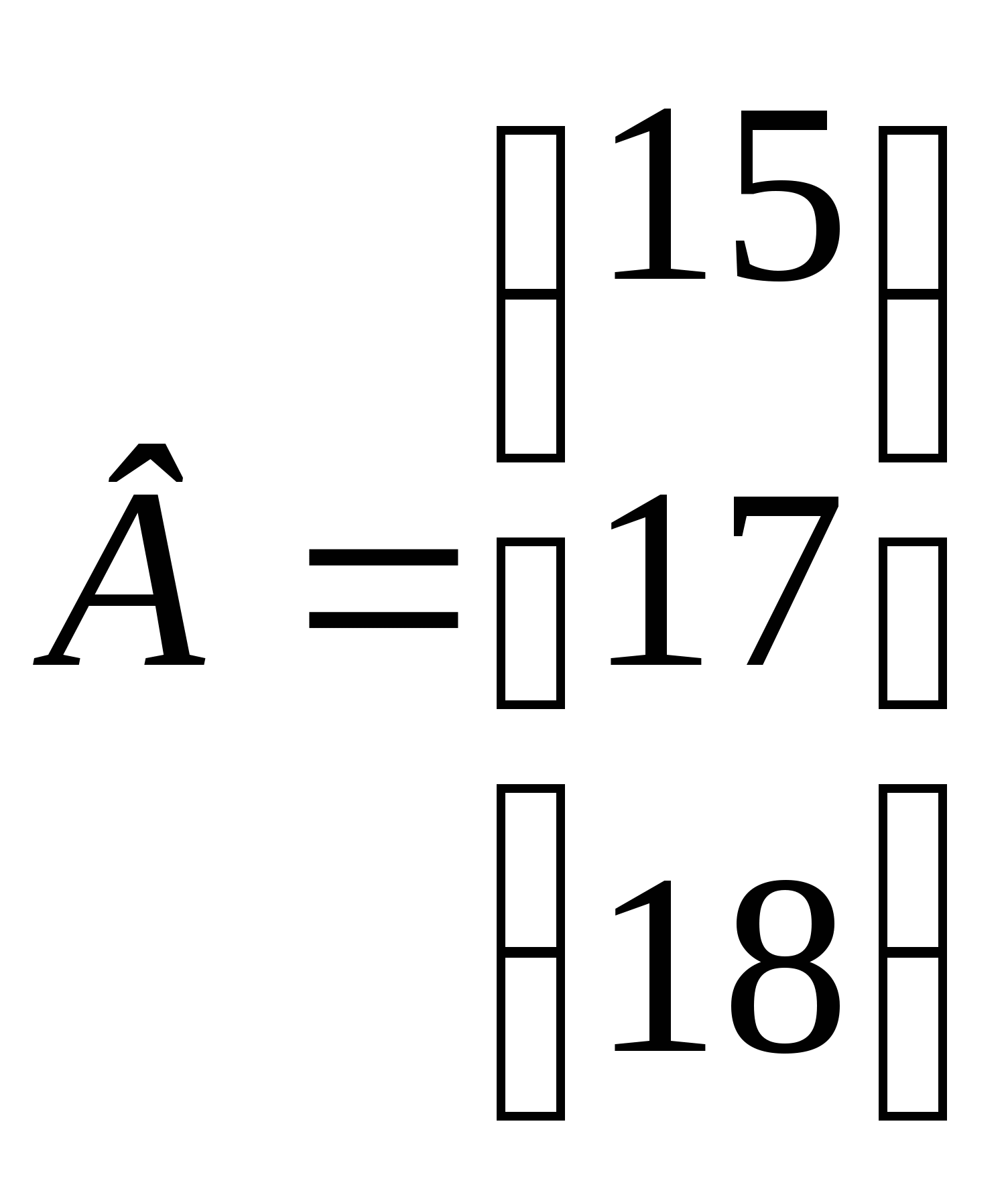 2)
2) 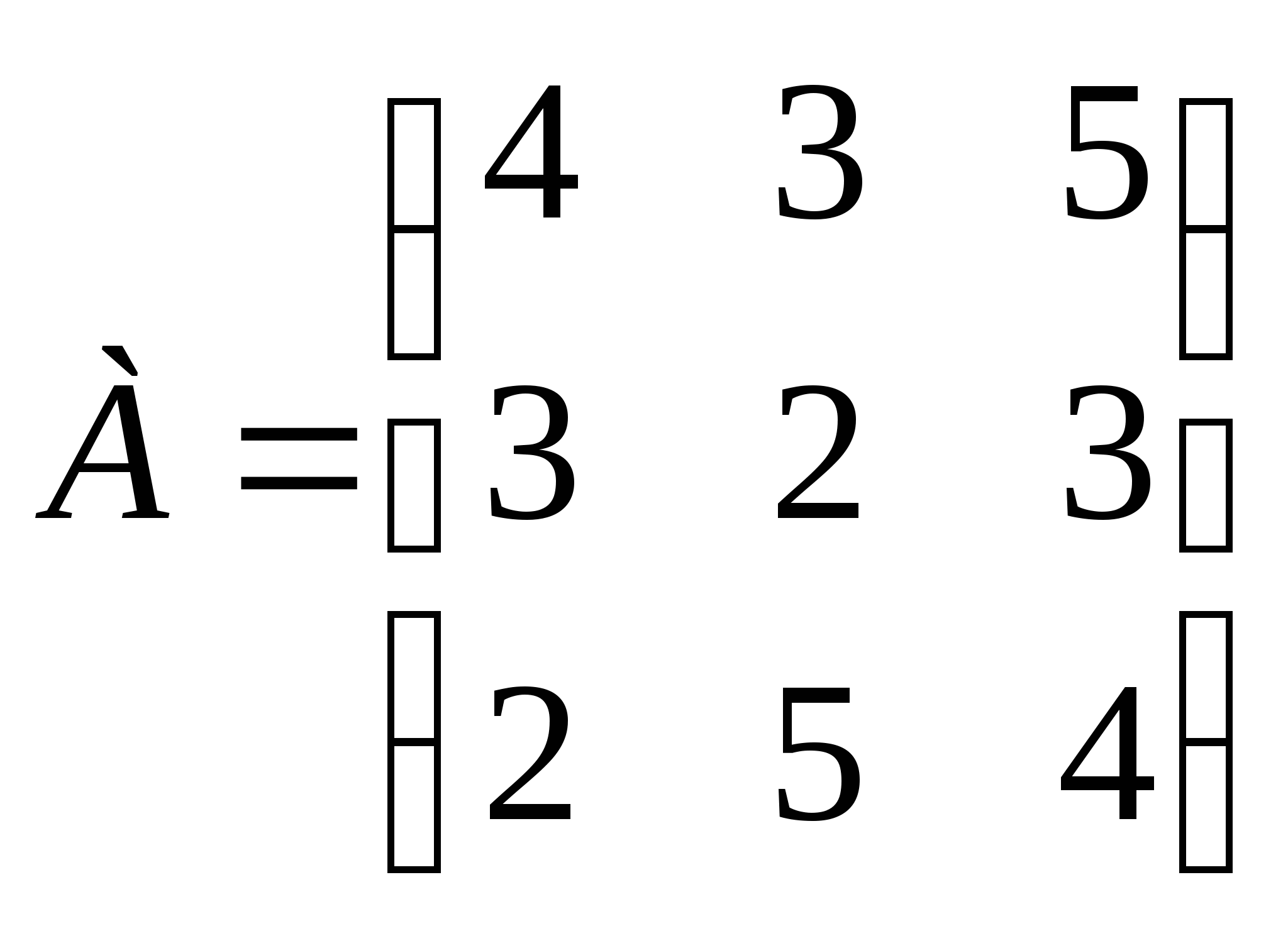 ,
, 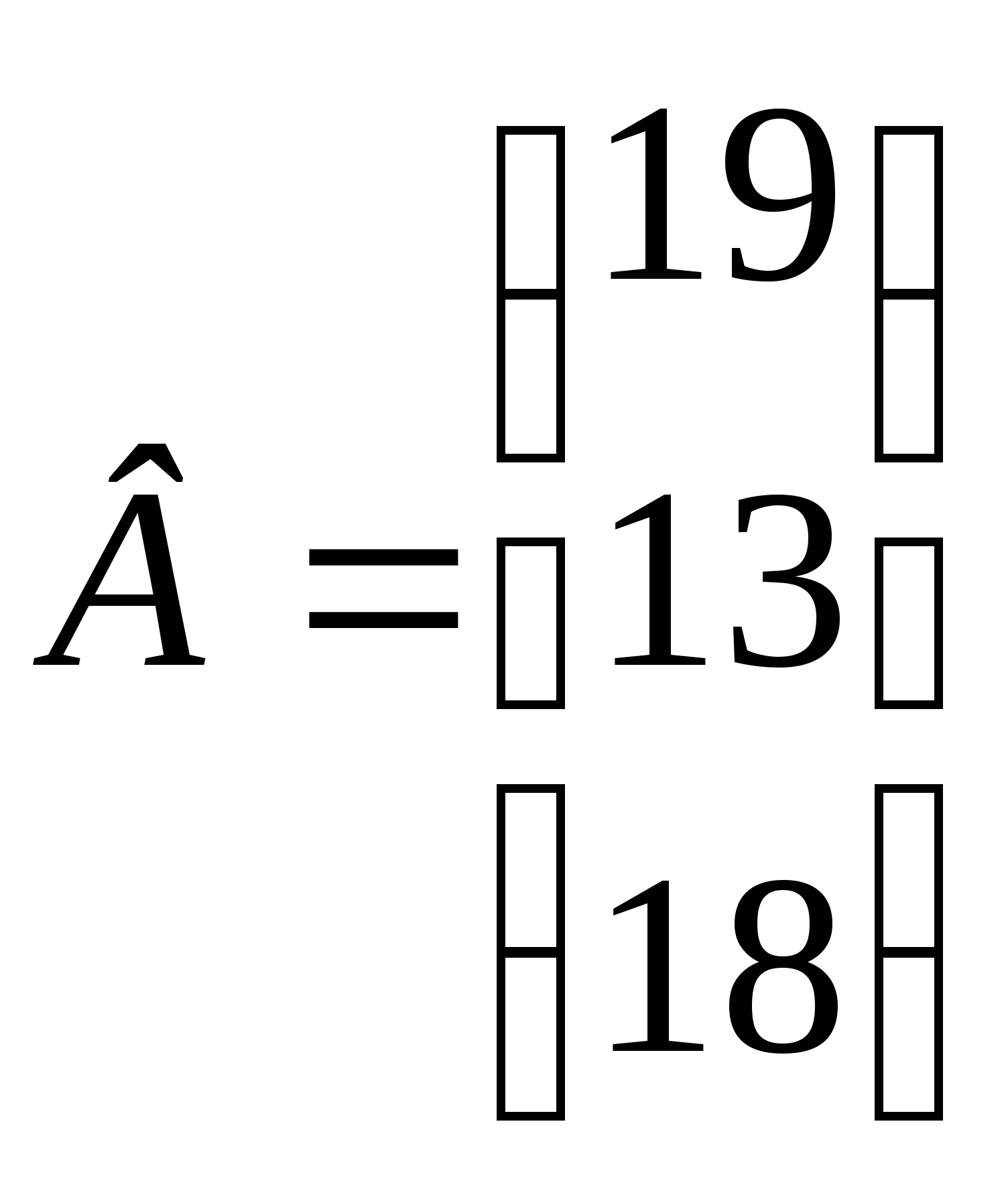 .
.
Практическое занятие 6
Практическая работа 5
По теме «Вычисление первого и второго замечательных пределов»
Цель работы: закрепить понятие предела функции , научиться вычислять первый и второй замечательные пределы.
Актуализация знаний
Фронтальный опрос
1. Дать понятие предела функции, свойства пределов.
2. Основные методы вычисления пределов..
3. Вычисление первого и второго замечательных пределов..
Краткие теоретические и учебно-методические материалы по теме практической работы
Тригонометрические функции, которые стоят под знаком предела, приводятся к первому замечательному пределу:
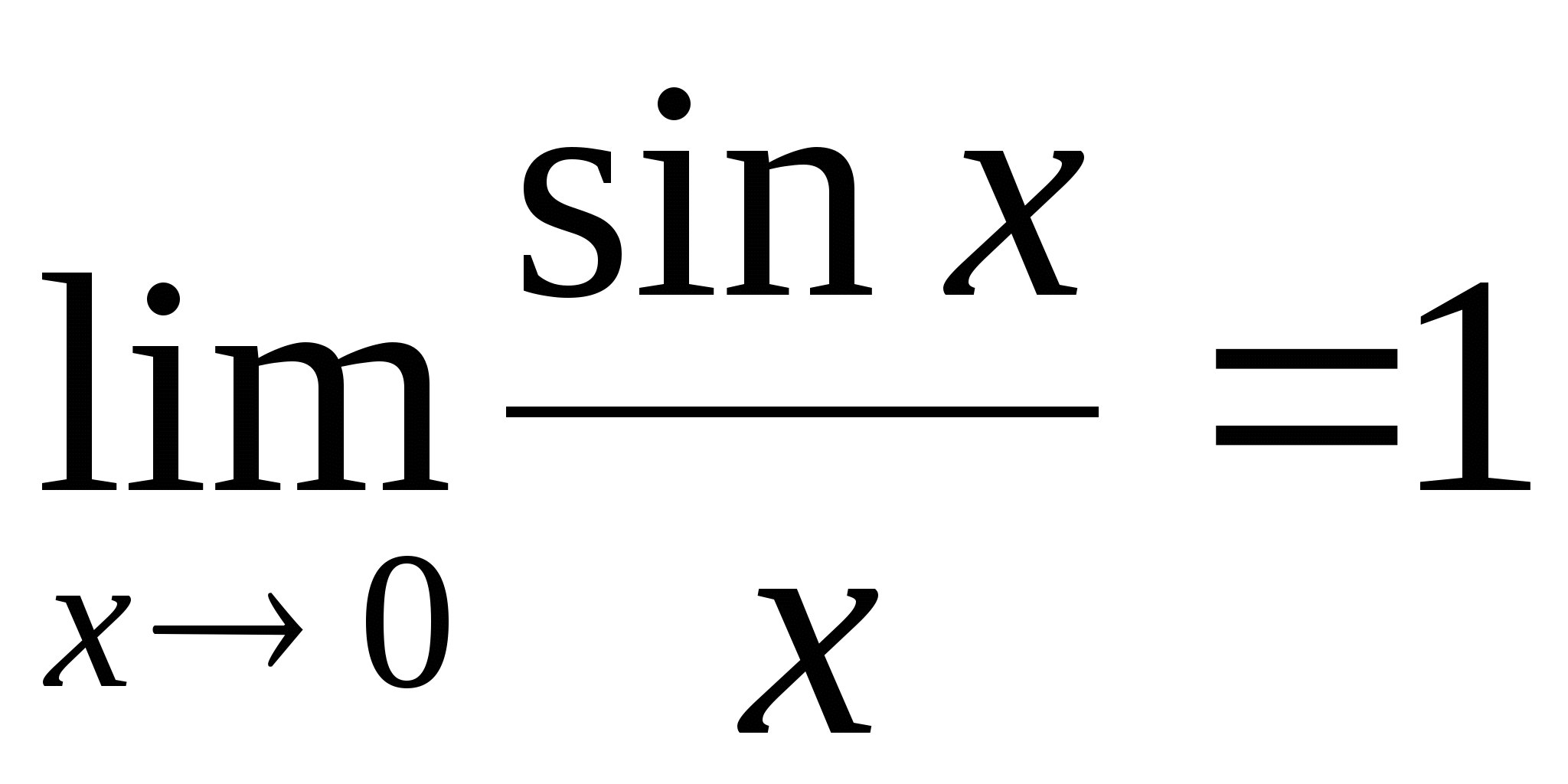
Дополнительные формулы: 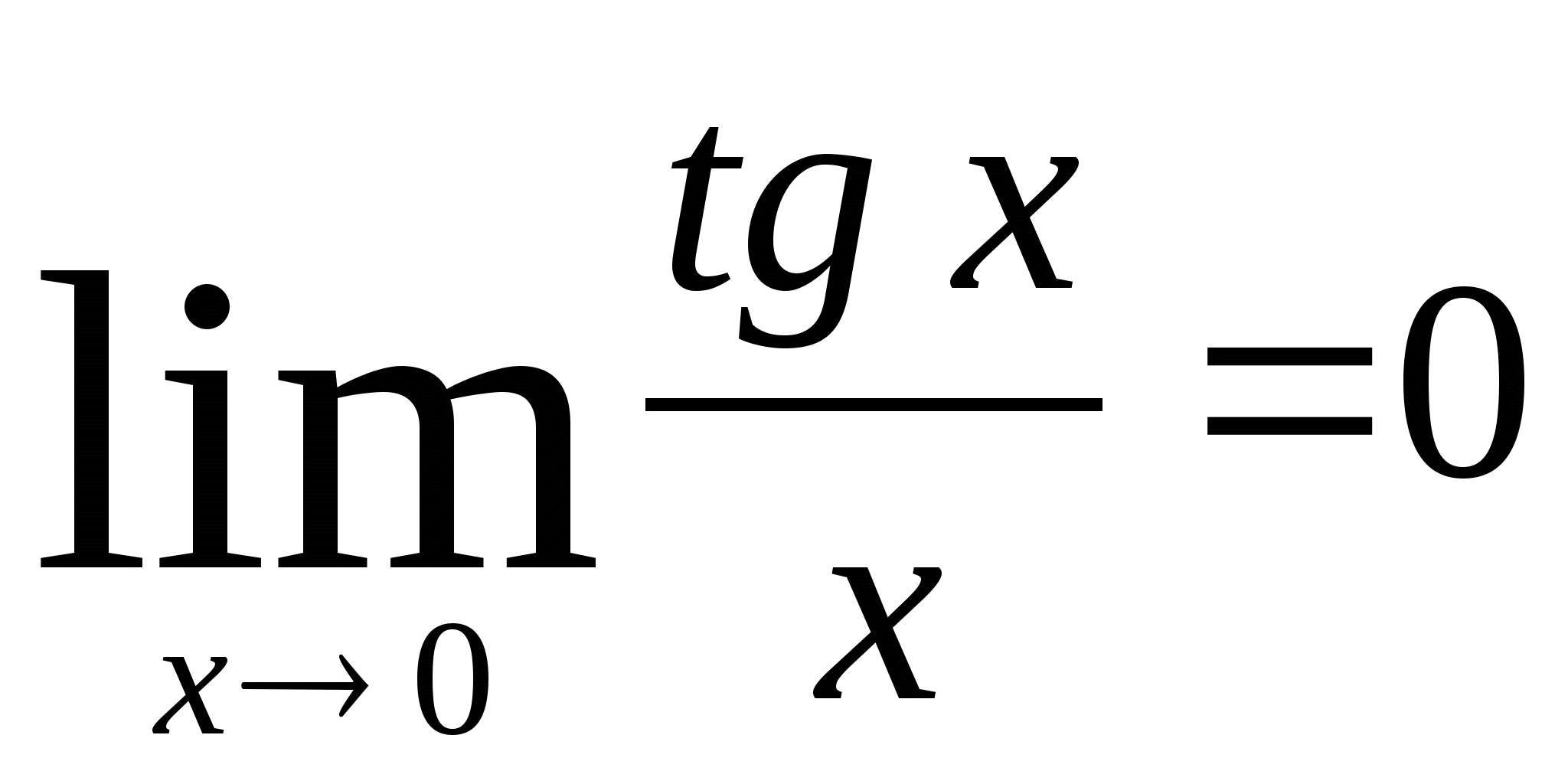

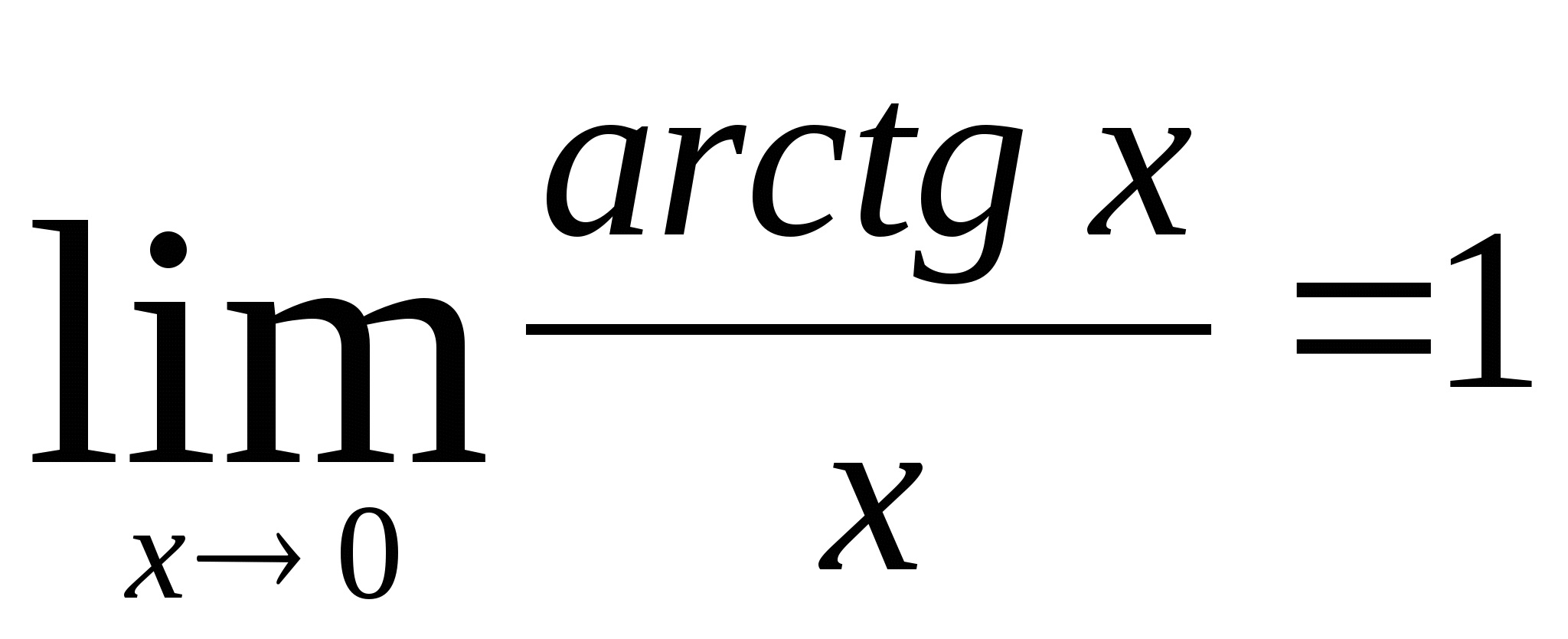
![]()
![]()
Второй замечательный предел:
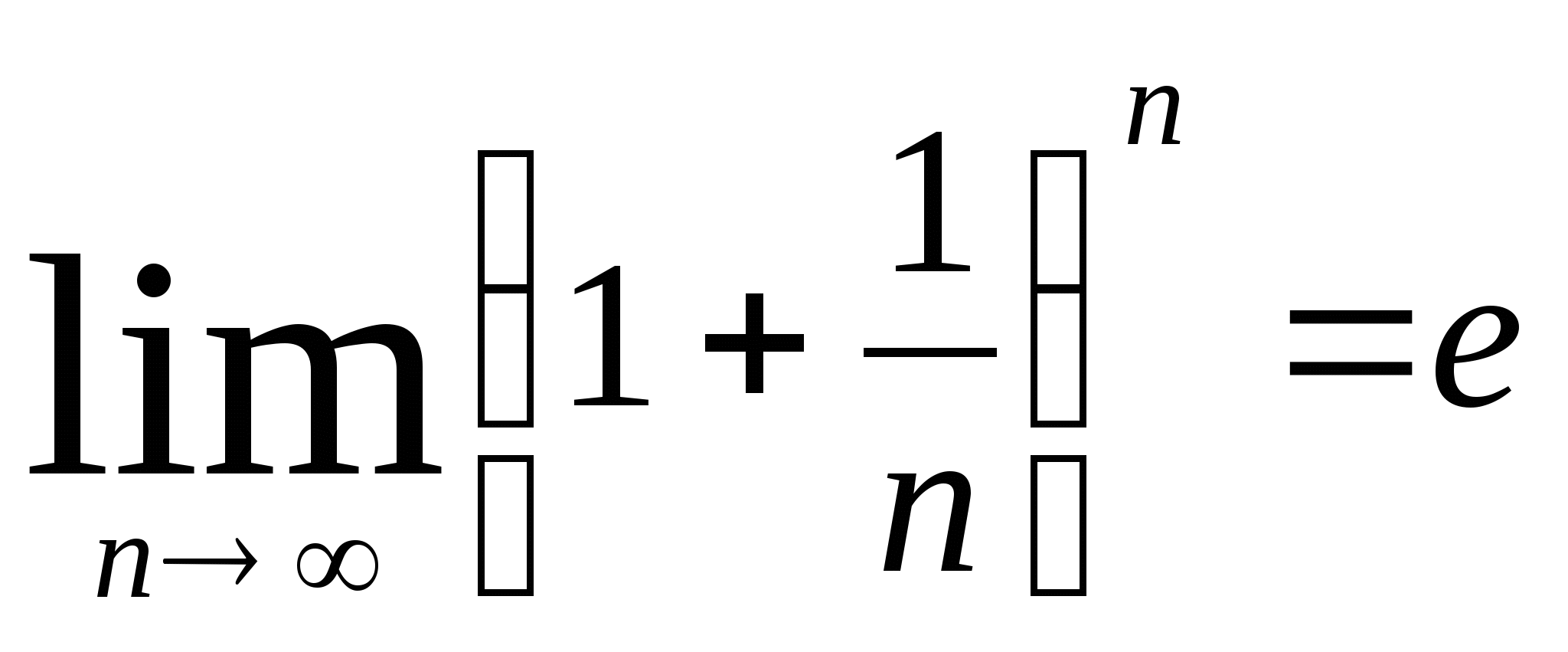
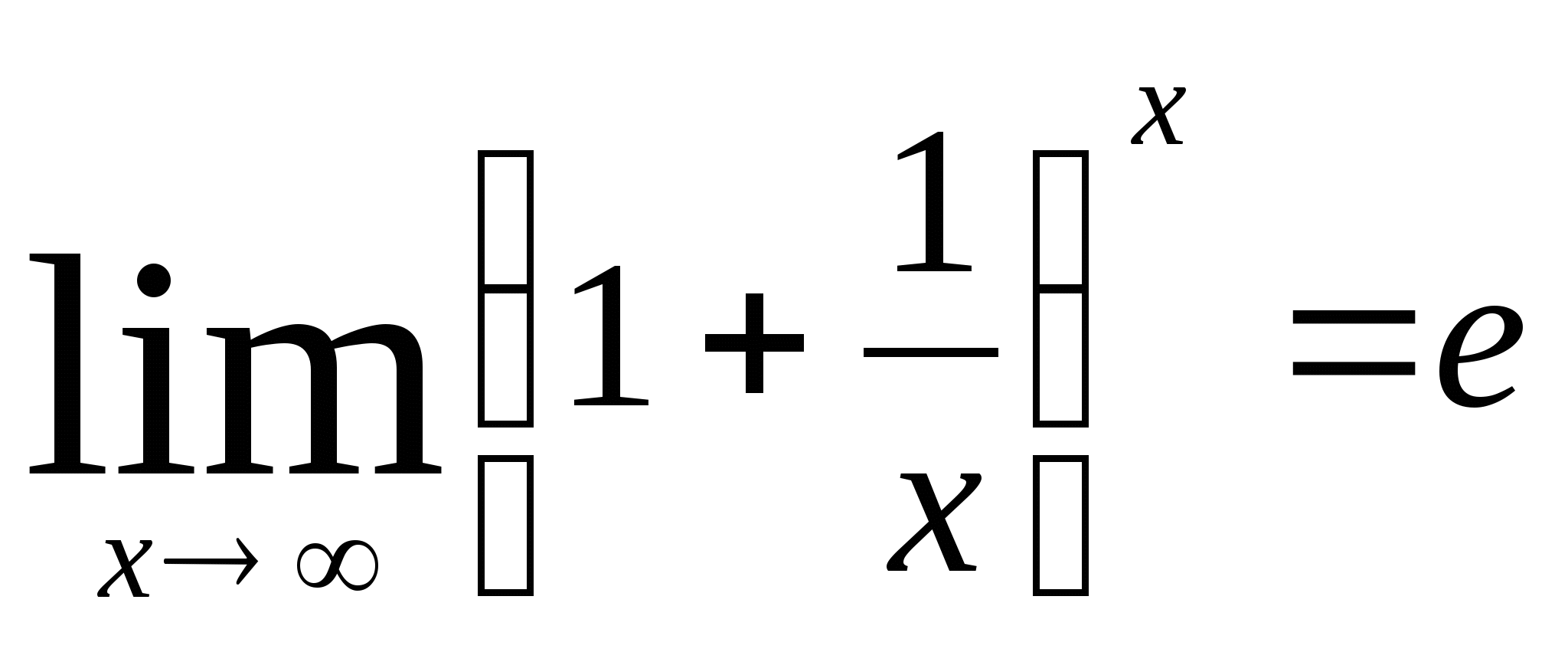
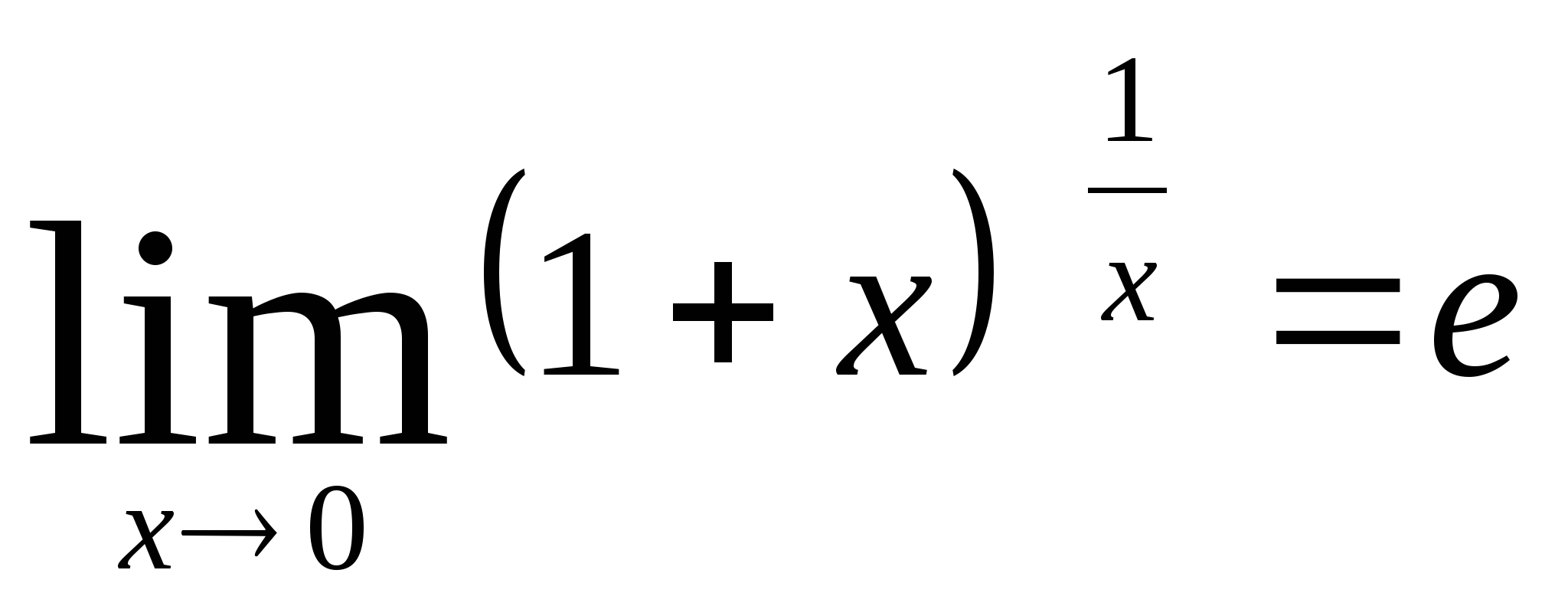
Формирование необходимых знаний и умений
Коллективное решение и обсуждение предложенных задач
1) 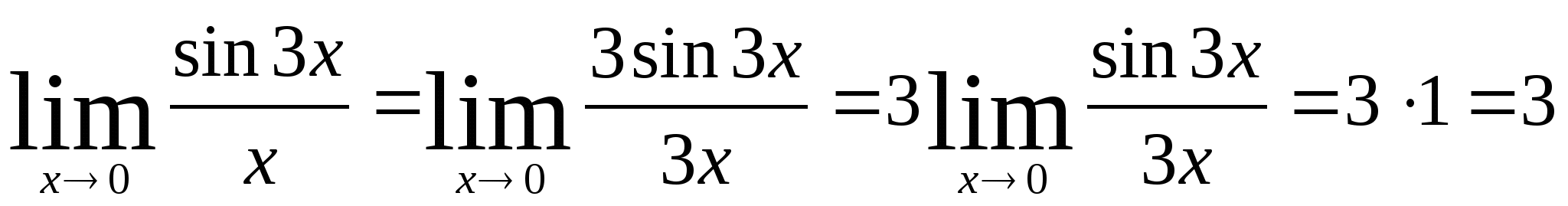
2) 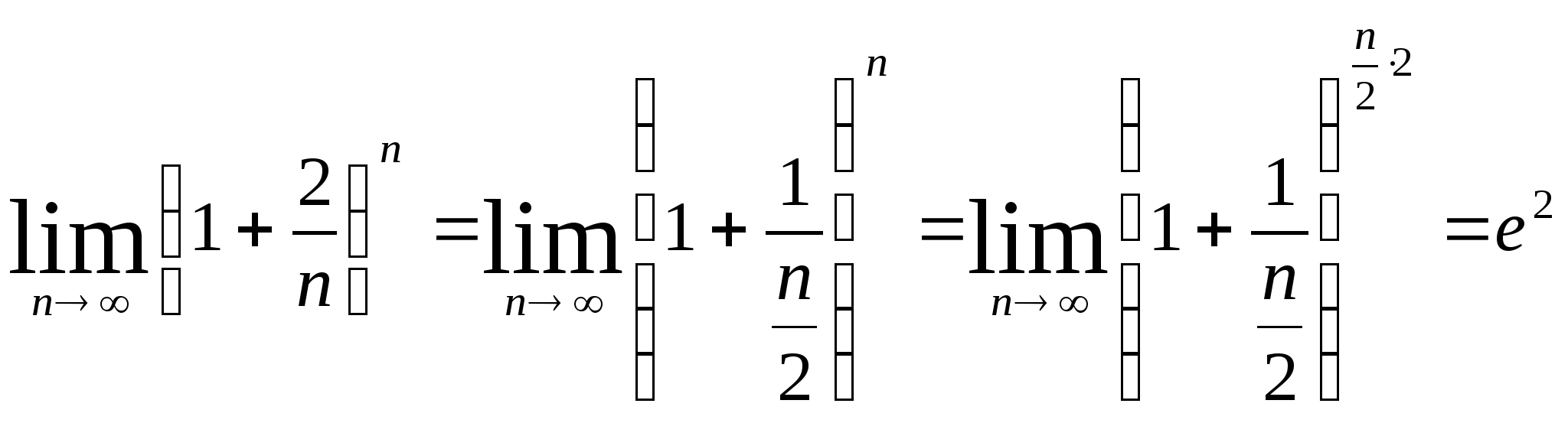
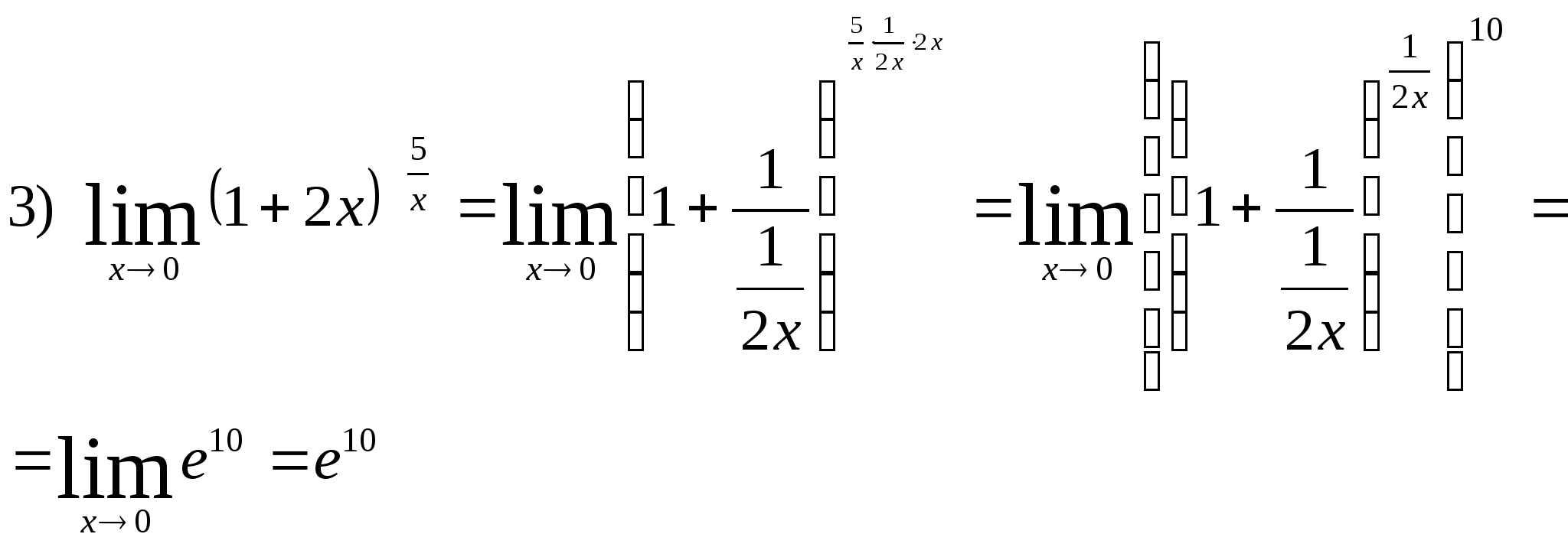
4) 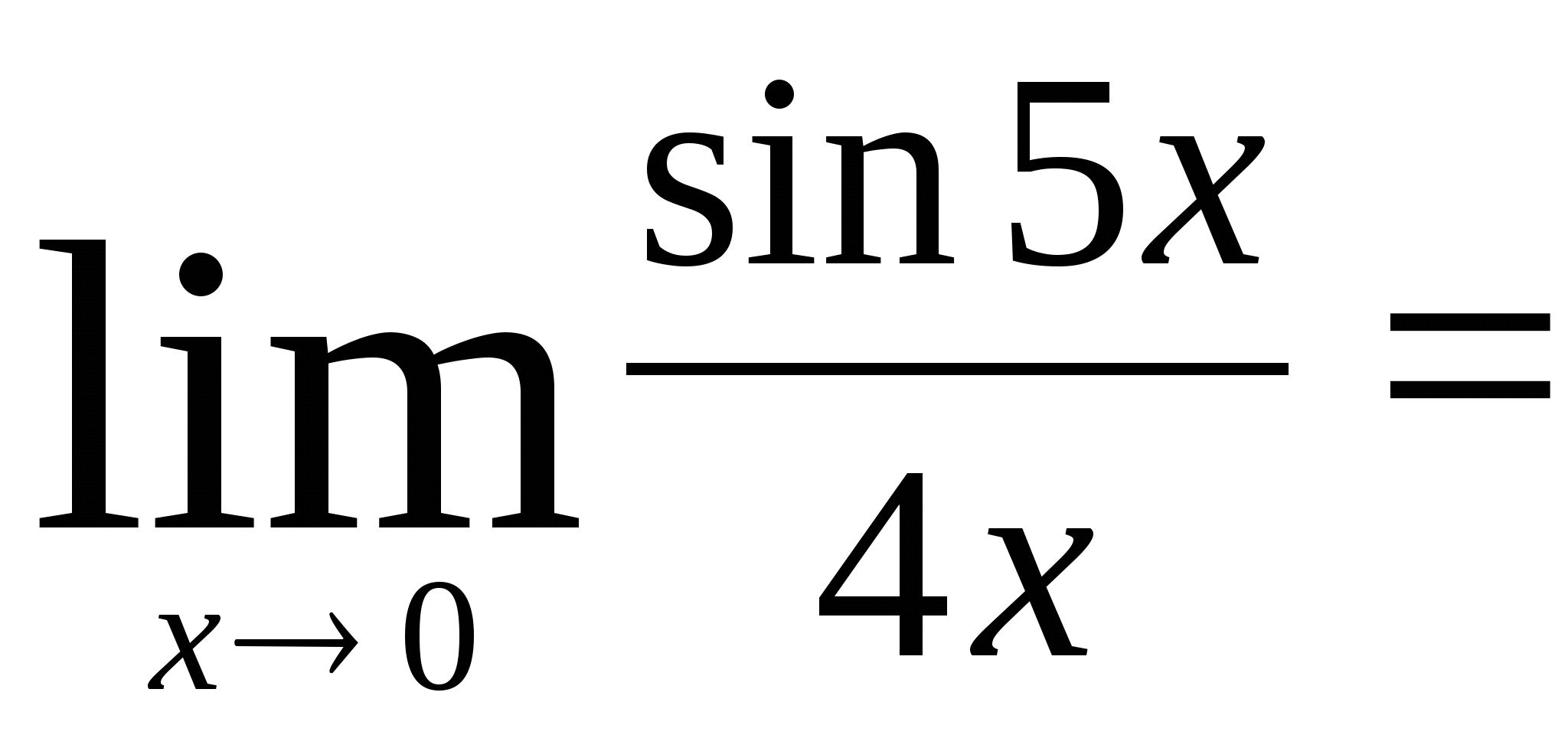
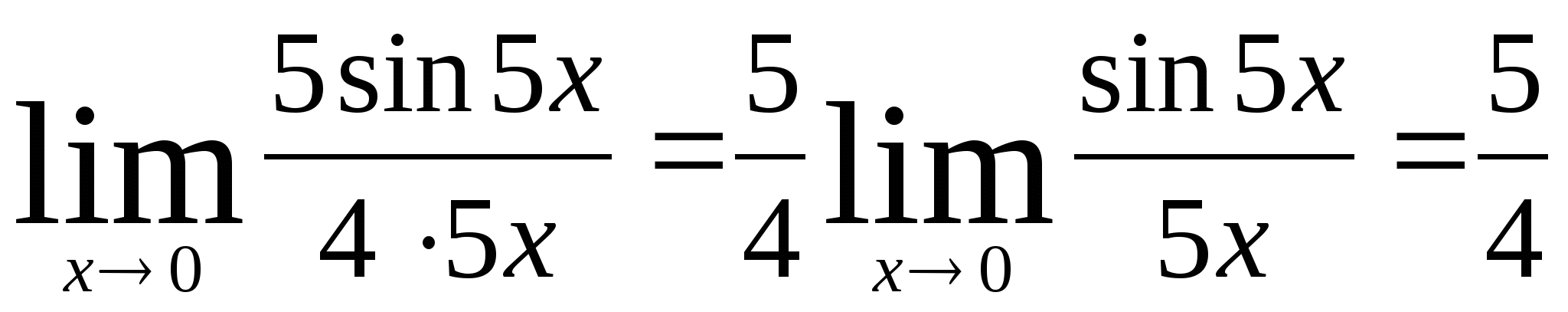
Примеры:
1) 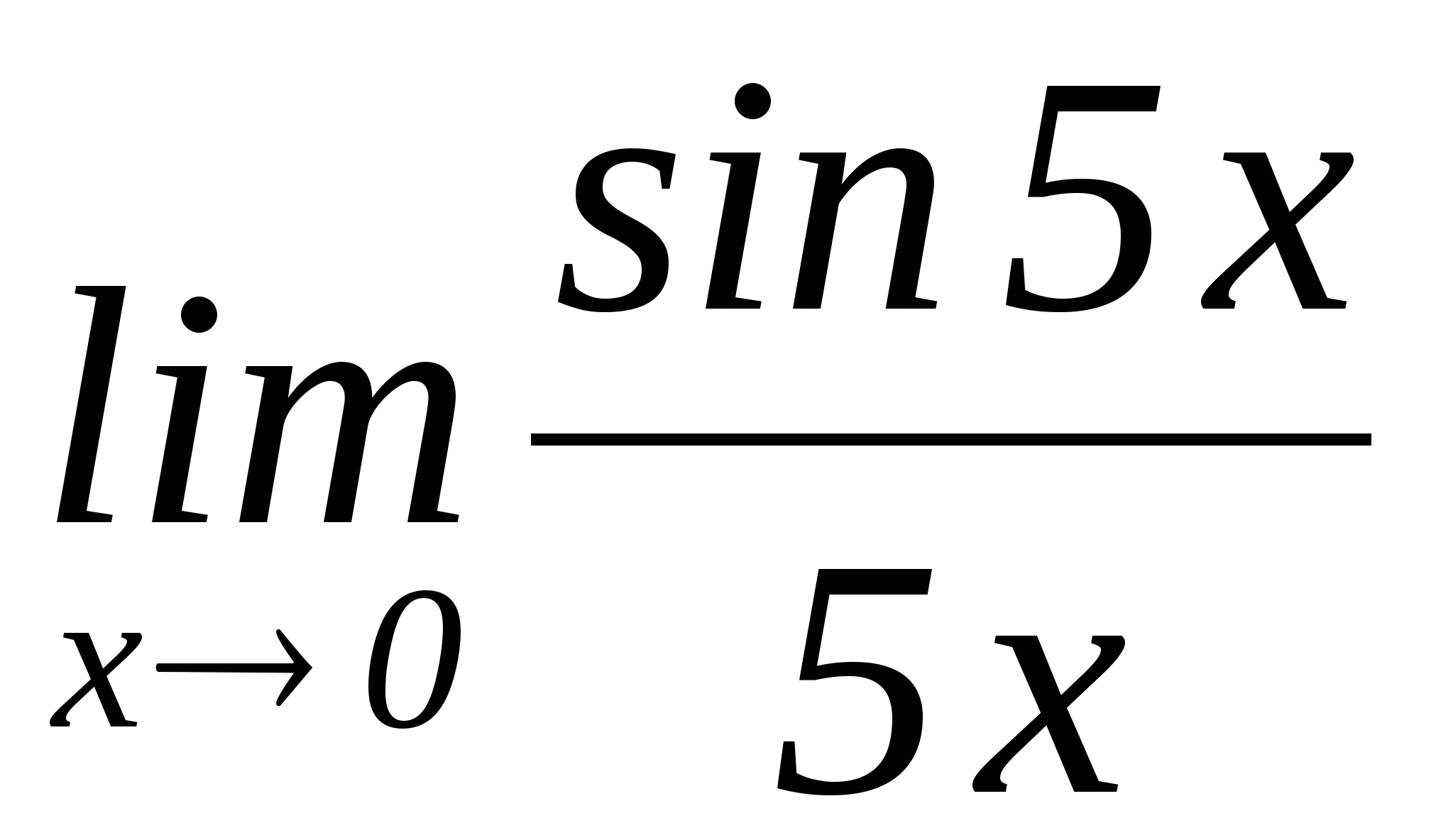 2)
2) 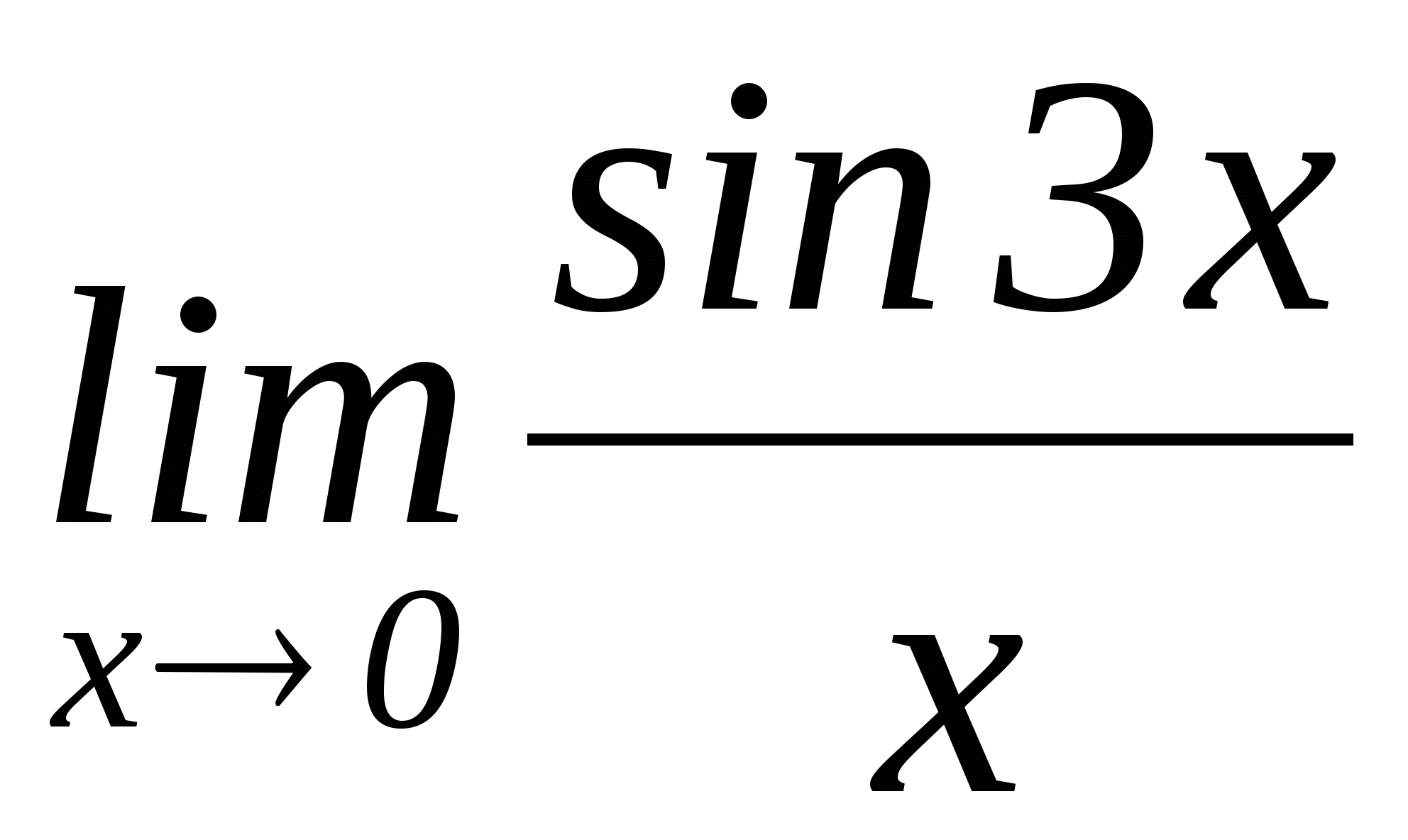
3) 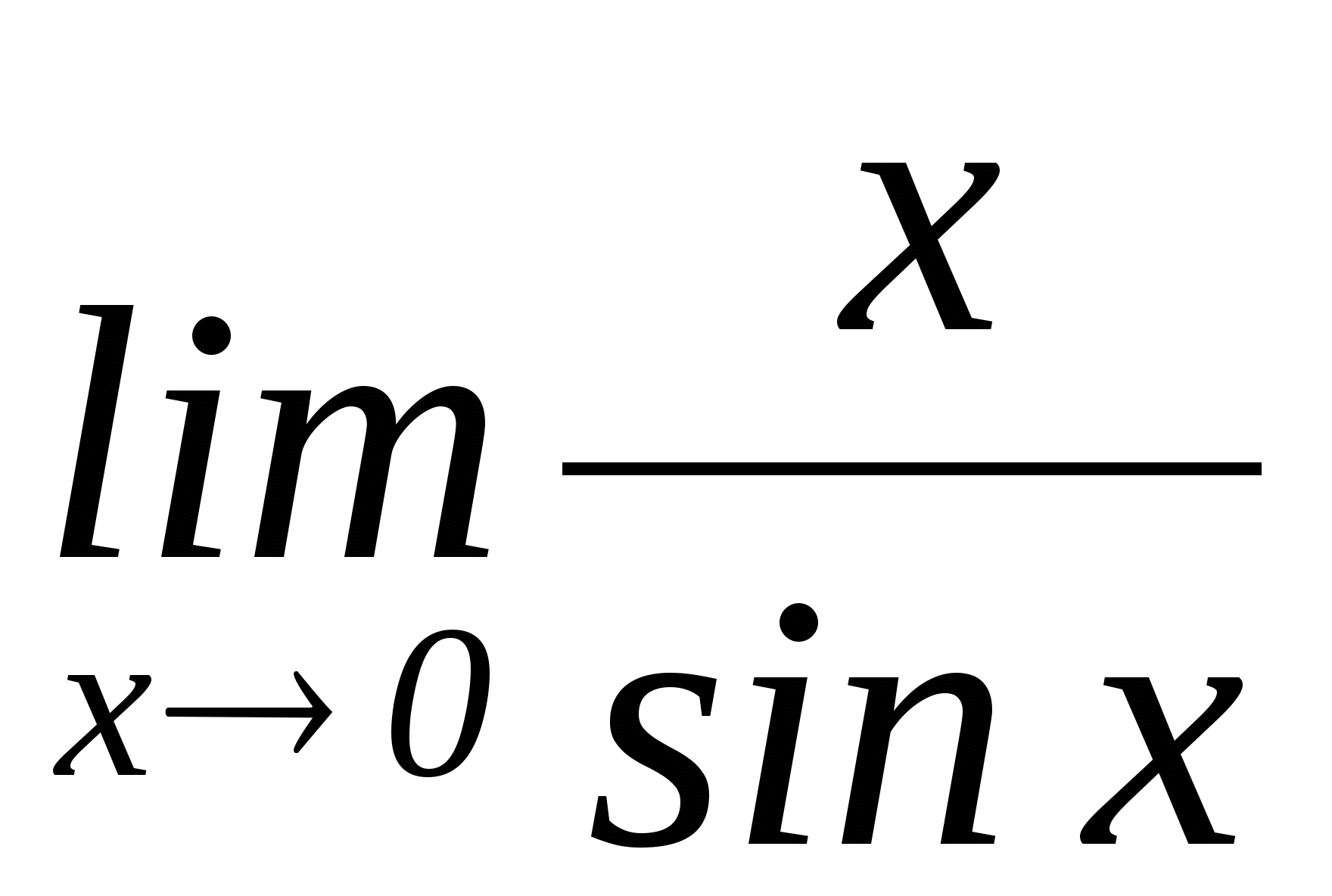 4)
4) ![]()
5) ![]() 6)
6) 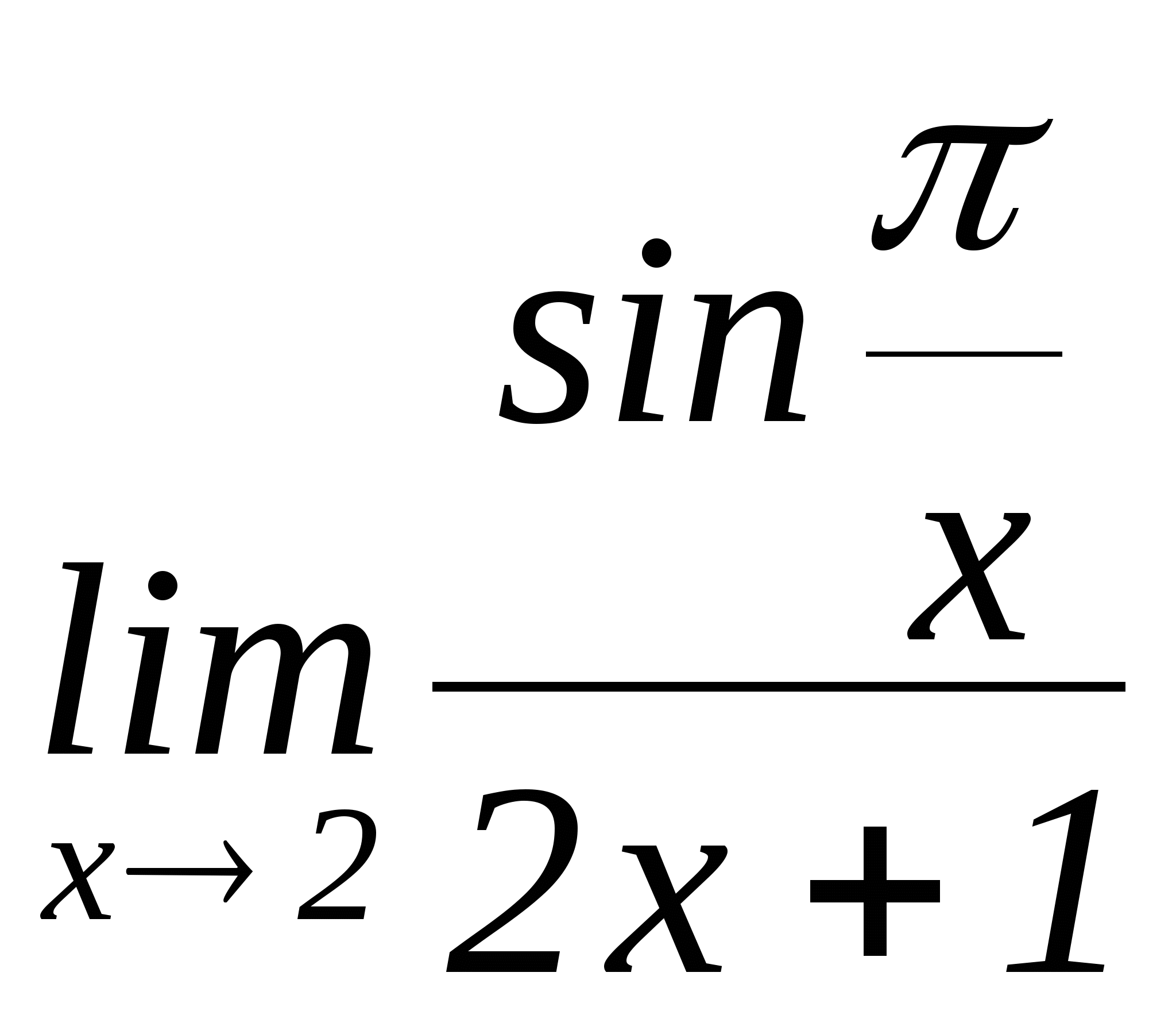
7) 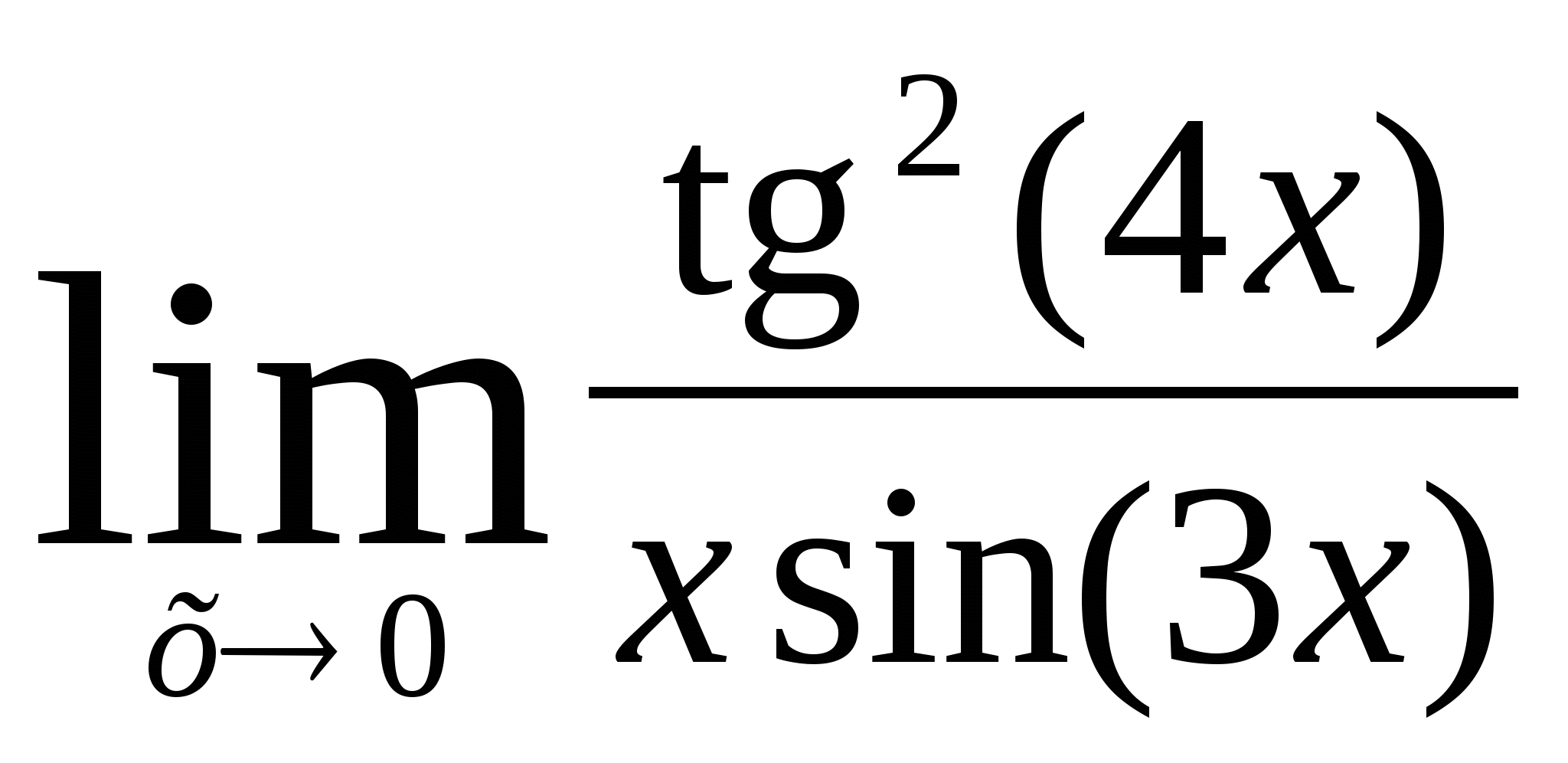 8)
8) 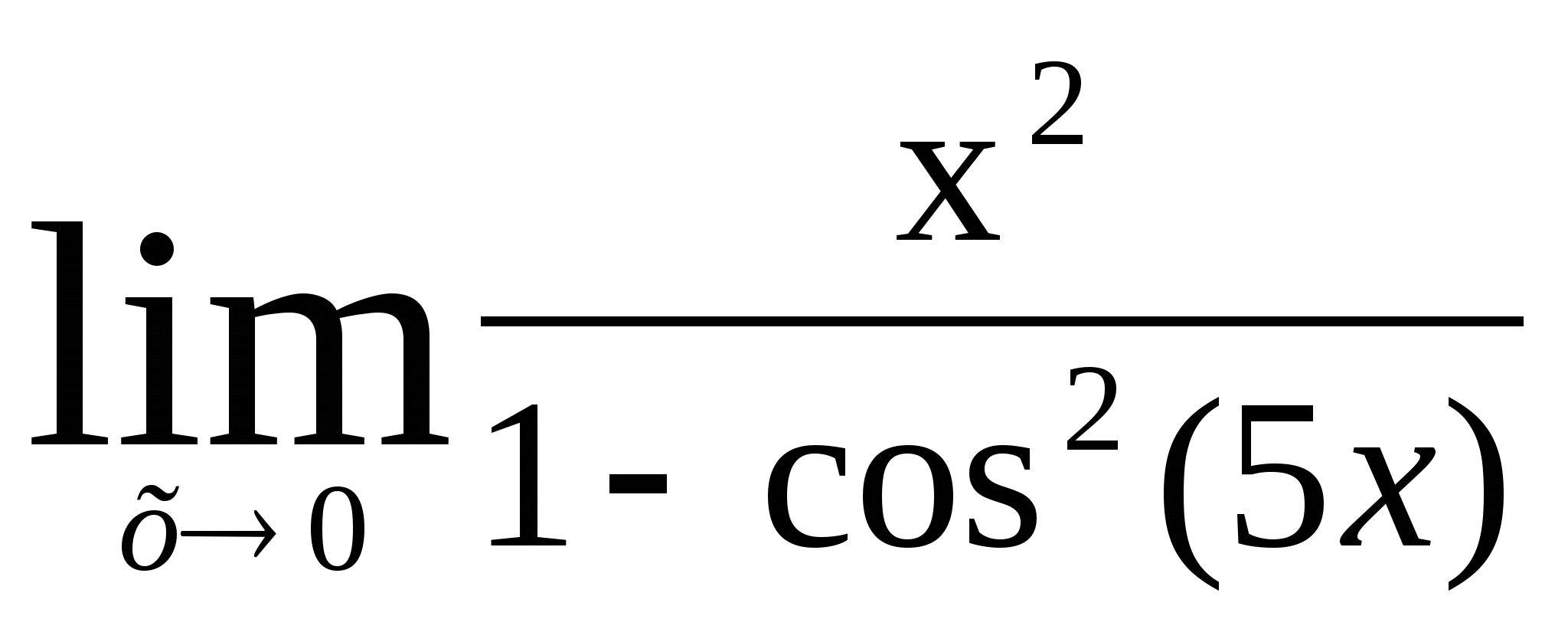
Закрепление сформированных знаний и учений:
Закрепление полученных знаний по данной теме проводится во время самостоятельного решения заданий
1) 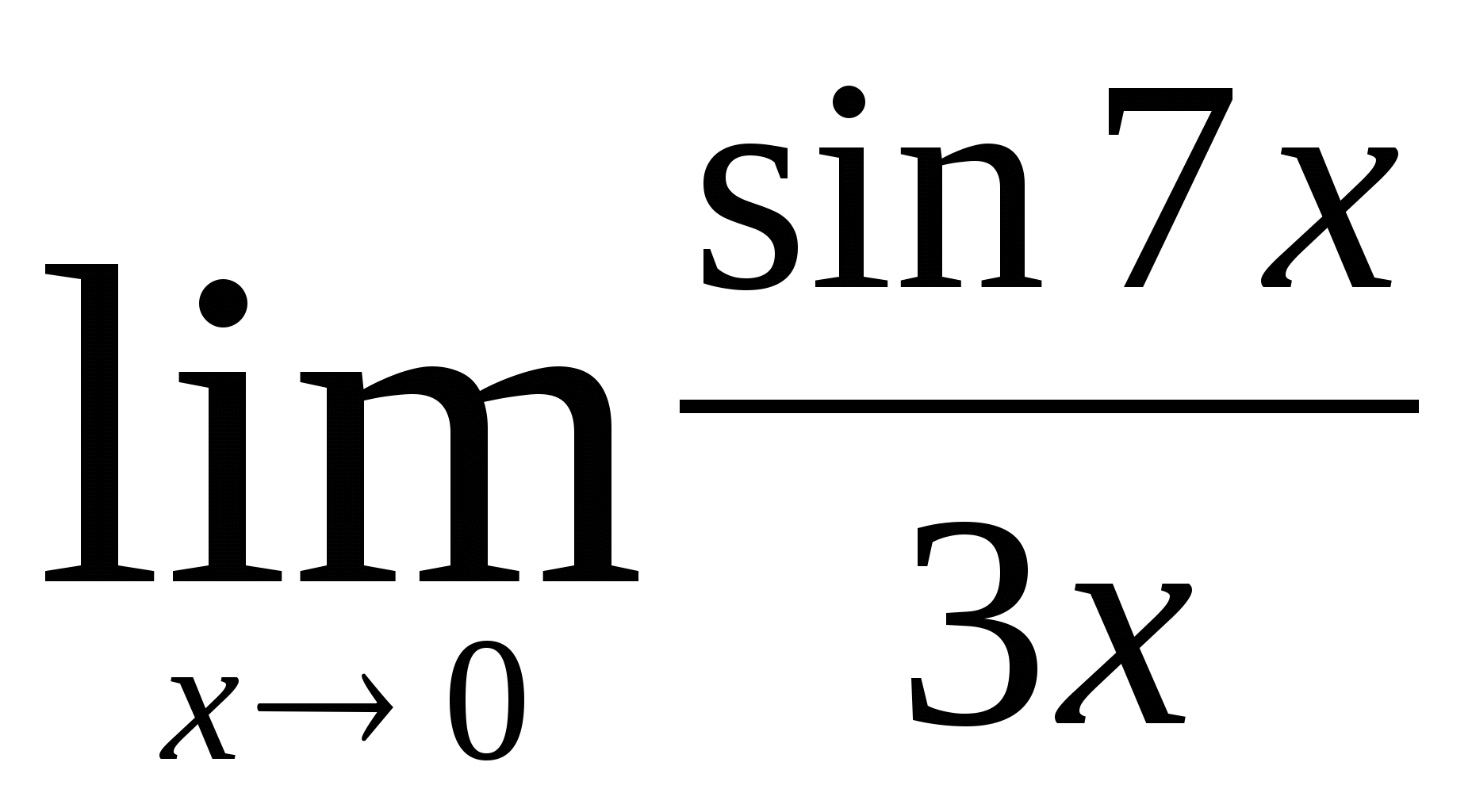 2)
2) 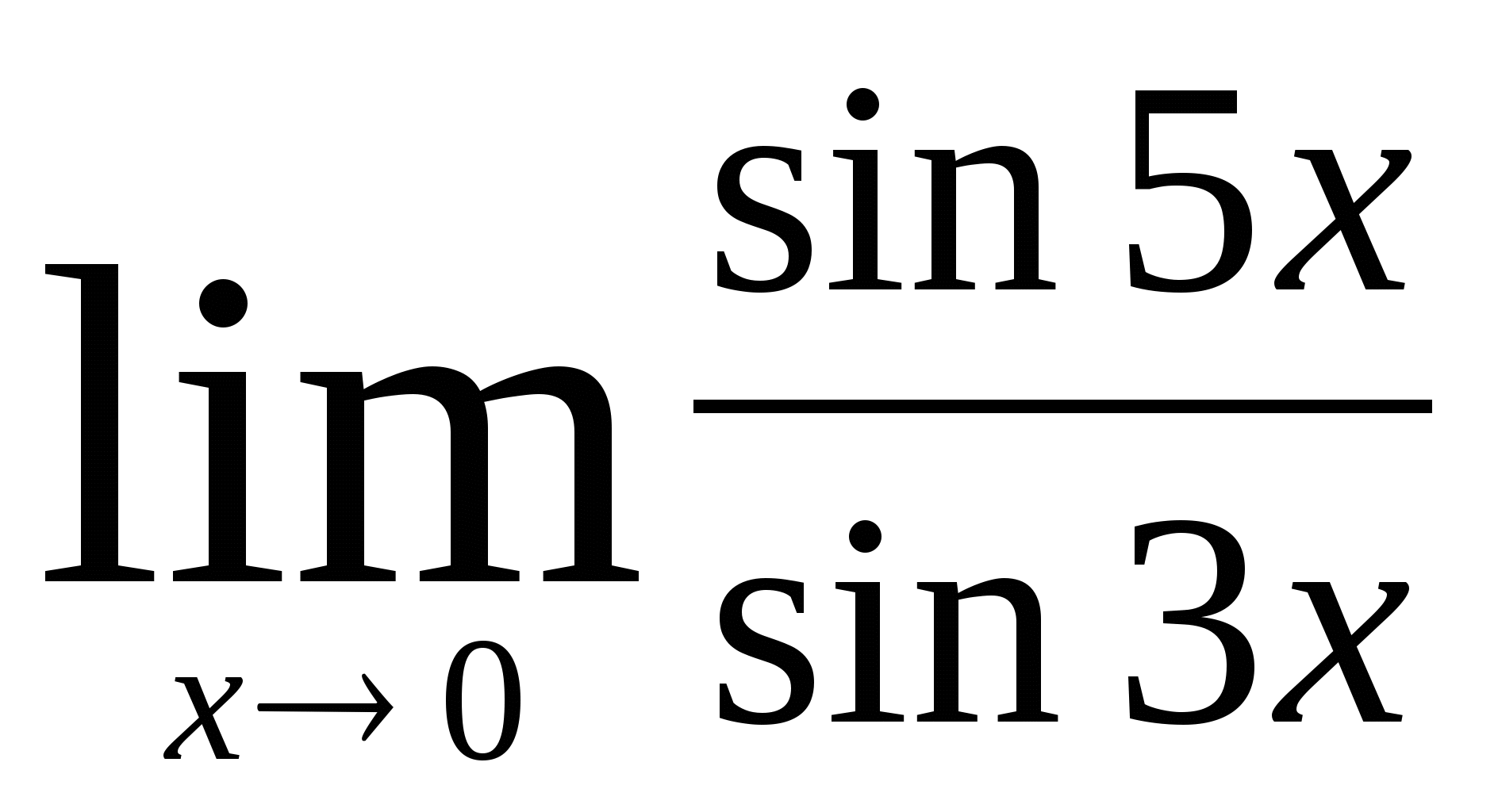
3) 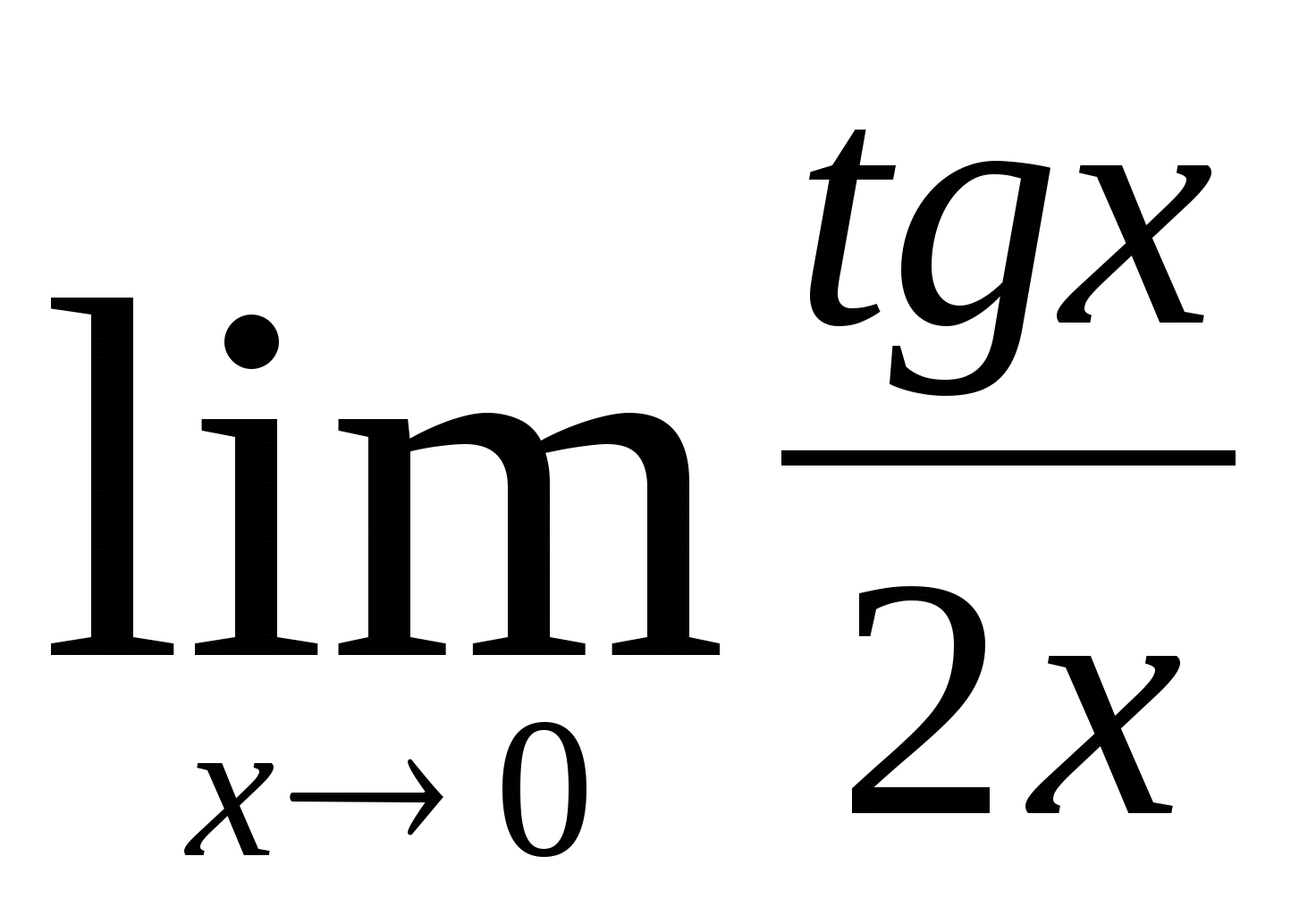 4)
4) 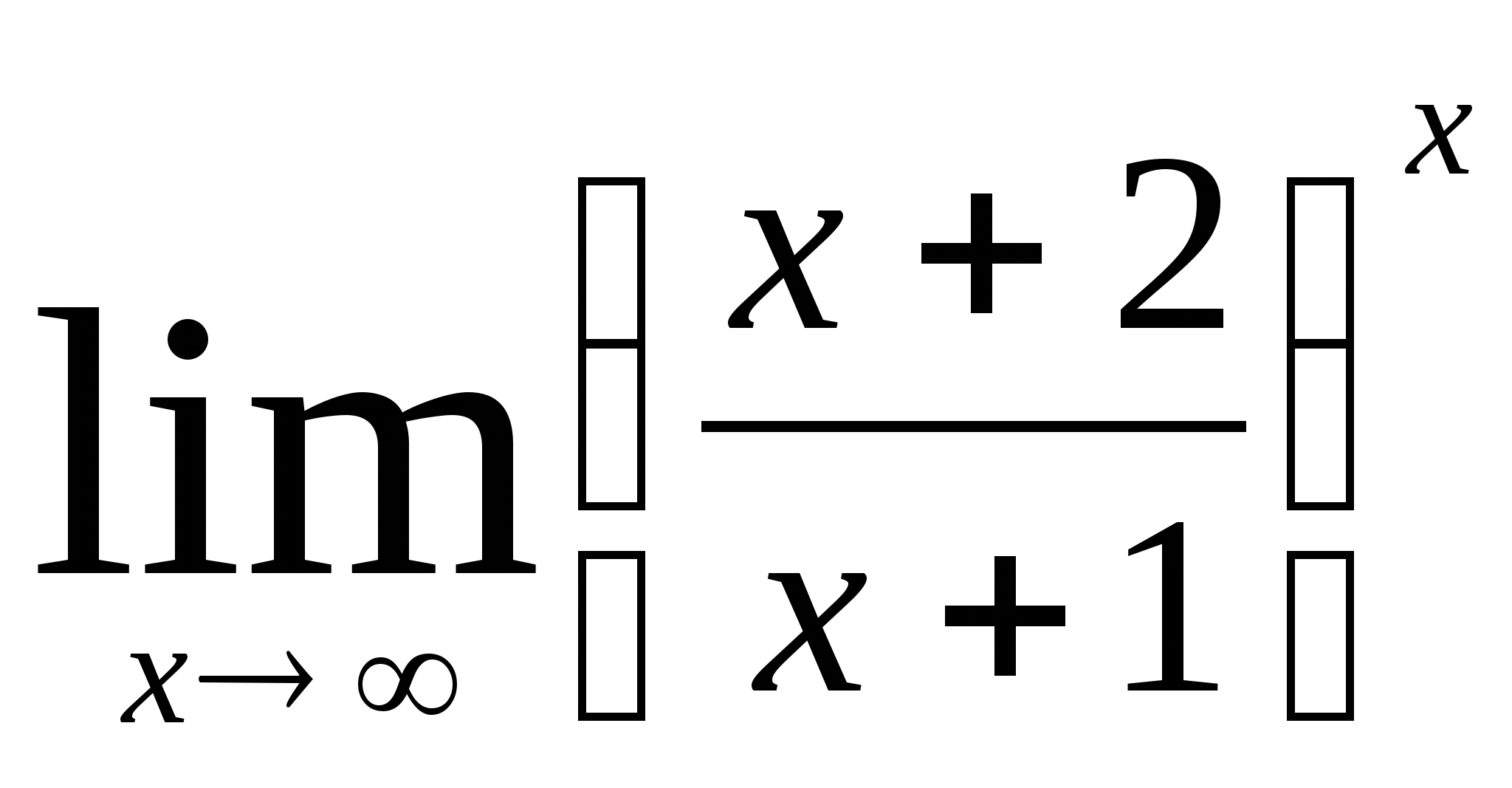 5)
5) 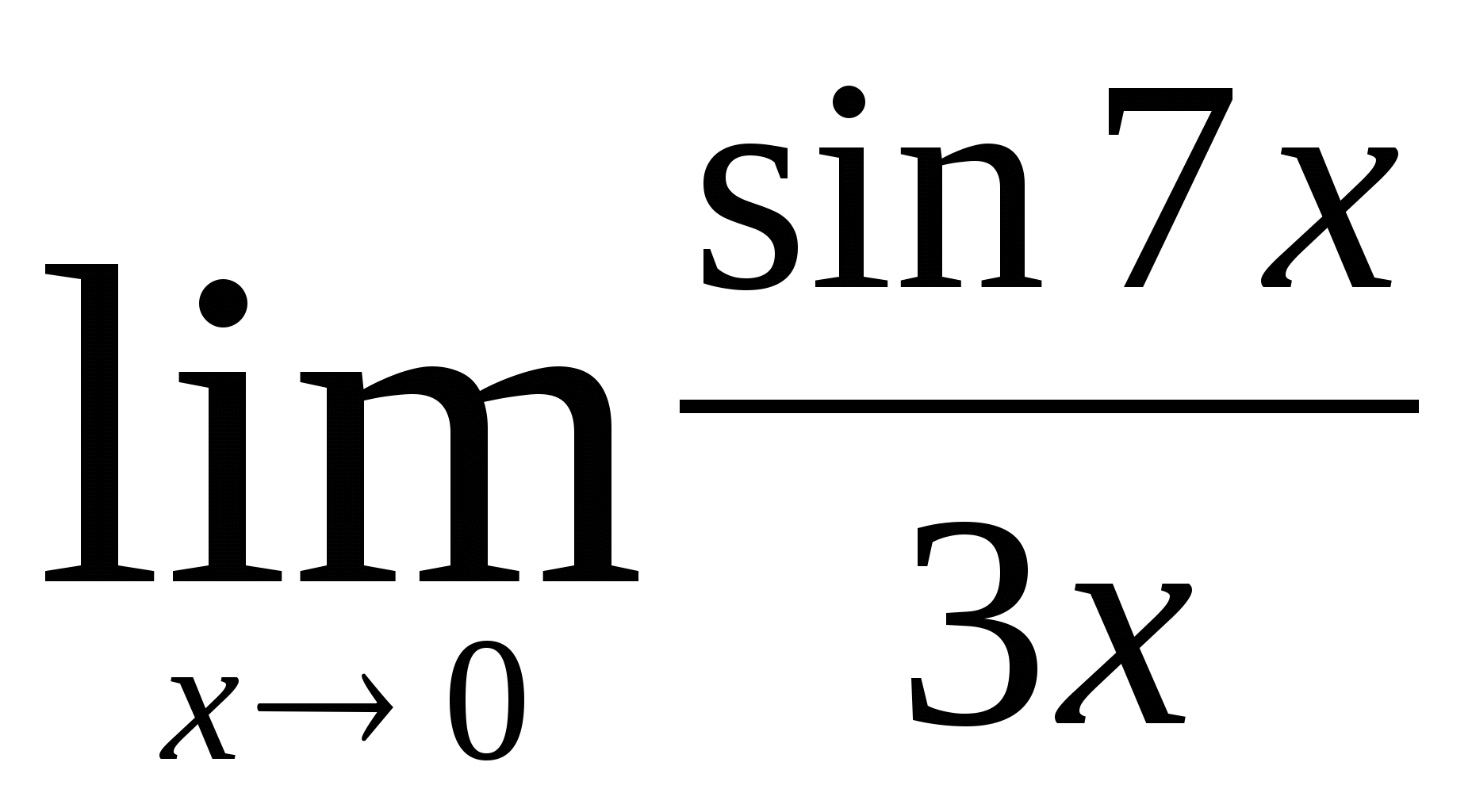
6) 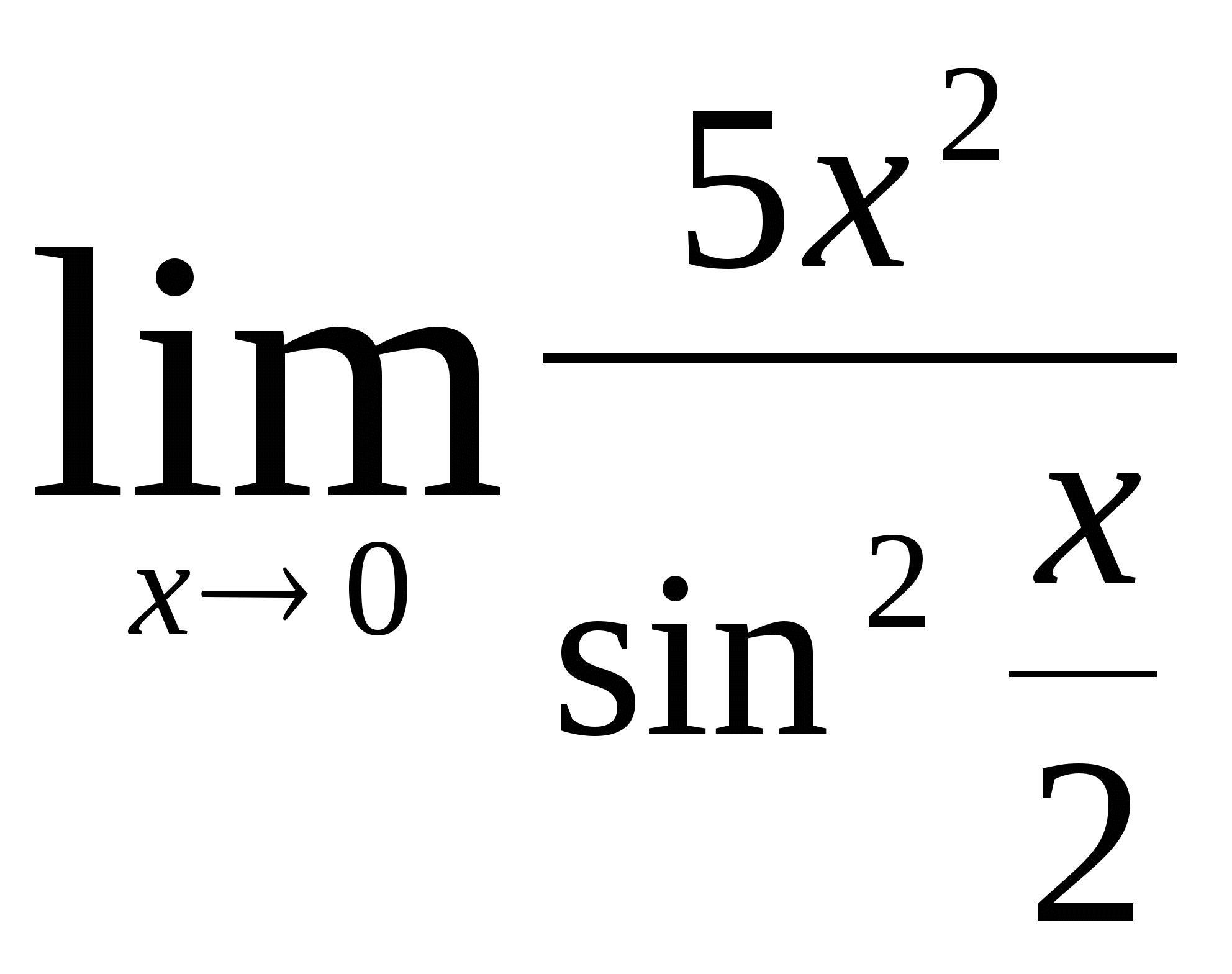 7)
7) 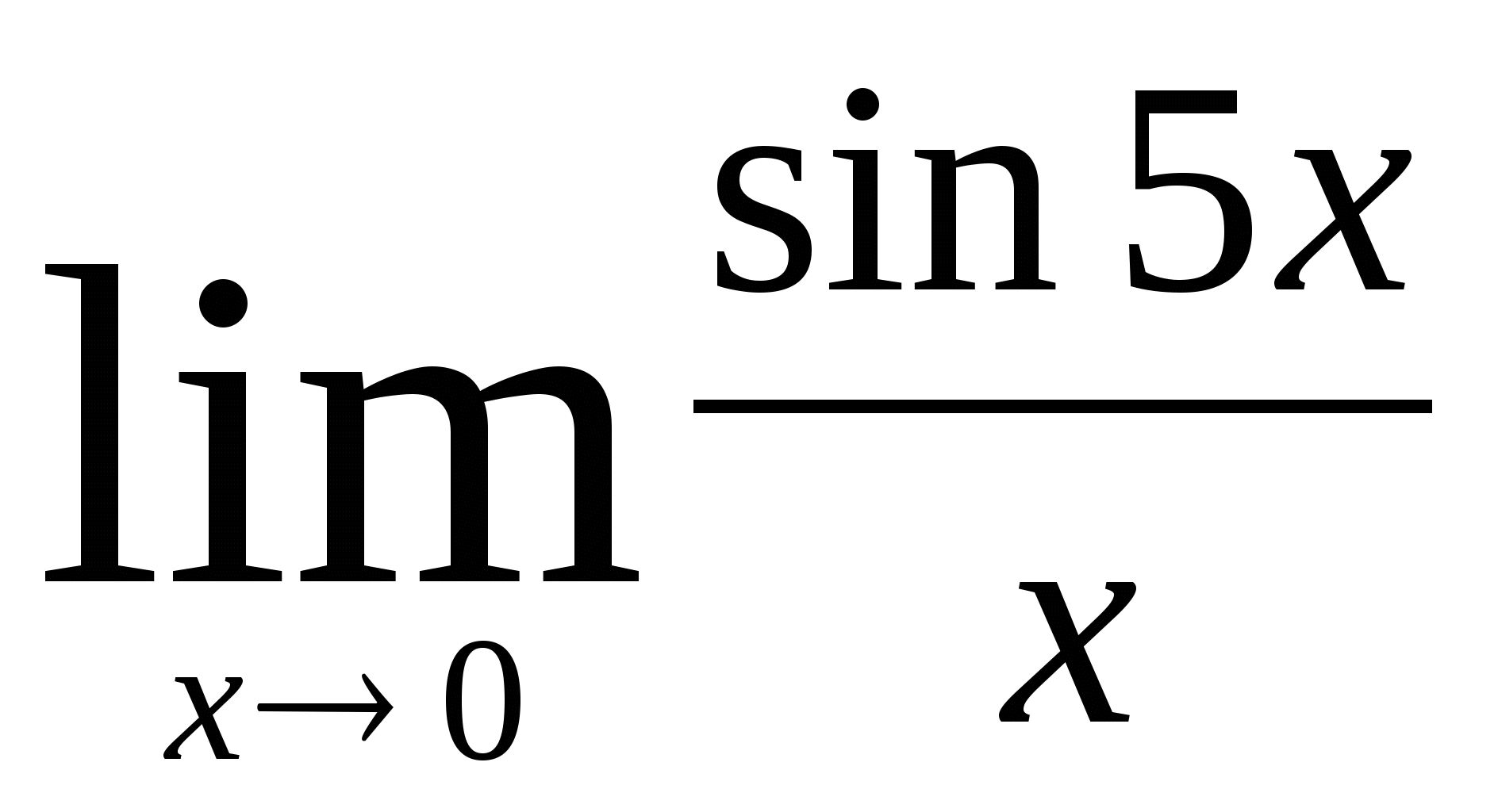 6)
6) 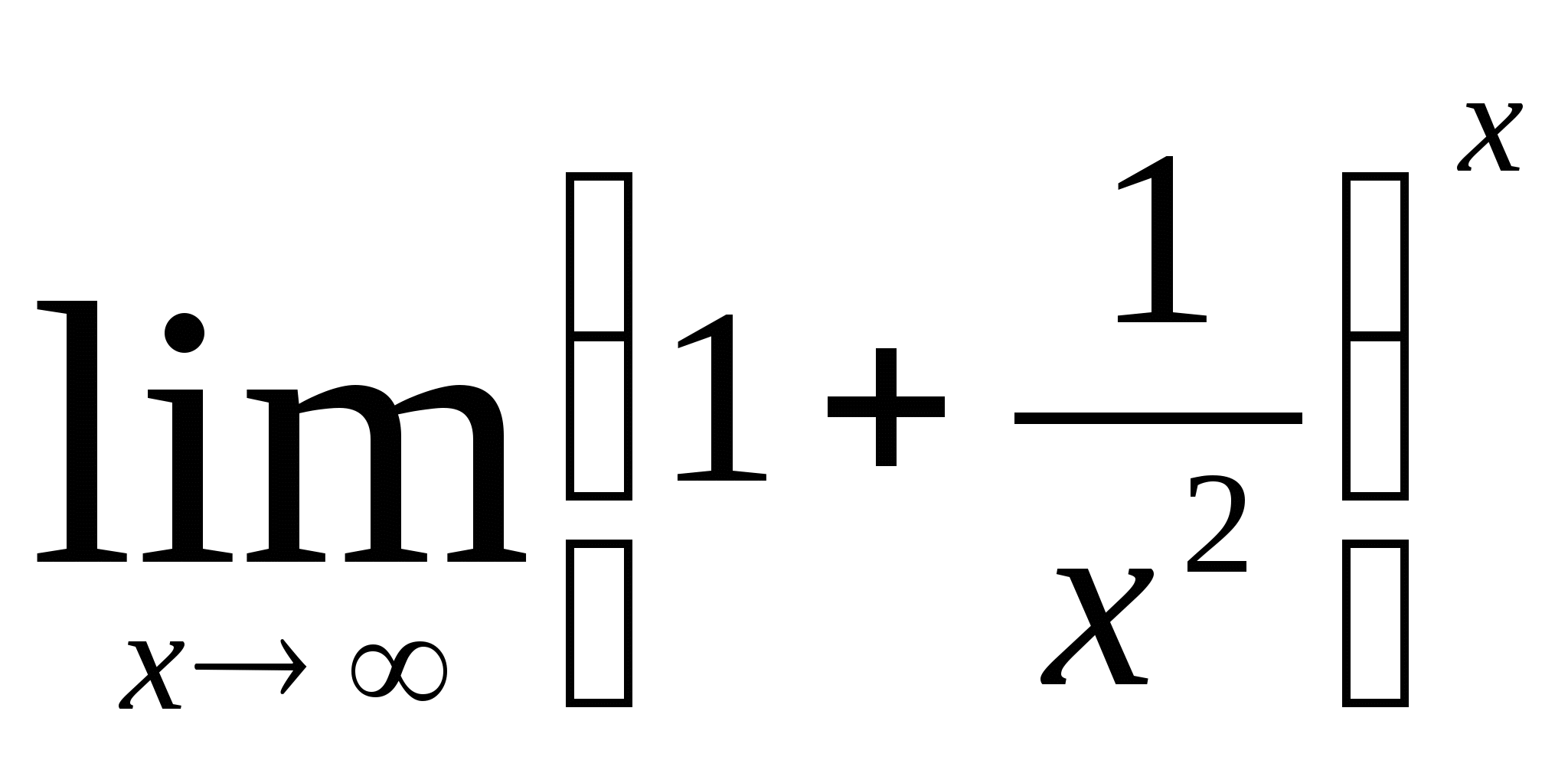
7) 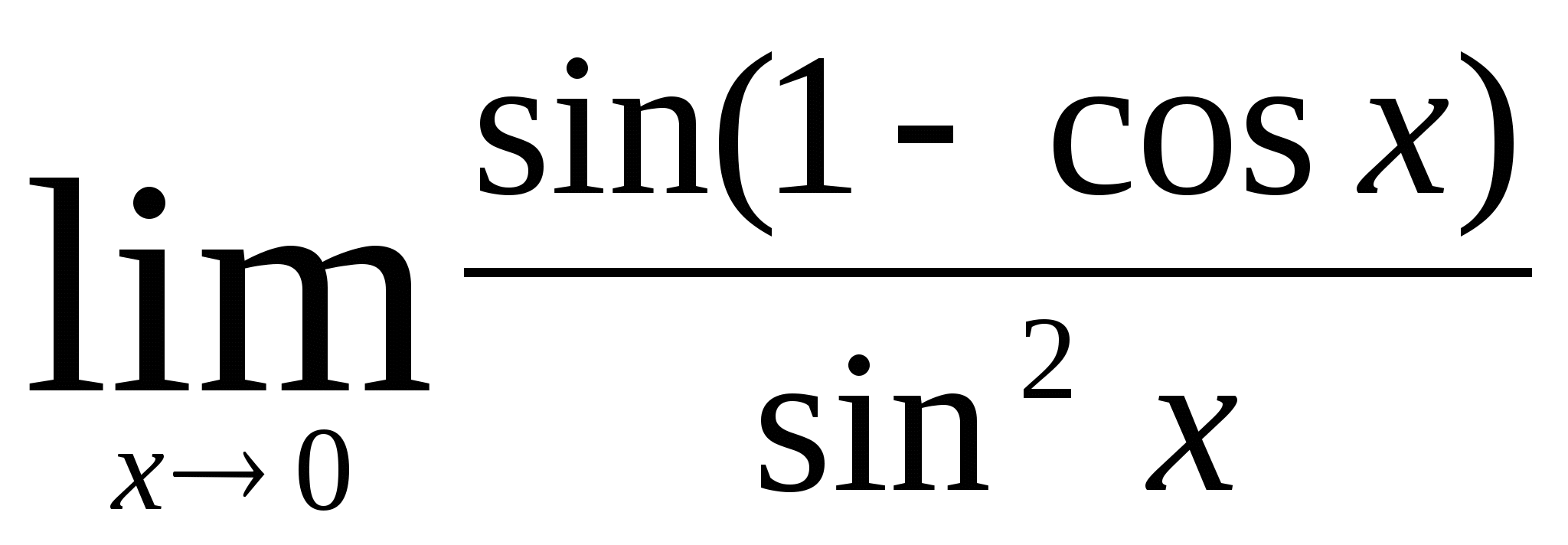 8)
8) 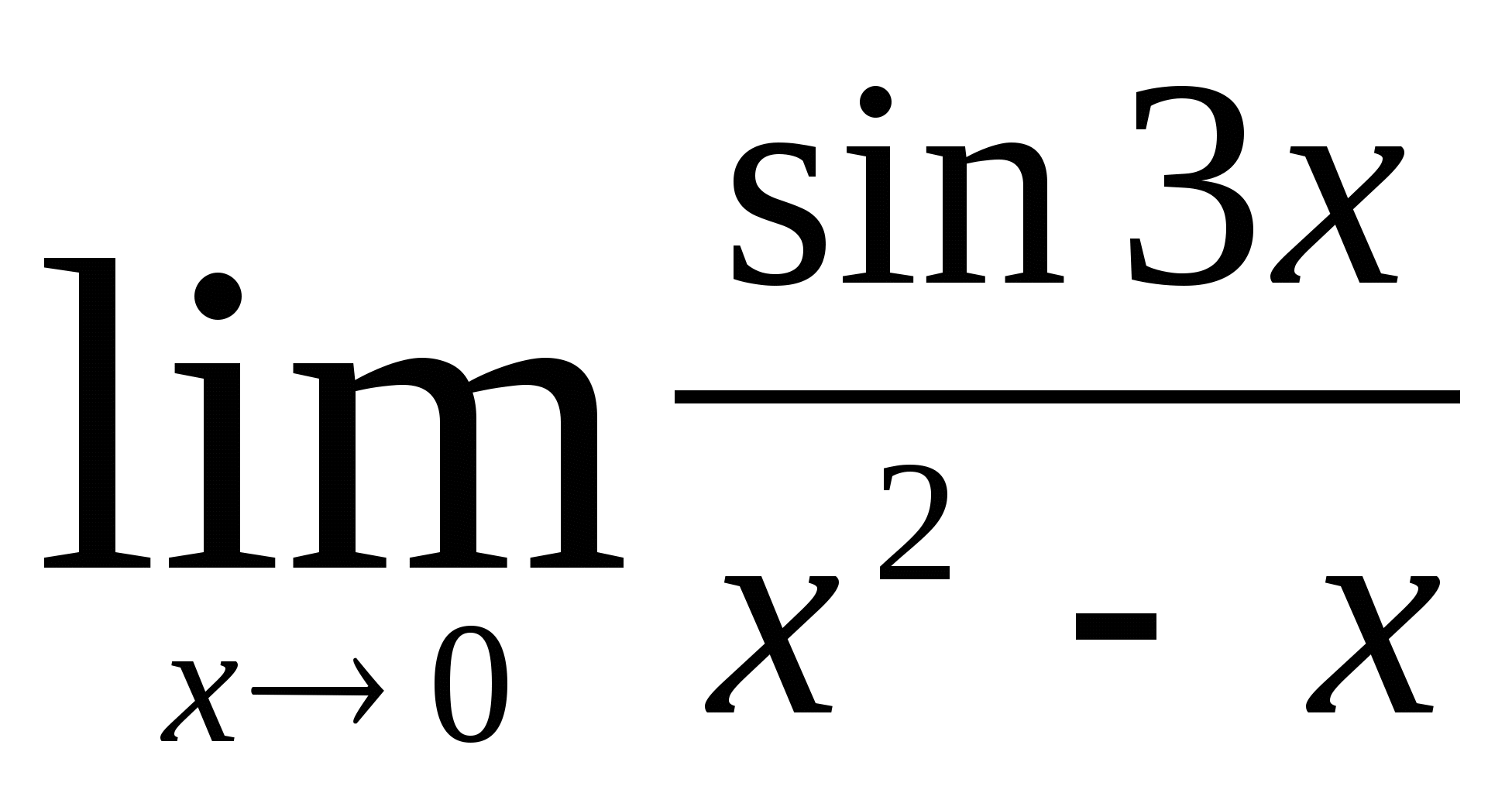 9)
9) 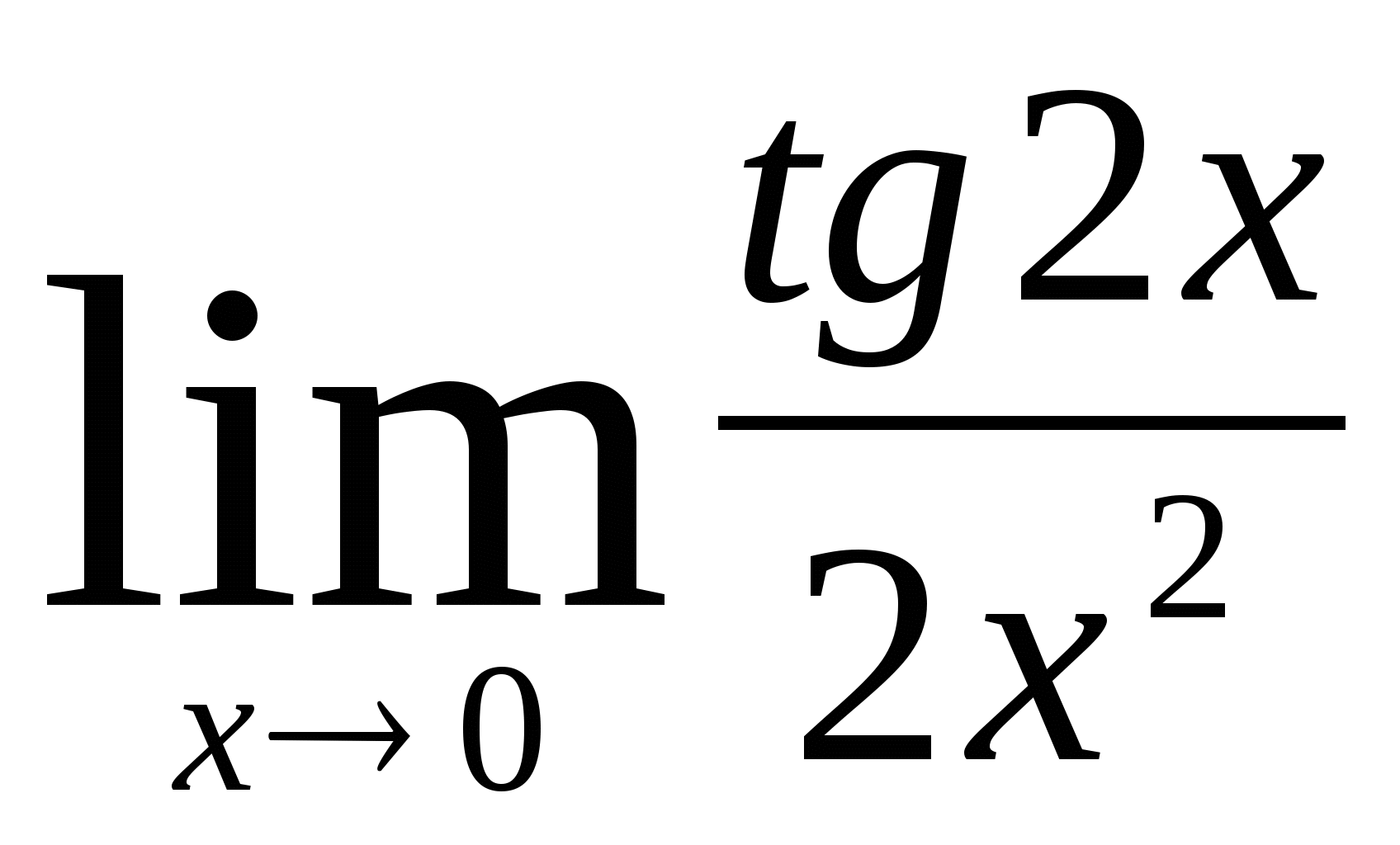
10) 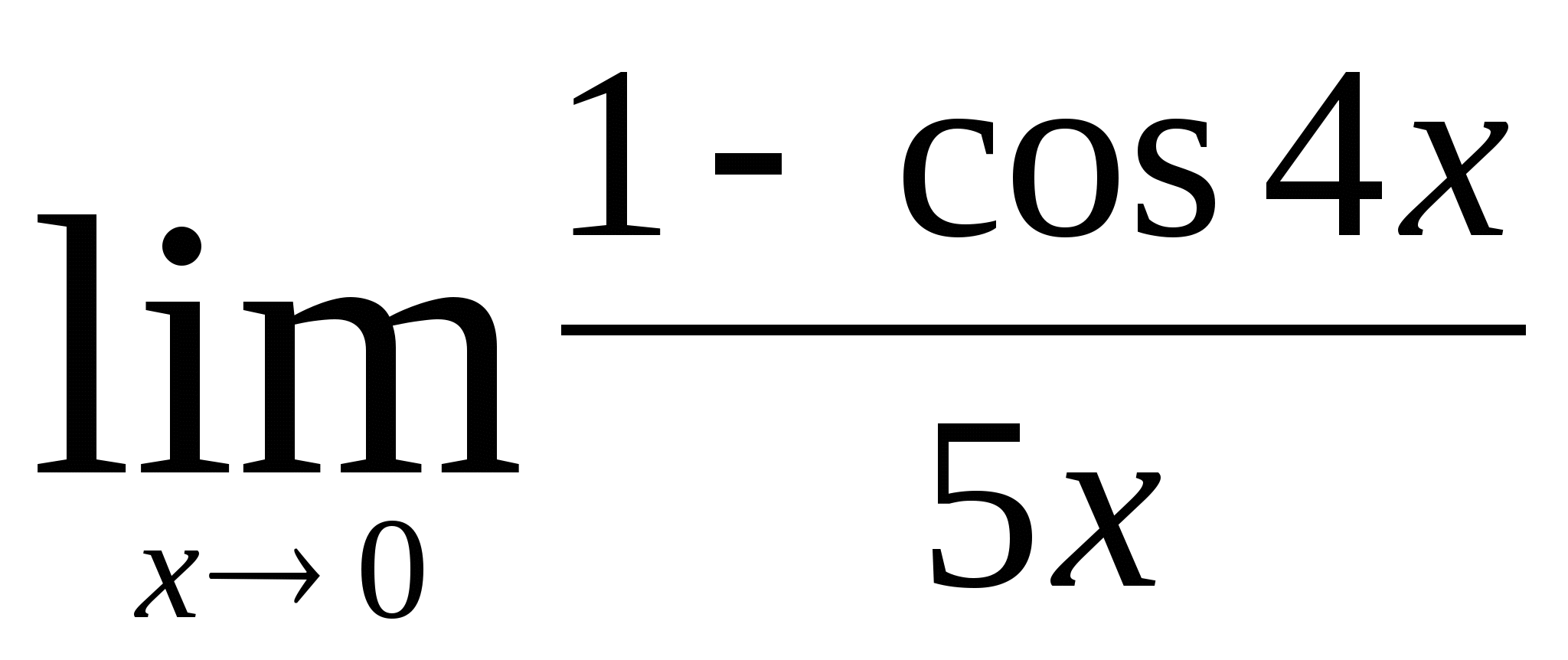 11)
11) 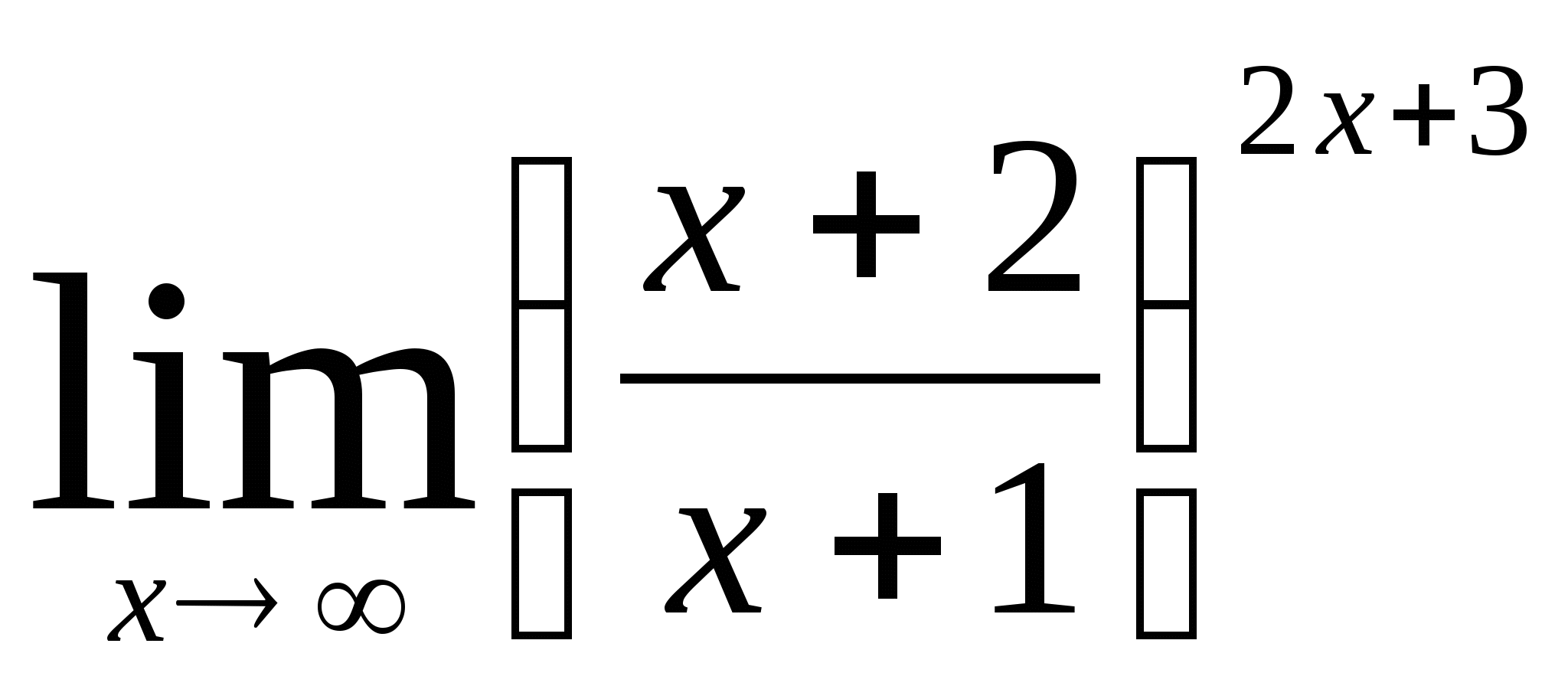 12)
12) 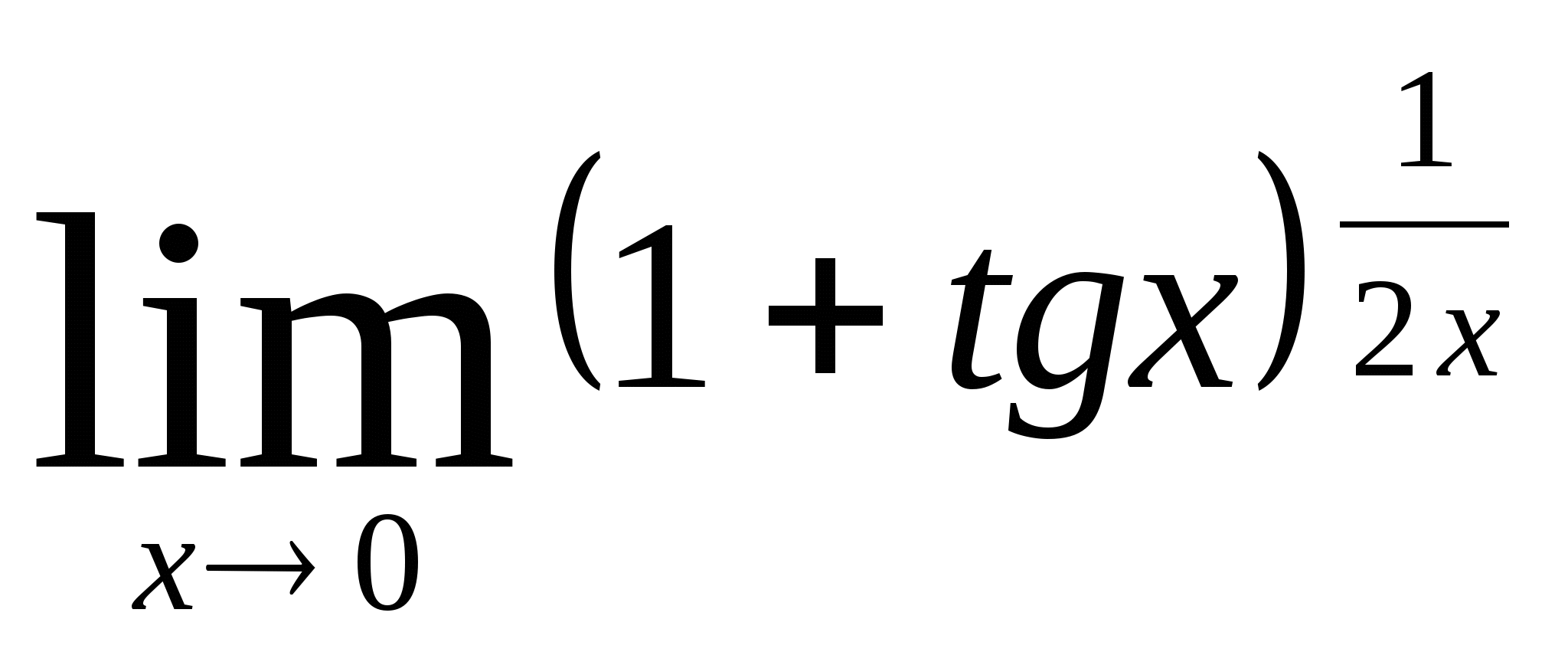
Задачи для домашнего решения
1) ![]() 2)
2) 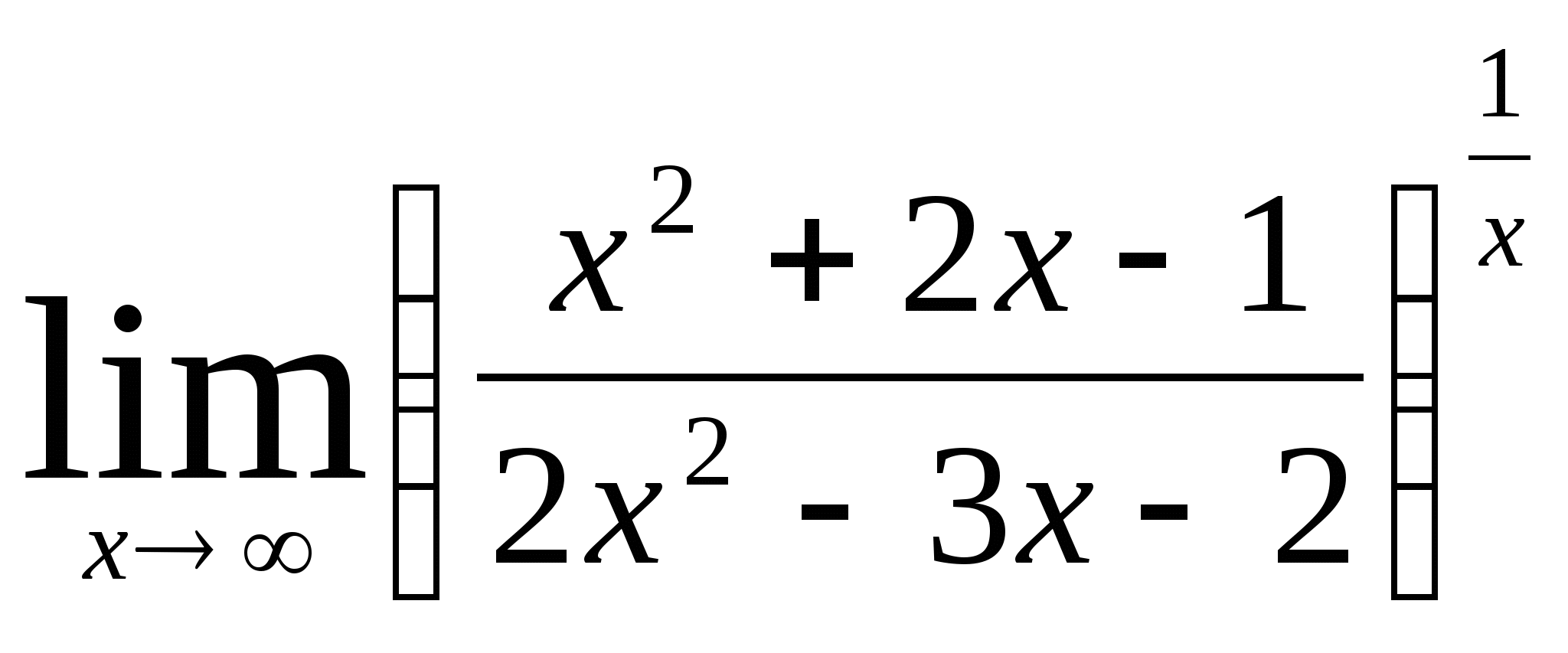
3) 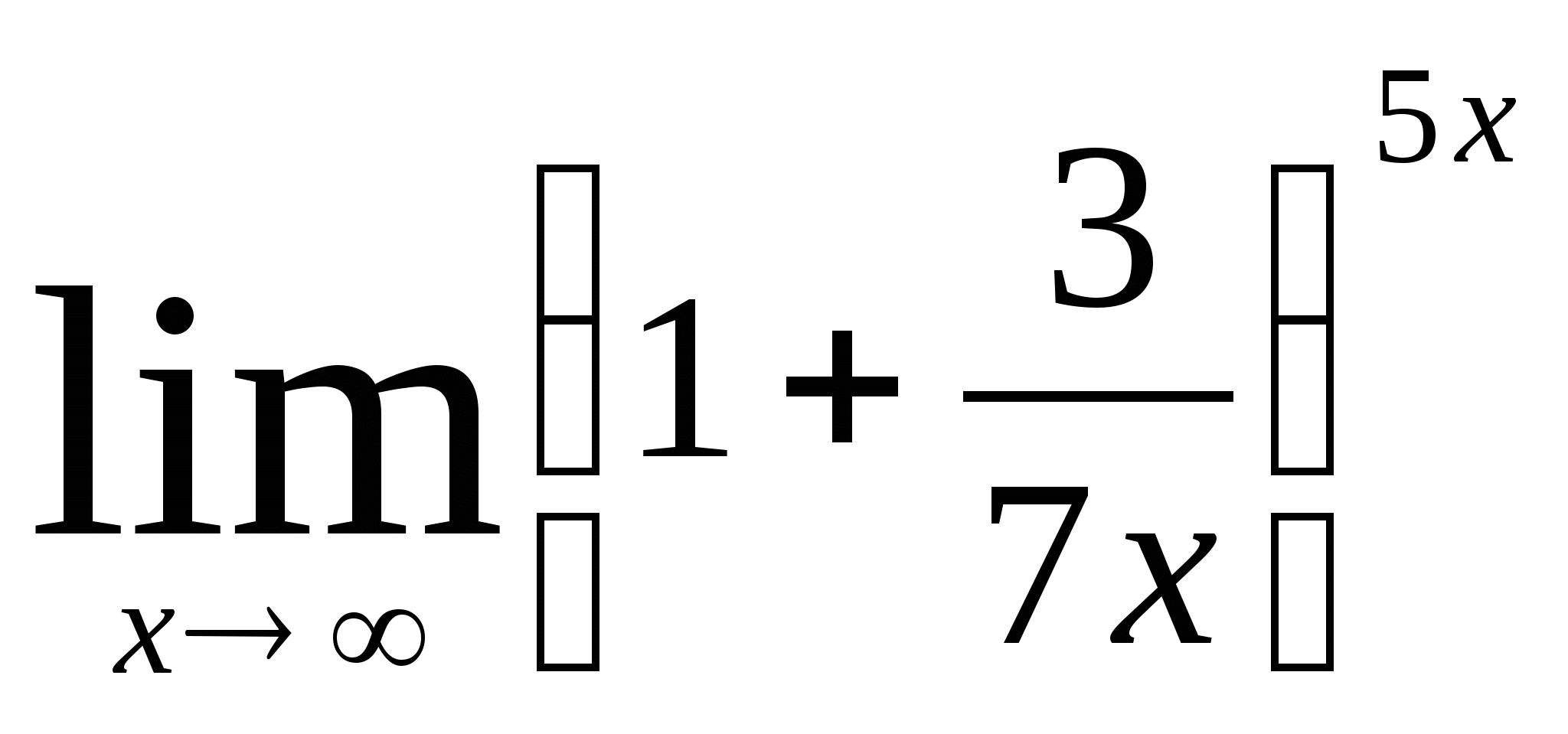 4)
4) 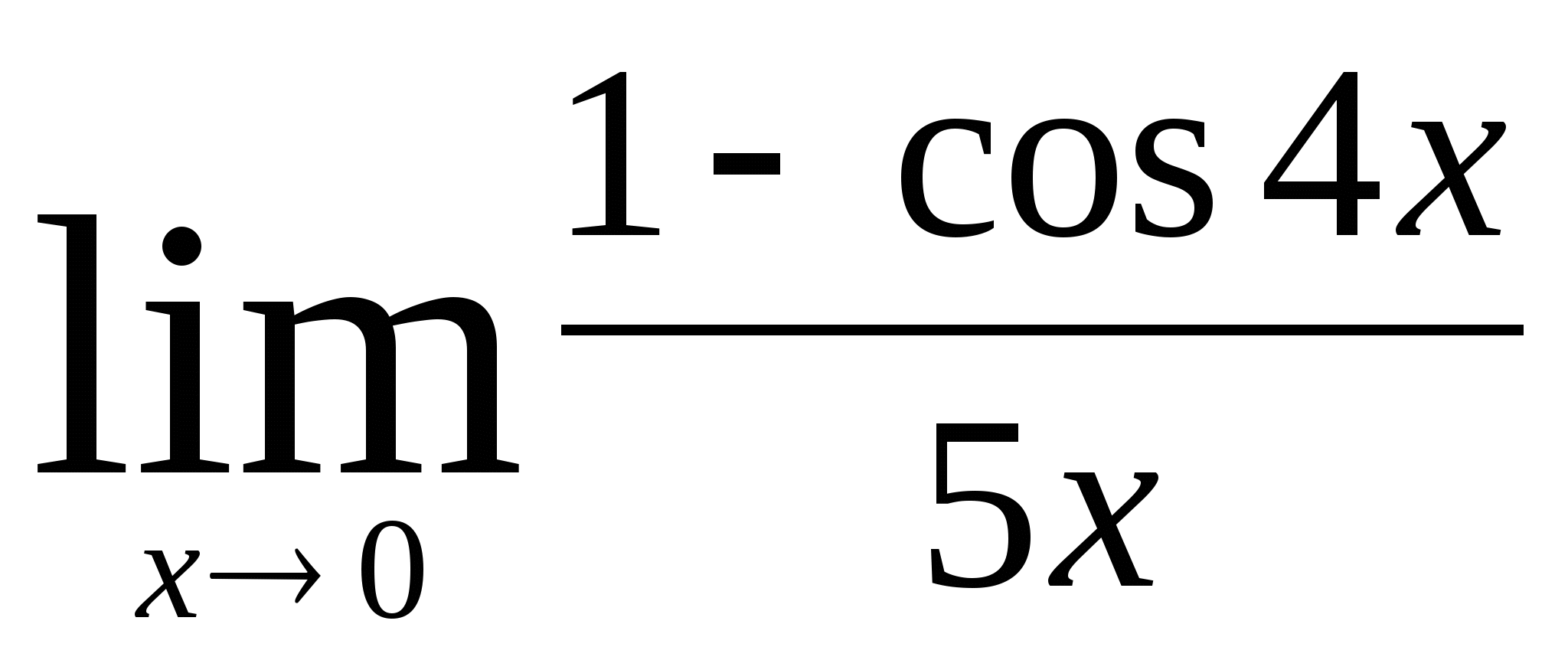
5) 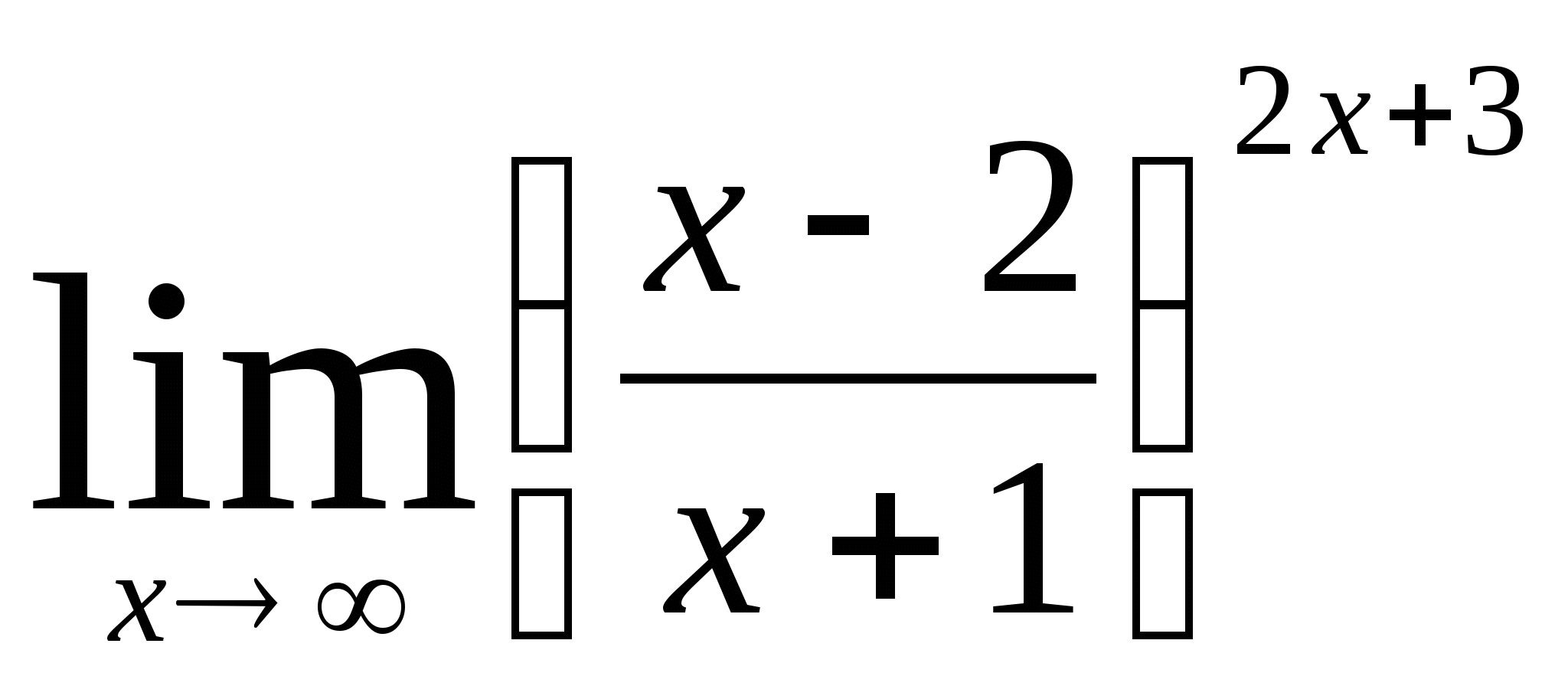
Практическое занятие 7
Практическая работа 6
по теме «Вычисление производных сложных функций. Дифференцирование сложной функции.»
Цель работы: закрепить понятие производной , научиться вычислять производные первого и второго порядков, используя правила дифференцирования и таблицу производных, вычислять производную сложной функции.
Актуализация знаний
Фронтальный опрос
1. Дать понятие производной функции, производной функции в точке.
2. Сформулировать теоремы про производную суммы, произведения и частного функций. Привести примеры.
3. Записать основные формулы дифференцирования.
4. Правило нахождения производной сложной функции.
Краткие теоретические и учебно-методические материалы по теме практической работы
Таблица производных основных элементарных функций.
1. (с)/ = 0, с - сonst 9. ![]()
2. (xα)/ = αx α - 1
10. ![]()
3. ![]() 11.
11. ![]()
4. 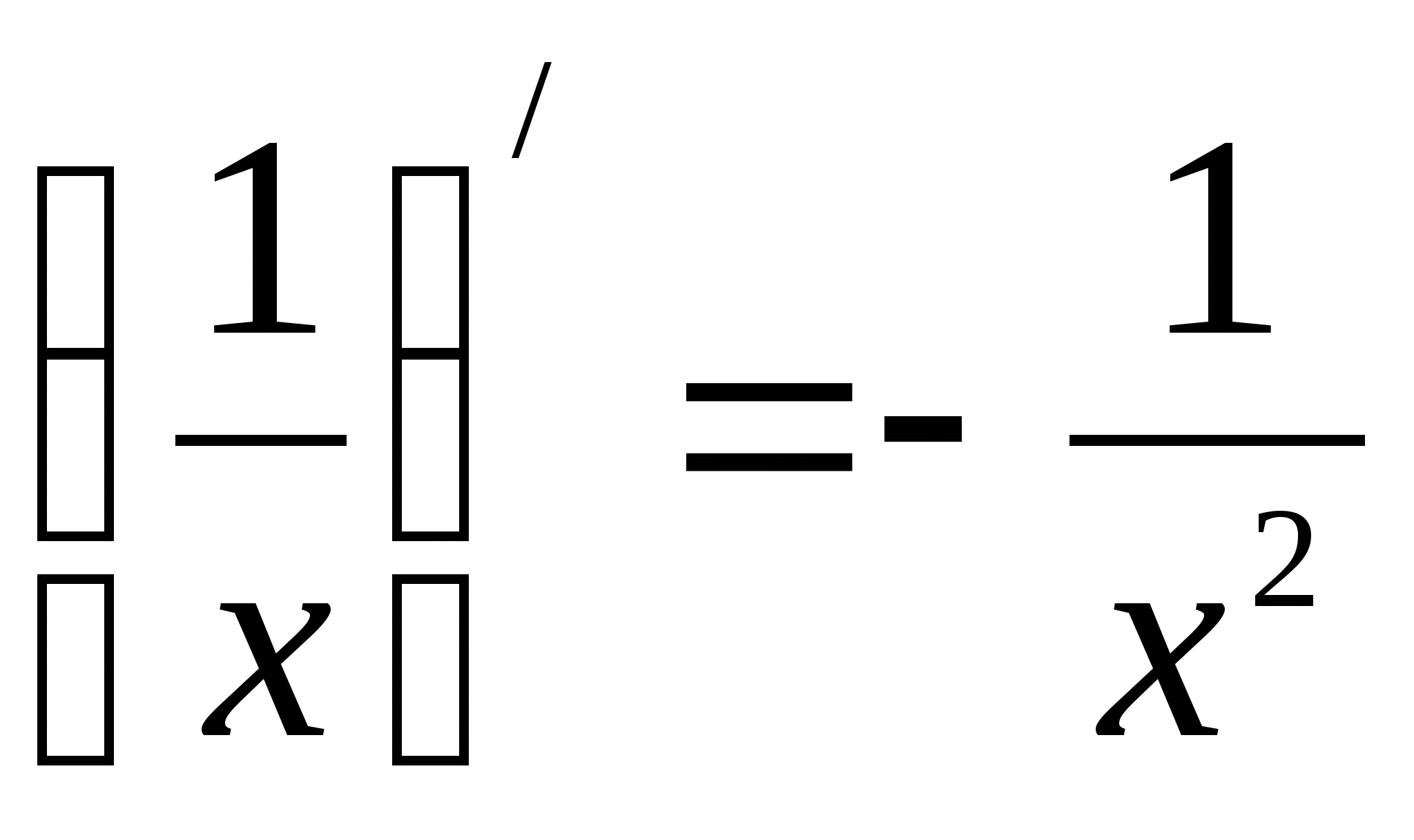 12.
12. ![]()
5. ![]() 13.
13. 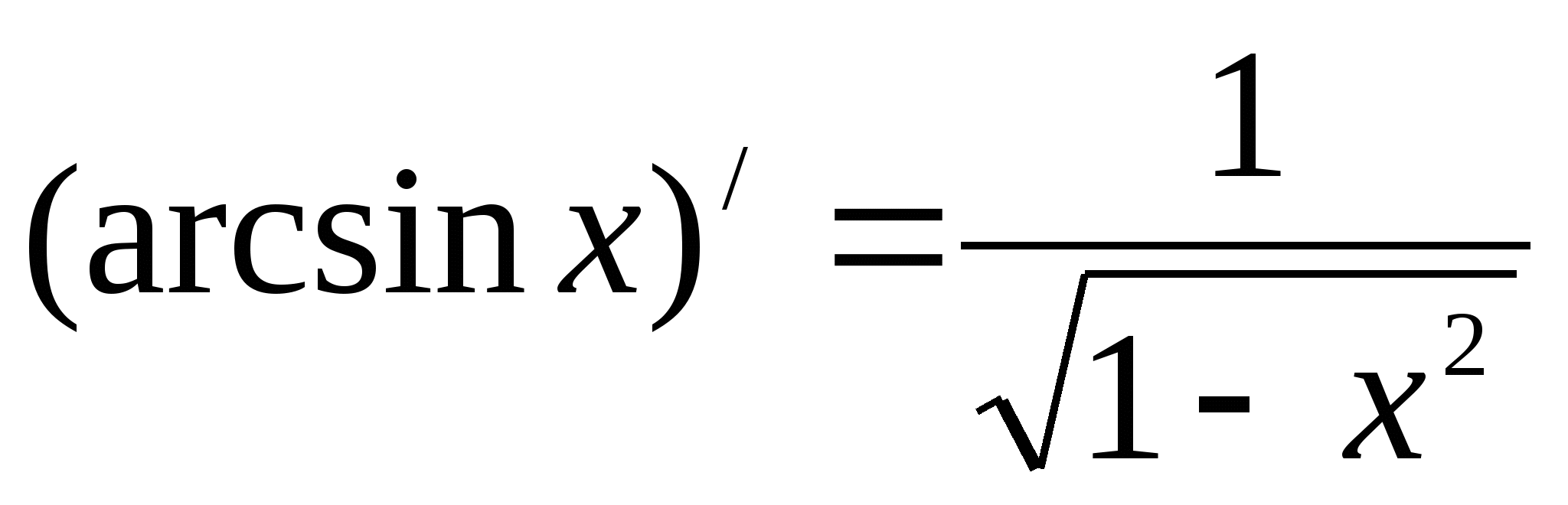
6. ![]() 14.
14. 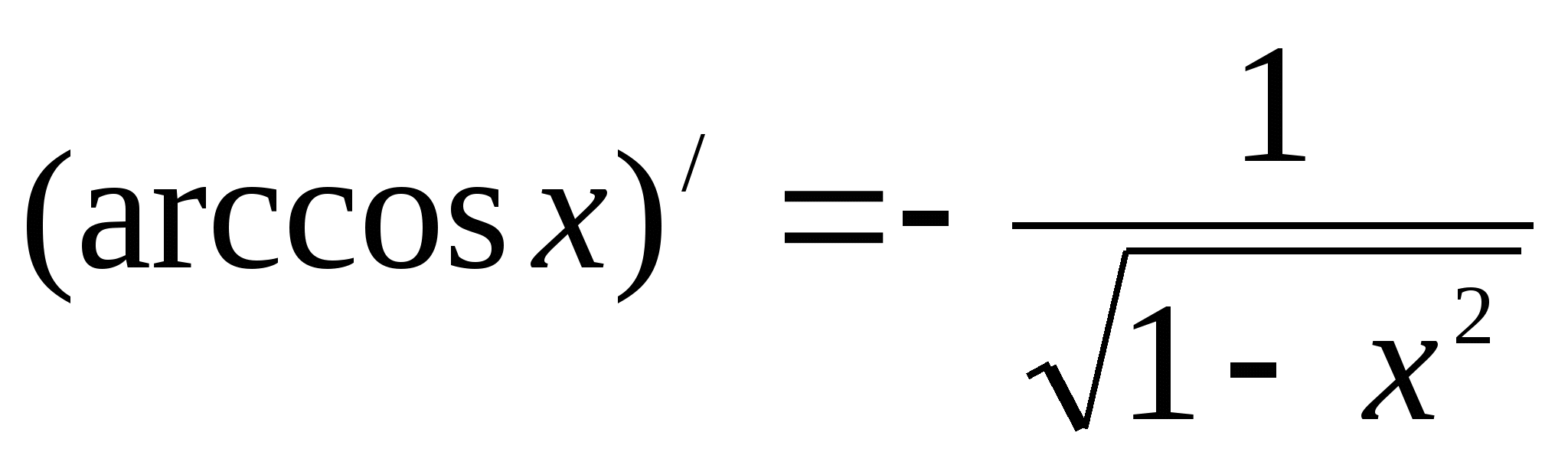
7. ![]() 15.
15. ![]()
8. ![]() 16.
16. ![]()
17. ![]()
Правила дифференцирования.
1. ![]() - вынесение константы за знак производной.
- вынесение константы за знак производной.
2.![]() -
производная суммы равна сумме производных.
-
производная суммы равна сумме производных.
3. ![]() - производная произведения.
- производная произведения.
4. 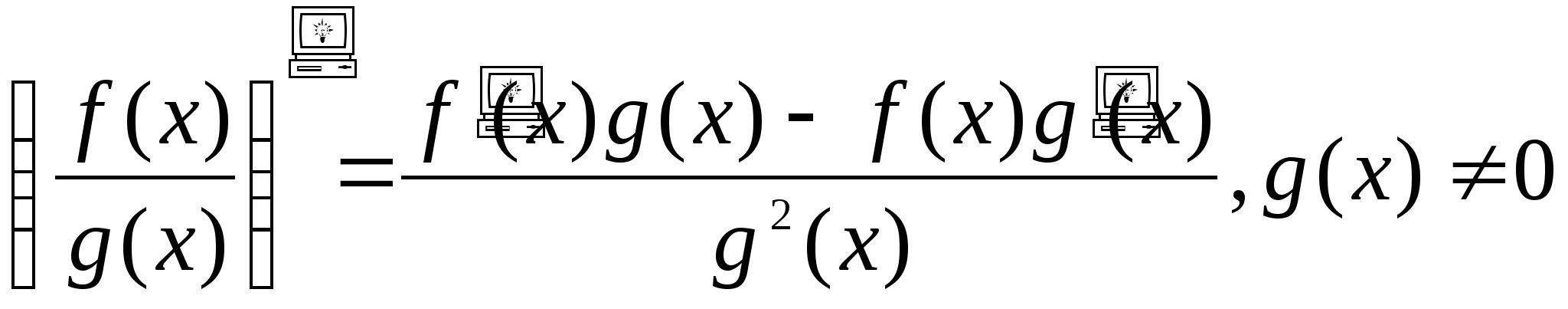 - производная частного.
- производная частного.
Пусть функция ![]() - сложная функция.
- сложная функция.
Теорема. Если y есть дифференцируемая функция от u, а u есть дифференцируемая функция от x, то
-
y есть дифференцируемая функция по x,
-
производная y по x равна произведению производной y по u на производную u по x, т.е. если
![]()
Определение. Пусть функция y = f(x) определена и дифференцируема на интервале (a, b). Если функция f ¢ (x) дифференцируема в точке х0 (a, b), то ее производную называют второй производной или производной второго порядка функции f(x) в точке х0 и обозначают f ′′ (x0), то есть
![]()
Определение. Пусть функция y = f(x) имеет на интервале (a, b) производные f ¢ (x), f ′′ (x), …, f (n − 1) (x). Если в точке х0 (a, b) существует производная функции f (n−1) (x0), то эту производную называют производной n-ого порядка, то есть
![]()
где производная нулевого порядка − это функция f(x).
Формирование необходимых знаний и умений
Коллективное решение и обсуждение предложенных задач
1. Найти производные следующих сложных функций.
Решение.
![]()
Решение:
Находим производную частного.
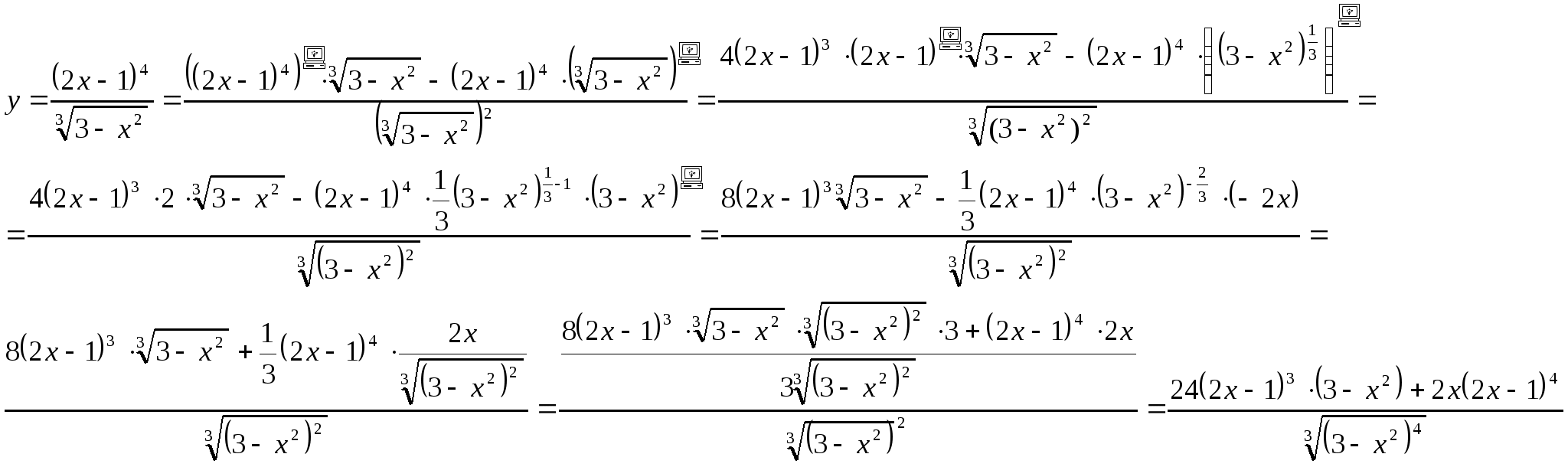
Решение:
![]()
1. Вычислить производную сложной функции:
1) ![]() ; 3)
; 3) ![]() ;
;
2) ![]() ; 4)
; 4) ![]() ;
;
5) ![]() ; 6.)
; 6.) ![]() ;
;
7) ![]() ; 8)
; 8) ![]() ;
;
9) ![]() ; 10)
; 10) ![]() ;
;
11) ![]() ; 12)
; 12) 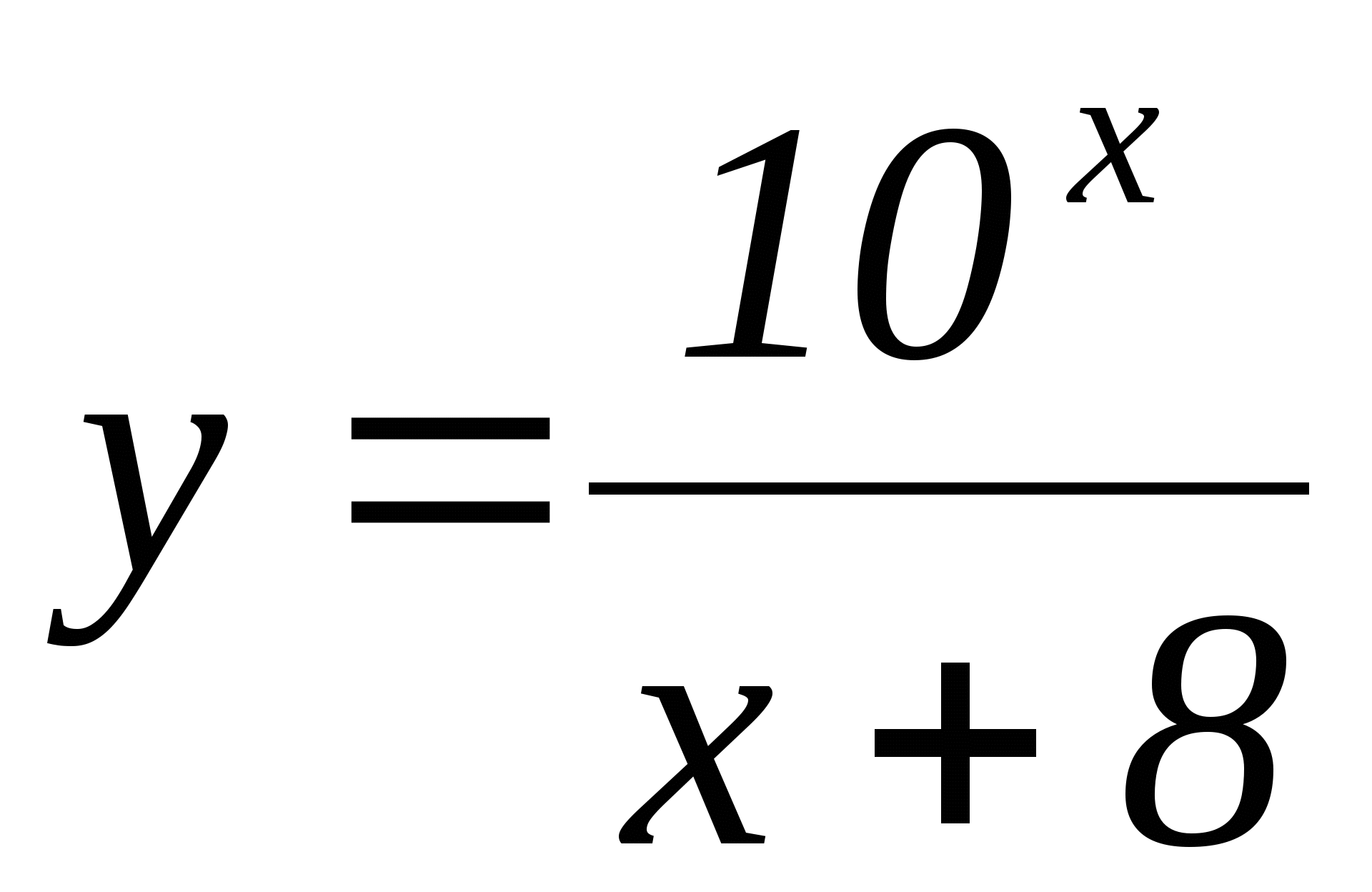 ;
;
13) ![]() ; 14)
; 14) ![]() ;
;
15) ![]() ; 16)
; 16) ![]() ;
;

2. Найти производную второго порядка
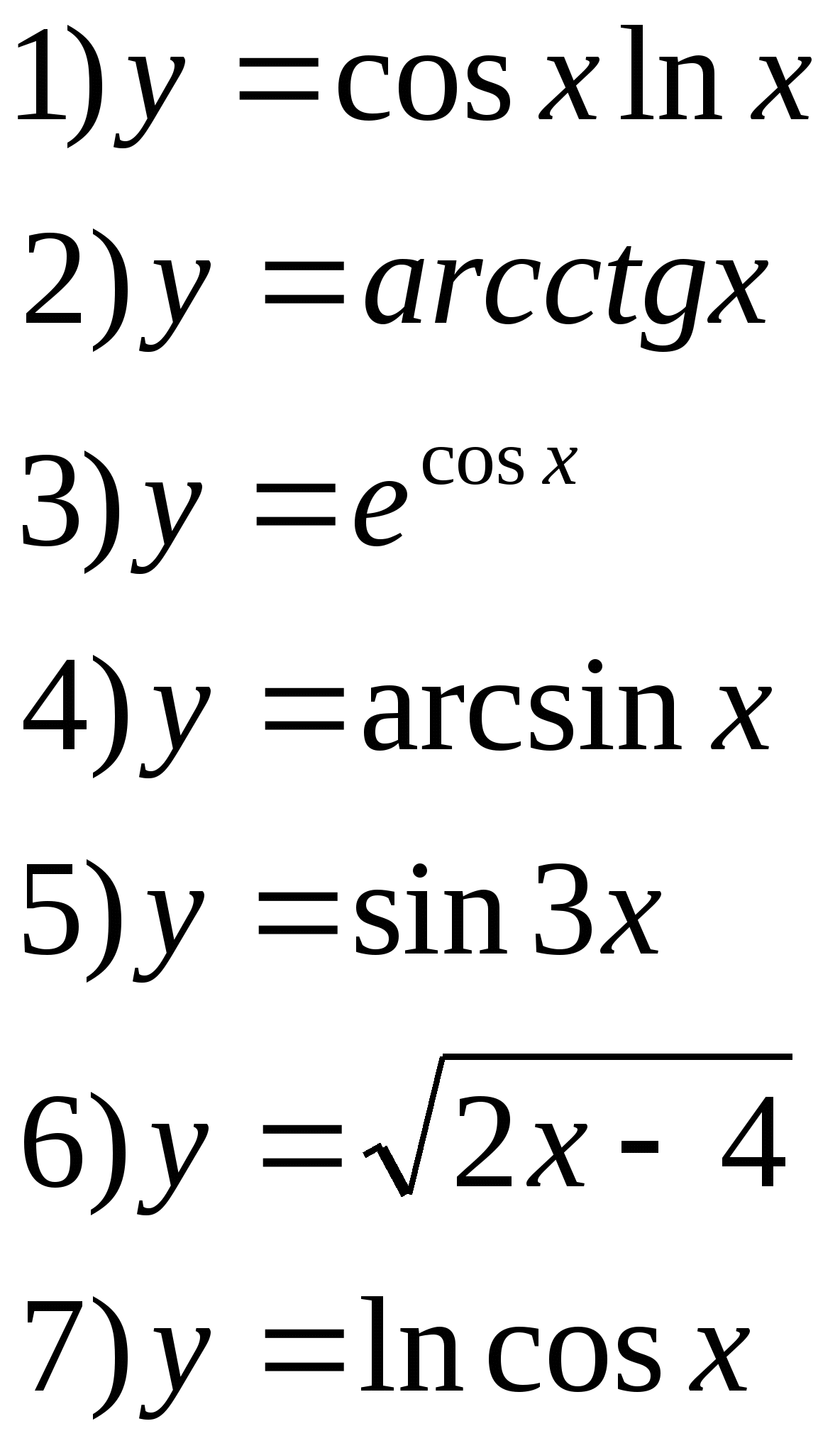
Закрепление сформированных знаний и учений:
Закрепление полученных знаний по данной теме проводится во время самостоятельного решения заданий
1. Найти производные следующих сложных функций.
-
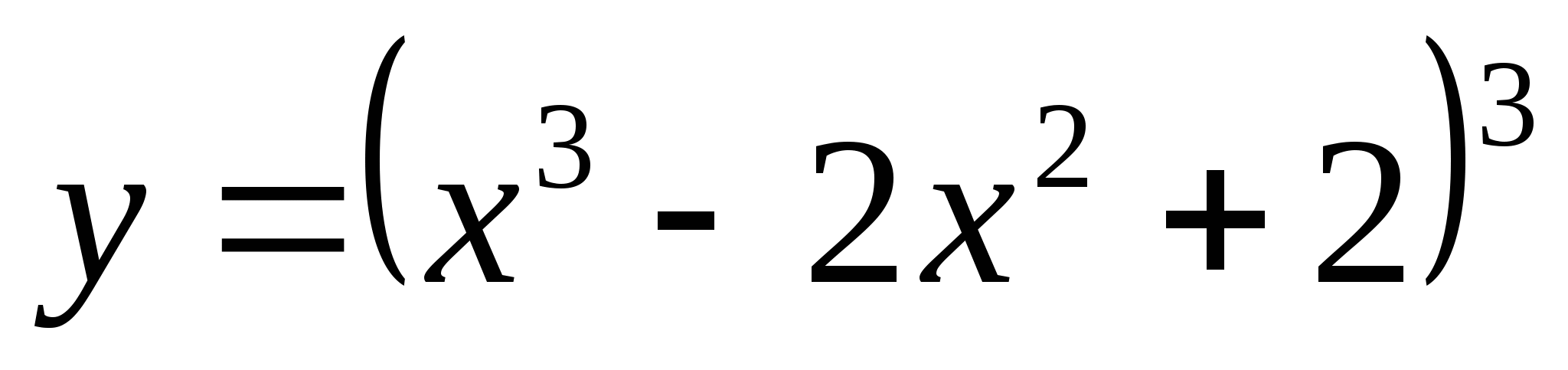 2)
2)
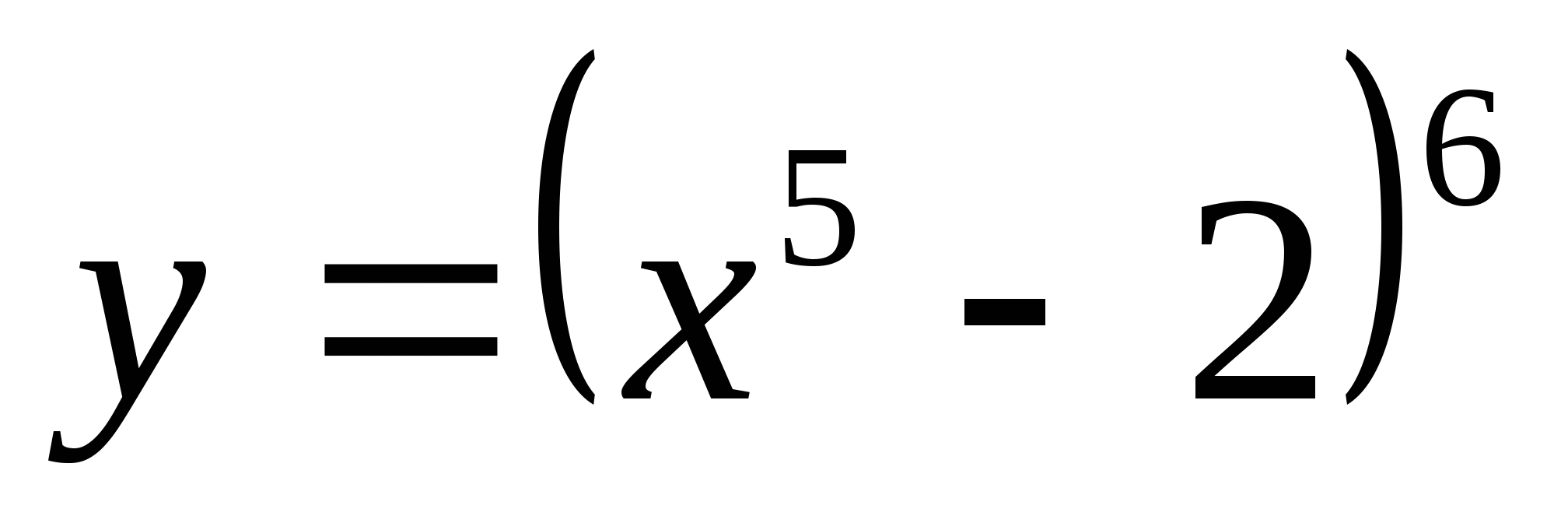
3)![]() 4)
4) ![]()
5) ![]() 6)
6) ![]()
7) ![]() 8)
8) ![]()
9) ![]() 10)
10) ![]()
2. Вычислите производные при заданных значениях аргумента.
-
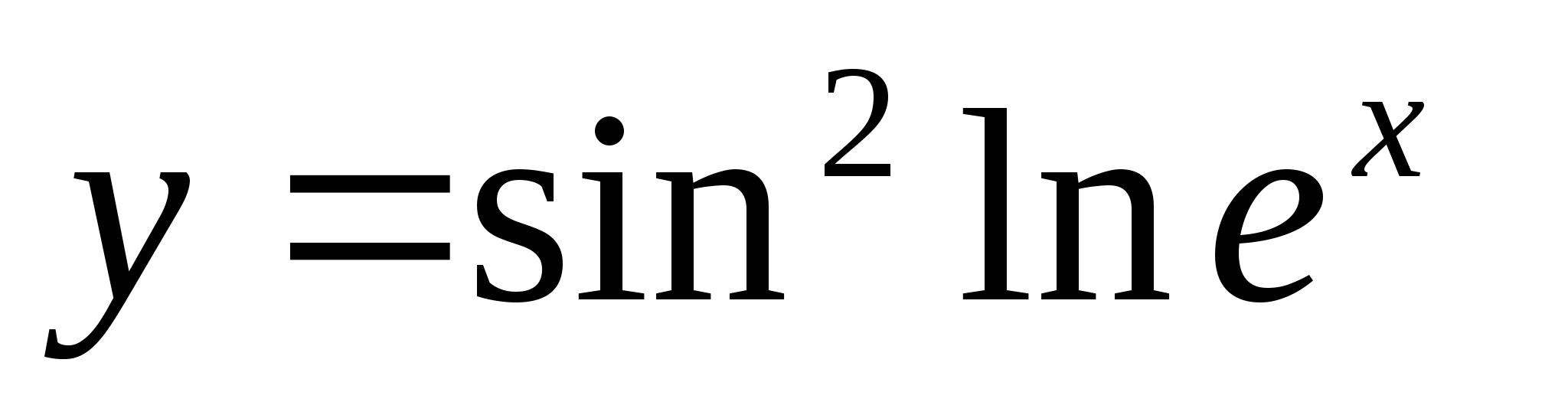 при
x = 0
при
x = 0
-
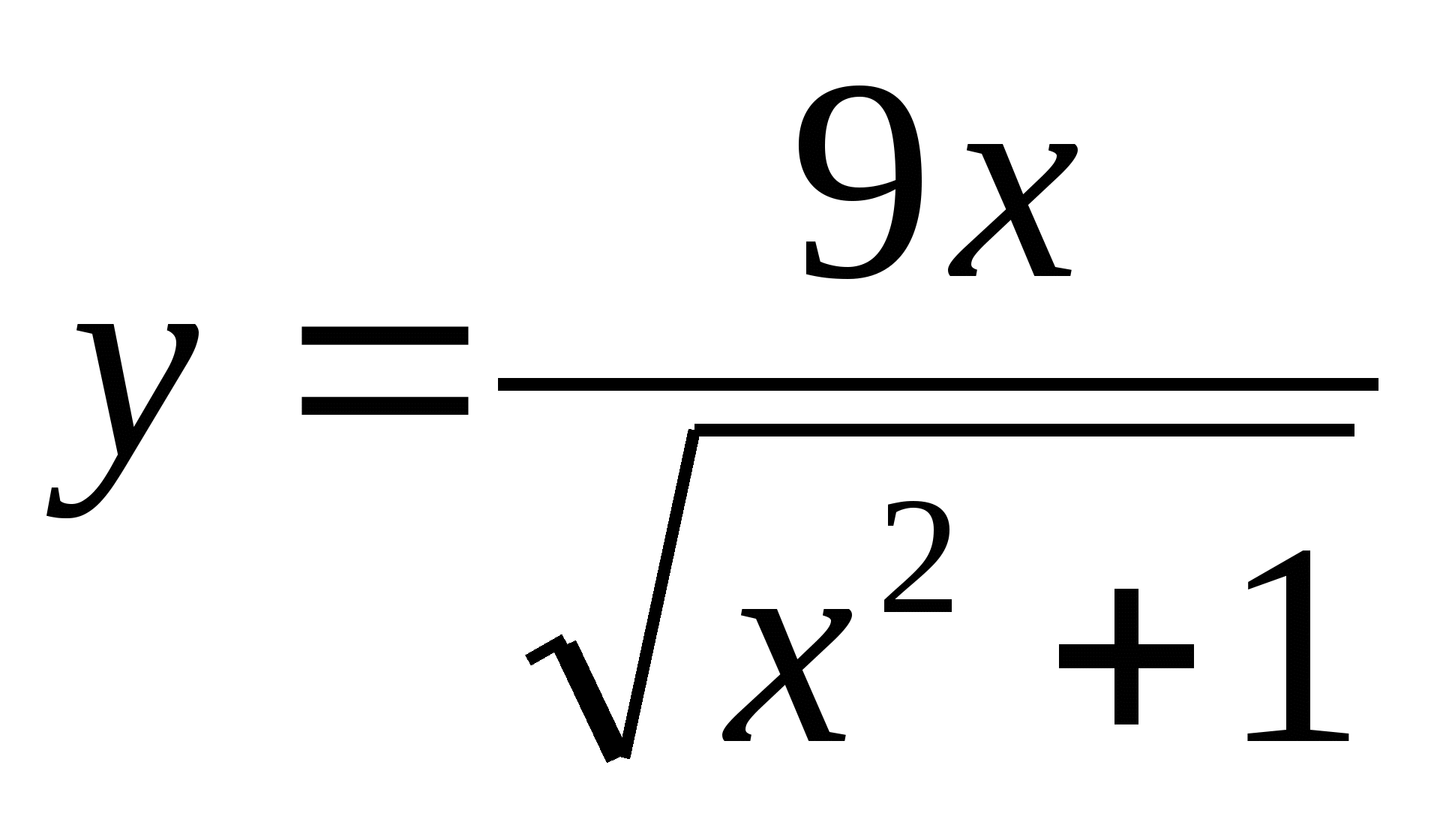 при
x =
при
x = 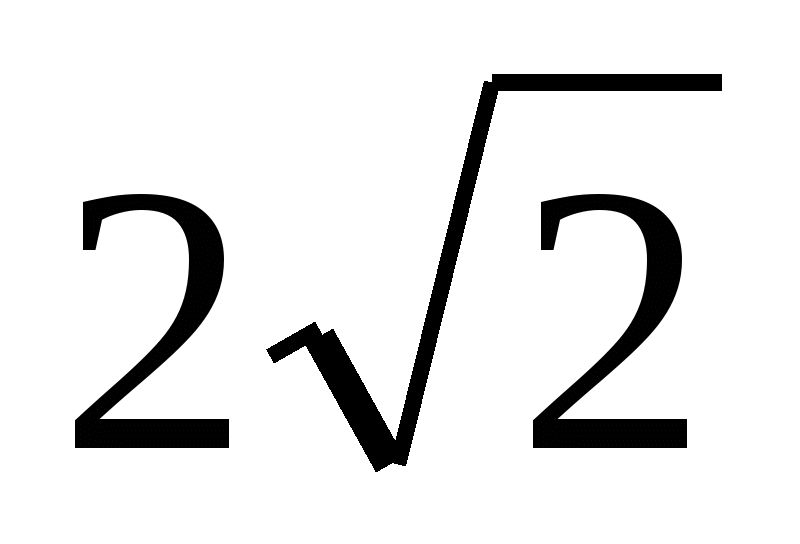
Задачи для домашнего решения
Вычислить производную функции:
1) ![]() , х0 = π; 2)
, х0 = π; 2) ![]() ; 3)
; 3) ![]() ;
;
4) 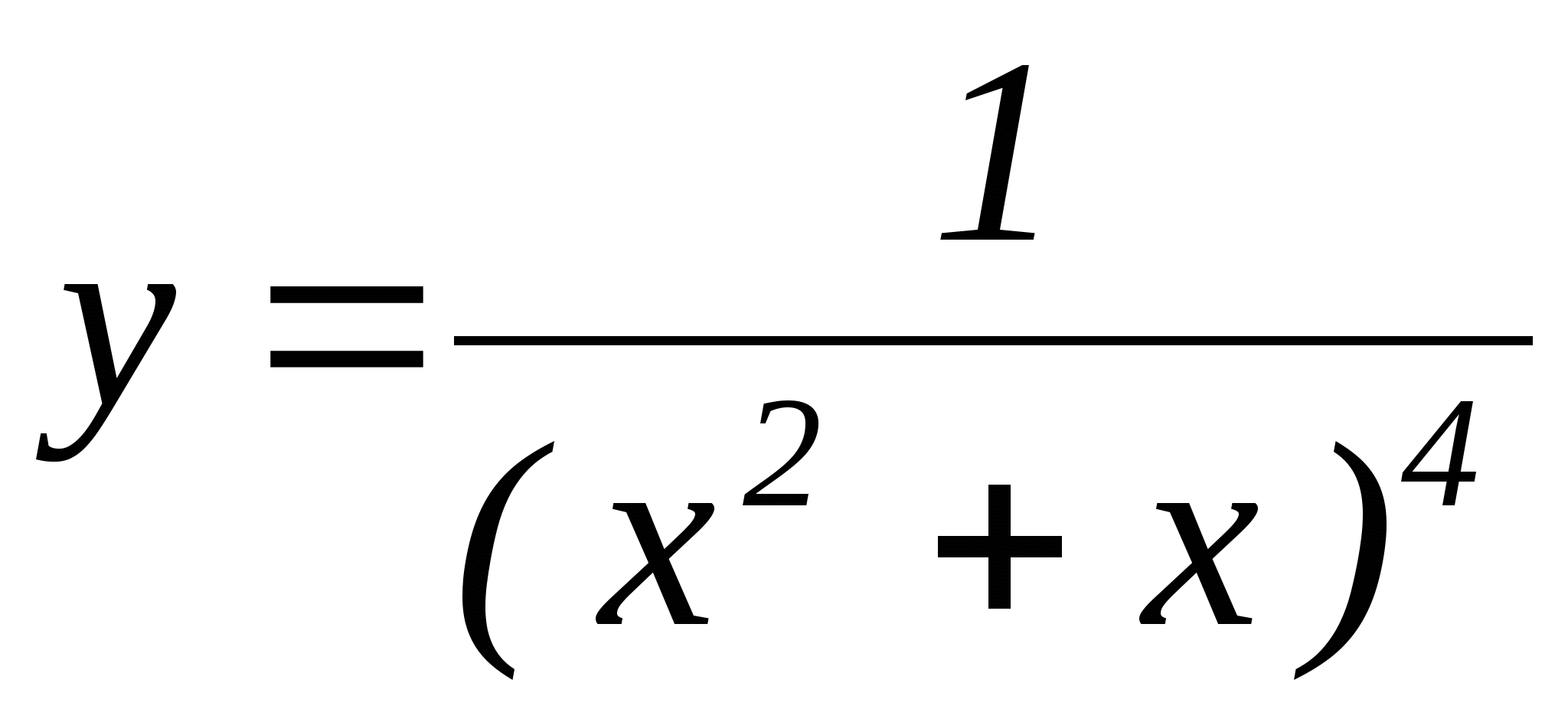 ; 5)
; 5) ![]() ; 6)
; 6) ![]()
Практическое занятие 8
Практическая работа 7
по теме «Решение заданий экономического смысла методом дифференциального исчисления»
Цель работы: Сформировать умения решать задания экономического смысла методом дифференциального исчисления.
Актуализация знаний
Фронтальный опрос
1. Определение точки минимума и точки максимума.
2. Определение критической точки.
3. Необходимое условие, чтобы точка х0 была точкой экстремума.
4. Алгоритм нахождения критических точек функции.
5. Определение стационарных точек.
6. Теорема Ферма (необходимое условие экстремума функции).
7. Достаточные условия существования экстремума функции .
8. Достаточный признак возрастания, убывания функции.
9. Алгоритм нахождения экстремумов функции.
10. Нахождение прибыли, дохода, рентабельности, налога на прибыль.
Краткие теоретические и учебно-методические материалы по теме практической работы
Необходимый признак экстремума. Если x=a является точкой экстремума функции y=f(x) и производная в этой точке существует,
то она равна нулю f(a)=0.
Достаточный признак экстремума. Если производная f '(x) при переходе x через a меняет знак, то а является точкой экстремума функции f(x)
Алгоритм исследования функции на экстремум:
1. Находят производную f '(x)
2. Находят все критические точки из области определения функции.
3. Устанавливают знаки производной функции при переходе через критические точки и выписывают точки экстремума.
4. Вычисляют значения функции f(x) в каждой экстремальной точке.
Правило нахождения интервалов монотонности f'(x).
1. Вычисляют производную f'(x) данной функции.
2. Находят точки, в которых f'(x) равна нулю или не существует. Эти точки называются критическими для функции f(x).
3. Найденными точками область определения функции f(x) разбивается на интервалы, на каждом из которых производная f'(x) сохраняет свой знак. Эти интервалы является интервалами монотонности.
4. Исследуют знак f'(x) на каждом из найденных интервалов. Если на рассматриваемом интервале f'(x)>0, то на этом интервале f(x) возрастает; если же f'(x)<0, то на таком интервале f(x) убывает.
Применение производной в экономике:
Пусть Р - стоимость одного изделия, а "х" - количество изделий, которые изготовлены и проданы за некоторый промежуток времени.
Функция дохода:
Д (х) = Р1 х
Функция прибыли:
П = Д - В
П = Р1 х -В (х)
Рентабельность:
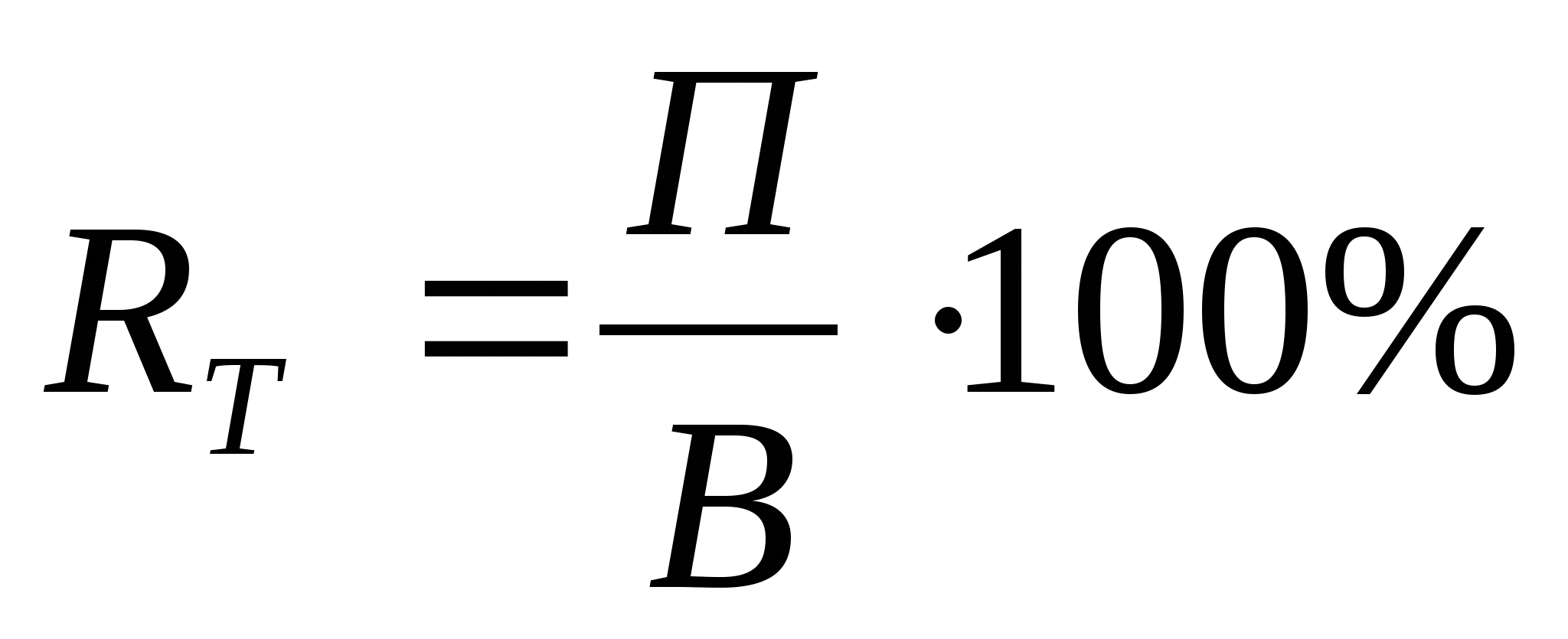
Налог на прибыль:
НП=18%∙П
Эластичность функции вычисляется по формуле: 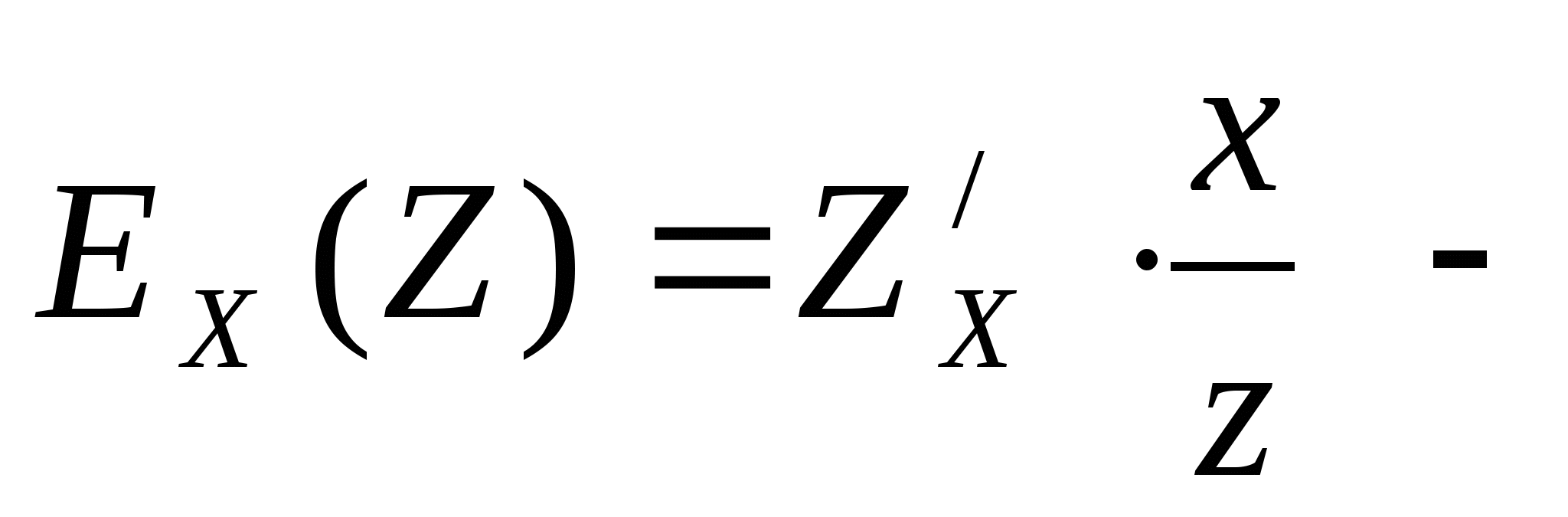
Это показатель возможного возрастания или функции Z, если аргумент "х" увеличивается на 1 %, а аргумент "у" остается неизменным. Выражается в процентах.
Если эластичность < 1, то функцию называют неэластичной. В этом случае изменение цены повлечет за собой меньшее изменение величины спроса.
Если эластичность > 1, то функцию называют эластичной. Иными словами, изменение цены в данном случае приведет к большему количественному изменению величины спроса.
Если эластичность =1, то говорят о единичной эластичности. В этом случае изменение цены приводит к такому же количественному изменению величины спроса.
Равновесная цена - цена, при которой спрос равен предложению.
Формирование необходимых знаний и умений
Коллективное решение и обсуждение предложенных задач
Пример 1
Торгово-производственное предприятия изготавливает для продажи некоторую продукцию. Затраты на производство задаются функцией В(х)=11х2 -8х-3, где х - объем продукции в десятках условных единиц. Покупательная функция имеет вид Р(х)=52 -4х . Необходимо:
1. Составить оптимальный план деятельности производства;
2. установить цену;
3. вычислить величину затрат производства на реализацию этого плана;
4. вычислить величину ожидаемой прибыли;
5. вычислить величину налога на прибыль;
6. вычислить рентабельность производства.
Решение:
Составим формулу прибыли: П=Д-В=Р∙х-В
Д=(52-4х)∙х=52х-4х2
П=52х-4х2-11х2+8х+3=-15х2+60х+3
П'=-30х+60
П'=0 -30х+60=0
х=2-критическая точка

П'(0)=60
П'(3)=-30
Вычислим величину ожидаемой прибыли:
П(2)=-15∙4+60∙2+3=63 (усл.ед)
Установим цену: Р(2)=52-4∙2=44 (усл.ед)
Вычислим величину затрат производства на реализацию этого плана:
В(2)=11∙4-8∙2-3=25 (усл.ед)
Вычислим величину налога на прибыль: НП=0,2∙63=12,6 (усл.ед)
Вычислим рентабельность производства: ![]()
Пример 2
Опытным путем установлены функции спроса S и предложения П
(S и П - объемы товаров, р - их цена). Найти:
1) Равновесную цену
2) Эластичность спроса и предложения относительно равновесной цены.
S=![]() ,
П=
,
П=![]() Р+0,5
Р+0,5
Решение:
1) ![]() = Р+0,5
= Р+0,5
Р1= -3,5 - не подходит
Р2=2 (ден. ед) - равновесная цена
2)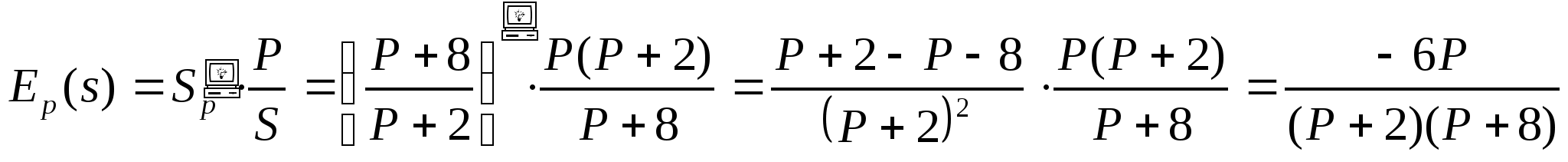
![]()
Для Р=2:
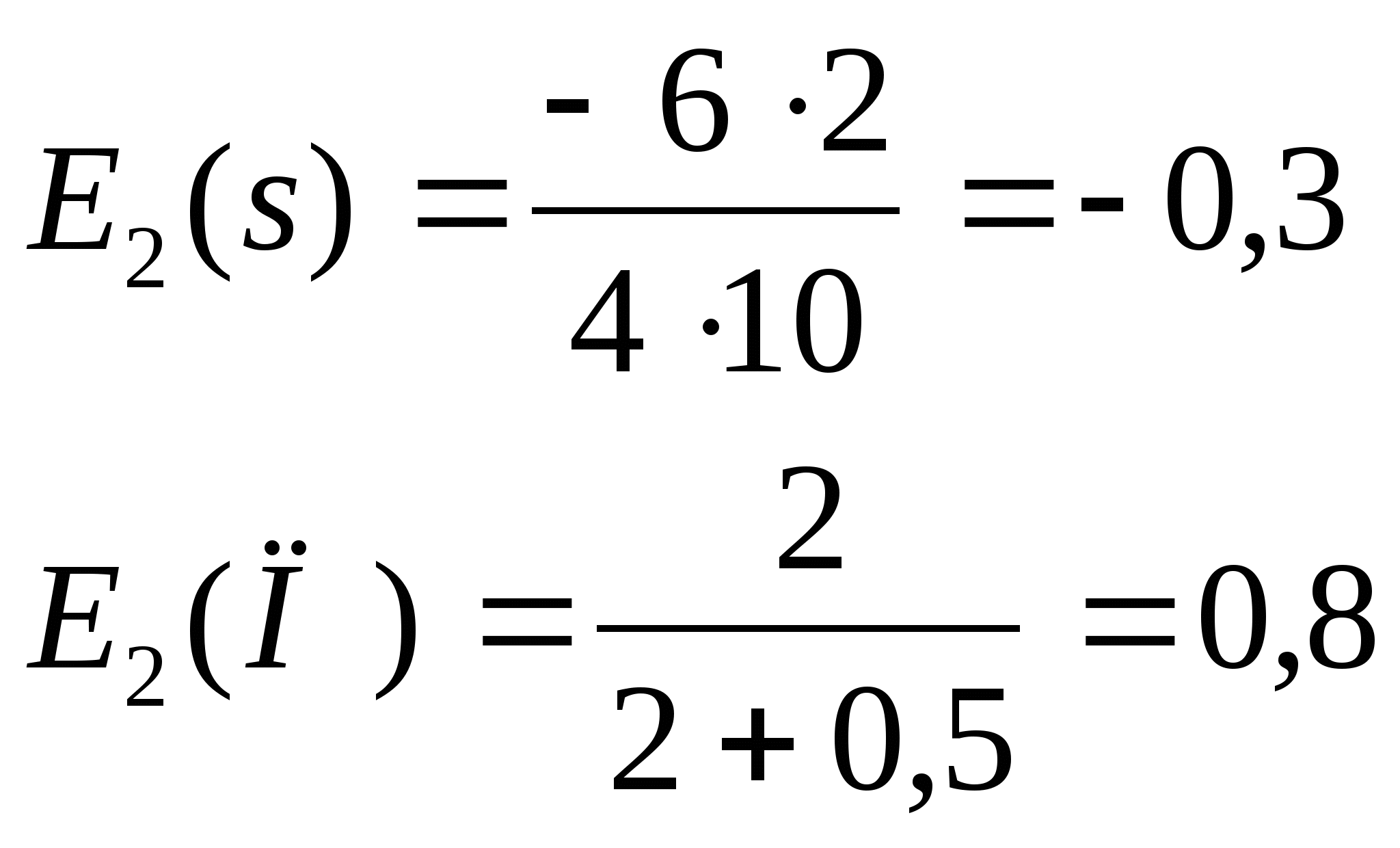
Спрос и предложение не эластичны относительно цены, значит, изменение цены не приведет к резкому изменению спроса и предложения.
При увеличении цены Р на 1% спрос уменьшается на 0,3%, а предложение увеличится на 0,8%.
Задачи
1. Торгово-производственное предприятия изготавливает для продажи некоторую продукцию. Затраты на производство задаются функцией В(х), где х - объем продукции в десятках условных единиц. Покупательная функция имеет вид Р(х). Необходимо:
-
Составить оптимальный план деятельности производства;
-
вычислить величину затрат производства на реализацию этого плана;
-
вычислить величину ожидаемой прибыли;
-
вычислить величину налога на прибыль;
-
вычислить рентабельность производства.
2. Опытным путем установлены функции спроса S и предложения П
(S и П - объемы товаров, р - их цена). Найти:
1) Равновесную цену
2) Эластичность спроса и предложения относительно равновесной цены.
Закрепление сформированных знаний и учений:
Закрепление полученных знаний по данной теме проводится во время самостоятельного решения заданий
1. Торгово-производственное предприятия изготавливает для продажи некоторую продукцию. Затраты на производство задаются функцией В(х), где х - объем продукции в десятках условных единиц. Покупательная функция имеет вид Р(х). Необходимо:
1. Составить оптимальный план деятельности производства;
2. установить цену;
3. вычислить величину затрат производства на реализацию этого плана;
4. вычислить величину ожидаемой прибыли;
5. вычислить величину налога на прибыль;
6. вычислить рентабельность производства.
2. Опытным путем установлены функции спроса S и предложения П
(S и П - объемы товаров, р - их цена). Найти:
1) Равновесную цену
2) Эластичность спроса и предложения относительно равновесной цены.
Задачи для домашнего решения
1. Торгово-производственное предприятия изготавливает для продажи некоторую продукцию. Затраты на производство задаются функцией В(х), где х - объем продукции в десятках условных единиц. Покупательная функция имеет вид Р(х). Необходимо:
1. Составить оптимальный план деятельности производства;
2. установить цену;
3. вычислить величину затрат производства на реализацию этого плана;
4. вычислить величину ожидаемой прибыли;
5. вычислить величину налога на прибыль;
6. вычислить рентабельность производства.
2. Опытным путем установлены функции спроса S и предложения П
(S и П - объемы товаров, р - их цена). Найти:
1) Равновесную цену
2) Эластичность спроса и предложения относительно равновесной цены.
Практическое занятие 9
Практическая работа 8
по теме «Вычисление неопределенных интегралов методом замены переменной и по частям»
Цель работы: научиться вычислять неопределенный интеграл методами замены переменной и по частям.
Актуализация знаний
Фронтальный опрос
1. Понятие неопределенного интеграла. Свойства неопределенного интеграла.
2. Интегрирование методом разложения..
Краткие теоретические и учебно-методические материалы по теме практической работы
Метод интегрирования по частям: данное
подынтегральное выражение представляют в виде произведения двух
множителей, которые обозначают u и dv. Множитель u выбирают так,
чтоб ![]() было проще найти, а за dv выбирают тот дифференциал, для которого
можно найти интеграл.
было проще найти, а за dv выбирают тот дифференциал, для которого
можно найти интеграл.
![]()
Метод замены переменной: заменяют новой переменной такую часть подынтегральной функции, при дифференцировании которой мы получим часть подынтегрального выражения, которая осталась.
1. Определяют, к какому табличному интегралу сводится данный интеграл (перед этим преобразовав подынтегральное выражение, если нужно).
2. Заменяют переменным такую часть подынтегральной функции, при дифференцировании которой, мы получим оставшуюся часть подынтегрального выражения, не учитывая постоянный множитель.
3. Находим полученный интеграл.
4. Выполняем в ответе обратную замену, то есть переходим к старой переменной.
Формирование необходимых знаний и умений
Коллективное решение и обсуждение предложенных задач
Пример 1
Проинтегрировать по частям:
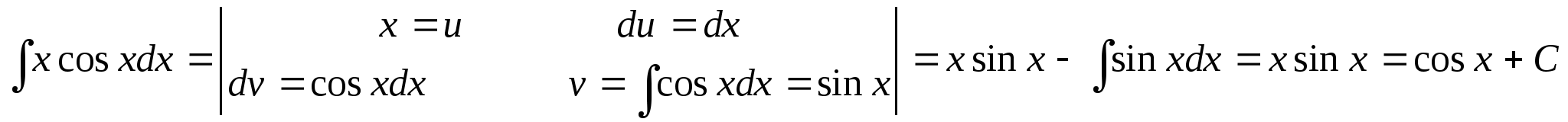
Пример 2
Вычислить интеграл методом замены переменной:
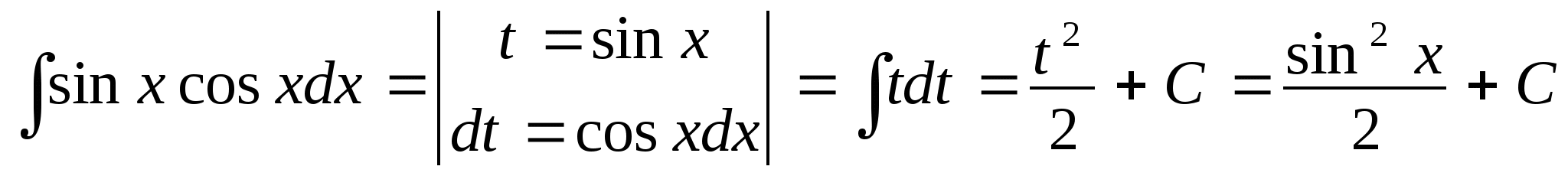
Пример 3
Вычислить интеграл
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
;
4) 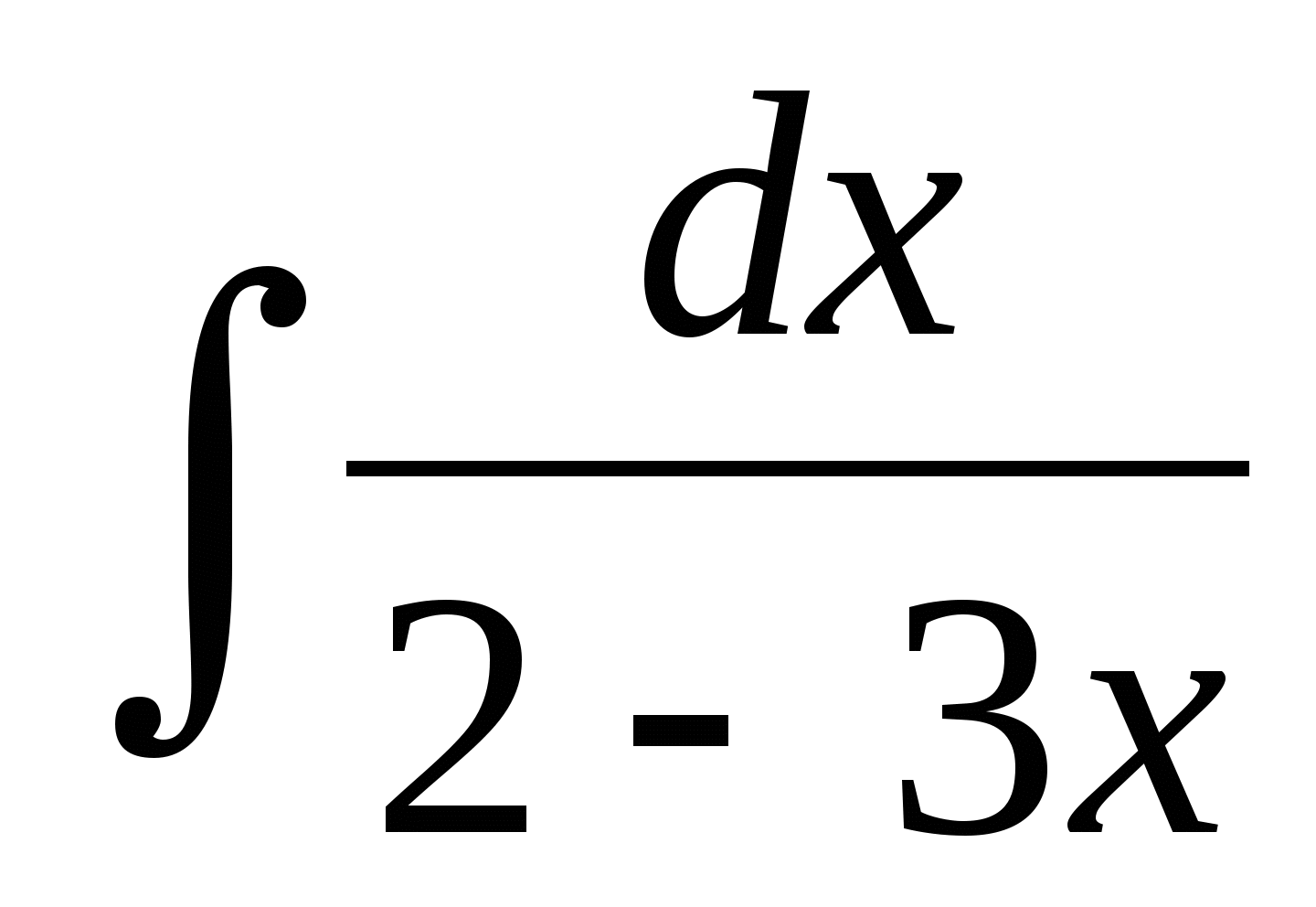
![]()
![]()
![]()
![]()
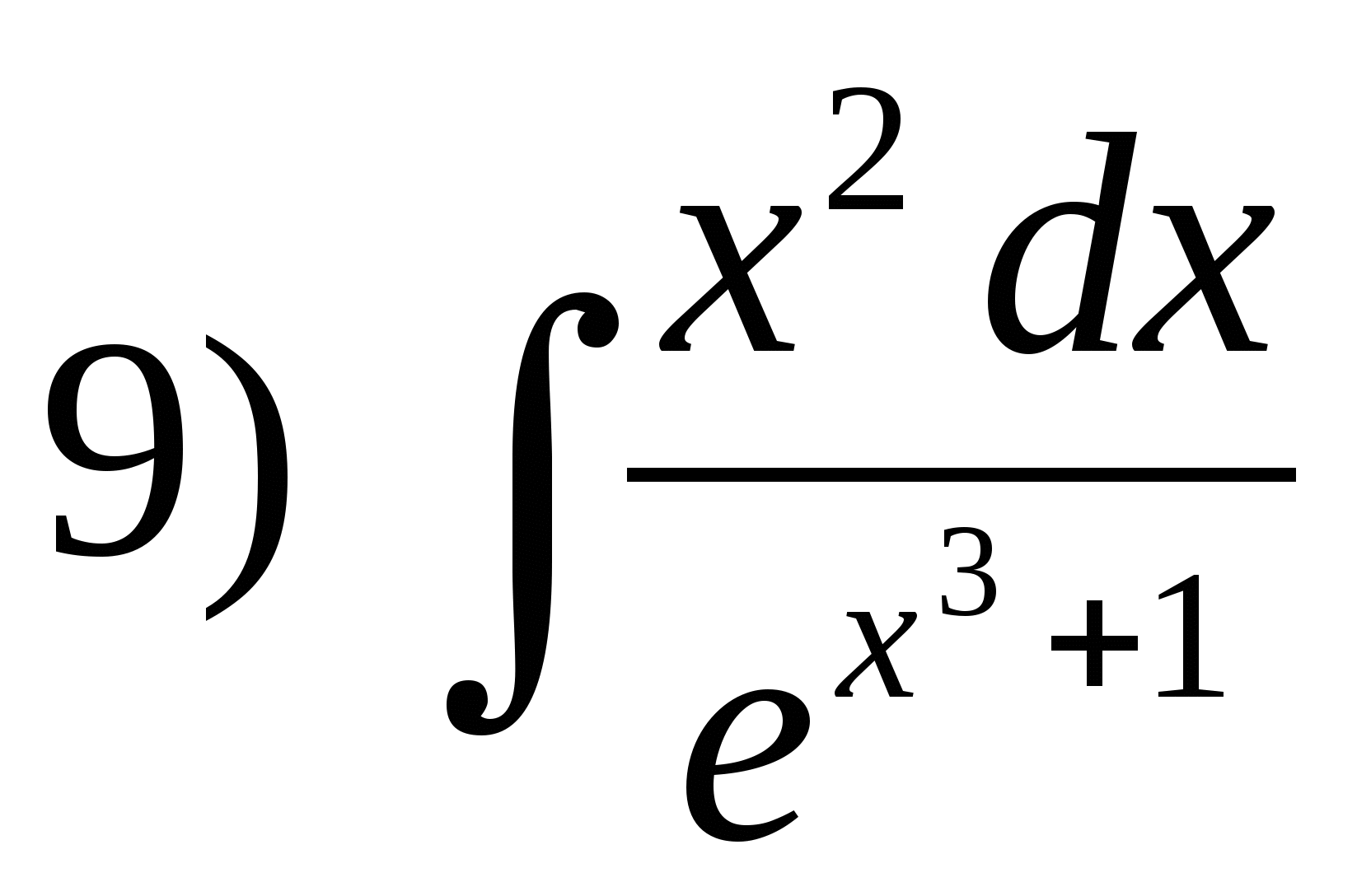
Закрепление сформированных знаний и умений
Закрепление полученных знаний по данной теме проводится во время самостоятельного решения заданий. Предлагаются 2 варианта:
7
![]()
![]()
Задачи для домашнего решения:
Вычислить интеграл:
![]() ;
;
![]() ;
;
![]() ;
;
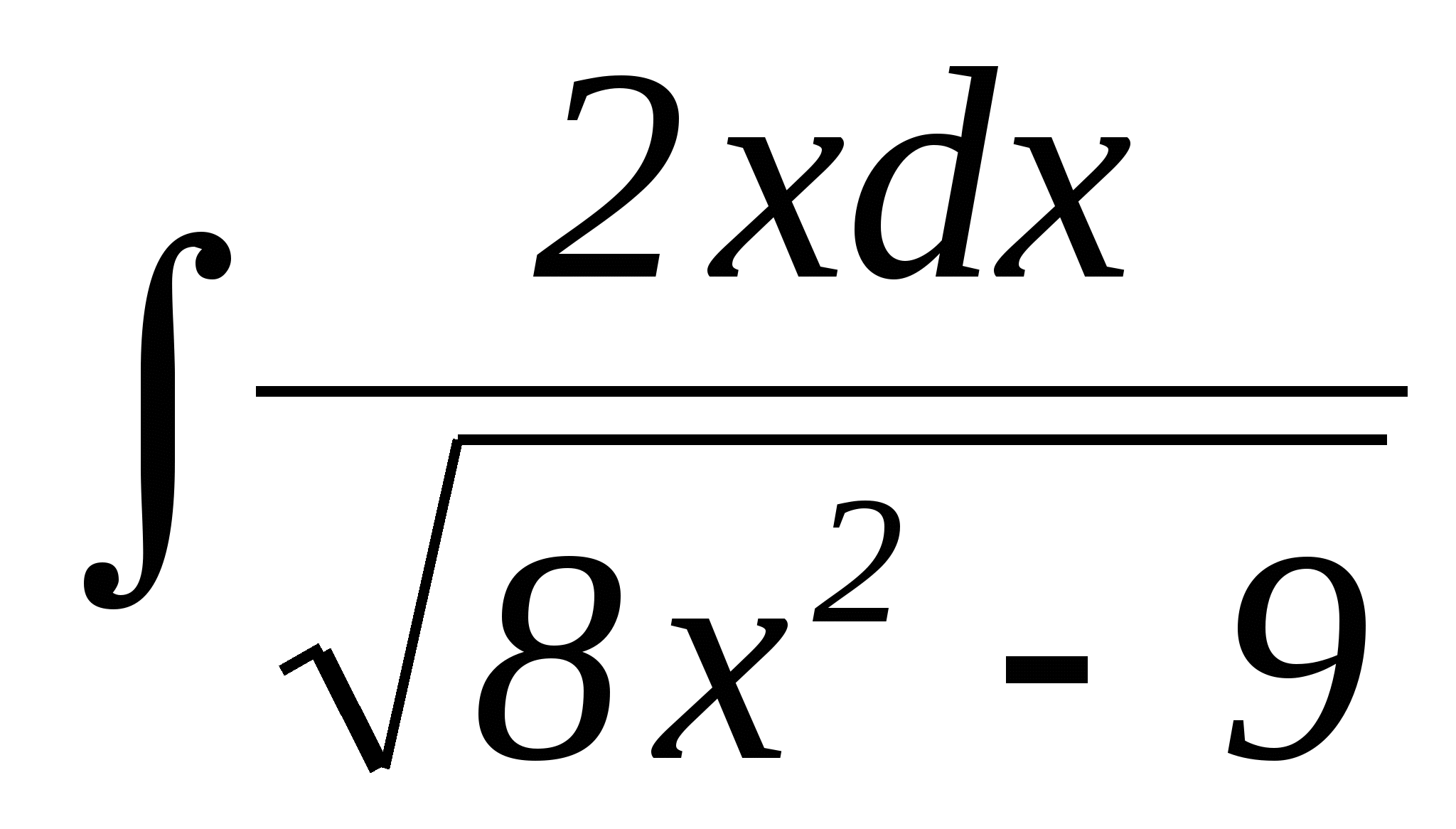 ;
;
![]() ;
;
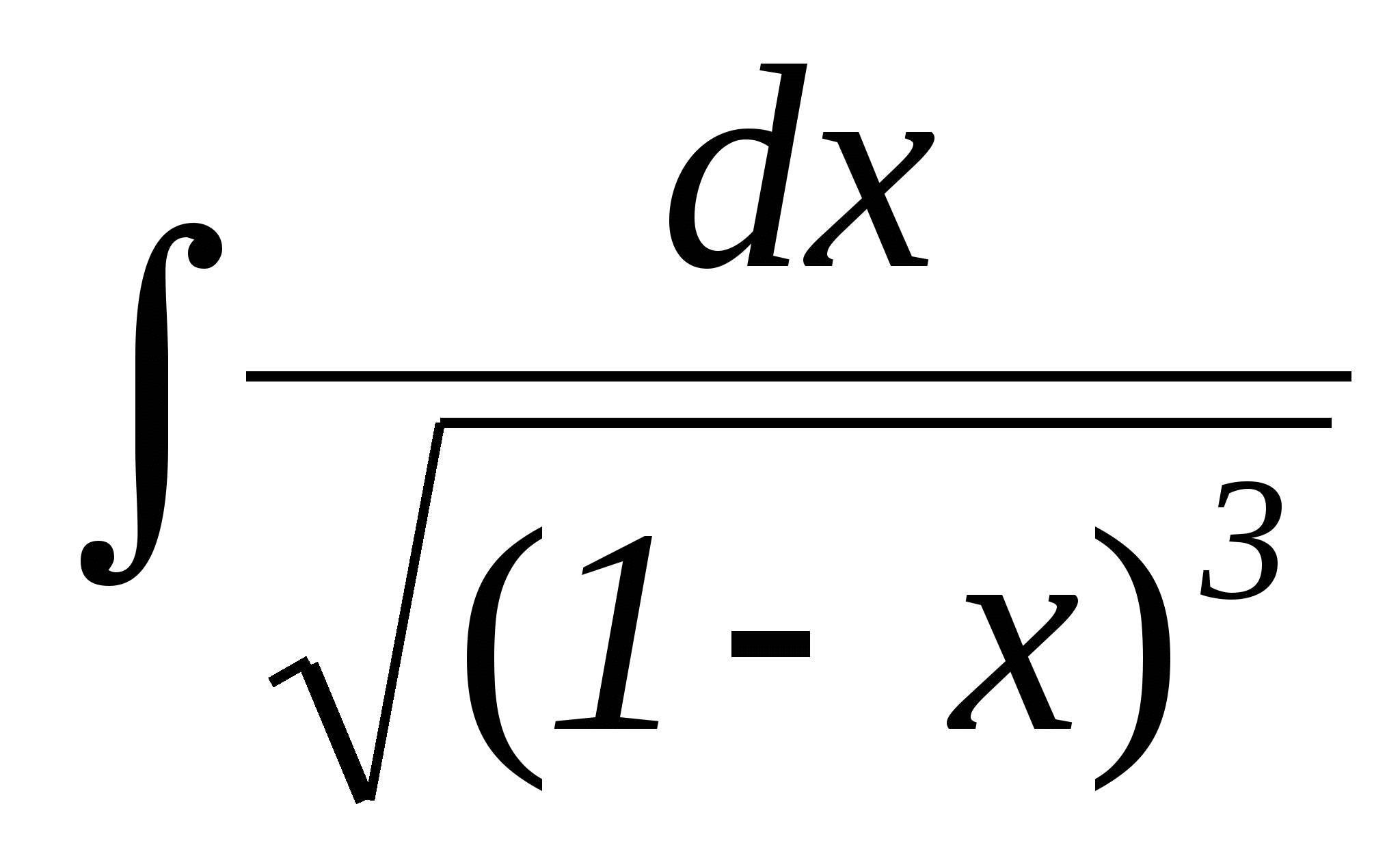
![]() .
.
Практическое занятие 10
Практическая работа 9
по теме «Вычисление определенного интеграла методом замены переменной и интегрированием по частям»
Цель работы: научиться вычислять определенный интеграл методами замены переменной и по частям.
Актуализация знаний
Фронтальный опрос
1. Понятие определенного интеграла. Свойства определенного интеграла.
2. Интегрирование методом замены переменной и по частям в определенном интеграле.
Краткие теоретические и учебно-методические материалы по теме практической работы
Замена переменной в определенном интеграле
Часто для упрощения вычисления интеграла
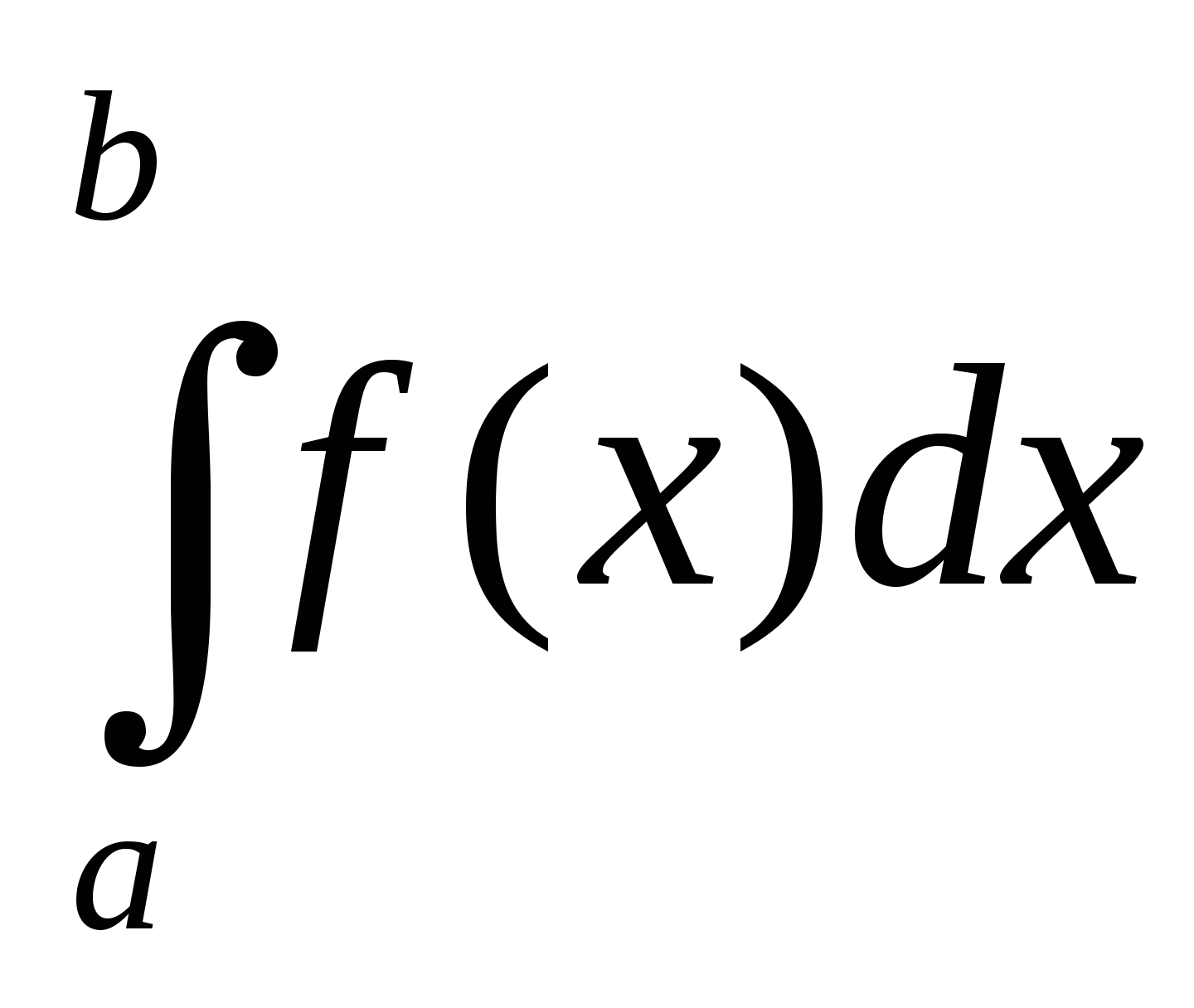 приходится заменять подынтегральное выражение или его часть новой
переменной. Подстановка должна упрощать вычисление интеграла. При
этом замена переменной в определенном интеграле сводится к
интегралу с новыми пределами интегрирования. Эти пределы находят
так: подставляется сначала нижний предел а заданного интеграла в
переменную, найденное значение и будет новым нижним пределом. Потом
для определения нового верхнего предела подставляется верхний
предел b заданного интеграла в переменную, найденное значение и
будет новым верхним пределом..
приходится заменять подынтегральное выражение или его часть новой
переменной. Подстановка должна упрощать вычисление интеграла. При
этом замена переменной в определенном интеграле сводится к
интегралу с новыми пределами интегрирования. Эти пределы находят
так: подставляется сначала нижний предел а заданного интеграла в
переменную, найденное значение и будет новым нижним пределом. Потом
для определения нового верхнего предела подставляется верхний
предел b заданного интеграла в переменную, найденное значение и
будет новым верхним пределом..
Выполнив замену, изменив пределы интегрирования, ми не переходим к старой переменной.
Интегрирование по частям в определенном интеграле
Замена происходит так же, как и в неопределенном
интеграле. Используется формула: 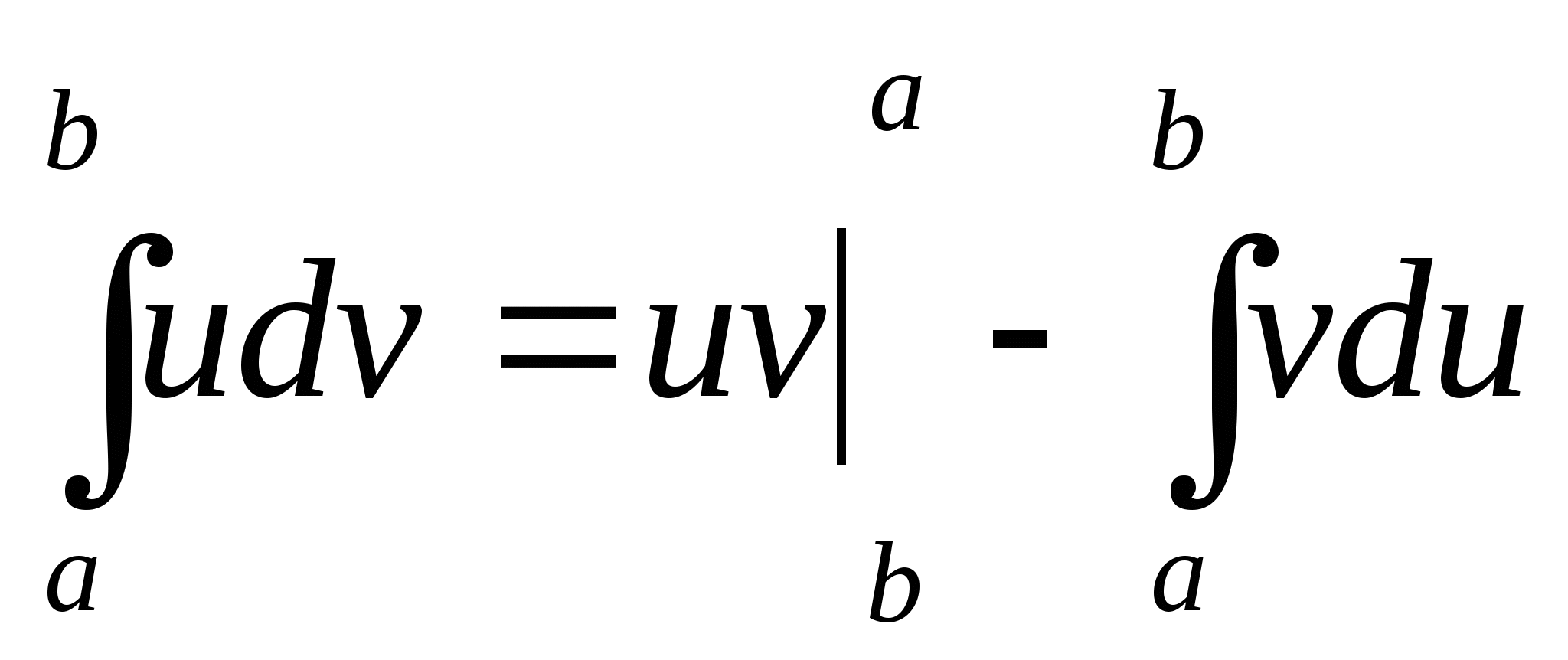
Формирование необходимых знаний и умений
Коллективное решение и обсуждение предложенных задач
Пример 1
Вычислить определенный интеграл:
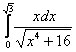
Главный вопрос здесь вовсе не в определенном интеграле, а в том, как правильно провести замену. Смотрим в таблицу интегралов и прикидываем, на что у нас больше всего похожа подынтегральная функция?
Очевидно, что на длинный логарифм: ![]() . Но есть одна неувязочка, в табличном интеграле под корнем
. Но есть одна неувязочка, в табличном интеграле под корнем
![]() а в нашем - «икс» в четвёртой степени. Из рассуждений следует и
идея замены - неплохо бы нашу четвертую степень как-нибудь
превратить в квадрат. Это реально.
а в нашем - «икс» в четвёртой степени. Из рассуждений следует и
идея замены - неплохо бы нашу четвертую степень как-нибудь
превратить в квадрат. Это реально.
Сначала готовим наш интеграл к замене:
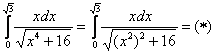
Из вышеуказанных соображений совершенно
естественно напрашивается замена: ![]()
Таким образом, в знаменателе будет : ![]() .
.
Выясняем, во что превратится оставшаяся часть xdx подынтегрального
выражения, для этого находим дифференциал dt:
![]()
По сравнению с заменой в неопределенном интеграле у нас добавляется дополнительный этап: находим новые пределы интегрирования.
Это достаточно просто. Смотрим на нашу замену
t=x2 и старые пределы интегрирования ![]() ,
, ![]() .
.
Сначала подставляем в выражение замены
t=x2 нижний предел интегрирования, то есть, ноль:
![]() /
/
Потом подставляем в выражение замены
t=x2 верхний предел интегрирования, то есть, корень из
трёх:
![]()
Готово. Продолжаем решение.

(1) В соответствии с заменой записываем новый интеграл с новыми пределами интегрирования.
(2) Это простейший табличный интеграл,
интегрируем по таблице. Константу ![]() лучше оставить за скобками (можно этого и не делать), чтобы она не
мешалась в дальнейших вычислениях. Справа отчеркиваем линию с
указанием новых пределов интегрирования
лучше оставить за скобками (можно этого и не делать), чтобы она не
мешалась в дальнейших вычислениях. Справа отчеркиваем линию с
указанием новых пределов интегрирования ![]() - это подготовка для применения формулы Ньютона-Лейбница.(3)
- это подготовка для применения формулы Ньютона-Лейбница.(3)
Используем формулу Ньютона-Лейбница
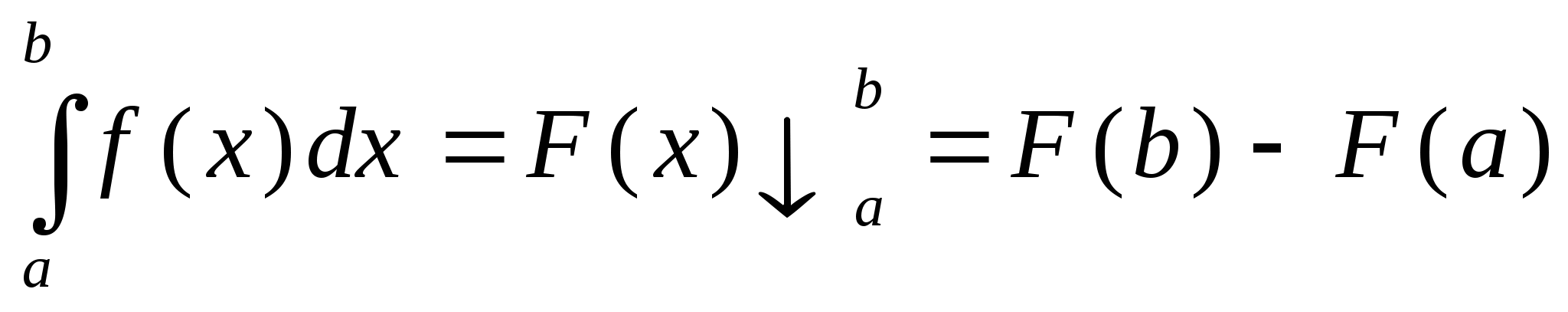
Ответ стремимся записать в максимально компактном виде.
Ещё одно отличие от неопределенного интеграла состоит в том, что, после того, как мы провели замену, никаких обратных замен проводить не надо.
Пример 2
Проинтегрировать по частям:
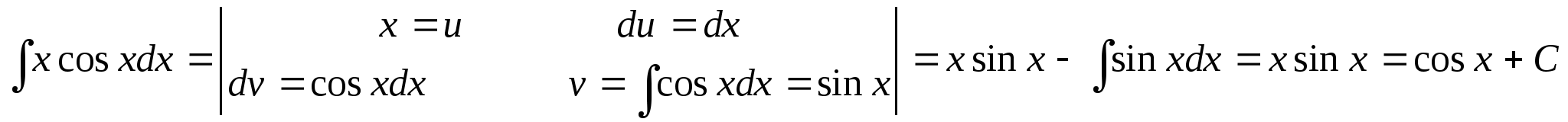
Пример 3
Вычислить )интеграл методом замены переменной:
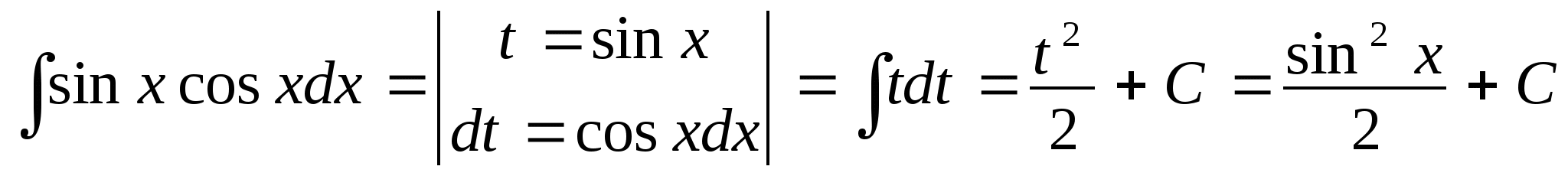
Примеры:
1) 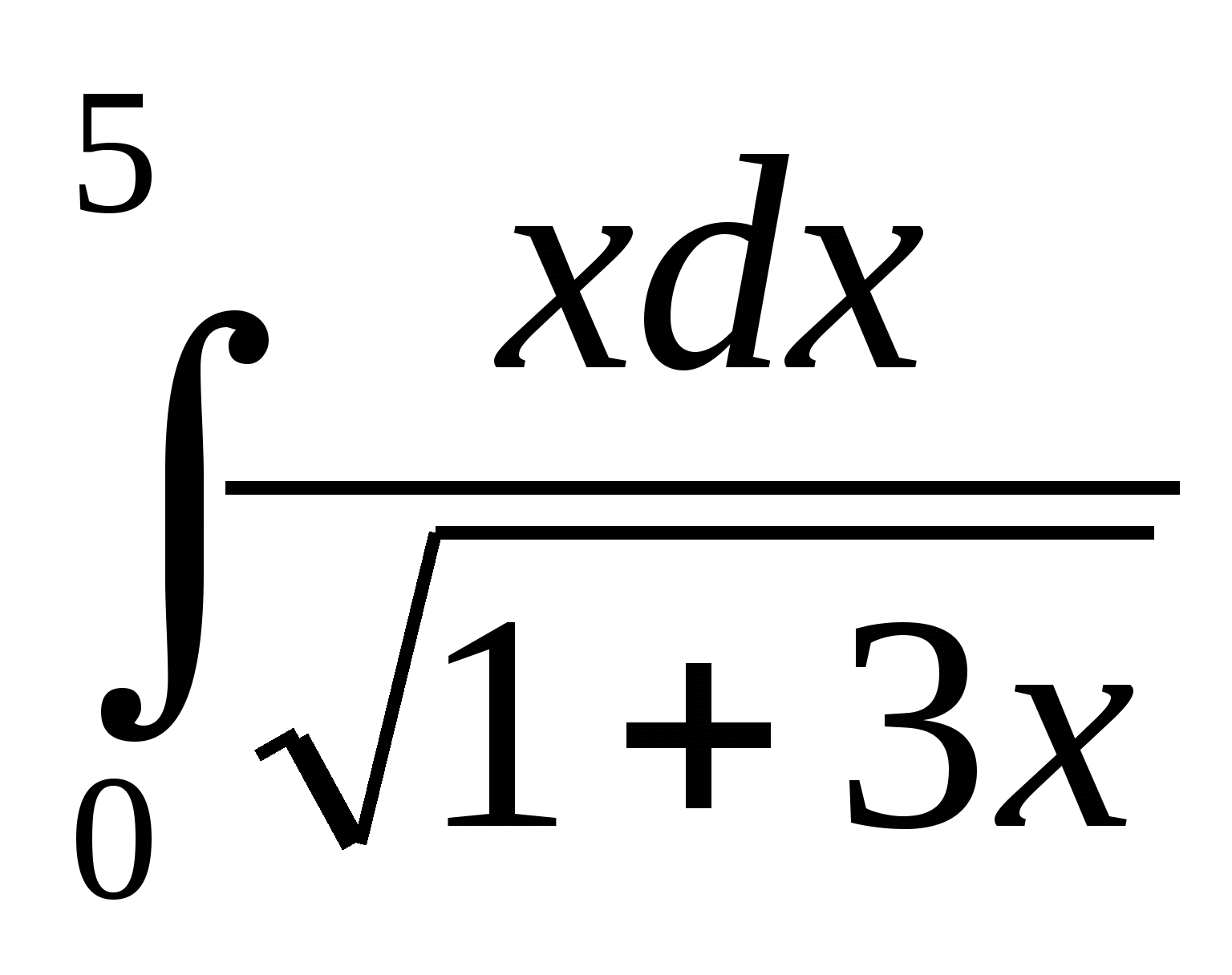 ; 2)
; 2) 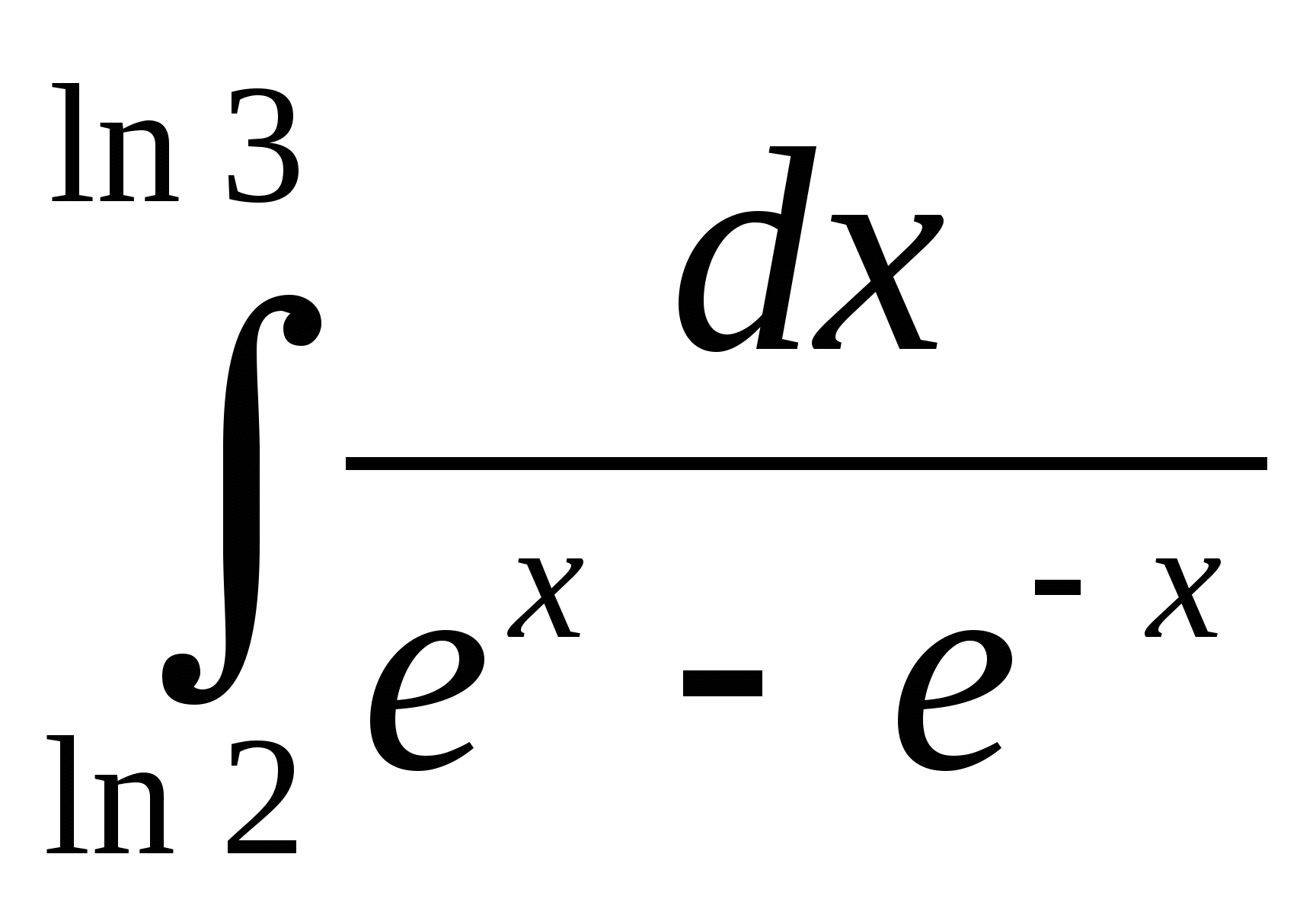 ; 3)
; 3) 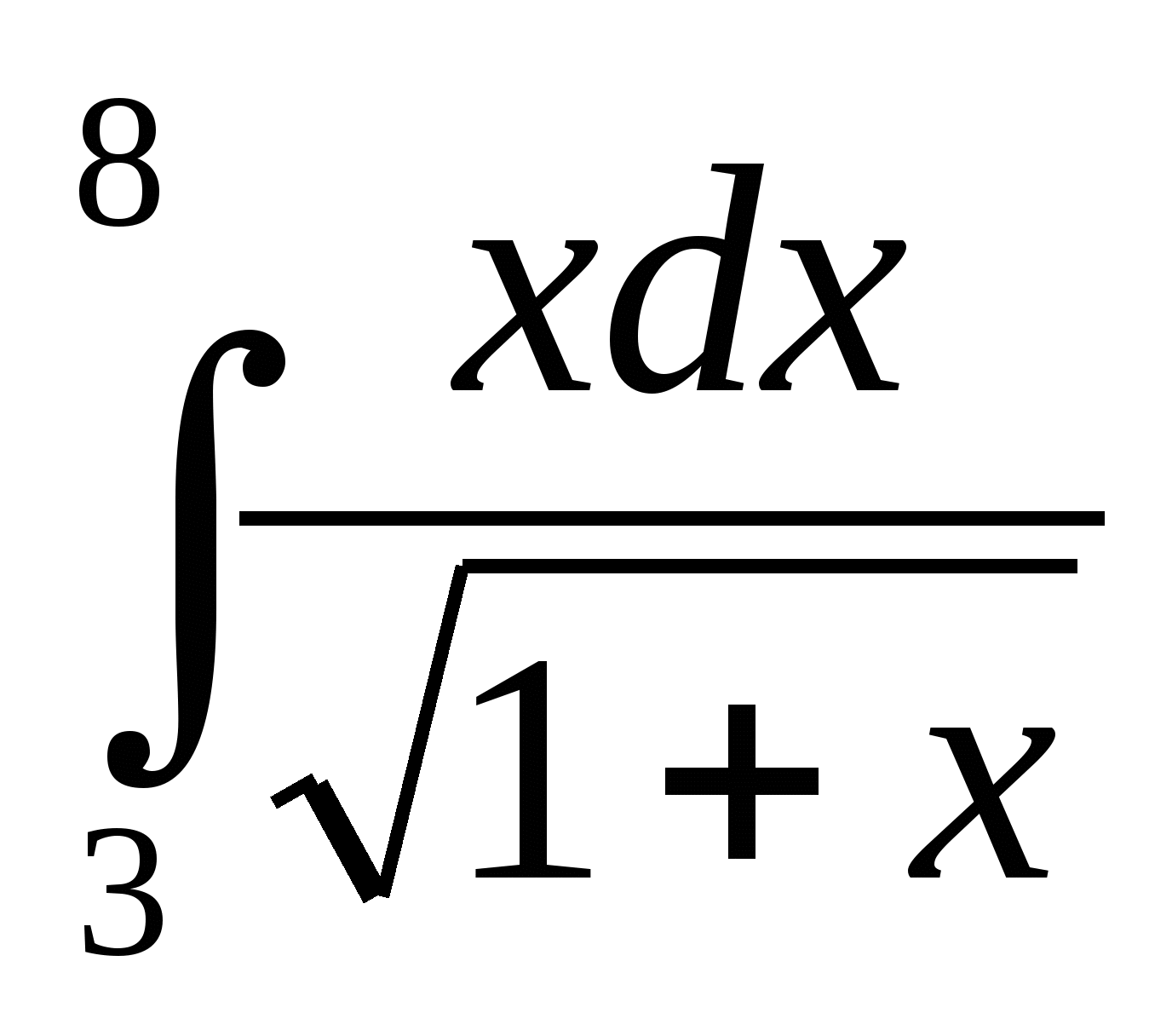 ;
;
4) 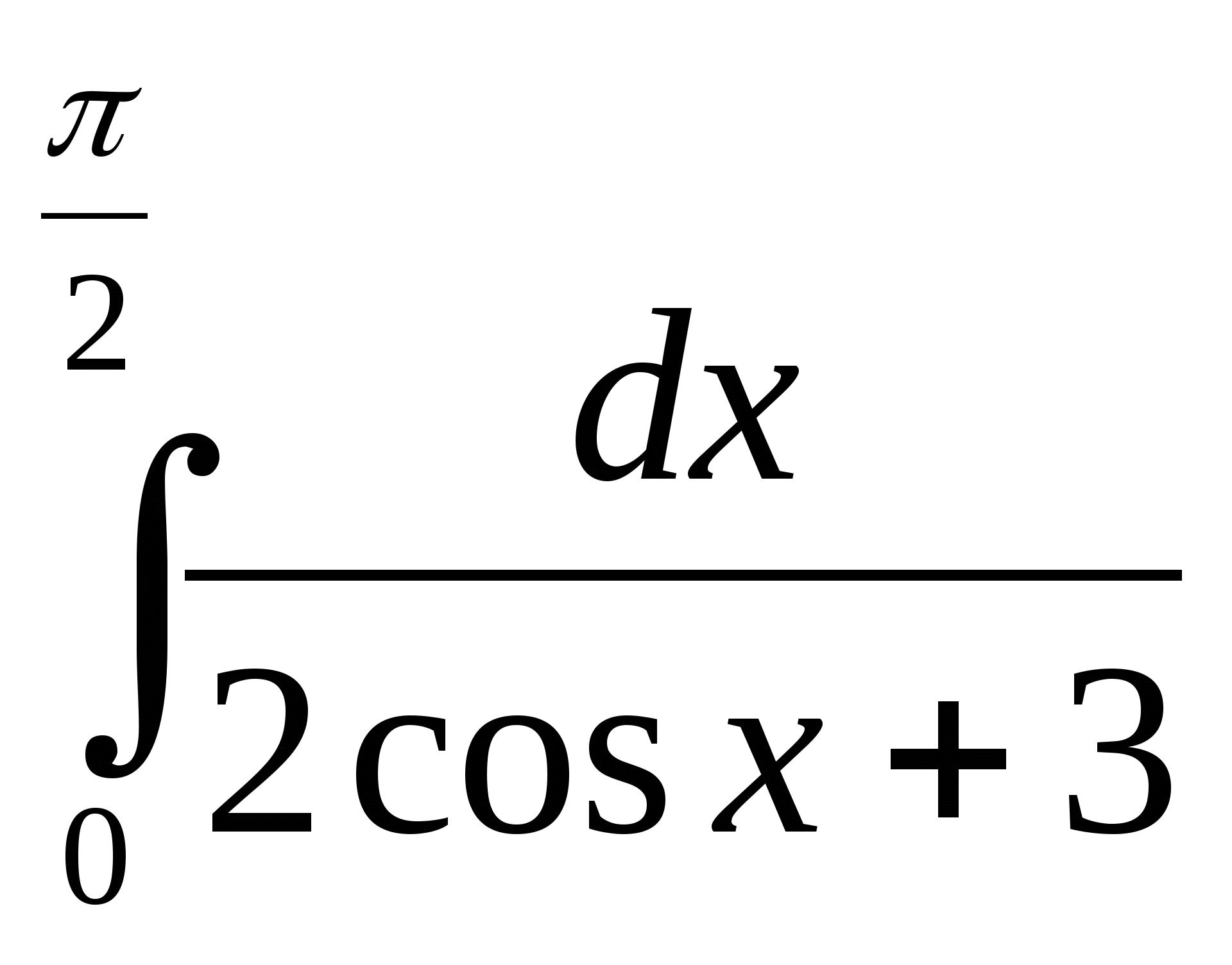 ; 5)
; 5)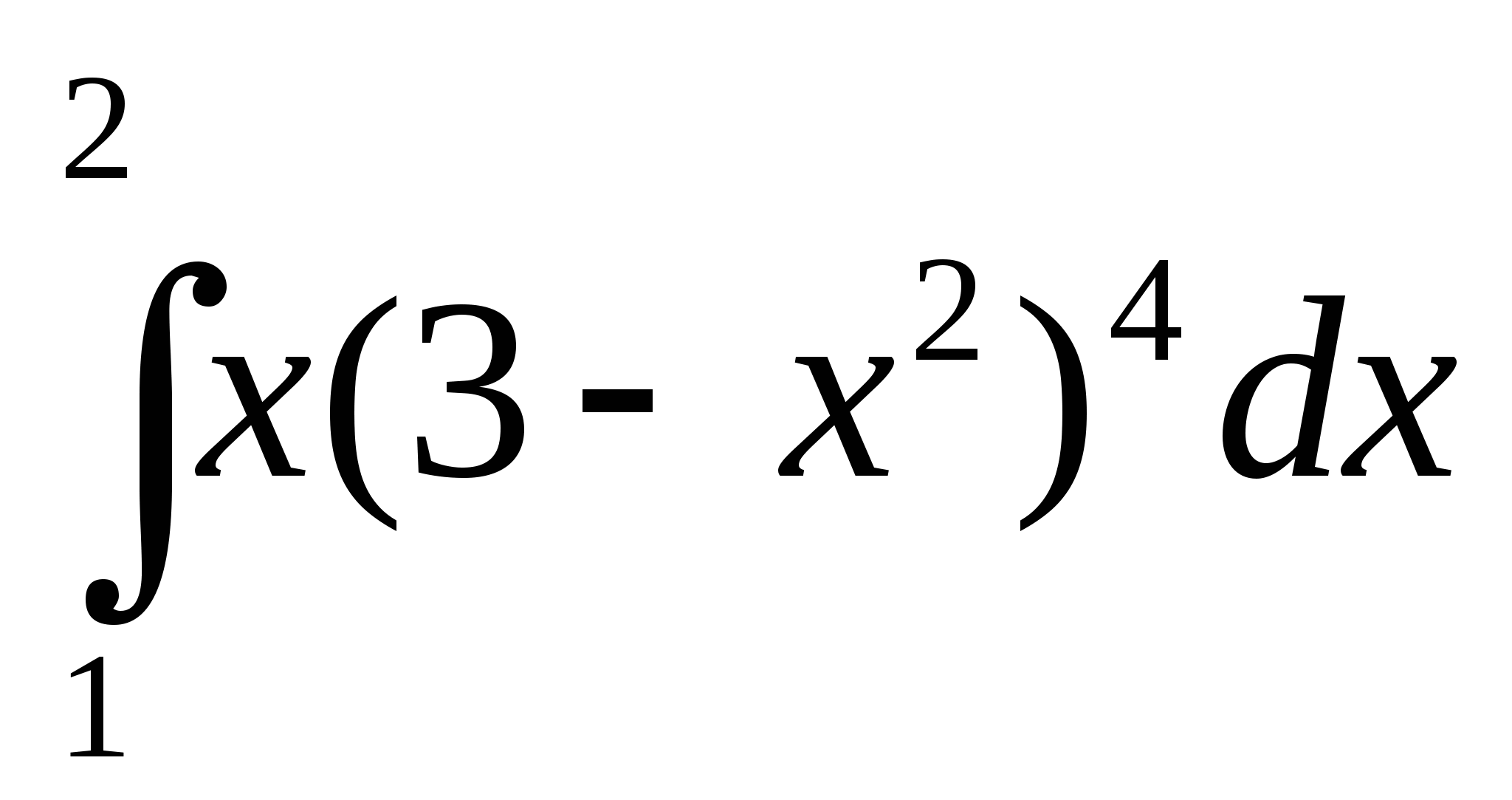
Закрепление сформированных знаний и умений
Закрепление полученных знаний по данной теме проводится во время самостоятельного решения заданий.
Примеры
1. Вычислить интеграл:
1) 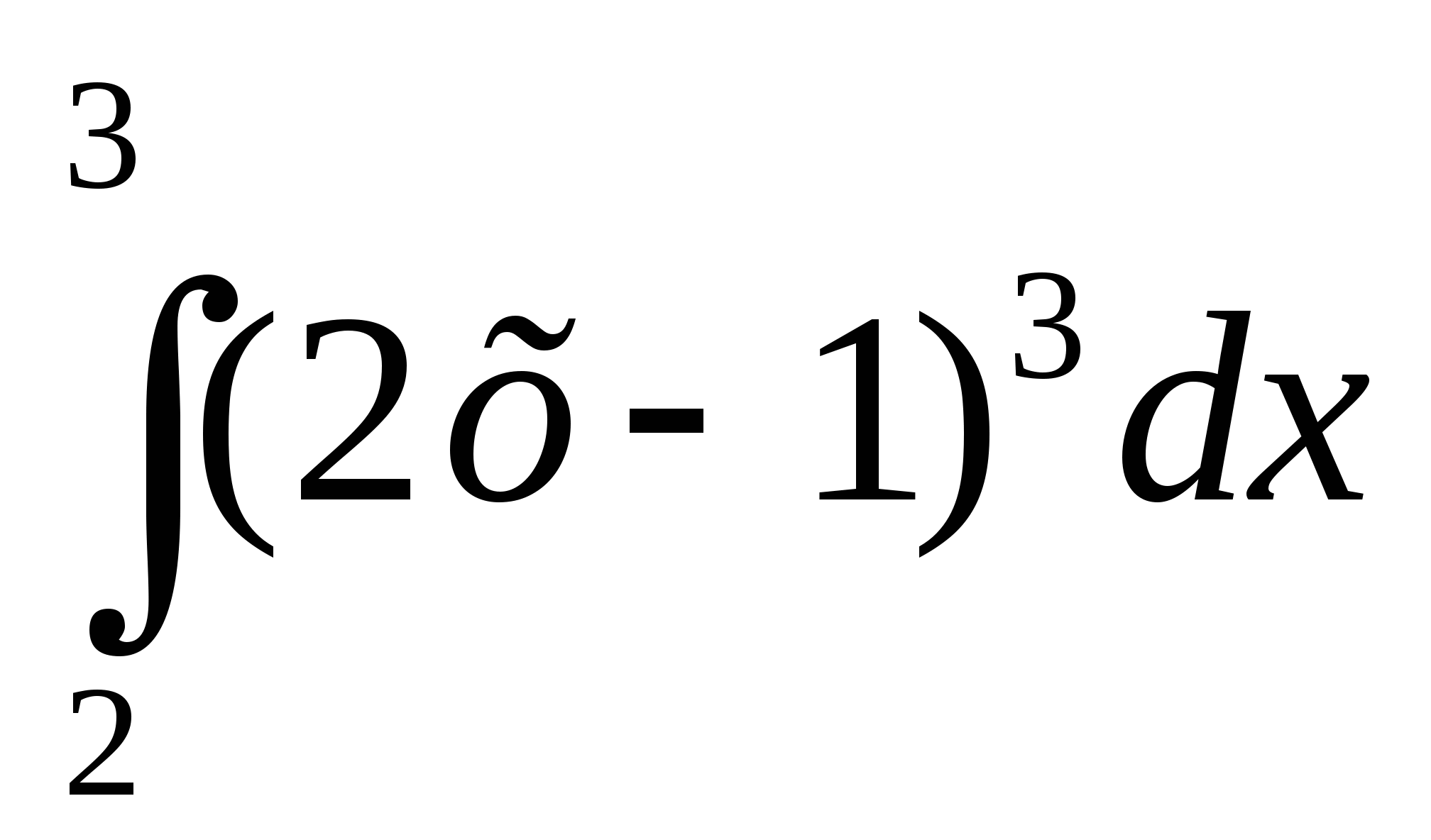 ; 2)
; 2) 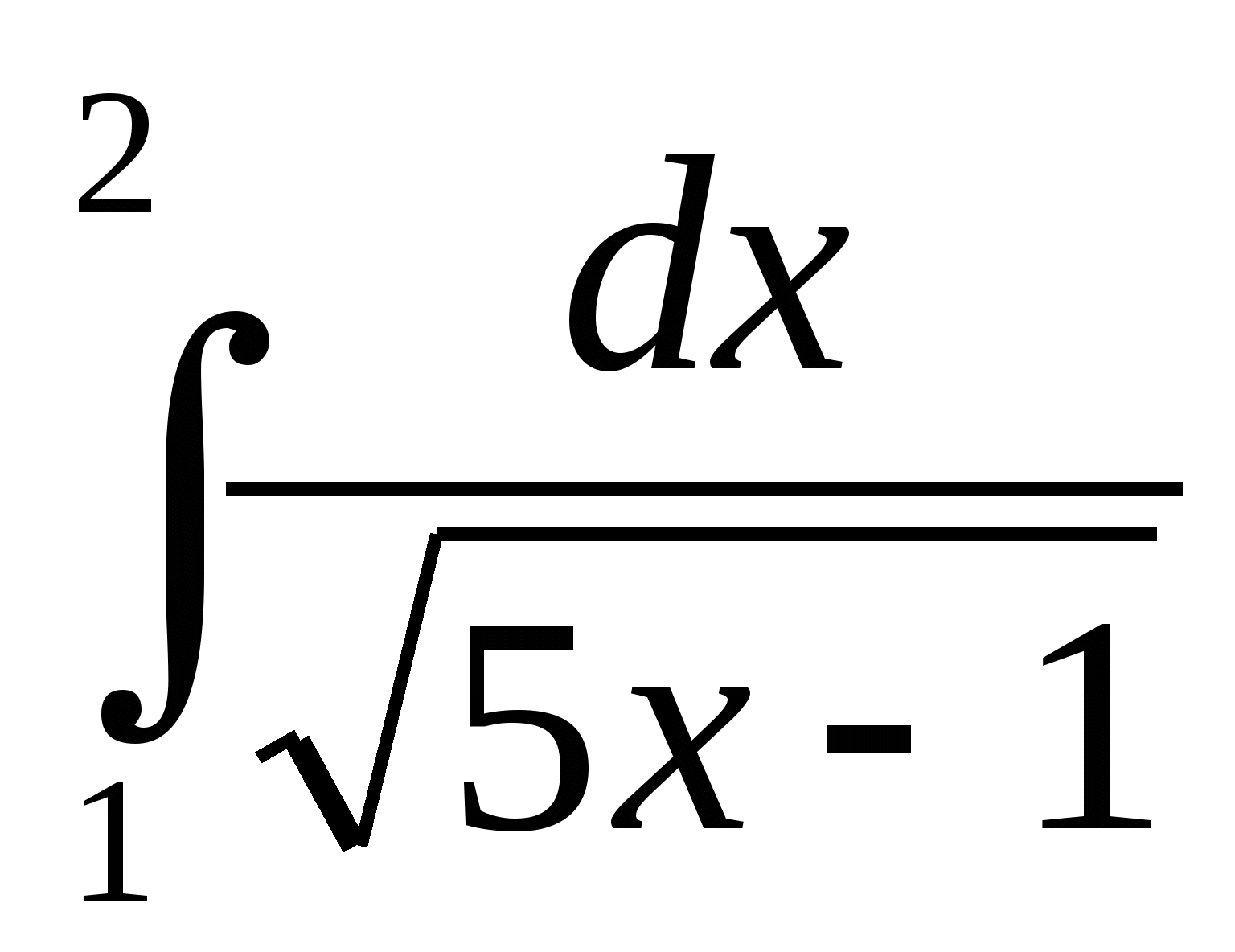 ; 3)
; 3) 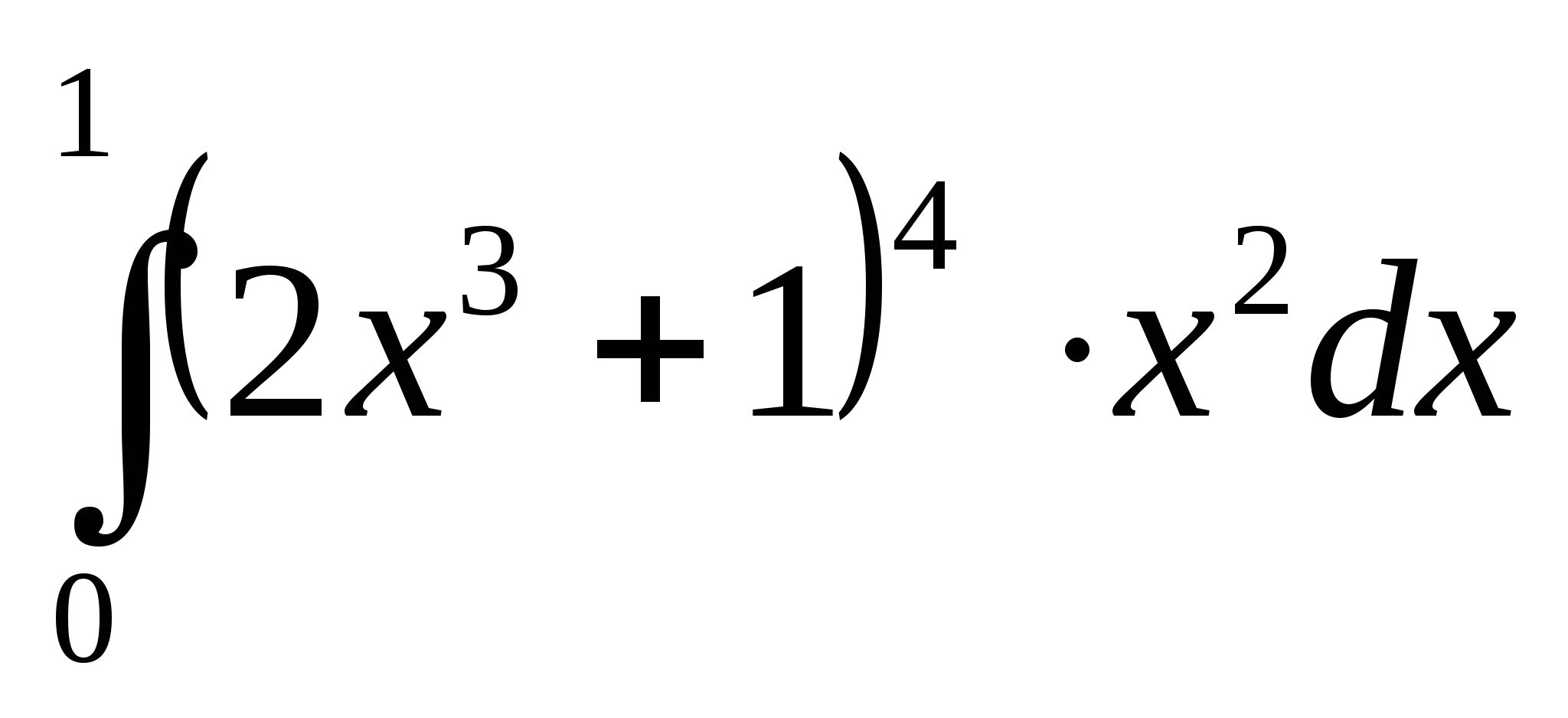 ;
;
4) 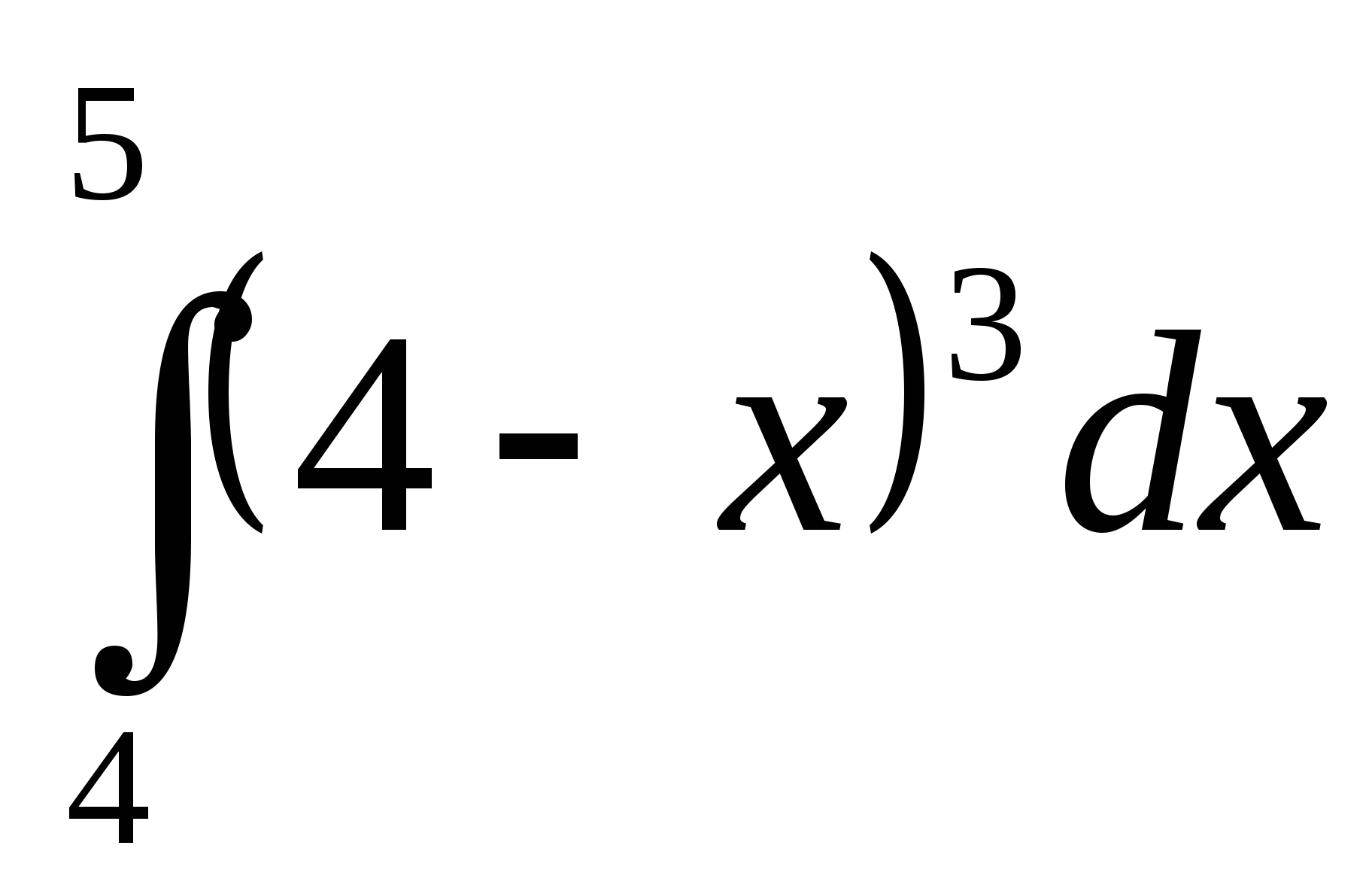 ; 5)
; 5) 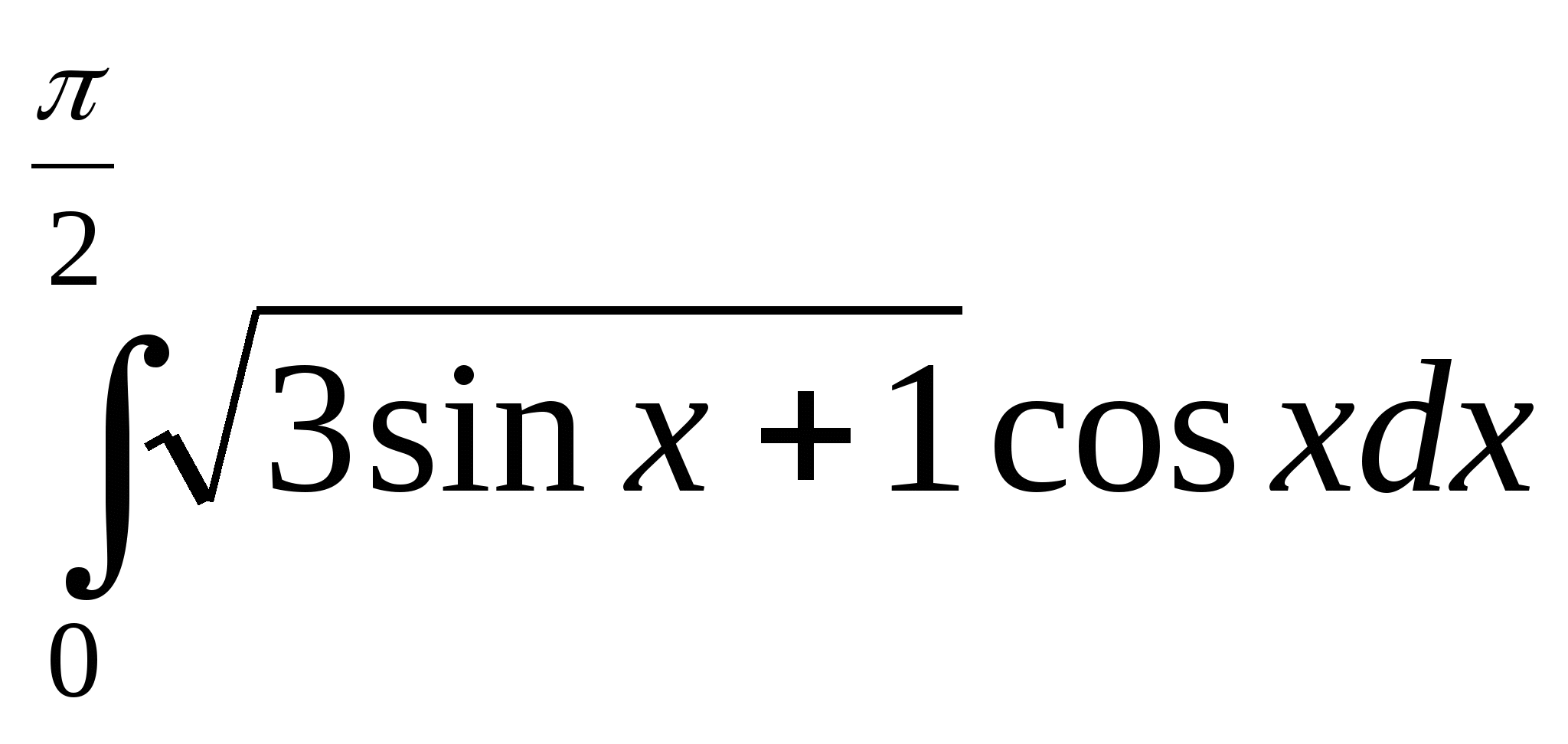 ; 6)
; 6) 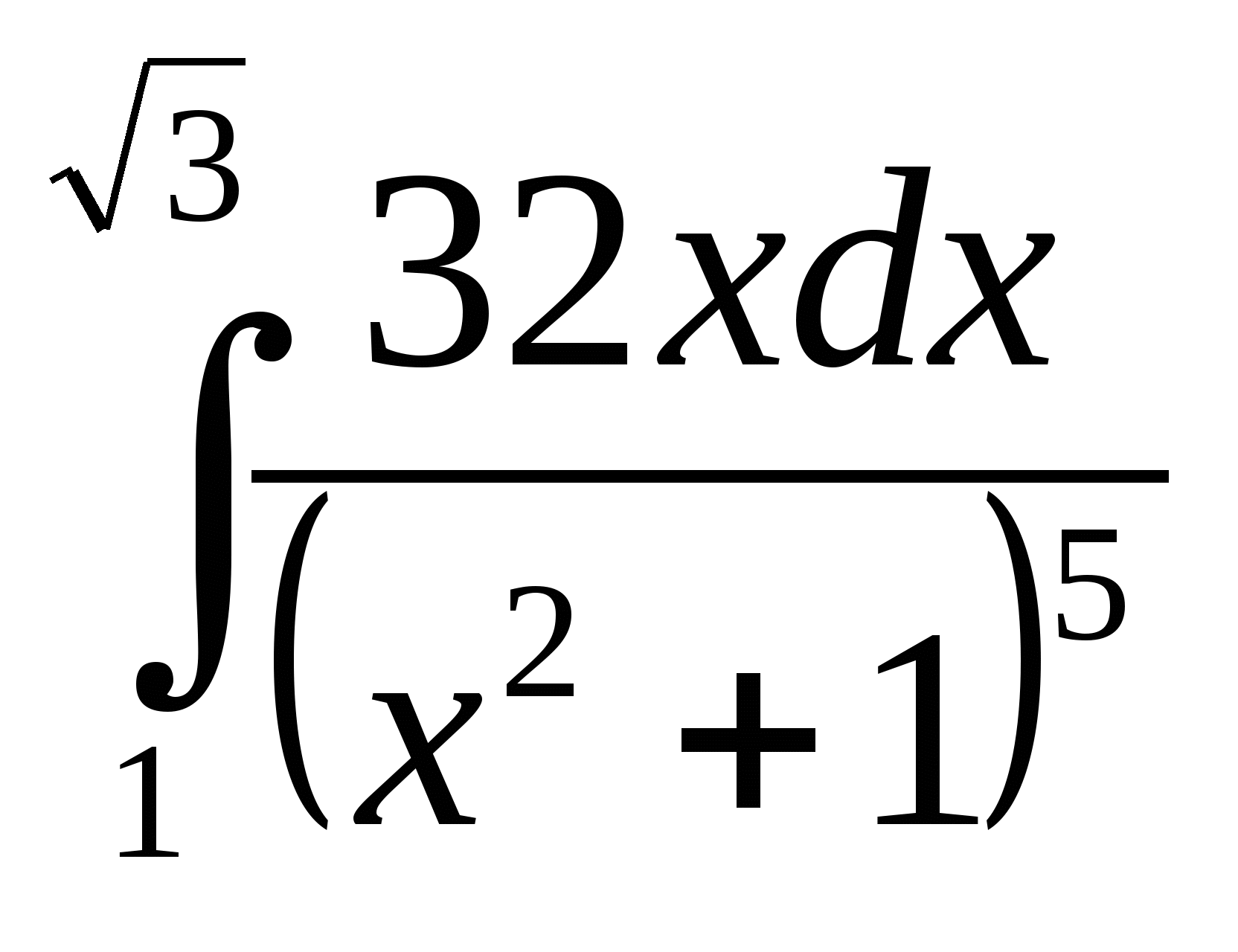 ;
;
7) 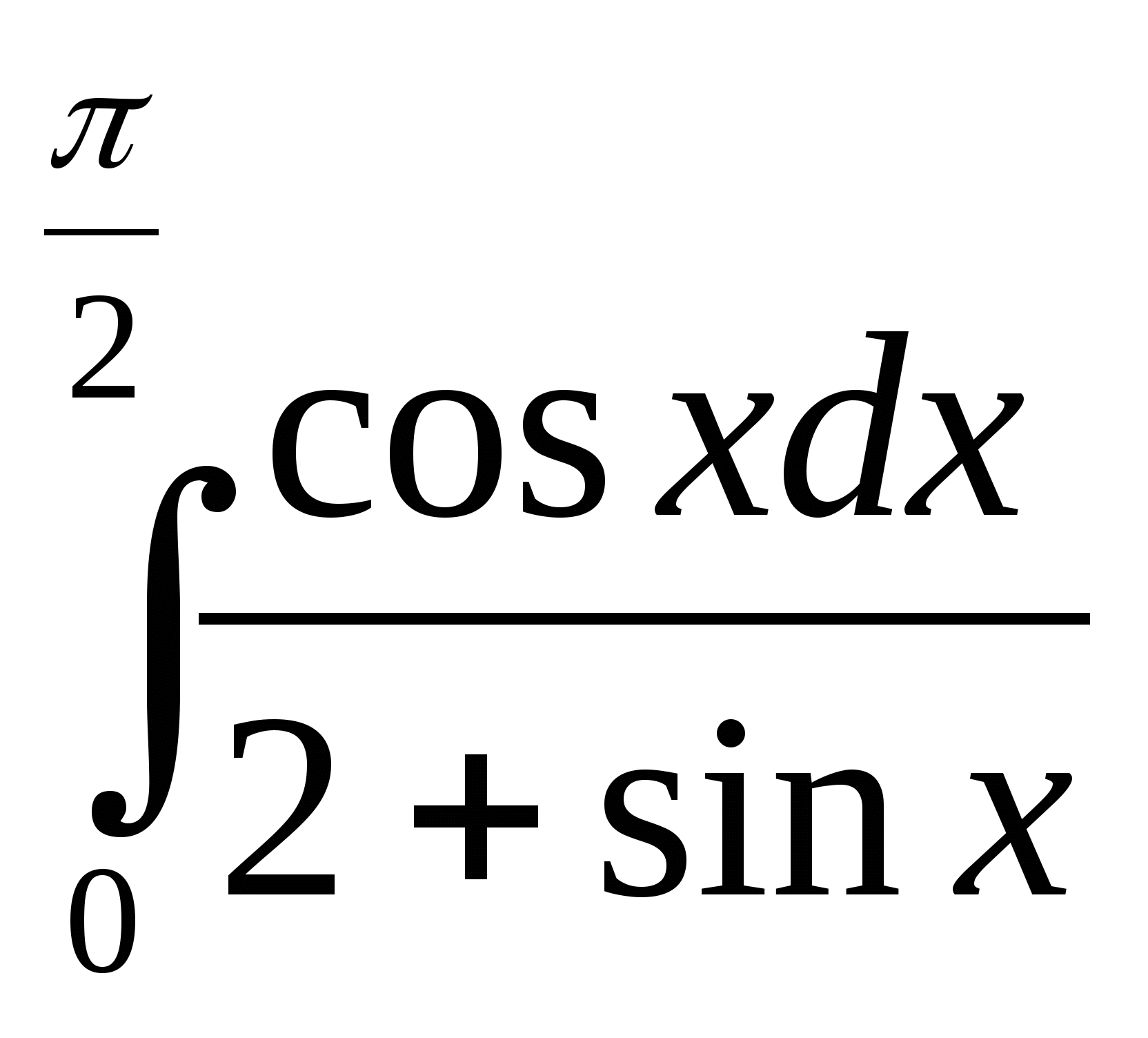 ; 8)
; 8) 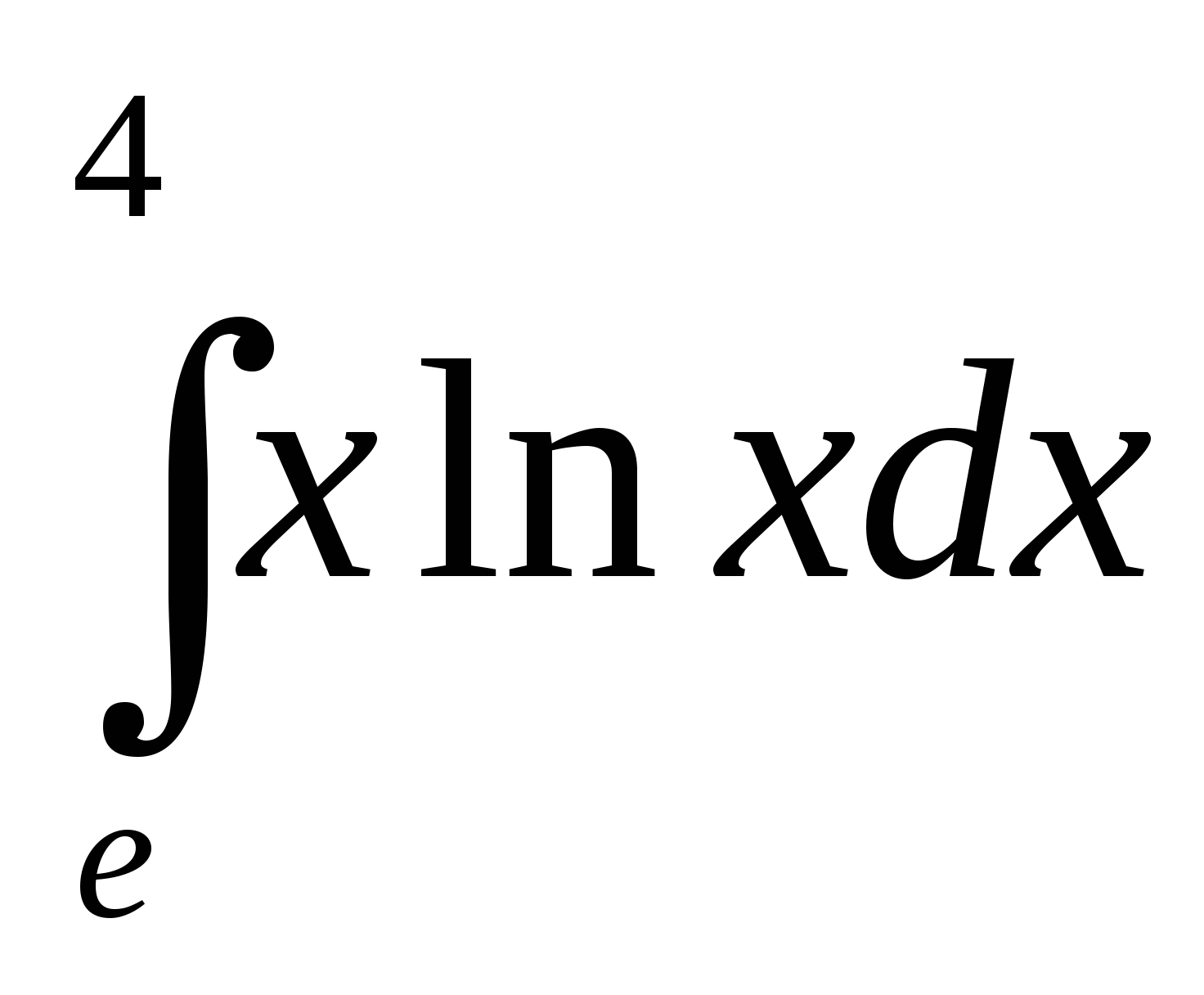 ; 9)
; 9) 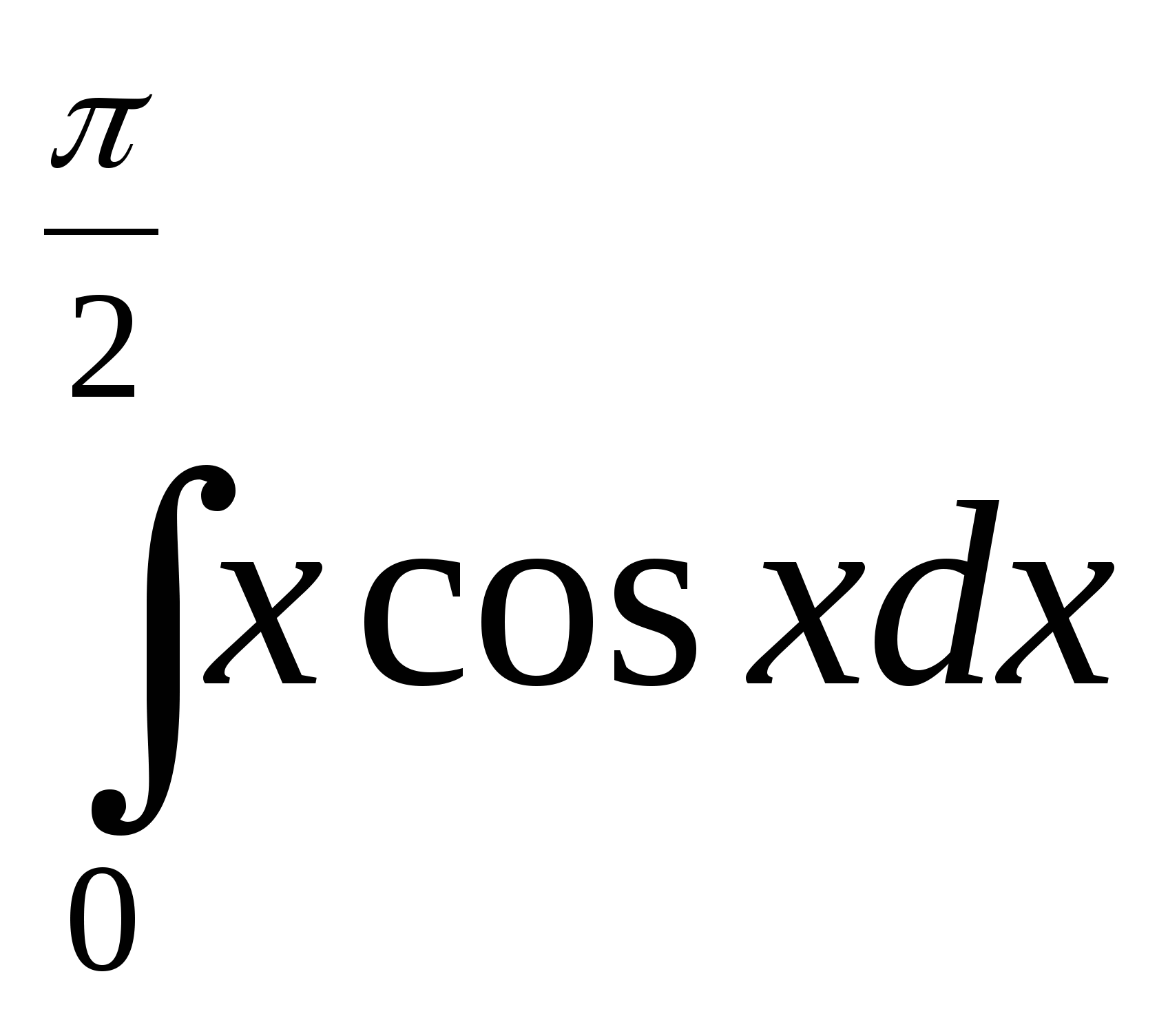 ;
;
10) 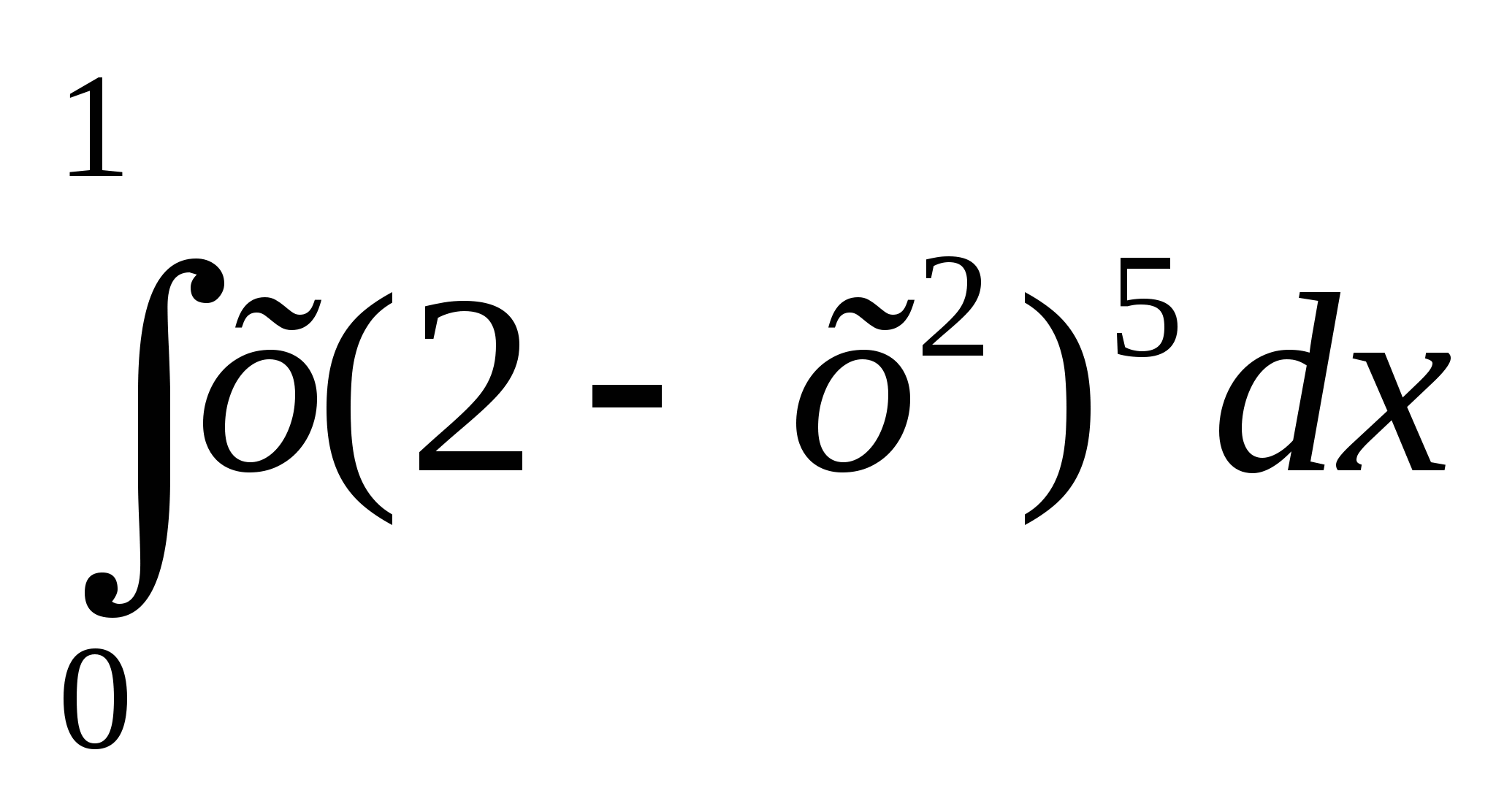
Задачи для домашнего решения:
Вычислить интеграл:
1) 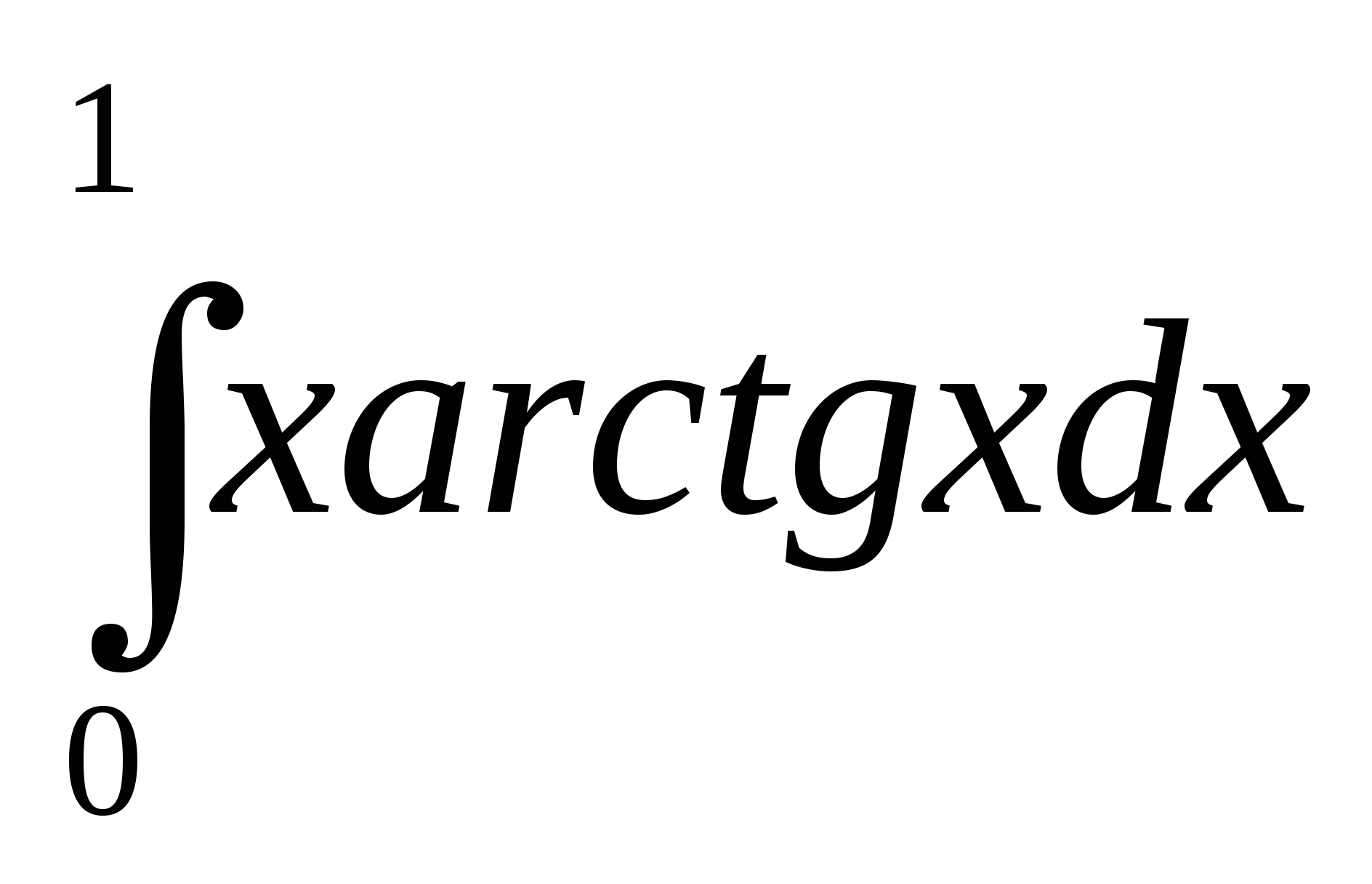 ; 2)
; 2) 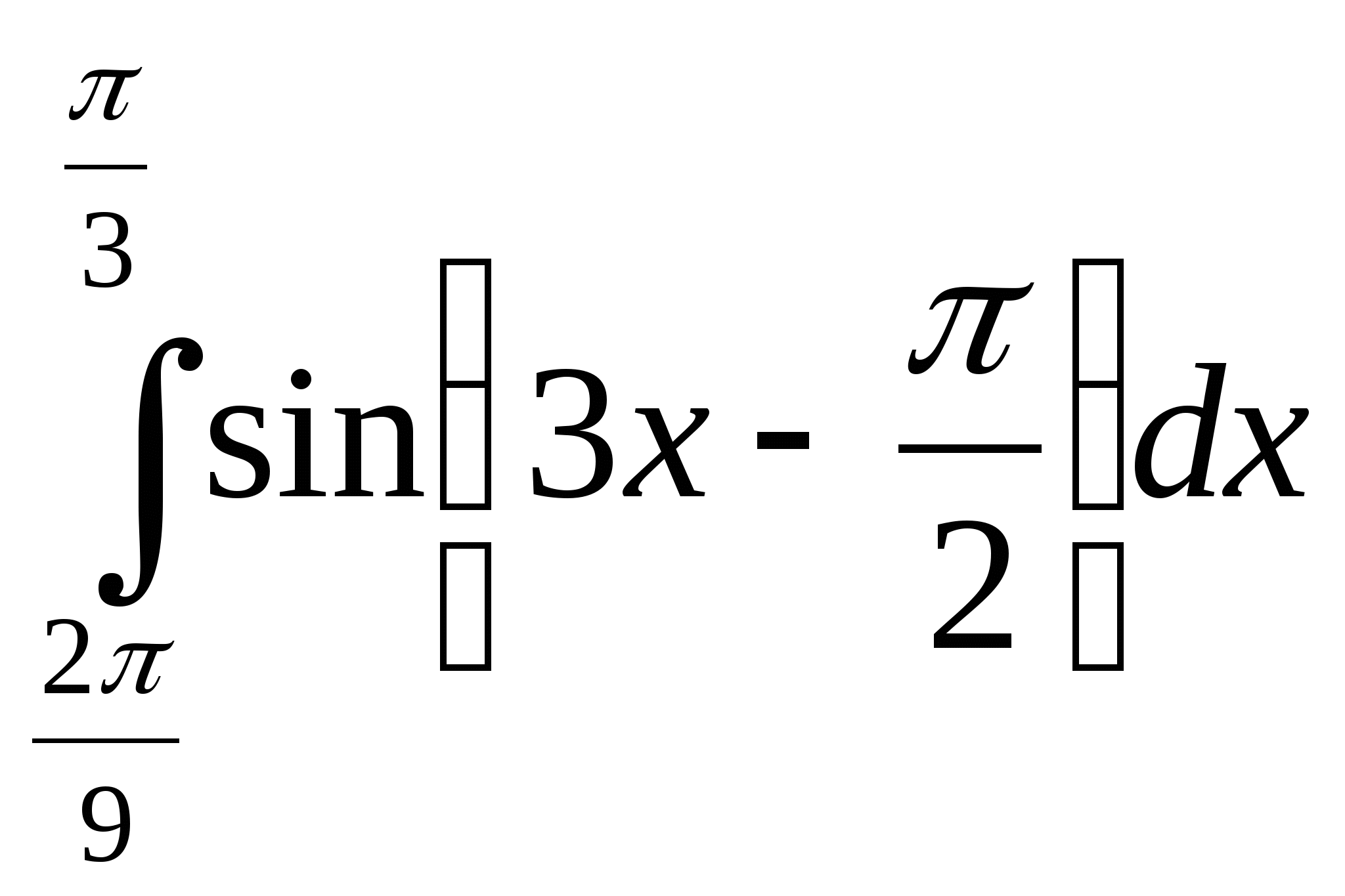 ;3)
;3) 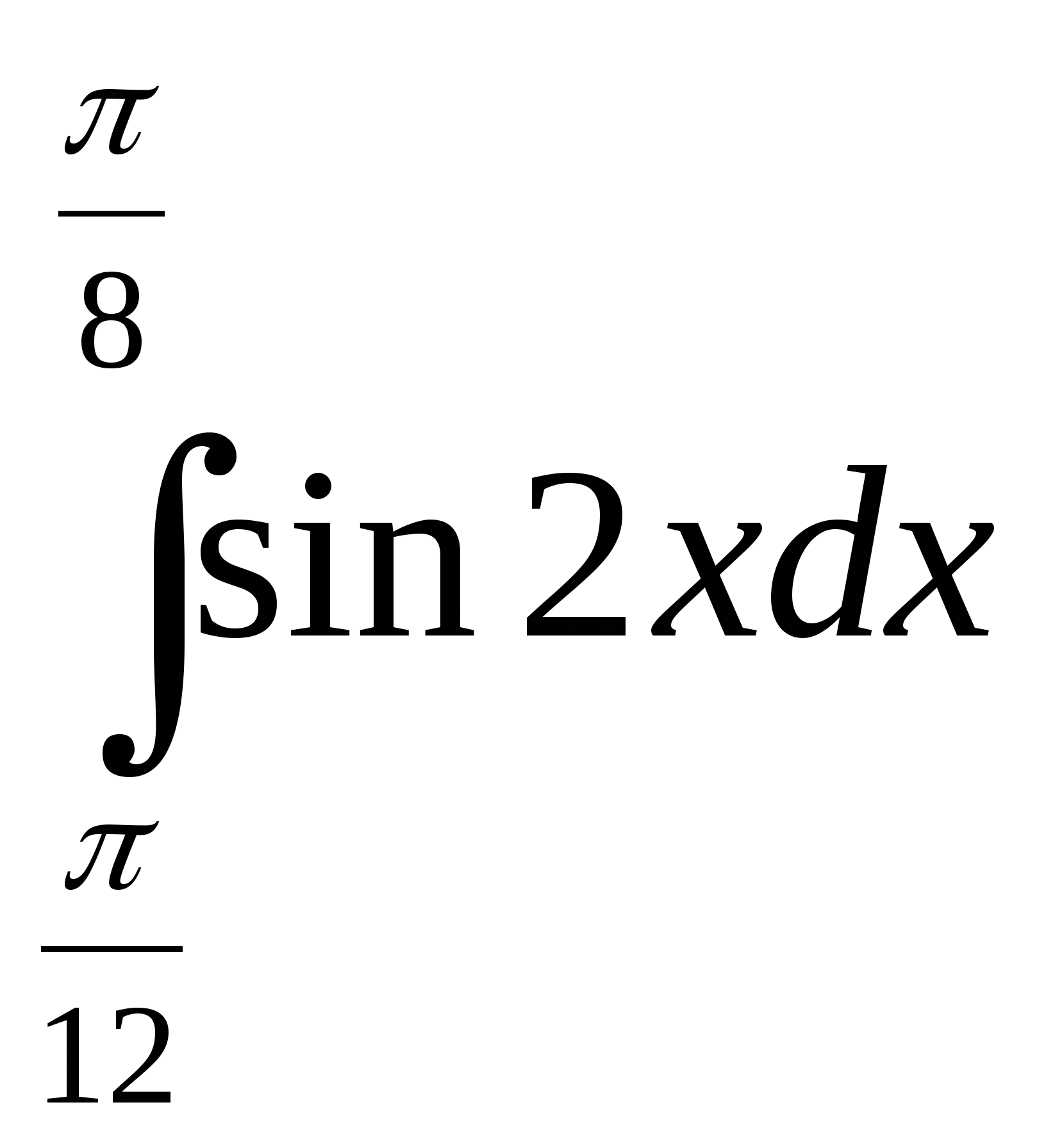 ;4)
;4) 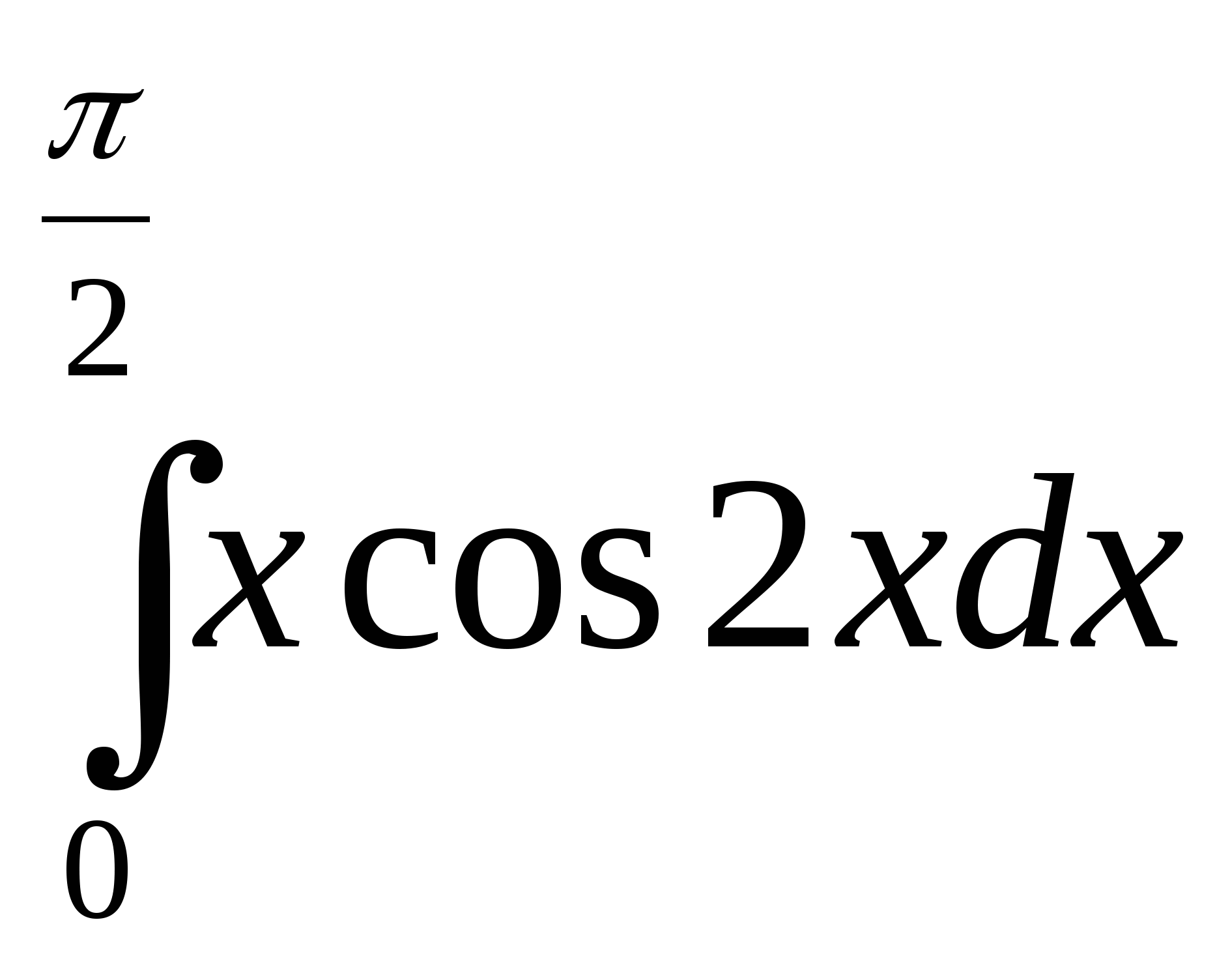
Практическое занятие 11
Практическая работа 10
по теме «Решение заданий экономического смысла методом интегрального исчисления»
Цель работы: научиться решать задания экономического смысла методом интегрального исчисления.
Актуализация знаний
Фронтальный опрос
1. Понятие определенного интеграла. Свойства определенного интеграла.
2. Интегрирование методом замены переменной и по частям в определенном интеграле.
3. Области применения определенного интеграла.
Краткие теоретические и учебно-методические материалы по теме практической работы
Объем продукции V, который был изготовлен за промежуток времени [0;Т] при изменении продуктивности труда предприятия, который описан функцией у=f(t), находится по формуле:
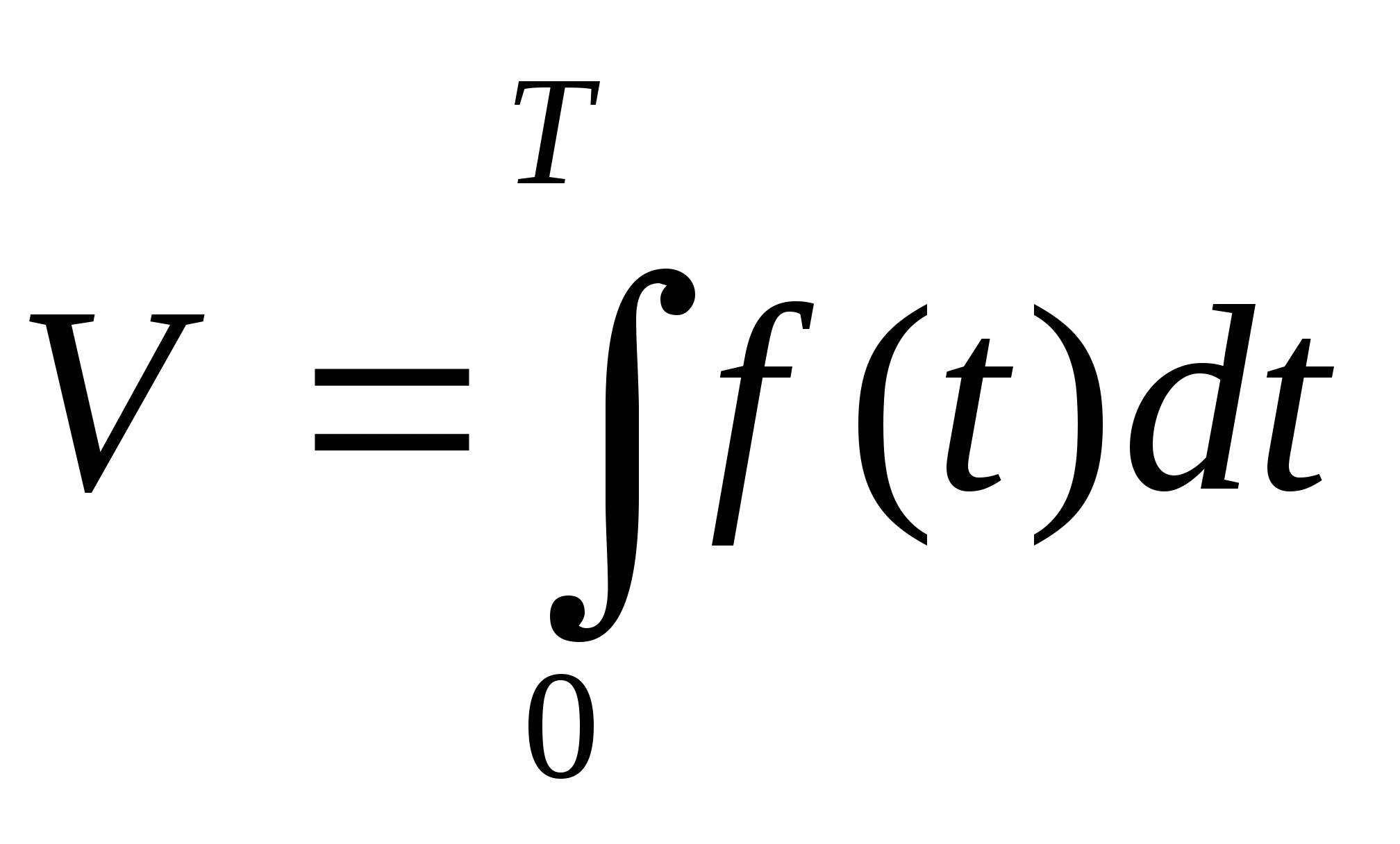
f - продуктивность труда в данный момент
t - время, которое прошло от начала рабочего дня
Теорема о среднем: если функция непрерывная на интервале (а;в), то существует такое число С из этого интервала, что:
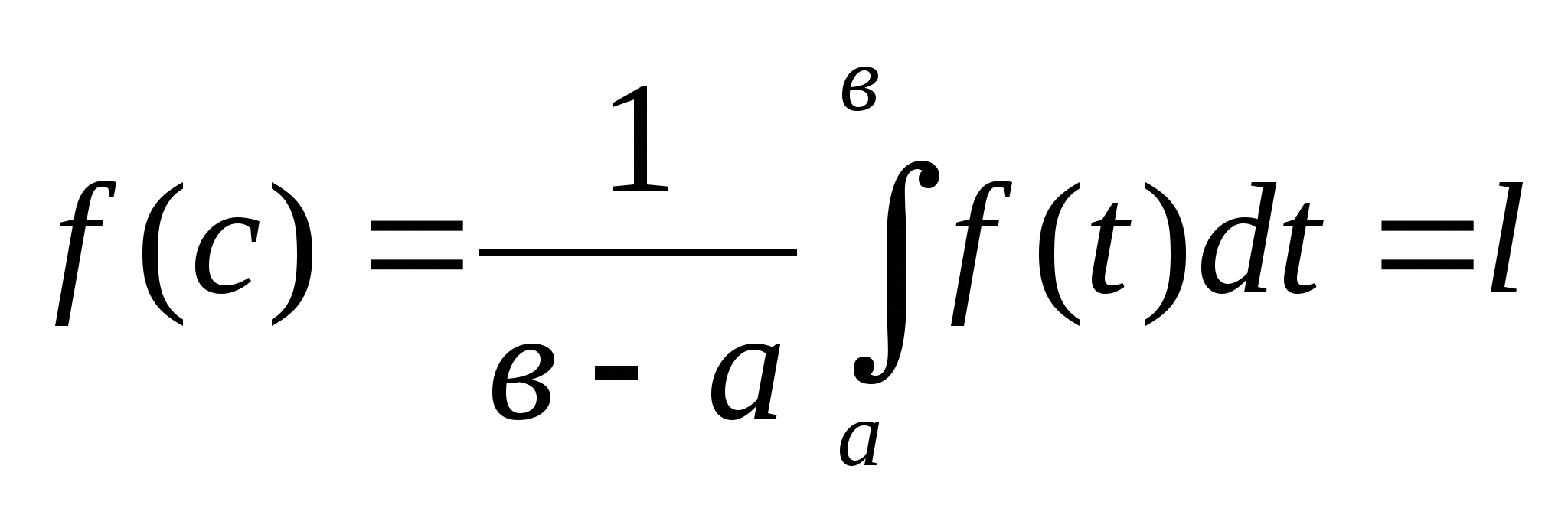 ,
,
l - среднее значение функции f(t) на интервале (а;в).
Среднее время ![]() , затраченное на изготовление одного изделия в период изготовления
от а до b изделий, вычисляется по формуле:.
, затраченное на изготовление одного изделия в период изготовления
от а до b изделий, вычисляется по формуле:. 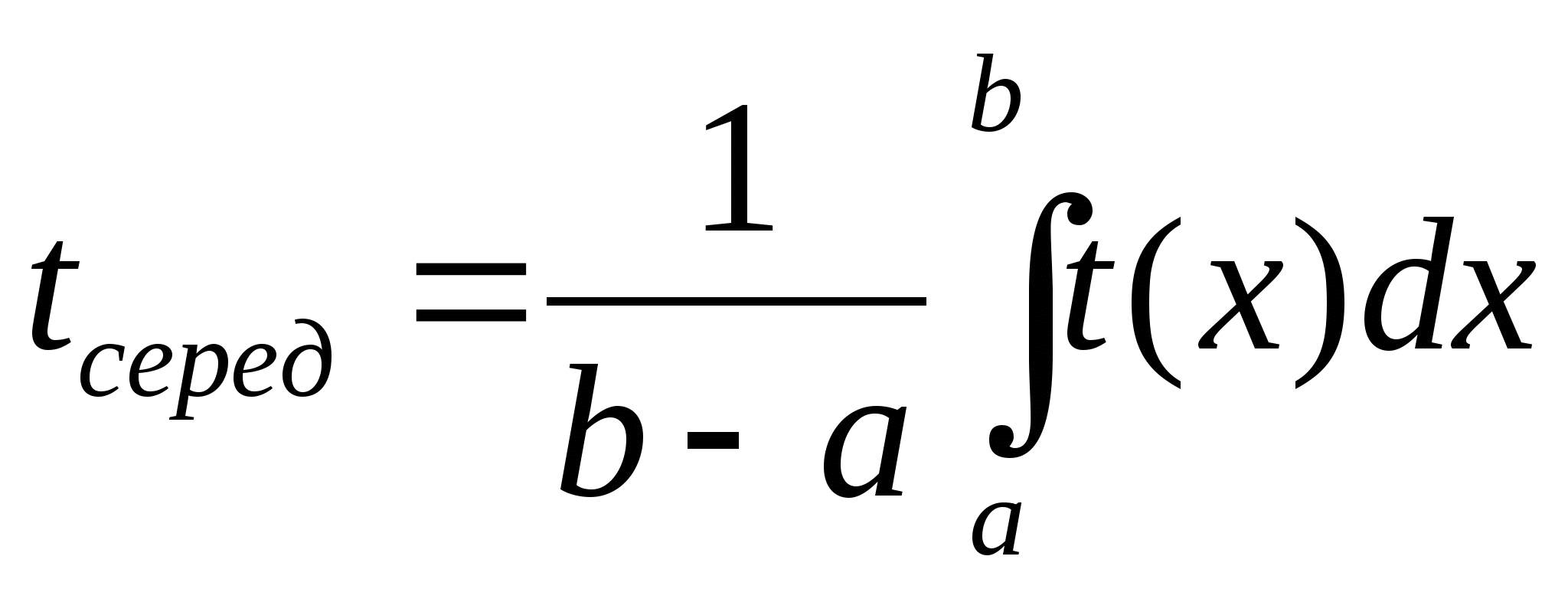
![]() ,
где α - затрата времени на одно изготовление, β - показатель
изготовительного процесса.
,
где α - затрата времени на одно изготовление, β - показатель
изготовительного процесса.
Формирование необходимых знаний и умений
Коллективное решение и обсуждение предложенных задач
Пример 1
Дневное изменение продуктивности труда характеризуется функцией f(t)=2t 2+23t+29.
Найти объем изготовленной продукции за 8 часов, среднее значение продуктивности труда за это время и момент времени, за которое это значение было достигнуто.
Решение:
Объем изготовленной продукции находится по формуле:
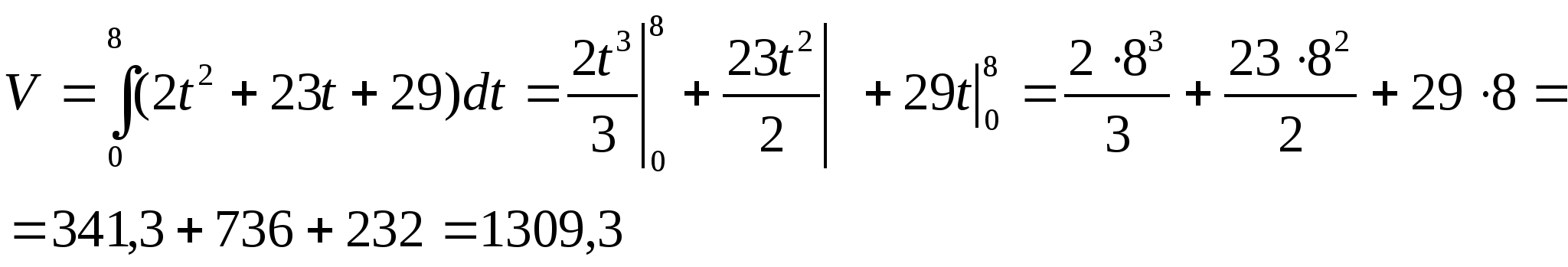
V=1309,3 усл.ед.
Найдем среднее значение продуктивности труда по формуле:
![]() (усл.ед.∕час)
(усл.ед.∕час)
Найдем момент времени, в которое было достигнуто среднее значение продуктивности труда:
2t 2+23t+29=164
2t2+23t+29-164=0
2t2+23t-135=0
D=b2-4ac=232-4∙2∙(-135)=529+1080=1609
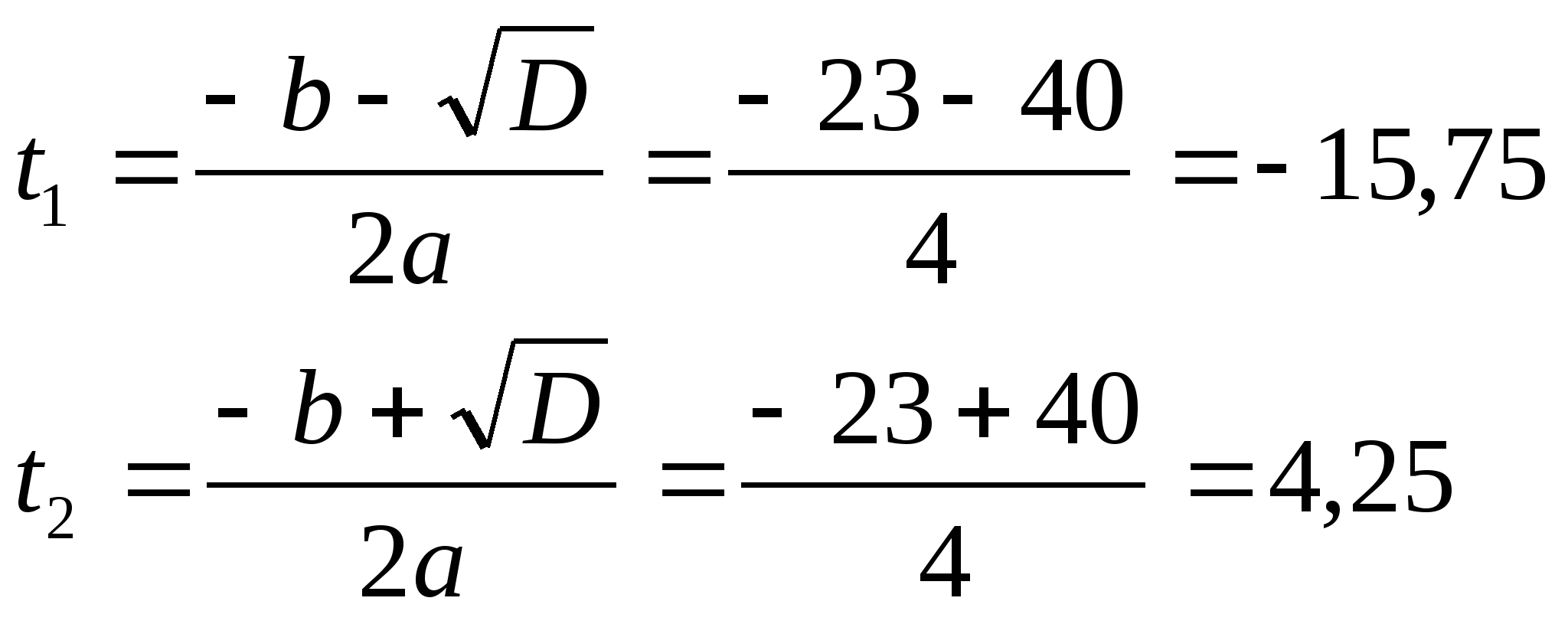
Первое значение не подходит, так как время не может быть отрицательным.
Таким образом, среднее значение продуктивности труда будет достигнуто через 4,25 часа, примерно в середине рабочего дня.
Ответ: 1309,3 усл.ед, 164 усл.ед.∕час, 4,24 ч
Пример 2
Найти среднее время, которое затрачено на изготовление выпуска одного изделия в период выпуска от 10 до20 изделий, если затраты времени на одно изготовление (по технологии) 200 мин, а показатель изготовительного процесса 0,7.
Решение:
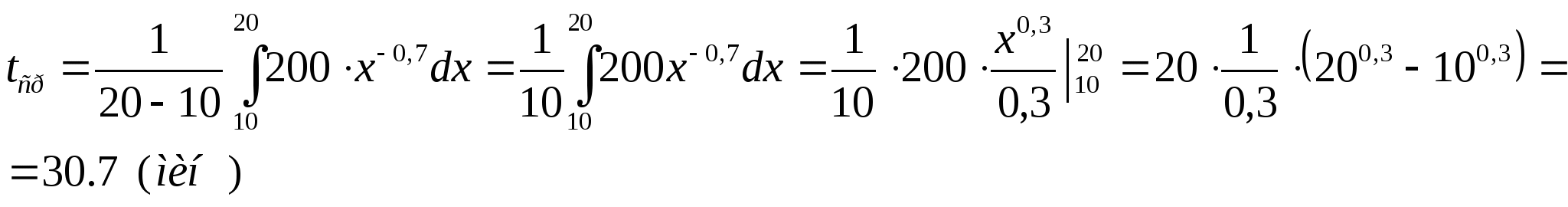
Примеры:
1. Дневное изменение продуктивности труда характеризуется функцией f(t)=at 2+bt+c.
Найти объем изготовленной продукции за m часов, среднее значение продуктивности труда за это время и момент времени, за которое это значение было достигнуто.
2. Найти среднее время, которое затрачено на изготовление выпуска одного изделия в период выпуска от m до n изделий, если затраты времени на одно изготовление (по технологии) α мин, а показатель изготовительного процесса β.
Закрепление сформированных знаний и умений
Закрепление полученных знаний по данной теме проводится во время самостоятельного решения заданий.
Самостоятельная работа
1. Дневное изменение продуктивности труда характеризуется функцией f(t)=at 2+bt+c.
Найти объем изготовленной продукции за m часов, среднее значение продуктивности труда за это время и момент времени, за которое это значение было достигнуто.
2. Найти среднее время, которое затрачено на изготовление выпуска одного изделия в период выпуска от m до n изделий, если затраты времени на одно изготовление (по технологии) α мин, а показатель изготовительного процесса β.
m
n
α
β
1
50
100
80
0,5
2
70
170
100
1/3
3
50
150
60
0,5
4
10
40
30
0,5
5
10
40
40
0,5
6
150
200
100
0,5
7
150
200
60
0,25
8
70
100
80
0,25
9
70
100
80
0,5
10
50
300
100
0,5
11
100
300
200
0,5
12
70
80
20
0,5
13
100
400
200
0,25
14
100
300
100
1/3
15
10
100
60
0,25
Задачи для домашнего решения:
Найти среднее время, которое затрачено на изготовление выпуска одного изделия в период выпуска от m до n изделий, если затраты времени на одно изготовление (по технологии) α мин, а показатель изготовительного процесса β.
m
n
α
β
1
100
200
60
0,5
2
100
150
100
0,5
3
100
200
60
0,25
4
100
150
100
0,25
5
100
150
60
0,25
Практическое занятие 13
Практическая работа 11
по теме «Действия над комплексными числами»
Цель работы: сформировать необходимые умения и навыки по выполнению основных действий на множестве комплексных чисел.
Актуализация знаний
- Фронтальный опрос
1. Формы задания комплексных чисел.
2. Геометрическая интерпретация комплексного числа.
3. Действия над комплексными числами во всех формах задания.
- тестирование на компьютере
Краткие теоретические и учебно-методические материалы по теме практической работы
Алгебраическая форма комплексного числа:
і2 = -1 і = 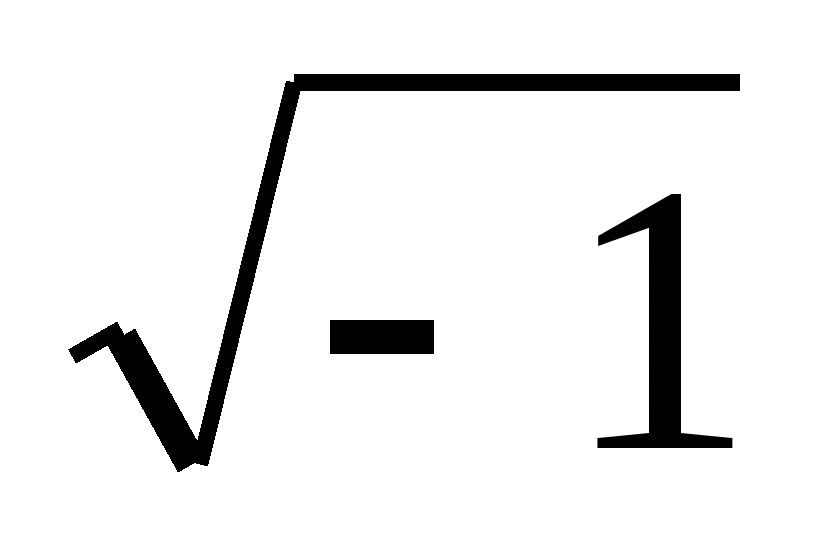
Действия над комплексными числами а алгебраической форме:
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами.
Можно использовать формулы сокращенного умножения.
Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью.
При делении надо умножить делимое и делитель на комплексное число, сопряженное делителю.
Модулем комплексного числа Z = а +
bііназывается длина вектора ![]() , которую можно найти по формуле:
, которую можно найти по формуле:
![]()
Аргументом комплексного числа называется угол
![]() , который образует вектор
, который образует вектор ![]() с положительным направлением оси абсцисс.
с положительным направлением оси абсцисс.
Величину угла можно найти с помощью формул:
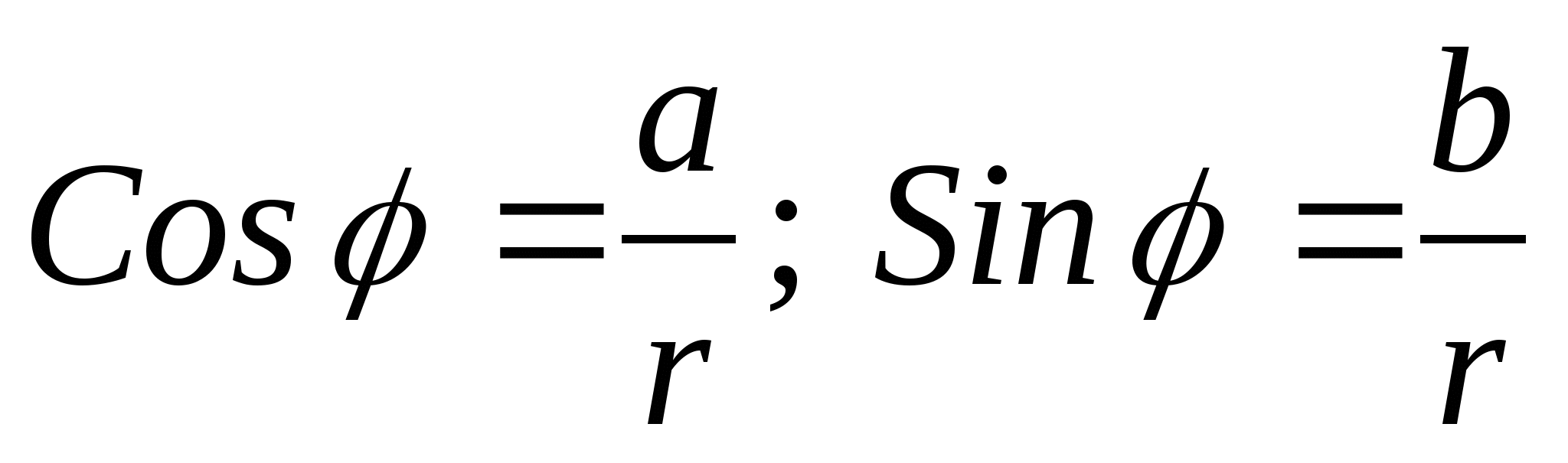 .
.
![]() -
тригонометрическая форма комплексного числа
-
тригонометрическая форма комплексного числа
Действия над комплексными числами в тригонометрической форме
1. Произведение:
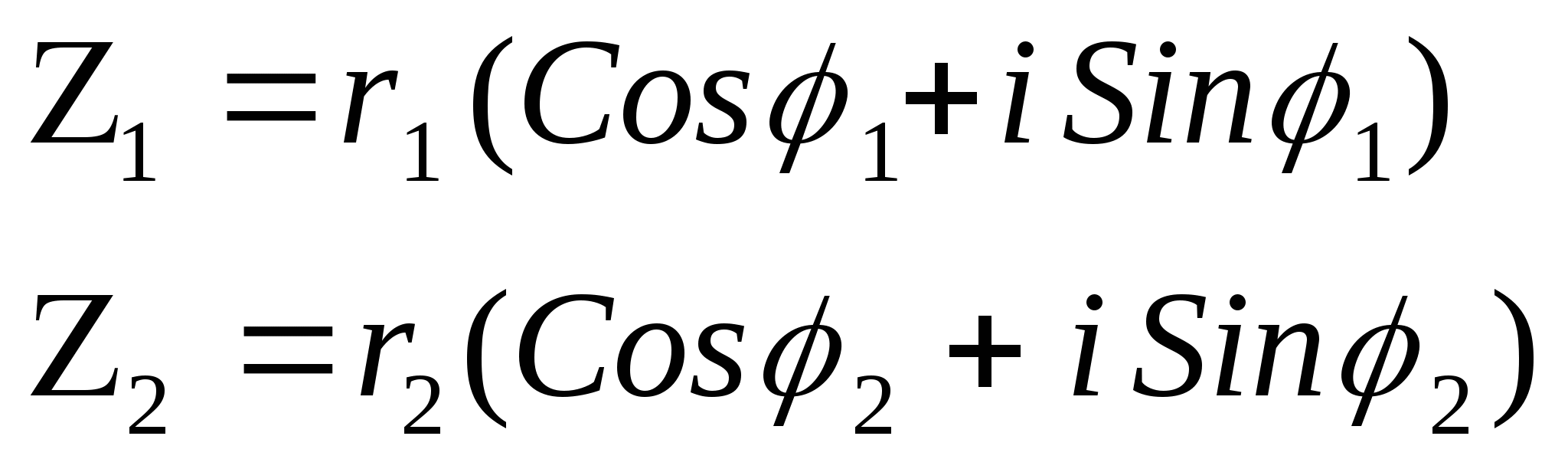
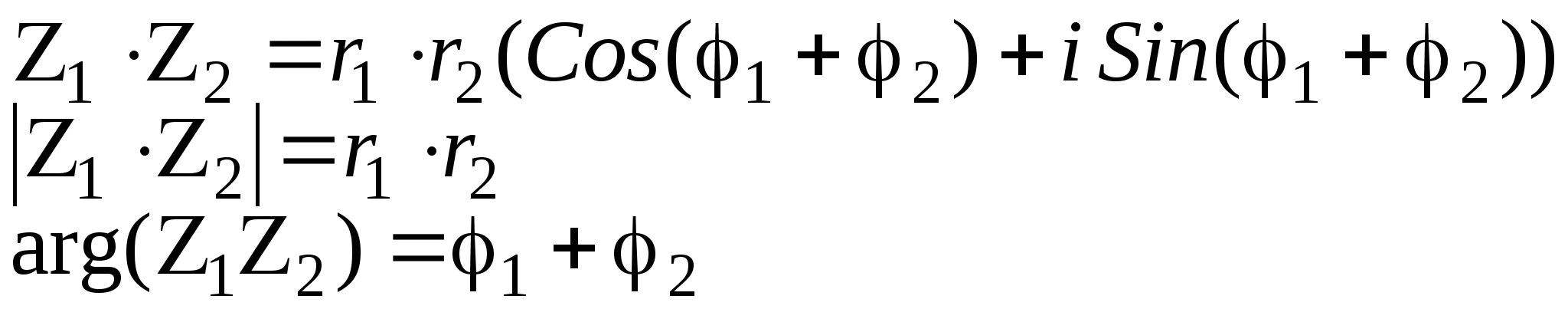
2 Частное:
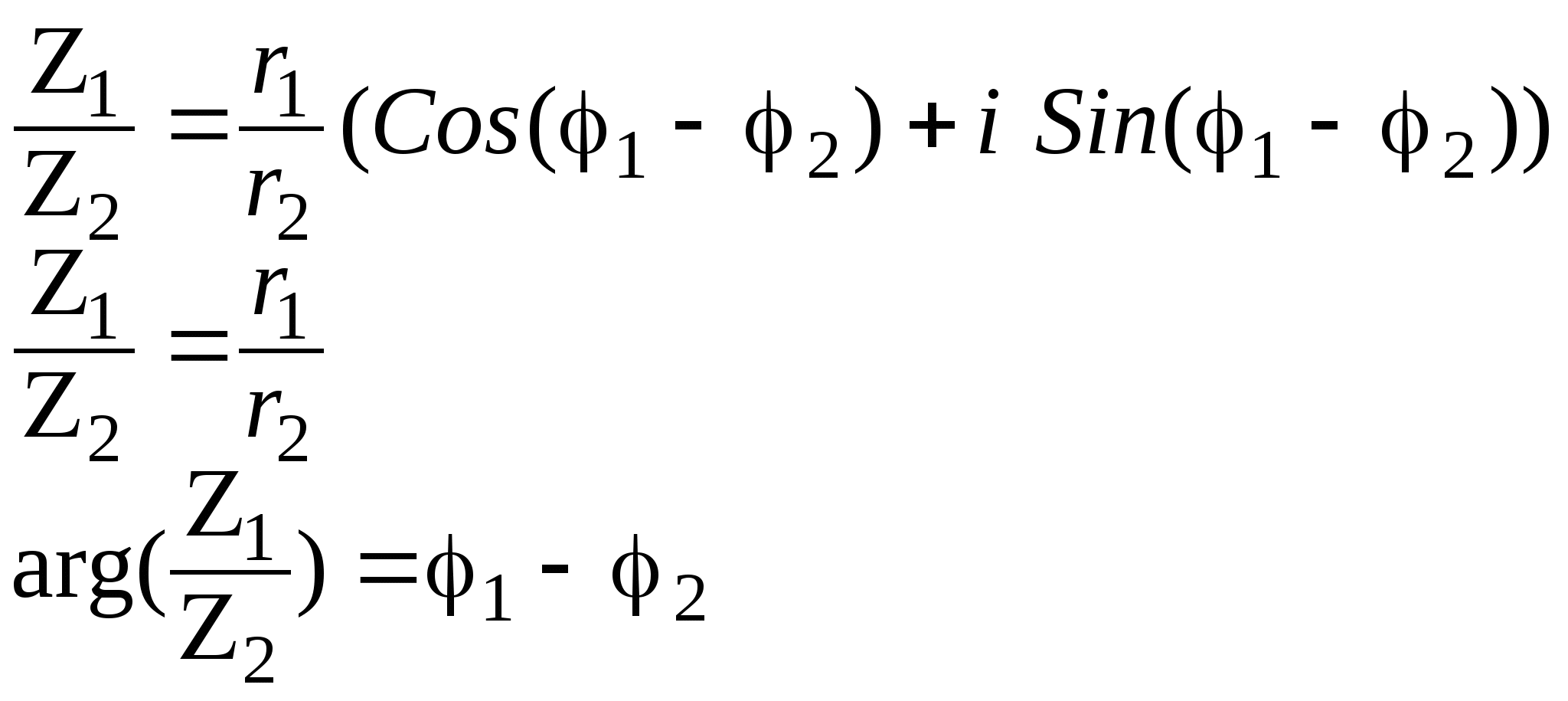
3. Возведение в степень:
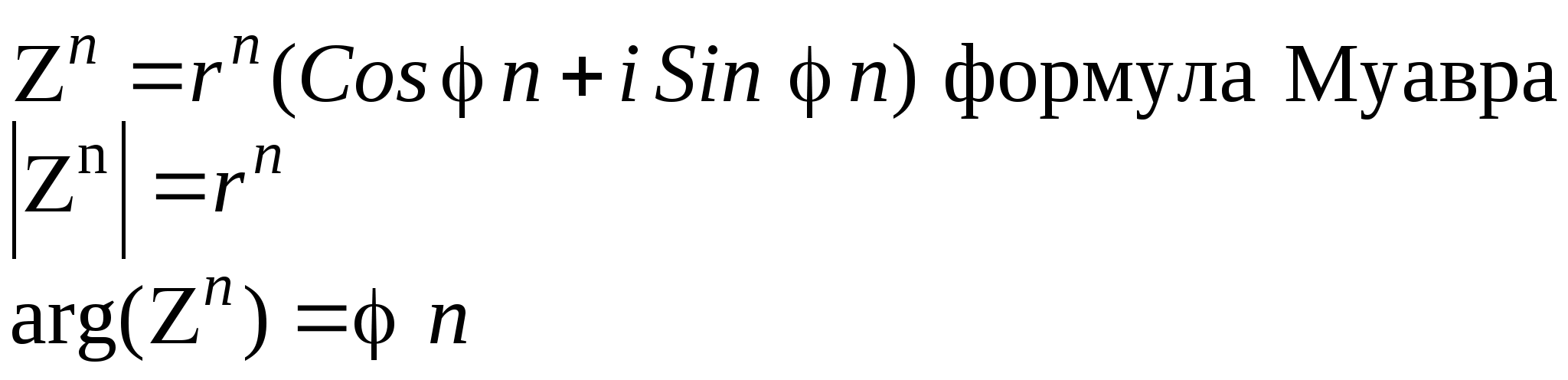
4. Корень n-й степени (n≥2)
![]()
![]()
![]()
R = 0, 1, ..., n - 1
![]() показательная
форма комплексного числа
показательная
форма комплексного числа
Формирование необходимых знаний и умений
Коллективное решение и обсуждение предложенных задач
Пример 1
Найти х и у из равенства:
(2х + 3у) + (х - у) і = 7 + 6і
Решение:
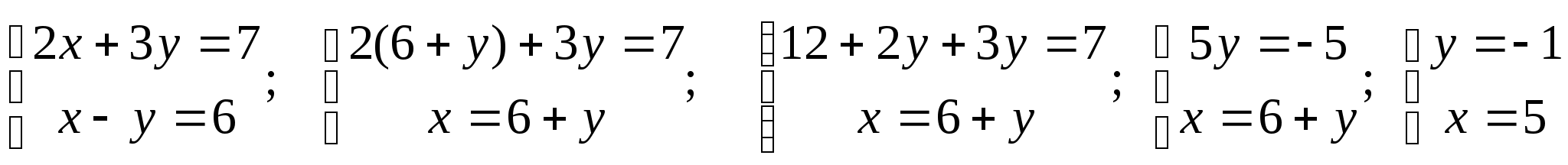
Ответ:: х = 5, у = -1.
Пример 2
![]()
Найти:
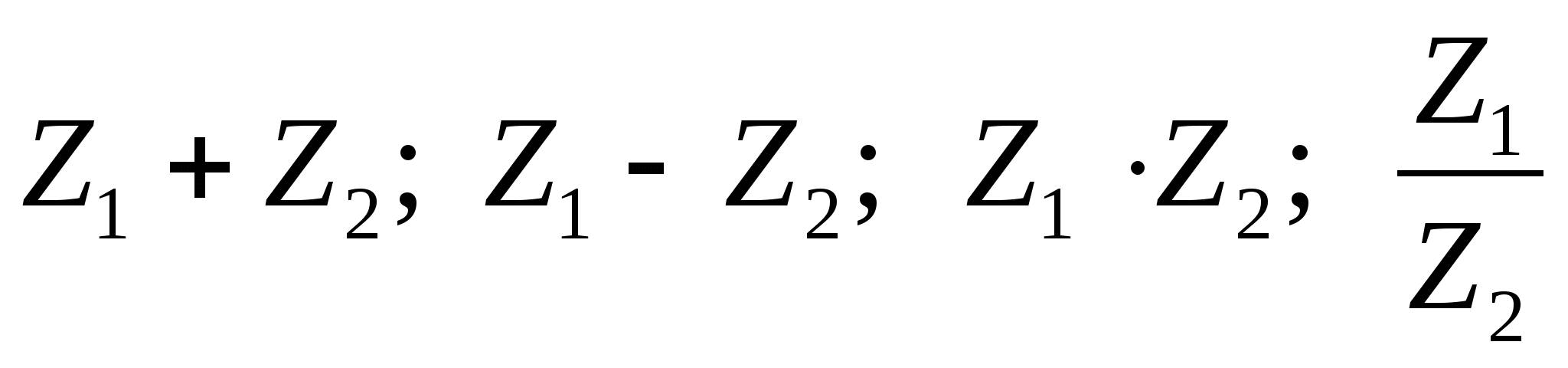
Решение:
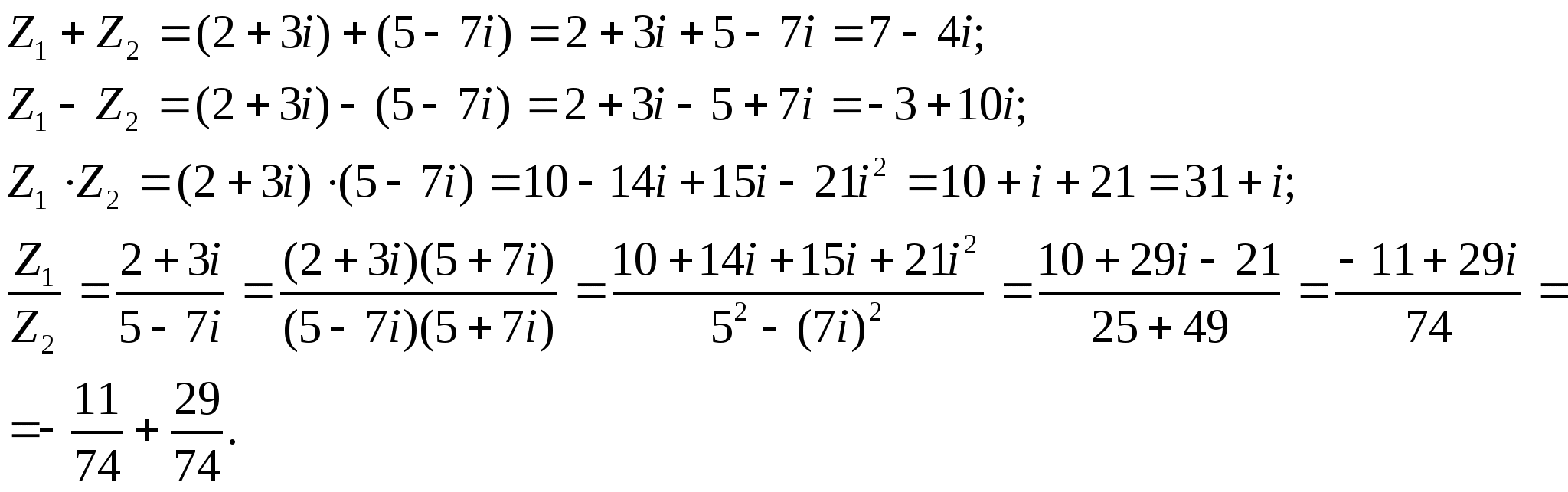
Пример 3
Решить уравнение:
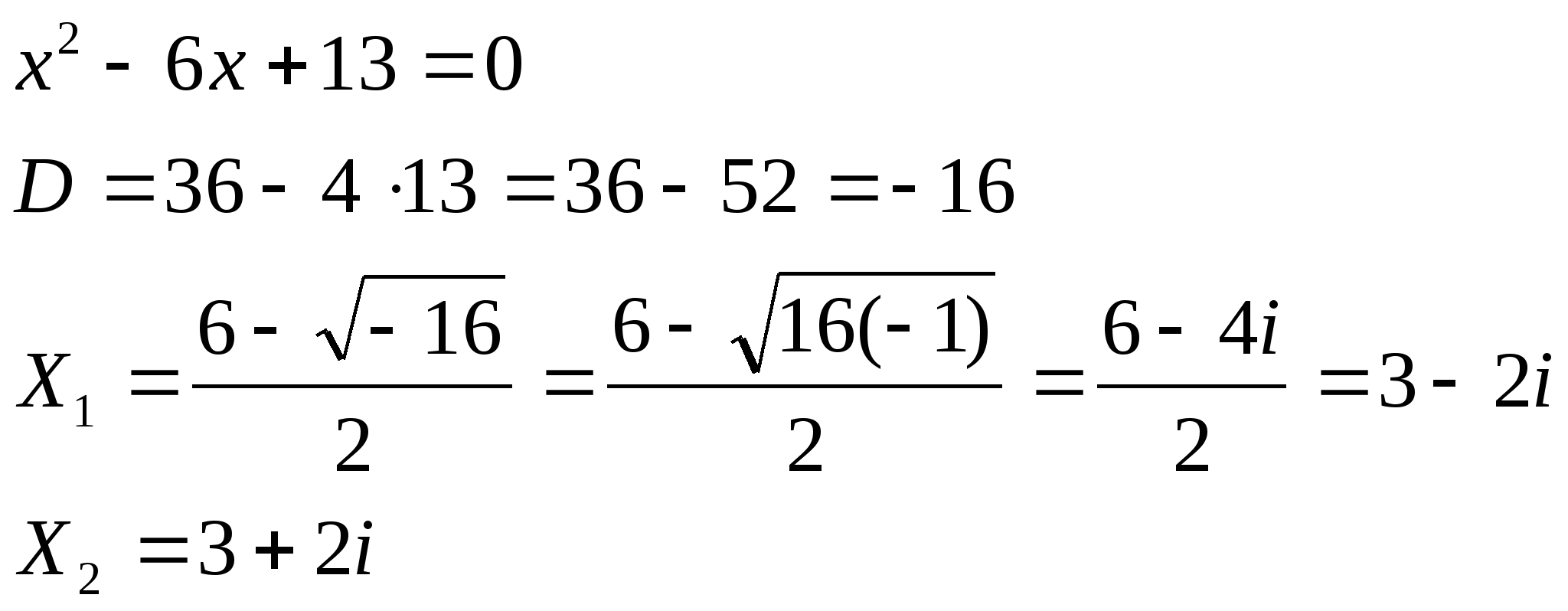
Ответ:: х1 = 3 - 2і, х2 = 3 + 2і.
Пример 4
Изобразить на плоскости:
![]()
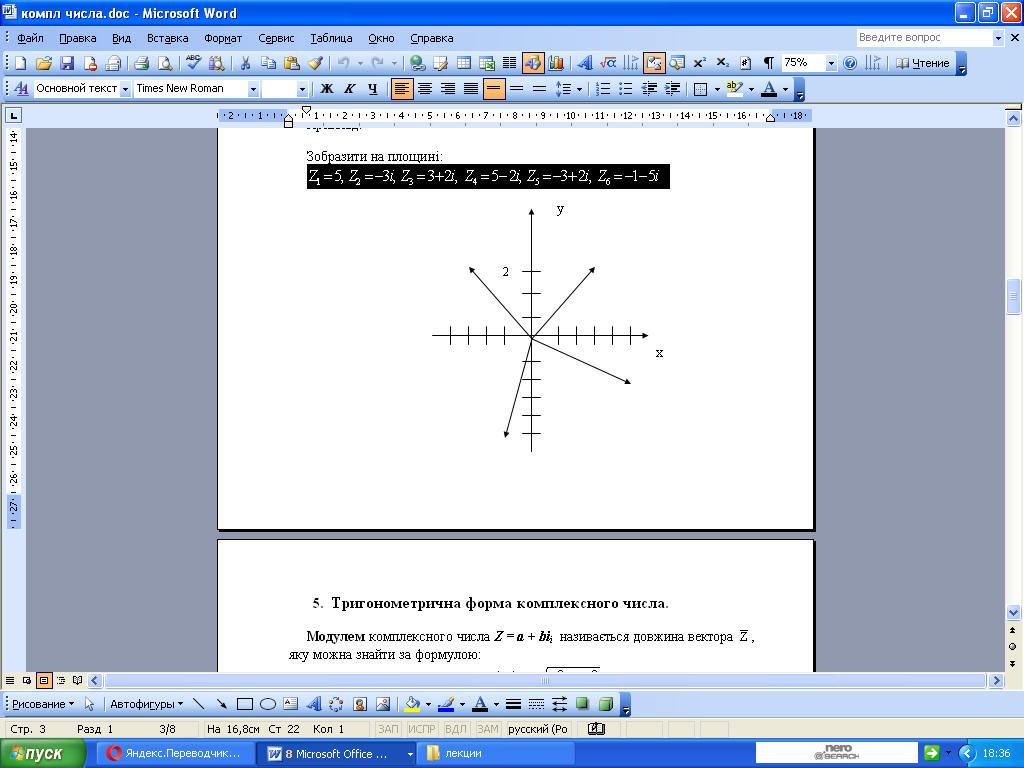
Пример 5
Записать в тригонометрической форме комплексное число::
а) Z =-1+і
Решение:
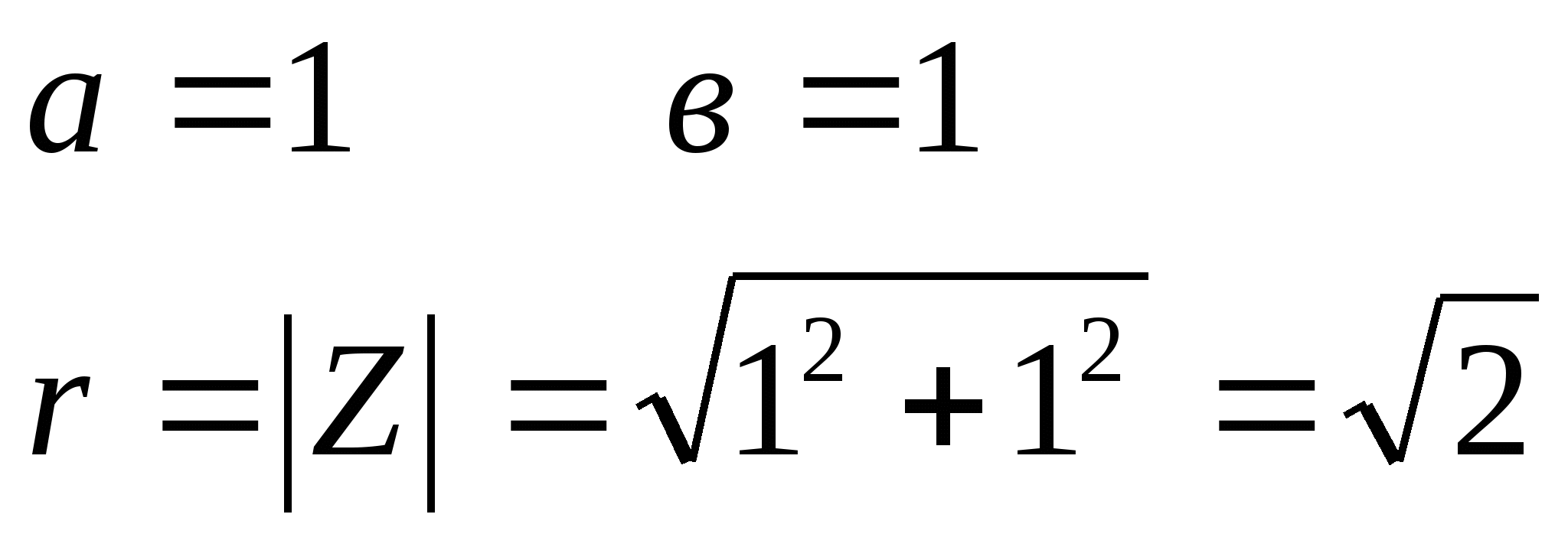
Числу Z соответствует точка Z (1;1), которая лежит в 1 четверти
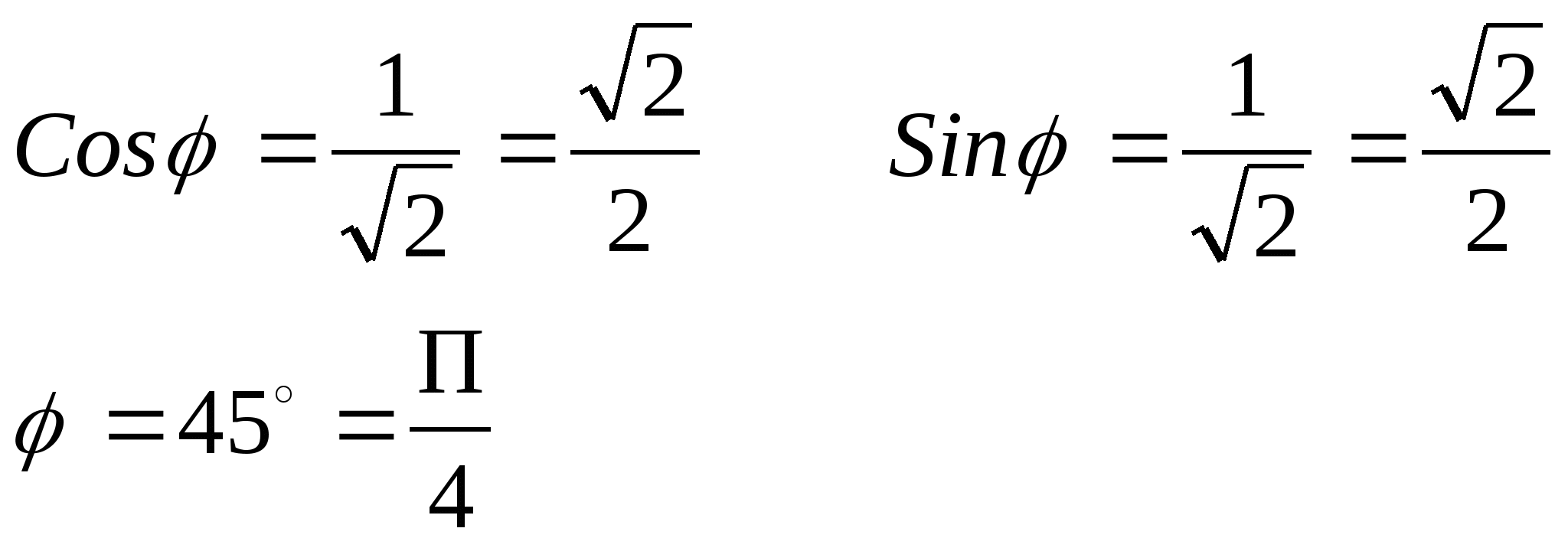
Z = 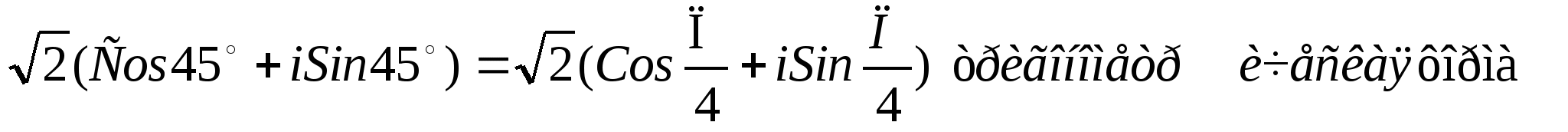
б) Z = ![]()
Решение:
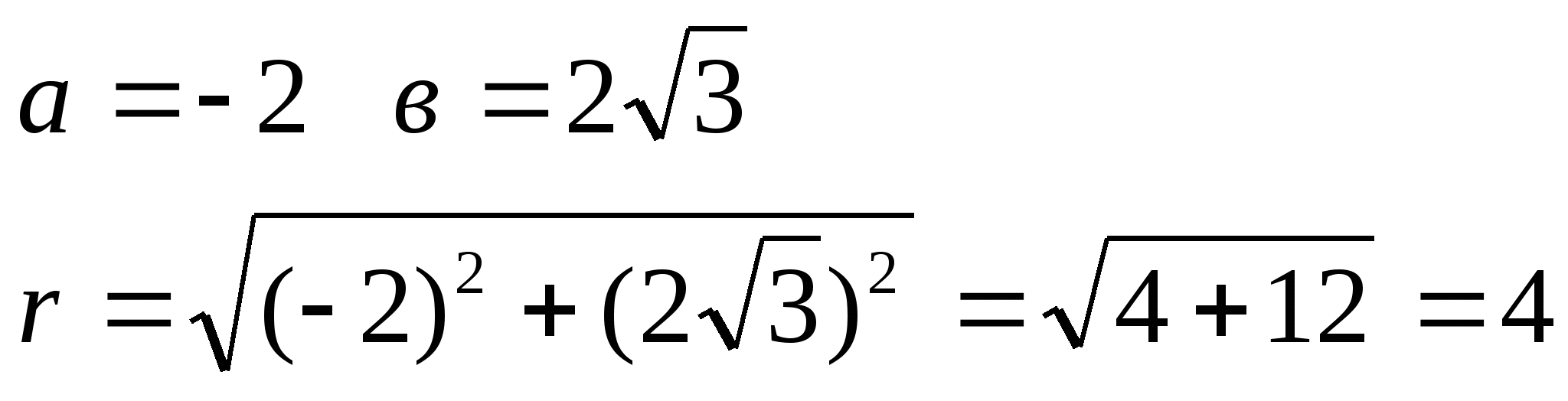
Числу Z соответствует точка Z (-2;2![]() ),
которая лежит во 2 четверти.
),
которая лежит во 2 четверти.
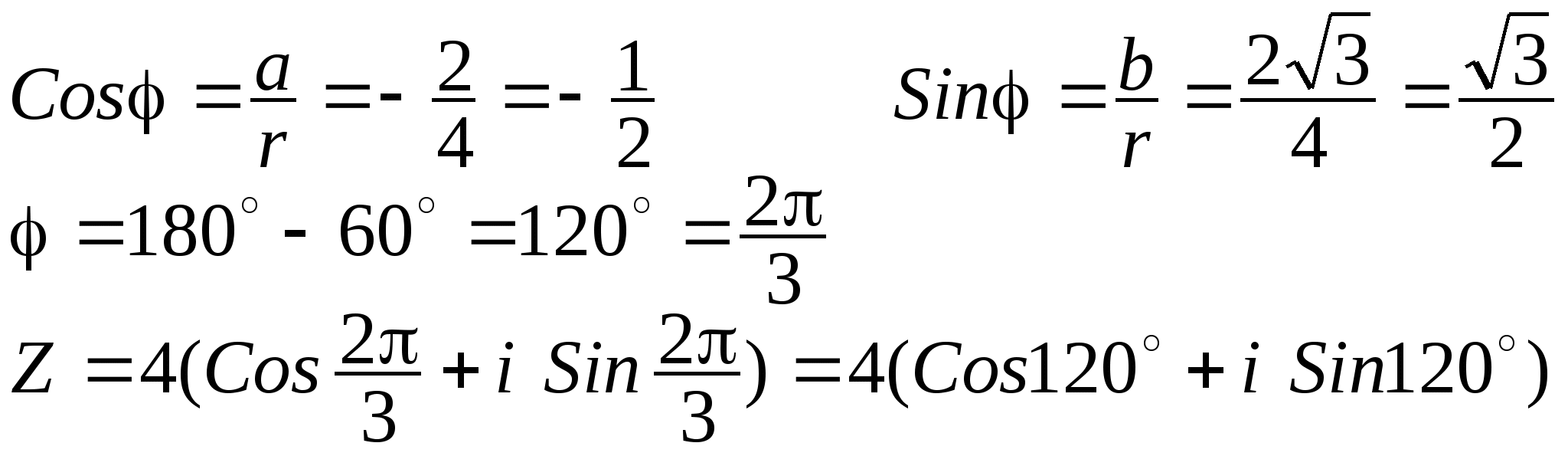
Пример 6
Записать число в показательной форме: ![]()
Решение:
Сначала запишем Z = -5i в тригонометрической форме:.
а = 0 b = -5
![]()
Аргумент находится на мнимой оси:
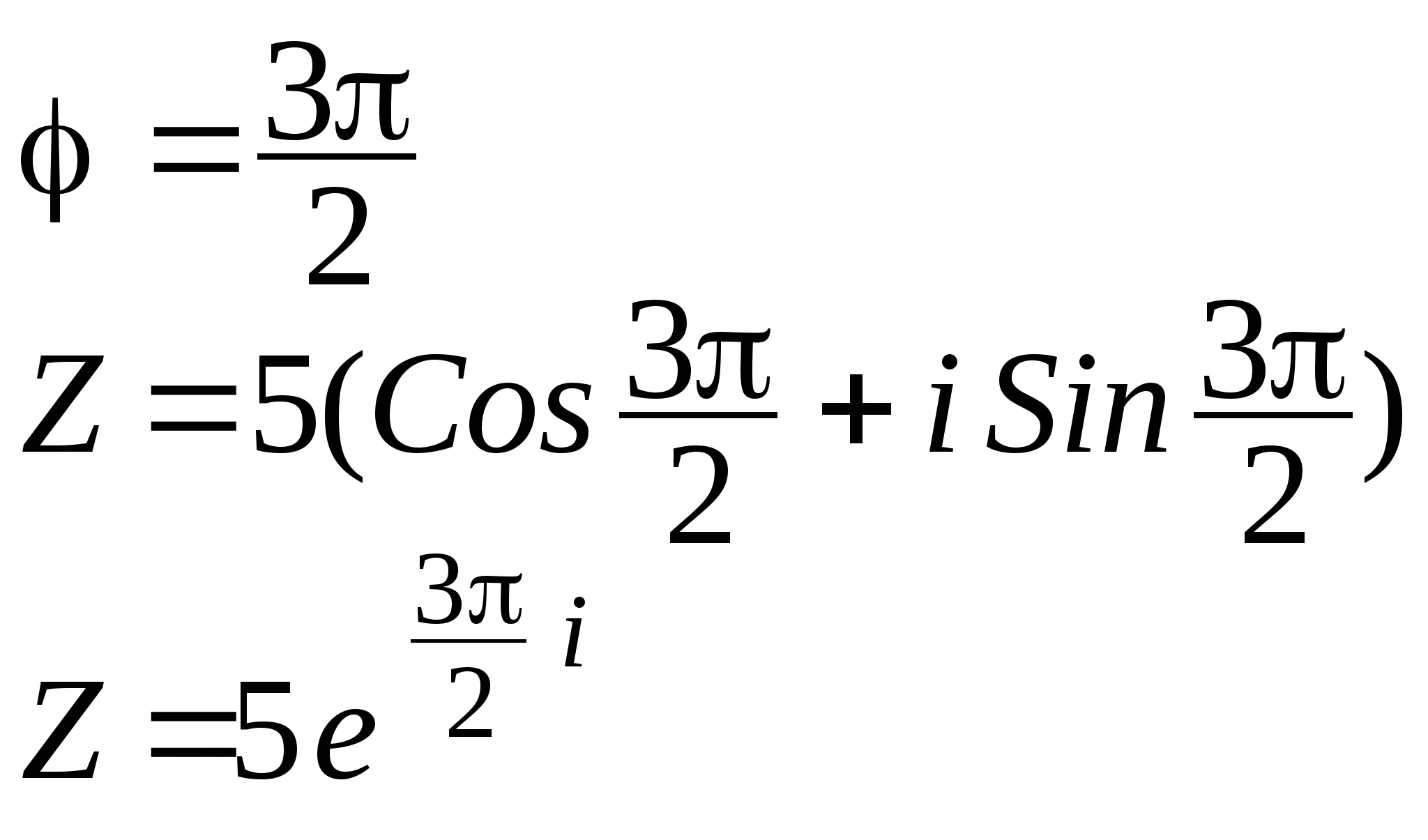
Ответ: ![]()
Пример 6
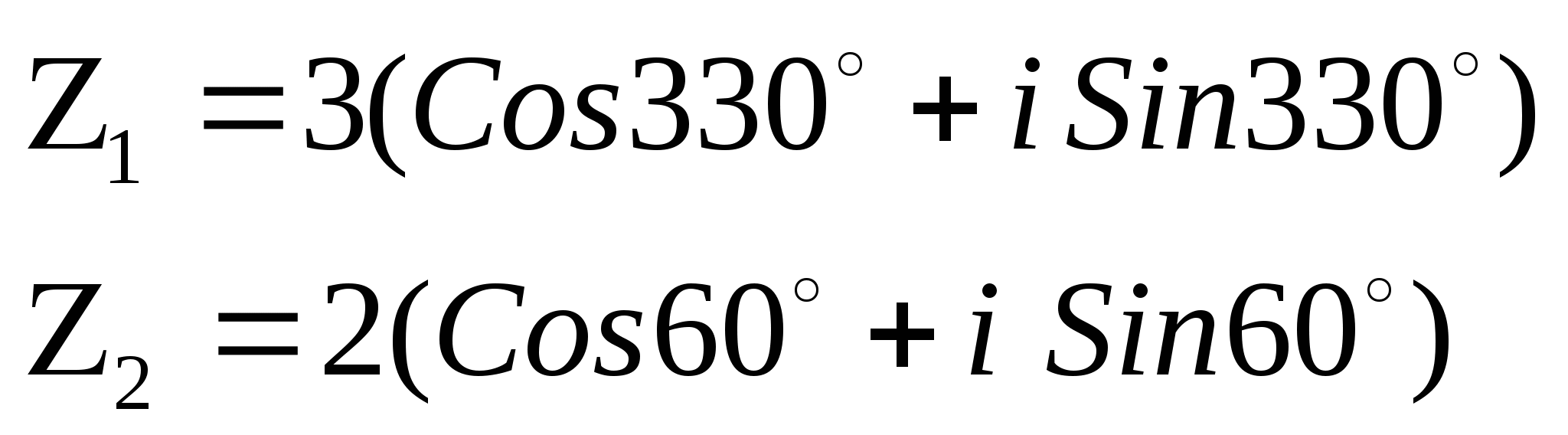
Найти:
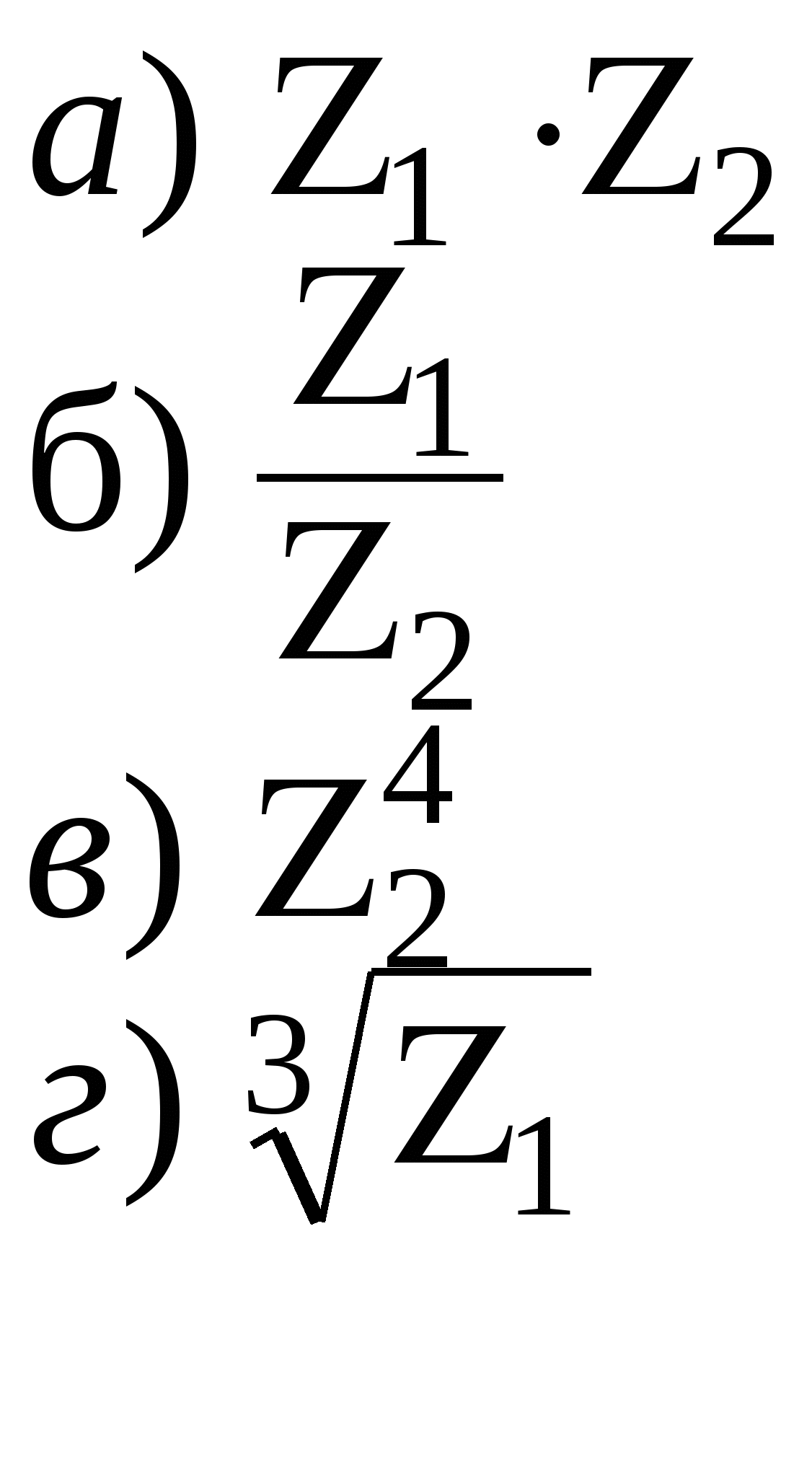
Решение:
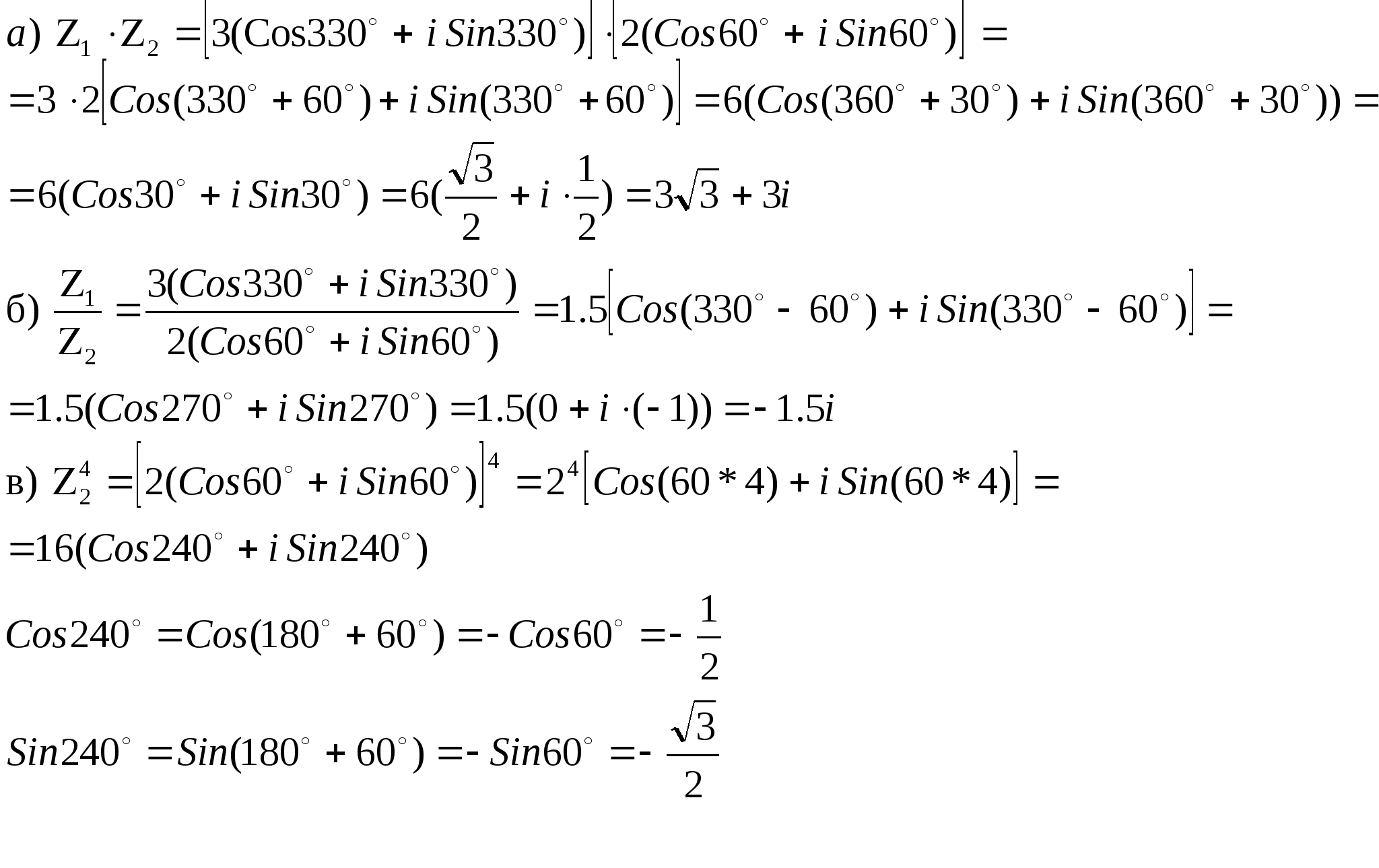
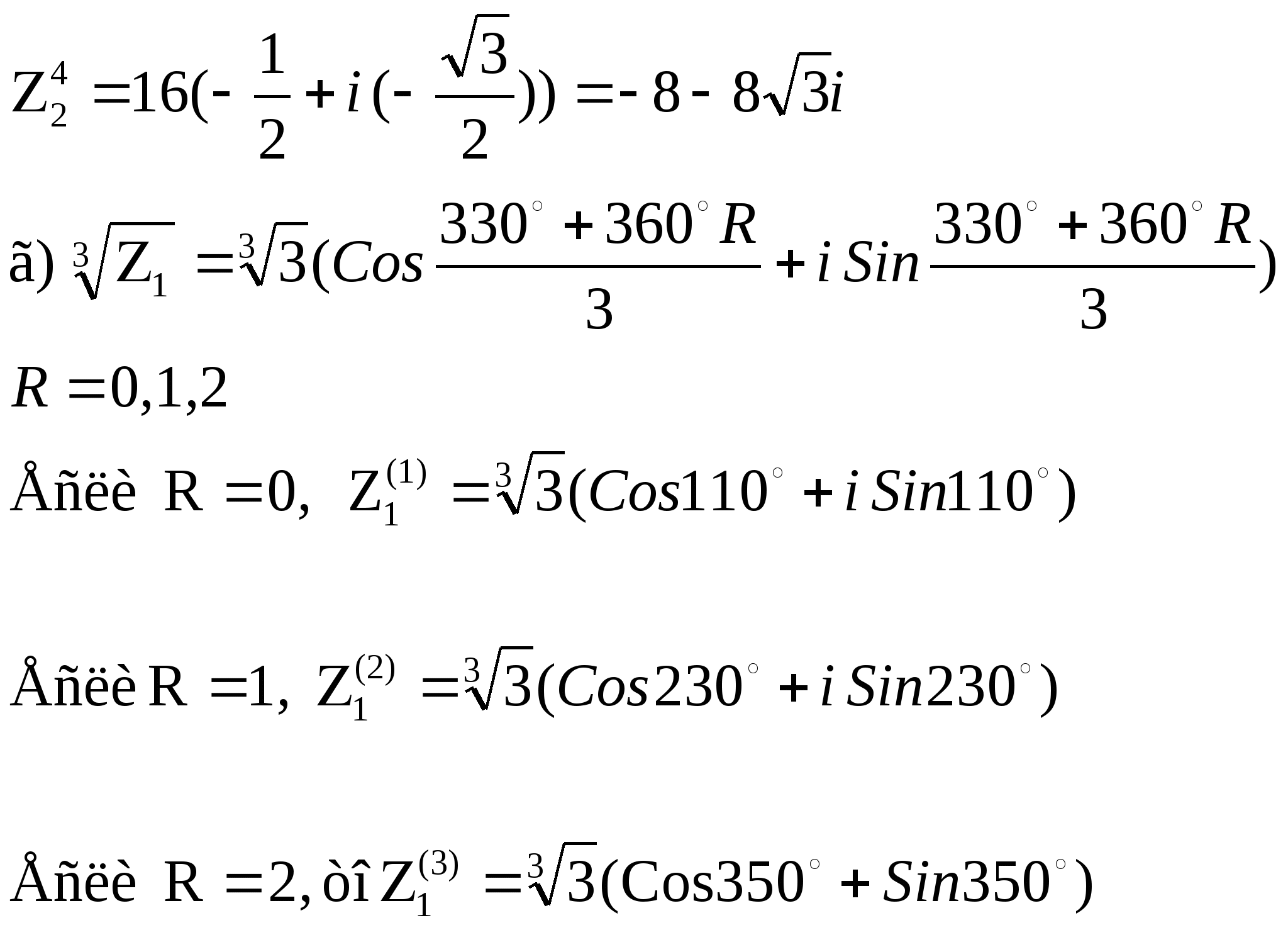
Примеры
Изобразить заданные комплексные числа Z1=х1+іу1 и Z2=х2+іу2 геометрически и выполнить следующие действия над ними в удобной форме задания:
-
аZ1+вZ2
-
сZ1• Z2
-
Z1n
-
Z2 ⁄ Z1
Закрепление сформированных знаний и учений:
Закрепление полученных знаний по данной теме проводится во время самостоятельного решения заданий
Самостоятельная работа:
Изобразить заданные комплексные числа Z1=х1+іу1 и Z2=х2+іу2 геометрически и выполнить следующие действия над ними в удобной форме задания:
-
аZ1+вZ2
-
сZ1• Z2
-
Z1n
-
Z2 ⁄ Z1
Задачи для домашнего решения
Изобразить заданные комплексные числа Z1=х1+іу1 и Z2=х2+іу2 геометрически и выполнить следующие действия над ними в удобной форме задания:
-
аZ1+вZ2
-
сZ1• Z2
-
Z1n
-
Z2 ⁄ Z1
Практическое занятие 15
Практическая работа 12
по теме «Выполнение операций над множествами»
Цель работы: сформировать навыки выполнения операций над множествами.
Актуализация знаний
Фронтальный опрос
1. Дать понятие множества, пустого множества.
2. Операции над множествами
Краткие теоретические и учебно-методические материалы по теме практической работы
Операции над множествами
-
Объединением множеств А и В называется множество С, которое состоит из всех элементов, которые принадлежат хотя бы одной из двух данных множеств.
Обозначается: "![]() ".
Читается "или".
".
Читается "или".
Г рафически
изображается:
рафически
изображается:
Например : А=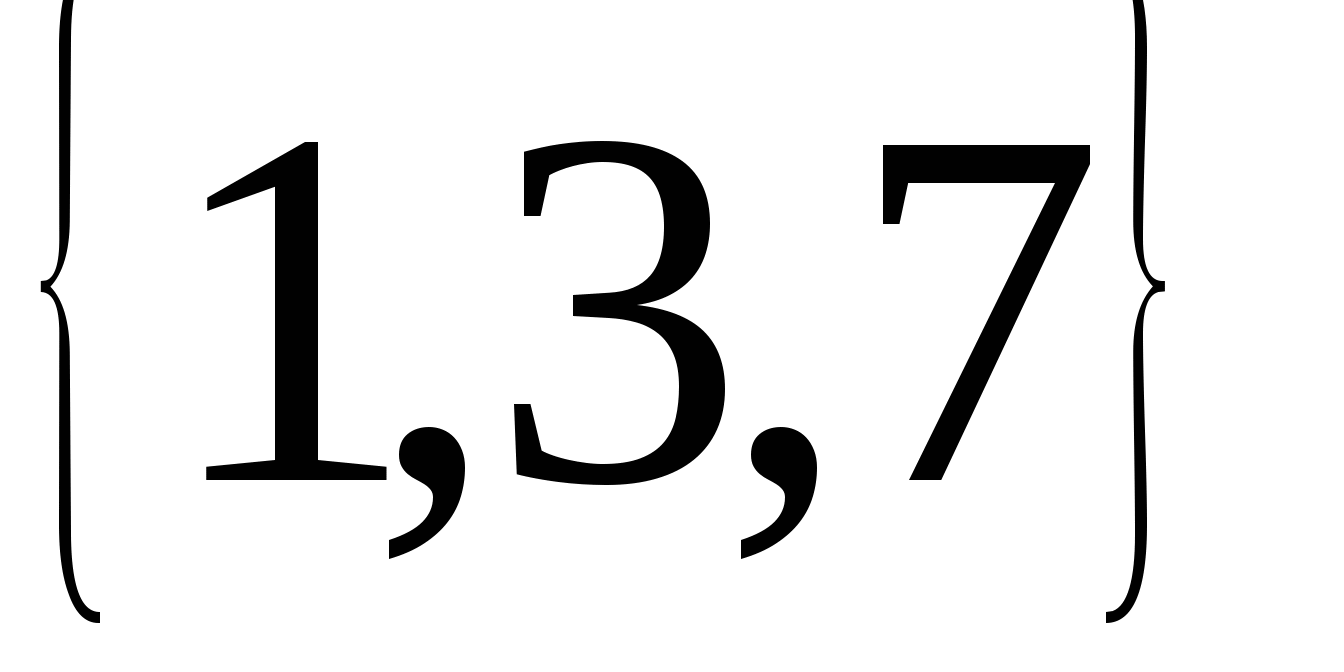 ,
В=
,
В=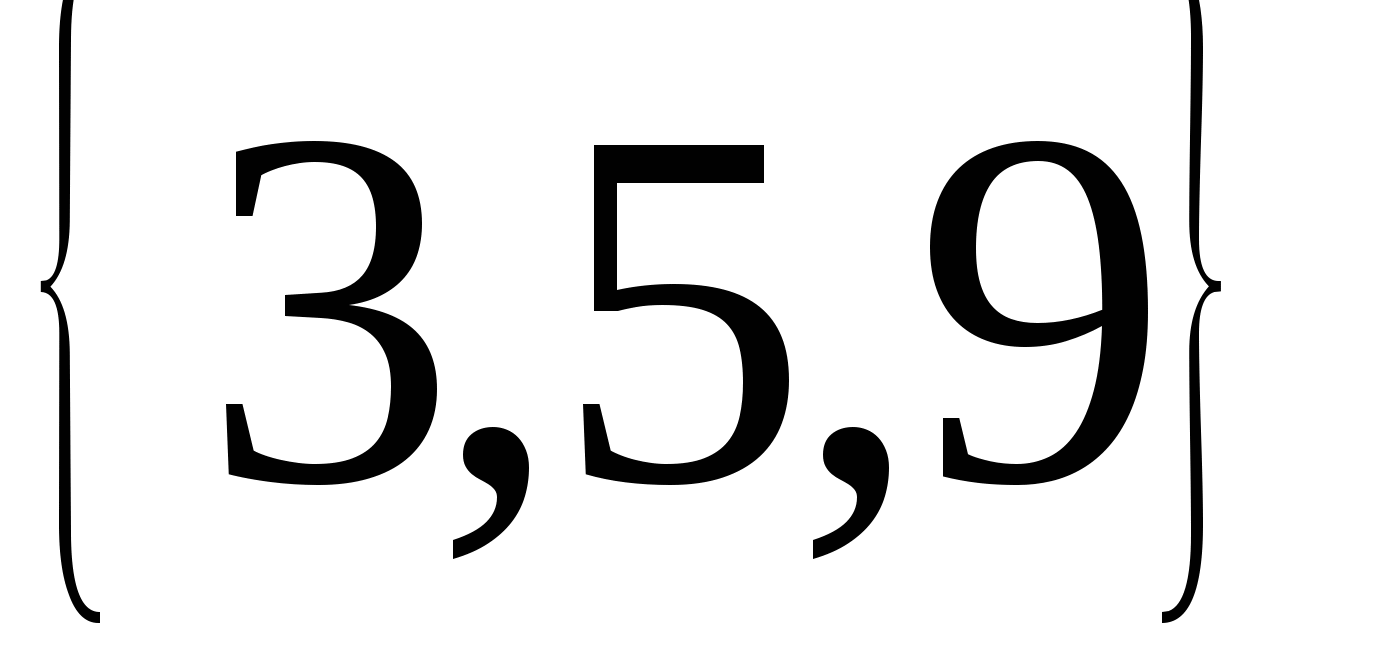
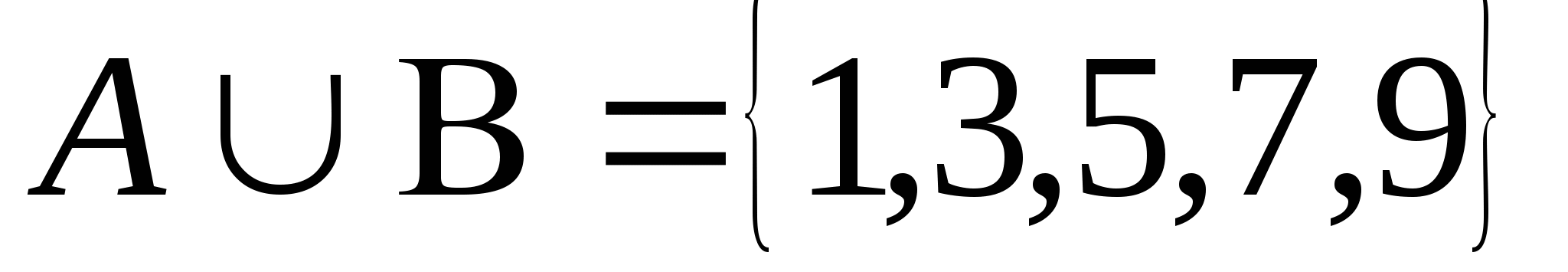
-
Пересечением множеств А и В называется множество, которое состоит из тех элементов, которые принадлежат и множеству А, и множеству В.
Обозначается: "![]() ".
Читается "и".
".
Читается "и".
Графически изображается:

-
п
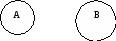 ересечение
ересечение
 (пустое множество)
(пустое множество)
Например:
![]()
![]()
![]()
3. Разностью множеств А и В называется множество, которое состоит из тех элементов множеств А, которые не принадлежат множеству В.
Обозначается: А\В
Г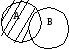 рафически:
рафически:
Например: ![]()
![]()
![]() \
\![]()
-
Симметрическая разность множеств А и В - это объединение их разностей.
Обозначается: ![]() \
\![]() \
\![]()
Г





А
Арафически:





В
Формирование необходимых знаний и умений
Коллективное решение и обсуждение предложенных задач
Пример1: ![]()
![]()
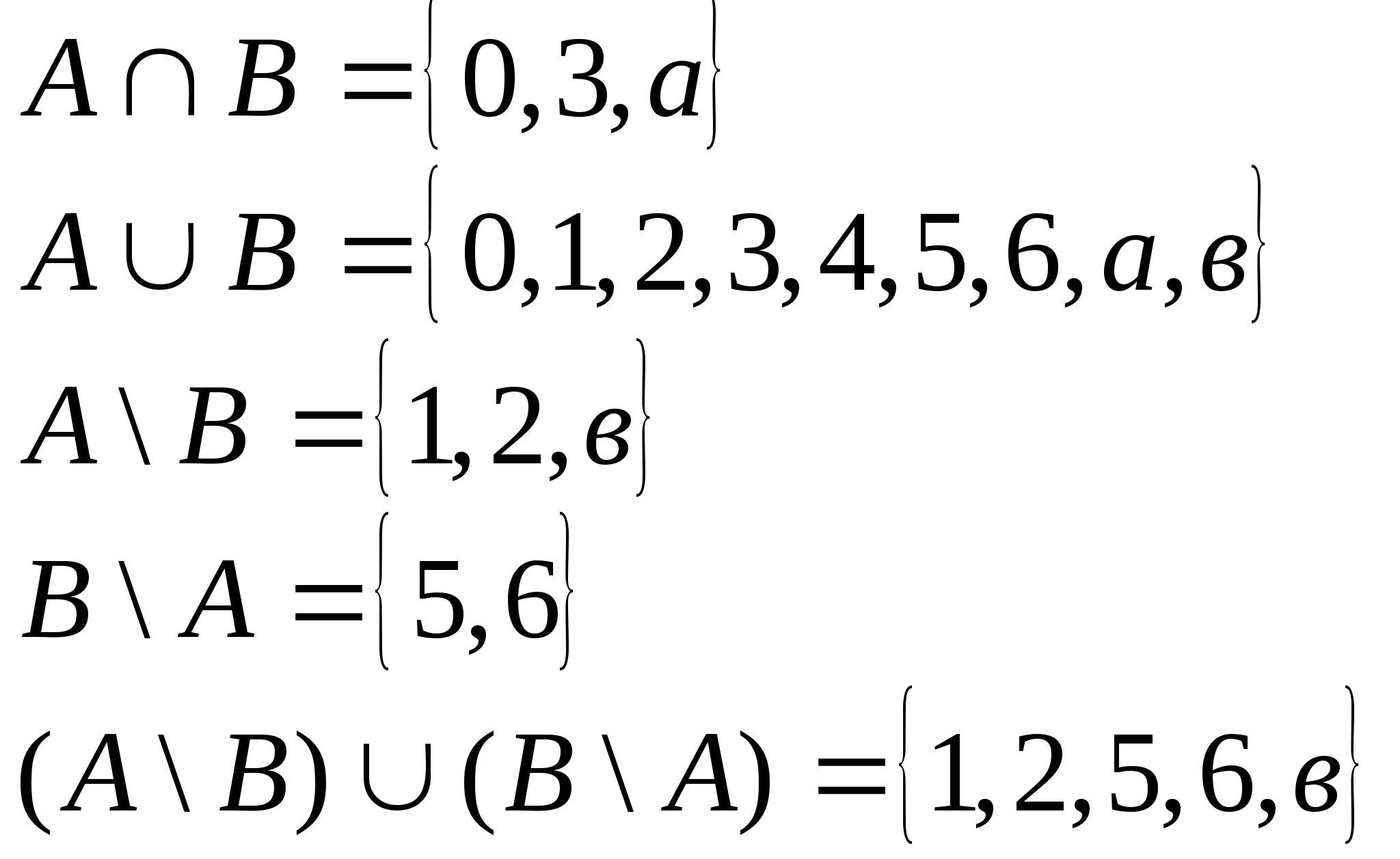
Пример 2
Среди перечисленных ниже множеств укажите конечные и бесконечные множества:
а) множество чисел, кратных 13;
б) множество делителей числа 15;
в) множество деревьев в лесу;
г) множество натуральных чисел;
д) множество рек Ростовской области;
е) множество корней уравнения х + 3 = 11;
ж) множество решений неравенства х + 1 < 3.
Пример 3
Задайте множество цифр, с помощью которых записывается число:
а) 3254; б) 8797; в) 11000; г) 555555.
Пример 4
Охарактеризуйте множество А:
а) А = {1, 3, 5, 7, 9};
б) А = {- 2, - 1, 0, 1, 2};
в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99};
Пример 5
Даны множества:
М = {5, 4, 6},
Р = {4, 5, 6},
Т = {5, 6, 7},
S = {4, 6}.
Какое из утверждений неверно?
а) М = Р б) Р ≠ S в) М ≠ Т г) Р = Т
Пример 6
Даны множества:
А = {2; 3; 8},
В = {2; 3; 8; 11},
С = {5; 11}.
Найдите: 1) АUВ; 2) АUС; 3) СUВ.
Пример 7
Даны множества:
А = {a, b, c, d},
B = {c, d, e, f},
C = {c, e, g, k}.
Найдите: (АUВ)UС.
Закрепление сформированных знаний и учений:
Закрепление полученных знаний по данной теме проводится во время самостоятельного решения заданий
Примеры
1) Перечислите элементы множества планет солнечной системы. (Ответ: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун).
2) Как называется множество цветов, стоящих в вазе? (Ответ: букет).
3) Приведите примеры множеств, элементами которого являются геометрические фигуры.
4) Задайте множество А описанием:
а) А = {1, 3, 5, 7, 9}; б) А = {- 2, - 1, 0, 1, 2}; в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99}; г) А = {0,1; 0,01; 0,001; 0,0001; }; д) А = {1/2, 2/3, 3/4, 4/5, … }.
5) Запишите на символическом языке следующее утверждение:
а) число 10 - натуральное;
б) число - 7 не является натуральным;
в) число - 100 является целым;
г) число 2,5 - не целое.
6) Даны множества: А = {10}, В = {10, 15}, С =
{5, 10, 15}, D = {5, 10, 15, 20}. Поставьте вместо … знак включения
(![]() или
или ![]() ) так, чтобы получилось верное утверждение: а) А… D; б) А…В; в)
С…А; г) С…В.
) так, чтобы получилось верное утверждение: а) А… D; б) А…В; в)
С…А; г) С…В.
Задачи для домашнего решения
1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}.
Найдите: а) А∩В; б) А∩С; в) С∩В.
2. Даны множества: А - множества всех натуральных чисел, кратных 10, В = {1; 2; 3;…, 41}. Найдите А∩В.
3. Даны множества: А = {a, b, c, d}, B = {c, d, e, f}, C = {c, e, g, k}.
Найдите (А∩В)∩С.
4. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}.
Найдите: а) АUВ; б) АUС; в) СUВ.
Практическое занятие 16
Практическая работа 13
по теме «Решение задач на применение формул Бернулли и Лапласа»
Цель работы: сформировать навыки нахождения вероятности по формулам Бернулли и Лапласа.
Актуализация знаний
Фронтальный опрос
1. Понятие факториала.
2. Понятие перестановок, размещений, сочетаний.
3. Классическое определение вероятности.
5. Формулы Бернулли и Лапласа.
Краткие теоретические и учебно-методические материалы по теме практической работы
Нахождение вероятностей при повторении испытаний
І. "Мелкосерийное производство", т.е. n < 20 единиц. Тогда ответ на первый вопрос находится по формуле Бернулли:
![]()
ІІ. "Крупносерийное производство", т.е. 20 единиц.
Ответы на поставленные вопросы могут быть получены с помощью функции Лапласа. Эти функции находятся соответственно к своему аргументы и с учетом свойств функции по таблицам. Аргумент любой функции Лапласа находится по формуле и зависит для одной и той же серии только от количества появления событий.
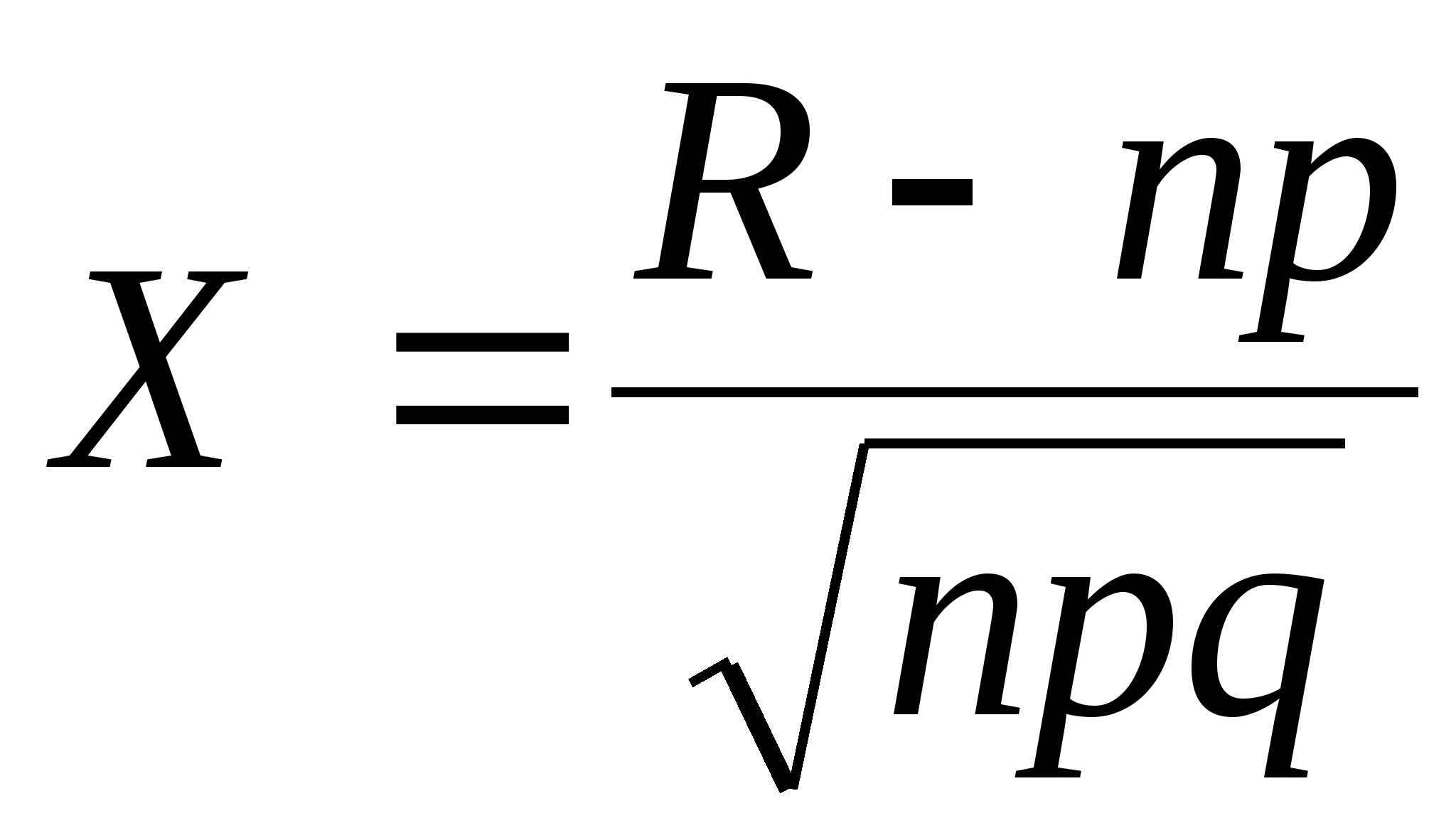
Ответ на первый вопрос может быть получен с помощью локальной функции Лапласа:
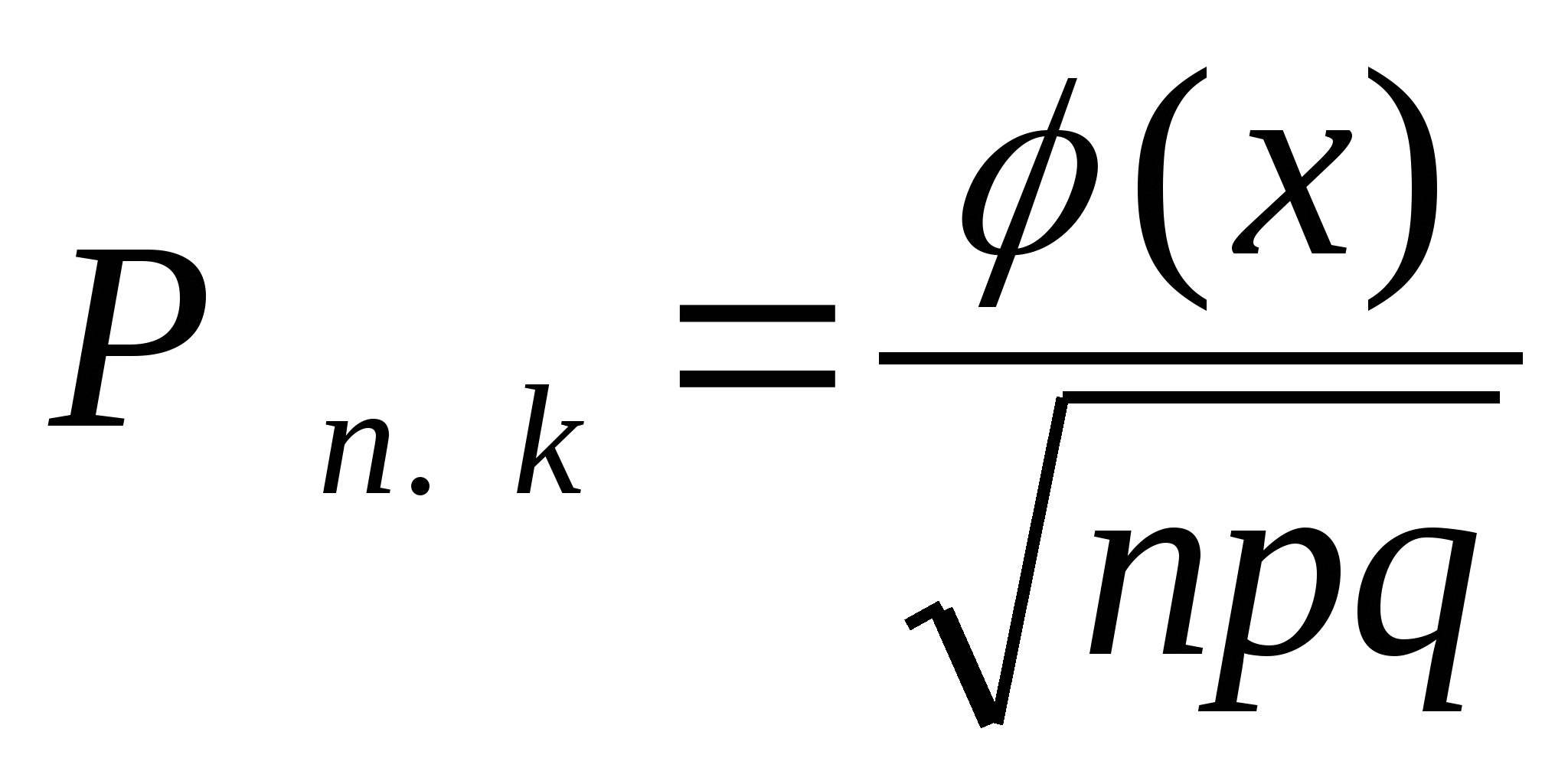
Свойства локальной функции ![]()
-
Область определения Д
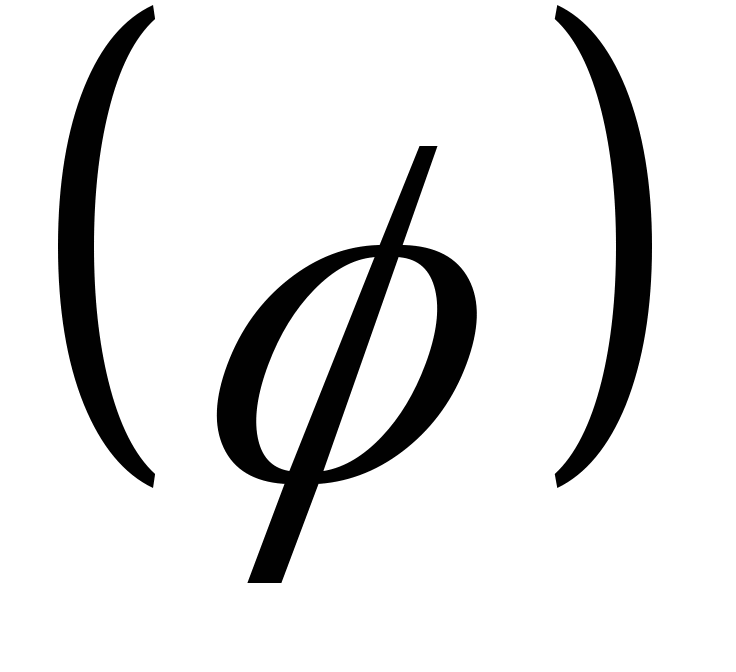 - все действительные числа.
- все действительные числа.
-
Функция четная, т.е.
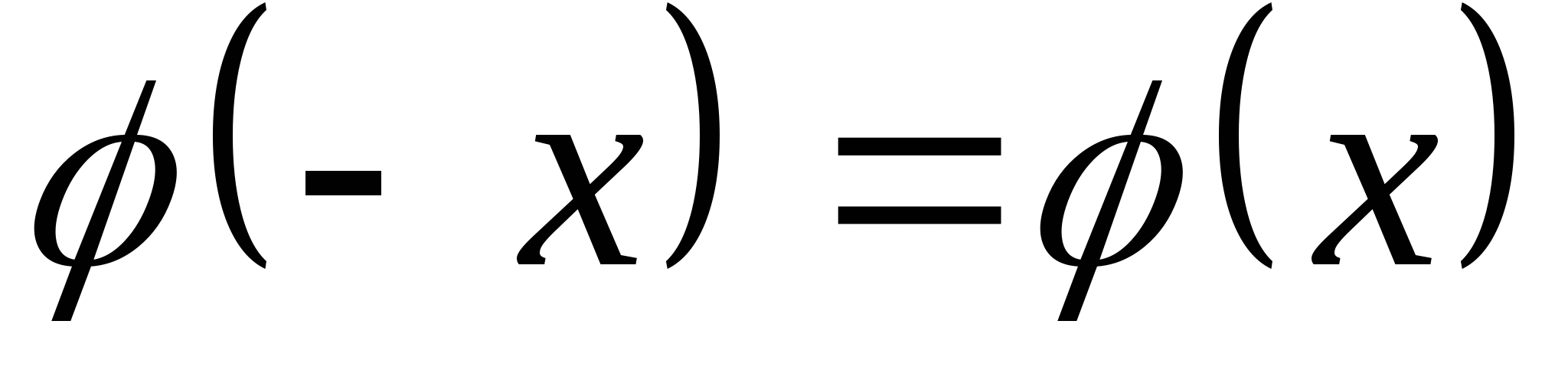 .
.
-
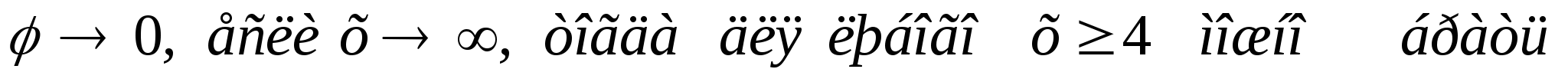
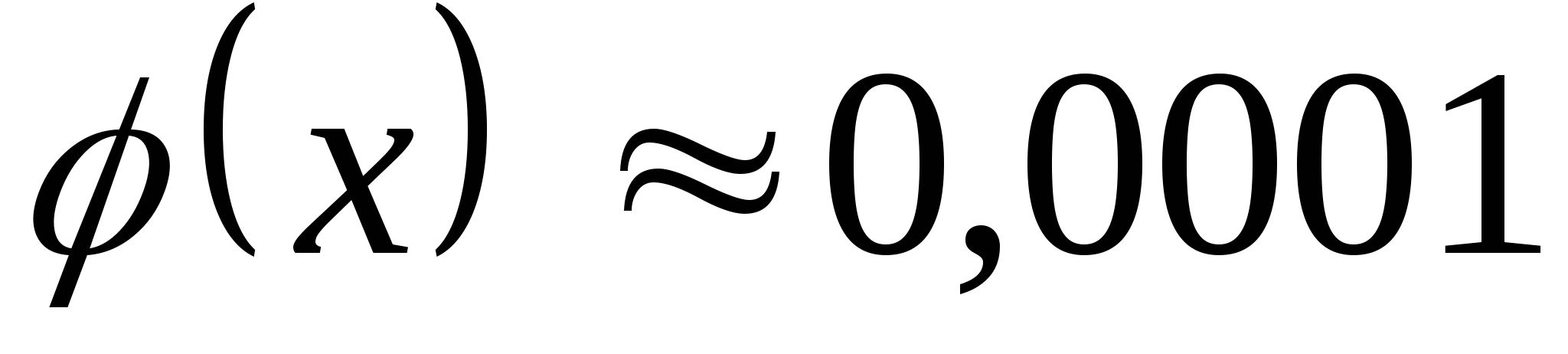
Ответ на второй вопрос может быть получен с помощью интегральной функции Лапласа:
![]()
Свойства интегральной функции (Ф)
-
Область определения Д (Ф) =
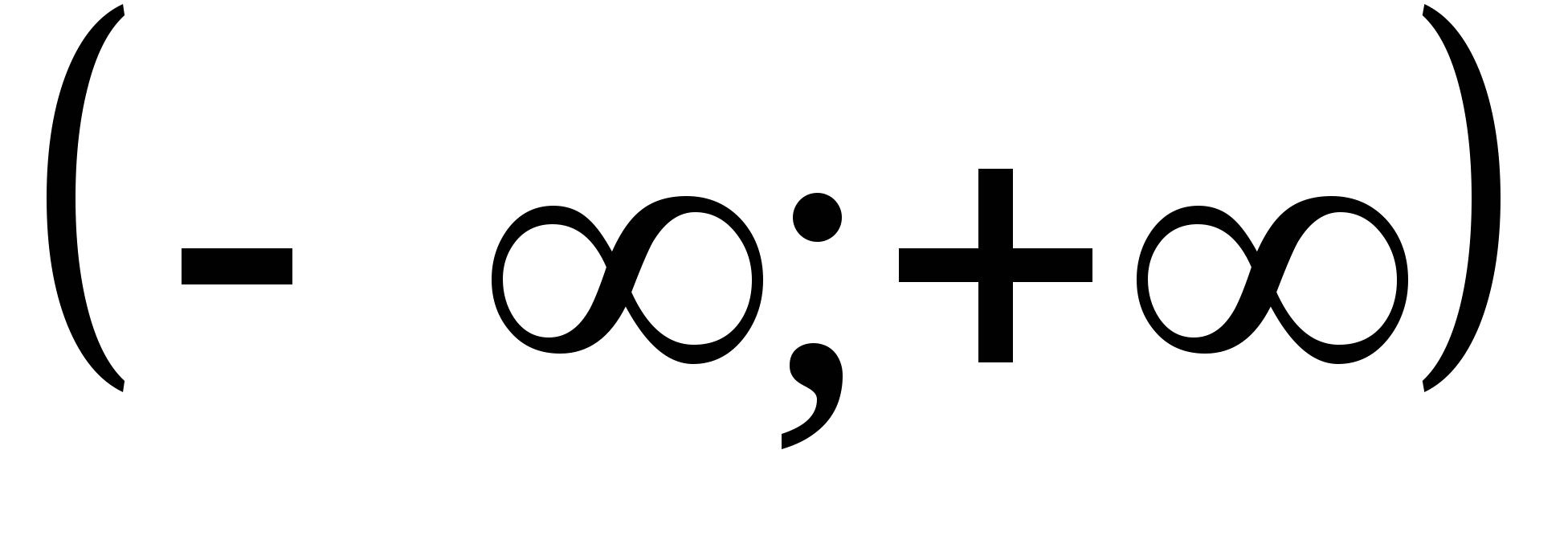
-
Функция нечетная, т.е. Ф (-х) = -Ф (х)
-
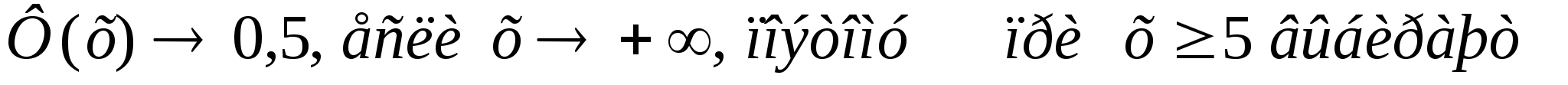
Ф (х) = 0,499997.
Таблица значений локальной функции Лапласах
0
1
2
3
4
5
6
7
8
9
0.0
0.3989
3989
3989
3988
3986
3984
3982
3980
3977
3973
0.1
3970
3965
3961
3956
3951
3945
3939
3932
3925
3918
0.2
3910
3902
3894
3885
3876
3867
3857
3847
3836
3825
0.3
3814
3802
3790
3778
3765
3752
3739
3726
3712
3697
0.4
3683
3668
3653
3637
3621
3605
3589
3572
3555
3538
0.5
3521
3503
3485
3467
3448
3429
3410
3391
3372
3352
0.6
3332
3312
3292
3271
3251
3230
3209
3187
3166
3144
0.7
3123
3101
3079
3056
3034
3011
2989
2966
2943
2920
0.8
2897
2874
2850
2827
2803
2780
2756
2732
2709
2685
0.9
2661
2637
2613
2589
2565
2541
2516
2492
2468
2444
1.0
0.2420
2396
2371
2347
2323
2299
2275
2251
2227
2203
1.1
2179
2155
2131
2107
2083
2059
2036
2012
1989
1965
1.2
1942
1919
1895
1872
1849
1826
1804
1781
1758
1736
1.3
1714
1691
1669
1647
1626
1604
1582
1561
1539
1518
1.4
1497
1476
1456
1535
1415
1394
1374
1354
1334
1315
1.5
1295
1276
1257
1238
1219
1200
1182
1163
1145
1127
1.6
1109
1092
1074
1057
1040
1023
1006
0989
0973
0957
1.7
0940
0925
0909
0893
0878
0863
0848
0833
0818
0804
1.8
0790
0775
0761
0748
0734
0721
0707
0694
0681
0669
1.9
0656
0644
0632
0620
0608
0596
0584
0573
0562
0551
х
0
1
2
3
4
5
6
7
8
9
2.0
0.0540
0529
0519
0508
0498
0488
0478
0468
0459
0449
2.1
0440
0431
0422
0413
0404
0396
0387
0379
0371
0363
2.2
0355
0347
0339
0332
0325
0317
0310
0303
0297
0290
2.3
0283
0277
0270
0264
0258
0252
0246
0241
0235
0229
2.4
0224
0219
0213
0208
0203
0198
0194
0189
0184
0180
2.5
0175
0171
0167
0163
0158
0154
0151
0147
0143
0139
2.6
0136
0132
0129
0126
0122
0119
0116
0113
0110
0107
2.7
0104
0101
0099
0096
0093
0091
0088
0086
0084
0081
2.8
0079
0077
0075
0073
0071
0069
0067
0065
0063
0061
2.9
0060
0058
0056
0055
0053
0051
0050
0048
0047
0046
3.0
0.0044
0043
0042
0040
0039
0038
0037
0036
0035
0034
3.1
0033
0032
0031
0030
0020
0028
0027
0026
0025
0025
3.2
0024
0023
0022
0022
0021
0020
0020
0019
0018
0018
3.3
0017
0017
0016
0016
0015
0015
0014
0014
0013
0013
3.4
0012
0012
0012
0011
0011
0010
0010
0010
0009
0009
3.5
0009
0008
0008
0008
0008
0007
0007
0007
0007
0006
3.6
0006
0006
0006
0005
0005
0005
0005
0005
0005
0004
3.7
0004
0004
0004
0004
0004
0004
0003
0003
0003
0003
3.8
0003
0003
0003
0003
0003
0002
0002
0002
0002
0002
3.9
0002
0002
0002
0002
0002
0002
0002
0002
0001
0001
Таблица значений интегральной функции Лапласах
0
1
2
3
4
5
6
7
8
9
0.0
0.0000
00399
00798
01197
01595
01994
02392
02790
03188
03586
0.1
03983
04380
04776
05172
05567
05962
06356
06749
07142
07535
0.2
07926
08317
08706
09095
09483
09871
10257
10642
11026
11409
0.3
11791
12172
12552
12930
13307
13683
14058
14431
14803
15173
0.4
15542
15910
16276
16640
17003
17364
17724
18082
18439
18793
0.5
19146
19497
19847
20194
20540
20884
21226
21566
21904
22240
0.6
22575
22907
23237
23565
23891
24215
24537
24857
25175
25490
0.7
25804
26115
26424
26730
27035
27337
27637
27935
28230
28524
0.8
28814
29103
29389
29673
29955
30234
30511
30785
31057
31327
0.9
31594
31859
32121
32381
32639
32894
33147
33398
33646
33891
1.0
0.34134
34375
344614
34850
35083
35314
35543
35369
35993
36214
1.1
36433
36650
36864
37076
37286
37493
37698
37900
38100
38298
1.2
38493
38686
38877
39065
39251
39435
39617
39796
39973
40147
1.3
40320
40490
40658
40824
40988
41149
41309
41466
41621
41774
1.4
41924
42073
42220
42364
42507
42647
42786
42922
43056
43189
1.5
43319
43448
43574
43699
43822
43943
44062
44179
44295
44408
1.6
44520
44630
44738
44845
44950
45053
45154
45254
45352
45449
1.7
45543
45637
45728
45818
45907
45994
46080
46164
46246
46327
1.8
46407
46485
46562
46638
46712
46784
46856
46926
46995
47062
1.9
47128
47193
47257
47320
47381
47441
47500
47558
47615
47670
х
0
1
2
3
4
5
6
7
8
9
2.0
0.47725
47778
47831
47882
47932
47982
48030
48077
48124
48169
2.1
48214
48257
48300
48341
48382
48422
48461
48500
48537
48574
2.2
48610
48645
48679
48713
48745
48778
48809
48840
48870
48899
2.3
48928
48956
48983
49010
49036
49061
49086
49111
49134
49158
2.4
49180
49202
49224
49245
49266
49286
49305
49324
49343
49361
2.5
49379
49396
49413
49430
49446
49461
49477
49492
49506
40520
2.6
49534
49547
49560
40573
49585
49598
49609
49621
49632
49643
2.7
49653
49664
49674
49683
49693
49702
49711
49720
49728
49736
2.8
49744
49752
49760
49767
49774
49781
49788
49795
49801
49807
2.9
49813
49819
49825
49831
49836
49841
49846
49851
49856
49861
3.0
0.49865
3.3
0.49952
3.6
0.49984
3.9
0.49995
5.0
0.499999
3.1
49903
3.4
49966
3.7
49989
4.0
499968
3.2
49931
3.5
49977
3.8
49993
4.5
499997
Формирование необходимых знаний и умений
Коллективное решение и обсуждение предложенных задач
Пример 1
Вероятность попадания в цель при одном выстреле составляет р=0,8. Найти вероятность четырёх попаданий при шести выстрелах.
Решение:
п = 6, R = 4, p = 0,8, q = 0,2
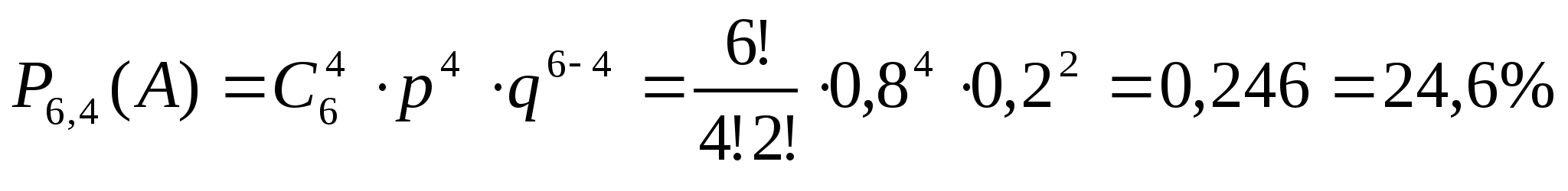
Пример 2
По рекламному проспекту всхожесть семян имеет вероятность того, что из 500 единиц семян:
-
взойдёт лишь 147
-
взойдет от 300 до 400 ед. семян
Решение:
п = 500, p = 0,7, q = 0,3
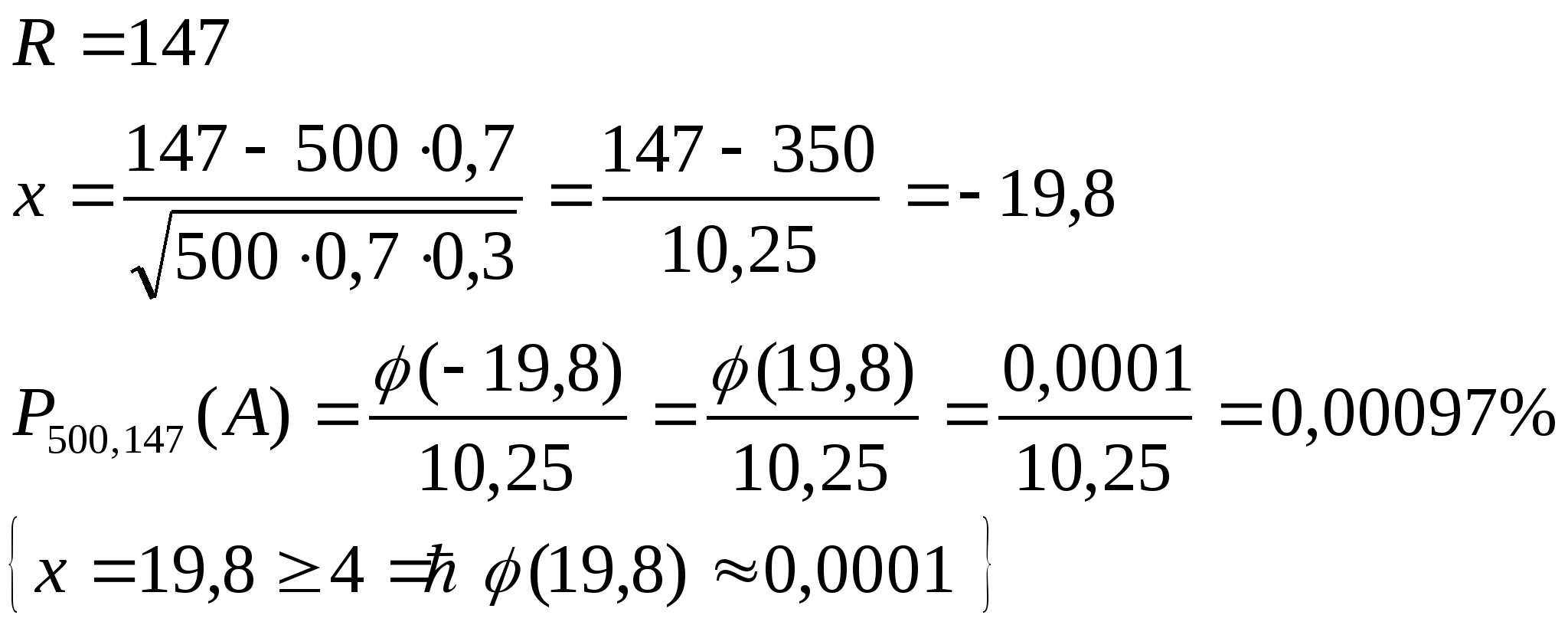
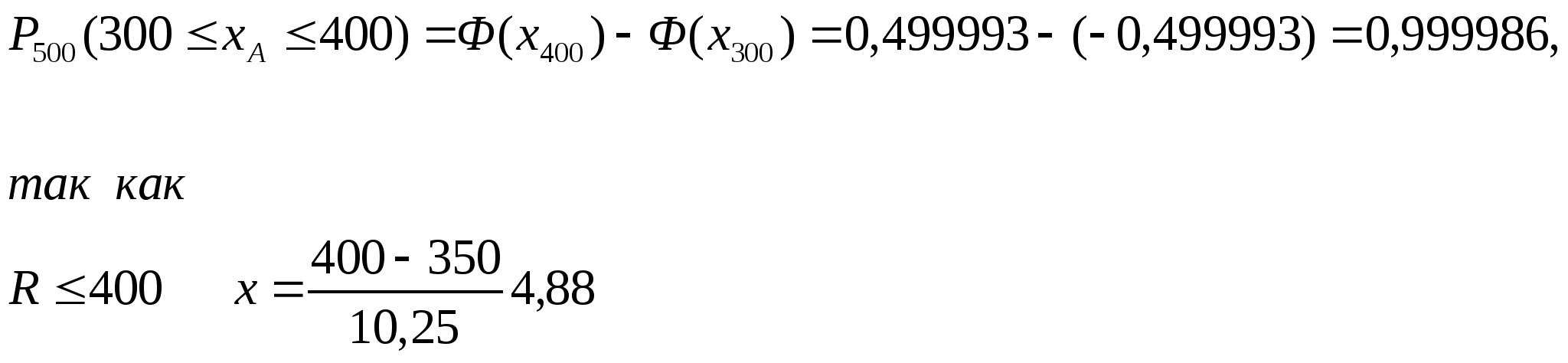
Ф (х400) = Ф (4,88) = 0,499993
Задачи:
1. Вероятность сбоя в работе компьютера в одном сеансе работы равна 0.1. Найти вероятность двух сбоев в шести сеансах работы.
2. Вероятность появления события А в одном испытании равна 0.4. произведено 5 испытаний. Найти вероятность того, что событие А наступит не более одного раза.
3. Фирма выпускает изделия, из которых 80% высшего качества. Какова вероятность при отборе 100 изделий обнаружить ровно 18 изделий высшего качества?
4. Хлебокомбинат выпускает 90% продукции первого сорта. Какова вероятность того, что из 400 изделий хлебокомбината первосортных окажется не менее 380?
Закрепление сформированных знаний и учений:
Закрепление полученных знаний по данной теме проводится во время самостоятельного решения заданий
1.Вероятность появления события А в одном испытании равна 0.9. произведено 100 испытаний. Найти вероятность того, что событие А наступит не менее 80 раз.
2. Известно, что в данном селе 80% семей имеют телевизоры. Найти вероятность того, что среди 6 случайно отобранных семей 2 окажутся без телевизора.
3. В квартире 8 электролампочек. Вероятность работы лампочки в течение года равна 0,9. Какова вероятность того, что в течение года придется заменить не менее половины лампочек.?
Задачи для домашнего решения
1. Всхожесть семян новой культуры 85%. На опытном участке посеяли 500 семян. Найти вероятность того, что прорастут от 400 до 450 семян.
2. Вероятность появления события А в одном испытании равна 0.4. произведено 400 испытаний. Найти вероятность того, что событие А наступит не менее 190 и не более 215 раз.
3. Типография гарантирует вероятность брака переплета книг 0.0001. Книга издана тиражом 25000 экземпляров. Какова вероятность того, что в этом тираже только одна книга имеет брак переплета?
Практическое занятие 17
Практическая работа 14
по теме «Составление и анализ случайных величин»
Цель работы: сформировать умения составления закона распределения случайной величины в двух формах и анализировать данные с помощью числовых характеристик.
Актуализация знаний
Фронтальный опрос
1. Дать понятие моды.
2. Виды случайных величин.
3. Свойства интегральной и локальной функции.
4. Понятие дисперсии , математического ожидания, среднеквадратичного отклонения, интервала рассеивания.
Краткие теоретические и учебно-методические материалы по теме практической работы
Формы задания случайных величин:
1. Табличная - ряд распределения. Используется и для НСВ и для ДСВ. Наиболее удобна для задания ДСВ.
Критерий правильности ЗРСВ: сумма вероятностей всех значений случайных величин равна 1.
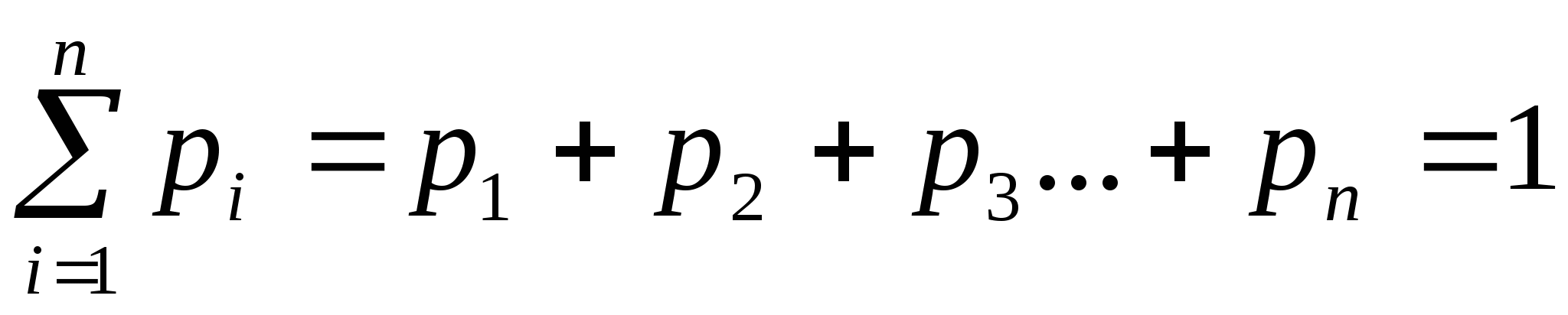
2)
(х2;х3)
р
р1
р2
...
рn
р
р1
р2
2. Графическая - полигон распределения. Используется только для ДСВ. Представляет собой ломаную, отрезки которой соединяют в системе координат точки (xi ; Pi). Практически, полигон распределения - наглядное отображение ряда распределения. Свойство полигона: он ограничен снизу осью ОХ, а сверху - прямой р=1.
1). Математическое ожидание, среднее значение распределения - это аналог центра тяжести фигуры, отдельные элементы которого имеют различную массу, аналогичную вероятностям значений СВ.
ДСВ: 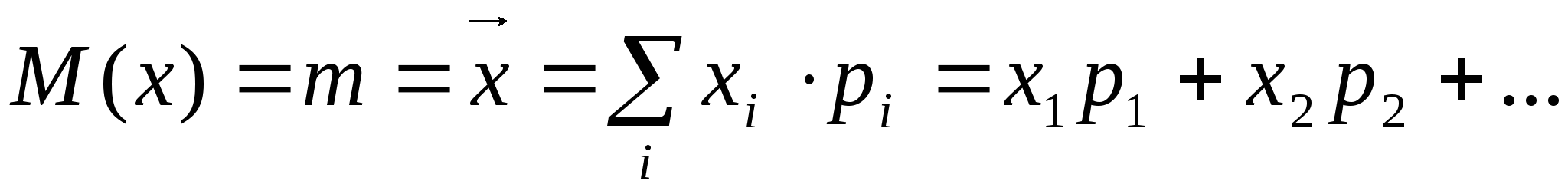
НСВ: 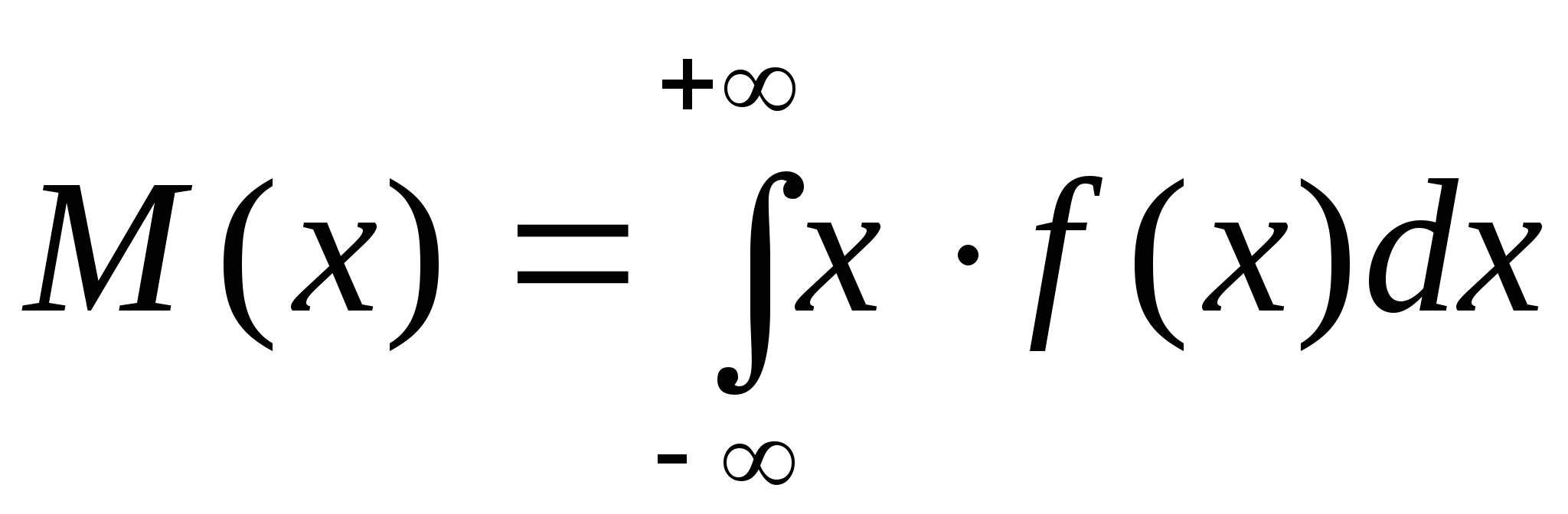
2). Дисперсия - показатель рассеяния наиболее "весомых" значений СВ возле математического ожидания; аналог площади круга наиболее весомой части фигуры с центром в математическом ожидании.
ДСВ: ![]()
НСВ: 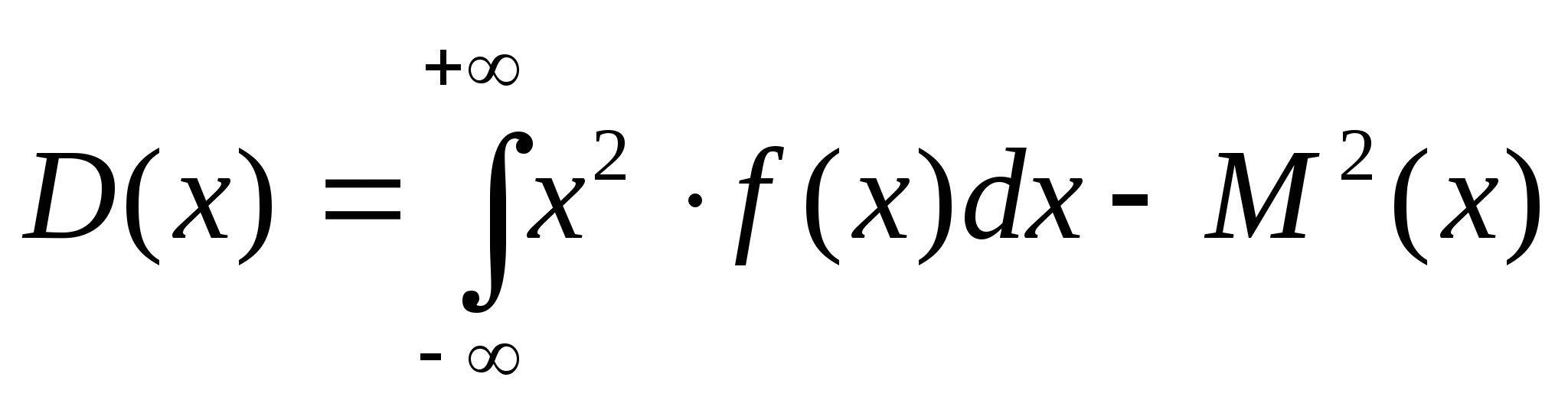
3). Среднее квадратическое отклонение -
показатель рассеивания, который является аналогом радиуса "весомого
круга", или ширины интервала около математического
ожидания.![]()
Для планирования используется наиболее вероятный интервал
рассеивания значений ВВ.![]()
4). Мода m0 - наиболее вероятное значение СВ (актуально для ДСВ).
Формирование необходимых знаний и умений
Коллективное решение и обсуждение предложенных задач
Пример 1
Задан ряд распределения суточного спроса на определенный продукт Х. Найти числовые характеристики этой ДСВ.
Решение:
1) Математическое ожидание находим по формуле:
M(X) = 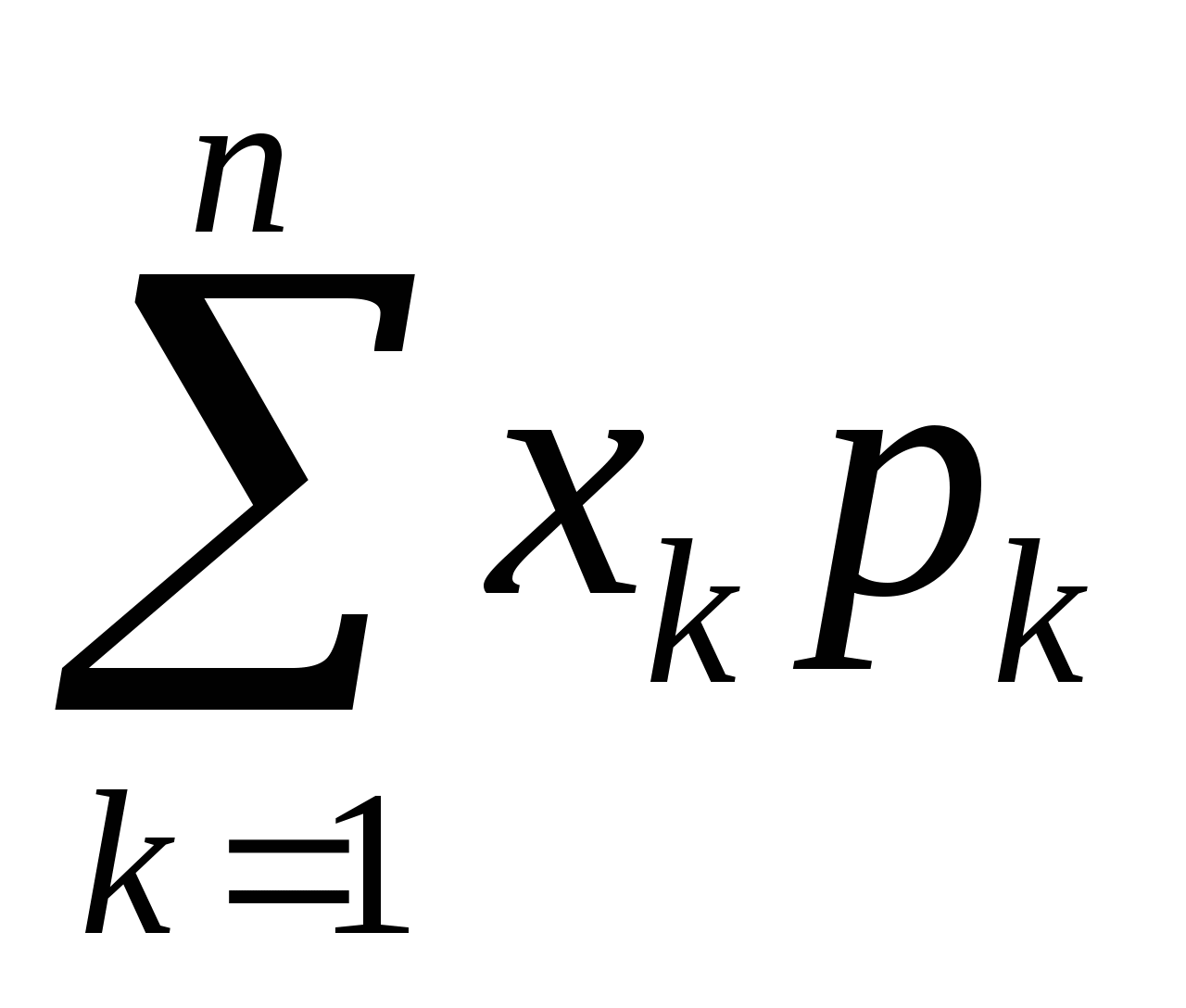 ,
,
Т.е. М(х) = 10*0,1 + 20*0,15 + 30*0,42 + 40*0,25 + 50*0,08 = 30,6.
2) Дисперсию находим по формуле: Д(X) =
![]() xi2pi - М(Х)2 ,
xi2pi - М(Х)2 ,
т.е. Д (Х) = 102*0,1 + 202*0,15 + 302*0,42 + 402*0,25 + 502*0,08-(30,6)2 =111,64.
3) Средне квадратичное отклонение находим по
формуле: ![]() , т.е
, т.е ![]() = 10,56.
= 10,56.
4) Мода: m0 = 30.
Пример 2
Дискретная случайная величина может принимать три значения:
Х1 = 1, Х2 = 3, Х3 = 4. Известны математическое ожидание М(Х) = 2,9 и дисперсия Д(Х) = 1,09. Составить ЗРСВ.
Решение:
ЗРСВ будем составлять в виде ряда распределения, для чего необходимо найти вероятности значений дискретной случайной величины. Для их нахождения составим и решим методом Гаусса систему линейных уравнений, используя для составления следующие органы:
-
сумма вероятностей значений СВ равна "1";
-
M(X) =
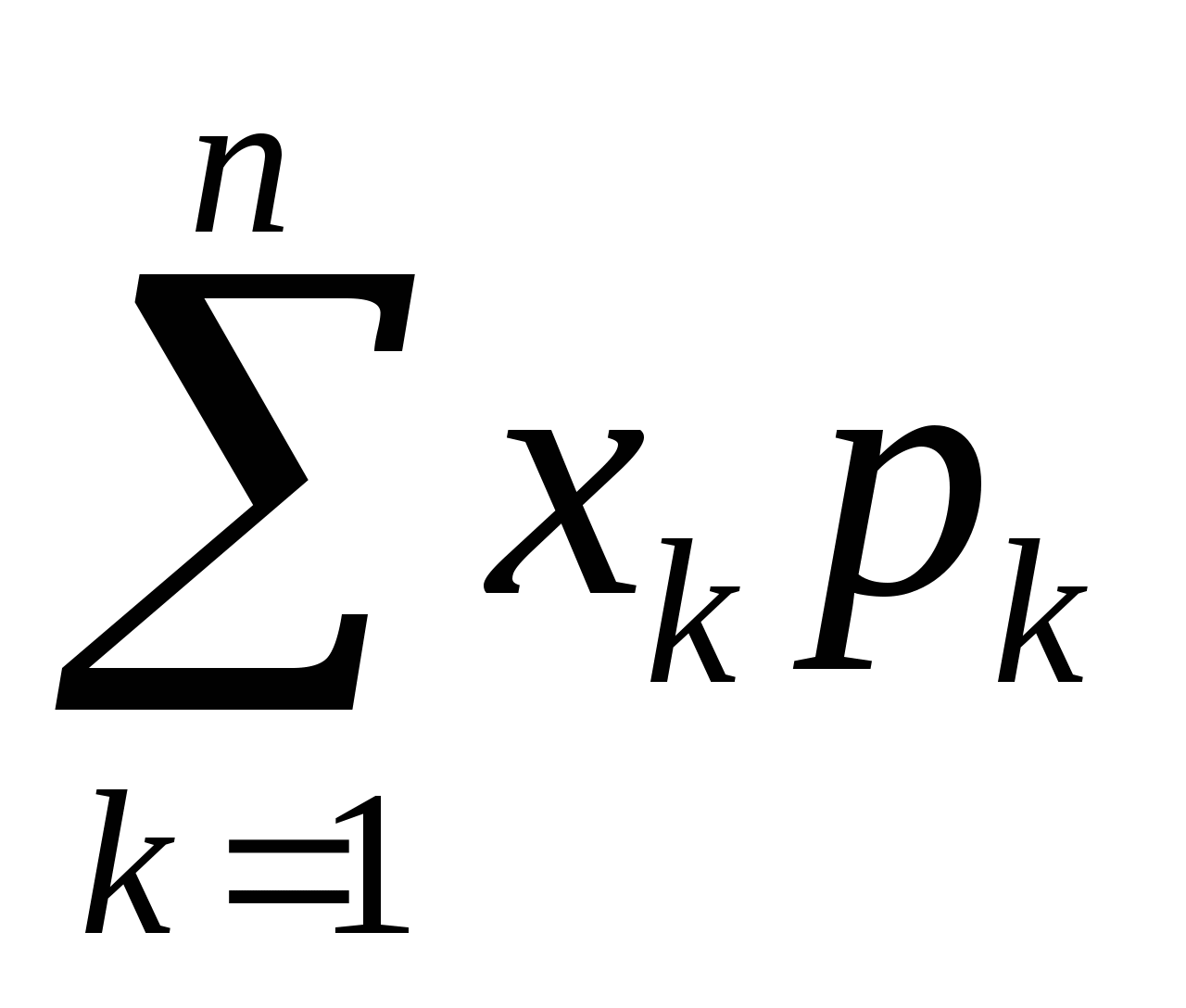 ;
;
-
Д(X) =
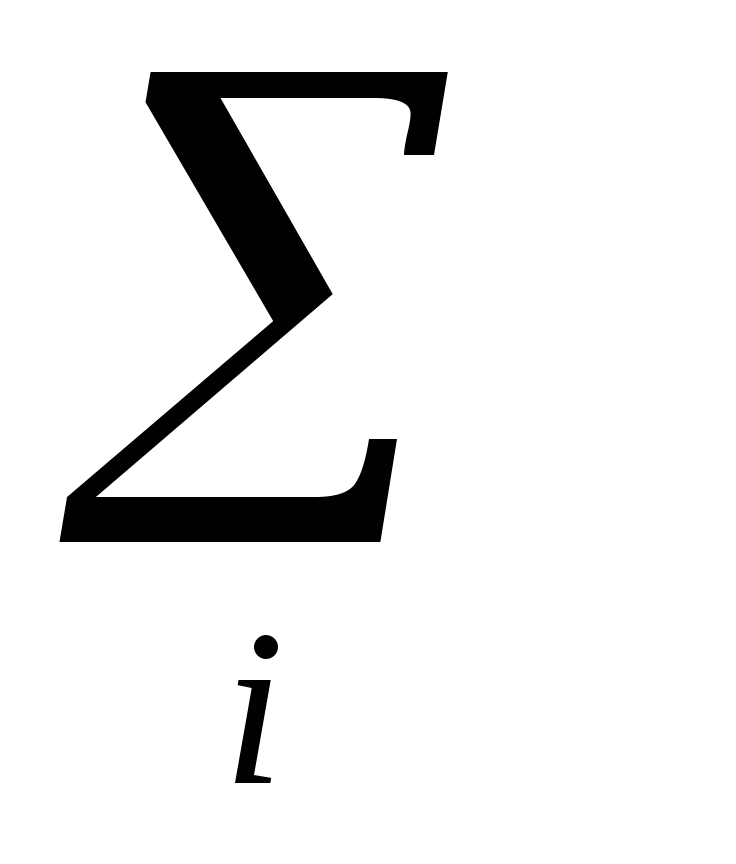 xi2pi - М(Х)2 .
xi2pi - М(Х)2 .
Таким образом, получим:
р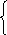 1
+ р2 + р3 = 1,
1
+ р2 + р3 = 1,
р1 + 3р2 + 4р3 = 2,9,
р1 + 9р2 + 16р3 - 8,41 = 1,09;
р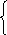 1
+ р2 + р3 = 1,
1
+ р2 + р3 = 1,
р1 + 3р2 + 4р3 = 2,9,
р1 + 9р2 + 16р3 = 9,5;
р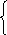 1
+ р2 + р3 = 1,
1
+ р2 + р3 = 1,
2р2 + 3р3 = 1,9,
8р2 + 15р3 = 8,5;
р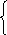 1
+ р2 + р3 = 1,
1
+ р2 + р3 = 1,
2р2 + 3р3 = 1,9,
3р3 = 0,9;
Следовательно, р3 = 0,3, р2 = 0,5*(1,9 - 0,9) = 0,5, р1 = 1 -0,3 - 0,5 = 0,2.
Ряд распределения СВ имеет вид:
Пример 3
Составить и проанализировать ЗРСВ Х = (количество стандартных изделий), если известно, что токарь обработал 5 изделий, а его квалификационный уровень позволяет предсказать 40% вероятность получения бракованного изделия.
Решение:
ЗРСВ будем составлять в биномиальном виде, с помощью формулы Бернулли, учитывая, что n = 5, q = 0,4, р = 1 - 0,4 = 0,6.
-
х1 = 0, р =
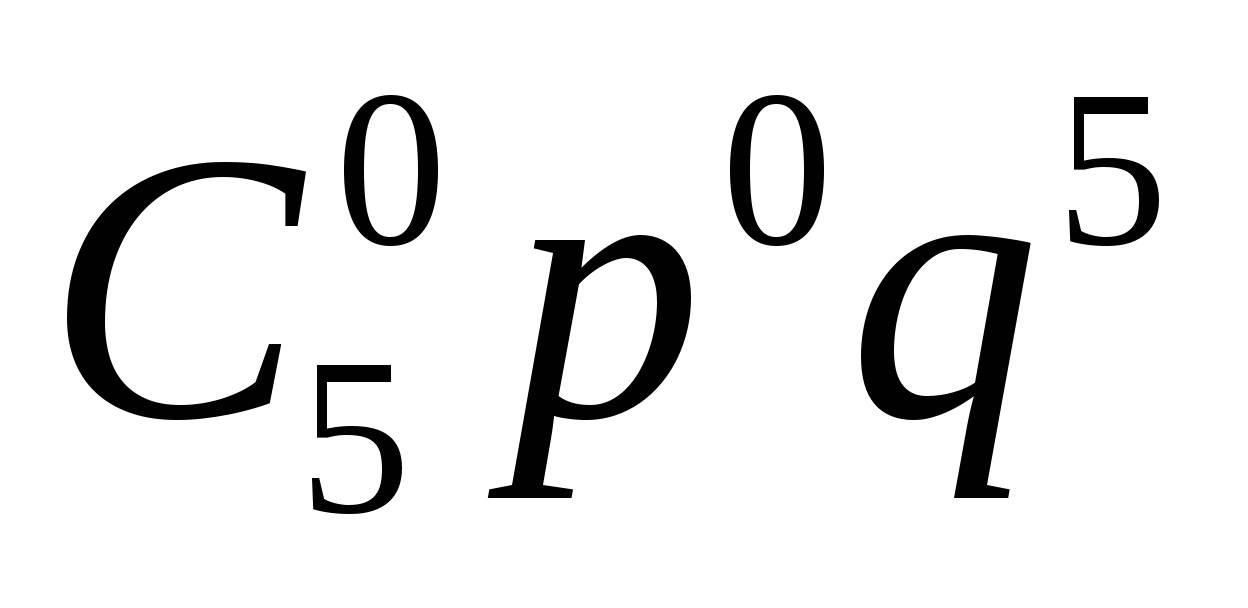 =
= 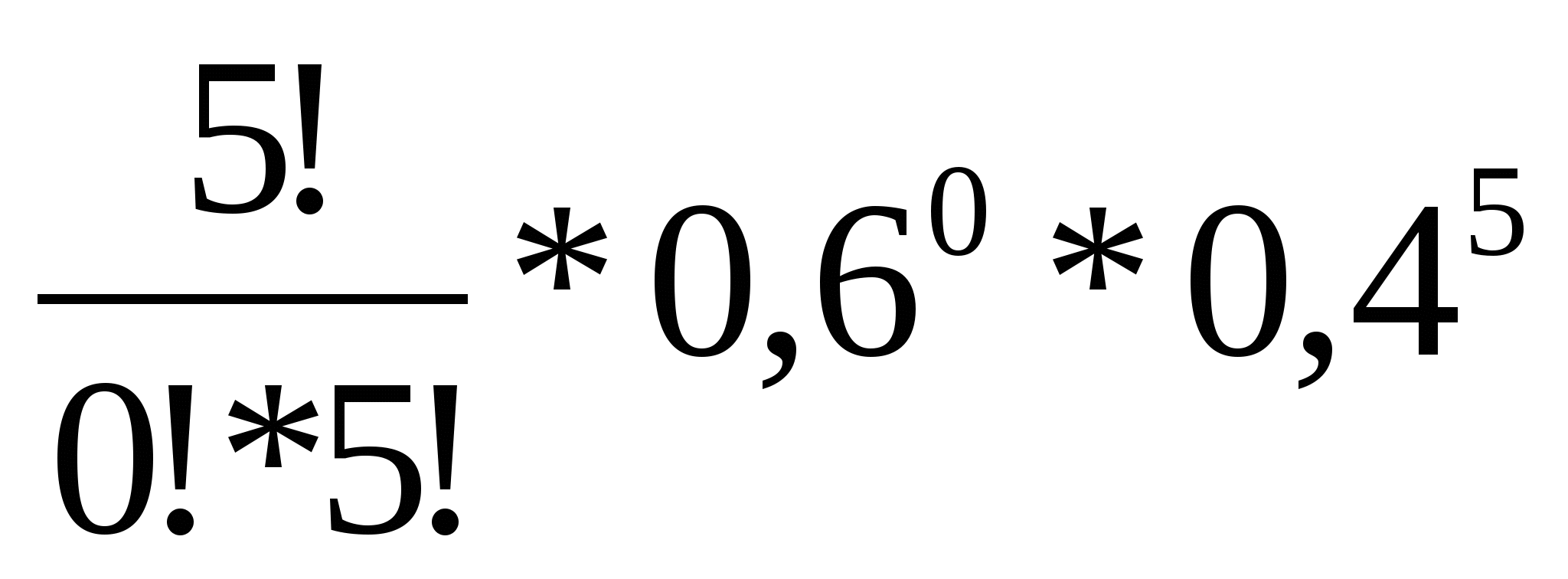 = 0,01024,
= 0,01024,
-
х2 = 1, р =
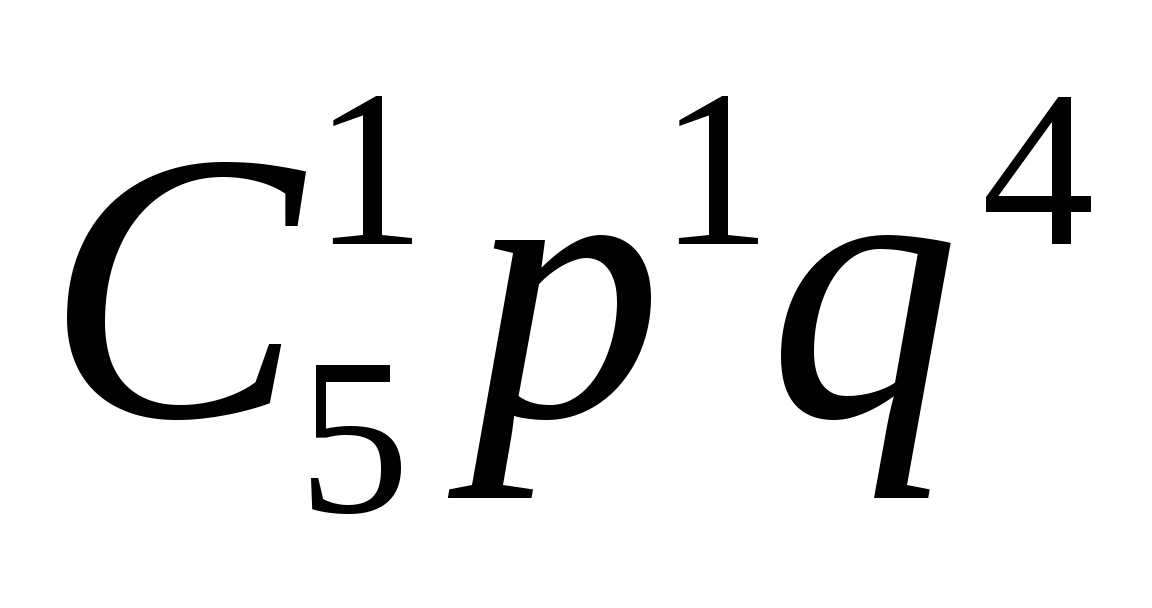 =
= 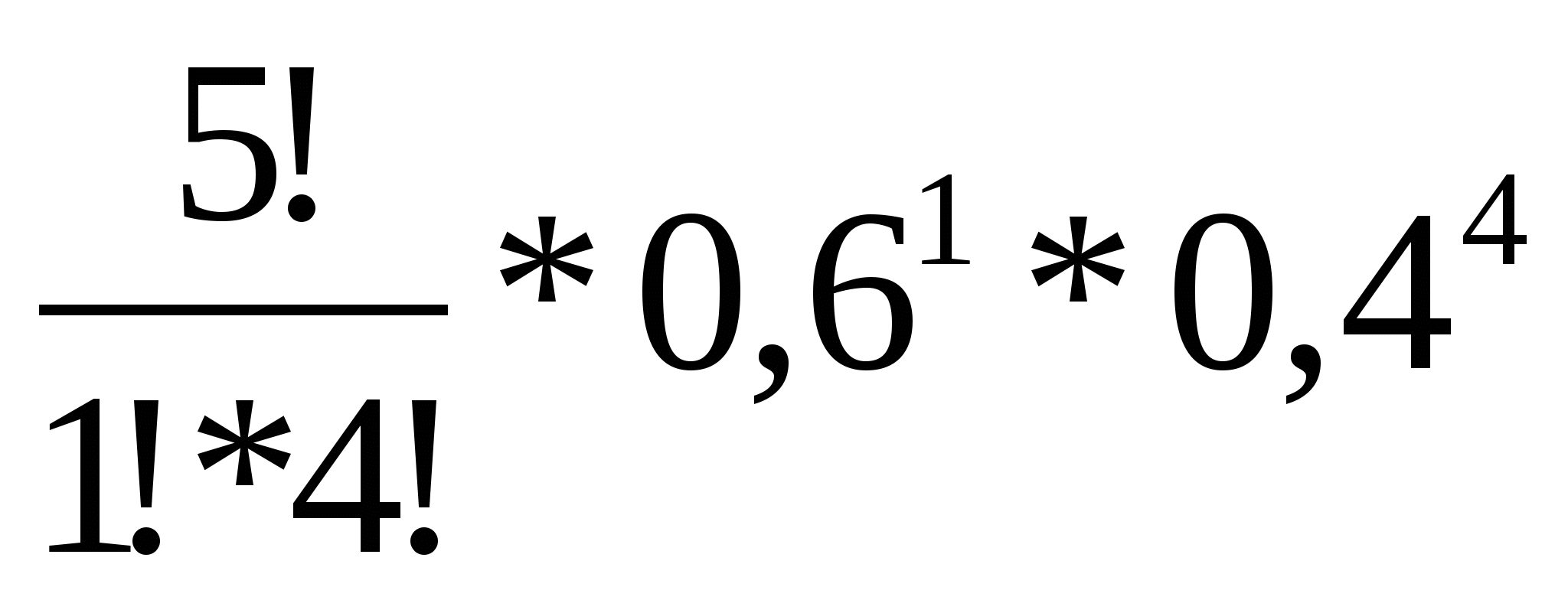 = 0,0768,
= 0,0768,
-
х3 = 2, р =
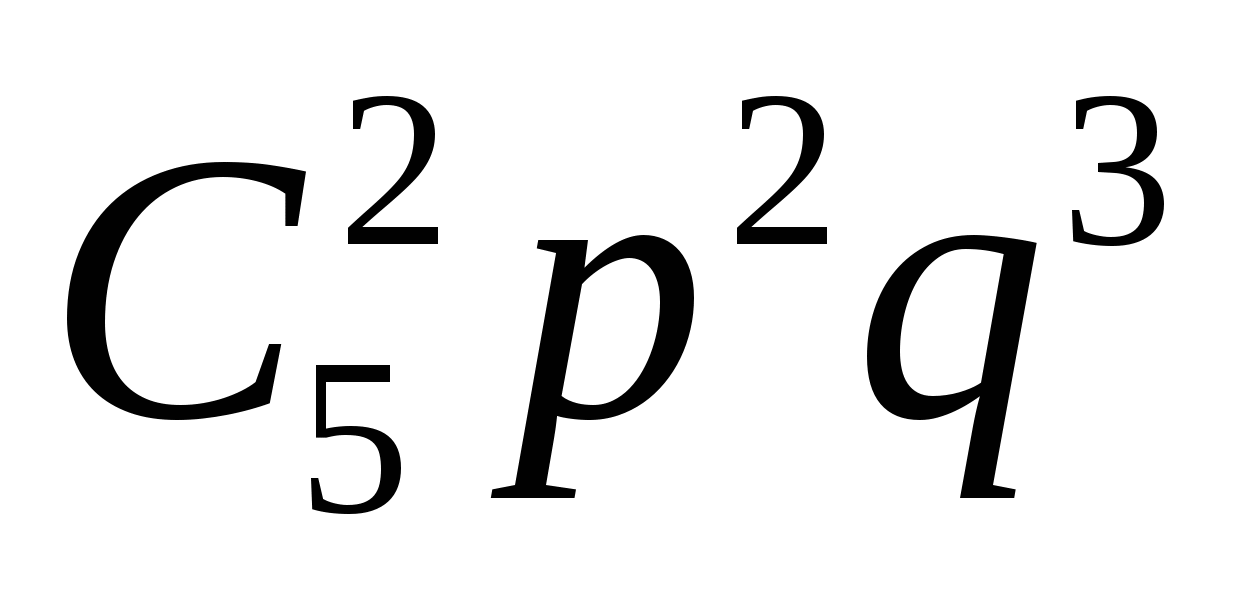 =
= 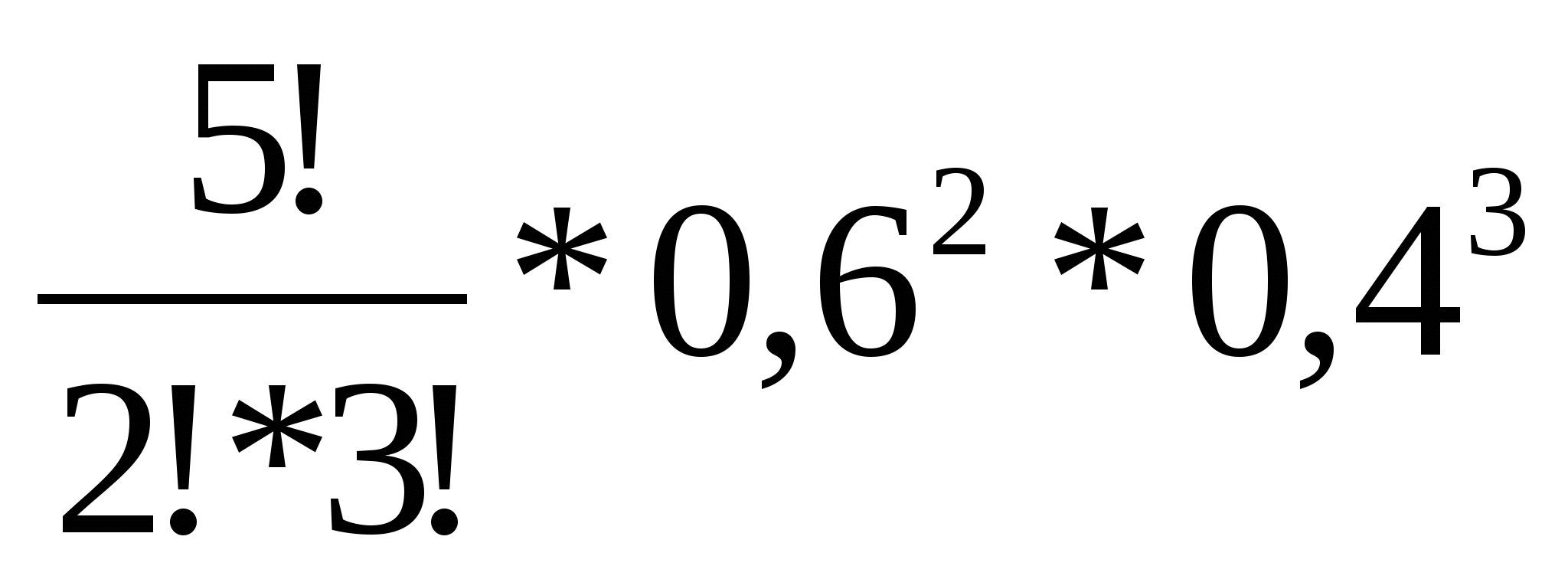 = 0,2304,
= 0,2304,
-
х4 = 3, р =
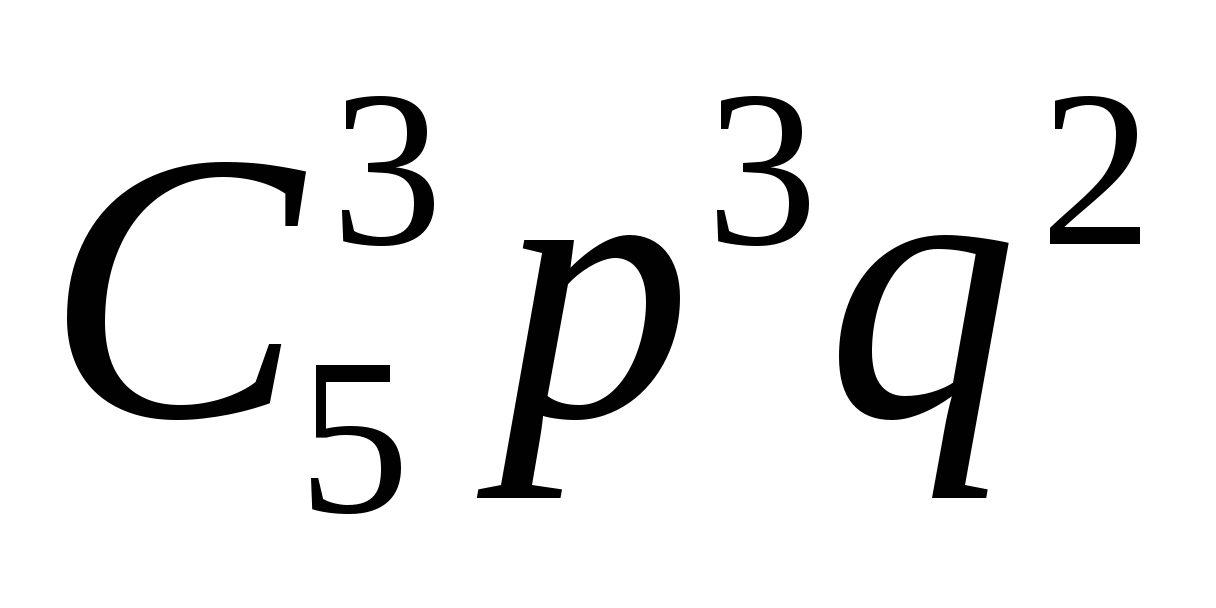 =
= 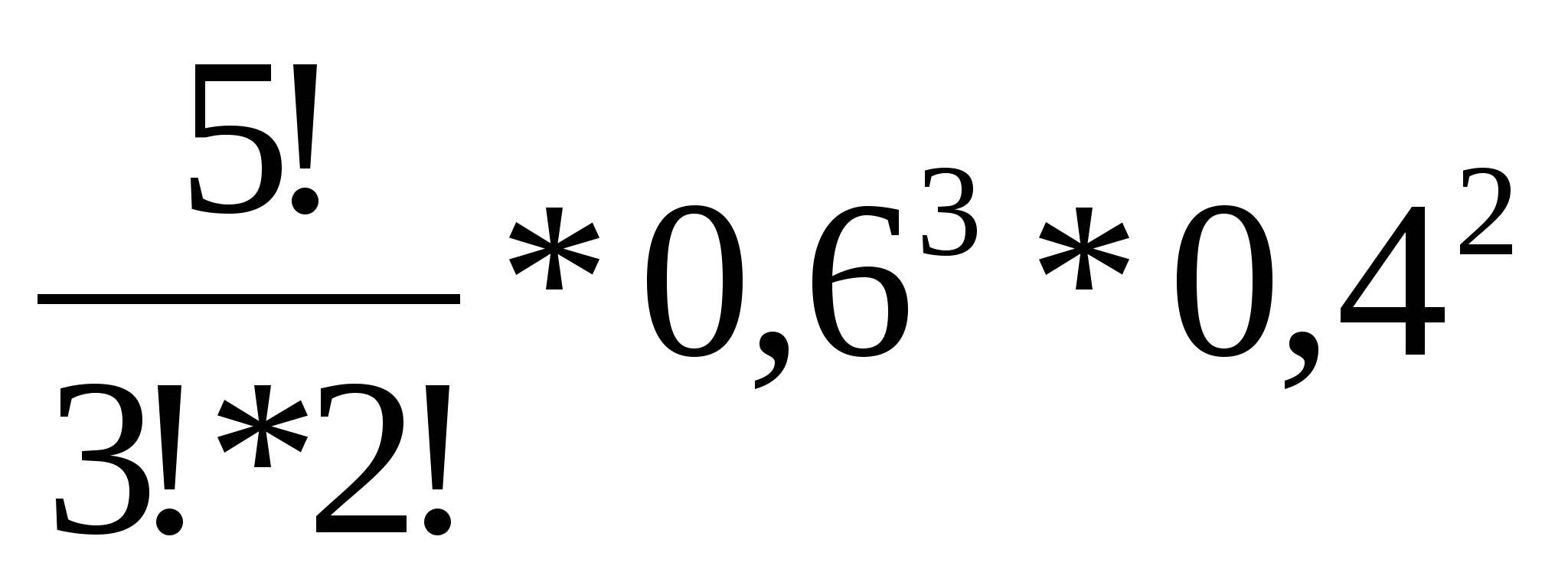 = 0,3456,
= 0,3456,
-
х5 = 4, р =
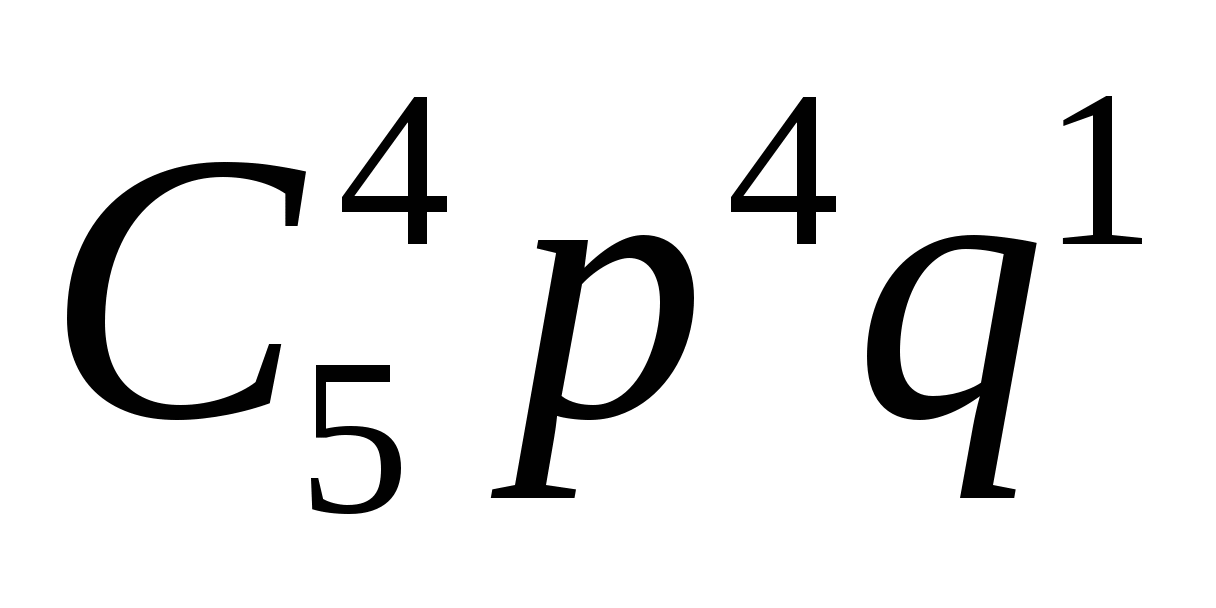 =
= 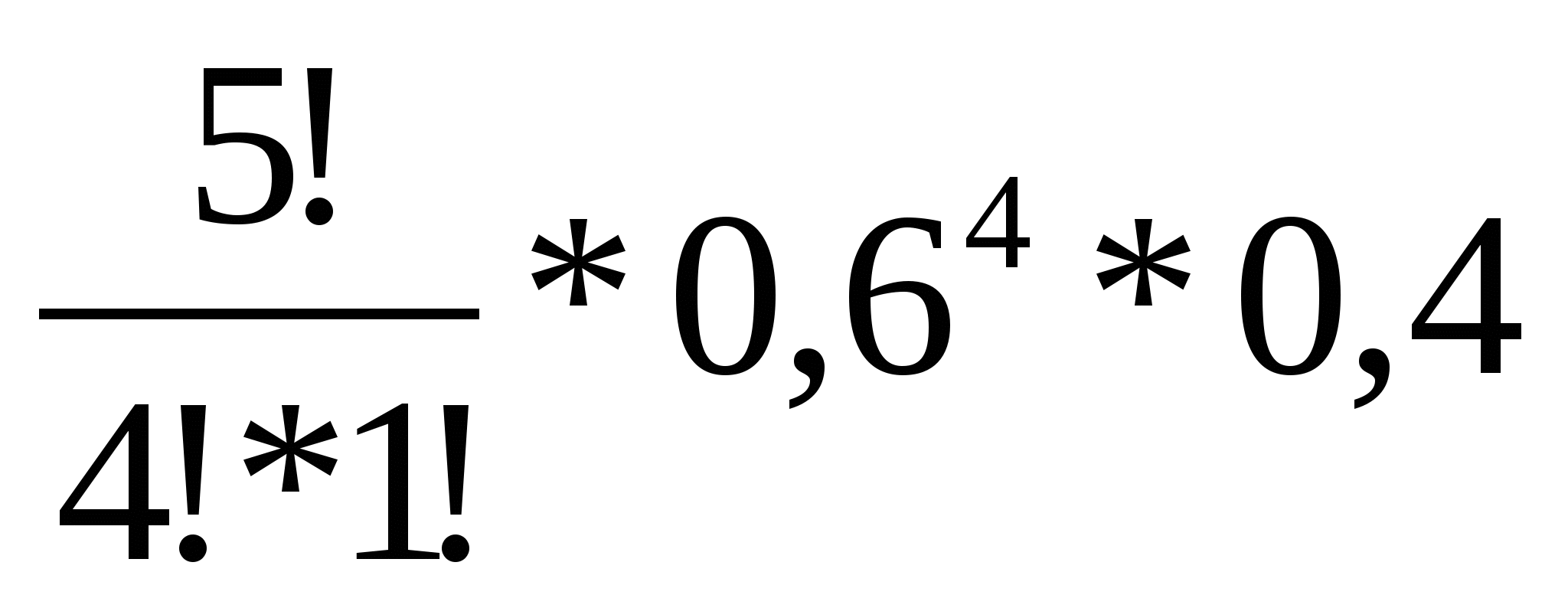 = 0,2592,
= 0,2592,
-
х6 = 5, р =
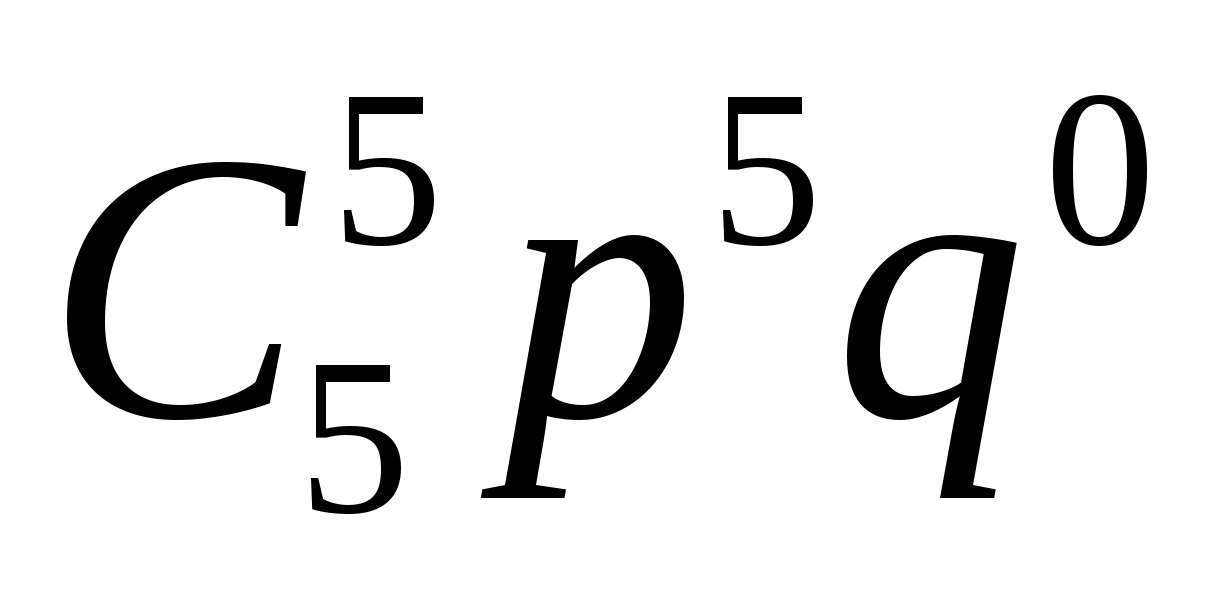 =
= 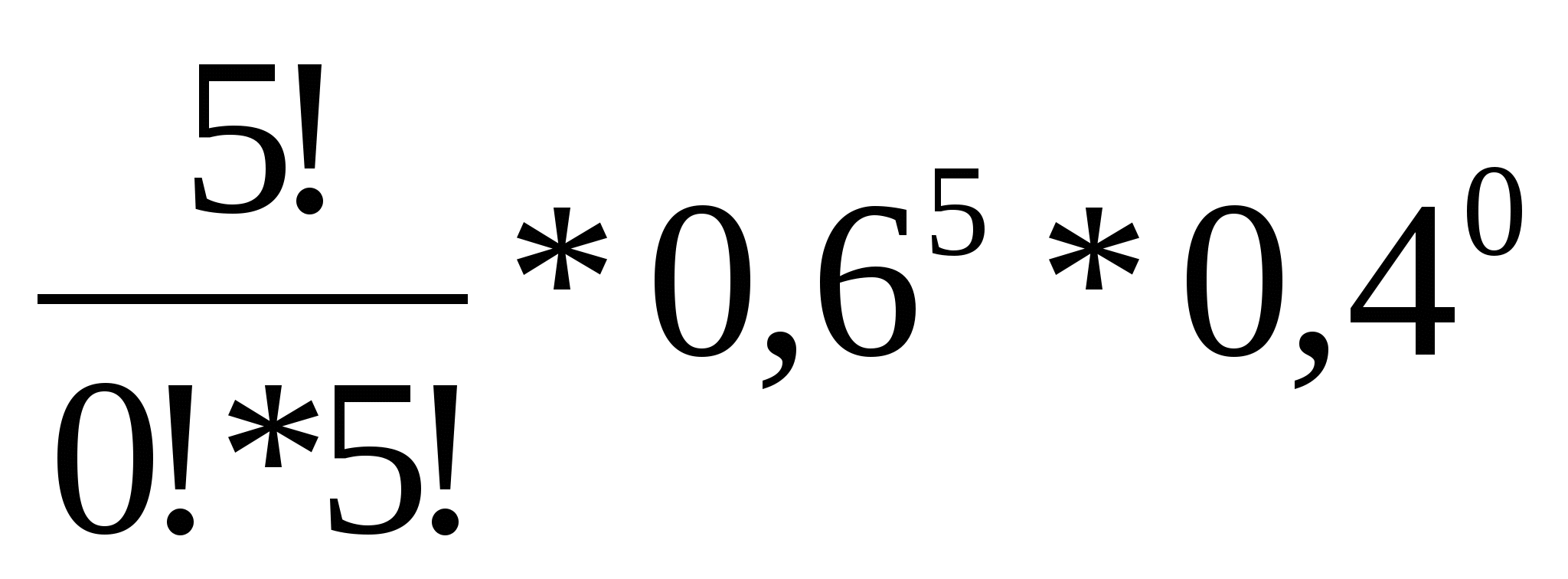 = 0,07776.
= 0,07776.
Таким образом, ряд распределения имеет вид:
Многоугольник решения имеет вид:
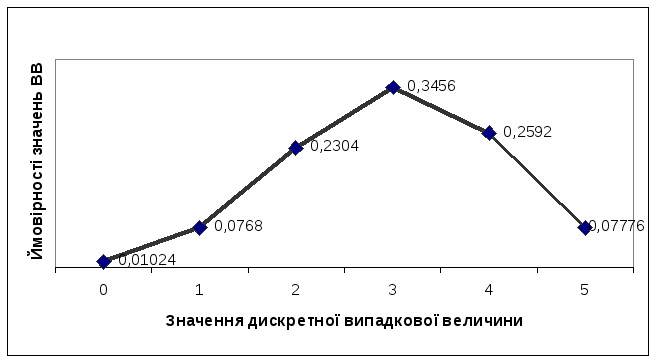
Задачи:
1. Задан ряд распределения суточного спроса на определенный продукт Х. Найти числовые характеристики этой ДСВ.
а) М (х), б) Д (х), в) G(x)
2. Дискретная случайная величина может принимать три значения: Х1, Х2, Х3. Известны математическое ожидание М(Х) и дисперсия Д(Х). Составить ЗРСВ и найти его моду.
Закрепление сформированных знаний и учений:
Закрепление полученных знаний по данной теме проводится во время самостоятельного решения заданий
1. Дискретная случайная величина может принимать два значения, причем Х1 < Х2. Известна вероятность появления меньшего значения ДСВ - Р1, математическое ожидание М(Х) и дисперсия Д(Х). Составить ЗРСВ.
2. Составить ЗРСВ Х = (количество подписанных соглашений на поставку определенной продукции в следующем месяце), если известно, что отдел маркетинга заключил "n" соглашений с известными потребителями, а по сведениям прошлого года месячную подписку получали от потребителей с вероятностью "p" от каждого.
Задачи для домашнего решения
Составить ЗРСВ Х = (количество соответствующих нормативам расчетно - платежных месячных ведомостей на зарплату за 2004 год среди "n", избранных работниками КРУ для проверки ), если известно, что в течение m месяцев бухгалтерия не учитывала при взыскании налогов наличие среди работников "чернобыльцев различных категорий.
Практические занятия 18,19
Практические работы 15,16
по теме «Составление и анализ случайных величин. Нахождение числовых характеристик.»
Цель работы: научиться составлять закон распределения случайной величины в двух формах и анализировать данные с помощью числовых характеристик.
Актуализация знаний
Фронтальный опрос
1. Дать понятие моды.
2. Виды случайных величин.
3. Свойства интегральной и локальной функции.
4. Понятие дисперсии , математического ожидания, среднеквадратичного отклонения, интервала рассеивания.
Краткие теоретические и учебно-методические материалы по теме практической работы
Формы задания случайных величин:
1. Табличная - ряд распределения. Используется и для НСВ и для ДСВ. Наиболее удобна для задания ДСВ.
Критерий правильности ЗРСВ: сумма вероятностей всех значений случайных величин равна 1.
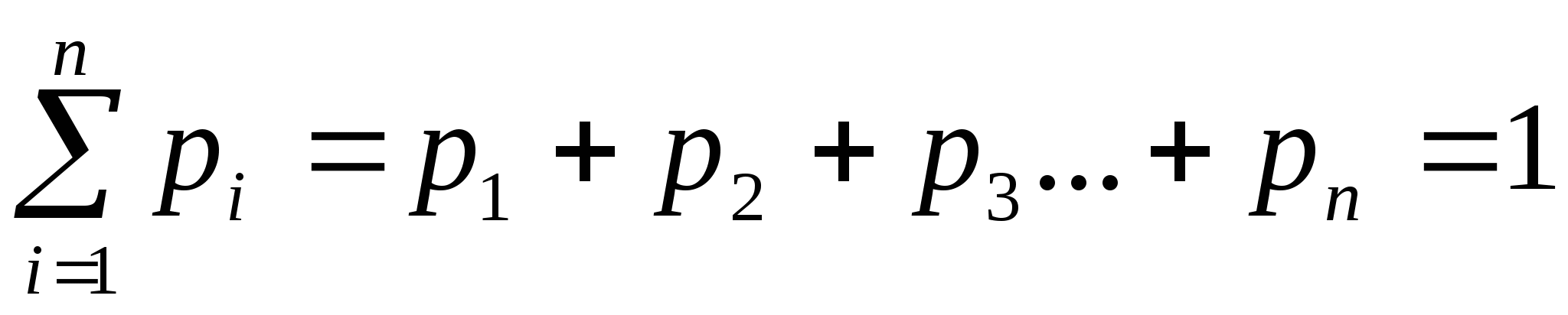
2)
(х2;х3)
р
р1
р2
...
рn
р
р1
р2
2. Графическая - полигон распределения. Используется только для ДСВ. Представляет собой ломаную, отрезки которой соединяют в системе координат точки (xi ; Pi). Практически, полигон распределения - наглядное отображение ряда распределения. Свойство полигона: он ограничен снизу осью ОХ, а сверху - прямой р=1.
1). Математическое ожидание, среднее значение распределения - это аналог центра тяжести фигуры, отдельные элементы которого имеют различную массу, аналогичную вероятностям значений СВ.
ДСВ: 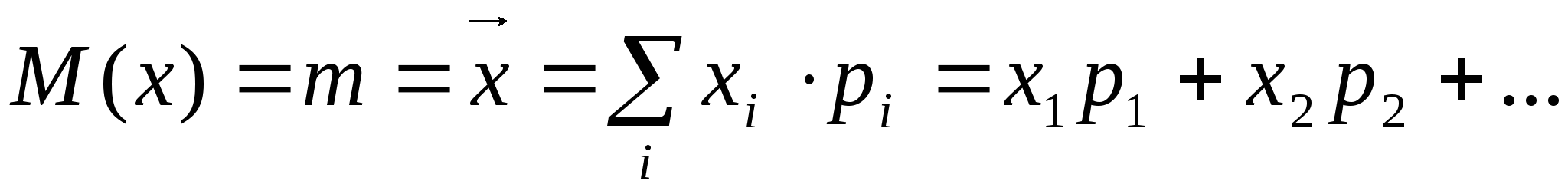
НСВ: 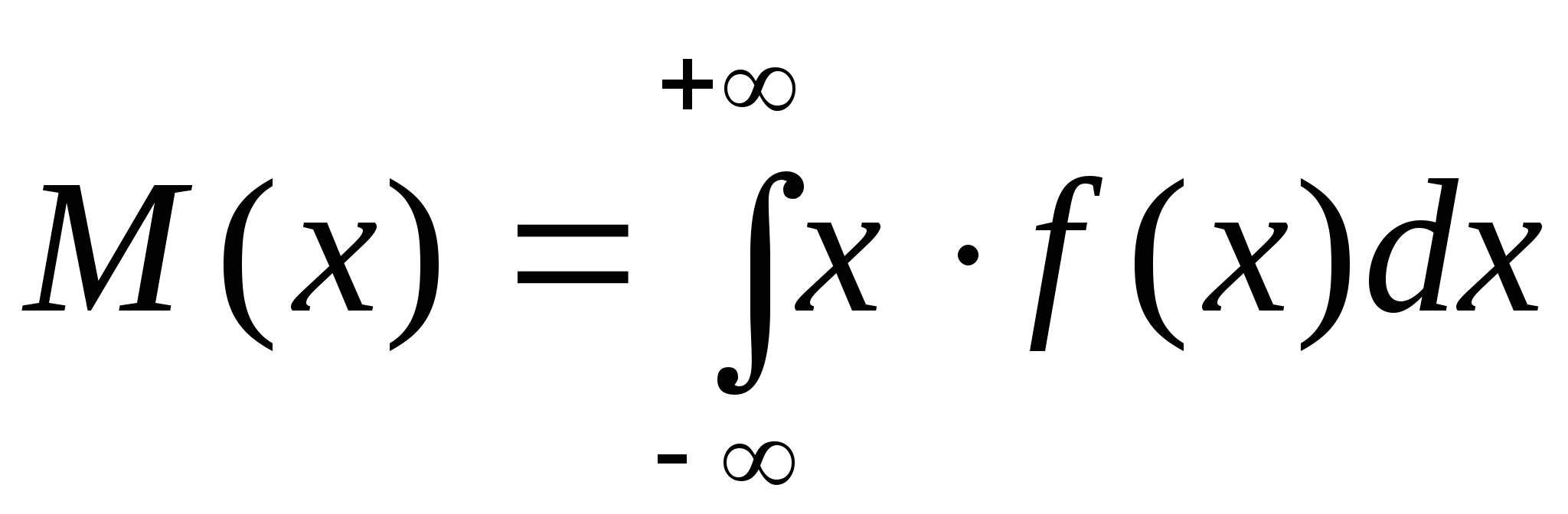
2). Дисперсия - показатель рассеяния наиболее "весомых" значений СВ возле математического ожидания; аналог площади круга наиболее весомой части фигуры с центром в математическом ожидании.
ДСВ: ![]()
НСВ: 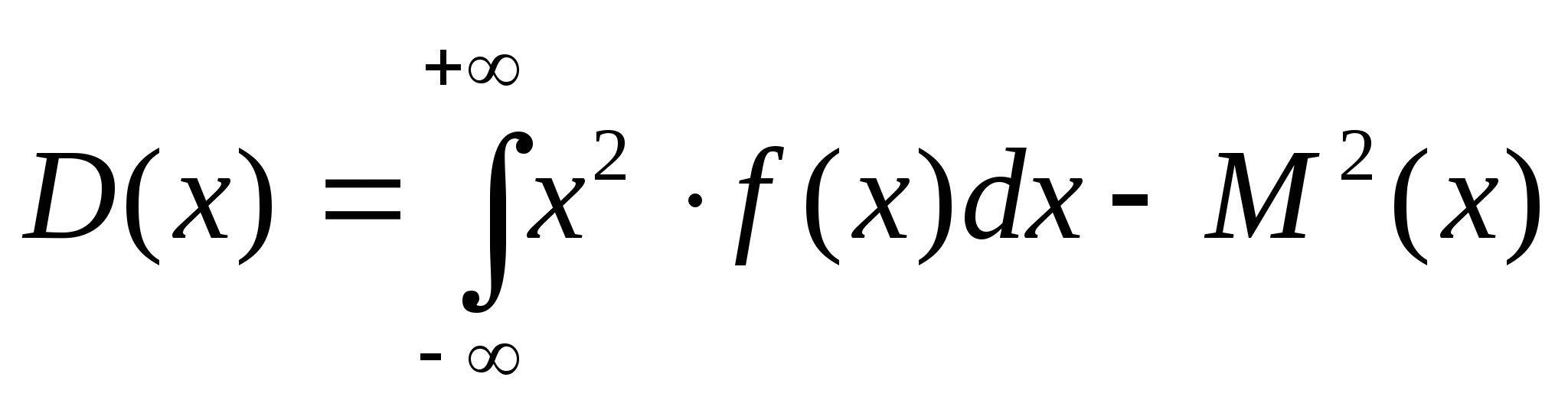
3). Среднее квадратическое
отклонение - показатель рассеивания, который является
аналогом радиуса "весомого круга", или ширины интервала
около математического ожидания.![]()
Для планирования используется наиболее вероятный
интервал рассеивания значений ВВ.![]()
4). Мода m0 - наиболее вероятное значение СВ (актуально для ДСВ).
Формирование необходимых знаний и умений
Коллективное решение и обсуждение предложенных задач
Пример 1
Вероятность появления нестандартной детали после обработки составляет 0,8. Составить закон распределения соответствия обработанных деталей и проанализировать его с помощью числовых характеристик, если задание токарю - 5 деталей.
Решение:
Количество появления нестандартной
детали после обработки -дискретная случайная величина.
Для составления закону ее распределения удобно
использовать ряд распределения , вычисляя вероятности
отдельных значений случайной величины с помощью формулы
Бернулли: ![]()
По условию задачи :n=5 , p=0,8 , тогда q=1-0,8=0,2; значения m совпадают со значениями случайной величины.
1). Х=m=0.Тогда ![]() 0,00032.
0,00032.
2). Х=m=1.Тогда ![]() 0,0064.
0,0064.
3). X=m=2. Тогда ![]() 0,0512.
0,0512.
4). Х=m=3. Тогда ![]() 0,2048.
0,2048.
5). Х=m=4. Тогда ![]() 0,4096.
0,4096.
6). Х=m=5. Тогда ![]() 0,32768.
0,32768.
Выполним проверку вычислений :
![]() 1.
1.
0,00032 + 0,0064 + 0,0512 + 0.2048 + 0,4096 + 0,32768=1,
т.е. вероятности значений случайной величины найдены верно. Получили ряд распределения:Находим числовые характеристики:
-
Математическое ожидание случайной величины:
М(Х)= ![]() = 4.
= 4.
-
Дисперсия : Д(Х)=М(Х2) - М2(Х)= 0,7936.
-
Среднеквадратичное отклонение :
![]()
![]() 0,89.
0,89.
Таким образом, наиболее весомые по
вероятности значения случайной величины будут
расположены в интервале : ( М- ![]() ; М+
; М+ ![]() ) , т.е.
) , т.е.
( 3,11 ; 4,89 ).
Примеры:
1. Вероятность появления нестандартной детали после обработки составляет "р". Составить закон распределения соответствия обработанных деталей и проанализировать его с помощью числовых характеристик, если задание токарю - "n" деталей.
2. Частично задан ряд распределения суточного
спроса на определенный продукт Х. найти интервал
доверия та моду ЗРСВ.
3. Составить и проанализировать с помощью числовых характеристик ЗРСВ Х = (количество бракованных деталей среди 6 выбранных для проверки), если известно, что выбор осуществлялся среди 12 деталей, из которых 7 были бракованные.
Закрепление сформированных знаний и учений:
Закрепление полученных знаний по данной теме проводится во время самостоятельного решения заданий.
1. Составить и проанализировать с помощью числовых характеристик ЗРСВ Х = (количество бракованных деталей среди 5 выбранных для проверки), если известно, что выбор осуществлялся среди 10 деталей, из которых 6 были именно бракованные.
2. Составить (в двух формах) и проанализировать с помощью числовых характеристик ЗРСВ Х = (количество стандартных деталей), если известно, что обработано 5 деталей, а уровень квалификации токаря предусматривает 20 - процентную вероятность появления бракованной детали.
Самостоятельная работа
Вероятность появления нестандартной детали после обработки составляет "р". Составить закон распределения соответствия обработанных деталей и проанализировать его с помощью числовых характеристик, если задание токарю - "n" деталей.
Задачи для домашнего решения
1. Задан ряд распределения суточного спроса на определенный продукт Х. Найти числовые характеристики этой дискретной случайной величины.
а) М (х), б) Д (х), в) G(x)
2. Вероятность появления нестандартной детали после обработки составляет "0,34". Составить закон распределения соответствия обработанных деталей и проанализировать его с помощью числовых характеристик, если задание токарю - "4" детали.
Практическое занятие 20
Практическая работа 17
по теме «Решение задач математической статистики»
Цель работы: научиться решать задачи математической статистики.
Актуализация знаний
- Фронтальный опрос
1. Понятие математической статистики.
2. Среднее арифметическое, среднее геометрическое.
3. Полигон частот.
- тестирование на компьютере
Краткие теоретические и учебно-методические материалы по теме практической работы
Мода - значение признака,
которая встречается чаще всего в данном ряду
распределения. Обозначается ![]() .
.
В случае, когда все значения в группе встречаются одинаково часто, считают, что группа оценок не имеет моды. (например: в группе 1,2; 1,2; 1,7; 1,7; 4,8; 4,8 моды нет).
Если два соседних значения имеют одинаковую частоту и они больше частоты какого-либо другого значения, то мода есть среднее этих двух значений. (Например, мода группы значений 1,2,3,3,3,4,4,4,5 равна 3,5) .
Если два несмежных значения в группе имеют равные частоты и они больше частот любого значения, то существуют две моды. (Например, в группе значений 7, 10, 10, 10, 20, 13, 14, 14, 14, 15, модами будут 10 и 14).
Медиана - средняя величина переменной признака, который находится в середине ряда, расположенного в порядке возрастания или убывания значений признака. Обозначается Me.
Если данные содержат нечетное число различных значений, например 9,11,15,18,20, то медиана является средним значением в случае их упорядоченности, то есть медиана равна 15.
Если данные содержат четное
число различных случаев, например 7,11,13,15, то
медиана равна среднему между двумя центральными
значениями, если они упорядочены, то есть ![]() .
.
Формирование необходимых знаний и умений
Коллективное решение и обсуждение предложенных задач
Пример 1
На протяжении 20 дней августа температура была такой:
17º, 18º, 19º, 20º, 18º, 18º, 18º, 19º, 19º, 20º, 20º, 19º, 19º, 19º, 20º,
19º, 18º, 17º, 16º, 19º.
Найти среднюю температуру по этим данным.
Решение:
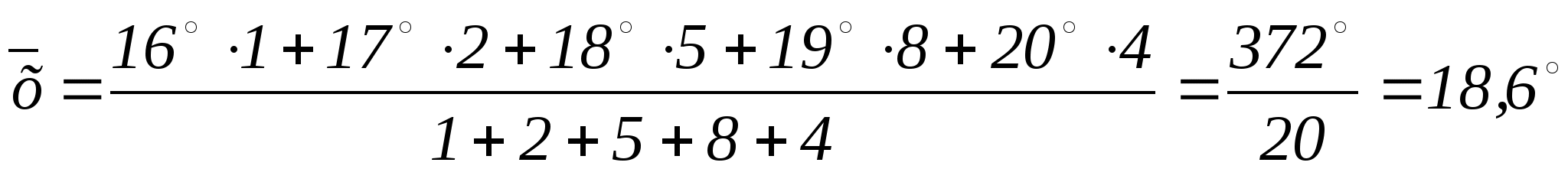
Пример 2
Найти среднее квадратичное отклонение значений 5,8,10,12,17,20.
Решение:
![]()
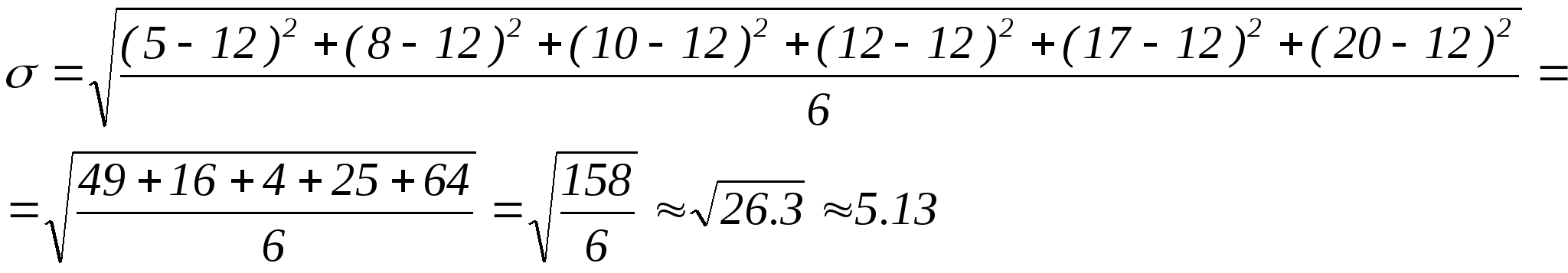
Пример 3
Найти центральные тенденции выборки:
1,3; 1,8; 1,2; 3,0; 2,1; 5; 2,4; 1,2; 3,2; 1,2; 4; 2,4.
Решение
Упорядочим выборку в порядке возрастания:
1,2; 1,2; 1,2; 1,3; 1,8; 2,1; 2,4; 2,4; 3,2; 3,8; 4; 5.
Мода m 0= 1,2
Среднее арифметическое::
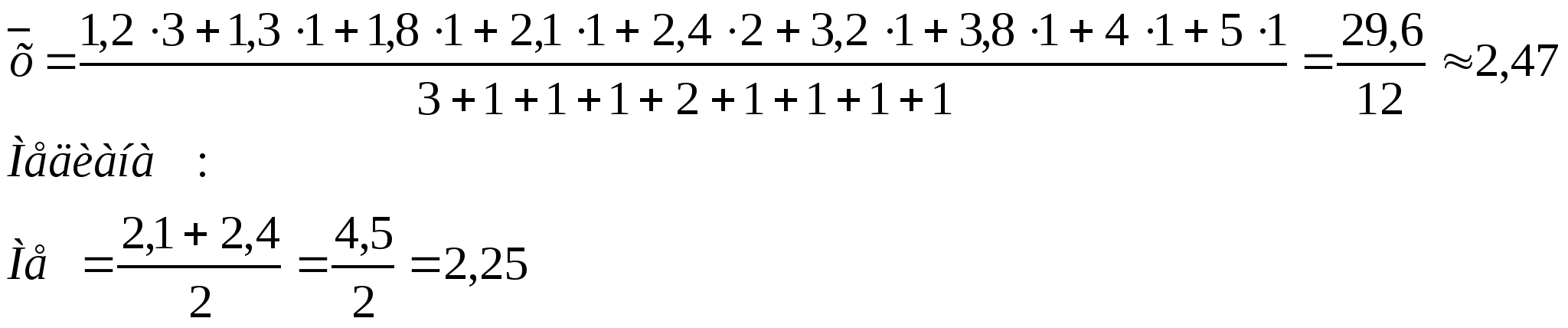
Пример 4
Задана выборка, характеризующая месячную прибыль предпринимателей (в тысячах гривен).
1. Составить вариационный ряд выборки
2. Построить гистограмму.
3. Вычислить средние значения.
1.
6, 10, 12, 11, 11, 14, 6, 8, 12, 10, 14, 8, 9, 11, 7, 7, 12, 10, 13, 16
2.
42, 57, 47, 43, 46, 53, 43, 50, 47, 49, 51, 45, 46, 50, 51, 55, 52, 47, 42, 56
3.
21, 19, 17, 23, 18, 22, 25, 20, 19, 18, 24, 21, 23, 17, 24, 25, 19, 20, 18, 22
Закрепление сформированных знаний и учений:
Закрепление полученных знаний по данной теме проводится во время самостоятельного решения заданий. Предлагаются 2 варианта.
Вариант 1
1. Для выборки, заданной вариационным рядом 2;3;1;0;-1;0;-2;5;6;5 найти моду, медиану, среднее значение, средне квадратичное отклонение. Постройте полигон частот.
2. Найти среднее значение х и среднее квадратичное отклонение. Построить гистограмму частот.
Вариант 2
1. Для выборки, заданной вариационным рядом 10;15;8;7;12;10;8;10;12;10. Найти моду, медиану, среднее значение, средне квадратичное отклонение. Постройте полигон частот.
2. Найти среднее значение х и среднее квадратичное отклонение. Построить гистограмму частот.
Задачи для домашнего решения
1. Для выборки, заданной вариационным рядом -40;-40;0;0;1;1;2;8;9;9. Найти моду, медиану, среднее значение, средне квадратичное отклонение. Постройте полигон частот.
2. . Найти среднее значение х и среднее квадратичное отклонение. Построить гистограмму частот.
Основная литература:
1. Богомолов Н.В. Практические занятия по математике. - М.: Дрофа - 2010.- 400 с.
Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. - 4-е изд., перераб. и доп. - М.: ЮНИТИ-ДАНА, 2010. - 573 с.
2. Спирина М.С. Дискретная математика: учебник для студ. учреждений сред. проф. образования / М.С. Спирина, П.А. Спирин. - М.: Издательский центр «Академия», 2010. - 368 с.
Электронные учебники:
1. Дадаян А.А. Математика: Учебник. - М.: Форум: ИНФРА-М, 2010. - 552с.;znanium.com/bookread.php?book=397662
2. В.А. Буслов, С.Л. Яковлев, Численные методы. Исследование функций. Решение уравнений; www.mat.net.ua/mat/Buslov-Yakovlev- Chislennie-metodi.htm
3. А.А. Самарский, Введение в численные методы; www.mat.net.ua/mat/Samarski-Vvedenie-chislennye- metody.htm</</u>
4. электронная библиотека по математике; www.mat.net.ua/mat/
Интернет - ресурсы:
1 Образовательный математический сайт: www.exponenta.ru;
2. Сайт учебно-методического журнала Математика: mat.1september.ru;
3. Математический портал: www.allmath.ru;
4. Сайт тесты по математике: www.mathtest.ru.