Урок геометрии на тему Векторы. Угол между векторами 9 класс

Поремская И.В., учитель математики

КГУ «СШ№2 г. Тайынша», Северо-Казахстанская область

Урок геометрии «Векторы. Угол между векторами» (9 класс).

Цель: повторить и закрепить с учащихся основные понятия, связанные с векторами, закрепить умение решать задачи, применяя теоретический материал.

Ученик должен знать: определение вектора и связанных с ним понятий, находить сумму, разность векторов.

Ученик должен уметь: применять теоретические знания при решении геометрических задач, уметь графически находить сумму, разность векторов, умножать вектор на число.

Тип урока: Комбинированный урок повторения и изучения нового материала.

Технология: Личностно-ориентированная, информационно-коммуникативная.

Методы:

• Наблюдение;

• Эвристическая беседа;

• Диалог;

• Создание ситуации успеха;

Формы: Фронтальный опрос, самостоятельная работа, индивидуальная работа.

Структура урока:

1.Организационный момент.

2. Повторение

3. Обобщение и систематизация

4. Практическое задание

5. Решение задач

6.Историческая справка

7. Изучение нового материала

8. Самостоятельная работа

9. Рефлексия

10. Домашнее задание.

Ход урокаI. Организационный момент

Цель: Настроить учащихся на эффективную работу на уроке.

Учитель приветствует учащихся, проверяет готовность класса к уроку. Настраивает учащихся на работу.

Здравствуйте, ребята. Садитесь. Сегодня у нас открытый урок, на котором присутствуют учителя.

Посмотрите на слайд. Какова же тема урока?

Учащиеся рассаживаются на свои места

На слайде изображены векторы, значит тема урока: Векторы. Угол между векторами.

II. Повторение теоретического материала

Цель:

Закрепить знания учащихся о векторах, модуле вектора и равенстве векторов

Мы сегодня на уроке повторим все понятия, все формулы, изученные по теме Векторы на плоскости.

Впервые понятие вектора появилось в трудах математика, фамилию которого вы узнаете в конце урока. При решении заданий вами будет открыта буква фамилии этого ученого.

1 задание. Распределить величины на скалярные и векторные (масса, сила, перемещение, площадь, скорость, длина, объем, время, температура, ускорение, вес)

Учащиеся на интерактивной доске классифицируют величины.

Скалярные: масса, площадь, длина, объем, время, температура.

Векторные: сила, перемещение, скорость, ускорение, вес.

III. Обобщение и систематизация

Цель:

Систематизировать знания по данной теме

2 задание. Из данных понятий выделить главное понятие и второстепенные.

Вектор, Коллинеарные векторы, Не коллинеарные векторы, Нулевой вектор, Единичный вектор, Сонаправленные векторы,

Противоположно направленные векторы, Равные векторы.

Вектор

Коллинеарные Не коллинеарные

векторы векторы

Нулевой вектор

Сонаправленные Единичный вектор

векторы

Противоположно

направленные

векторы

Равные векторы

Учащиеся данным понятиям дают определения.

Вектор - направленный отрезок.

Нулевой вектор - вектор, у которого начало совпадает с концом.

Единичный вектор- вектор длина которого равна 1.

Коллинеарные векторы - это ненулевые векторы, которые лежат на параллельных прямых или на одной прямой.

В противном случае векторы называют неколлинеарными.

Векторы называются сонаправленными, если они коллинеарные и имеют одинаковое направление.

Векторы называются противоположно

направленными, если они коллинеарные

и имеют противоположные направления.

Все определения повторили, а теперь выполним следующее задание. Установите соответствие между понятием и выполненным чертежом.

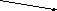
Не коллинеарные векторы

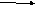
коллинеарные векторы

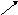
Сонаправленные векторы

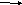
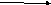
Противоположно направленные векторы

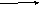
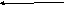
Равные векторы

Нулевой вектор

Учитель задает вопросы.

Какие действия выполняются над векторами?

Сложение векторов

Вычитание векторов

Умножение вектора на число

Как можно сложить два вектора?

По правилу треугольника и по правилу параллелограмма

IV. Практическое задание

Цель:

Повторить и закрепить умение выполнять сложение, вычитание векторов, умножение вектора на число

На доске изображены два неколлинеарных вектора. Нужно сложить их двумя способами.

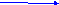
1 способ. Правило треугольника. Вектор переносим параллельным переносом так, чтобы начало вектора совпало с концом вектора . Суммой векторов и будет такой вектор , начало которого совпадает с началом вектора , а конец с концом вектора .

А теперь нужно сложить эти же векторы по правилу параллелограмма.

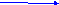
2 способ. Правило параллелограмма. Вектор переносим параллельным переносом так, чтобы начало вектора совпало с началом вектора . Дополняем до параллелограмма. Суммой векторов и будет такой вектор , диагональ параллелограмма, начало которого совпадает с началом векторов и .

Следующее задание: вычесть эти векторы.

Вектор переносим параллельным переносом так, чтобы начало вектора совпало с началом вектора . Разностью векторов и будет такой вектор начало которого совпадает с началом вектора , а конец с концом вектора .

Повторение формул

Вспомним формулы, которые будут необходимы при решении задач. На доске разбросаны начало и конец формул. Ваша задача собрать правильно все формулы.

А(x_1;у₁), В(х₂;у₂), (а₁;а₂), (в₁;в₂).

= (х₂-х₁; у₂-у₁) ǀǀ=√а₁²+а₂²

+ = (а₁+в₁; а₂+в₂)

- = (а₁-в₁; а₂-в₂)

k= (kв_1;kв₂)

V. Решение задач

Цель:

Закрепить навыки учащихся выполнять действия над векторами в координатах

Задача №1

Дано:

(4; 8) , (-3; 5)

+ =?

Учащиеся в ходе решения проговаривают правила.

+ = (4;8)+(-3;5) = (1;13)

Задача№2

Дано:

(4; 8) , (-3; 5)

- =?

Учащиеся в ходе решения проговаривают правила.

- = (4;8)-(-3;5) = (7;3)

Задача№3

Дано:

(4; 8) , (-3; 5)

ǀ3+4 ǀ =?

3+4 = 3(4;8)+4(-3;5) = (12;24)+

(-12;20) = (0;44);

ǀ3+4 ǀ = √0²+44² = √44

Задача№4

(-6; 8)

ǀλǀ = 5

λ -?

λ= λ(-6;8) = (-6λ; 8λ)

ǀλǀ=√(-6λ) ²+( 8λ)² =√36 λ ²+64 λ ² =10ǀλǀ 10ǀλǀ =5

ǀλǀ = λ=; λ=- Ответ: при полученных значениях λ=; λ=- длина вектора ǀλǀ = 5

Задача№5

(1; -1) , (-2; m)

и - коллинеарные

m -?

У коллинеарных векторов соответствующие координаты пропорциональны

= m= = 2

Ответ: при m=2 векторы и - коллинеарные

Задача№6

А(6; -2), В(-4; -7), С(0; -8), К(5;0)

АС-? КВ-?

АС(-6;-6)

КВ(-9;-7)

VI. Историческая справка

Цель:

Ознакомить учащихся с биографией ученого математика

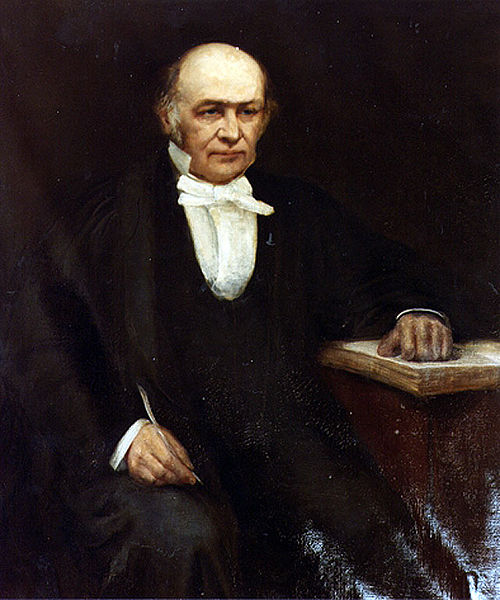
4 августа 1805 - 2 сентября 1865) - выдающийся ирландский математик, механик и физик XIX века.

Уже в детстве мальчик проявил необыкновенные дарования. В 7 лет он знал древнееврейский язык; в 12 - под руководством дяди Джеймса, хорошего лингвиста, знал уже 12 языков и среди них персидский, арабский. В 13 лет он написал руководство по сирийской грамматике.

После языков настала пора увлечения математикой. Двумя годами раньше Гамильтону попался латинский перевод «Начал» Евклида, и он детально изучил это сочинение; в 13 лет он прочел «Универсальную арифметику» Ньютона; в 16 лет - большую часть «Математических начал натуральной философии» Ньютона, в 17 лет - начал изучение «Небесной механики» Лапласа</</u>.

VII. Изучение нового материала

Цель: ввести понятие угол между векторами

Алгоритм:

1. Построить два неколлинеарных вектора

2. Обозначить их а и в

3. Перенести векторы так, чтобы они выходили из одной точки

4. При помощи транспортира измерить угол между этими векторами

Сделать вывод:

Углом между двумя векторами называется угол между векторами выходящими из одной точки.

1. Угол между векторами.

а)

 (, ) = 30°

30°

б)

120°  (, ) = 120°

в)

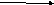
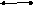
 (, ) = 180°

2. Если векторы сонаправлены, то

 (, ) = 0°

VIII. Самостоятельная работа

Цель:

Проверить знания учащихся

Вариант №1

1. Если два коллинеарных вектора направлены в разные стороны, то они - __________________.

2. Любая точка плоскости является __________________.

3. _______________ или модулем ненулевого вектора называется длина этого отрезка.

4. Ненулевые вектора называются___________________, если они лежат либо на одной прямой, либо на параллельных прямых.

5. Вектор разности выходит из ____________вектора ___________ и приходить в ________________ вектора _____________.

6. Отрезок, для которого указано, какая из его граничных точек считается началом, какая - концом, называется ____________.

7. Если два коллинеарных вектора направлены в одну сторону, то они - ______________.

8. Два вектора называются _______________ если они сонаправлены и их длины равны.

9. От любой точки можно отложить вектор равный данному и притом только __________.

10. Нулевой вектор _________ коллинеарным любому вектору.

11. По правилу треугольника вектор суммы выходит их _____________ первого вектора и заканчивается в _________ второго.

Самостоятельно выполняют тест на заполнение пропусков

Вариант №2

1. Отрезок, для которого указано, какая из его граничных точек считается началом, какая - концом, называется ____________.

2. Любая точка плоскости является __________________.

3. ____________ или модулем ненулевого вектора называется длина этого отрезка.

4. Ненулевые вектора называются __________________, если они лежат либо на одной прямой, либо на параллельных прямых.

5. Нулевой вектор _____________ коллинеарным любому вектору.

6. Если два коллинеарных вектора направлены в одну сторону, то они - ______________.

7. Если два коллинеарных вектора направлены в разные стороны, то они - ______________.

8. Два вектора называются _______________ если они сонаправлены и их длины равны.

9. От любой точки можно отложить вектор равный данному и притом только __________.

10. По правилу треугольника вектор суммы выходит их ______________ первого вектора и заканчивается в _______________ второго.

11. Вектор разности выходит из ____________вектора ___________ и приходить в ________________ вектора ____________.

IX. Рефлексия

- У каждого из вас ребята на столе карточки. Уходя с урока, прикрепите на доску одну их них.

урок был полезен для меня,

я много с пользой и хорошо работал на уроке, получил заслуженную оценку, я понимал всё,

о чем говорилось и

что делалось на уроке.

Урок был интересен,

я принимал активное

участие, урок был

в определенной степени

полезен для меня,

я отвечал на вопросы,

выполнил некоторые

задания, мне было

достаточно комфортно.

Пользы от урока

я получил мало,

я не очень понимаю,

о чем идет речь, мне это

не очень нужно,

домашнее задание я

не смогу сделать, мне

это не интересно и

всё не понятно.

Ребята проводят анализ своей деятельности на уроке

X. Д/З

Повторить §6 №66

Записывают в дневники домашнее задание

Маршрутный лист

Г

А теперь нужно сложить эти же векторы по правилу параллелограмма.

А

Нужно вычесть эти векторы.

М

Задача №1

(4; 8) , (-3; 5)

+ =?

И

Задача№2

(4; 8) , (-3; 5)

- =?

Л

Задача№3

(4; 8) , (-3; 5)

׀3+4 ׀ =?

Ь

Задача№4

(-6; 8)

׀λ׀ = 5

λ -?

Т

Задача№5

(1; -1) , (-2; m)

и - коллинеарные

m -?

О

Задача№6

А(6; -2), В(-4; -7), С(0; -8), К(5;0)

АС-? КВ-?

Н