Урок алгебры в 10 классе «Производная и её применение»

Урок алгебры в 10 классе «Производная и её применение»

Цель:

• закрепление знаний учащихся о производной и её приложении к исследованию свойств функций;

• проверить сформированность у учащихся умений устанавливать характер изменения функции по знаку производной; выделять точки, подозрительные на экстремум;

• установить, могут ли учащиеся применять метод дифференциального исчисления для решения задач;

• проверить сформированность качества знаний: глубину, оперативность мышления, прочность.

Тип урока: обобщающий урок.

Форма проведения: урок-зачёт.

Оформление: компьютер, проектор, презентация

Ход урока:

I. Организационный момент

Вступительное слово учителя:

а) сообщение целей (слайд 2);

б) часто можно услышать, что математики и физики - это лирики. Софья Ковалевская говорила: «Математик должен быть поэтом в душе». Послушайте слова из учительского фольклора, дающие алгоритм нахождения производной (слайд 3):

В данной функции от х,

Наречённой игреком.

у = f(x)

Вы фиксируете х,

Отмечая индексом.

x_o; f(x_o)

Придаёте вы ему

Тотчас приращение

x_o + ∆х

Тем у функции самой

Вызвав изменение.

∆y = f(x_o + ∆х) - f(x_o)

Приращений тех теперь

Взявши отношение

∆y

∆х

Пробуждаете к нулю

У ∆х стремление.

∆х  0

Предел такого отношения

Вычисляется

Он производною

В науке называется.

y ′ =
II. Математический диктант

За каждый правильный ответ - 1 балл. За этот вид работы учащиеся имеют возможность получить до 14 баллов. Работу выполняют на отдельных листочках. Вопросы на слайде 4.

1. Запишите определение производной с помощью математических символов.

2. Ответьте на вопрос: «Когда функция дифференцируема в некоторой точке?»

3. Запишите четыре правила дифференцирования.

4. Чему равна производная функции у = х ⁿ?

5. Найдите производную функции у = sin x - 2 cos x.

6. Найдите производную функции у = 3х⁴ - х³ + х² - 7х + 1.

7. Что можно сказать о производной функции в точке экстремума?

8. Найдите производную функции у = (2х - 5)³ + cos 2x.

9. В чём заключается геометрический смысл производной?

10. В чём заключается механический смысл производной?

11. Запишите уравнение касательной в общем виде.

III. Сведения из истории

Материал можно взять из предметной газеты, № 2за 2000 год, стр. 19.

IV. Теоретический конкурс

Учащиеся рассказывают о различных случаях применения производной. Например, раскрывают такие вопросы:

1. Написание уравнения касательной.

2. Нахождение критических точек.

3. Нахождение промежутков возрастания и убывания.

4. Нахождение точек экстремума.

5. Нахождение наибольшего и наименьшего значения функции на отрезке.

6. При решении задач на оптимум.

7. При исследовании свойств функции и построении графиков.

Учащиеся имеют возможность за каждый раскрытый вопрос получить до 2 баллов. За дополнение, исправление - 1 балл.

V. Конкурс «Задачи-картинки»

Задания и ответы к ним приготовлены на слайдах 5 - 10 презентации. Учащиеся записывают номер того ответа, который считают правильным. Работают на отдельных листочках. За этот вид работы имеют возможность получить 6 баллов.

1. у

Какое значение принимает производная функции у = f(x) в точке А?

1) f ′ (x) = 0. 2) f ′ (x) < 0. 3) f ′ (x) > 0.А у = f(x)



0 х

2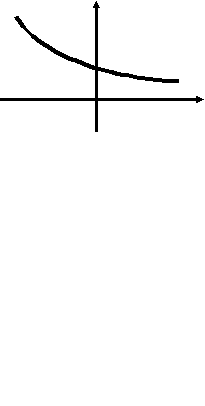. у = f(x) у

Какое значение принимает производная функции у = f(x) в точке В?

1) f ′ (x) = 0. 2) f ′ (x) < 0. 3) f ′ (x) > 0.

В 

0 х

3. у

у = f(x)

Назовите промежутки убывания функции у = f(x).

1) 0 < x <3. 2) 0 < x < 2. 3) x > 2.

1

-1 0 1 2 3 4 5 6 7 х

Назовите промежутки, на которых производная функции у = f(x) положительна.

1) x < 0. 2) x > 0. 3) - ∞ < x < + ∞.у

4. у = f(x)

0 х

5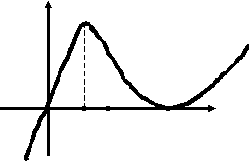. у

Назовите точки, в которых производная функции у = f(x) равна нулю.

1) ; 1. 2) 0; 1. 3) 0;1.у = f(x)

0 1 х

у у = f(x)

6.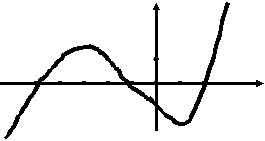

Назовите промежутки возрастания функции у = f(x) , если график её производной имеет вид.

1) (- ∞; - 3]; [1; + ∞). 2) [- 3; 1].

3) [- 5; - 1]; [2; + ∞).

1

-5 -4 -3 -2 -1 0 1 2 х

VI. Конкурс «Верно, неверно»

Задание выполняется письменно на отдельном листочке. Если учащиеся согласны с утверждением, то ставят знак «+», а если не согласны, то ставят знак «-». Учащиеся имеют возможность заработать до 11 баллов. (слайд 11)

1. В точке возрастания функции её производная больше нуля.

2. Если производная функции в некоторой точке равна нулю, то в этой точке она имеет экстремум.

3. х_о - точка максимума функции у = f(x), если для всех х из окрестности точки х_о выполняется неравенство f (x) ≤ f (x_o).

4. Если функция имеет производную на некотором промежутке, то она непрерывна на этом промежутке.

5. В точках экстремума касательные необязательно параллельны оси абсцисс.

6. Если производная функции при переходе через критическую точку меняет знак с «+» на «-», то это - точка минимума.

7. Если при переходе через критическую точку производная не меняет свой знак, то эта точка не является точкой экстремума.

8. Если угловой коэффициент касательной к графику функции в точке х_о равен 0,5, то f ′ (x_о) = 0,5.

9. Для функции у = точка х = 0 является критической.

10. Касательная к графику непрерывной функции существует в любой точке.

VII. Промежуточный итог

Оцениваются следующие виды работы:

1. Математический диктант - 14 баллов.

2. Теоретический конкурс - 2 балла.

3. Конкурс «Задачи-картинки» - 6 баллов.

4. Конкурс «Верно, неверно» - 11 баллов.

Учащиеся имели возможность набрать 31 балл и выше. При выставлении оценок используется следующая шкала: 31 балл и выше - оценка «5»;

24 - 30 баллов - оценка «4»;

16 - 23 балла - оценка «3»;

меньше 16 баллов - оценка «2».

VIII. «Думай и соображай»

1. Найдите соответствие между функцией и её производной.

Это задание учащиеся выполняют письменно в тетрадях, затем - взаимопроверка и обсуждение. (слайд 12)

Ответ: 1  4; 2 5; 3  2; 4  3; 5  1.

2. Заполните таблицу (слайд 13):

Это задание учащиеся выполняют письменно в тетрадях, затем - самопроверка и обсуждение.

IX. Прочитайте график (слайд 14)

Учащиеся проводят по общей схеме исследование функции, заданной графиком. Это задание выполняется устно.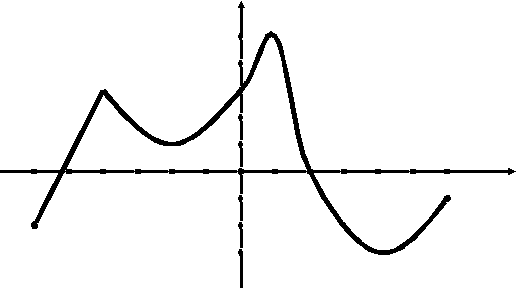у

5

4

3

2

1

-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 х

-2

-3

Х. «Думай и соображай» (слайд 15)

Три ученика решали задачу: «Исследуйте функцию f(x) = х⁴ - 2х² - 3 и постройте её график». Каждый из них выполнил исследование функции, и результаты занёс в таблицу. Вот что получилось:

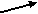
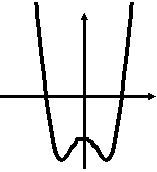
Но график каждым был построен по-разном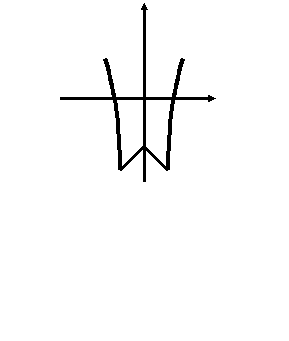у.

у у у

о х 0 х 0 х

а) б) в)

1. Почему у учащихся получились различные графики для одной и той же функции?

2. Какой из представленных графиков является правильно построенным? Ответ объясните.

XI. Решение задачи

Задачу ученики решают в тетрадях, один ученик с подробными комментариями у доски. Условие задачи на слайде 16.

Число 144 разложили на два отрицательных множителя так, что сумма их оказалась наибольшей из возможных. Найдите эти множители.

XII. Самостоятельная работа (слайд 17)

Задания дифференцированные. Оценивается каждый учащийся.

1. Найдите число, которое, будучи сложено со своим квадратом, даёт наименьшую сумму.

2. Исследуйте функцию у = 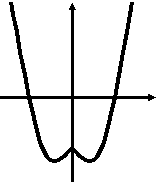и постройте её график.

3. Найдите значение функции f(x) = 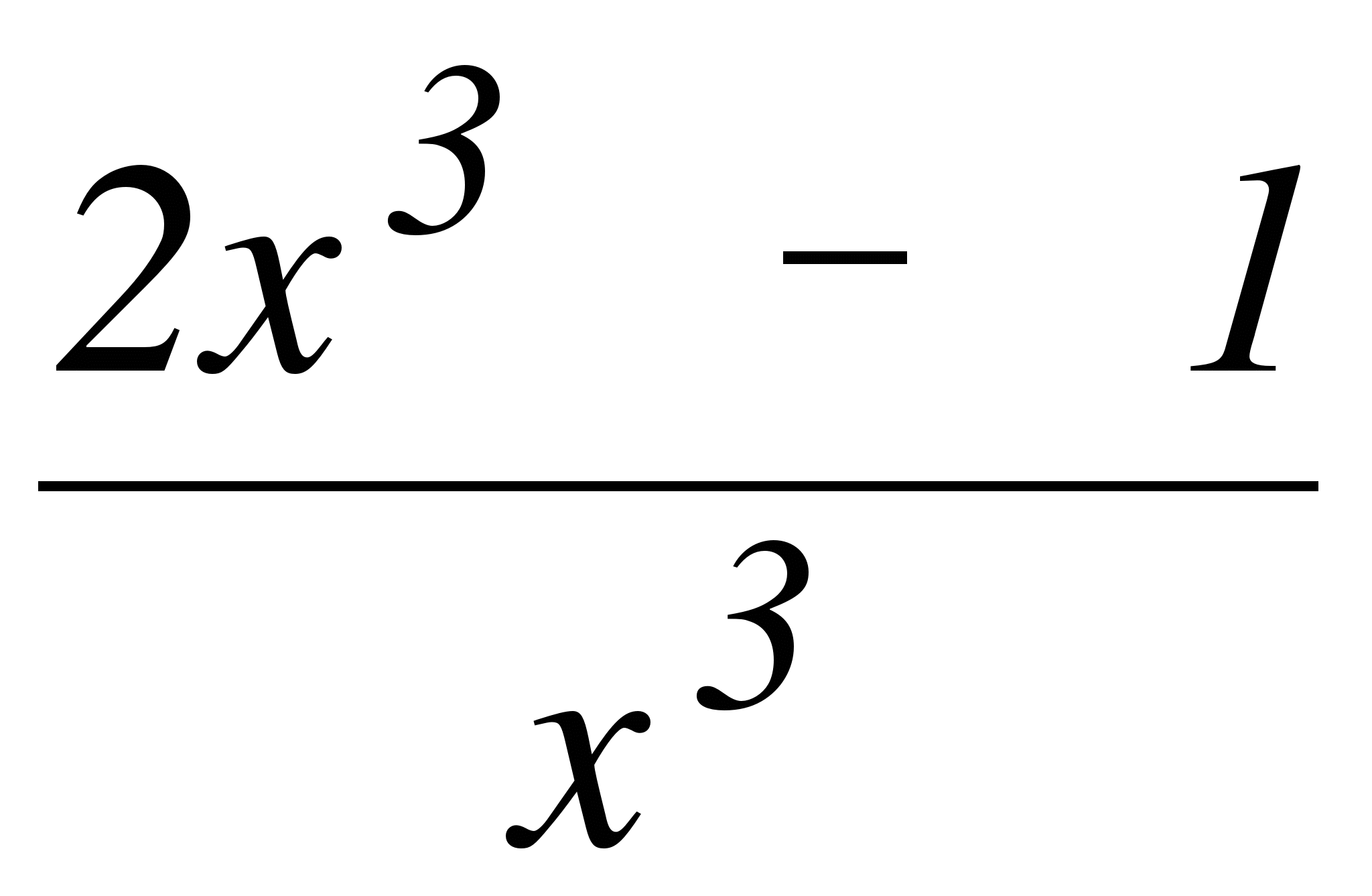в точках экстремума.

4. Найдите промежутки возрастания и убывания функции f(x) =х⁴ - 8х².

5. Найдите критические точки функции f(x) = х³ + .

6. Напишите уравнение касательной к графику функции f(x) = х³ - х в точке х_о = 2.

7. На отрезке [- 4; 3] постройте график непрерывной функции f(x), пользуясь данными, приведёнными в таблице. Учесть, что f(0) = 2.

XIII. Итог урока

а) Объявляются оценки.

б) Оценки за самостоятельную работу объявляются на следующем уроке.