Менелай Александрийский (, I в.) - древнегреческий математик</ и астроном. Автор работ по сферической тригонометрии: написал 6 книг о вычислении хорд и 3 книги "Сферики'', сохранившиеся в арабском переводе. Для получения формул сферической тригонометрии использовал теорему, известную сегодня как теорема Менелая.

Теорема Менелая. Пусть прямая пересекает треугольник , причем - точка ее пересечения со стороной , - точка ее пересечения со стороной , и - точка ее пересечения с продолжением стороны . Тогда

Доказательство. Проведем через точку прямую, параллельную . Обозначим через ее точку пересечения с прямой .

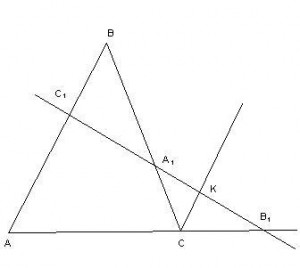
Треугольники и подобны (). Следовательно,

Треугольники и также подобны (). Значит,

Из каждого равенства выразим :

откуда

что и требовалось доказать.

Теорема (обратная теорема Менелая). Пусть дан треугольник . Пусть точка лежит на стороне , точка - на стороне , а точка - на продолжении стороны , причем выполняется соотношение

Тогда точки и лежат на одной прямой.

Доказательство. Заметим для начала, что , поскольку, по условию, это выражение равно . Следовательно, прямые и не параллельны.

Проведем прямую через точки и . Она пересечет прямую в некоторой точке . Для точек и справедлива теорема Менелая, так что

Отсюда следует, что

Из этого равенства следует, что обе точки и лежат на продолжении отрезка за одну и ту же точку, ибо правее данное отношение меньше , а левее оно строго больше . Пусть . Тогда, учитывая, что и , перепишем полученное равенство в виде

Из равенства следует, что , и доказано, что точка , совпадающая с , лежит на прямой .

Замечание. Теоремы Менелая (прямая и обратная) верны также и в том случае, когда все три точки лежат на продолжениях сторон треугольника . То есть справедлива следующая

Теорема. Пусть дан треугольник . Точки лежат на продолжениях сторон и соответственно. Три точки и лежат на одной прямой тогда и только тогда, когда выполняется равенство

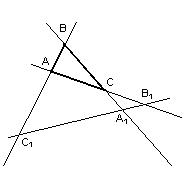Доказательство этой теоремы точно такое же, как и доказательство, приведенное выше.

Источники: В.В. Ткачук, "Математика абитуриенту", М.: Изд-во МЦНМО, 2004.

Я.П. Понарин, "Элементарная геометрия. Т.1. Планиметрия, преобразования плоскости", М.: Изд-во МЦНМО, 2004.

Введение.

Мой реферат посвящен применению подобия к доказательству теорем и решению задач, а именно глубоко изучить обобщение теоремы Фалеса, теоремы Чевы и Менелая, которые не изучаются в школьной программе. Теме подобия, которая проходится в восьмом классе, отведено всего лишь 19 часов, что недостаточно для изучения этой темы более углубленно. В тему подобия входят: определение подобных треугольников, признаки подобия, отношение площадей подобных треугольников, средняя линия треугольника, пропорциональные отрезки и т.д.

Источники информации:

Дополнительные главы по геометрии 8 класса (Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, С. А. Шестаков, И. И. Юдина) - настоящее пособие является дополнением к учебнику `Геометрия, 7-9` авторов Л.С.Атанасяна, В.Ф.Бутузова и др. (М.: Просвещение, 1990 и последующие издания). Оно полностью соответствует программе углубленного изучения математики.

Сайты:

festival.1september.ru

www.problems.ru

Вывод.

С помощью обобщения теоремы Фалеса, теорем Чевы и Менелая, не изучаемых в школьной программе, можно быстрее и легче доказывать определенные теоремы и решать более широкий круг задач. Я смогла доказать такие теоремы: теорема о пропорциональных отрезках (с помощью обобщения теоремы Фалеса), теоремы о пересечении медиан, высот и биссектрис треугольника в одной точке (воспользовалась теоремами Чевы и Менелая).

Историческая справка

Теорема Менелая - это классическая теорема аффинной геометрии. Эта теорема доказывается в третьей книге "Сферики" древнегреческого математика и астронома Менелая Александрийского (ок. 100 г. н.э.). Менелай сначала доказывает теорему для плоского случая, а потом центральным проектированием переносит её на сферу. Возможно, что плоский случай теоремы рассматривался ранее в несохранившихся "Поризмах" Евклида.

Сферическая теорема Менелая была основным средством, с помощью которого решались разнообразные прикладные задачи позднеантичной и средневековой астрономии и геодезии. Ей посвящён ряд сочинений под названием "Книга о фигуре секущих", составленных такими математиками средневекового Востока, как Сабит ибн Кора (836 - 901, астроном, математик, механик и врач), ан-Насави (1010 - 1075, газневидский математик и астроном), ал-Магриби (1220 - 1283, математик и астроном государства Хулагу), Абу Саид ибн Мухаммад ибн Абд-ал-Джалил ас-Сиджизи (951 - 1024, газневидский математик и астроном), Хусам ад-Дин Али ибн Фадлаллах ас-Салар аш-Шами (ум. 1262, среднеазиатский математик и астроном Хорезшахов), Абу Мухаммад Джабир ибн Афлах ал-Ишбили (первая половина 12 в., западноарабский математик и астроном), Абу Джафар Мухаммад ибн Мухаммад Насир ад-Дин ат-Туси (1201 - 1274, персидский математик, механик и астроном).

В начале нашей исследовательской работы мы поставили проблему - Зачем нужна математика? В ходе изучения литературы и материалов сети интернет мы выяснили, что изначально математика возникла из повседневных нужд человека (подсчеты, измерения) и многие годы служила мощным инструментом познания окружающего мира. Значит, если бы математические знания не передавались из поколения в поколение люди бы надолго застряли на уровне пещерного человека. В ходе проведения экспериментов мы выяснили, что полученные в школе знания очень помогают при решении практических задач с которыми мы сталкиваемся постоянно. Проведенные нами статистические исследования помогли убедиться в правильности выдвинутой гипотезы: математические знания полученные в школе применимы в жизни. Теоретическая значимость нашей работы заключается в том, что познакомившись с нашим исследованием, многие ученики, на вопрос о необходимости изучать математику, ответят положительно. Практическая значимость ее в том, что она может быть использована школьниками для повышения своего образовательного уровня, а также научить применять полученные в школе знания на практике, что сегодня очень актуально.

Введение

Я хочу изучить треугольник Рёло , потому что мне стала интересна его история. Если в древние времена наиболее широко применялся прямоугольный треугольник Пифагора, то в настоящий момент людей больше интересуют необычные свойства треугольника Рёло.

Цель моей работы - выяснить, что такое треугольник Рёло, узнать его историю и где он применяется.

Для этого поставлены задачи:

1.Узнать что такое треугольник Рёло

2.Узнать историю Треугольника Рёло

3.Построить треугольник Рёло самостоятельно

4.Узнать где используется треугольник Рёло

Гипотеза

Мне кажется, что Треугольник Рёло является ненужным механизмом в истории человечества. В конце работы я узнаю, прав я или нет. Заключение.

Я рассмотрел применение треугольника Рело в некоторых архитектурных строениях, механических устройствах, в автомобильных двигателях.

Я считаю, что изобретенная крышка люка для рекуперированной воды в Сан-Франциско, является очень интересной для человечества. За счет своей формы, такая крышка никогда не перевернется. Если бы архитекторы пересмотрели наши канализационные люки, и взяли бы для примера такую крышку, то можно было бы избежать множество трагических ситуаций, когда люди падали в канализационные люки.

Поиски альтернативных видов топлива для автомобилей заставил вновь обратить внимание на роторно-поршневой двигатель Ванкеля. Разработчики Mazda уверяют, что по природе своей роторно-поршневой агрегат гораздо лучше приспособлен для работы на водороде, нежели традиционные моторы. По прогнозам специалистов, уже к 2025 году более четверти мирового автопарка будет использовать в качестве топлива водород. Сколько из этого количества придется на традиционные ДВС и как будет меняться пропорция по мере удешевления себестоимости производства компонентов привода на топливных элементах? Увидим в ближайшие годы.

Я опровергнул свою гипотезу, так как Треугольник Рёло используется во многих механизмах. Я думаю, что он будет использоваться и в будущем.

.