- Учителю
- Урок по математике для 5 класса «Объёмы. Объем прямоугольного параллелепипеда»
Урок по математике для 5 класса «Объёмы. Объем прямоугольного параллелепипеда»
Предмет: математика
Класс: 5
Тема урока: «Объемы. Объем прямоугольного параллелепипеда»
Базовый учебник: Математика 5 класс. В.Я. Виленкин, В.И. Жохов М.: Мнемозина, 2011г
Цель урока: дать учащимся понятие объема; научить находить объем прямоугольного параллелепипеда.
Задачи:
Обучающие:
-
сформировать понятие объема;
-
помочь учащимся вывести формулу для нахождения объема прямоугольного параллелепипеда и куба;
-
научить вычислять объем прямоугольного параллелепипеда и куба;
-
научить переводить одни единицы объема в другие;
-
совершенствовать вычислительные навыки.
Развивающие:
-
развитие математической речи (устной и письменной);
-
развитие внимания, логического мышления;
-
научить анализировать, сравнивать, обобщать, делать выводы.
Воспитательные:
-
активизировать познавательную деятельность учащихся;
-
развивать навыки самостоятельной работы при выполнении различных заданий на уроке;
-
демонстрация значимости математических знаний в практической деятельности;
-
воспитывать аккуратность, дисциплинированность.
Тип урока: изложение нового материала.
Формы работы учащихся: фронтальная, индивидуальная.
Необходимое оборудование: персональный компьютер, интерактивная доска или проектор и экран, презентация «Объемы. Объем прямоугольного параллелепипеда».
План урока
1. Организационный момент 1 мин.
2. Устный счёт (Самостоятельная работа) 7 мин.
3. Сообщение темы урока 1 мин.
4. Изложение нового материала 10 мин.
5. Физкультминутка 1 мин.
6. Закрепление нового материала 15 мин.
7. Повторение изученного материала 3 мин.
8. Решение комбинаторной задачи 5 мин.
9. Домашнее задание. 1 мин.
10. Подведение итогов урока 1 мин.
ХОД УРОКА
-
Организационный момент. (1 мин)
Взаимное приветствие учителя и учеников, проверка подготовки к уроку, проверка отсутствующих.
-
Устный счёт. (7 мин)
1. Блиц- опрос Слайд №1
Р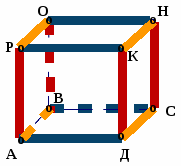 ассмотрите рисунок и назовите пропущенные слова:
ассмотрите рисунок и назовите пропущенные слова:
- АВСДРОНК - это…(прямоугольный параллелепипед)
- Точка Д - его… (вершина)
- Отрезок АВ - его…(ребро)
- Прямоугольник АВСД - его…(грань)
Назовите равные ребра прямоугольного параллелепипеда
- АВ = СД = КН = РО
- АД = РК = ОН = ВС
- АР = ДК = СН = ВО
Найдите площадь фигуры Слайд №2
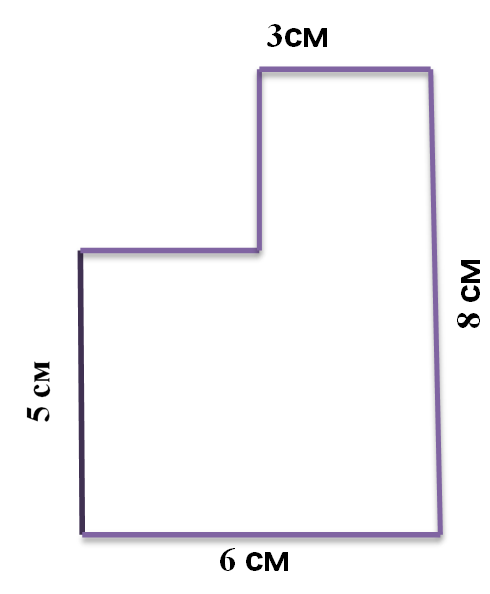
S = 5 6 + 3 3 = 39 см2 или
S = 6 8 - 3 3 = 39 см2
2. Самостоятельная работа.
Вариант I
Вычисли площадь поверхности каждого прямоугольного параллелепипеда.
Решение:
S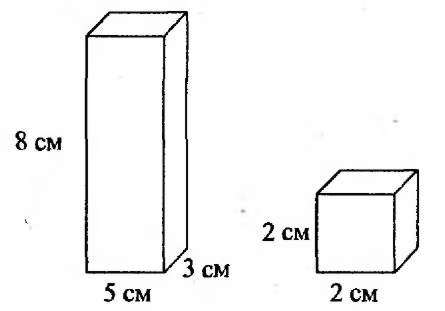 1=582+532+832=80+30+48 =158 (см2)
1=582+532+832=80+30+48 =158 (см2)
S2 =226 = 24 (см2)
Вариант II
Вычисли площадь поверхности каждого прямоугольного параллелепипеда.
Решение:
S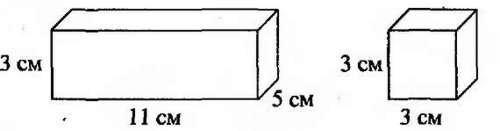 1=1132+1152+532=66+110+30 =206 (см2)
1=1132+1152+532=66+110+30 =206 (см2)
S2 =336 = 54 (см2)
3. Вычислите и расположите трехзначные ответы в порядке возрастания. Слайд №3 И вы сможете прочитать, что мы будем учиться вычислять сегодня.
1710 = 170 Ъ
16 4 = 64 У
936 : 3 = 312 Е
171 : 9 = 19 Ж
102 = 100 О
218 2 = 436 М
5! = 120 Б
-
Сообщение темы урока. (1 мин)
Сегодня на уроке мы продолжим изучение прямоугольного параллелепипеда, введем понятие объема, научимся находить объем прямоугольного параллелепипеда и куба.
Откройте тетради, запишите число, классная работа и тему урока.
(Тема урока и основные понятия пишутся учителем на доске, а учащимися в тетради.) (Классная работа «Объемы. Объем прямоугольного параллелепипеда») Слайд №4 (Урок сопровождается показом презентации)
-
Изложение нового материала. (10 мин)
Чтобы сравнить вместимость двух сосудов, можно наполнить один из них водой и перелить ее во второй сосуд. Если второй сосуд окажется заполненным, а воды в первом сосуде не останется, то объемы сосудов равны. Если в первом сосуде вода останется, то его объем больше объема второго сосуда. А если заполнить водой второй сосуд не удастся, то объем первого сосуда меньше объема второго.
Слайд №5 Если наполнить формочку влажным песком, а потом перевернуть и снять ее, получится фигура, имеющая одинаковый объем, что и формочка.
Слайд №6 Для измерения объемов применяют следующие единицы: кубический миллиметр (мм3), кубический сантиметр (см3), кубический дециметр (дм3), кубический метр (м3), кубический километр (км3).
Например: кубический сантиметр - это объем куба с ребром 1 см.
Кубический дециметр называют также литром.
1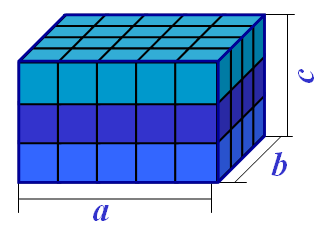 л = 1 дм3
л = 1 дм3
Чтобы найти объем прямоугольного параллелепипеда, надо найти, сколько кубиков с объемом 1 куб. единица входит в этот прямоугольный параллелепипед.
Слайд №7 Выведем правило для вычисления объема прямоугольного параллелепипеда. Пусть прямоугольный параллелепипед имеет длину 5 кубиков, ширину 4 кубика и высоту 3 кубика. Один кубик с ребром 1 см имеет объем 1 см3.
Разобьем его на три слоя толщиной 1 см. Каждый из этих слоев состоит из 5 кубиков в длину и 4 кубиков в ширину с ребром 1 см. Значит, объем первого слоя - 4 • 5 (см3), а всего прямоугольного параллелепипеда - (4 • 5) • 3, то есть 60 см3.
Чтобы найти объем прямоугольного параллелепипеда, надо его длину умножить на ширину и на высоту.
Слайд №8 Формула объема прямоугольного параллелепипеда имеет вид
V = abc
V = Sосн. с
где V - объем, Sосн. - площадь основания; а, b, с - измерения.
Слайд №9 Задача. Если ребро куба равно 5 см, то объем куба равен 5 • 5 • 5 = 53 (см3), то есть 125 см3.
Если ребро куба равно а, то объем V куба равен a • a • a = a3
Слайд №10 Формула объема куба имеет вид
V = a3
Запись а3 называют кубом числа а.
Слайд №11 Объем куба с ребром 1 м равен 1 м3.
1 м = 10 дм
1 м3 = 1000 дм3 = 1000 л
1 л = 1 дм3 = 1000 см3
1 см3 = 1000 мм3
1 км3 = 1 000 000 000 м3
Фигуры пространства Слайд №12
Тело, ограниченное несколькими плоскими гранями, называется многогранником. Особенно важную роль играют выпуклые многогранники. Среди всех выпуклых многогранников только пять называются правильными. У правильного многогранника все грани правильные многоугольники с одинаковым числом сторон. Куб - один из них. У трёх других правильных многогранников все грани - равносторонние треугольники. Их называют тетраэдром (4 грани), октаэдром (8 граней) и икосаэдром (20 граней). Наконец, ещё у одного правильного многогранника имеются 12 граней, все они правильные пятиугольники. Его называют додекаэдром. Выпуклые многогранники изучают в науке о кристаллах.
-
Физкультминутка. (1 мин)
-
Закрепление нового материала. (15 мин)
1. Работа по статье учебника (стр. 125-126)
- Прочитайте статью учебника и приготовьтесь отвечать на вопросы.
- Что такое кубический сантиметр, кубический метр?
- Как еще называют кубический дециметр?
- Запишите на доске формулу объема прямоугольного параллелепипеда.
- Скажите словами, как найти объем прямоугольного параллелепипеда.
- Что можно сказать про длину, ширину и высоту куба?
- Как записать формулу объема куба?
- Посмотрите внимательно на формулу объема прямоугольного параллелепипеда.
- Что обозначают а и b.
- Что обозначает произведение а и b?
- Как иначе можно записать формулу объема прямоугольного параллелепипеда?
Запись в тетрадь:
V = abc
V = Sосн. с
V=a3
-
Выполнение упражнений. Слайд №15
-
Учебник стр.127 №819 (устно) Слайды №13-14
VА = 4 см3; SА = 4 + 4 + 4 + 4 + 1 + 1 = 18 см2;
VВ = 4 см3; SB = 3 + 1 + 2 + 4 + 4 + 4 = 18 см2;
VС = 4 см3; SC = 2 + 2 + 2 + 2 + 4 + 4 = 16 см2;
VК = 4 см3; SK = 4 + 4 + 2 + 1+ 3 + 1 + 3 = 18 см2;
VМ = 7 см3; SM = 4 + 7 + 2 + 2 + 7 + 6 = 28 см2;
VE = 30 см3; SE = 7 + 7 + 4 + 8 + 8 + 3 + 3 = 40 см2;
VF = 10 см3; SF = 10 4 + 1 + 1 = 18 см2;
VR = 1 10 10 = 100 см3; SR = 10 10 2 + 10 4 = 240 см2;
VN = 10 10 10 = 1000 см3; SN = 10 10 6 = 600 см2;
-
Учебник стр.127 №820
V = abc = 6 10 5 = 300 (см3)
V = abc = 30 20 30 = 18 000 (см3)
V = abc = 8 60 120 = 57 600 (см3)
V= abc = 21 17 8 = 2856 (см3)
V= abc = 300 20 15 = 90 000 (см3)
-
Учебник стр.127 №821
V = S c, 96 = 24 c, с = 96 : 24, с = 4 см
-
Учебник стр.127 №822
V = abc, 60 = 3 4 b, b = 60 : 12, b = 5 м - длина
Sпола = Sпотолка = 4 5 = 20 м2
Sстены = 2(3 4) + 2(5 3) = 24 + 30 = 54 м2
-
Учебник стр.127 №823
V = a3
если а = 8 дм, V = 83 = 512 дм3
если а = 36 см, V = 363 = 46 656 см3
-
Повторение изученного материала. (3 мин)
Учебник стр.129 №836 (устно)
а) АВХС и АВКР; АВХС и АРDC
б) АВКР - верхняя; АВХС - задняя; РКМD - передняя; СХМD - нижняя
в) АС, ВХ, КМ, РD
-
Решение комбинаторной задачи. (5 мин)