Программа элективного курса 9 класса Модуль действительного числа

Муниципальное общеобразовательное учреждение

Селтинская средняя общеобразовательная школа

Программа курса по выбору

Модуль действительного числа.

Для учащихся 9 класса

Селты, 2014.

Элективный курс по математике для учащихся 9 класса по теме

«Модуль действительного числа»

Пояснительная записка.

Концепция российского образования предлагает организацию профильного образования учащихся для формирования их готовности к ответственному выбору дальнейшего жизненного пути. В соответствии с этой концепцией и в нашей школе введены элективные курсы.

Данный элективный курс разработан для 9 класса и посвящен одну из вопросов алгебры - модуль действительного числа. Данный курс содействует профессиональной ориентации учащихся в области математики и ее приложений, облегчая тем самым выбор специальности и дальнейшее совершенствование в ней.

С понятием модуля действительного числа учащиеся знакомы еще с 6 класса. Однако в программах общеобразовательных школ и соответствующих учебниках в дальнейшем это понятие ни в теоретических материалах, ни в задачах и упражнениях почти не применяется. В то же время на ГИА и ЕГЭ задачи с модулями все и чаще и чаще предлагаются выпускникам, а учащиеся не всегда могут справиться с такими заданиями. По этой причине возникла необходимость более глубокого изучения этого раздела элементарной математики.

Материал курса имеет большое образовательное значение. Задания курса позволяют повысить учебную мотивацию. Особенность этого курса заключается в том, что он дает учащимся дополнительный материал, и помогает школьникам систематизировать полученные на уроках знания, открывать новые методы решения задач, которые не рассматриваются в рамках школьного курса программы.

Проводить занятия можно в форме обзорных лекций с разбором ключевых задач или в форме семинаров, нацелив учащихся на предварительную подготовку и самостоятельный поиск материалов с их последующим обсуждением.

Рассматриваемые вопросы, позволяют сделать курс практико-ориентированным, показать учащимся, что приобретаемые ими математические знания нужны при решении многих задач в курсе математики, физики и других предметов. Это служит достаточно сильным мотивом для решения предлагаемых задач. Внутрипредметные связи ориентированы на формирование приемов решения задач.

Цели курса:

• определить уровень способностей учащихся и уровень их готовности к профильному обучению в школе;

• систематизировать ранее полученные знания о модуле.

Задачи курса:

• ознакомление учащихся с разными типами задач, особенностями методики и различными способами их решения;

• реализация межпредметных связей.

• создание условий для подготовки к экзаменам по выбору и наиболее вероятным предметам будущего профилирования.

Ожидаемые результаты

После изучения курса учащиеся должны:

• знать определение абсолютной величины действительного числа; основные операции и свойства абсолютной величины;

• знать правила построения графиков уравнений (в т.ч. функций), содержащих знак абсолютной величины;

• знать алгоритмы решения уравнений, неравенств, содержащих переменную под знаком модуля.

• знать и уметь правильно употреблять термины, связанные с понятием модуля;

• уметь представлять геометрическую интерпретацию уравнения и неравенств и ;

• уметь пользоваться техникой решения уравнений и неравенств, содержащих неизвестную под знаком модуля;

• знать и уметь правильно переходить от одного способа решения к другому;

• уметь пользоваться простейшими приёмами преобразования графиков и их построение;

Формы текущего и итогового контроля: самостоятельная работа, индивидуальные задания, тестирование.

Содержание курса.

Модуль действительного числа.

1. История происхождения. Определение модуля. Основные свойства модуля числа. Геометрический смысл модуля числа. (1ч)

Исторические сведения о модуле, понятие модуля и абсолютной величины, основные свойства модуля

,

,

, где q - положительное число

.

Геометрический смысл модуля числа а заключается в том, что модуль числа а есть расстояние от начала отсчета до точки, изображающей это число а.

2. Решение уравнений, содержащих знак модуля. (1ч)

Наиболее распространенным методом решения уравнений и систем уравнений, содержащих абсолютные величины, является метод , при котором знак модуля раскрывается на основании её определения.

Иногда уравнения могут содержать не один , а несколько абсолютных величин , тогда выше изложенный способ окажется слишком громоздким и может запутать ученика.

В таких случаях более приемлем другой способ решения уравнений по следующему алгоритму:

1) Находятся те значения неизвестных, при которых каждое подмодульное выражение обращается в ноль;

2) Числовая прямая разбивается этими значениями на промежутки ;

3) Для каждого промежутка раскрыть каждый модуль. Получаются несколько уравнений, в каждом из которых на неизвестное наложено ограничение;

4) Решить полученные уравнения и корни соотнести с ограничениями.

Решение уравнений вида │х - b│+ │х - с│= а,

│ f₁(х)│+ │ f₂(х │+….│ f_к(х)│= g(х).

Способы решения уравнений: по определению, метод интервалов, возведение в квадрат, способ перебора, графический.

3. Решение уравнений с модулями с параметрами. (2ч)

Несколько методов решения уравнений, содержащих модуль и параметр.

Например,

1.Решите относительно х уравнение:

│ах-1│=2;

│ах²-1│=8;

2.Сколько корней может иметь уравнение │х²-5│=а.

4. Решение неравенств, содержащих знак модуля. (2ч)

Обычный путь решения неравенств, содержащих абсолютные величины, состоит в том, что числовая прямая разбивается на участки ,на каждом из которых на основании определения абсолютной величины ,знак модуля можно снять.

5. Построение графиков функций, содержащих знак модуля. (1ч)

Построение графиков функций:

. Алгоритмы построения графиков, содержащих модуль.

6. Зачет. (1ч)

Тестовая работа.

Тестирование можно провести с помощью программы MyTest X или раздать тесты на бумажном носителе.

Учебно-тематический план.

Литература

1. Галицкий М.Л. и др. Сборник задач по алгебре 8 - 9 кл. - М.: Просвещение, 1995.

2. Горнштейн П.И. и др. Задачи с параметрами. - М.: Илекса, Харьков: Гимназия, 2003.

3. Мерзляк А.Г. и др. Алгебраический тренажер. - М.: Илекса, 2001.

4. Нешков К.И. и др. Множества. Отношения. Числа. Величины. - М.: Просвещение, 1978.

5. Никольская И.Л. Факультативный курс по математике. - М.: Просвещение, 1995.

6. Ястребинецкий Г.А. Задачи с параметрами. - М.: Просвещение, 1986.

7. Ю.Н. Макарычев и др. Алгебра: Дополнительные главы к школьному учебнику 8 - 10 класс(9 - 10 класс). - М.; Просвещение, 1998(2000)

8. В.В.Локоть. Задачи с параметрами. Иррациональные уравнения, неравенства, системы, задачи с модулем. Издательство Аркти, Москва, 2010.

9. Подготовка к ГИА. Математика 9 класс. Под редакцией Ф.Ф.Лысенко. Издательство «Легион-М», 2010.

10. www.resolventa.ru Учебный центр «Резольвента» К.Л.Самаров. Уравнения и неравенства с модулями, 2010.

11. www.hi-edu.ru/PDF/8.pdf

12. www.tutoronline.ru

13. festival.1september.ru/authors/101-168-781

14. pages.marsu.ru/iac/resurs/demenec/ur_na_gqe.html

15. pages.marsu.ru/iac/resurs/demenec/kvadrat_ur.gif

16. rodnik.3dn.ru.

17. mirurokov.ru/</ Модуль числа.

Приложение.

Модуль действительного числа 8ч

История происхождения. Определение модуля. Основные свойства модуля числа. Геометрический смысл модуля числа. 1ч

Модуль числа

«Сначала я открывал то, что известно многим,

затем то, что известно некоторым,

а потом - то, что неизвестно никому».

К.Э. Циолковский:

Историческая справка: термин "модуль" (от лат.modulus - мера) ввел английский математик Р. Котес (1682-1716), а знак модуля немецкий математик К.Вейерштрасс (1815-1897), в 1841 г. Карл Теодор Вильгельм (31.10.1815, Остенфельде, - 19.2.1897, Берлин), немецкий математик. Изучал юридические науки в Бонне и математику в Мюнстере. Профессор Берлинского университета (с 1856). Исследования В. посвящены математическому анализу, теории функций, вариационному исчислению, дифференциальной геометрии и линейной алгебре.

Модулем неотрицательного действительного числа a называют само это число: |а| = а

Модулем отрицательного действительного числа х называют противоположное число: |а| = - а

Короче это записывают так:

Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А(а).

Модуль числа 5 равен 5, так как точка В(5) удалена от начала отсчета на 5 единичных отрезков. Пишут: |5| = 5

Расстояние точки М(-6) от начала отсчета О равно 6 единичным отрезкам. Число 6 называют модулем числа -6. Пишут: |-6| = 6

Геометрический смысл модуля числа а заключается в том, что модуль числа а есть расстояние от начала отсчета до точки , изображающей это число а .

Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного - противоположному числу. Противоположные числа имеют равные модули: |-а| = |а|

Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом отсчета 0, т.е. удалена от нее на 0 единичных отрезков: |0| = 0

На практике используют различные свойства модулей:

,

,

, где q - положительное число

.

Значение равно расстоянию на числовой прямой между точками, изображающими числа a и b.

Пример 1.

.

Пример 2.

Упростить выражение , если a< 0.

Решение.

Так как по условию а < 0, то |а| = -а. В результате получаем

Ответ:

Пример 3.

Вычислить .

Решение.

Имеем

Теперь раскроем знаки модулей.

Воспользуемся тем, что 1<<2. Значит, .

Но тогда

В итоге получаем

.

Ответ: 1.

Задания для самостоятельной работы.

Упростите выражения.

1) при а) х<1 , б) х

2) при а) х<1 б) 1 в) х>3

3) (2-a) при а) а>2, б) a<2

4) (х-3) при а) x>3, б) x<3

5) y= при а) х<4 б) 4 в) x>6

6) у= при а) х< б) в)x>

7) , где a>b

8) Упростить выражения:; ; ;

; +

Решение уравнений, содержащих знак модуля.

Решение уравнений вида:

│х│= а, │х - b│= а, │f(х)│= а, │f(х)│= g(х)

Наиболее распространенным методом решения уравнений и систем уравнений, содержащих абсолютные величины, является метод , при котором знак модуля раскрывается на основании определения.

Например, решить уравнение =х+5.

Решение.

1) Если 3х-40 , то =3х-4 , т.е.

х 3х-4=х+5

х=4.5

Корень х=4.5 принадлежит х

2) Если 3х-4<0 , то = -(3х-4) , т.е.

х< -(3х-4) = х+5

х=-0,25

Корень х=0,25принадлежит х<

Ответ: х₁=-0,25 , х₂=4,5

Иногда уравнения могут содержать не один , а несколько абсолютных величин , тогда выше изложенный способ окажется слишком громоздким и может запутать ученика.

В таких случаях более приемлем другой способ решения уравнений по следующему алгоритму:

1.Находятся те значения неизвестных, при которых каждое подмодульное выражение обращается в ноль;

2.Числовая прямая разбивается этими значениями на промежутки ;

3.Для каждого промежутка раскрыть каждый модуль. Получаются несколько уравнений, в каждом из которых на неизвестное наложено ограничение;

4.Решить полученные уравнения и корни соотнести с ограничениями.

Пример. Решить уравнение

Решение.

1. Найдем значения при которых подмодульные выражения обращаются в ноль

2х+1=0 5-3х=0

х=- х=1

2. Отметим числовые промежутки на которые разбивается числовая прямая

х<- , -х1 , х>1.

3. Решим уравнение на каждом из промежутков отдельно, корни соотнесем с ограничениями

а) х<- 2х+1<0 5-3x>0

-(2x-1)+(5-3x)+1-4x=0

x=

б) - 2х+1>0 5-3x>0

(2х+1)+(5-3х)+1-4х=0

х=

в) х> 2x+1>0 5-3x<0

(2x+1)+(3x-5)+1-4x=0

x=3 3

Ответ. х= х=3

Или несколько другой способ решения уравнений.

Пример. Решить уравнение

Исходя из определения модуля,

можно наложить условие для 2х-1 2х-1

х (1)

тогда исходному уравнению соответствуют два уравнения:

3х+5х-4=-(2х-1) 3х+5х-4=2х-1

3х+7х-5=0 3х-3х-3=0

Далее решаем квадратные уравнения, находим корни и записываем ответ, учитывая условие (1).

Геометрический метод решения уравнений с модулем.

- расстояние между точками a и b.

Пример 1.

Расстояние от точки х до 3 равно 4.

Ответ: х=-1, х=7.

Пример 2.

Расстояние от х до 2 плюс расстояние от х до -4 равно 12.

Запишем

Изобразим схематически на чертеже

.

Пусть х<-4, тогда

Пусть х>2, тогда

Ответ: х=-7, х=5.

Задания для закрепления.

Решить уравнения:

1)

2)

3)

4)

5)

6) х-4+3=0

7) (х-1)

8) 2х-7=

9)

10)

11)

12)

17)

18) С помощью геометрической интерпретации решите уравнение .

Задания для самостоятельной работы.

│х│= - 5; │х│= 0 ; │х - 5│= 3 ; │2х- 4│= 10 - 5х;

│х + 4│= - 2 ; │3 - х│= 7 ; │28х - 37│= 93; │х² + 5х + 6│= 2;

│2х - 3│= 3 - 2х ; ( х + 2)² = 2│х + 2│+ 3; 3│х² + 4х + 2│= 5х + 16;

2х² - 3│х│+ 4 = 0.

Решение уравнений вида │х - b│+ │х - с│= а,

│ f₁(х)│+ │ f₂(х │+….│ f_к(х)│= g(х)

_{Задания для практики.}

│х - 2│=│х + 3│; 3│х² - 4│=│х - 1│; │5 - х│-│х + 4│= 0;

│5- х│+│х - 1│= 10; │5х- 13│-│6 - 5х│= 7; │х- 2│+│х - 4│= 3;

│2х- 7│= │х - 4│; 2│х - 2│=│х - 1│; │3х - 1│+│4 - х│= 5;

│х + 6│=│2х│.

Решите уравнение .

1 способ: ( по определению). Имеем 4 системы:

2. 0=2

6. Нет решений.

12. Нет решений.

20. −4

25. Ответ:

26. 2 способ: Метод интервалов. 1) х < 1 2) 1 < х < 3

27. 3 - х - 1 + х = 0 3 - х - х + 1 = 0

28. 0 ∙ х = 2 2х = - 2

29. нет решений х = 1

30. 1 ( 1: 3)

31. нет решений

33. 2х = 4

34. х = 2

35. Ответ: х = 2.

36. 3 способ:

38. Возведение в квадрат.

39. │х - 3│² =│х - 1│²

40. (х - 3) ² =( х - 1)²

41. х² - 6 х + 9 = х² - 2х + 1

42. - 4х = - 8

43. х = 2.

44. Ответ: 2.

45. 4 способ: Способ перебора. │х - 3│=│х - 1│

46. 1) х - 3 = х - 1

47. 0 ∙ х = 2

48. нет решений

49. 2) х - 3 = - х + 1

50. 2х = 4

51. х = 2.

52. 5 способ: Графический.

53. у = │х - 3│

54. у = │х - 1│

55. Ответ: 2.

56. Подводя итог занятия, спросить учащихся: Какой способ самый эффективный?; Самый трудный?; Самый простой? Попросить их придумать и решить аналогичные уравнения.

57. Решение уравнений с модулями с параметрами.

58. Решение уравнений, содержащих модуль и параметр, на примерах от простого к сложному.

1. Решить уравнения: а), б).

60. Решим данные уравнения графическим способом.

61. а)

62. Построим графики функций и .

63. По графикам видно,

64. Если a<0, нет корней.

65. Если a=0, то x=0.

66. Если a>0, то x=-a, x=a.

67. б)

68. Построим графики функций и .

69. По графикам видно,

70. Если a<0, нет корней.

71. Если a=0, то x=3.

72. Если a>0, то x=3-a, x=3+a.

2. Решим уравнение

74. Мы знаем, что , поэтому данное уравнение разобьем на два уравнения или . Корнем первого уравнения является число , второго . Уравнение имеет два корня при любом а, кроме 0.

3. Найти все значения р, при которых уравнение имеет хотя бы один корень.

76. Сумма модулей положительное число, поэтому число должно быть положительным.

77. Приравняем подмодульные выражения к нулю.

78. ,

79. , .

80. Разобьем числовую прямую на промежутки

81. Решим уравнение на каждом промежутке отдельно

82. а) если , то оба подмодульных выражения отрицательны, имеем уравнение

85. , где

86. Решим неравенство , получим .

87. б) если , первое подмодульное выражение положительное, второе - отрицательное, имеем уравнение

90. При p=1 уравнение представляет собой верное равенство, поэтому решением уравнения будет .

91. в) если , оба подмодульных выражения положительны, имеем уравнение

94. , где

95. Решим неравенство , получим .

96. Ответ: уравнение имеет хотя бы один корень при .

4. Найти множество значений параметра p , при которых уравнение

97. имеет ровно два корня.

98. Решение:

1. , получаем

102. ,

103. , при .

109. Решим методом интервалов

2. , получаем

114. , при .

120. Решим методом интервалов

3. Объединяя первое и второе решение получаем, что уравнение имеет два решения при .

122. Ответ: .

5. Решите относительно х уравнение

123. Решить по аналогии с примером 2.

6. Сколько корней может иметь уравнение .

124. Решение: при а<0, уравнение не имеет решений.

125. При а=0,

126. , два корня.

127. При а>0, имеем два уравнения

130. Верно при а>0

131. , но а>0.

132. Рассматриваем все решения видим что уравнение имеет два решения,

133. При четыре корня, по два корня из уравнений

134. При a=5, три корня.

135. Ответ: уравнение может иметь 0, 2, 3,4 корней.

137. Задачи для самостоятельного решения.

1. Решите относительно х уравнение

2. Найти все значения параметра p , при которых уравнение

138. имеет хотя бы один корень.

3. Найдите множество значений параметра p, при которых уравнение

139. не имеет корней.

140. Решение неравенств с модулями с параметрами.

141. Обычный путь решения неравенств, содержащих абсолютные величины, состоит в том, что числовая прямая разбивается на участки, на каждом из которых на основании определения абсолютной величины ,знак модуля можно снять.

1. Решите неравенство

142. Решение: Если , то неравенство верно при любых , так как .

143. Если , то верно при всех .

145. Если , то решим геометрическим методом

147. .

148. Ответ: , ,

149. .

2. Решите неравенство

150. Решение: Так как , то при неравенство решений не имеет.

151. При , то .

152. .

153. Ответ: при , то ;

154. при решений нет.

3. Решить неравенство .

155. Решение: Неравенство равносильно системе

157. Корни квадратного трехчлена ;

159. Множество решений неравенства зависит от знаков .

161. Решением первого неравенство будет множество

163. Решением второго неравенства .

164. Решением системы будет множество .

165. ,

166. .

168. Решением первого неравенство будет множество

169. Решением второго неравенства .

170. Решением системы будет множество

173. .

175. Решением первого неравенство будет множество

176. Решением второго неравенства .

177. Решением системы будет

179. Решением системы будет

181. Решением первого неравенство будет множество

182. Решением второго неравенства .

183. Решением системы будет множество .

184. Ответ: при ,

185. ,

186. ,

187. ,

188. при

189. при .

4. При каких а неравенство выполняется для любых пар чисел (x,y) таких, что ?

190. Решение: неравенство должно выполнятся при

1. . Неравенство имеет вид

193. Рассмотрим функцию , квадратичная функция, графиком которой является парабола, направление ветвей зависит от знака .

194. Чтобы неравенство (1) было верным для , надо чтобы уравнение

196. имело один корень или не имело корней.

197. Значит ветви параболы направлены вверх, и с осью Ох может быть только одна общая точка, получаем систему неравенств.

199. Откуда получаем

2. Неравенство имеет вид

203. Рассмотрим функцию , квадратичная функция, графиком которой является парабола, направление ветвей зависит от знака .

204. Если неравенство (2) верно для , значит ветви параболы направлены вверх, получаем неравенство , то есть.

205. Таким образом, оба неравенства выполняются при всех , если a=2.

206. Ответ: а=2

207. Задания для самостоятельной работы:

1. Решить неравенства:

2. Решить неравенство:

3. Решить неравенство ; .

4. Найдите а, при которых неравенство выполняется для всех

5. При каком а уравнение имеет ровно три решения?

6. При каких а неравенство имеет хотя одно положительное решение?

208. Построение графиков функций, содержащих знак модуля.

209. Построение графиков функций

210. Алгоритмы построения графиков, содержащих модуль.

1. Используя определение модуля построить график функции .

2. Используя правила преобразования графиков функций, построить графики

211. на конкретных примерах.

212. Например, и т.д.

213. По графикам обратить внимание на свойства функций.

3. Используя определение модуля построить график функции.

214. , поэтому все значения функции должны быть неотрицательные.

215. Вместе с ребятами составить алгоритм построения графика.

1. Построить график .

2. Часть графика, которая находится ниже оси Ох, отобразить симметрично више оси Ох.

216. Построим график функции

4. Построение графика функции .

219. Заметим, что , значит функция четная и график симметричен относительно оси Оу.

220. Алгоритм построения.

1. Для построить график функции .

2. Для отобразить построенную часть графика симметрично относительно оси Оу.

221. Например, построить график функции +12.

222. 

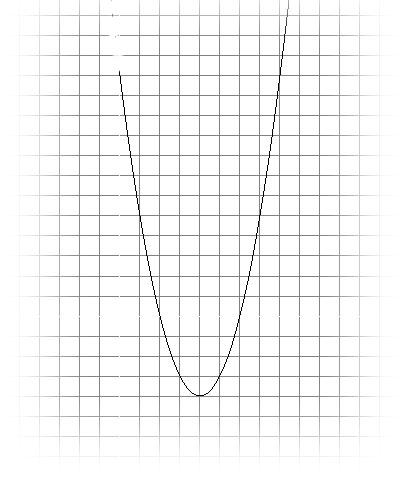
223. Задания для самостоятельной работы.

1. Постройте графики функций:

224. .

2. Постройте графики функций: , .

3. Постройте графики функций: , , .

28