- Учителю
- Конспект урока в 9 классе по теме: Решение треугольников с помощью теоремы синусов
Конспект урока в 9 классе по теме: Решение треугольников с помощью теоремы синусов
ТЕМА «Решение треугольников с помощью теоремы синусов»
Цель урока: сформировать умение решать задачи на нахождение неизвестных элементов произвольного треугольника с помощью теоремы синусов.
Оборудование:
-
компьютер,
-
мультимедийный проектор,
-
экран,
-
меловые записи.
Ход урока
I. Организационный момент. Постановка цели и задач урока.
II. Актуализация опорных знаний.
1. Что значит решить прямоугольный треугольник.
2. Рассказать о ходе решения прямоугольных треугольников:
- по двум катетам;
- по катету и гипотенузе;
- по катету и острому углу;
- по гипотенузе и острому углу;
Таблица «Решение прямоугольных треугольников» проектируется с помощью мультимедийного проектора на экран.
III. Мотивация практической необходимости рассмотрения теоремы синусов.
Проверка задач из домашнего задания.
Дано:
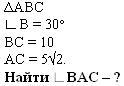
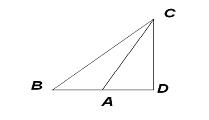
Решение.
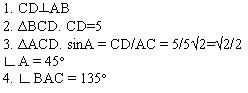
Необходимо обратить внимание ребят, что такое решение нерациональное. Эти задачи можно решать проще, если будет известна теорема, называемая теоремой синусов.
Формулируется теорема синусов. На доске и в тетрадях записывается тема урока, условие теоремы.
IV. Объяснение нового материала.
Теорема синусов: ![]()
Задача.
Дано:
ABC
Доказать:
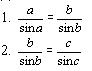
План доказательства.
1. Провести высоту СD
2. Выразить СD через b и ![]() A.
A.
3. Выразить СD через a и ![]() B.
B.
4. Приравнять полученные для CD выражения
Учащиеся выполняют эту работу на местах самостоятельно.
Затем доказательство разбирается..
V. Формирование умений и навыков.
Применение теоремы синусов для решения задач.
1. Двое у доски показывают решение задач №1 и №2 из домашнего задания с помощью теоремы синусов.
2. Решить самостоятельно:
а) а = 20, ![]() A = 750,
A = 750, ![]() В = 600. Найти b.
В = 600. Найти b.
б) a = 8,7, b = 6,5, ![]() A =450. Найти LB.
A =450. Найти LB.
в) c = 14, ![]() A = 600,
A = 600, ![]() C = 400. Найти a.
C = 400. Найти a.
г) LA = 800, a = 16, b = 10. Найти LB.
Ответы изображаются на экране с помощью мультимедийного проектора.
VI. Итоги урока.
1. Ставится вопрос.
Будет ли теорема синусов справедлива для прямоугольного треугольника.
2. Делается вывод, что теорема синусов справедлива для любого треугольника.
VII. Домашнее задание. №1025(б, г), №1026, № 1027 (учебник
геометрии Л.С. Атанасян)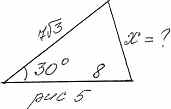
Рисунок 1
1) х = 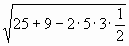 =
= ![]() ; х =
; х = ![]()
2) х = 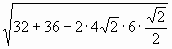 =
= ![]() ; х =
; х = ![]()
3) х = 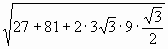 =
= ![]() ; х =
; х = ![]()
4) х = 10, т.к. данный треугольник равносторонний
5) х = 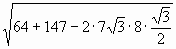 =
= ![]() ; х =
; х = ![]()
- Какая![]() теорема
помогла вам найти третью сторону треугольника?
теорема
помогла вам найти третью сторону треугольника?
- Сформулируйте теорему.
3. Новая тема
- формулируется теорема синусов.
- при доказательстве теоремы на доске полезно сделать следующие чертежи и записи.
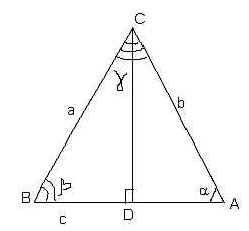
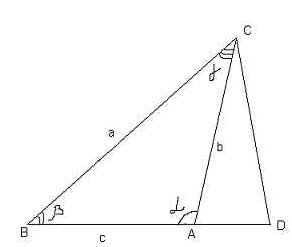
Рисунок 2
-
СD = b x sin
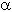
 BCD: СD = a x sin
BCD: СD = a x sin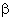
 BCD: СD = a x sin
BCD: СD = a x sin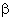
 ACD: СD = b x sin(1800-
ACD: СD = b x sin(1800- 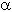 )
)
из (а) и (б), следует b x sin![]() = a x sinb , поделив обе части на a x b, получим:
= a x sinb , поделив обе части на a x b, получим:
![]()
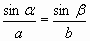
аналогично доказывается, что,
![]()
4. Закрепление (составление пропорций для вычисления стороны треугольника)
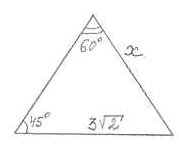
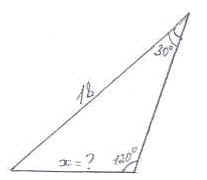
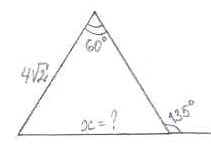
Рисунок 3
1) 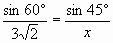 ;
; 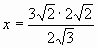
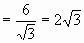 ;
;
![]()
2) ![]() ;
; 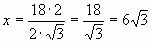 ;
; ![]()
3) 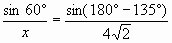 ;
; 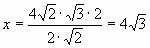 ;
; ![]()
5. Итог урока (решение задач по группам)
- класс делится на группы по 3 человека;
- каждая группа получает по две задачи