Урок по алгебре на тему Прогрессии.Подготовка к ОГЭ по математике (9 класс)

Урок по алгебре в 9-в классе

Тема урока: «Прогрессии»

Цель урока:

Образовательная: повторение и обобщение знаний по теме, проверка умения и навыков учащихся, подготовка к ОГЭ.

Развивающая: развитие умения видеть и применять изученные формулы в решении задач; формирование интереса к изучению математики.

Воспитательная: развитие навыков самостоятельной учебной деятельности, умения общаться, умения оценивать свои достижения.

Тип урока: Совершенствование умений и навыков.

Необходимое техническое оборудование:

Мультимедийное оборудование, раздаточный материал, мел, классная доска, рабочие карты урока (карты самооценки).

ХОД УРОКА

1. Организационный момент

1. Здравствуйте, ребята! Садитесь. Я очень рада вас видеть, и очень хочу начать работу с вами! Посмотрите друг на друга, улыбнитесь, приготовьтесь к сотрудничеству на уроке.

2. Не забудьте, что в течение всего урока вы работаете с листом самооценки, которые лежат у вас на столе.

3. Сегодня у нас с вами урок подготовки к итоговой аттестации. Какой раздел математики мы закончили изучать? Значит тема урока «Прогрессии». Каким выпускником школы вы хотите быть? Придумаем качества выпускника

П-(продвинутый)

Р- (решительный)

О- (ответственный)

Г- (грамотный)

Р- (рассудительный)

Е-(естествовед)

С-(смелый)

С- (способный)

И- (интеллигентный)

И-(интеллектуальный)

Давайте стремиться к этому не только на уроках, но и во всех делах.

Каковы цели нашего урока?

2. Актуализация знаний.

1).Какие прогрессии вы изучили? (арифметическая и геометрическая)

2). Дадим определение им.

3).Чем похожи?

4) Чем отличаются?

5) Что называют разностью арифметической прогрессии? Знаменателем геометрической прогрессии?

• На слайде даны последовательности чисел. Какие из них являются прогрессиями?

13; 10; 7; 4; …(арифметическая)

1; 3; 9; 27; …(геометрическая)

1; 3; 4; 7; 11; …(последовательность)

24; 12; 6; 3; …(геометрическая)

5; 10; 25; 100; 125...(последовательность)

0,5; 1; 1,5; 2; … (арифметическая)

• Чему равна разность арифметических прогрессий? (d=-3, d=0,5)

• Найдите следующие три члена прогрессий.

следующие члены : 1) 1, -2, -5;

2) 2,5; 3; 3,5;

• Чему равен знаменатель геометрических прогрессий? (q = 3, q = 0,5)

• Найдите следующие два члена прогрессий.

следующие члены: 1) 81; 243.

2) 1,5; 0, 75.

3. Подготовка учащихся к работе на основном этапе.

- Что необходимо знать для решения задач по теме «Прогрессии»?

Проверим знание формул по теме "Арифметическая и геометрическая прогрессии".

Прогрессии

Арифметическая (a_n)

Геометрическая ( b_n)

1

Определение

2

Формула для нахождения n-го члена

3

Сумма n-первых членов прогрессии

4

Свойства

Посмотрите на слайд, проверьте правильность записи формул, исправьте ошибки, если они есть.

Поставьте оценки в лист самооценки.

Прогрессии

Арифметическая (a_n)

Геометрическая ( b_n)

1

Определение

2

Формула для нахождения n-го члена

3

Сумма n-первых членов прогрессии

4

Свойства

4. Этап закрепления знаний и совершенствования способов действий.

- Решение задач в парах с последующей проверкой.

Выполнение заданий

- Оцените работу соседа и поставьте оценку за вклад его в решение.

- В чем были ошибки?

- Для чего вы выполняли данное задание?

(Для того, чтобы уметь самостоятельно выбирать формулы и для решения, правильно вычислять по формулам, хорошо решить задачи по теме в ОГЭ)

5. Этап психологической разгрузки.

- У Вас на столах лежат листы, на которых написаны цифры от 1 до 9. Теперь раскрасьте ряд двумя разными цветами в любом порядке.

А пока Вы раскрашиваете, я расскажу про замечательного математика по фамилии Рамсей. Он жил в начале ХХ века. Им была создана теория, доказывающая, что в мире нет абсолютного хаоса. Что даже, казалось бы, самая неупорядоченная система имеет определенные математические закономерности. Вспомните, когда Вы смотрите на звезды, то может показаться, что расположены они в самом случайном порядке. Но еще в древности люди увидели там созвездия.

И вот на ваших карточках казалось бы цифры раскрашены в случайном порядке. Но Рамсей доказал, что это не так, доказав следующий факт: Обратите внимание, что хотя бы три каких - либо числа одного цвета обязательно составляют арифметическую прогрессию. Как я это сделала, показано на слайде. Какие числа образуют прогрессию? (3, 6, 9)

Найдите такие числа в своих рядах.

6. Этап контроля и самоконтроля знаний и способов действий.

-Для того, чтобы проверить свои умения использовать знания при решении задач, я предлагаю вам выполнить тестовую самостоятельную работу, (с последующей самопроверкой):

Тест: «Числовые последовательности».

Ответы на тест внесите в бланки ОГЭ.

1. Выписаны первые несколько членов геометрической прогрессии: 1,5;−3; 6; …. Какое из следующих чисел есть среди членов этой прогрессии?

1) 9 2) -12 3) -9 4) 12

2. Арифметическая прогрессия может быть задана формулой a_n=7n+3. Какое из следующих чисел не является членом этой прогрессии?

1) 73 2) 80 3) 24 4) 63

3. Дана арифметическая прогрессия y₁ = −3,y₂ = −1, … Найдите сумму первых шести членов этой прогрессии.

Ответ____________

4. Первый член арифметической прогрессии равен 12, а третий равен −4. Найдите разность этой прогрессии.

Ответ_______

5. Выписано несколько последовательных членов геометрической прогрессии: ; -5; 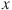; -80; -320; . Найдите член прогрессии, обозначенный буквой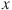

Ответ__________

6. В арифметической прогрессии 2; 5; 8; … один из членов равен 23. Найдите его номер.

1) 3 2) 4 3) 5 4) 6

7. Арифметическая прогрессия задана первыми двумя членами: a₁=−11, a₂=−8. Найдите первый положительный член этой прогрессии.

Ответ____________

8. Дана геометрическая прогрессия (b_n) , знаменатель которой равен 5, b₁=25.

Найдите сумму первых четырех её членов.

Ответ____________

Предлагает выполнить взаимопроверку результатов по слайду. Помогает выполнить разбор заданий, вызвавший затруднения.

7. Подведение итогов

Предлагает ответить на вопросы:

1. Какая из изученных прогрессий, на Ваш взгляд, более сложная?

Почему?

2. Поднимите руку, кто доволен своей работой? кто из вас остался не довольным своей работой? Почему?

3. Какую тему вам необходимо повторить?

4. Что для этого вы должны сделать?

8. Этап информации о домашнем задании.

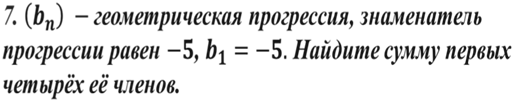
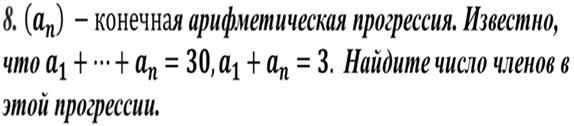
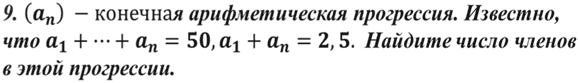
9. Рефлексия.

Проанализируйте предложения и ответьте на вопросы.

1.Сегодня на уроке я узнал(а) (что?)

2.Сегодня на уроке я научился(лась) (чему?)

3.Сегодня на уроке научился(лась) делать лучше (что?)

4.Самым неожиданным для меня стало (Что?)

5.Сегодня на уроке я мог(ла) бы сделать лучше (что сделать?)

6.Осталось непонятным (что?)

Урок сегодня завершен,

Но каждый должен знать:

Познание, упорство, труд

К прогрессу в жизни приведут!

Прогрессии

Арифметическая (a_n)

Геометрическая ( b_n)

1

Определение

2

Формула для нахождения n-го члена

3

Сумма n-первых членов прогрессии

4

Свойство прогрессии

№

Прогрессии

Арифметическая ()

Геометрическая ()

1

Определение

2

Формула для нахождения n-го члена

3

Сумма n-первых членов прогрессии

4

Свойства

1

2

3

4

5

6

7

8

9

1

2

3

4

5

6

7

8

9

1

2

3

4

5

6

7

8

9

Арифметическая

(a_n)

Геометрическая

( b_n)

1) Дано: (а _n) арифметическая прогрессия а₁ = 5,d = 3 .

Найти: а₆ ; а₁₀.

Ответ: ____________

2) Дано: (b_n) геометрическая прогрессия b₁= 5 ,q = 3 .

Найти: b₃ ;b₅.

Ответ:_____________.

3)Дано: (а _n) арифметическая прогрессия а₄=12,5; а₆=17,5.

Найти: разность арифметической прогрессии.

Ответ: ____________

4) Дано: (b_n) геометрическая прогрессия b₄=6; b₆=24.

Найти: знаменатель геометрической прогрессии, если известно, что он положительный.

Ответ: ______________

5) Дано: (а _n) арифметическая прогрессия а₁ = 11,d = 2 .

Найти: S₁₀ .

Ответ: ___________

6) Дано: (bn) геометрическая прогрессия b₁= 40 ,q = 2 .

Найти: S₅.

Ответ: ______________

Арифметическая (a_n)

Геометрическая ( b_n)

1) Дано: (а n) арифметическая прогрессия а1 = 5,d = 3 .

Найти: а6 ; а10.

Ответ: ____________

2) Дано: (bn) геометрическая прогрессия b1= 5 ,q = 3 .

Найти: b3 ;b5.

Ответ:_____________.

3)Дано: (а n) арифметическая прогрессия а4=12,5; а6=17,5.

Найти: разность арифметической прогрессии.

Ответ: ____________

4) Дано: (bn) геометрическая прогрессия b4=6; b6=24.

Найти: знаменатель геометрической прогрессии, если известно, что он положительный.

Ответ: ______________

5) Дано: (а n) арифметическая прогрессия а1 = 11,d = 2 .

Найти: S10 .

Ответ: ___________

6) Дано: (bn) геометрическая прогрессия b1= 40 ,q = 2 .

Найти: S5.

Ответ: ______________

Ф.И.__________________________ Класс___________

Тест: «Числовые последовательности».

1. Выписаны первые несколько членов геометрической прогрессии: 1,5;−3; 6; …. Какое из следующих чисел есть среди членов этой прогрессии?

1) 9 2) -12 3) -9 4) 12

2. Арифметическая прогрессия может быть задана формулой a_n=7n+3. Какое из следующих чисел не является членом этой прогрессии?

1) 73 2) 80 3) 24 4) 63

2. Дана арифметическая прогрессия y₁ = −3,y₂ = −1, … Найдите сумму первых шести членов этой прогрессии.

Ответ____________

2. Первый член арифметической прогрессии равен 12, а третий равен −4. Найдите разность этой прогрессии.

Ответ_______

2. Выписано несколько последовательных членов геометрической прогрессии: ; -5; 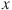; -80; -320; . Найдите член прогрессии, обозначенный буквой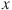

Ответ__________

2. В арифметической прогрессии 2; 5; 8; … один из членов равен 23. Найдите его номер.

1) 3 2) 8 3) 5 4) 6

2. Арифметическая прогрессия задана первыми двумя членами: a₁=−11, a₂=−8. Найдите первый положительный член этой прогрессии.

Ответ____________

2. Дана геометрическая прогрессия (b_n) , знаменатель которой равен 5, b₁=25.

Найдите сумму первых четырех её членов.

Ответ____________