- Учителю
- План урока по математике на тему Решение тригонометрических неравенств
План урока по математике на тему Решение тригонометрических неравенств
Ход урока по теме "Решение простейших тригонометрических неравенств"
Преподаватель математики Киселева Л.А.
Разделы: Математика</</font>
Тип урока: объяснение нового материала.
Цель урока: Выработать у учащихся последовательность решения тригонометрических неравенств с помощью единичной окружности.
План урока (2 часа).
-
Организационный момент.(1-2 мин.)
-
Объяснение нового материала.(30 мин.)
-
Закрепление изученного материала.(50мин.)
-
Подведение итогов.(5 мин.)
-
Задание на дом.(2-3 мин.)
Ход урока
Организационный момент.
Учитель здоровается с учениками, проверяет их готовность к уроку, оглашает цель урока. Учащиеся приветствуют учителя.
Объяснение нового материала.
Объясняет материал, делая чертежи на доске. Удобно будет воспользоваться шаблоном единичной окружности, изготовленным заранее.
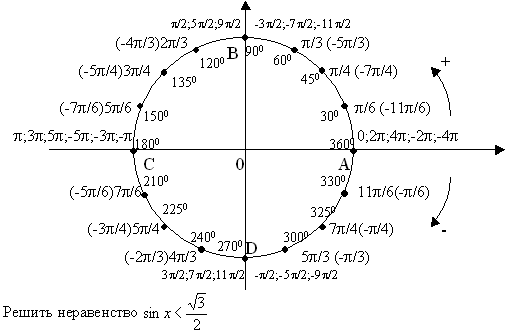
Алгоритм решения:
-
Начертите единичную окружность.
-
Найдите на ней точки, ординаты которых равны (синус равен ординате точки единичной окружности)
-
Отметьте точки, удовлетворяющие данному неравенству.
-
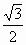 Найдите
несколько значений х, соответствующие отличным точкам.
Найдите
несколько значений х, соответствующие отличным точкам.
-
Найдите значения двух - трёх углов, синус которых равен
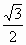 .
.
-
Этими точками единичная окружность разделилась на две дуги: меньшую (
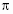 /3;2
/3;2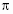 /3)
и большую (-4
/3)
и большую (-4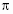 /3;
/3;
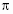 /3). При записи промежутков слева всегда записывают меньшее
число, а справа - большее, что соответствует на окружности
движению против часовой стрелки.
/3). При записи промежутков слева всегда записывают меньшее
число, а справа - большее, что соответствует на окружности
движению против часовой стрелки.
-
Чтобы убедиться, что дуга отмечена верно, возьмём контрольную точку на этой дуге, например х = 0 тогда
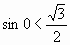 , так как
, так как 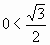
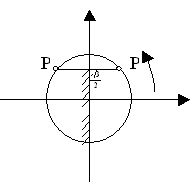
![]() ,
при -4
,
при -4![]() /3
< x <
/3
< x < ![]() /3;
/3;
Все решения данного неравенства принадлежат промежутку:
-4![]() /3+2
/3+2![]() n
< x <
n
< x <![]() /3+2
/3+2![]() n.
n.
Рассмотрим ещё пример.
![]() (Задача
1, учебник)
(Задача
1, учебник)
По определению косинуса cos x - это абсцисса точки единичной окружности.
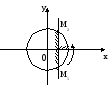
-/3< x < /3.
Все решения данного неравенства принадлежат промежутку:
-/3+2n < x < /3+2n, nZ.
Закрепление изученного материала
Разобрать №4 (стр.193) по учебнику.
Записать задания на доске, контролировать действия учащихся. №1648(1,4), №649(2,3), №650(2,3), №651(2,3), 652(1).
Учащиеся выполняют задания №649(3) и №651(3) у доски (2 человека); остальные выполняют упражнения в тетрадях. Оставшиеся задания учащиеся выполняют самостоятельно
Решения.
№648.
-
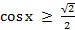 ;
;
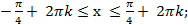 k
k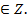
4. ![]() ;
; ![]() k
k![]()
№649.
-
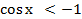 ;
решений нет.
;
решений нет.
3. ![]() ; выполняется при
; выполняется при ![]() ; х =
; х = ![]() k
k![]()
№650..
2.![]()
![]() k
k![]()
3. ![]()
![]() k
k![]()
№651.
2.![]() решений нет.
решений нет.
3.![]() выполняется при
выполняется при ![]()
![]() k
k![]()
№652.
![]()
![]()
![]() k
k![]()
![]() k
k![]()
Подведение итогов урока
Учитель задаёт вопросы ученикам.
-
Абсцисса точки единичной окружности есть ... (косинус)
-
Ордината точки единичной окружности есть ...(синус)
-
Как проверить что дуга на единичной окружности отмечена верно?
-
Назовите алгоритм решения тригонометрического неравенства.
Учитель объявляет оценки за урок.
Задание на дом.
§37 «Решение тригонометрических уравнений и неравенств», №649(4), №651(4), 652(2).
Учитель отвечает на вопросы учеников, прощается с ними.
Учащиеся записывают задания на дом в дневник, спрашивают, что непонятно по пройденному материалу.
Список литературы.
(Алгебра и начала анализа: учебник для 10-11 классов средней школы.
Ш.А. Алимов, Ю.М.Колягин. М.: Просвещение, 2004г.)