7


  • Учителю
  • Решение задач повышенной сложности при подготовке к ГИА по геометрии

Решение задач повышенной сложности при подготовке к ГИА по геометрии

Автор публикации:
Дата публикации:
Краткое описание:
предварительный просмотр материала

Задача №1- 3

Дано.ABCD- трапеция

A=8 , b=6 , R=5.

Найти. AB , СD,площадь ABCD,h1, h2.

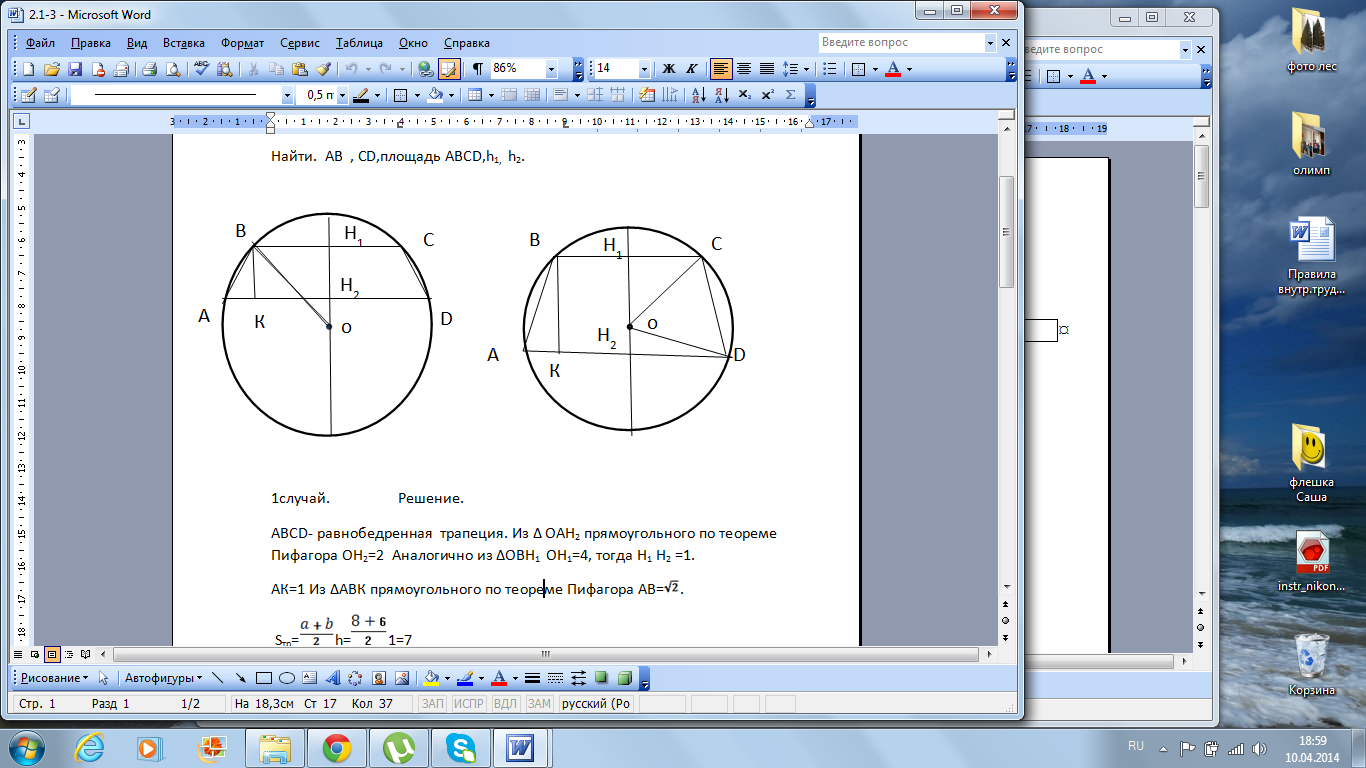
Решение задач повышенной сложности при подготовке к ГИА по геометрии

1случай. Решение.

ABCD- равнобедренная трапеция. Из Δ ОАН2 прямоугольного по теореме Пифагора ОН2=2 Аналогично из ΔОВН1 ОН1=4, тогда Н1 Н2 =1.

АК=1 Из ΔАВК прямоугольного по теореме Пифагора АВ=Решение задач повышенной сложности при подготовке к ГИА по геометрии.

Sтр=Решение задач повышенной сложности при подготовке к ГИА по геометрииh=Решение задач повышенной сложности при подготовке к ГИА по геометрии1=7

2случай.

ABCD- равнобедренная трапеция .Из ΔODH2 прямоугольного по теореме Пифагора ОН2=3 ,из ΔОСН1 прямоугольного по теореме Пифагора ОН2=4, тогда Н1 Н2=7

АК=1 Из ΔАВК прямоугольного по теореме Пифагора АВ=Решение задач повышенной сложности при подготовке к ГИА по геометрии.

Sтр=Решение задач повышенной сложности при подготовке к ГИА по геометрииh=Решение задач повышенной сложности при подготовке к ГИА по геометрии ·7=49.

Ответ:Задача № 4

Найдите угла А, В ,С и D трапеции.



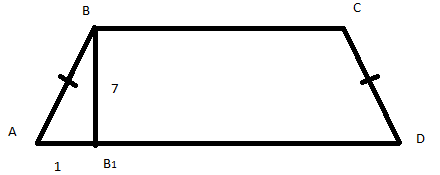
Решение задач повышенной сложности при подготовке к ГИА по геометрии

Дано:

ABCD - трапеция,

ВС=6, AD=8

Найти:

Решение задач повышенной сложности при подготовке к ГИА по геометрии





Решение:

Из вершины Решение задач повышенной сложности при подготовке к ГИА по геометрии опустим высоту Решение задач повышенной сложности при подготовке к ГИА по геометрии .

Из задачи 1 следует, что Решение задач повышенной сложности при подготовке к ГИА по геометрии .

По свойству равнобедренной трапеции Решение задач повышенной сложности при подготовке к ГИА по геометрии .

Так же по свойству равнобедренной трапеции Решение задач повышенной сложности при подготовке к ГИА по геометрии .

Рассмотрим Решение задач повышенной сложности при подготовке к ГИА по геометрии - прямоугольный. По определению тангенса острого угла прямоугольного треугольника получим:

Решение задач повышенной сложности при подготовке к ГИА по геометрии

Решение задач повышенной сложности при подготовке к ГИА по геометрии

По условию задачи трапеция Решение задач повышенной сложности при подготовке к ГИА по геометрии вписана в окружность. Следовательно, Решение задач повышенной сложности при подготовке к ГИА по геометрии .

Решение задач повышенной сложности при подготовке к ГИА по геометрии

Ответ: Решение задач повышенной сложности при подготовке к ГИА по геометрии Решение задач повышенной сложности при подготовке к ГИА по геометрии



Задача № 5

Найти диагонали Решение задач повышенной сложности при подготовке к ГИА по геометрии трапеции.

Д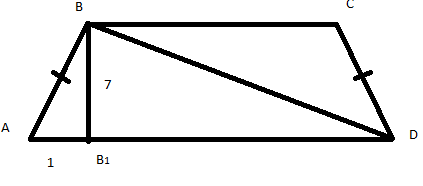Решение задач повышенной сложности при подготовке к ГИА по геометрииано: Решение задач повышенной сложности при подготовке к ГИА по геометрии -трапеция, Решение задач повышенной сложности при подготовке к ГИА по геометрии . Найти: Решение задач повышенной сложности при подготовке к ГИА по геометрии .











Решение:

По свойству равнобедренной трапеции Решение задач повышенной сложности при подготовке к ГИА по геометрии .

Рассмотрим Решение задач повышенной сложности при подготовке к ГИА по геометрии - прямоугольный. По теореме Пифагора

Решение задач повышенной сложности при подготовке к ГИА по геометрии

Решение задач повышенной сложности при подготовке к ГИА по геометрии

Ответ: Решение задач повышенной сложности при подготовке к ГИА по геометрии







Задача № 6

Найти угол между диагоналями Решение задач повышенной сложности при подготовке к ГИА по геометрии трапеции.

Д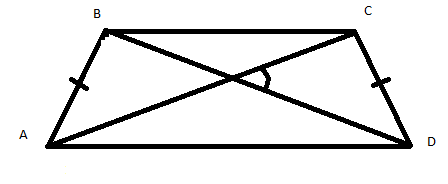Решение задач повышенной сложности при подготовке к ГИА по геометрииано: Решение задач повышенной сложности при подготовке к ГИА по геометрии -трапеция,

Решение задач повышенной сложности при подготовке к ГИА по геометрии.

Найти: Решение задач повышенной сложности при подготовке к ГИА по геометрии .











Решение:

Пусть Решение задач повышенной сложности при подготовке к ГИА по геометрии

Площадь трапеции можно найти по формуле:

Решение задач повышенной сложности при подготовке к ГИА по геометрии

По свойству равнобедренной трапеции Решение задач повышенной сложности при подготовке к ГИА по геометрии Следовательно, формула принимает вид:

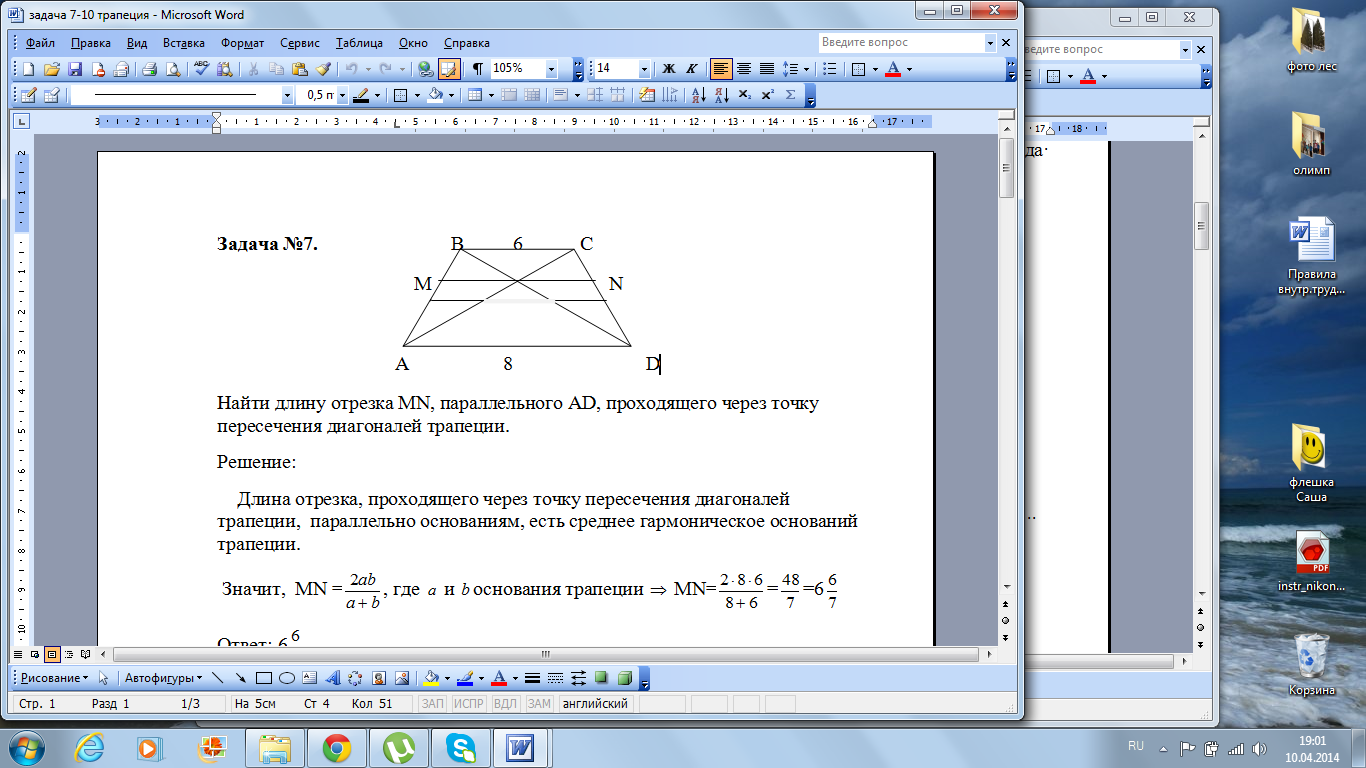
Решение задач повышенной сложности при подготовке к ГИА по геометрии

Из задачи 3 известно, что Решение задач повышенной сложности при подготовке к ГИА по геометрии Составим и решим уравнение:

Решение задач повышенной сложности при подготовке к ГИА по геометрии

Решение задач повышенной сложности при подготовке к ГИА по геометрии

Решение задач повышенной сложности при подготовке к ГИА по геометрии

Ответ: Решение задач повышенной сложности при подготовке к ГИА по геометрии





ЗРешение задач повышенной сложности при подготовке к ГИА по геометрииадача №7



Решение задач повышенной сложности при подготовке к ГИА по геометрии

Найти длину отрезка МN, параллельного АD, проходящего через точку пересечения диагоналей трапеции.

Решение:

Длина отрезка, проходящего через точку пересечения диагоналей трапеции, параллельно основаниям, есть среднее гармоническое оснований трапеции.

Значит, МN =Решение задач повышенной сложности при подготовке к ГИА по геометрии, где Решение задач повышенной сложности при подготовке к ГИА по геометрии и Решение задач повышенной сложности при подготовке к ГИА по геометрии основания трапеции Решение задач повышенной сложности при подготовке к ГИА по геометрии МN=Решение задач повышенной сложности при подготовке к ГИА по геометрии=Решение задач повышенной сложности при подготовке к ГИА по геометрии=6Решение задач повышенной сложности при подготовке к ГИА по геометрии

Ответ: 6Решение задач повышенной сложности при подготовке к ГИА по геометрии



Задача №8

Найти длину отрезка средней линии трапеции АВСD, заключенного между диагоналями (длину отрезка ЕF).

Решение:

В треугольнике АСD ЕN - средняя линия ЕN АD и ЕN=АD.

В треугольнике ВСD FN - средняя линия FN ВС и FN=ВС. Тогда ЕF= ЕN- FN=( АD- ВС)

Значит, длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности оснований.

Длина отрезка равна =1

Ответ: 1

Задача №9

В каком отношении отрезок МN делит площадь трапеции (вычислить Решение задач повышенной сложности при подготовке к ГИА по геометрии ).

Решение:

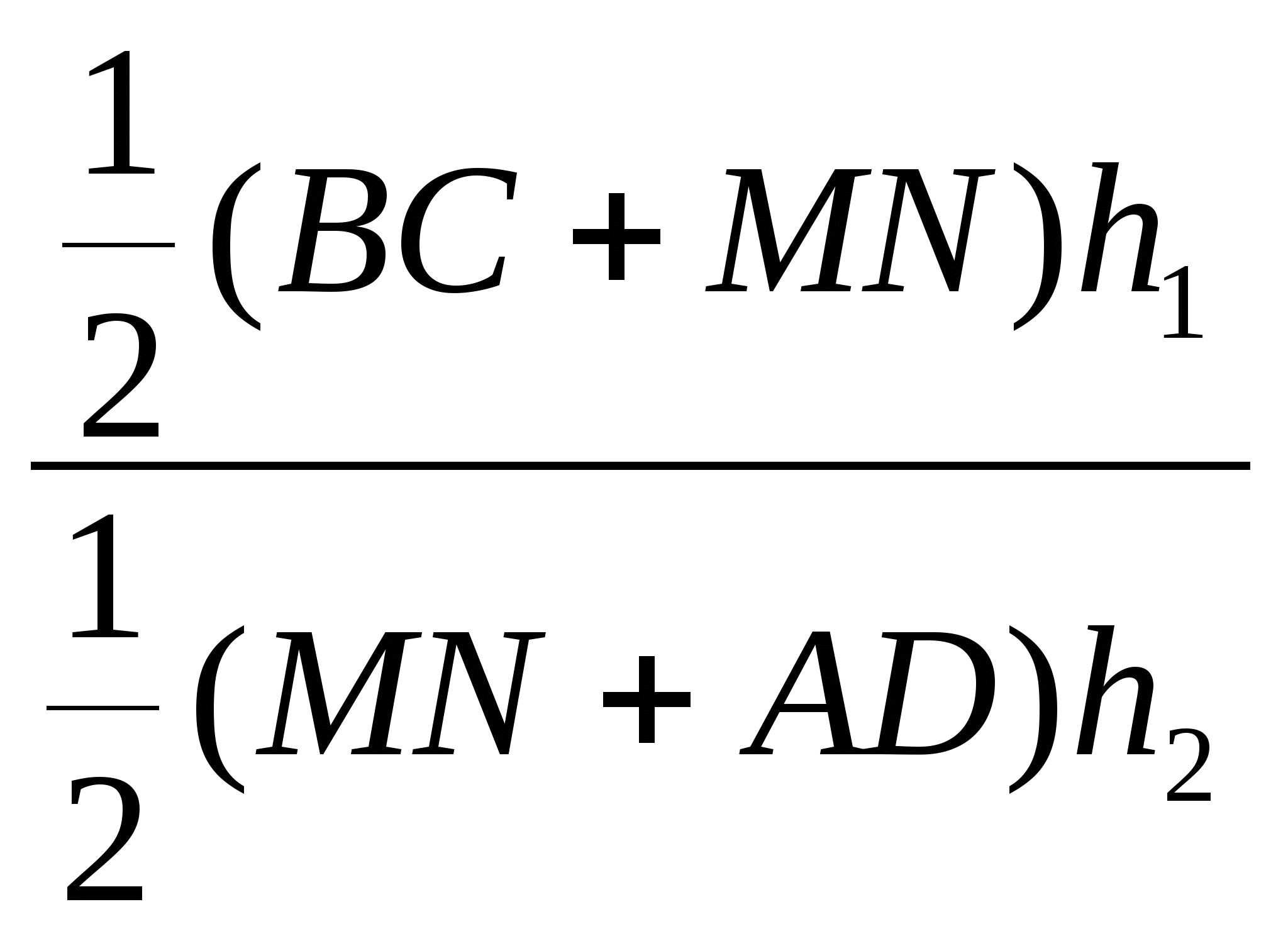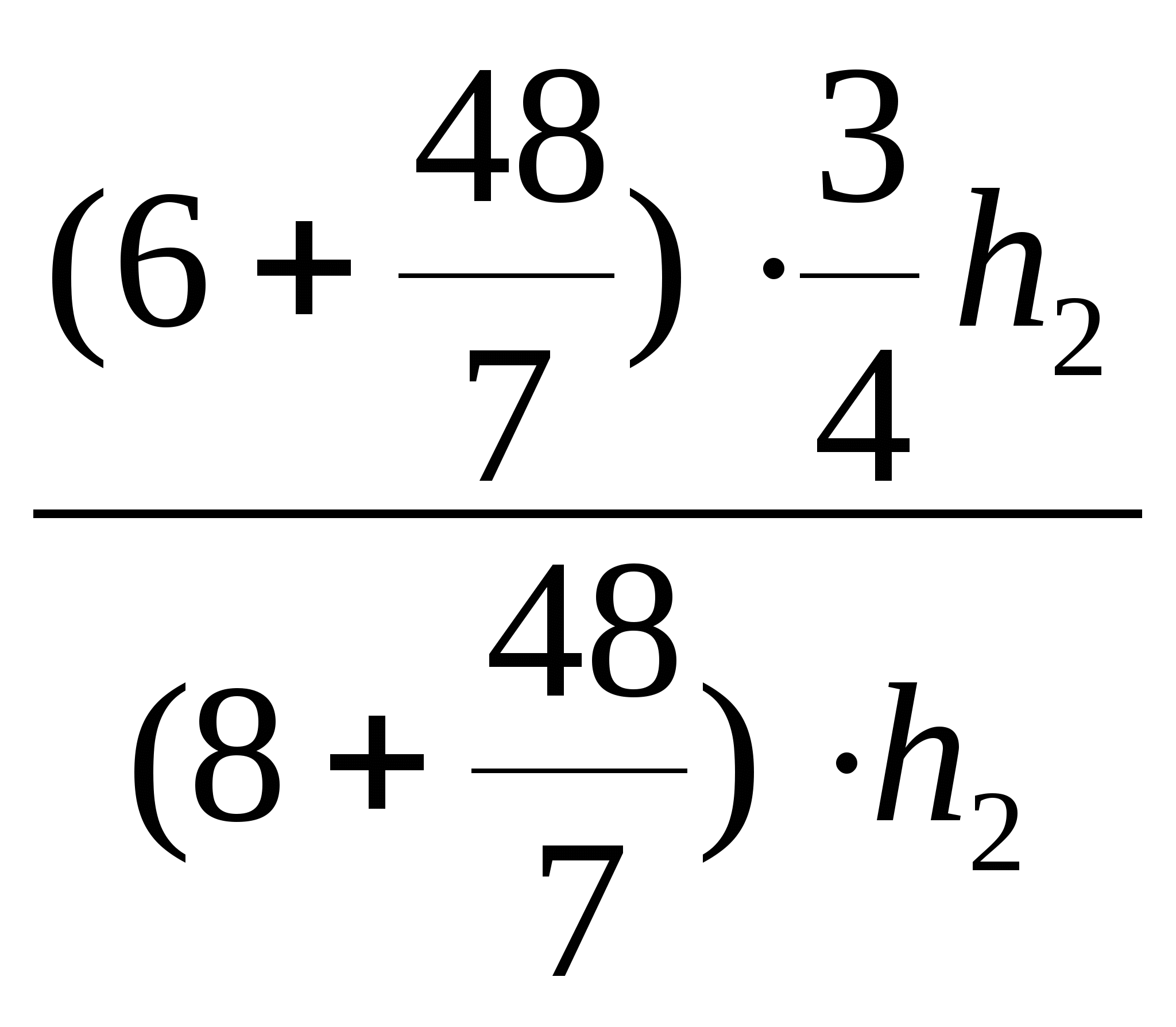Решение задач повышенной сложности при подготовке к ГИА по геометрии=Решение задач повышенной сложности при подготовке к ГИА по геометрии, где Решение задач повышенной сложности при подготовке к ГИА по геометрии иРешение задач повышенной сложности при подготовке к ГИА по геометриивысоты трапеций MNCB и ADNM соответственно. Так как Решение задач повышенной сложности при подготовке к ГИА по геометрии , то Решение задач повышенной сложности при подготовке к ГИА по геометрии =Решение задач повышенной сложности при подготовке к ГИА по геометрии.

Значит, Решение задач повышенной сложности при подготовке к ГИА по геометрии =Решение задач повышенной сложности при подготовке к ГИА по геометрии=Решение задач повышенной сложности при подготовке к ГИА по геометрии

Ответ: Решение задач повышенной сложности при подготовке к ГИА по геометрии .

Задача №10.





Н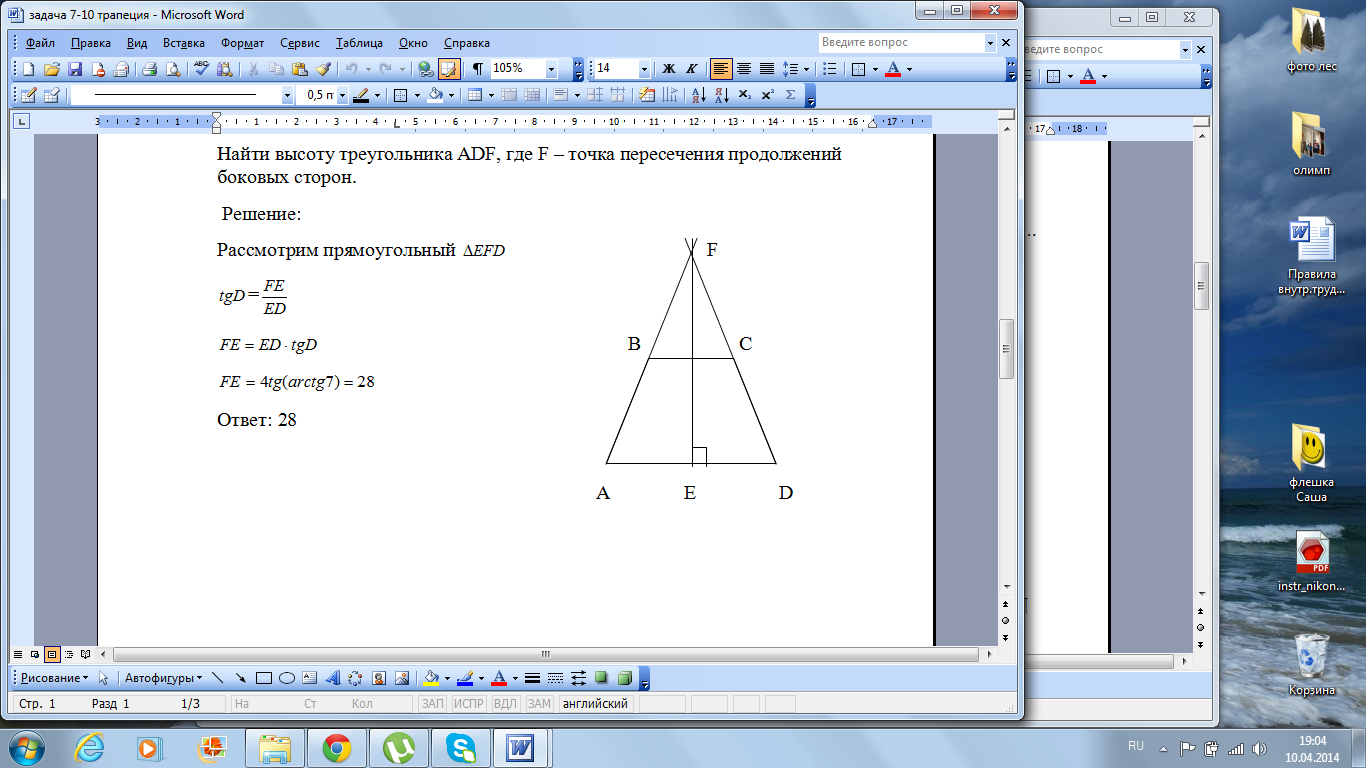Решение задач повышенной сложности при подготовке к ГИА по геометрииайти высоту треугольника ADF, где F - точка пересечения продолжений боковых сторон.

Решение: 1 способ.

Рассмотрим прямоугольный Решение задач повышенной сложности при подготовке к ГИА по геометрии

Решение задач повышенной сложности при подготовке к ГИА по геометрии=Решение задач повышенной сложности при подготовке к ГИА по геометрии

Решение задач повышенной сложности при подготовке к ГИА по геометрии

Решение задач повышенной сложности при подготовке к ГИА по геометрии

Ответ: 28

2 способ.

Треугольники Решение задач повышенной сложности при подготовке к ГИА по геометрии и Решение задач повышенной сложности при подготовке к ГИА по геометрии подобны по двум углам (угол Решение задач повышенной сложности при подготовке к ГИА по геометрии -общий, угол Решение задач повышенной сложности при подготовке к ГИА по геометрии равен углу Решение задач повышенной сложности при подготовке к ГИА по геометрии как соответственные углы при параллельных прямых Решение задач повышенной сложности при подготовке к ГИА по геометрии и Решение задач повышенной сложности при подготовке к ГИА по геометрии ).

Значит, Решение задач повышенной сложности при подготовке к ГИА по геометрии , где Решение задач повышенной сложности при подготовке к ГИА по геометрии .

Пусть Решение задач повышенной сложности при подготовке к ГИА по геометрии = Решение задач повышенной сложности при подготовке к ГИА по геометрии , тогда Решение задач повышенной сложности при подготовке к ГИА по геометрии = Решение задач повышенной сложности при подготовке к ГИА по геометрии +7 (Решение задач повышенной сложности при подготовке к ГИА по геометрии= 7 из задачи № 1)

Решение задач повышенной сложности при подготовке к ГИА по геометрииРешение задач повышенной сложности при подготовке к ГИА по геометрииРешение задач повышенной сложности при подготовке к ГИА по геометрии=21. Значит, Решение задач повышенной сложности при подготовке к ГИА по геометрии

Ответ:28





Задача №11

Известны длины оснований a=8 см и b=6 см вписанной в окружность трапеции АВСD, ВС||АD и радиус окружности R=5 см. Найдите площади четырех треугольников, на которые делят диагонали трапецию.





Дано: АВСD - трапеция,

ВС||АD

основания 8 см и 6 см

R=5



Найти S треугольников, на которые диагонали делят трапецию





Решение:

1. Δ ВОС подобен Δ АОD по двум углам (Решение задач повышенной сложности при подготовке к ГИА по геометрииВОС =Решение задач повышенной сложности при подготовке к ГИА по геометрии СОD (вертикальные), Решение задач повышенной сложности при подготовке к ГИА по геометрии ОВС = Решение задач повышенной сложности при подготовке к ГИА по геометрии ОDА (накрест лежащие при параллельных прямых (ВС и АD) и секущей ВD).

k = 4/3

Отношение S подобных треугольников равно k2

Обозначим S Δ ВОС за х, тогда S Δ АОD = 16/9х

S Δ ВОА = S Δ СОD = 4/3х (см. БЗ 2.8)

2. S Δ АВСD = 1/2* (8+6)*7=49

S Δ АВСD = S Δ ВОА+ S Δ АОD + S Δ ВОС +S Δ СОD

х+ 16/9х+4/3х+4/3х = 49

х= 9 см2 - S Δ ВОС

S Δ АОD = 16/9*9=16 см2

S Δ ВОА = S Δ СОD = 4/3*9=12 см2

Ответ: 9 см2, 16 см2 , 12 см2



Задача №12

а) Найдите длину отрезка, .параллельного основаниям трапеции, который делит трапецию на две равновеликие трапеции.









Дано: АВСD - трапеция,

ВС|| АD

основания 8 см и 6 см



Найти: длину MN



Решение:

Согласно БЗ2.12 MN = Решение задач повышенной сложности при подготовке к ГИА по геометрии = 4Решение задач повышенной сложности при подготовке к ГИА по геометрии см



б) Найдите длину отрезка, .параллельного основаниям трапеции, который делит трапецию на две подобные трапеции.









Дано: АВСD - трапеция,

ВС|| АD

основания 8 см и 6 см



Найти: длину MN



Решение:

Согласно БЗ2.11 MN = Решение задач повышенной сложности при подготовке к ГИА по геометрии = 5Решение задач повышенной сложности при подготовке к ГИА по геометриисм



Задача №13

Можно ли в трапецию вписать окружность?



В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы противоположных сторон равны. (БЗ2.5)

Проверим АВ + СD = ВС + АD,

8 см + 6 см Решение задач повышенной сложности при подготовке к ГИА по геометрии 5Решение задач повышенной сложности при подготовке к ГИА по геометриисм+5Решение задач повышенной сложности при подготовке к ГИА по геометриисм

В данную трапецию окружность вписать нельзя.

⇧
⇩
скачать материал


 
 
X

Чтобы скачать данный файл, порекомендуйте его своим друзьям в любой соц. сети.

После этого кнопка ЗАГРУЗКИ станет активной!

Кнопки рекомендации:

загрузить материал