Исследование к уроку математики Золотое сечение

ШКОЛЬНАЯ НАУЧНО-ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ

СЕКЦИЯ «ВОКРУГ НАС МИР, 5-7 классы»

Автор: Хребтова Вера Сергеевна.

Дата рождения: 18.10.2002г

Место учёбы: муниципальное казённое общеобразовательное учреждение «Кондинская средняя общеобразовательная школа».

Адрес образовательного учреждения: 641971, Шатровский район, с. Кондинское, ул. Центральная, д.9.

Тема работы: «Золотое сечение»

Секция: «ВОКРУГ НАС МИР, 5-7 классы»

Руководитель: Фефелова Татьяна Кузьминична, учитель математики МКОУ «Кондинская средняя общеобразовательная школа».

Место работы: МКОУ «Кондинская средняя общеобразовательная школа».

Содержание:

1. Введение…………………………………………………………. 3стр.

2. Проведение исследования .………………………... ……… …. 5стр.

3. Золотое сечение в природе, искусстве, архитектуре (Практическое применение) .………………………………………………………5стр.

4. Заключение……………………………………………………….. 7стр.

5. Список литературы……………………………………………….8 стр.

6. Приложение……………………………………………………….8 стр.

1. ВВЕДЕНИЕ

В математике пропорцией (лат. proportio) называют равенство двух отношений:a : b = c : d.

Отрезок прямой АВ можно разделить на две части следующими способами:

• на две равные части - АВ : АС = АВ : ВС;

• на две неравные части в любом отношении (такие части пропорции не образуют);

• таким образом, когда АВ : АС = АС : ВС.

Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.

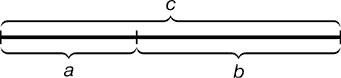
Золотое сечение - это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему

a : b = b : c или с : b = b : а.

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования».

Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа - важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела - длина плеча, предплечья и кисти, кисти и пальцев и т.д.

Мы решили исследовать в своём классе, кто ближе всех подходит под эталоны пропорциональности - Аполлона Бельведерского и Венеру Милосскую

Объект исследования: обучающиеся 6 класса МКОУ «Кондинская СОШ»

Цель исследования: Определить, в каком отношении делит тело человека точка пупка.

Задачи исследования:

1. Изучить учебную и дополнительную литературу.

2. Провести практические исследования и выяснить, в каком отношении делит тело человека точка пупка.

3. Обработать полученную информацию.

4. Интерпретировать результаты практических исследований.

5. Наглядно представить полученную информацию.

Методы исследования: изучение литературы, проведение опытов, обработка полученных данных, анализ, сравнение полученных результатов.

Этапы работы:

1. Изучение учебной и дополнительной литературы по данному вопросу.

2. Проведение опытов.

3. Обработка полученных данных.

2. ПРОВЕДЕНИЕ ИССЛЕДОВАНИЙ.

a

b

c=a+b

b/a

c/b

1

Вера

59

100

159

1.695

1,59

2

Люда

54

95

149

1.759

1,568

3

Настя

59

97

156

1,644

1,608

4

Максим

58

100

158

1,724

1,58

5

Саша

56

96

152

1.714

1,583

6

Егор

57

93

150

1,631

1,612

7

Юра

54

85

139

1,574

1,635

ВЫВОД: По исследованию Цейзинга пропорция составляет к 13 годам отношение равное 8:5 = 1,6. Из таблицы исследования, проведённого в нашем классе, видно, что ближе всех к этому отношению подходят параметры Егора и Насти, у большей части учеников нашего класса ноги длиннее, чем в среднестатистических значениях, а у Юры - короче.

3. ЗОЛОТОЕ СЕЧЕНИЕ В ПРИРОДЕ, ИСКУССТВЕ, АРХИТЕКТУРЕ.

Среди придорожных трав растет ничем не примечательное растение - цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок

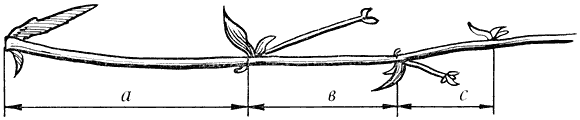
Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий - 38, четвертый - 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

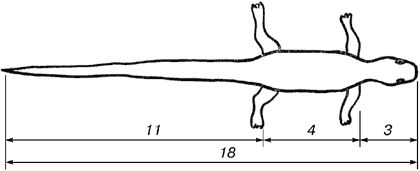
В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции - длина ее хвоста так относится к длине остального тела, как 62 к 38.

И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы - симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.

Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.

На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны - освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Слева от главной сосны находится множество сосен - при желании можно с успехом продолжить деление картины по золотому сечению и дальше.

</</font>

Гармония в архитектурном произведении зависит не столько от размеров самого сооружения, сколько от соотношений между размерами составляющих его частей. Для того чтобы выполнялся основной принцип гармонии "все во всем", взаимосвязь частей и целого в архитектурном произведении должна иметь единое математическое выражение.

4. ЗАКЛЮЧЕНИЕ

В процессе исследования мы выполнила все поставленные перед собой задачи:

изучила учебную и дополнительную литературу, провела практические исследования для выяснения, в каком отношении делит тело человека точка пупка, обработала полученную информацию, проведя математические расчёты, данные поместила в таблицу для наглядного представления информации.

Исследование в своём классе, кто ближе всех подходит под эталоны пропорциональности - Аполлона Бельведерского и Венеру Милосскую, показало, что это Егор и Настя

5. СПИСОК ЛИТЕРАТУРЫ И ДРУГИХ ИСПОЛЬЗУЕМЫХ РЕСУРСОВ

1. «Математика 6» Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд.

2. Яндекс-картинки.

3. Википедия.

6. ПРИЛОЖЕНИЯ