Дидактические материалы тема 'Множества' (7-9 классы)

Дидактические материалы по теме

МНОЖЕСТВА

Составитель: Мелькис А.И.

1. Вова выучил 12 вопросов, 5 - вообще не смотрел, остальные из 20 вопросов кое-что знает. Сколько можно составить билетов?

Ответ. С_п^к =п!/(п-к)!*к! С₂₀³ =20*19*18/1*2*3=1140 билетов.

Сколько билетов, которые Вова полностью знает?

Ответ. С₁₂³ =12*11*10/1*2*3=220 билетов.

Сколько билетов будет, в которые включены каждый из вопросов (знает, немного знает, не знает)?

Ответ. 12*5*3=180 билетов.

Всего 1, 2, 3, …, 12 вопросов. Сколько билетов, за которые Вова получит положительную оценку?

Ответ. С₁₂² =12*11/1*2=66 билетов.

Элементы теории множества

Множество - это совокупность объектов, предметов, объединенных в единое целое по какому-либо признаку.

Предметы, из которых состоит множество, называют элементами множества.

А,В,С, …-множество

а, б, с, …-элементы множества

Существует элемент, принадлежащий множеству и элемент, не принадлежащий множеству.

Примеры множеств: люди, множество натуральных чисел, …

Множество может содержать 1, 2, 3, .. бесконечное множество элементов, может не содержать ни одного элемента.

А=[3] пустое множество

Конечное множество - это множество, элементы которого можно сосчитать.

Бесконечное - множество, содержащее бесконечное число элементов.

5х-3=2 Можно записывать корни уравнения [1]

а в а в

(а;в) [а;в)

Способы задания множеств

Множество считается заданным, если мы владеем способом, позволяющим определить, принадлежит данный предмет множеству или нет.

1. Словесное описание множества (записать множество нечетных чисел).

2. Перечисление всех элементов данного множества (А=[1. 2. 3. 6. 9])

3. Указание характеристических свойств элементов данного множества, т.е. таких свойств, которыми обладают элементы данного множества и не обладает ни один элемент, не входящий в это множество. (С=[х / х принадлежит N, х - четное] 7х-13=1 В=[х / х принадлежитN, х - корень уравнения 7х-13=1] В=[2] 44х+15=6 С=[х / х принадлежит N, х - натуральное и х - корень уравнения 4х+15=6]

Отношения между множествами

А=[1, 2, 3, 4, 5, 6, 7, 8, 9] В=[3, 6, 9] C=[21,72]

Все элементы множества В являются элементами множества А.

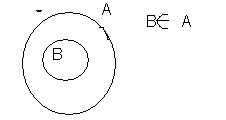
Множество В называется подмножеством множества А, если каждый элемент множества В принадлежит множеству А.

Множества А и В называются равными, если А принадлежит В и В принадлежит А, т.е. А=В.

1)

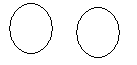
А = В

2)

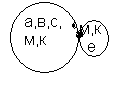
А В

3)

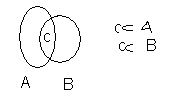
4)

5)

А=В

6)

конъюнкция «и» дизъюнкция «или»

Объединением множеств А и В называется множество, состоящее из всех и только тех элементов, которые принадлежат множеству А или множеству В.

А=[3, 4, 5, 6] В=[6, 7, 8, 9]

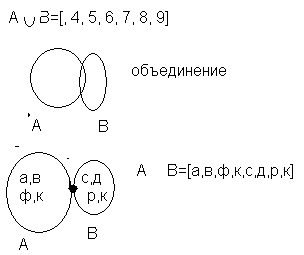
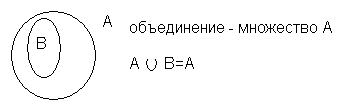
Пересечением двух множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат множеству А и множеству В.

А=[2, 7, 8, 11] В=[3, 4, 11, 19]

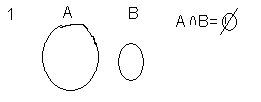
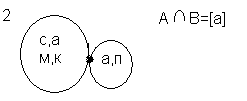
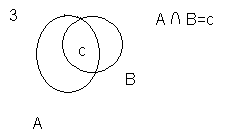
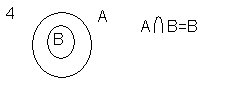
Свойства операций объединения и пересечения

(если множество А пересекает множество В, то и множество В пересекает множество А)

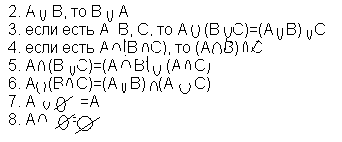
Дополнением С подмножества В до множества А называется такое множество, что