Урок по алгебре 9 класс Решение систем нелинейных уравнений второй степени

Урок по алгебре в 9 классе по теме: «Решение систем нелинейных уравнений второй степени»

Материал прислала: Никитина Наталья Ивановна, учитель математики

Горловской ОШ№12 І-ІІІ ступеней с углубленным изучением отдельных предметов

Тип урока: объяснение нового материала

Цели урока:

• составлять системы нелинейных уравнений второй степени для графических моделей и находить их решения; рассмотреть способы решения систем уравнений второй степени;

формировать умения и навыки решать системы уравнений.

• развивать логическое и критическое мышление, умение пояснять свои действия, анализировать и сравнивать, делать выводы.

• воспитывать внимательность, работоспособность, формировать духовную потребность и мотивы деятельности.

Оборудование: таблицы, опорный конспект

Ход урока

I. Организационный момент.

Наш урок начинается с высказывания известного российского

ученого М.Ломоносова - «Математика-это гимнастика ума».

Если ежедневно тренировать свой ум, то развивается логическое мышление, интеллектуальные способности. Развивать способности

будем при изучении данной темы (представление темы и целей урока ) .

На этом уроке у нас общие цели - рассмотреть способы решения систем и научиться находить их решения. Чтобы дойти до цели, нужно прежде всего, идти вперед.

Я жду от вас активности, четких ответов и смелых идей. Ваша задача, собрать как можно больше информации и фактов по этой теме. В этом вам поможет опорный конспект(приложение№1)

II. Мотивация.

Рассмотрим прямоугольную систему координат - в центре Солнце.

Планета движется по закону +у=25, а траектория кометы

у = х-5 . Найдем точки пересечения орбит.

Что для этого нужно?

- построить графики.

- что есть графиком функции +у=25?

- какому графику функции соответствует закон движения кометы?

- какие точки важны для построения параболы?

- как найти координаты вершины параболы?

- с осью абсцисс?

Постройте траекторию движения кометы. Самоконтроль.

- сколько точек пересечения?

- назвать точки пересечения орбит.

Обратим внимание на графическую модель №2 . По каким законам движутся астрономические тела? Сколько точек пересечения имеют их траектории?

Как переформулировать задание?

Постановка проблемы.

Решить систему

Результат

III. Актуализация опорных знаний.

Завершить формулировки основных понятий

- систему образуют два или ________________________________

- системы, которые имеют одни и те же решения называются ________________________________­________________________

- чем является пара чисел, которое обращает каждое уравнение в верное равенство _________________________________________

- решить систему, это значит _______________________________

Устно решить систему:

Для решения систем нужно повторить решение квадратных уравнений. Опорный конспект .

а)

б)

в)

IV. Решение упражнений.

Вернемся к таблице. Если мы решили систему графическим способом ( заметили, что способ неточный), то решим эту систему аналитическим способом.

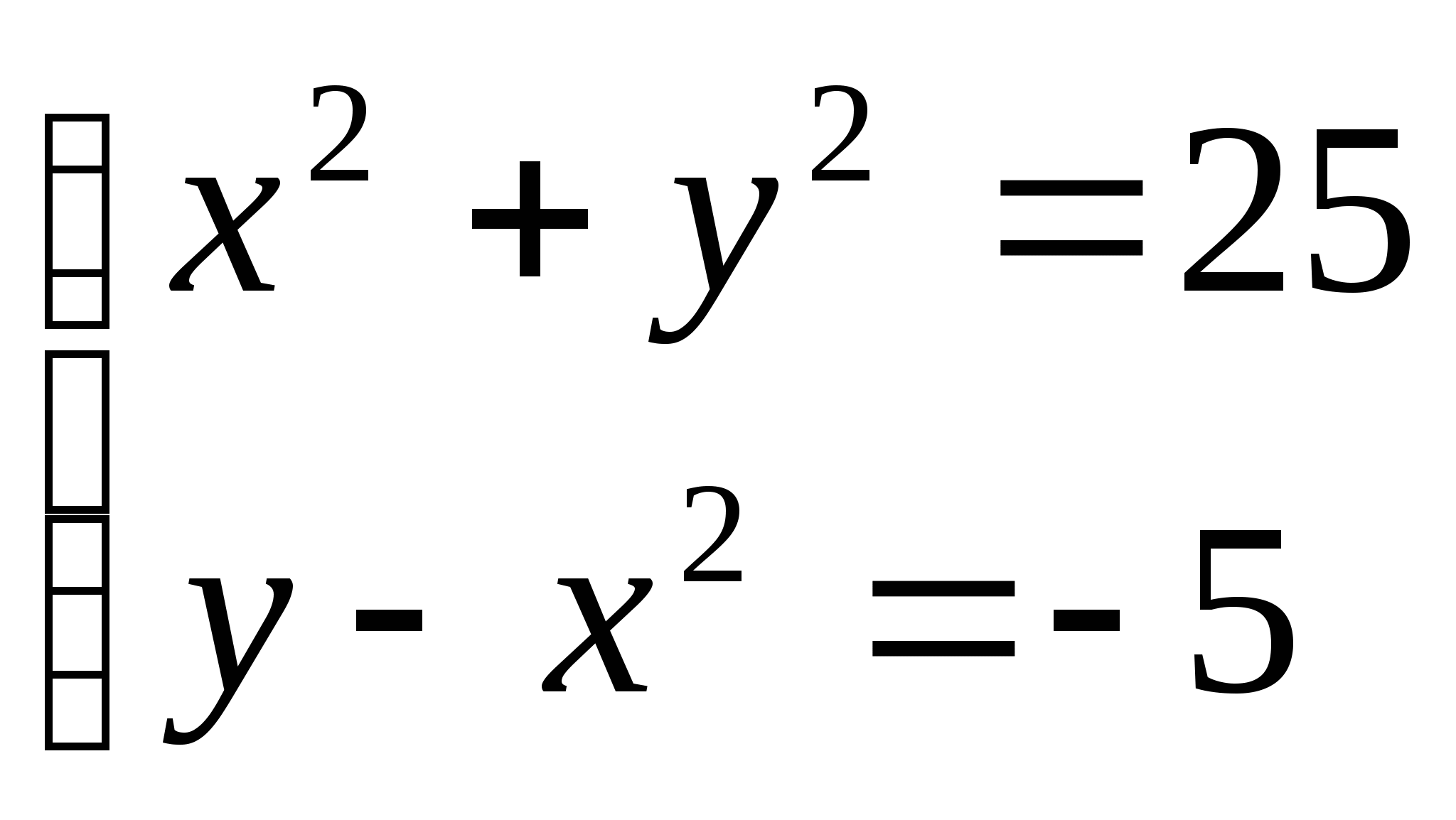
Какой способ рационально применить? Запишите ответ.

Ответ: ( 0; -5), (3; 4), (-3;4).

Ученик у доски. Решить систему:

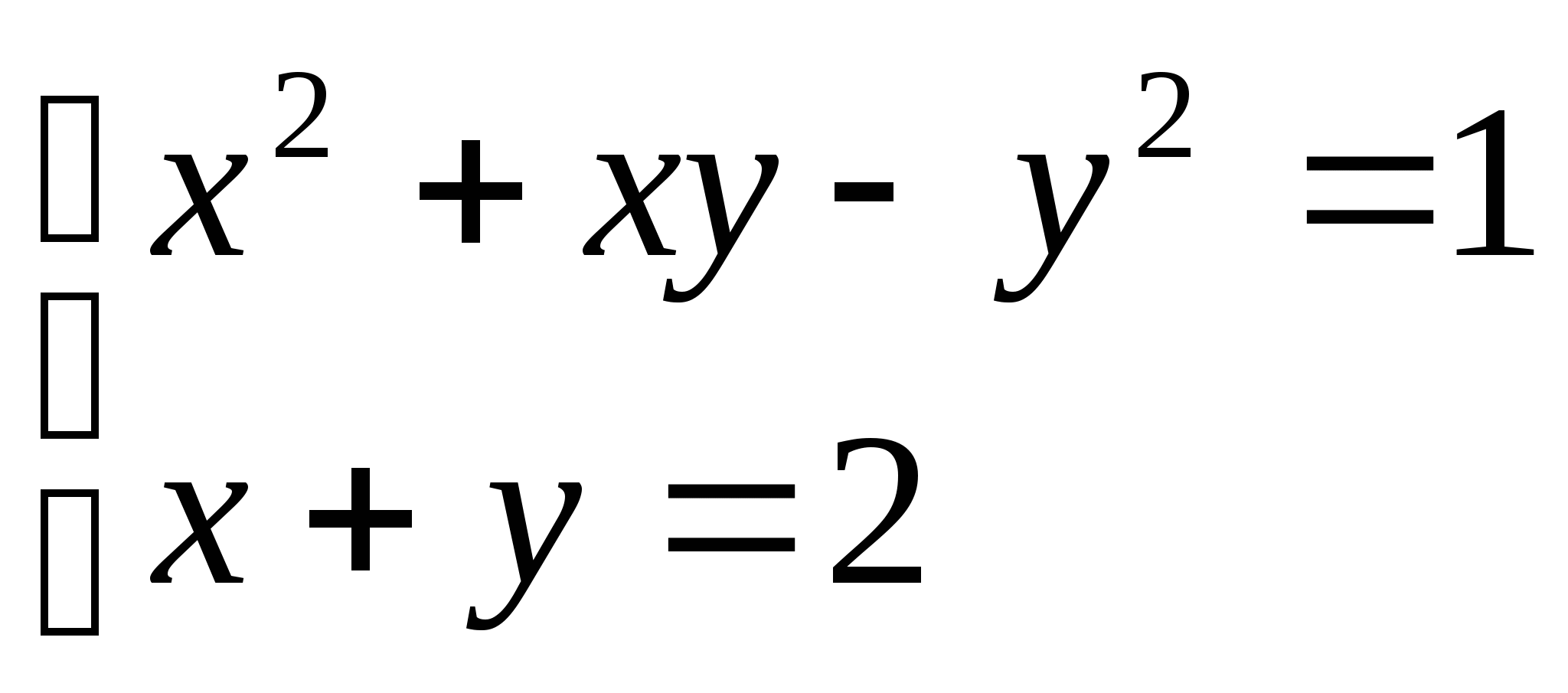
Ваш выбор?

Ответ: (5;-3) , (1;1)

Открываем практическую лабораторию. Два ученика делают открытия, решают системы (остальные могут решать самостоятельно).

№178а) 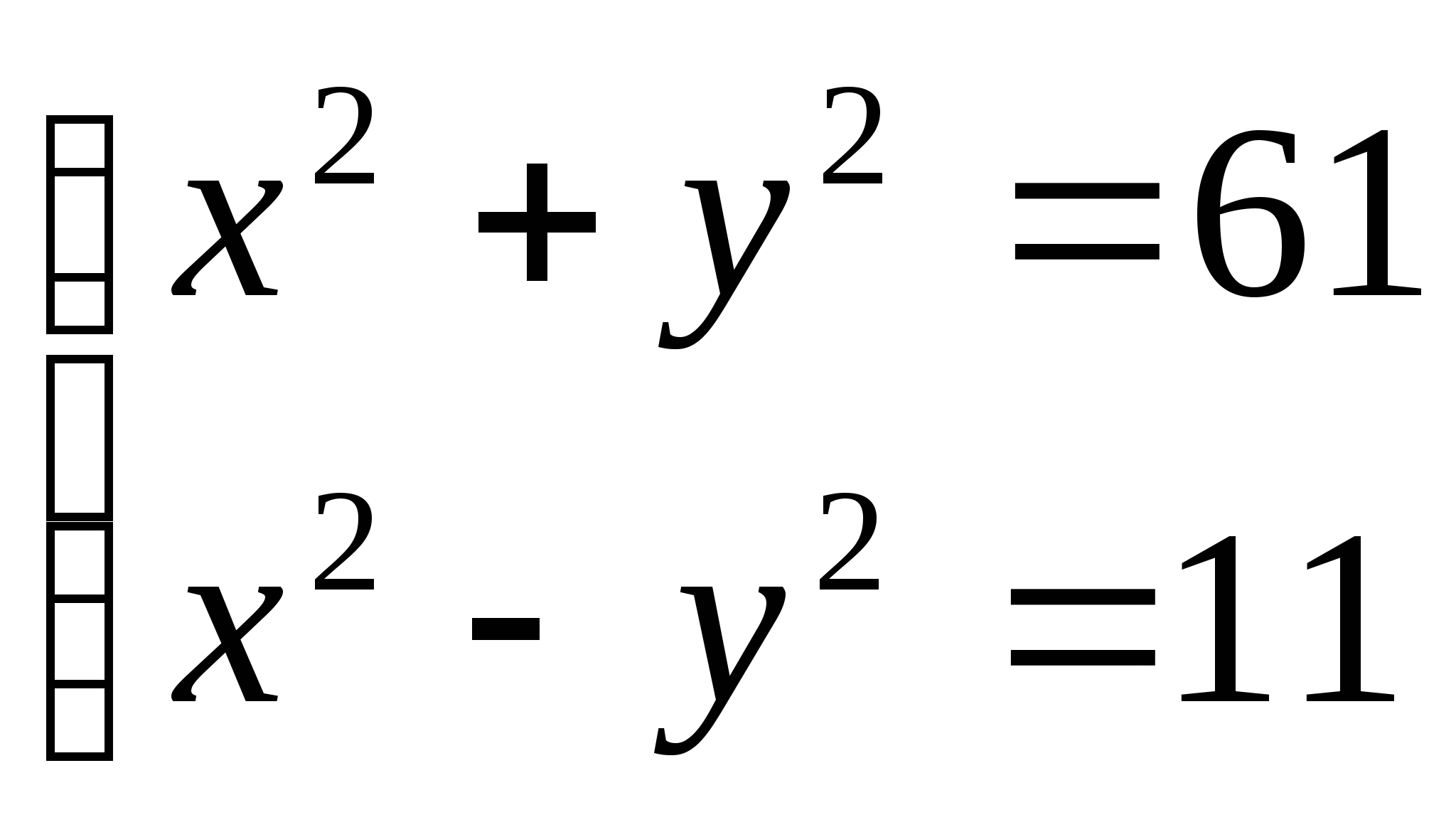№2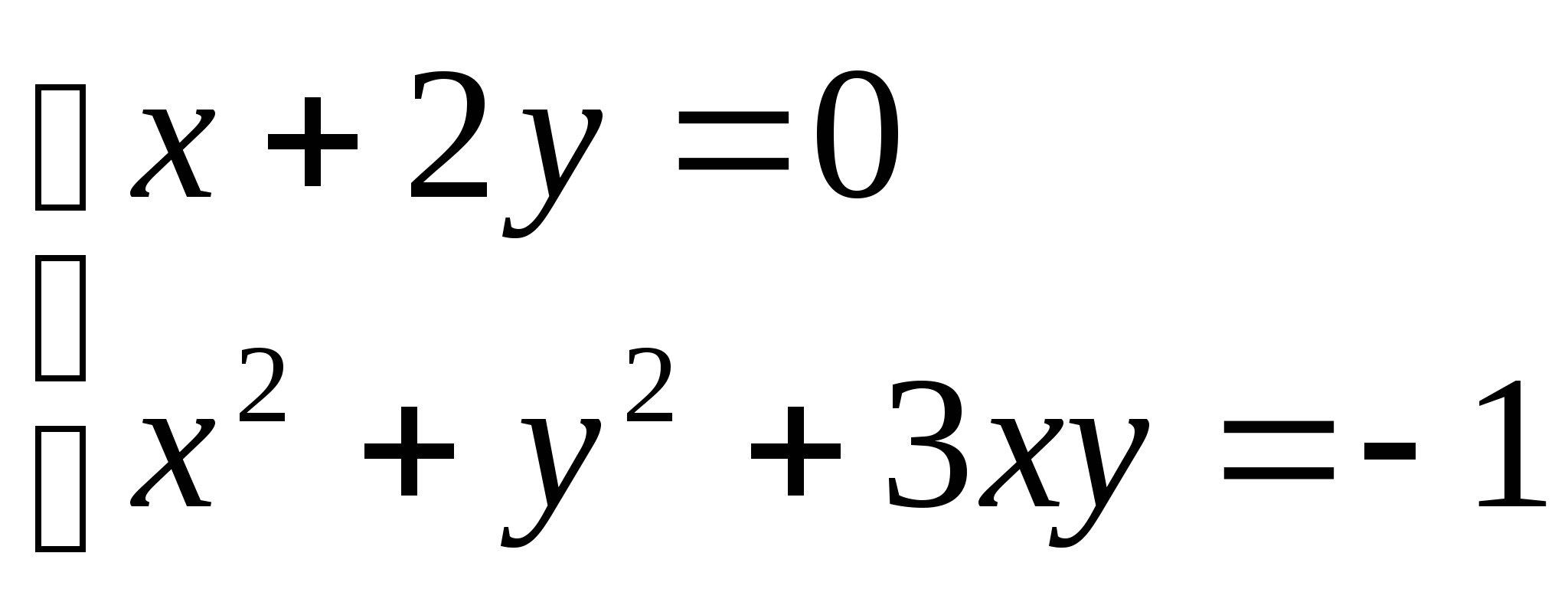

Ответ: (6;5), (6;-5) Ответ: (2;-1), (-2;1)

(-6;5), (-6;-5)

Способ замены. Решить систему:

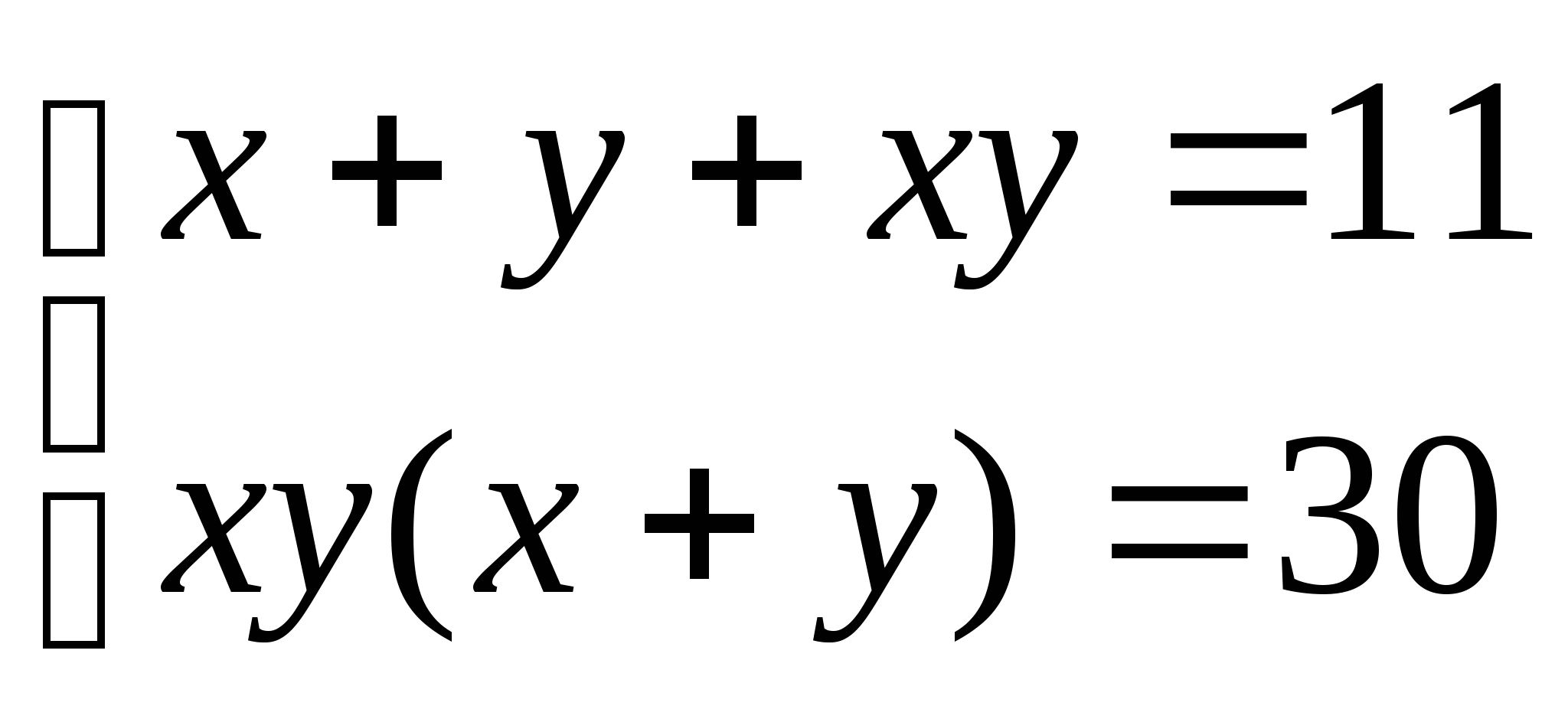
Ответ: (2;3), (3;2), (1;5), (5;1).

V. Домашнее задание : п. 57 решить О. 169а), № 176а)

Д. № 176б), № 170б)

В. № 172а), № 178б)

VI. Подведение итогов урока.

Подошло время вернуться к началу урока, к целям.

- что делали на уроке?

- какие способы применяли?

- есть ли универсальный способ решения систем?

- над чем нужно работать?

- сможете ли вы решать системы самостоятельно?

Сможете ли Вы, решать системы уравнений второй степени самостоятельно?

ДА НАДО НЕТ

ДОРАБОТАТЬ

Домашняя работа: п.57

№172а № 178б

№176б

№170б

№169а

№176а