- Учителю
- Рабочая программа по математике для 7 класса
Рабочая программа по математике для 7 класса
| 3Рассмотрено на ШМО «Математика» Руководитель_________ /Лапина О.Д./ От « »_______20_14___ г | Согласовано Зам директора по УВР _______ /Жильцова И.В./ от « » ______2014___ г. | «Утверждаю» Директор МБОУ«Курьинская сош» им. М.Т.Калашникова __________ /Лёгоньких JI.H./ Приказ № _______ от « » _______2014___ г
|
.
.
Администрация Курьинского района Алтайского края
Муниципальное бюджетное образовательное учреждение
«Курьинская средняя общеобразовательная школа»
имени М.Т. Калашникова
Рабочая программа
по математике для 7 класса
по учебному курсу «Алгебра», «Геометрия»
базовый уровень
на 2014-2015 учебный год
Образовательная область: Математика
Сроки реализации: 2013-2014 учебный год
Разработчик: Лапина Ольга Дмитриевна, учитель математики, высшей квалификационной категории
с. Курья
2014 год
Пояснительная записка
к рабочей программе по математике для 7 класса
Рабочая программа составлена на основании:
-
федерального компонента Государственного образовательного стандарта основного общего образования по математике. Базовый уровень;
-
федерального перечня учебников на 2013-2014 учебный год, рекомендованного Министерством образования и науки РФ к использованию в образовательном процессе в ОУ;
-
Программы общеобразовательных учреждений. Алгебра. 7-9 классы. Составитель: Бурмистрова Т. А. - Москва «Просвещение» 2010 г.
-
Программы общеобразовательных учреждений. Геометрия. 7-9 классы. Составитель: Бурмистрова Т. А. - Москва «Просвещение» 2009 г.
-
Государственный стандарт основного общего образования по математике.
Программа соответствует учебнику: Алгебра. 7 класс: учебник для общеобразовательных учреждений / Ю. Н. Макарычев, Н. Г. Миндюк и др.; под ред. С. А. Теляковского. - М.: Просвещение, 2009. Геометрия 7-9 класс: учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И Юдина. - М.: Просвещение, 2009.
-
Базисного учебного плана 2004 года.
-
Основной общеобразовательной программы МБОУ «Курьинская средняя общеобразовательная школа» им М.Т. Калашникова
Структура документа:
рабочая программа по математике включает разделы:
-
пояснительную записку;
-
цели изучения математики; обоснование выбора умк
-
основное содержание с примерным распределением учебных часов по разделам курса;
-
требования к уровню подготовки выпускников;
-
учебно-методический комплект;
-
календарно-тематическое планирование.
-
лист коррекции рабочей программы
-
контрольные работы
Место предмета в базисном учебном плане
Согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации для обязательного изучения математики на этапе осовного общего образования на изучение математики в 7 классе отводится 204 часов (в неделю 6 часов). Из них алгебра - 136 часов, геометрия - 68 часов по II варианту (алгебра: 4 часа в неделю, геометрия: 2 часа в неделю. Резерв 6 часов из расчёта 35 рабочих недель за год.
Срок реализации рабочей учебной программы - один учебный год.
Уровень обучения: базовый.
Изучение курса в 7 классе направлено на достижение следующих целей:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
В задачи обучения математики входит:
-
овладение навыками дедуктивных рассуждений;
-
получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и т.д.);
-
развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.
Содержание обучения курса алгебры.
-
Выражения, тождества, уравнения.
Числовые выражения с переменными. Простейшие преобразование выражений. Уравнения, корень уравнения. Линейное уравнения с одной переменной. Решение текстовых задач методом составления уравнений. Статистические характеристики.
Основная цель - систематизировать и обобщить сведения о преобразованиях алгебраических выражений и решении уравнений с одной переменной.
Первая тема курса 7 класса является связующим звеном между курсом математики 5-6 классов и курсом алгебры. В ней закрепляются вычислительные навыки, систематизируются и обобщаются сведения о преобразованиях выражений и решении уравнений.
Нахождение значений числовых и буквенных выражений дает возможность повторить с учащимися правила действий с рациональными числами. Умения выполнять арифметические действия с рациональными числами являются опорными для всего курса алгебры. Следует выяснить, насколько прочно овладели ими учащиеся, и в случае необходимости организовать повторение с целью ликвидации выявленных пробелов. Развитию навыков вычислений должно уделяться серьезное внимание и в дальнейшем при изучении других тем курса алгебры.
В связи с рассмотрением вопроса о сравнении значений выражений расширяются сведения о неравенствах: вводятся знаки ![]() и
и ![]() , дается понятие о двойных неравенствах.
, дается понятие о двойных неравенствах.
При рассмотрении преобразований выражений формально-оперативные умения остаются на том же уровне, учащиеся поднимаются на новую ступень в овладении теорией. Вводятся понятия «тождественно равные выражения», «тождество», «тождественное преобразование выражений», содержание которых будет постоянно раскрываться и углубляться при изучении преобразований различных алгебраических выражений. Подчеркивается, что основу тождественных преобразований составляют свойства действий над числами.
Усиливается роль теоретических сведений при рассмотрении уравнений. С целью обеспечения осознанного восприятия учащимися алгоритмов решения уравнений вводится вспомогательное понятие равносильности уравнений, формируется и разъясняется на конкретных примерах свойства равносильности. Дается понятие линейного уравнения и исследуется вопрос о числе его корней. В системе упражнений особое внимание уделяется решению уравнений вида ax=b при различных значениях a и b. продолжается работа по формированию у учащихся умения использовать аппарат уравнений как средство для решения текстовых задач. Уровень сложности задач здесь остается таким же, как и в 6 классе.
Изучение темы завершается ознакомлением учащихся с простейшими статистическими характеристиками: средним арифметическим, модой, медианой, размахом. Учащиеся должны уметь использовать эти характеристики для анализа ряда данных в несложных ситуациях.
-
Функции.
Функция, область определения функции. Вычисление значений функции по формуле. График функции. Прямая пропорциональность и ее график. Линейная функция и ее график.
Основная цель - ознакомить учащихся с важнейшими понятиями и графиками прямой пропорциональности и линейной функции общего вида.
Данная тема является начальным этапом в систематической функциональной подготовке учащихся. Здесь вводятся такие понятия, как функция, аргумент, область определения функции, график функции. Функция трактуется как зависимость одной переменной от другой. Учащиеся получают первое представления о способах задания функции. В данной теме начинается работа по формированию у учащихся умений находить по формуле значение функции по известному значению аргумента, выполнять ту же задачу по графику и решать по графику обратную задачу.
Функциональные понятия получают свою конкретизацию при изучении линейной функции и ее частного вида - прямой пропорциональности. Умение строить и читать графики этих функций широко используется как в самом курсе алгебры, так и в курсах геометрии и физики. Учащиеся должны понимать, как влияет знак коэффициента на расположение в координатной плоскости графика функции y=kc, где k≠0, как зависит от значений k и b взаимное расположение графиков двух функций вида y=kc+b.
Формирование всех функциональных понятий и выработка соответствующих навыков, а также изучение конкретных функций сопровождаются рассмотрением примеров реальных зависимостей между величинами, что способствует усилению прикладной направленности курса алгебры.
-
Степень с натуральным показателем.
Степень с натуральным показателем и ее свойства. Одночлен. Функции ![]() ,
, ![]() и их графики.
и их графики.
Основная цель - выработать умения выполнять действия над степенями с натуральными показателями.
В данной теме дается определение степени с натуральным показателем. В курсе математики 6 класса учащиеся уже встречались с примерами возведения чисел в степень. В связи с вычислением значений степени в 7 классе дается представление о нахождении значений степени с помощью калькулятора. Рассматриваются свойства степени с натуральным показателем. На примере доказательства свойств am![]() an=am+n, am:an=am-n, где m>n, (am)n=amn, (ab)n=anbn учащиеся впервые знакомятся с доказательствами, проводимыми на алгебраическом материале. Указанные свойства степени с натуральным показателем находят применение при умножении одночленов и возведении одночленов в степень. При нахождении значений выражений, содержащих степени, особое внимание следует обратить на порядок действий.
an=am+n, am:an=am-n, где m>n, (am)n=amn, (ab)n=anbn учащиеся впервые знакомятся с доказательствами, проводимыми на алгебраическом материале. Указанные свойства степени с натуральным показателем находят применение при умножении одночленов и возведении одночленов в степень. При нахождении значений выражений, содержащих степени, особое внимание следует обратить на порядок действий.
Рассмотрение функций ![]() ,
, ![]() позволяет продолжить работу по формированию умений строить и читать графики функций. Важно обратить внимание учащихся на особенности графика функции
позволяет продолжить работу по формированию умений строить и читать графики функций. Важно обратить внимание учащихся на особенности графика функции ![]() : график проходит через начало координат, ось Oy является его осью симметрии, график расположен в верхней полуплоскости.
: график проходит через начало координат, ось Oy является его осью симметрии, график расположен в верхней полуплоскости.
Умение строить графики функций ![]() ,
, ![]() используется для ознакомления учащихся с графическим способом решения уравнений.
используется для ознакомления учащихся с графическим способом решения уравнений.
-
Многочлены.
Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочленов на множители.
Основная цель - выработать умения выполнять сложение, вычитание, умножение многочленов и разложение многочленов на множители.
Данная тема играет фундаментальную роль в формировании умения выполнять тождественные преобразования алгебраических выражений. Формируемые здесь формально-оперативные умения являются опорными при изучении действий с рациональными дробями, корнями, степенями с рациональными показателями.
Изучение темы начинается с введения понятия многочлена, стандартного вида многочлена, степени многочлена. Основное место в этой теме занимают алгоритмы действий с многочленами - сложение, вычитание и умножение. Учащиеся должны понимать, что сумму, разность, произведение многочленов всегда можно представить в виде многочлена. Действия сложения, вычитание и умножение многочленов выступает как составной компонент в заданиях на преобразования целых выражений. Поэтому нецелесообразно переходить к комбинированным заданиям прежде, чем усвоены основные алгоритмы.
Серьезное внимание в этой теме уделяется разложению многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки. Соответствующие преобразования находят широкое применение как в курсе 7 класса, так и в последующих курсах, особенно в действиях с рациональными дробями.
В данной теме учащиеся встречаются с примерами использования рассматриваемых преобразований при решении разнообразных задач, в частности при решении уравнений. Это позволяет в ходе изучения темы продолжить работу по формированию умения решать уравнения, а также решать задачи методом составления уравнений. В число упражнений включаются несложные задания на доказательство тождества.
-
Формулы сокращенного умножения.
Формулы (a±b)2=a2±2ab+b2, (a±b)3=a3±3a2b+3ab2±b3, (a±b)(a2±ab+b2)=a3±b3. Применение формул сокращенного умножения в преобразовании выражений.
Основная цель - выработать умения применять формулы сокращенного умножения в преобразованиях целых выражений в многочлены и в разложении многочленов на множители.
В данной теме продолжается работа по формированию у учащихся умений выполнять тождественные преобразования целых выражений. Основное внимание в теме уделяется формулам (a-b)(a+b)=a2-b2, (a±b)2=a2±2ab+b2. Учащиеся должны знать эти формулы и соответствующие словесные формулировки, уметь применять их как «слева направо», так и «справа налево».
Наряду с указанными рассматриваются также формулы (a±b)3=a3±3a2b+3ab2±b3, (a±b)(a2±ab+b2)=a3±b3. Однако они находят меньшее применение в курсе, поэтому не следует излишне увлекаться выполнением упражнений на их использование.
В заключительной части темы рассматривается применение различных приемов разложения многочленов на множители, а также использование преобразований целых выражений для решения широкого круга задач.
-
Системы линейных уравнений.
Система уравнений. Решение систем двух линейных уравнений с двумя переменными и его геометрическая интерпретация. Решение текстовых задач методом составления систем уравнений.
Основная цель - ознакомить учащихся со способами решения систем линейных уравнений с двумя переменными, выработать умения решать системы уравнений с двумя переменными, выработать умения решать системы уравнений и применять их при решении текстовых задач.
Изучение систем уравнений распределяется между курсами 7 и 9 классов. В 7 классе вводится понятие системы и рассматриваются системы линейных уравнений.
Изложение начинается с введения понятия «линейное уравнение с двумя переменными». В систему упражнений включаются несложные задания на решение линейных уравнений с двумя переменными в целых числах.
Формируется умение строить график уравнения a+by=c, где a≠0 или b≠0, при различных значениях a, b, c. введение графических образов дает возможность наглядно исследовать вопрос о числе решений системы двух уравнений с двумя переменными.
Основное место в данной теме занимает изучение алгоритмов решения систем двух линейных уравнений с двумя переменными способом подстановки и способом сложения. Введение систем позволяет значительно расширить круг текстовых задач, решаемых с помощью аппарата алгебры. Применение систем упрощает процесс перевода данных задач с обычного языка на язык уравнений.
-
Повторение.
Содержание обучения курса геометрии.
1. Начальные геометрические сведения.
Простейшие геометрические фигуры: прямая, точка, отрезок, луч, угол. Понятие равенства геометрических фигур. Сравнение отрезков и углов. Измерение отрезков, длина отрезка. Измерение углов, градусная мера угла. Смежные и вертикальные углы, их свойства. Перпендикулярные прямые.
Основная цель - систематизировать знания учащихся о простейших геометрических фигурах и их свойствах: ввести понятие равенства фигур.
В данной теме вводятся основные геометрические понятия и свойства простейших геометрических фигур на основе наглядных представлений учащихся путем обобщения очевидных или известных из курса математики 1-6 классов геометрических фактов. Понятие аксиомы на начальном этапе обучения не вводится, и сами аксиомы не формируются в явном виде. Необходимые исходные положения, на основе которых изучаются свойства геометрических фигур, приводятся в описательной форме. Принципиальным моментом данной темы является введение понятия равенства геометрических фигур на основе наглядного наложения. Определенное внимание должно уделяться практическим приложениям геометрических понятий.
2. Треугольники.
Треугольник. Признаки равенства треугольников. Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника. Равнобедренный треугольник и его свойства. Задачи на построение с помощью циркуля и линейки.
Основная цель - ввести понятие теоремы; выработать умения доказывать равентсва треугольников с помощью изученных признаков; ввести новый класс задач - на построение с помощью циркуля и линейки.
Признаки равенства треугольников являются основным рабочим аппаратом всего курса геометрии. Доказательства большей части теорем курса и также решение многих задач проводится по следующей схеме: поиск равных треугольников - обоснование их равенства с помощью какого-то признака - следствия, вытекающие из равенства треугольников. Применение признаков равенства треугольников при решение задач дает возможность постепенно накапливать опыт проведения доказательных рассуждений. На начальном этапе изучения и применения признаков равенства треугольников целесообразно использовать задачи с готовыми чертежами.
3.Параллельные прямые.
Признаки параллельности прямых. Аксиома параллельных прямых. Свойства параллельных прямых.
Основная цель - ввести одно из важнейших понятий - понятие параллельных прямых; дать первое представление об аксиомах и аксиоматическом методе в геометрии; ввести аксиому параллельных прямых.
Признаки и свойства параллельных прямых, связанные с углами, образованными при пересечении двух прямых секущей (накрест лежащими, односторонними, соответственными), широко используются в дальнейшем при изучении четырехугольников, подобных треугольников, при решении задач, а также в курсе стереометрии.
-
Соотношение между сторонами и углами треугольника.
Сумма углов треугольника. Соотношение между сторонами и углами треугольника. Неравенства треугольника. Прямоугольные треугольники, их свойства и признаки равенства. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Построение треугольника по трем элементам.
Основная цель - рассмотреть новые интересные и важные свойства треугольников.
В данной теме доказывается одна из важнейших теорем геометрии - теорема о сумме углов треугольника. Она позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный), а также установить некоторые свойства и признаки равенства прямоугольных треугольников.
Понятие расстояния между параллельными прямыми вводится на основе доказанной предварительно теореме о том, что все точки каждой из двух параллельных прямых равноудалены от другой прямой. Это понятие играет важную роль, в частности используется в задачах на построение.
При решении задач на построение в 7 классе следует ограничиться только выполнением и описанием построения искомой фигуры. В отдельных случаях можно провести устно анализ и доказательство, а элементы исследования должны присутствовать лишь тогда, когда это оговорено условием задачи.
5. Повторение. Решение задач.
Требования к уровню подготовки выпускников.
В результате изучения курса математики 7-го класса учащиеся должны знать/понимать
-
существо понятие математического доказательства; приводить примеры доказательств;
-
существо понятия алгоритма; приводить примеры алгоритмов;
-
как используются математические формулы, уравнения; примеры их применения для решения математических и практических задач;
-
как математически определить функции могут описывать реальные зависимости; приводить примеры такого описания;
-
как потребности практики привели математическую науку к необходимости расширения понятия числа;
-
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
-
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.
В результате изучения курса математики 7-го класса учащиеся должны уметь:
-
выполнять устно арифметические действия: сложения и вычитание двухзначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
-
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты - в виде дроби и дробь - в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
-
выполнять арифметические действия с рациональными числами; находить значение числовых выражений;
-
округлять целые числа и десятичные дроби, выполнять оценку числовых выражений;
-
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
-
решать текстовые задачи, включая задачи связанные с отношением и с пропорциональностью величин, дробями и процентами;
-
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
-
выполнять основные действия с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
-
решать линейные уравнения, системы двух линейных уравнений;
-
решать текстовые задачи алгебраическим методом;
-
изображать числа точками на координатной прямой;
-
определять координаты точки плоскости, строить точки с заданными координатами;
-
находить значение функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
-
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений;
-
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
-
вычислять средние значения результатов измерений;
-
пользоваться математическим языком для описания предметов окружающего мира;
-
распознавать геометрические фигуры, различать их взаимное расположение;
-
изображать геометрические фигуры: выполнять чертежи по условию задач; осуществлять изображение фигур;
-
решать геометрические задачи, опираясь на изученные свойства фигур и отношения между ними;
-
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
Применять полученные знания:
-
для решения несложных практических задач, в том числе с использованием, при необходимости, справочных материалов и простейших расчетных устройств;
-
для устной прикидки и оценки результата вычислений; проверки результата вычисления на правдоподобие, используя различные приемы; интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;
-
для выполнения расчетов по формулам, понимая формулу как алгоритм вычисления; для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
-
при моделировании практических ситуаций и исследовании построенных моделей (используя аппарат алгебры);
-
при интерпретации графиков зависимостей между величинами; переводя на язык функций и исследуя реальные зависимости;
-
при построениях геометрическими инструментами (линейка, угольник, циркуль, транспортир);
-
для вычисления длин, площадей основных геометрических фигур с помощью формул (используя при необходимости справочники и технические средства).
Учебно-тематический план по алгебре
№
Содержание материала
Кол-во часов
1
Выражения, тождества, уравнения
26
2
Функции
18
3
Степень с натуральным показателем
18
4
Многочлены
23
5
Формулы сокращенного умножения
23
6
Системы линейных уравнений
17
7
Повторение
11
Всего
136
Учебно-тематический план по геометрии
№
Содержание материала
Кол-во часов
1
Начальные геометрические сведения
10
2
Треугольники
17
3
Параллельные прямые
13
4
Соотношения между сторонами и углами треугольника
18
5
Повторение. Решение задач
10
Всего
68
Контрольных работ предусмотрено 15.
Критерии оценивания письменных контрольных работ учащихся
Отметка «5» ставится, если:
-
работа выполнена полностью;
-
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
-
в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
-
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
-
допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).
Отметка «3» ставится, если:
-
допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
-
допущены существенные ошибки, показавшие, что учащийся не владеет
обязательными умениями по данной теме в полной мере.
Материально-техническое и учебно-методическое обеспечения
-
Алгебра. Программы образовательных учреждений 7-9 классы. Составитель: Бурмистрова Т.А. Москва «Просвещение» 2010.
-
Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина Геометрия 7-9 классы. М.: Просвещение, 2009.
-
Гаврилова Н.Ф. Поурочные разработки по геометрии. 7 класс. М.: «ВАКО», 2004.
-
Геометрия. Программы образовательных учреждений 7-9 классы. Составитель: Бурмистрова Т.А. Москва «Просвещение» 2010.
-
Ю.П. Дудницын, Е.Е. Тульчинская. Алгебра 7 класс. Контрольные работы. М.: Мнемозина, 2004г.
-
Л.И. Звавич, Л.В. Кузнецова, С.Б. Суворова. Дидактические материалы по алгебре 7 класс. М.: Просвещение, 2005г.
-
Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова Алгебра 7 класс. М.: Просвещение, 2009г.
-
Т.М. Мищенко. Дидактические карточки-задания по геометрии. «Экзамен», 2004г.
-
Рурукин А.Н., Лупенко Г.В., Масленникова И.А. Поурочные разработки по алгебре: 7 класс.- М.: ВАКО, 2011.
-
Тесты. Алгебра. 7 класс. Л.М. Короткова, Н.В. Савинцева. М.: айрис-пресс, 2006г.
Информационно- методическое обеспечение:
1). Интерактивное учебное пособие:
-тригонометрические функции, уравнения и неравенства; «Наглядная математика»:
-стереометрия; «Наглядная математика»:
-генератор заданий по математике, контрольные и самостоятельные работы; « Экзамен»
-математика 5-11 класс, Практикум; образовательный комплекс «Школа»
-геометрия 7-9 классы Издательство « Учитель»
-алгебра и начала анализа 10-11 класс «Медиа»
-интерактивная математика 5-9 классы, Издательство «Дрофа»
Математика планиметрия 7-9 классы « Умник»
Интернет - ресурсы:
-
Интерактивная доска Interwrite
-
Мультимедийный проектор epson
-
Компьютер в сборе монитор Acer
-
Ноутбуки roverbook
-
Планшетники roverbook
-
документ-камера dymo
Приложение
Календарно-тематическое планирование (всего 136 часов, 4 часа в неделю)
Алгебра-7 класс
№ урока
Содержание учебного материала
Кол-во часов
Время проведения
Глава I. Выражения, тождества, уравнения
26
1-5
Выражение.
5
6-11
Преобразование выражений
6
12
Контрольная работа №1
1
13-21
Уравнения с одной переменной
9
22-25
Статистические характеристики
4
26
Контрольная работа №2
1
Глава II. Функции
18
27-33
Функции и их графики.
7
34-43
Линейная функция
10
44
Контрольная работа №3
1
Глава III. Степень с натуральным показателем
18
45-54
Степень и ее свойства
10
55-61
Одночлены
7
62
Контрольная работа №4
1
Глава IV. Многочлены
23
63-66
Сумма и разность многочленов
4
67-73
Произведение одночлена и многочлена
7
74
Контрольная работа №5
1
75-84
Произведение многочленов
10
85
Контрольная работа №6
1
Глава V. Формулы сокращенного умножения
23
86-91
Квадрат суммы и квадрат разности
6
92-97
Разность квадратов. Сумма и разность кубов
6
98
Контрольная работа №7
1
99-107
Преобразование целых выражений
9
108
Контрольная работа №8
1
Глава VI. Системы линейных уравнений
17
109-114
Линейные уравнения с двумя переменными и их системы
6
115-124
Решение систем линейных уравнений
10
125
Контрольная работа №9
1
Повторение
11
126-134
Повторение
9
135
Итоговый зачет
1
136
137-140
Итоговая контрольная работа
Резерв
1
4
Лист корректировки рабочей программы
№ урока
Тема урока
Причины корректировки
Способ корректировки
Календарно-тематическое планирование (всего 68 часов, 2 часа в неделю)
Геометрия-7 класс
№ урока
Содержание учебного материала
Кол-во часов
Время проведения
Глава I. Начальные геометрические сведения
10
1-2
Прямая и отрезок. Луч и угол
2
3
Сравнение отрезков и углов
1
4-6
Измерение отрезков. Измерение углов
3
7-8
Перпендикулярные прямые
2
9
Решение задач
1
10
Контрольная работа №1
1
Глава II. Треугольники
17
11-13
Первый признак равенства треугольников.
3
14-16
Медианы, биссектрисы и высоты треугольника
3
17-20
Второй и третий признаки равенства треугольников
4
21-23
Задачи на построение
3
24-26
Решение задач
3
27
Контрольная работа №2
1
Глава III. Параллельные прямые
13
28-31
Признаки параллельности двух прямых
4
32-36
Аксиома параллельных прямых
5
37-39
Решение задач
3
40
Контрольная работа №3
1
Глава IV. Соотношения между сторонами и углами треугольника
18
41-42
Сумма углов треугольника
2
43-45
Соотношения между сторонами и углами треугольника
3
46
Контрольная работа №4
1
47-50
Прямоугольные треугольники
4
51-54
Построение треугольника по трем элементам
4
55-57
Решение задач
3
58
Контрольная работа №5
1
59-70
Повторение. Решение задач +2 часа резерв
10
Лист корректировки рабочей программы
№ урока
Тема урока
Причины корректировки
Способ корректировки
Контрольные работы по алгебре.
Контрольная работа №1
Вариант I
-
Найдите значение выражения 6x - 8y, при x =
 , у =
, у =  .
. -
Сравните значения выражений -0,8x - 1 и 0,8x - 1 при x = 6.
-
Упростите выражение:
а) 2x - Зy - 11х + 8у; б) 5(2а + 1) - 3; в) 14x - (x - 1) + (2х + 6).
-
Упростите выражение и найдите его значение:
-4 (2,5а - 1,5) + 5,5а - 8, при а = - ![]() .
.
-
Из двух городов, расстояние между которыми s км, одновременно навстречу друг другу выехали легковой автомобиль и грузовик и встретились через t ч. Скорость легкового автомобиля v км/ч. Найдите скорость грузовика. Ответьте на вопрос задачи, еcли s = 200, t = 2, v = 60.
-
Раскройте скобки: Зx - (5x - (3x - 1)).
Вариант II
-
Найдите значение выражения 16а + 2y, при а =
 , у = -
, у = -  .
. -
Сравните значения выражений 2 + 0,3а и 2 - 0,3а, при а = - 9.
-
Упростите выражение:
а) 5а + 7b - 2а - 8b; б) 3 (4x + 2) - 5; в) 20b - (b - 3) + (Зb - 10).
-
Упростите выражение и найдите его значение:
-6 (0,5x - 1,5) - 4,5x - 8, при x = ![]() .
.
-
Из двух городов одновременно навстречу друг другу выехали автомобиль и мотоцикл и встретились через t ч. Найдите расстояние между городами, если скорость автомобиля v1 км/ч, а скорость мотоцикла v2 км/ч. Ответьте на вопрос задачи, если: t = 3, v1 = 80, v2 = 60.
-
Раскройте скобки: 2р - (3р - (2р - с)).
Контрольная работа №2
Вариант I
-
Решите уравнение:
а) ![]() x = 12; б) 6x - 10,2 = 0; в) 5x - 4,5 = 3x + 2,5; г) 2x - (6x - 5) = 45.
x = 12; б) 6x - 10,2 = 0; в) 5x - 4,5 = 3x + 2,5; г) 2x - (6x - 5) = 45.
-
Таня в школу сначала едет на автобусе, а потом идет пешком. Вся дорога у нее занимает 26 мин. Идет она на 6 мин дольше, чем едет на автобусе. Сколько минут она едет на автобусе?
-
В двух сараях сложено сено, причем в первом сарае сена в 3 раза больше, чем во втором. После того как из первого сарая увезли 20 т сена, а во второй привезли 10 т, в обоих сараях сена стало поровну. Сколько всего тонн сена было в двух сараях первоначально?
-
Решите уравнение 7х - (х + 3) = 3 (2х - 1).
Вариант II
-
Решите уравнение:
а) ![]() х = 18; б) 7x + 11,9 = 0; в) 6х - 0,8 = 3х + 2,2; г) 5х - (7х + 7) = 9.
х = 18; б) 7x + 11,9 = 0; в) 6х - 0,8 = 3х + 2,2; г) 5х - (7х + 7) = 9.
-
Часть пути в 600 км турист пролетел на самолете, а часть проехал на автобусе. На самолете он проделал путь, в 9 раз больший, чем на автобусе. Сколько километров турист проехал на автобусе?
-
На одном участке было в 5 раз больше саженцев смородины, чем на другом. После того как с первого участка увезли 50 саженцев, а на второй посадили еще 90, на обоих участках саженцев стало поровну. Сколько всего саженцев было на двух участках первоначально?
-
Решите уравнение 6х - (2х - 5) = 2 (2х + 4).
Контрольная работа №3
Вариант I
-
Функция задана формулой у = 6х + 19. Определите: а) значение у, если x = 0,5; б) значение x, при котором у = 1; в) проходит ли график функции через точку А (-2; 7).
-
а) Постройте график функции у = 2х - 4.
б) Укажите с помощью графика, чему равно значение у, при x = 1,5.
-
В одной и той же системе координат постройте графики функций: а) у = -2х; б) у = 3.
-
Найдите координаты точки пересечения графиков функций y= 47х - 37 и у = -13х + 23.
-
Задайте формулой линейную функцию, график которой параллелен прямой у = 3х - 7 и проходит через начало координат.
Вариант II
-
Функция задана формулой у = 4х - 30. Определите:
а) значение у, если x = -2,5; б) значение x, при котором у = -6; в) проходит ли график функции через точку В (7; -3).
-
а) Постройте график функции у = -3х + 3.
б) Укажите с помощью графика, при каком значении x значение у равно 6.
-
В одной и той же системе координат постройте графики функций: а) у = 0,5х; б) у = -4.
-
Найдите координаты точки пересечения графиков функций у=-38х + 15 и у = -21х - 36.
-
Задайте формулой линейную функцию, график которой параллелен прямой у = -5х + 8 и проходит через начало координат.
Контрольная работа №4
Вариант I
-
Найдите значение выражения 1 - 5х2, при x = -4.
-
Выполните действия:
а) y7 • y12; б) y20 : y5; в) (y2)8; г) (2у)4.
-
Упростите выражение: а) -2аb3 • 3а2 • b4; б) (- 2а5 b2)3.
-
Постройте график функции у = х2. С помощью графика определите значение у при x = 1,5; x = -1,5.
-
Вычислите:

-
Упростите выражение: а)
 x2y8
x2y8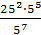 (
(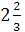 xy3)4; б) x-2
xy3)4; б) x-2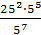 x3-n
x3-n 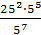 x
x
Вариант II
-
Найдите значение выражения -9р3, при р =
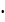 .
. -
Выполните действия: а) с3 • с22; б) с18 : с6; в) (с4)6; г) (3с)5.
-
Упростите выражение: а) -4x5y2 • Зху4 ; б) (3x2y3)2.
-
Постройте график функции у = х2. С помощью графика функции определите, при каких значениях х значение y равно 4.
-
Вычислите:
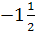
-
Упростите выражение: a) 3
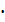 x5y6
x5y6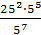 (
(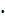 x5y)2; б) (an+1)2 : a2n.
x5y)2; б) (an+1)2 : a2n.
Контрольная работа №5
Вариант I
-
Выполните действия: а) (За - 4ах + 2) - (11а - 14ах); б) 3у2 (у3 + 1).
-
Вынесите общий множитель за скобки: а) 10аb - 15b2; б) 18а3 + 6а2.
-
Решите уравнение 9х - 6 (х - 1) = 5 (х + 2).
-
Пассажирский поезд за 4 ч прошел такое же расстояние, какое товарный за 6 ч. Найдите скорость пассажирского поезда, если известно, что скорость товарного на 20 км/ч меньше.
-
Решите уравнение
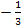 -
- 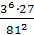 =
= 
-
Упростите выражение 2а (а + b - с) - 2b (а - b - с) + 2с (а - b + с).
Вариант II
-
Выполните действия: а) (2а2 - За + 1) - (7а2 - 5а); б) 3х (4х2 - х).
-
Вынесите общий множитель за скобки: а) 2ху - 3ху2; б) 8b4 + 2b3.
-
Решите уравнение 7 - 4 (3х - 1) = 5 (1 - 2х).
-
В трех шестых классах 91 ученик. В 6 «А» на 2 ученика меньше, чем в 6 «Б», а в 6 «В» на 3 ученика больше, чем в 6 «Б». Сколько учащихся в каждом классе?
-
Решите уравнение
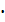 =
= 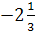 +
+ 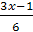
-
Упростите выражение 3х (х + у + с) - 3у (х - у - с) - 3с (х + у - с).
Контрольная работа №6
Вариант I
-
Выполните умножение:
а) (с + 2) (с - 3); б) (2а - 1) (За + 4); в) (5х - 2у) (4х - у); г) (а - 2) (а2 - 3а + 6).
-
Разложите на множители: а) а (а + 3) - 2 (а + 3); б) ах - ау + 5х - 5у.
-
Упростите выражение -0,1x (2х2 + 6) (5 - 4х2).
-
Представьте многочлен в виде произведения:
-
а) х2 - ху - 4х + 4у; б) ab - ас - bх + сх + с - 6.
-
Из прямоугольного листа фанеры вырезали квадратную пластинку, для чего с одной стороны листа фанеры отрезали полосу шириной 2 см, а с другой, соседней, - 3 см. Найдите сторону получившегося квадрата, если известно, что его площадь на 51 см2 меньше площади прямоугольника.
Вариант II
-
Выполните умножение:
а) (а - 5) (а - 3); б) (5х + 4) (2х - 1); в) (3р + 2с) (2р + 4с); г) (6 - 2) (b2 + 2b - 3).
-
Разложите на множители: а) х (х - у) + а (х - у); б) 2а - 2b + са - сb.
-
Упростите выражение 0,5х (4х2 - 1) (5х2 + 2).
-
Представьте многочлен в виде произведения:
-
а) 2а - ас - 2с + с2; б) bx + by - х - у - ах - ау.
-
Бассейн имеет прямоугольную форму. Одна из его сторон на 6 м больше другой. Он окружен дорожкой, ширина которой 0,5 м. Найдите стороны бассейна, если площадь окружающей его дорожки 15 м2.
Контрольная работа №7
Вариант I
-
Преобразуйте в многочлен:
а) (у - 4)2; б) (7х + а)2; в) (5с - 1) (5с + 1); г) (3а + 2b) (3а - 2b).
-
Упростите выражение (а - 9)2 - (81 + 2а).
-
Разложите на множители: а) х2 - 49; б) 25х2 - 10ху + у2.
-
Решите уравнение (2 - х)2 - х (х + 1,5) = 4.
-
Выполните действия: а) (у2 - 2а) (2а + у2); б) (3х2 + х)2; в) (2 + m)2 (2 - m)2.
-
Разложите на множители: а) 4x2y2-9a4; б) 25а2 - (а + 3)2; в) 27m3 + n3.
Вариант II
-
Преобразуйте в многочлен:
а) (3а + 4)2; б) (2х - b)2; в) (b + 3) (b - 3); г) (5у - 2х) (5у + 2х).
-
Упростите выражение (с + b) (с - b) - (5с2 - b2).
-
Разложите на множители: а) 25у2 - а2; б) с2 + 4bс + 4b2.
-
Решите уравнение 12 - (4 - х)2 = х (3 - х).
-
Выполните действия: а) (3х + у2) (3х - у2); б) (а3 - 6а)2; в) (а - х)2 (х + а)2.
-
Разложите на множители: а) 100а4 -
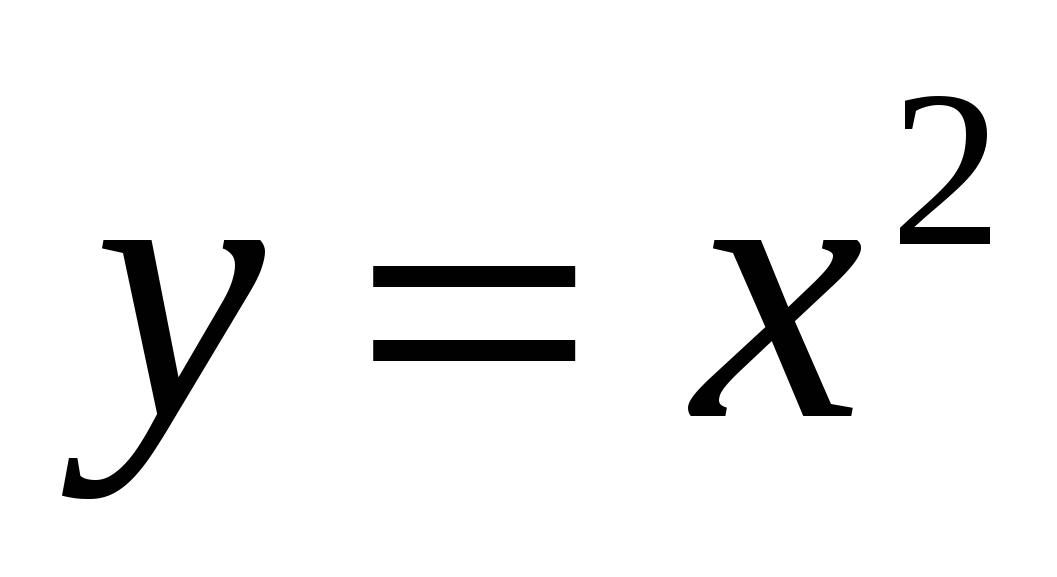 b2; б) 9х2 - (х - 1)2; в) х3 + у6.
b2; б) 9х2 - (х - 1)2; в) х3 + у6.
Контрольная работа №8
Вариант I
-
Упростить выражение:
а) ( х - 3)( х - 7) - 2х( 3х - 5); б) 4а( а - 2) - ( а - 4)2; в) 2( m + 1)2 - 4m
-
Разложите на множители: а) х3 - 9х; б) - 5а2 - 10ав - 5в2
-
Упростите выражение: (у2 - 2у)2 - у2(у + 3)(у - 3) + 2у(2у2 + 5)
-
Разложите на множители: а) 16х4 - 81; б) х2 - х - у2 - у
-
Докажите, что выражение х2 - 4х + 9 при любых значениях х принимает положительные значения.
Вариант II
-
Упростить выражение:
а) 2x(x-3)-3x(x+5); б) (a+7)(a-1)+(a-3)2; в) 3(y+5)2-3y2.
-
Разложите на множители: а) с3 - 16с; б) 3а2 - 6ав + 3в2
-
Упростите выражение: (3а - а2)2 - а2(а - 2)(а + 2) + 2а(7 + 3а2)
-
Разложите на множители: а) 81а4 - 1; б) а - а2 + в + в2
-
Докажите, что выражение - а2 + 4а - 9 может принимать лишь отрицательные значения.
Контрольная работа №9
Вариант I
-
Решите систему уравнений:
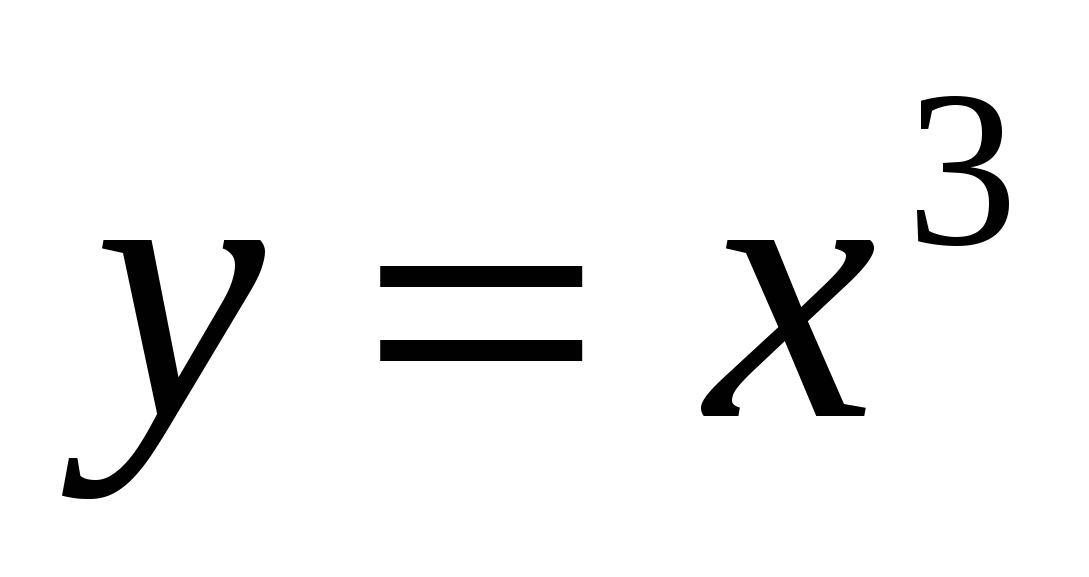
-
Банк продал предпринимателю г-ну Разину 8 облигаций по 2000 р и 3000р. Сколько облигаций каждого номинала купил г-н Разин, если за все облигации было заплачено 19000р?
-
Решите систему уравнений:
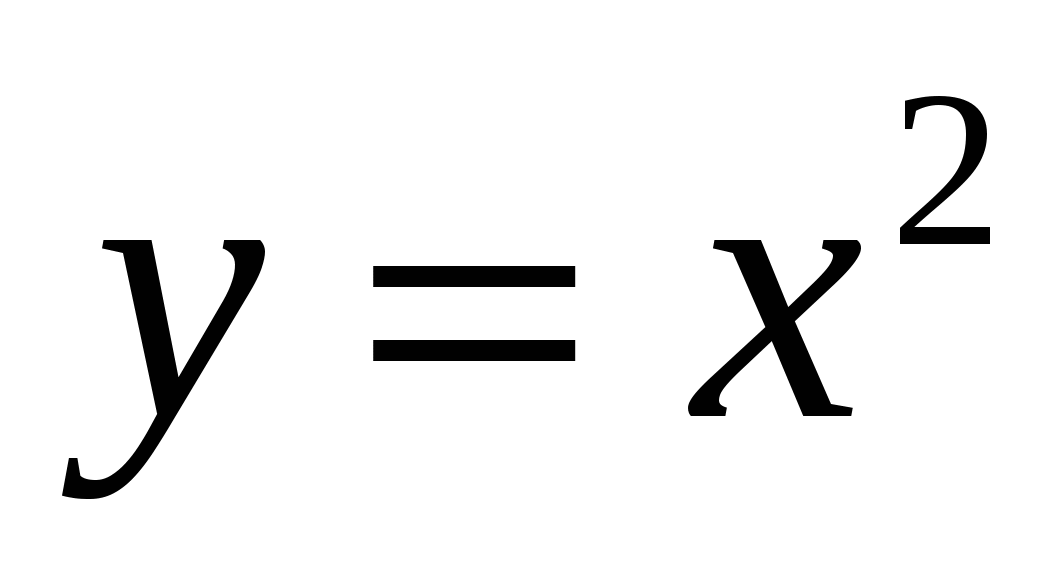
-
Прямая у = kx + b проходит через точки А (3; 8) и В (- 4; 1) . Напишите уравнение этой прямой
-
Выясните, имеет ли решение система:
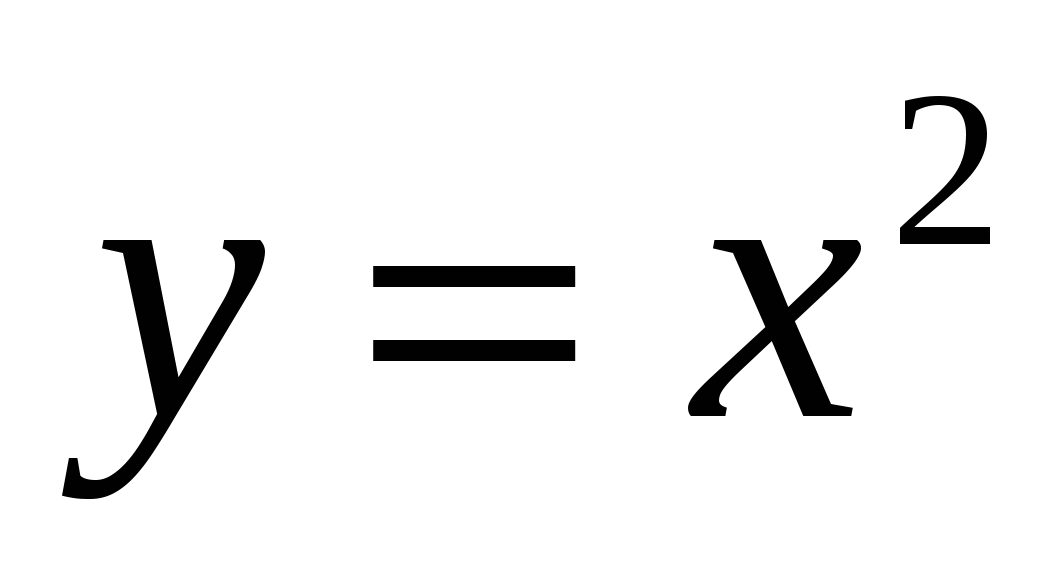
Вариант II
-
Решите систему уравнений:
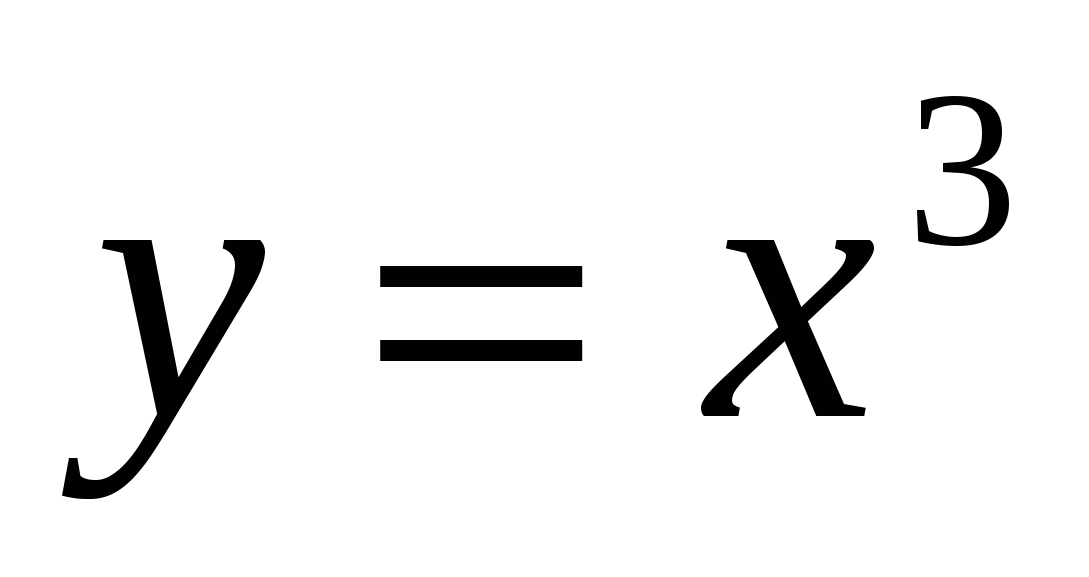
-
Велосипедист ехал 2 часа по лесной дороге и 1 час по шоссе, всего он проехал 40 км. Скорость его по шоссе была на 4 км/ч больше, чем скорость на лесной дороге. С какой скоростью велосипедист ехал по шоссе, и с какой по лесной дороге?
-
Решите систему уравнений:

-
Прямая у = kx + b проходит через точки А (5; 0) и В (- 2; 21) . Напишите уравнение этой прямой.
-
Выясните, имеет ли решение система и сколько:
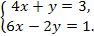
Итоговая контрольная работа
Вариант I
-
Упростить выражение: а) 3a2b
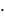 (-5a3b); б) (2x2y)3.
(-5a3b); б) (2x2y)3. -
Решите уравнение 3x-5(2x+1)=3(3-2x).
-
Разложите на множители: а) 2xy-6y2; б) a3-4a.
-
Периметр треугольника ABC равен 50см. сторона AB на 2 см больше стороны BC, а сторона FC в 2 раза больше стороны BC. Найдите стороны треугольника.
-
Докажите, что верно равенство (a+c)(a-c)-b(2a-b)-(a-b+c)(a-b-c)=0
-
На графике функции y=5x-8 найдите точку, абсцисса которой противоположна ее ординате.
Вариант II
-
Упростите выражение: а) -2xy2
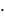 3x3y5; б) (-4ab3)2.
3x3y5; б) (-4ab3)2. -
Решите уравнение 4(1-5x)=9-3(6x-5).
-
Разложите на множители: а) a2b-ab2; б) 9x-x3.
-
Турист прошел 50 км за 3 дня. Во второй день он прошел на 10 км меньше, чем в первый день, и на 5 км больше, чем в третий. Сколько километров проходил турист каждый день?
-
Докажите, что при любых значениях переменных верно равенство
(x-y)(x+y)-(a-x+y)(a-x-y)-a(2x-a)=0
-
На графике функции y=3x+8 найдите точку, абсцисса которой равна ее ординате.
Контрольные работы по геометрии
Контрольная работа №1
Вариант I
-
Три точки B, C и D лежат на одной прямой. Известно, что BD=17 см, DC=25 см. какой может быть длина отрезка BC?
-
Сумма вертикальных углов MOE и DOC, образованных при пересечении прямы MC и DE, равна 2040. Найдите угол MOD.
-
С помощью транспортира начертите угол, равный 780 и проведите биссектрису смежного с ним угла.
Вариант II
-
Три точки M, N и K лежат на одной прямой. Известно, что MN=15 см, NK=18 см. Каким может быть расстояние MK?
-
Сумма вертикальных углов AOB иCOD, образованных при пересечении прямы AD и BC, равна 1080. Найдите угол BOD.
-
С помощью транспортира начертите угол, равный 1320 и проведите биссектрису одного из смежных с ним углов.
Контрольная работа №2
Вариант I
-
На рисунке отрезки АВ и CD имеют общую середину О.Докажите, что DAO = СBO
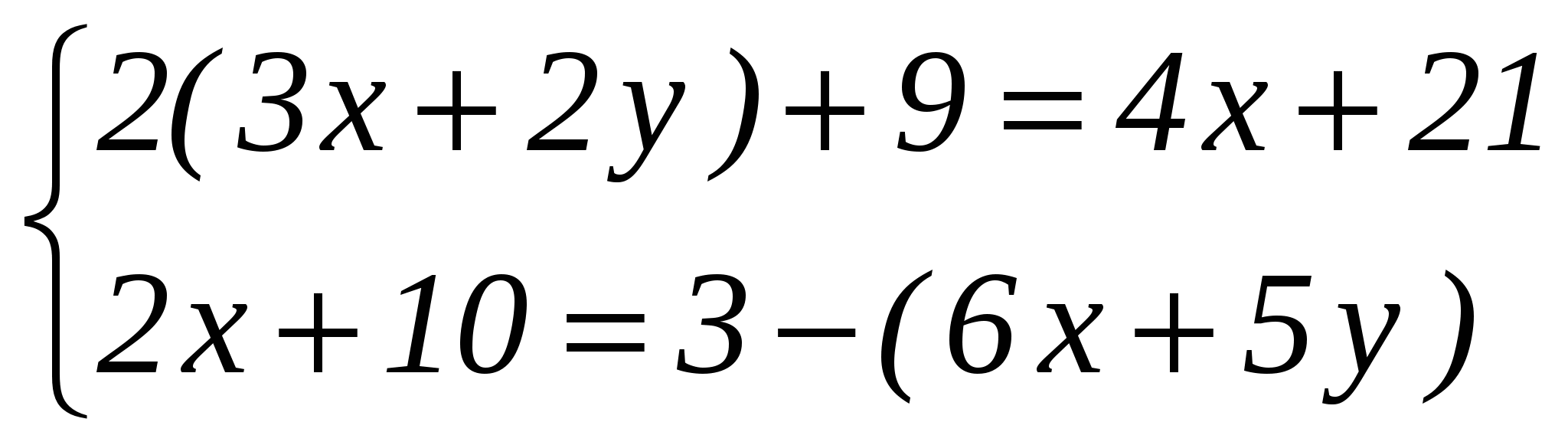
-
Луч AD - биссектриса угла А. На сторонах угла А отмечены точки В и С так, что ADB = ADC. Докажите, что АВ = АС.
-
Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ1 к боковой стороне АС.
Вариант II
-
На рисунке отрезки ME и PK точкой D делятся пополам. Докажите, что KMD = PED.
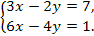
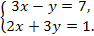
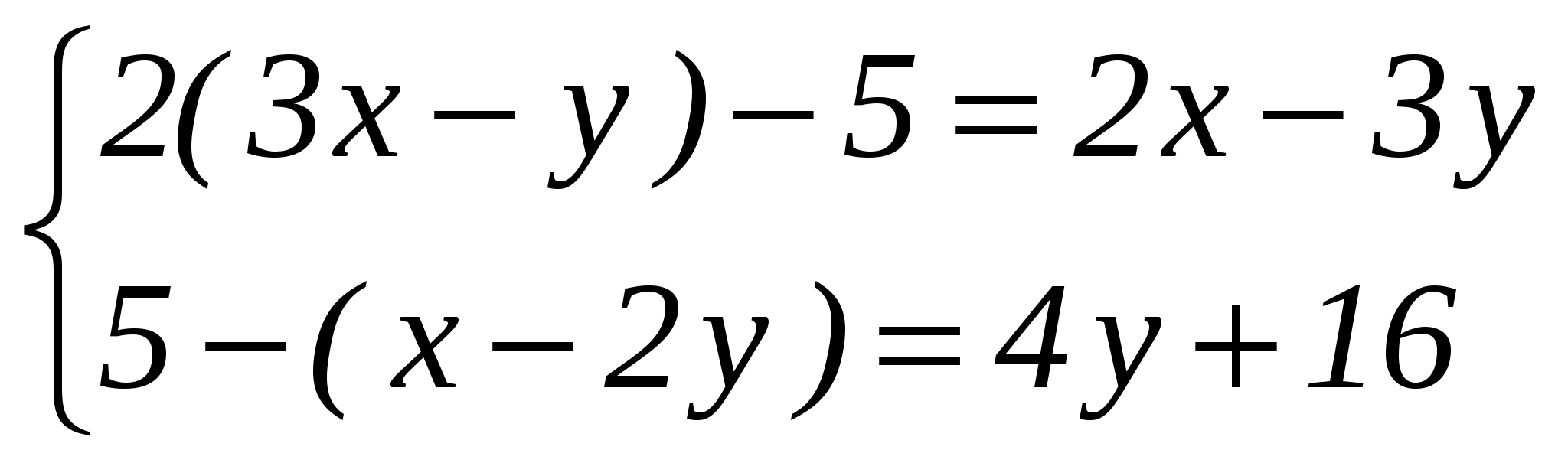 M K
M K
D
P E
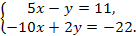
-
На сторонах угла D отмечены точки М и К так, что DM = DK. Точка Р лежит внутри угла D, и РК = РМ, Докажите, что луч DP - биссектриса угла MDK.
-
Начертите равнобедренный треугольник АВС с основанием AС и острым углом В. С помощью циркуля и линейки проведите высоту из вершины угла А.
Контрольная работа №3
Вариант I
-
Отрезки EF и PQ пересекаются в их середине М. Докажите, что PE || QF
-
Отрезок DM - биссектриса треугольника CDE. Через точку М проведена прямая, параллельная стороне CD и пересекающая сторону DE в точке N. Найти углы треугольника DMN, если СDЕ = 68о
Вариант II
-
Отрезки EF и MN пересекаются в их середине P. Докажите, что EN || MF
-
Отрезок АD - биссектриса треугольника АВC. Через точку D проведена прямая, параллельная стороне AB и пересекающая сторону AC в точке F. Найти углы треугольника ADF, если BAС = 72о
Контрольная работа №4
Вариант I
-
ABE = 104о, DCF = 76о, AC = 12 см. Найти сторону АВ треугольника АВС.
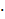
-
В треугольнике CDE точка М лежит на стороне СЕ, причем СМD - острый. Докажите, что DE > DM
-
Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см, Найти стороны треугольника.
Вариант II
-
BАE = 112о, DВF = 68о, ВC = 9 см. Найти сторону АС треугольника АВС.
-
В треугольнике MNP точка K лежит на стороне MN, причем NKP - острый. Докажите, что KP < MP
-
Одна из сторон равнобедренного тупоугольного треугольника на 17 см меньше другой. Найти стороны треугольника, если его периметр равен 77 см.
Контрольная работа №5
Вариант I
-
В остроугольном треугольнике MNP биссектриса угла М пересекает высоту NK в точке О, причем ОК = 9 см. Найти расстояние от точки О до прямой MN
-
Постройте прямоугольный треугольник по гипотенузе и острому углу.
-
С помощью циркуля и линейки постройте угол, равный 150о
Вариант II
-
В прямоугольном треугольнике DCE с прямым углом С проведена биссектриса EF, причем FC = 13 см. Найти расстояние от точки F до прямой DE
-
Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу.
-
С помощью циркуля и линейки постройте угол, равный 105о