- Учителю
- Материал по математике для 9 класса «Решение неравенств методом интервалов»
Материал по математике для 9 класса «Решение неравенств методом интервалов»
Алгебра 9 класс
Инструкция
Дорогой друг!
Выполняя задания, придерживайся следующих правил:
-
Внимательно изучи тот материал, который тебе выслали.
-
Разбери самостоятельно, прорешай те задачи и примеры, которые приведены в качестве образца.
-
Оформляя задачи для самостоятельного решения, приводи полные решения, опираясь на эти образцы. Не забывай выписывать ответы.
-
Если что-то не получилось, не огорчайся. С проверенной работой вышлем рекомендации по ее решению.
-
Методички возвращать не надо. Рекомендуем хранить их в специальной папке вместе с проверенными работами и периодически к ним обращаться.
-
Срок выполнения контрольной работы - 4 дня с момента получения задания.
Решение неравенств методом интервалов
Решим неравенство: 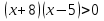
Неравенство положительно, если оба множителя положительны или отрицательны одновременно. Значит надо решить две системы неравенств:
1)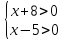 или 2)
или 2)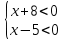
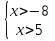
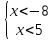
(5;+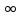 ) (-
) (-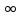 ;-8)
;-8)
Ответ: (-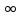 ;-8)
;-8)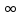 (5;+
(5;+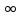 )
)
Решим другое неравенство: (x-2)(x+5)(x-12)>0
Если рассуждать как в предыдущем примере о возможных знаках каждого из трёх множителей, то вычисления будут громоздкими, потому необходим другой метод решения. Таким методом является метод интервалов.
Если левая часть неравенства является произведением, а правая часть - 0, то есть 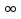 (
(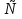 ) и
) и 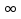 , где х - переменная, а
, где х - переменная, а 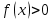 ,
, 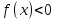 …,
…,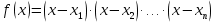 - не равные друг другу числа, то такие неравенства решаются методом интервалов.
- не равные друг другу числа, то такие неравенства решаются методом интервалов.
Числа 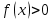 ,
, 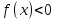 …,
…,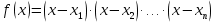 - нули функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль её знак меняется.
- нули функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль её знак меняется.
Для решения неравенства (x-2)(x+5)(x-12)>0 воспользуемся следующим алгоритмом.
Алгоритм:
-
Найти область определения функции.
-
Найти нули функции.
-
Отметить на координатной прямой интервалы, на которые область определения разбивается нулями функции.
-
Определить знак функции на каждом промежутке (интервале), для этого выбираем число из данного промежутка и подставляем в функцию.
-
Записать ответ, удовлетворяющий знаку неравенства.
Решение
(x-2)(x+5)(x-12)>0
-
x
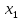 R
R -
(x-2)(x+5)(x-12)=0
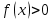 =2,
=2, 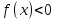 =-5,
=-5, 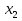 =12
=12
-5
2
12
-
+
-
+
-5
2
12
-
Ответ: x
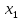 (-5;2)
(-5;2)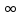 (12:+
(12:+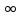 ).
).
Решим первое неравенство методом интервалов:
(х+8)(х-5)>0
-
х
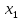 R
R -
(х+8)(х-5)=0
х1 = - 8, х2 = 5
-8
5
+
+
-
-8
5
-
Ответ: х
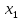 (-
(-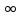 ;-8)
;-8)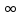 (5;+
(5;+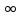 )
)
Применение метода интервалов
Рассмотрим метод интервалов для решения неравенств высоких степеней.
Пример 1. Решим неравенство 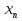
Решение:
Прежде всего, отметим, что если в разложении многочлена на множители входит сомножитель 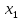 , то говорят, что
, то говорят, что 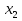 - корень многочлена кратности
- корень многочлена кратности 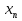 .
.
Данный многочлен имеет корни:  кратности 6;
кратности 6; 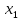 кратности 3;
кратности 3; 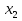 кратности 1;
кратности 1; 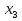 кратности 2;
кратности 2;  кратности 5.
кратности 5.
Нанесем эти корни на числовую ось. Отметим корни четной кратности двумя черточками, нечетной кратности - одной чертой.

Определим знак многочлена на каждом интервале, при любом значении х не совпадающем с корнями и взятом из данного интервала. Получим полную диаграмму знаков многочлена на всей числовой оси:

Теперь легко ответить на вопрос задачи, при каких значениях х знак многочлена неотрицательный. Отметим на рисунке нужные нам области, получим:

Из рисунка видно, что такими х являются 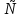 .
.
Ответ: 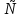 .
.
Проанализируем смену знаков в корнях различной кратности.
Посмотрите внимательно на диаграмму знаков, что можно заметить? В корнях четной кратности смена знаков не произошла, а в корнях нечетной кратности - знак меняется.
Важные выводы:
-
Для решения неравенства важно знать, является ли k четным или нечетным числом.
-
При четном k многочлен справа и слева от
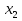 имеет один и тот же знак (т.е. знак многочлена не меняется),
имеет один и тот же знак (т.е. знак многочлена не меняется), -
При нечетном k многочлен справа и слева от
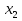 имеет противоположные знаки (т.е. знак многочлена изменяется).
имеет противоположные знаки (т.е. знак многочлена изменяется).
Еще небольшое замечание, что бы применять метод интервалов, нужно сначала привести в неравенство к указанному виду (т.е. разложить на множители).
Рассмотрим способы решения рациональных неравенств 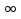 методом интервалов.
методом интервалов.
Заметим, что рациональные неравенства легко сводятся к решению неравенств высоких степеней. Умножим обе части такого неравенства на многочлен  , который положителен при всех допустимых значениях х (т.к.
, который положителен при всех допустимых значениях х (т.к. 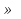 ). Тогда знак исходного неравенства не меняется, и получаем неравенство
). Тогда знак исходного неравенства не меняется, и получаем неравенство 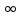 , эквивалентное данному неравенству.
, эквивалентное данному неравенству.
Итак: 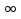 эквивалентно системе неравенств
эквивалентно системе неравенств 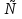 которая далее решается методом интервалов.
которая далее решается методом интервалов.
Пример 2. Решим неравенство 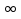
Отметим, прежде всего, что знаменатель неравенства не может быть равен нулю и найдем область определения неравенства:
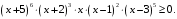 откуда
откуда 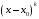
Сведем данное рациональное неравенство к алгебраическому. Для этого умножим обе части неравенства на положительное выражение - квадрат знаменателя (замети, что при этом знак неравенства не меняется).
Получаем: 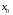 . Разложив квадратный трехчлен на множители, имеем:
. Разложив квадратный трехчлен на множители, имеем: 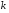 . Решаем это неравенство методом интервалов. Находим корни многочлена и определяем их кратность: х =1 (четная кратность), остальные корни 3, -1, 0, 5, -2 (нечетной кратности). Отмечаем корни на числовой оси с учетом области определения неравенства и определяем знаки на промежутках с учетом кратности корней.
. Решаем это неравенство методом интервалов. Находим корни многочлена и определяем их кратность: х =1 (четная кратность), остальные корни 3, -1, 0, 5, -2 (нечетной кратности). Отмечаем корни на числовой оси с учетом области определения неравенства и определяем знаки на промежутках с учетом кратности корней.

Ответ: 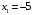 .
.
Литература
Алгебра: Учеб. для 9 кл. общеобразоват. учреждений/ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; Под ред. С.А. Теляковского. - 8-е изд. - М.: Просвещение, 2001. - 207 с.
Контрольная работа
-
Решите неравенства методом интервалов:
а) 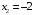 ; б)
; б) 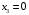 ;
;
в) 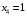 .
.
-
Решите неравенство, разложив его левую часть на множители:
а) 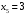 ; б)
; б) 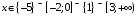 ;
;
б)  .
.
-
Найдите область определения функции:
а) 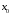 ; б)
; б) 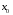 .
.
-
Решите неравенство:
а) 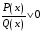 ; б)
; б) 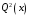 ;
;
в) 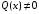 .
.
-
Решите неравенство:
а) 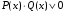 ; б)
; б) 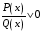 .
.