- Учителю
- урок геометрии в 11 классе
урок геометрии в 11 классе
ГУ «Отдел образования Астраханского района»
Конкурс «Методический портфель учителя математики»
Номинация «Современный урок математики»
Геометрия 11 класс
Цилиндр

Дзёма В.И.
учитель математики
ГУ «Каменская средняя школа»
Акмолинская область
Астраханский район
Тема: Цилиндр. Сечения цилиндра. Площадь поверхности цилиндра
Цель:
1. Образовательная:
Ввести понятия цилиндрической поверхности цилиндра и его элементов (боковая поверхность, основания, образующие, ось, высота, радиус).
Рассмотреть сечения цилиндра плоскостью, площадь боковой и полной поверхности цилиндра.
2. Развивающая:
Способствовать развитию у учащихся умения самостоятельно формулировать цели и задачи.
Формировать понимание взаимосвязи между предметами математика и физика.
Развивать пространственное воображение.
3. Воспитывающая:
Воспитывать внимание, аккуратность, бережное отношение к техническим средствам.
Способствовать осознанию ценности коллективной мыслительной деятельности.
Формировать представление о математике, как о части общечеловеческой культуры.
Тип урока: комбинированный урок
Методы обучения: словесный, наглядный, метод практической работы
Формы работы: общеклассная, дифференцированная, самостоятельная,
работа в группе
Оборудование и материалы: компьютеры, презентация "Цилиндр",
физминутка, дидактический материал, лист
успеха, тесты, музыка, таблицы к задачам
Ход урока
-
Организация класса.
-
Целевая и тематическая установка урока.
Звучит музыка (релаксация)
Эпиграф урока
Через математические знания, полученные в
школе, лежит широкая дорога к огромным,
почти необозримым областям труда и открытий.
Здравствуйте ребята, на сегодняшнем уроке мы рассмотрим цилиндр и его элементы, сечения цилиндра плоскостью, площадь боковой и полной поверхности цилиндра (слайд 1-3).
В течение 45 минут вы должны смотреть и видеть, замечать и отмечать, а главное правильно мыслить и рассуждать.
Вы самостоятельно оцените свои знания и определите, как вами усвоен материал. Выполняя задания, вы будете заполнять лист УСПЕХА учащегося. Подпишите его и ознакомьтесь с его содержанием.
-
Актуализация основных знаний учащихся.
I. Работа по вопросам (слайд 4)
1) Формула радиуса описанной окружности для правильного многоугольника.
2) Формула радиуса вписанной окружности для правильного многоугольника.
2) Для правильного многоугольника центры вписанной в него и описанной около него окружностей …..(совпадают)
3) В каком случае пирамида называется правильной?
4) Что такое правильная усеченная пирамида? высота усеченной пирамиды? апофема правильной усеченной пирамиды?
II. Решение задач (устно)- таблицы к задачам на магнитной доске
1) Сторона основания правильной шестиугольной пирамиды равна 3. Высота равна 4. Найдите боковое ребро пирамиды.
2)Боковое ребро правильной шестиугольной пирамиды равно 12 и наклонено к плоскости основания под углом 60°. Найдите сторону основания пирамиды.
III. Решение задач (разноуровневые задания на карточках)- самостоятельно, учащиеся выбирают задание на оценку «3», «4» и «5» (слайд 5-7)
Оценка «5»
Найдите полную поверхность правильной треугольной усеченной пирамиды, если высота h, а стороны оснований а и b.
Ответ: Sполн = 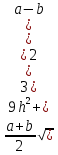
Оценка «4»
Высота правильной четырехугольной пирамиды равна 7 см, сторона ее основания 8 см. Вычислите:
А) длину бокового ребра пирамиды;
Б) площадь боковой поверхности пирамиды.
Ответ: 9 см; 4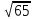 см.
см.
Оценка «3»
1. Если основание пирамиды правильный многоугольник и вершина проектируется в центр основания, то она
А) наклонная Б) правильная В) усеченная
2. Перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания
А) ось Б) апофема В) высота
3. Высота боковой грани правильной пирамиды, проведенная из вершины пирамиды
А) ось Б) апофема В) высота
4. Часть пирамиды, заключенная между ее основанием и секущей плоскостью, параллельной основанию называется
А) правильной пирамидой Б) тетраэдром В) усеченной пирамидой
5. Может ли быть гранью правильного многогранника правильный шестиугольник?
А) да Б) нет в) не знаю
6. Боковая поверхность пирамиды состоит из:
А) квадратов Б) треугольников В) параллелограммов
7. Общие стороны боковых граней
А) ребра Б) апофема в) ось
8. Сколько существует типов правильных многогранников
А) 4 Б) 3 В) 5
9. Правильный многогранник - это
А) ромб Б) додекаэдр В) эллипс.
10. Площадь боковой поверхности правильной пирамиды равна
А) 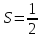 Pk Б)
Pk Б) 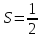 hk
hk 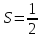 (P+P1)k
(P+P1)k
11. Площадью полной поверхности пирамиды называют
А) сумму площадей всех ее боковых граней;
Б) часть пирамиды, заключенная между ее основанием и секущей плоскостью;
В) сумму площадей всех ее граней.
12. Высотой усеченной пирамиды называется
А) перпендикуляр, проведенный из какой-нибудь точки одного основания на плоскость другого;
Б) отрезок, проведенный из какой-нибудь точки одного основания на плоскость другого;
В) сумму площадей всех ее граней.
(правильные ответы на слайде 8)
Задание на оценку «3» -(самопроверка), задание на оценку «4» и «5» - решение комментируется, затем выставление оценок и заполнение листа успеха.
-
Изучение нового материала (показ презентации)
Вступительное слово учителя:
На сегодняшнем уроке мы начинаем изучать новую главу «Тела вращения». Рассмотрим такие тела вращения как цилиндр, конус, шар (слайд 9-10)
Говорят, что фигура Ф в пространстве получена вращением фигуры F вокруг оси а, если точки фигуры Ф получаются всевозможными поворотами точек фигуры F вокруг оси а. Фигура Ф при этом называется фигурой вращения.
Вращение точки а вокруг прямой а - окружность, вращение окружности вокруг ее диаметра - сфера, вращение прямоугольника вокруг одной из его сторон - цилиндр (слайд 11).
Вращение прямоугольного треугольника вокруг одного из катетов - конус, вращение трапеции, один из углов которой является прямым, вокруг боковой стороны - усеченный конус, вращение окружности вокруг прямой, лежащей в плоскости окружности и не имеющей с этой окружностью общих точек - тор (слайд 12). Вращение эллипса вокруг его оси - эллипсоид вращения, вращение параболы вокруг ее оси - параболоид вращения, вращение гиперболы вокруг ее оси - гиперболоид вращения (слайд 13-14).
Тело вращения - это пространственная фигура, полученная вращением плоской ограниченной области вместе со своей границей вокруг оси, лежащей в той же плоскости (слайд 15).
Задание.
1) Приведите примеры из окружающего мира тел, похожих на тело, полученное вращением треугольника вокруг оси, содержащей его сторону (слайд 16).
2) Из каких геометрических тел состоит тело, полученное вращением трапеции вокруг оси, содержащей большее основание трапеции (слайд 17).
Ученик - консультант:
Слово цилиндр означает от греческого слова «валик», «каток» (слайд 18).
Зададим две параллельные плоскости α и . В плоскости α расположим окружность некоторого радиуса. Если из каждой точки окружности провести взаимно параллельные прямые пресекающие плоскость , то в плоскости получится окружность такого же радиуса. Отрезки прямых, заключенных между параллельными плоскостями образуют в этом случае цилиндрическую поверхность(слайд 19).
Цилиндр - это тело, заключенное между двумя кругами, расположенными в параллельных плоскостях и цилиндрической поверхностью.
Цилиндр - это тело, которое описывает прямоугольник при вращении около оси, содержащей его сторону.
Верхний и нижний круги - это основания цилиндра.
Прямая проходящая через центры кругов - это ось цилиндра.
Отрезок параллельный оси цилиндра, концы которого лежат на окружностях основания - это образующая цилиндра
Радиус основания - это радиус цилиндра.
Высота цилиндра - это перпендикуляр между основаниями цилиндра (слайд 20).
Виды цилиндров: прямой круговой, наклонный круговой, прямой некруговой (слайд 21).
Ученик- консультант:
(ученик- консультант проводит показ сечений на цилиндрическом куске колбасы)
Сечения цилиндра:
Осевое сечение: Плоскость сечения содержит ось цилиндра и перпендикулярна основаниям. В сечении - прямоугольник.
Сечение плоскостью параллельной оси цилиндра.
Плоскость сечения параллельна оси цилиндра и перпендикулярна основаниям. В сечении - прямоугольник.
Сечение плоскостью параллельной основанию цилиндра.
Плоскость сечения параллельна основаниям цилиндра и перпендикулярна оси. В сечении - круг (слайд 22-23).
Сечение цилиндра плоскостью, проходящей под углом к оси.
Сечением является эллипс (слайд 24).
Ученик- консультант:
Площадь боковой поверхности цилиндра (слайд 24-25).
L= 2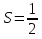
Sбок=2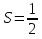
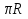
Для вывода формулы площади полной поверхности цилиндра потребуется развертка цилиндра.
Полная поверхность состоит из 2 оснований и боковой поверхности.
Площадь основания находим как площадь круга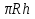 , R-радиус основания цилиндра. Боковая поверхность цилиндра есть прямоугольник. Одна сторона прямоугольника - это высота цилиндра (h), другая - длина окружности основания (2πR). Площадь боковой поверхности цилиндра равна произведению сторон прямоугольника. Получаем, Sполн=Sбок+2Sосн=2πRh + 2πR2
, R-радиус основания цилиндра. Боковая поверхность цилиндра есть прямоугольник. Одна сторона прямоугольника - это высота цилиндра (h), другая - длина окружности основания (2πR). Площадь боковой поверхности цилиндра равна произведению сторон прямоугольника. Получаем, Sполн=Sбок+2Sосн=2πRh + 2πR2
-
Физминутка для глаз (слайд 26)
-
Закрепление нового материала.
А) Тест (слайд 27)- кол-но
1. Расстояние между плоскостями цилиндра:
А) высота Б) радиус В) апофема
2. Прямая, проходящая через центры оснований цилиндра:
А) радиус Б) образующая В) ось
3. Сечением цилиндра плоскостью, проходящей через ось является
А) прямоугольник Б) круг В) окружность
4. Сечением цилиндра плоскостью, перпендикулярной оси является
А) прямоугольник Б) круг В) эллипс
5. Сечение цилиндра плоскостью, проходящей под углом к оси.
А) прямоугольник Б) круг В) эллипс
6. Цилиндр называют равносторонним, если осевое сечение:
А) эллипс Б) прямоугольник В) квадрат
7. Отрезки, соединяющие соответствующие точки окружностей кругов цилиндра называются
А) оси Б) образующие В) основания
Заполнение листа успеха
Б) Решение задач (работа в группе). (слайды 28-32)
1) (устно) Радиус основания цилиндра 2 м, высота 3 м. Найдите диагональ осевого сечения.
2) (устно) Площадь осевого сечения цилиндра 42 см2, высота цилиндра 7 см. Найдите площадь основания цилиндра.
3) (устно) Высота цилиндра 24 см, радиус основания 4 см. Найдите площадь осевого сечения цилиндра.
4) (устно) Высота цилиндра 6 см, радиус основания 5 см. Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4 см от нее.
5) Цилиндрический паровой котел имеет диаметр 1 м, длина котла равна 3,8 м, давление пара 10 атм. Найдите силу давления пара на поверхность котла.
6. Цилиндры вокруг нас ( слайды 33-53).
7. Итоги урока (звучит музыка -релаксация).
На сегодняшнем уроке мы рассмотрели определение цилиндра и связанных с ним понятий (образующие, основания, радиус, высота, ось), рассмотрели основные виды сечений цилиндра, площадь боковой и полной поверхности цилиндра. Подведем итог, были ли сегодня на уроке:
И-интересные, запоминающиеся моменты урока;
Т- трудные, тяжелые моменты урока;
О- оценка работы в группе и своего вклада в общее дело;
Г- главный вывод по сегодняшнему уроку:
- усвоил полностью, могу применять:
- усвоил, но затрудняюсь применять:
- усвоил частично:
- не усвоил.
Комментирование и выставление оценок, учащиеся сдают листы успеха.
8. Домашнее задание:
Группа «А» - стр.27-30 , № 11,12
Группа «В» - стр. 27-30, № 11,12,13
Заключительное слово учителя.
Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг - геометрия.
Ле Корбюзье
Приложение 3.
Лист успеха ___________________________
№ п/п
Задание
Материал
Усвоил, могу применять
Усвоил, но затрудняюсь применять
Усвоил частично
Не усвоил
1.
Актуализация основных знаний учащихся
2.
Работа в разноуровневых группах
3.
Изучение нового материала
А) тела вращения
Б) цилиндр
В) сечения цилиндра
Г) площадь боковой и полной поверхности цилиндра
4.
Закрепление нового материала
А)Тест
Б)Решение задач
(работа в группе)
5.
Цилиндры вокруг нас