- Учителю
- Урок по математике для 6 класса «Смешанные числа»
Урок по математике для 6 класса «Смешанные числа»
 Муниципальное казенное общеобразовательное учреждение Жигаловская средняя общеобразовательная школа
Муниципальное казенное общеобразовательное учреждение Жигаловская средняя общеобразовательная школа
№1 им.Г.Г. Малкова
Урок новых знаний
по математике
6 класс
Тема: «Смешанные числа»
учитель математики
первой категории
Репешко Валентина Юрьевна
2013г.
Цель: Научить записывать неправильные дроби в смешанные числа, расширить знания о числах.
Задачи:
1) Научиться переходить от записи неправильной дроби к смешанному числу, отработать алгоритм записи смешанных чисел.
2) УУД: - Познавательные: овладение основами логического и алгоритмического мышления;
Регулятивные: развитие умения читать и записывать информацию в виде различных математических моделей, планировать действия в соответствии с поставленной задачей;
Коммуникативные: строить высказывания, аргументировано доказывать свою точку зрения;
Личностные: развитие навыков сотрудничества со сверстниками,
Оборудование: презентация, конспект урока, компьютер, проектор, магнитный муляж апельсинов, листы достижений.
Ход урока:
Деятельность учителя и обучающегося. Формирование УУД:
№ слайда
-
Мотивация к учебной деятельности
На слайде эпиграф к уроку: «С малой удачи начинается успех»
- Какое ключевое слово в этом высказывании? (УСПЕХ)
- Что необходимо для успешной работы на уроке?
-Я желаю Вам успешно поработать на уроке. В конце урока каждый из вас оценит свою работу и работу соседа по шкале достижений (приложение 1)
Посмотрим отрывок из мультфильма «Апельсин»
На данном этапе урока происходит вовлечение учащихся в деятельность на личностно-значимом уровне. Формируются личностные УУД.
№1
№2
-
Актуализация и фиксирование индивидуального затруднения в пробном действии.
Приступим к работе. Предложите способы делениятрёх апельсинов среди трёх друзей (на доске магнитный муляж трёх апельсинов).
Подумайте и предложите свои версии.
- Сколько достанется каждому?
- Как найдём? (действие сложение)
Возможные варианты:
I способ: 1/2+1/2+1/2=3/2 (каждому)
II способ: 1/4+1/4+1/4+1/4+1/4+1/4=6/4 (каждому)
III способ: 1+1/2=?
IV способ: 1+1/4+1/4=1+2/4=?
- Сформулируйте способы деления.
Какой вывод можно сделать? (Способы различные, но количество доставшихся долей будет одинаково. Количество долей, доставшихся каждому будет записано по разному.
3/2=6/4=1+1/2=1+2/4 Умеем?!
Выявление сложности:
- Что нам не даёт сложить эти числа? (Не знаем правила сложения натуральных чисел и обыкновенных дробей)
- Каковы ваши предположения по поводу записи данного ответа (союз «и» - действие сложение).
Ситуация разрыва:
Не хватает чисел для полного и понятного математического ответа.
Сумму 1+1/2 принято записывать в виде смешанного числа 1 ½
целая часть дробная часть
Определение: Смешанное число - число, содержащее целую и дробную часть.
- Назовите дробные части смешанных чисел (на экране)
- Вернёмся к нашим способам деления. Какой по вашему мнению удачней? Почему? (II способ, так как неправильной дробью не понятно, какое количество апельсинов нам необходимо взять)
цдоО
ССуммуvjhС
На этапе актуализации идёт повторение изученного материала, необходимого для «открытия нового знания», и выявление затруднений в индивидуальной деятельности каждого учащегося. Формируются регулятивные УУД.
Учитель использует побуждающий от проблемной ситуации диалог, происходит обсуждение затруднений. Дети учатся обнаруживать и формулировать учебную проблему, задачу совместно с учителем. Формируются регулятивные УУД.
№3
№4
№5
-
Построение проекта выхода из затруднения (тема, цель, задачи, план, способ, средство)
- На какой вопрос предстоит ответить? (Как выделить целую часть из неправильной дроби?)
- Какова тема урока? (Смешанные числа).
- Есть необходимость смешанных чисел?
- Скажите, значит должен существовать математический способ перехода из неправильной дроби в смешанное число. Ваши предложения.
Ориентируемся на пример:
3/2=1 ½ 49/3= ?
Проверяем гипотезы.
Что используем при переходе из неправильной дроби к смешанному числу (формула деления с остатком).
3/2=3:2=1 (ост.1)= 1 ½
49/3= 49:3= 16 1/3
Составим алгоритм перехода из неправильной дроби в смешанное число: (Дети выдвигают предположения самостоятельно)
-
Разделить с остатком числитель на знаменатель;
-
Неполное частное будет целой частью чисел;
-
Остаток- числитель, делитель-знаменатель дробной части.
Подтверждение своей версии где можно найти (учебник стр.168).
(Дети читают текст учебника, делают выводы)
С обучающимися можно не согласиться, так как в учебнике указан алгоритм выделения целой части из неправильной дроби.
Высказывания равносильные:
«Выделить целую часть» и « перевести из неправильной дроби в смешанное число».
Дети учатся определять цель учебной деятельности с помощью учителя и самостоятельно, искать средства её осуществления; составлять план выполнения задач, решения проблем поискового характера. Формируются регулятивные УУД.
А так же дети учатся добывать информацию различными способами: наблюдение, чтение, слушание Происходит открытие нового знания. Формируются познавательные УУД.
Учатся доносить свою позицию до других (строить высказывания, пользуясь математической терминологией), слушать других, пытаться принимать другую точку зрения, быть готовым изменить свою точку зрения, при необходимости отстаивать свою точку зрения, аргументировать её.. Формируются коммуникативные УУД,
№6
№7
№8
-
Мультминутка
№9
5. Первичное закрепление с проговариванием во внешней речи
(- Проговаривание нового знания)
1) Сколько шагов должны выполнить при переходе из неправильной дроби в смешанное число ( 3 шага)?
При решении заданий не забываем делать пометки на полях «+» или «-«
2) Заменить многоточие числами (один ученик выполняет задание за закрытой доской, остальные в тетрадях)
…=15:2=7(ост.1)=…
…=… : 20=3(ост.2)=…
40/4= …
3) Задача (самостоятельно, ответы сличаются с решением на экране)
Турист прошёл 25 км за 4 часа. Найдите его скорость?
4) Решить уравнение (самостоятельно, ответы сличаются с решением на экране):
2х+10=31
На данном этапе формируются познавательные УУД: использовать полученную информацию в деятельности, развитие мыслительных операций, решать задания по аналогии, используя алгоритм действий, применять данное действие в новых ситуациях.
№10
№11
№12
-
Самостоятельная работа в парах с самопроверкой по эталону (пятиминутка)
-
Из обыкновенных дробей выпишите:
![]()
а) правильные дроби; б) неправильные дроби.
-
Запишите все дроби, у которых: а) знаменатель 7, числитель меньше знаменателя; б) числитель 9, знаменатель меньше числителя.
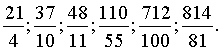
-
Выделите целую часть из дроби:
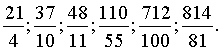
Проверка по эталону (обмен тетрадями)
На данном этапе дети учатся самостоятельно применять знания в новой ситуации. Формируются регулятивные УУД.
Каждый делает для себя вывод, что он уже умеет. Формируются личностные УУД (самоконтроль, самооценка, саморефлексия, способность к саморазвитию)
№13
№ 14
№ 15
№ 16
-
Рефлексия
Ответьте на вопросы:
1. Что повторили в ходе урока?
2. Что нового узнали?
3. Что понравилось?
4. Было ли трудно? В чём заключалась трудность?
Оцените работусвою и соседа по парте по шкале достижений.
В диалоге с учителем дети учатся определять степень успешности выполнения своей работы и работы все, осознание своей УД. Понимать причины своего неуспеха и находить способы выхода из этой ситуации. Регулятивные УУД.
№17
-
Домашнее задание (по выбору).
а) №1109, №1107
б) Написать рассказ или сказку об «Обыкновенных дробях».
Большое спасибо за работу!
Д/з включает в себя как репродуктивное задание, так и творческое, что позволяет вызвать у детей познавательный интерес. Формируются познавательные УУД,
№18
Приложение 1
Действия с обыкновенными дробями. Смешанные числа.