Технологическая карта по геометрии 8 класс по теме Теорема Пифагора

Технологическая карта урока по теме «Теорема Пифагора» 8 классГеометрия

Класс:

8

Учитель:

Попова Раиса Иннокентьевна

Базовый учебник:

Л.С. Атанасян «Геометрия 7-9»

Тема урока:

Теорема Пифагора

Количество часов, отведенное на изучение темы:

3

№ урока:

1

Тип урока:

Урок открытия нового знания

Цель урока:

Ознакомить и обеспечить учащихся приемами при нахождении сторон прямоугольного треугольника при помощи теоремы Пифагора

Планируемые результаты:

УУД

Личностные: формирование коммуникативной компетентности в общении со сверстниками, умеют ясно, четко излагать свои мысли в устной и письменной речи

Познавательные: самостоятельно добывают новые знания

Регулятивные: уметь анализировать, делать выводы, рефлексия способов и условий действия

Коммуникативные: уметь слушать и вступать в диалог, строить в группе продуктивное взаимодействие

Планируемые результаты обучения, в том числе и формирование УУД:

Предметные: знать теорему Пифагора, находить сторону прямоугольного треугольника при помощи теоремы Пифагора

Личностные: мотивация учебной деятельности, уметь работать группами

Метапредметные: уметь слушать собеседника, формулировать собственное мнение и позицию

Основные понятия темы:

Теорема Пифагора

Методы:

Эвристический метод (метод мозгового штурма), метод иллюстрации и демонстрации, учебная дискуссия, беседа

Межпредметные связи:

История, алгебра

Необходимое учебное оборудование:

Компьютер, проектор, электронная презентация, выполненная в программе Power Point

Основные этапы организации учебной деятельности

Цель этапа

Содержание педагогического взаимодействия

Деятельность учителя

Деятельность обучающихся

Личностная

Познавательная

Коммуникативная

Регулятивная

1. Этап мотивации (самоопределения) к учебной деятельности.

Создание благоприятного психологического настроя на работу. Выявление сущности значения темы, определение его места в системе знания

Приветствует учащихся, проверяет готовность к уроку. Мотивирует учащихся на получение новых знаний. Организует устную работу, подводит к целям и к теме урока

Мотивация учения

Проявление активности во взаимодействии для устной работы

Организация своей учебной деятельности. Определять последовательность промежуточных целей и соответствующих им действий с учетом конечного результата

2. Этап актуализации и фиксирования индивидуального затруднения в пробном действии

Подготовка мышления учащихся, организация осознания ими внутренней потребности к построению учебных действий и фиксирование каждым из них индивидуального затруднения в пробном действии.

Задает вопросы для повторения, актуализируя знания .

Структурирование собственных знаний. Отвечают на вопросы учителя. Практическая работа.

Проявление активности во взаимодействии для устной работы.

Уметь использовать речь для регуляции своего действия

3. Этап выявления места и причины затруднения

Организовать анализ учащимися возникшей ситуации и на этой основе выявить места и причины затруднения, осознать то, в чем именно состоит недостаточность их знаний, умений или способностей

Подводит учащихся к теореме Пифагора. Ставит проблему - доказательство.

Мотивация к целенаправленной познавательной деятельности, мобилизация внимания.

Структурирование знаний, постановка и формулирование проблемы.

В ситуации затруднения регулируют ход мыслей.

Целеполагание, планирование, прогнозирование

4. Этап построения проекта выхода из затруднения

Постановка целей учебной деятельности и на этой основе - выбор способа и средств их реализации.

Доказывают теорему Пифагора, пользуется эвристической беседой.

Структурирование знаний.

Участие в эвристической беседе.

волевая саморегуляция в ситуации затруднения

5. Этап реализации построенного проекта

Построение учащимися нового способа действий и формирование умений его применять как при решении задачи, вызвавшей затруднение, так и при решении задач такого класса или типа вообще.

Разделяет учащихся на команды. Каждой команде раздаются карточки, где теорема доказывается другими способами. Задача учащихся: понять доказательство и доказать теорему на доске другим учащимся.

Структурирование знаний, поиск и выделение необходимой информации, осознают ответственность за работу в команде.

В ситуации затруднения регулируют ход мыслей. Работа в команде.

Проявляют познавательную инициативу.

6. Этап первичного закрепления с проговариванием во внешней речи.

Усвоение учащимися нового способа действия при решении типовых задач

Рассматривает задачи на нахождение стороны треугольника с помощью теоремы Пифагора.

Структурирование знаний.

Проявление активности.

Закрепляют новую тему.

7. Этап самостоятельной работы с самопроверкой по эталону

Интериоризация (переход извне внутрь) нового способа действия и исполнительская рефлексия (коллективная и индивидуальная) достижения цели пробного учебного действия, применение нового знания в типовых заданиях

Задает задачи на самостоятельную работу с самопроверкой по эталону.

Извлечение из математических текстов необходимой информации. Подведение под понятие.

Выполнение действий по алгоритму.

Использование критериев для обоснования своего суждения

Контроль, коррекция, оценка.

8. Этап рефлексии учебной деятельности на уроке

Самооценка учащимися результатов своей учебной деятельности, осознание метода построения и границ применения нового способа действия

Задает вопросы, проводит рефлексию.

Самооценка на основе критерия

Успешности.

Контроль и оценка процесса и

результатов деятельности.

Выражение своих мыслей с

достаточной полнотой и точностью

Планирование учебного сотрудничества.

</<font face="Times New Roman, serif">Ход урокаПриветствие. Проверка готовности к уроку.

- Что вы знаете о Пифагоре? Пифагор - древнегреческий ученый. Считается, что он открыл доказательство теоремы, носящей теперь его имя. И важно то, что свойство прямоугольного треугольника было установлено не случайно, не опытом, не измерением, а исключительно путём доказательства, т.е. только усилием человеческого разума. Вот именно с этого момента, когда убедились, что путём логических рассуждений можно открывать новые факты, и пошла геометрия как дедуктивная наука.

Приветствие.

Мотивируются на урок.

2

2

Этап актуализации и фиксирования индивидуального затруднения в пробном действии

-Какая геометрическая фигура называется треугольником?

-Треугольник - это геометрическая фигура, состоящая из трех точек, не лежащих на данной прямой, соединенные между собой отрезками.

-Перечислите виды треугольников в зависимости от сторон.

-Равнобедренный, равносторонний.

-Перечислите виды треугольников в зависимости от углов.

-Тупоугольный, остроугольный, прямоугольный.

-Какой треугольник называется прямоугольным?

-Треугольник называется прямоугольным, если у него один угол прямой.

-Как называются стороны в прямоугольном треугольнике?

Катеты и гипотенуза.

-1) Сумма двух острых углов прямоугольного треугольника равна .

-Сформулируйте свойства прямоугольного треугольника.

2) Катет прямоугольного треугольника, лежащий против угла, равен половине гипотенузы.

3) Если катет прямоугольного треугольника равен половине гипотенузе, то угол, лежащий против этого катета, равен .

3

Этап выявления места и причины затруднения.

Теорема Пифагора:

В прямоугольном треугольнике квадрат гипотенузы равен сумме

квадратов катетов.

-Выполните задания:

1) Начертите прямоугольный треугольник ABC с прямым углом C.

2) Измерьте длины его сторон.

3) Вычислите, чему равен квадрат гипотенузы.

4) Найдите сумму квадратов катетов.

5) Какой можно сделать вывод?

-То, к чему мы пришли, называется теоремой Пифагора. Пифагор доказал теорему в 6 веке до н.э.-Давайте попробуем доказать теорему. Что мы будем делать?

Выполняют задание.

-Квадрат гипотенузы равен сумме квадратов катетов.

Предлагают свои варианты.

4

Этап построения проекта выхода из затруднения

Теорема Пифагора:

В прямоугольном треугольнике квадрат гипотенузы равен сумме

квадратов катетов.

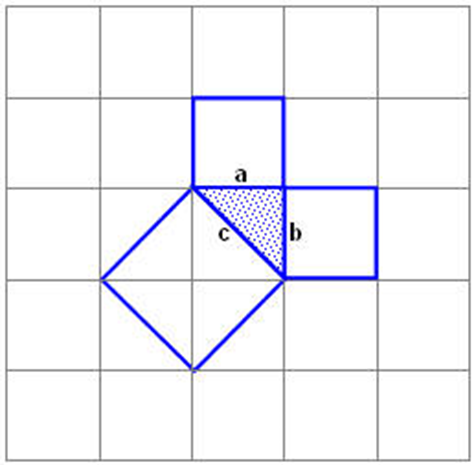
- Докажем теорему Пифагора:

-Что вы видите на рисунке?

- Квадраты, составленные на сторонах треугольника.

- Как нам доказать теорему Пифагора?

- Найти их площади.

Выполните задания:

1. Определить вид выделенного треугольника.

1. Нам дан прямоугольный треугольник, катеты которого равны a и b, а гипотенуза равна c.

2. Вставить пропущенные слова в предложении.

Квадраты, построенные на катетах, состоят из ……. одинаковых треугольников, а квадрат, построенный на гипотенузе состоит из …….таких треугольников.

2. Квадраты, построенные на катетах, состоят из двух одинаковых треугольников, а квадрат, построенный на гипотенузе состоит из четырех таких треугольников.

3. Найдите площади всех квадратов

3. ;

;

;

4. Сформулируйте теорему Пифагора

4.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

5

Этап реализации построенного проекта

Карточка 1: Доказательство древнеиндийских математиков с одним словом «Смотри!»

Карточка 2: Доказательство методом Гарфилда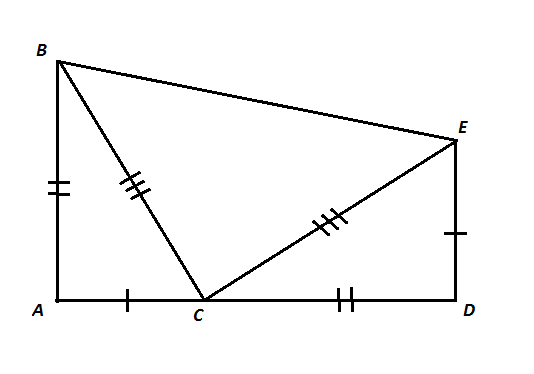

Карточка 3: Доказательство древнеиндийского математика Бхаскари

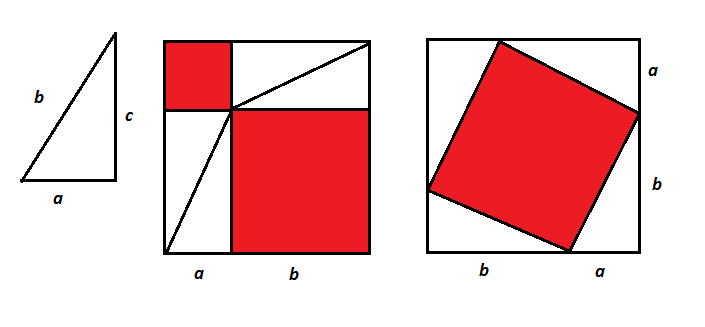
- А знаете ли вы, что теорема Пифагора входит в книгу рекордов Гиннеса? Потму что она имеет больше ста доказательство. А теперь предлагаю вам творческую работу - мозговой штурм. Разделитесь на команды. Каждой команде раздам карточки с рисунками разных доказательств. Вам дается 15 минут разобраться и расписать доказательство.

Разбиваются на группы и доказывают теорему Пифагора разными доказательствами, предложенными в карточках. После выходят на доску и рассказывают свои доказательства по группам.

6

Этап первичного закрепления с проговариванием во внешней речи

1.Катеты прямоугольного треугольника равны 15 см и 20 см.

Найди гипотенузу.

2. Катет прямоугольного треугольника равен 9 см, а гипотенуза равна 15 см.

Найди площадь треугольника.

3. Основания прямоугольной трапеции равны 10 дм и 25 дм. Меньшая боковая сторона равна 8 дм.

Вычисли большую боковую сторону трапеции.

- Решим задачи с применением теоремы Пифагора.

Решают задачи вместе с учителем.

7

Этап самостоятельной работы с самопроверкой по эталону.

1. Катет прямоугольного треугольника равен 60 см, а гипотенуза равна 100 см.

Вычисли длину второго катета.

2. Сторона квадрата равна 25 см.

Вычисли диагональ квадрата.

3. Основание равнобедренного треугольника равно 16 см, а боковая сторона равна 17 см.

Вычисли высоту, проведённую к основанию.

- Решите самостоятельно три задачи.

Решают задачи с самопроверкой по эталону.

8

Этап рефлексии учебной деятельности на уроке

- В чем заключается теорема Пифагора? Сколько доказательств мы рассмотрели? Какое доказательство вам больше понравилось? Почему?

Рефлексия. Отвечают на вопросы учителя.