Школьный этап олимпиады по математике. 5 класс

Школьный этап олимпиады по математике

Олимпиада по математике. 5 класс

1. Решите уравнение (6 099 948 - 756 : ((30 +х) : 336) · 201) : 407 025 = 12

2. Три туриста решили вместе поесть. Один из них дал две булки, другой три булки, а третий - 10 руб. Сколько из этих денег должен взять первый и сколько - второй турист?

3. Сумма шести последовательных четных чисел равна 3 018. Найдите эти числа

4. Длина прямоугольного параллелепипеда 250 мм, ширина - 120 мм, высота - 40 мм. Его разрезали на кубические сантиметры и разместили в один ряд вплотную друг к другу. Какой длины (в метрах) получился ряд?

5. В выражении 4+32:8+4·3 расставьте скобки так, чтобы получилось как можно большее число, как можно меньшее число.

6. Найдите все трехзначные числа, которые в 12 раз больше суммы своих цифр

Ответы:

1. х = 12

2. 5 * 3 = 15 (р.) - стоимость булок для троих.

15 : 5 = 3 (р.) - стоимость одной булки.

1 * 2 = 6 (р.) - стоимость двух булок.

6 - 5 = 1 (р.) - надо отдать первому туристу.

3 - 3 = 9 (р.) - стоимость трёх булок.

9 - 5 = 4 (р.) - надо отдать второму туристу.

Ответ: 1 рубль должен взять первый турист и 4 рубля второй

3. 498 + 500 + 502 + 504 + 506 + 508

4. 12 метров

5. Наибольшее число (4 + 32 : 8 + 4) * 3 = 36. Наименьшее число (4 + 32) : [(8 + 4) * 3] = 1

6. Если а, в и с - это цифры трёхзначного числа, то его можно записать как
   
   100а+10в+с. Сумма цифр - а+в+с. Уравняем сумму цифр и число:
   
   12(а+в+с) =100а+10в+с;
   
   12а+12в+12с=100а+10в+с;
   
   88а-11с=2в.
   
   88а и 11с делятся на 11, значит их разность (2в) тоже делится на 11. 2 на 11 не делится, поэтому в должно делится на 11. Но в - это цифра, из всех цифр только 0 делится на 11, в=0. Получаем
   
   88а-11с=0,|:11
   
   8а-с=0,
   
   с=8а.
   
   а и с - это цифры, значит а=1, с=8 (если а>1, то с>10).
   
   Получили число 108.

Олимпиада по математике. 5 класс

1. Установите, какой цифрой оканчивается разность 43⁴³ - 17¹⁷.

2. Произведение четырех последовательных чисел равно 7920. Найти эти числа.

3. Из книги выпала какая-то часть. Первая страница выпавшего куска имеет номер 387, а номер последней страницы состоит из тех же цифр, но записанных в другом порядке. Сколько листов выпало из книги?

4. Сумма двух чисел равна 80, а их разность равна 3. Найдите эти числа.

5. Расшифруйте ребус: КНИГА + КНИГА + КНИГА = НАУКА

6. Над имеющимся числом разрешается производить два действия: умножать его на 2 или прибавлять к нему 2. За какое минимальное число действий вы сможете получить из числа 1 число 100?

Ответы:

1. Следует поискать закономерность для последней цифры натуральной степени числа, оканчивающегося цифрой 3.Последовательность этих цифр 3, 9, 7, 1, 3, 9, 7, 1... Четвертое, восьмое, двенадцатое и т.д. места занимает цифра 1.Значит, 43⁴⁰ заканчивается цифрой 1, а 43⁴³ - цифрой 7, далее аналогично 17¹⁶ оканчивается цифрой 1, а 17¹⁷ - цифрой 7. Так как оба числа 43 и 17 оканчивается одной и той же цифрой 7, то их разность оканчивается нулем.

2. 7920 = 2*2*2*2*3*3*5*11 = 8*9*10*11

3. (738 - 386):2 = 176 листов

4. 41,5 и 38,5

5. 28375 + 28375 + 28375 = 85125.

6. 1+2*2*2*2*2+2*2. За 7 действий.

Олимпиада по математике. 5 класс

1. </ Сумма цифр двузначного числа равна 12. Если цифру десятков умножить на 2, а цифру единиц на 3 и сложить оба произведения, то в результате получится 29. Найдите это число.

2. Какое самое большое число можно записать четырьмя единицами?

3. Два путешественника одновременно подошли к реке. У берега была привязана лодка, в которой мог переправиться только один человек. Путешественники не умели плавать, но каждому из них удалось переправиться через реку. Как это могло случиться?

4. Разрежьте прямоугольник, длина которого 9 см, а ширина 4 см, на две равные части, из которых можно составить квадрат.

5. Мальчик и поросенок весят столько, сколько 5 ящиков. Поросенок весит столько, сколько 4 кошки; 2 кошки и поросенок весят столько, сколько 3 ящика. Сколько кошек уравновесят мальчика?

6. Проведите через 6 точек четыре прямые так, чтобы на каждой прямой было по три точки.

Ответы:

1. 75

2. 11¹¹

3. Путешественники подошли к реке с разных берегов.

4)

5. М + П = 5Я

П = 4К

2К + П = 3Я. Из 2 и 3 ур получаем: 2К + 4К = 3Я. Я = 2К

Подставляем в 1 уравнение: М + 4К = 10К, М = 6К. Ответ. 6 кошек

Олимпиада по математике. 5 класс

1. Сколькими различными способами можно прочитать слово «Точка» на этой схеме? (начинать с «т» и спускаться вниз до «а»)

2. Из восьмилитрового ведра, наполненного молоком, надо отлить 4л с помощью 3-хлитрового и 5-и литрового бидона. Как это сделать?

3. Счетчик автомобиля показывал 12 921. Через два часа на счетчике опять появилось число, которое читалось одинаково в обоих направлениях. С какой скоростью ехал автомобиль?

4. Тетя Груша продает кабачки. Три кабачка она продает за 5 у.е, 4 кабачка - за 6 у.е, 5 кабачков - за 7 у.е. Ни в каком другом количестве кабачки тетя Груша не продает. Вчера она продала 100 кабачков и выручила за них 160 у.е. Сколько продаж вчера совершила тетя Груша?

5. Как разделить круг тремя прямыми на 4, 5, 6, 7 частей?

Ответы:

1)

Т

О О

Ч Ч Ч

К К К К

А А А А А Ответ. 16 способов

2)

3) (13 031 - 12 921) : 2 = 55 км/ч

4) Пусть х продаж 3 каб по 5 у.е., у продаж - 4 каб по 6 у.е, z продаж - 5 каб по 7 у.е.

3х + 4у + 5z = 100

5х + 6у + 7z = 160

1. 15х + 20у + 25z = 500

15х + 18у + 21z = 480. Отсюда 2у + 4z = 20 или у + 2z = 10 или у = 10 - 2z

2. 9х + 12у + 15z = 300

10х + 12у + 14z = 320. Отсюда х - z = 20 или х = 20 + z

Итак, х + у + z = 20 + z + 10 - 2z + z = 30. Ответ. 30

5)

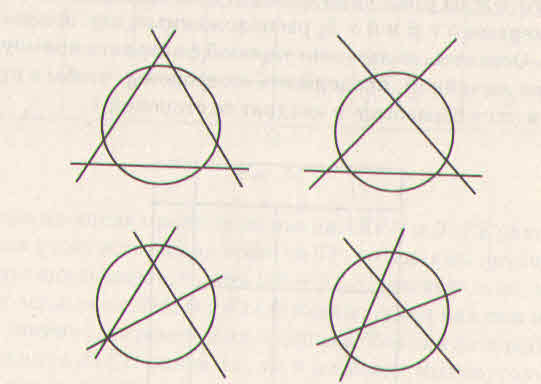
Олимпиада по математике. 5 класс

1. Три яблока, четыре груши и один персик стоят 40 руб. Одно яблоко, четыре груши и персик стоят 32 руб. Сколько стоят одно яблоко, одна груша и один персик, если персик стоит столько, сколько стоят два яблока?

2. Расшифруйте ребус:

C И Н И Ц А

+

С И Н И Ц А

____________

П Т И Ч К И

3. Кенгуру мама прыгает за 1 секунду на 3 метра, а её маленький сынишка прыгает на 1 метр за полсекунды. Они одновременно стартовали от бассейна к эвкалипту по прямой. Сколько секунд мама будет ждать сына под деревом, если расстояние от бассейна до дерева 240 метров?

4. В числе 3 728 954 106 зачеркнуть три цифры так, чтобы оставшиеся цифры в том же порядке составили бы наименьшее семизначное число.

5. Четыре ученика - Витя, Петя, Юра и Сергей - заняли на математической Олимпиаде четыре первых места. На вопрос, какие места они заняли, были даны ответы:

а) Петя - второе, Витя - третье;

б) Сергей - второе, Петя - первое;

в) Юра - второе, Витя - четвертое.

Укажите, кто какое место занял, если в каждом ответе правильна лишь одна часть. Ответ обоснуйте.

Ответ.

1. Решение.

40 - 32 = 8 (руб.) - стоят два яблока или один персик;

8:2 = 4 (руб.) - стоит одно яблоко;

4+8 = 12 (руб.) - стоят одно яблоко и персик;

32 - 12 = 20 (руб.) - стоят четыре груши;

20:4 = 5 (руб.) - стоит груша.

Ответ: 4 руб., 8 руб., 5 руб.

2. Решение.

342 457 + 342 457 = 684 914.

3. Решение.

1 шаг: 240:3 = 80 (с) - скакала мама Кенгуру;

2 шаг: за 1 секунду сын прыгает на 2 метра;

3 шаг: 80×2 = 160 (м) - проскачет кенгурёнок за 80 секунд:

4 шаг: 240-160 = 80 (м) - осталось проскакать кенгурёнку, когда мама была уже под эвкалиптом;

5 шаг: 80:2 = 40 (с).

Ответ. 40 секунд.

4. Ответ: 2 854 106.

5. Ответ: I - Петя, II - Юра, III - Витя, IV - Сергей.

Олимпиада по математике. 5 класс

1. Все треугольники, изображенные на рисунке, имеют равные стороны. Радиус каждой из окружностей равен 2 см. Окружности касаются друг друга и сторон квадрата. Чему равен периметр «звездочки», нарисованной жирной линией?

2. В данном примере различные цифры зашифрованы различными буквами. Определите, какое равенство зашифровано: ОТВЕТ + ОЧЕНЬ = ПРОСТ

3. Как разложить семь алмазов в четыре одинаковые шкатулки, чтобы вес всех шкатулок получился одинаковым, если вес алмазов 1, 2, 3, 4, 5, 6, 7. граммов. Ответ обоснуйте.

4. На уроке физкультуры мальчики построились в шеренгу. Потом между каждыми двумя мальчиками встала девочка. Всего в шеренге оказалось 25 детей. Сколько мальчиков стояло в шеренге?

5. Кот Матроскин прикинул, что он может выложить пол квадратной комнаты квадратной плиткой, и ему не понадобится ни одну из них разрезать. Сначала он положил плитки по краям комнаты, и на это у него ушло 84 плитки. Сколько всего ему надо иметь плиток, чтобы покрыть весь пол?

Ответы.

1. Решение. Сторона каждого треугольника 2+2+2+2=8см, тогда периметр равен 8*8=64 см. Ответ: 64 см

2. Зашифрованное равенство: 34214 + 35170 = 69384.

3. Вес одной доли алмазов равен 7 г. Ответ: 7 + (1 + 6) + (2 + 5) + (3 + 4).

4. Уберем самого правого мальчика. Тогда мальчиков и девочек будет поровну,

то есть по 12. Значит, в шеренге стояло 12 + 1 = 13 мальчиков.

5. Ответ. 484.

На каёмке, не считая угловых, лежит 84 - 4 = 80 плиток. Значит, на каждой стороне лежит 20 плиток, не считая угловых, а вместе с угловыми - 22 плитки. Поэтому

общее число плиток равно 484.

Олимпиада по математике. 5 класс

1. Даны числа 1,2,3,4,5,6,7,8,9. Расставьте их так, чтобы сумма их на каждой стороне треугольника была равна 20.

2. Как разложить гирьки весом 1, 2, ..., 9 г в три коробочки так, чтобы в первой было две гирьки, во второй - три, в третьей - четыре, а суммарный вес гирек в коробочках был одинаковым?

3. Мальчик по чётным числам всегда говорит правду, а по нечётным всегда врёт. Как-то его три ноябрьских дня подряд спрашивали: «Как тебя зовут?». На первый день он ответил: «Андрей», на второй: «Борис», на третий: «Виктор». Как зовут мальчика? Объясните, как вы рассуждали.

4. Мышь, мышонок и сыр вместе весят 180г. Мышь весит на 100г больше, чем мышонок и сыр вместе взятые. Сыр весит в три раза меньше, чем мышонок. Сколько весит каждый из них? Ответ нужно подтвердить вычислениями.

5. Есть 24 палочки. Длина первой палочки - 1 см, второй - 2 см, …, двадцать

четвёртой - 24 см (длина каждой следующей палочки на 1 см больше длины предыдущей). Как, использовав все эти палочки, составить три различных квадрата? Ломать палочки нельзя, каждая палочка должна входить только в один квадрат.

Ответы.

1. Например: 9 + 6; 8 + 5 + 2; 7 + 4 + 3 + 1.

2. Суммарный вес гирек равен 45, поэтому в каждой коробочке суммарный вес

гирек равняется 15 г.

3. Борис.

Решение. Так как мальчик дал три разных ответа, он хотя бы два раза соврал. Поэтому

два дня из трёх, когда мальчику задавали вопросы, пришлись на нечётные числа. Поскольку чётные и нечётные числа месяца чередуются, это должны были быть первый и третий дни. Стало быть, второй день пришёлся на чётное число. В этот день мальчик и назвал своё настоящее имя.

4. Мышь - 140г, сыр - 10г, мышонок - 30г.

Решение. Из условия следует, что удвоенный вес мыши равен 180 + 100 = 280г.

Поэтому вес мыши равен 140г. Тогда мышонок и сыр вместе весят 180 - 140 = 40г. А вес

сыра, согласно условию, равен четверти этого веса.

5. Разобьем палочки на три группы: от 1 до 8, от 9 до 16, от 17 до 24. В каждой

группе первую палочку соединим с последней, вторую - с предпоследней, третью - с третьей с конца, оставшиеся две палочки тоже соединим. Получим в каждой группе по четыре одинаковых палки, из которых сложим квадрат. Стороны полученных квадратов: 9, 25, 41.