- Учителю
- Самостоятельные работы по геометрии (8 класс)
Самостоятельные работы по геометрии (8 класс)
Самостоятельные работы по геометрии
(8 класс)
Самостоятельная работа обучающего характера № 1.
1 вариант.
-
Найдите сумму углов выпуклого одиннадцатиугольника.
-
Каждый угол выпуклого многоугольника равен 1350. Найти число сторон этого многоугольника.
2 вариант.
-
Найдите сумму углов выпуклого двенадцатиугольника.
-
Сумма углов выпуклого многоугольника равна 12600. Найти число сторон этого многоугольника.
Проверочная самостоятельная работа № 2.
1 вариант
-
ABCD - параллелограмм. Луч AN - биссектриса угла BAD; луч ВМ - биссектриса угла АВС. Докажите, что ABNM - параллелограмм.
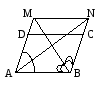
2 вариант
-
ABCD - параллелограмм. Луч AM - биссектриса угла BAD; луч CN - биссектриса угла ВСD. Докажите, что ANCM - параллелограмм.
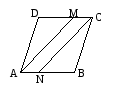
Проверочная самостоятельная работа № 3.
1 вариант
-
Найти боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов равен 1200.
2 вариант
-
Найти меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая сторона - 10 см, а один из углов равен 600.
Самостоятельная работа обучающего характера № 4.
Прямоугольник, ромб, квадрат
1 вариант.
-
Найдите углы ромба, если его диагонали составляют с его стороной угол, равный 300 .
-
В квадрате АВСD проведена диагональ ВD. Найти углы треугольника ВСD.
2 вариант.
-
Угол между диагоналями прямоугольника равен 500. Найти углы между диагональю прямоугольника и его сторонами.
-
В ромбе АВСD проведены диагонали, которые пересекаются в точке О. Найти углы треугольника АОВ, если тупой угол ромба 1200 .
Проверочная самостоятельная работа № 5.
1 вариант
-
Через точку пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AD и ВС в точках Е и F соответственно. Найти стороны параллелограмма, если его периметр равен 28 см, АЕ = 5 см, BF = 3 см
-
Найти меньшую боковую сторону прямоугольной трапеции, основания которой равны 10 см и 6 см, а один из углов равен 450.
2 вариант
-
Биссектрисы углов А и D параллелограмма ABCD пересекаются в точке М, лежащей на стороне ВС. Найти стороны параллелограмма, если его периметр равен 36 см.
-
Найти боковую сторону равнобедренной трапеции, основания которой равны 12 см и 6 см, а один из углов равен 600.
Самостоятельная работа обучающего характера № 6.
1 вариант.
-
ABCD - прямоугольник, точка М - середина стороны ВС. Периметр прямоугольника равен 48 см, а сторона AD вдвое больше стороны АВ. Найти: а) площадь прямоугольника ABCD; б) площадь треугольника ADN;
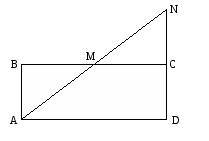
2 вариант.
-
ABCD - прямоугольник, точка C - середина стороны ВF. Периметр прямоугольника равен 46 см, а сторона BC вдвое больше стороны АВ. Найти: а) площадь прямоугольника ABCD; б) площадь треугольника ABF;
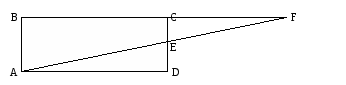
Самостоятельная работа обучающего характера № 7.
1 вариант.
-
Стороны параллелограмма равны 10 см и 6 см, а угол между ними 1500. Найти площадь этого параллелограмма.
2 вариант.
-
Острый угол параллелограмма равен 300 , а высоты, проведенные из вершины тупого угла, равны 4 см и 3 см. Найти площадь этого параллелограмма.
Самостоятельная работа обучающего характера № 8.
1 вариант.
-
ОА = ОВ, ОС = 2ОD, SAOD = 12 см2. Найти площадь треугольника ВОС

2 вариант.
-
ОB = ОC, ОD = 3AО, SAOC = 16 см2. Найти площадь треугольника ВОD
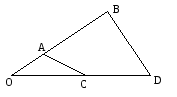
Самостоятельная работа обучающего характера № 9.
1 вариант.
-
Высота и основания трапеции относятся как 5 : 6 : 4. Найдите меньшее основание трапеции, если ее площадь равна 88 см2.
2 вариант.
-
Высота трапеции равна меньшему основанию и в два раза меньше большего основания этой трапеции. Найдите высоту трапеции, если ее площадь равна 54 см2.
Проверочная самостоятельная работа № 10.
1 вариант
-
В прямоугольной трапеции основания равны 22 см и 6 см, а большая боковая сторона - 20 см. Найти площадь трапеции.
2 вариант
-
Боковые стороны прямоугольной трапеции равны 7 см и 25 см, а меньшее основание - 2 см. Найти площадь трапеции.
Итоговая самостоятельная работа № 11.
1 вариант
-
В треугольнике АВС угол А равен 450, ВС = 13 см, а высота BD отсекает на стороне АС отрезок DC, равный 12 см. Найти площадь треугольника АВС и высоту, проведенную к стороне ВС.
-
Одна из диагоналей ромба на 4 см больше другой, а площадь ромба равна 96 см2. Найти стороны ромба.
2 вариант
-
В треугольнике АВС угол В равен 450, высота AN делит сторону ВС на отрезки BN = 8 см, NC = 6 см. Найти площадь ∆ АВС и сторону АС.
-
Найдите площадь ромба, если его сторона равна 20 см, а диагонали относятся как 3 : 4.
Самостоятельная работа обучающего характера № 12.
1 вариант.
-
∆АВС ∞ ∆KMN, АС = 3 см, MN = 4 см, А = 300. Найти: а) ВС, MKN; б) SABC : SKMN ; в) отношение, в котором биссектриса угла С делит сторону АВ
2 вариант.
-
∆PQR ∞ ∆АВС , PQ = 3 см, PR = 4 см, А = 400. Найти: а) AС, QPR; б) SPQR : SABC ; в) отношение, в котором биссектриса угла P делит сторону RQ
Проверочная самостоятельная работа № 13.
1 вариант
-
Высота CD прямоугольного треугольника АВС делит гипотенузу АВ на части AD = 16 cм и BD = 9 см. Докажите, что ∆АСD ∞ ∆CBD и найдите высоту CD
-
Точки М и N лежат на сторонах АС и ВС треугольника АВС соответственно; АС = 16 см, ВС = 12 см, СМ = 12 см, CN = 9 см. Докажите, что MN || BC.
2 вариант
-
Высота CD прямоугольного треугольника АВС отсекает от гипотенузы АВ = 9 см отрезок AD = 4 cм. Докажите, что ∆АВС ∞ ∆АCD и найдите высоту АC
-
Диагонали АС и ВD четырехугольника АВСD пересекаются в точке О; АО = 18 см, ОВ = 15 см, ОС = 12 см, ОD = 10 см. Докажите, что ABCD - трапеция.
Проверочная самостоятельная работа № 14.
1 вариант
-
Площадь ромба равна 48 см2. Найдите площадь четырехугольника, вершинами которого являются середины сторон данного ромба.
2 вариант
-
Площадь прямоугольника равна 36 см2. Найдите площадь четырехугольника, вершинами которого являются середины сторон данного прямоугольника.
Проверочная самостоятельная работа № 15.
1 вариант
-
На рис. 197 в учебнике AD = 16 см, CD = 12 см. Найти АС, ВС, АВ, BD.
-
Начертите отрезок и разделите его в отношении 2 : 7.
2 вариант
-
На рис. 197 в учебнике ВС = 3 см, CD =
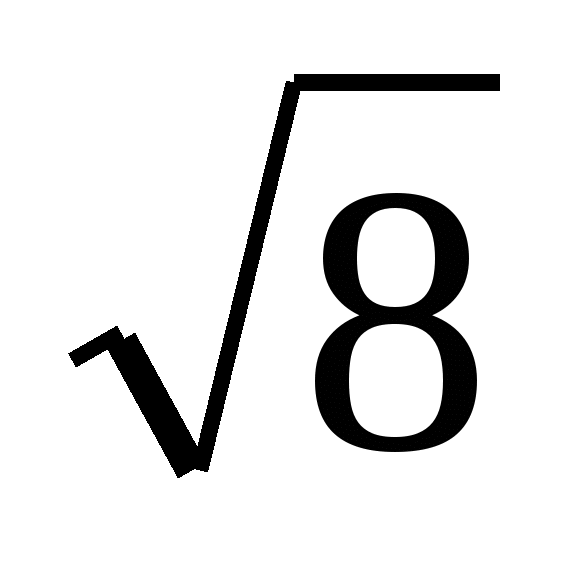 см. Найти АВ,
АС, AD, BD.
см. Найти АВ,
АС, AD, BD.
-
Начертите отрезок и разделите его в отношении 5 : 4.
Проверочная самостоятельная работа № 16.
1 вариант
-
Постройте прямоугольный треугольник по острому углу и медиане, проведенной из вершины этого угла.
2 вариант
-
Постройте прямоугольный треугольник по острому углу и биссектрисе прямого угла.
Проверочная самостоятельная работа № 17.
1 вариант
-
В равнобедренной трапеции меньшее основание равно 4 см, боковая сторона - 6 см, а один из углов - 1200. Найти площадь трапеции.
2 вариант
-
В прямоугольной трапеции меньшее основание равно 3 см, большая боковая сторона - 4 см, а один из углов - 1500. Найти площадь трапеции.
Проверочная самостоятельная работа № 18.
1 вариант
-
Из точки К к окружности с центром О проведены две прямые, касающиеся данной окружности в точках M и N. Найти КМ и КN, если ОК = 12 см, MON = 1200.
-
Диагонали ромба ABCD пересекаются в точке О. Докажите, что прямая BD касается окружности с центром А и радиусом, равным ОС.
2 вариант
-
Из точки К к окружности с центром О проведены две прямые, касающиеся данной окружности в точках M и N. Найти КМ и КN, если ОМ = 9 см, MКN = 1200.
-
BD - медиана равнобедренного треугольника АВС с основанием АС. Докажите, что прямая BD касается окружности с центром С и радиусом, равным AD.
Проверочная самостоятельная работа № 19.
1 вариант
-
Вершины треугольника АВС лежат на окружности с центром О, АOВ = 800, АС : ВС = 2 : 3. Найти углы треугольника АВС.
-
Хорды MN и KL окружности пересекаются в точке А, причем хорда MN делится точкой А на отрезки, равные 10 см и 6 см. На какие отрезки точка А делит хорду KL, если KL больше MN на 3 см.
2 вариант
-
Вершины треугольника АВС лежат на окружности с центром О, АВС = 800, ВС : АВ = 3 : 2. Найти углы треугольника ОАВ.
-
Хорды MN и KL окружности пересекаются в точке А, причем хорда MN делится точкой А на отрезки, равные 1 см и 15 см. На какие отрезки точка А делит хорду KL, если KL в два раза меньше MN.
Самостоятельная работа обучающего характера № 20.
1 вариант.
-
Радиус окружности, вписанной в прямоугольный треугольник, равен 2 см, гипотенуза этого треугольника равна 10 см. Найти периметр этого треугольника и его площадь.
-
вариант.
-
Радиус окружности, вписанной в прямоугольный треугольник, равен 2 см, сумма катетов - 17 см. Найти периметр этого треугольника и его площадь.
Проверочная самостоятельная работа № 21.
1 вариант
-
Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, равные 5 см и 13 см. Найти площадь этого треугольника.
2 вариант
-
Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, меньший из которых равен 8 см, основание треугольника - 12 см. Найти площадь этого треугольника.
Самостоятельная работа обучающего характера № 22.
1 вариант.
-
Перечертите рисунок в тетрадь. Постройте векторы
 и
и  такие, что
такие, что
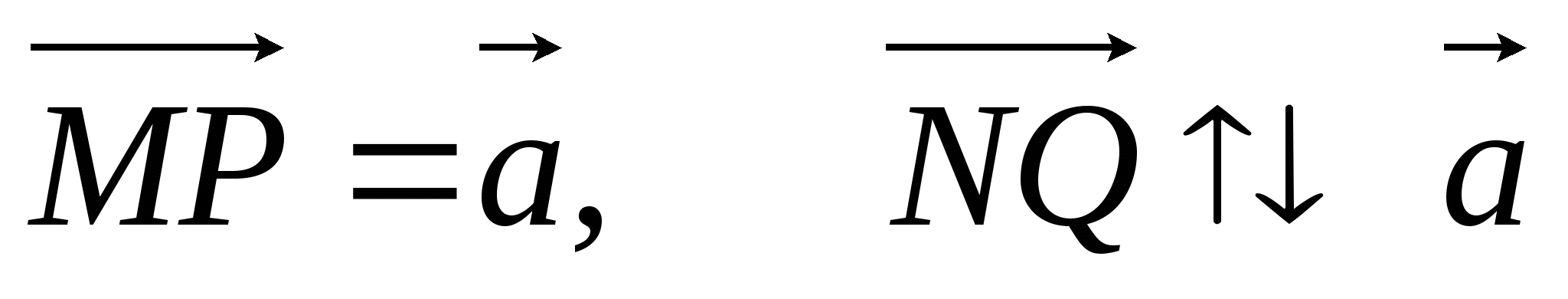
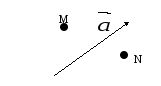
-
ABCD - параллелограмм. Докажите, что
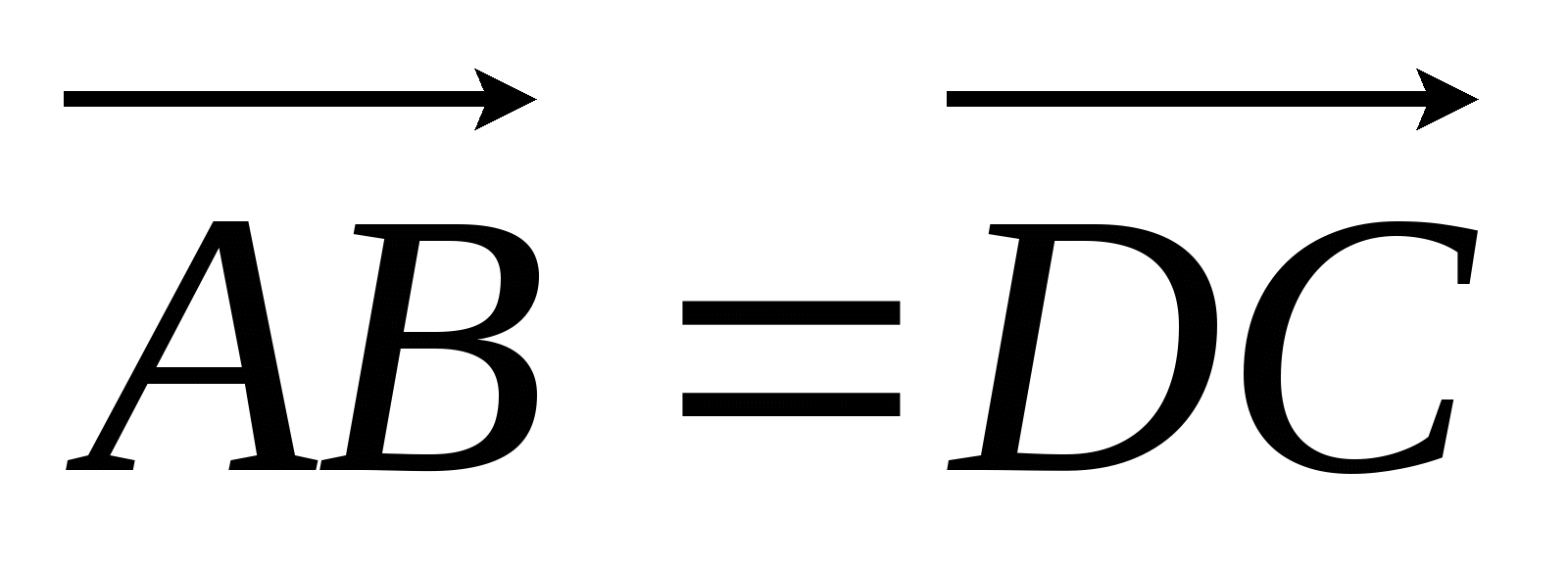
-
вариант.
-
Перечертите рисунок в тетрадь. Постройте векторы
 и
и  такие, что
такие, что
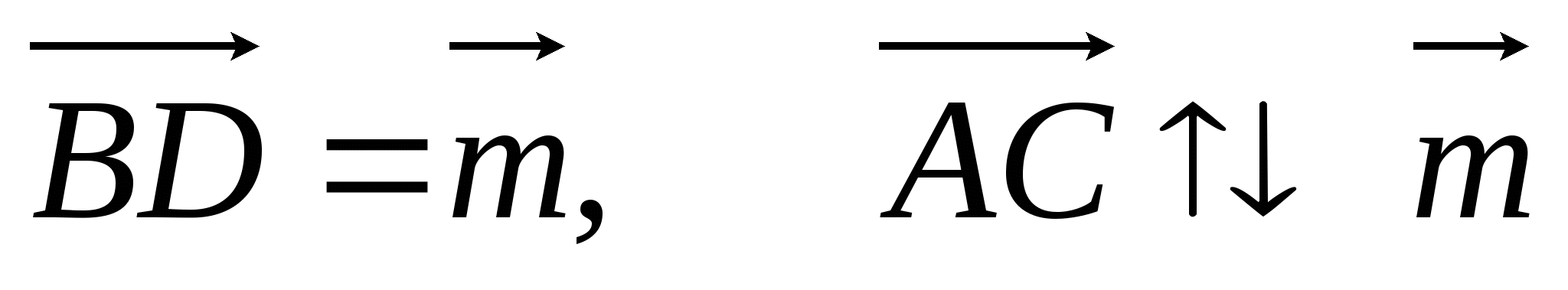
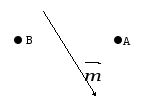
-
Точки M, K, N, P не лежат на одной прямой и
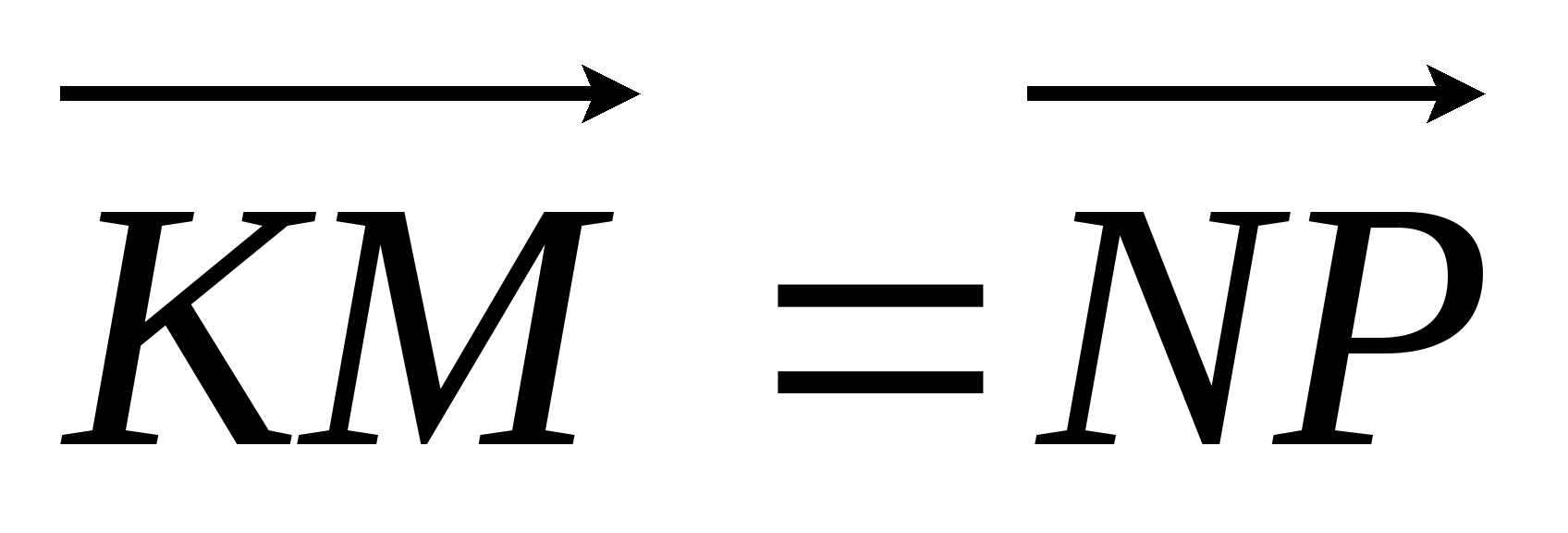 . Докажите, что
KMNP - параллелограмм.
. Докажите, что
KMNP - параллелограмм.
Самостоятельная работа обучающего характера № 23.
1 вариант.
-
Начертите четыре попарно неколлинеарных вектора
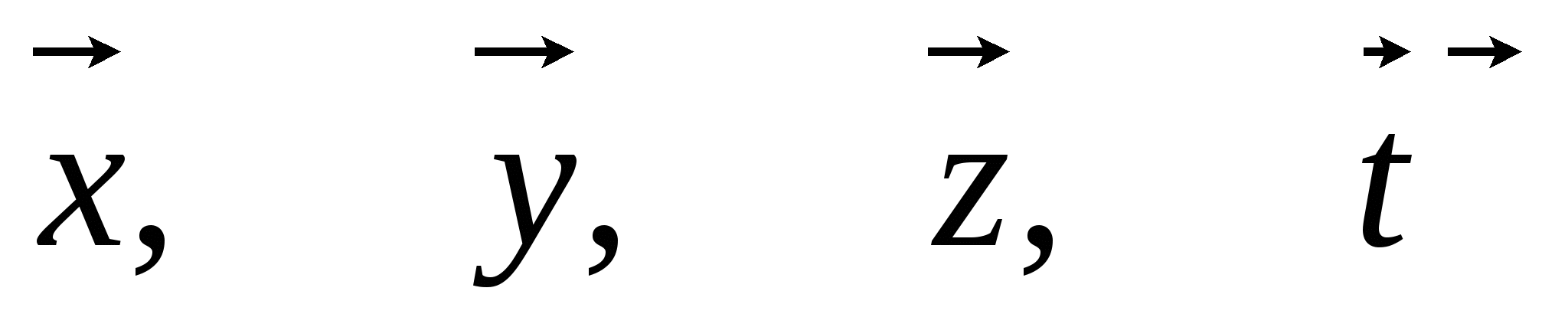 . Постройте
вектор
. Постройте
вектор 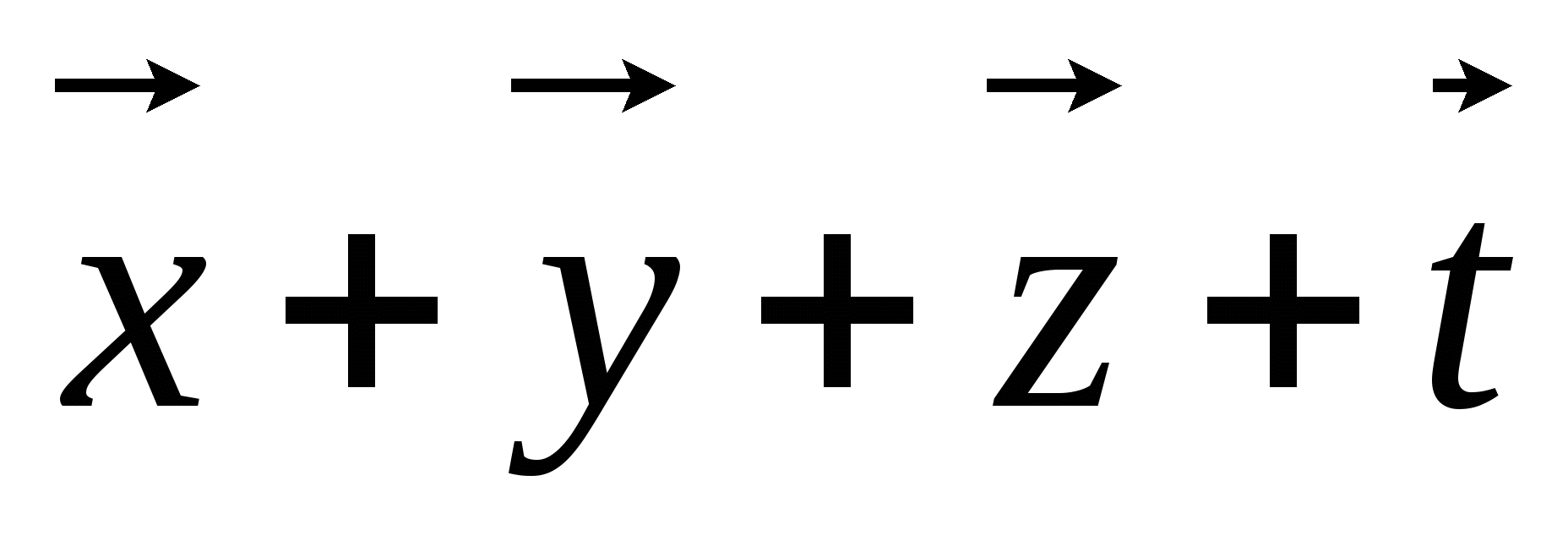
-
Упростите выражение:

2 вариант.
-
Начертите пять попарно неколлинеарных вектора
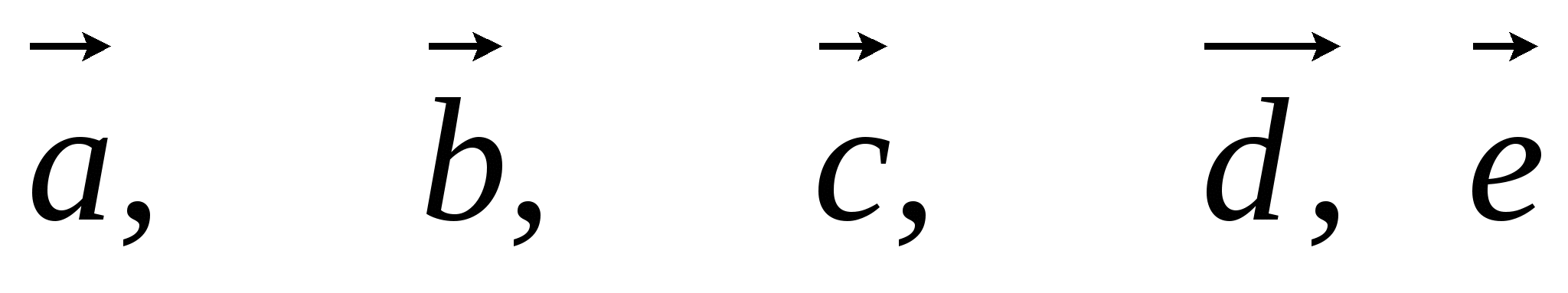 . Постройте
вектор
. Постройте
вектор 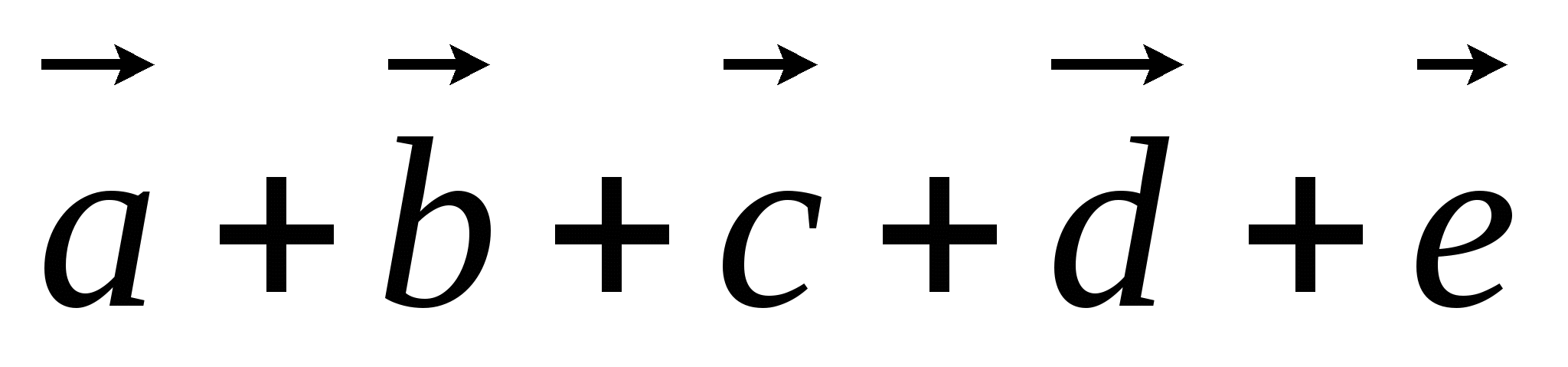
-
Упростите выражение:
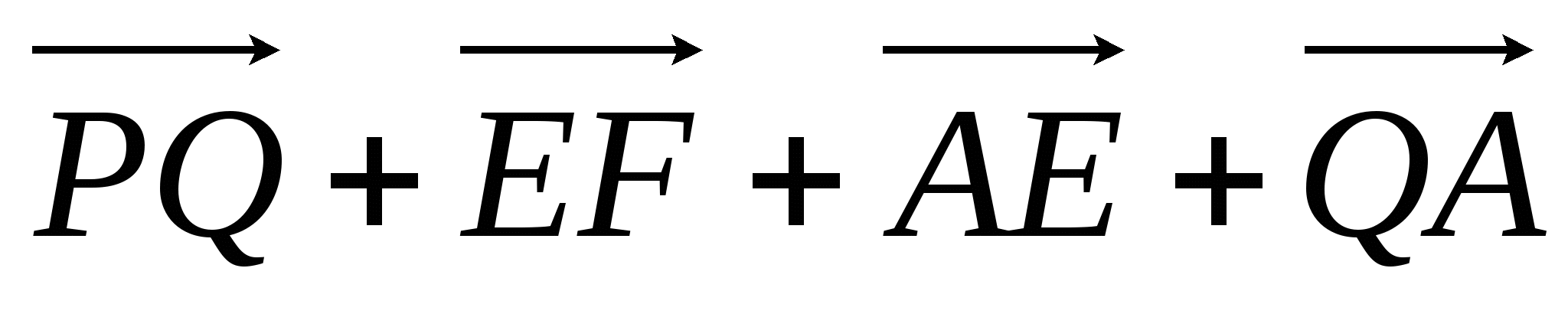
Проверочная самостоятельная работа № 24.
1 вариант
-
Дан прямоугольный треугольник АВС с гипотенузой ВС. Постройте вектор
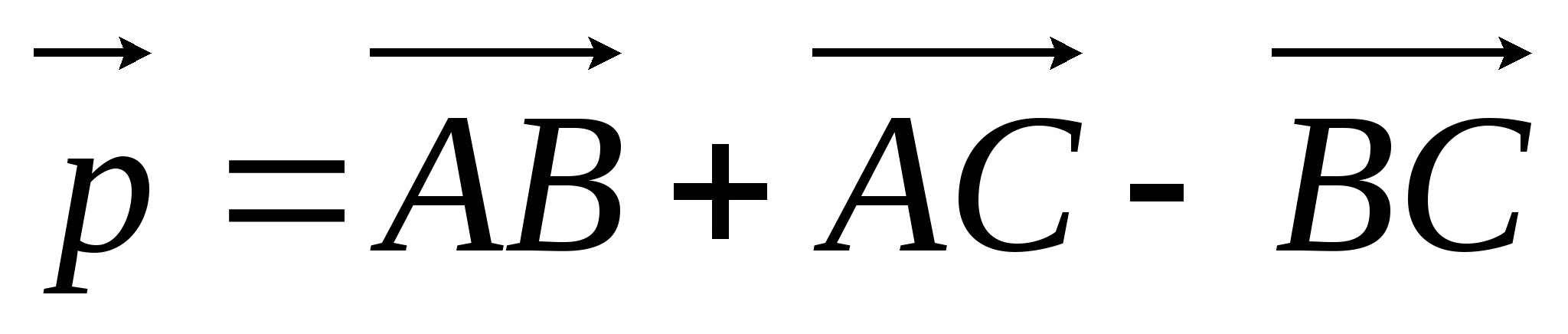 и найдите
и найдите
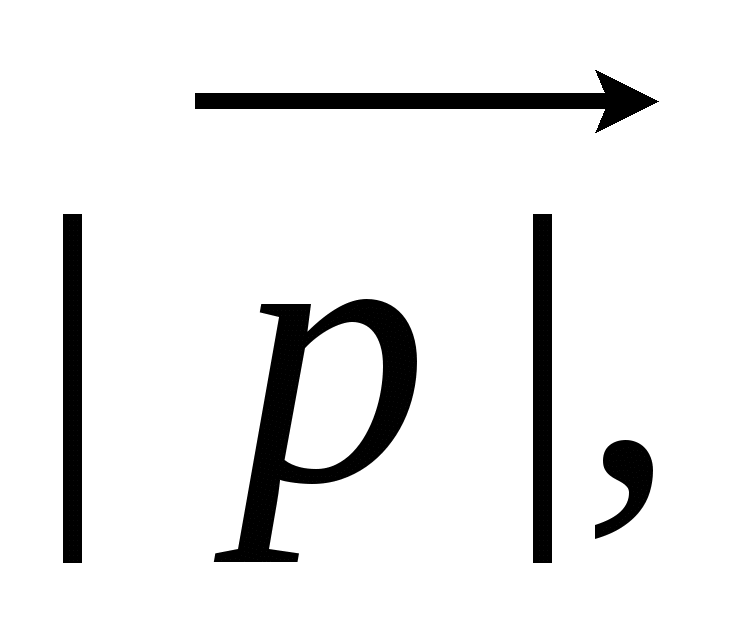 если АВ = 8 см.
если АВ = 8 см.
2 вариант
-
Дан прямоугольный треугольник АВС с гипотенузой АВ. Постройте вектор
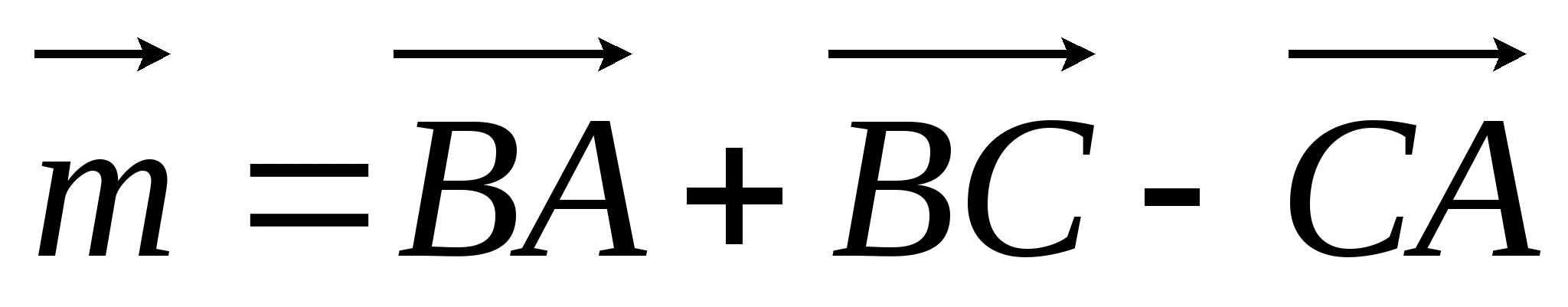 и найдите
и найдите
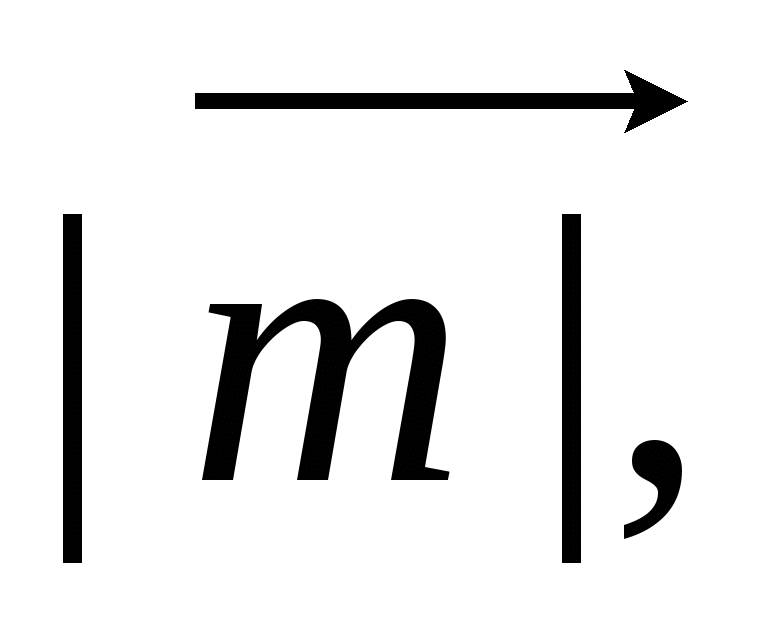 если ВС = 9 см.
если ВС = 9 см.
Практическое задание № 25
-
Начертите произвольный вектор
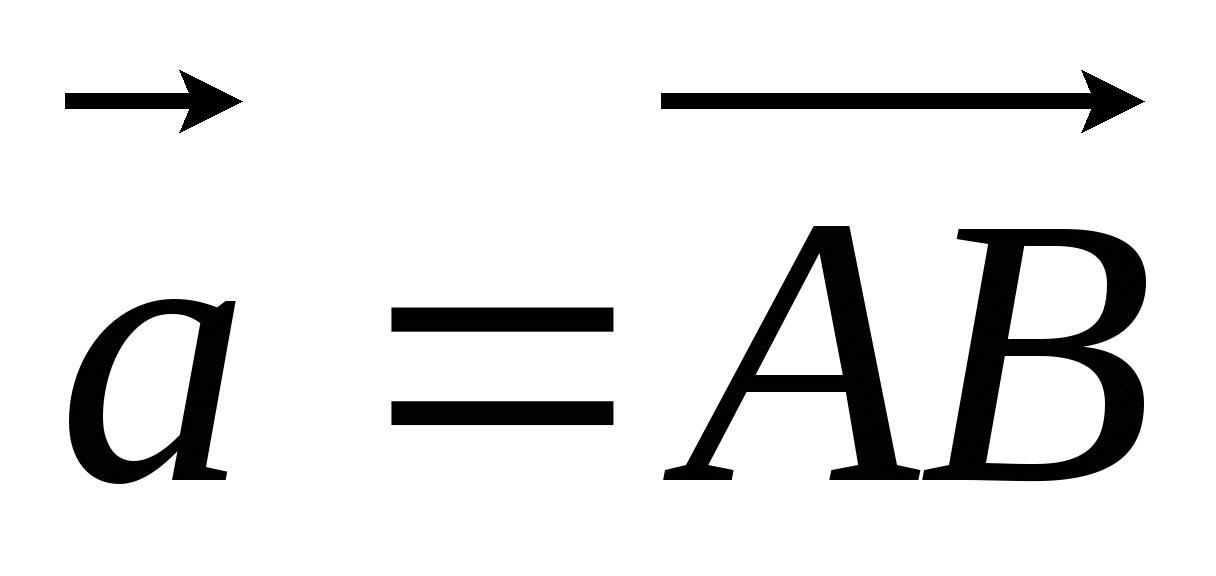 и отметьте
точки K, M, N, не лежащие на прямой АВ.
и отметьте
точки K, M, N, не лежащие на прямой АВ.
Постройте: а) вектор ![]() ,
равный вектору
,
равный вектору ![]() б) вектор
б) вектор
![]() такой, что
такой, что
![]() в) вектор
в) вектор
![]() такой, что
такой, что
![]() г) вектор
г) вектор
![]() такой, что
такой, что
![]()
Проверочная самостоятельная работа № 26.
1 вариант
-
Начертите два неколлинеарных вектора
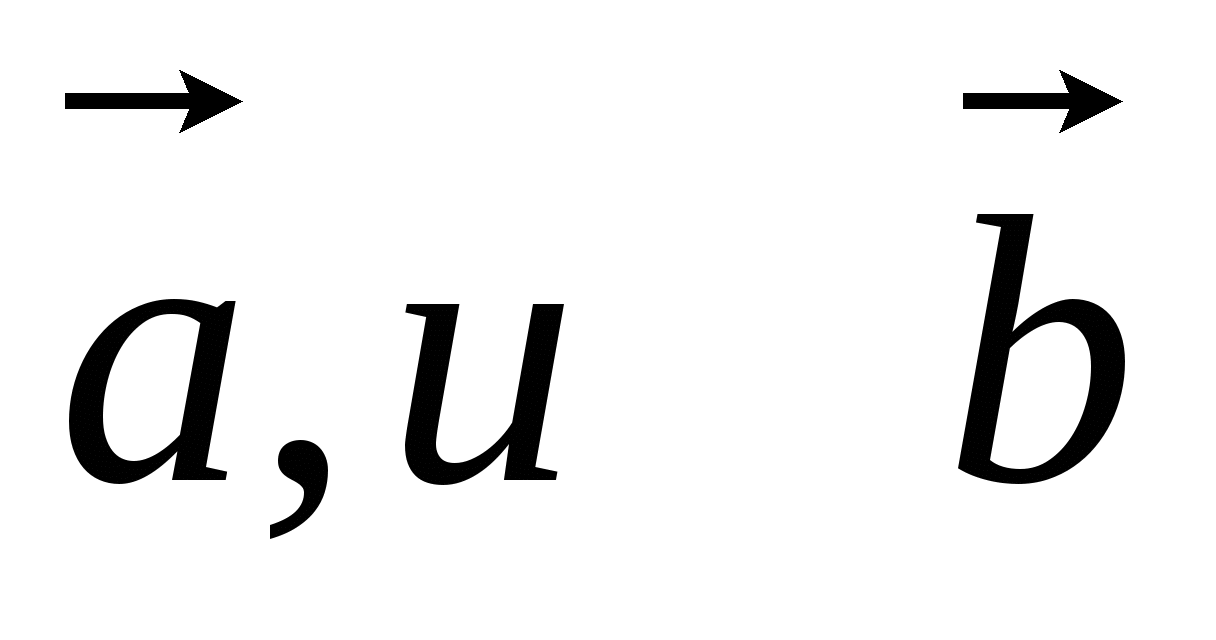 так, что
так, что
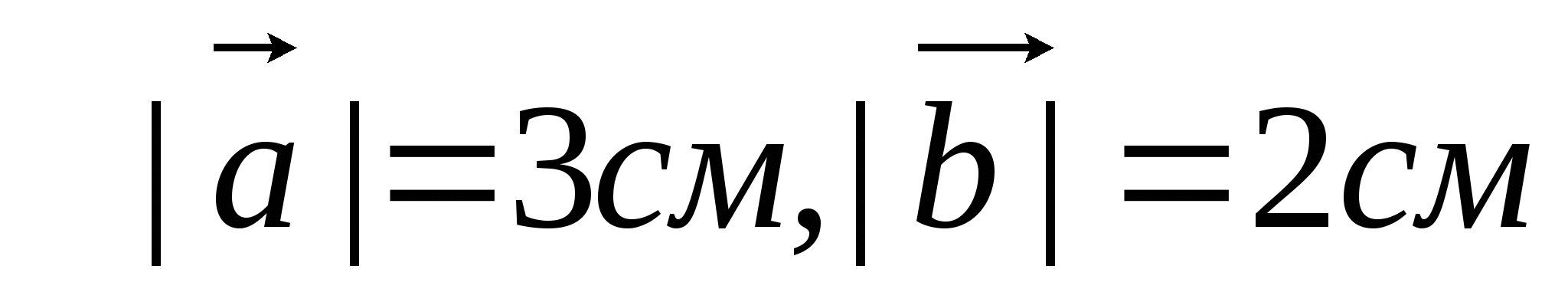 . Постройте
вектор
. Постройте
вектор 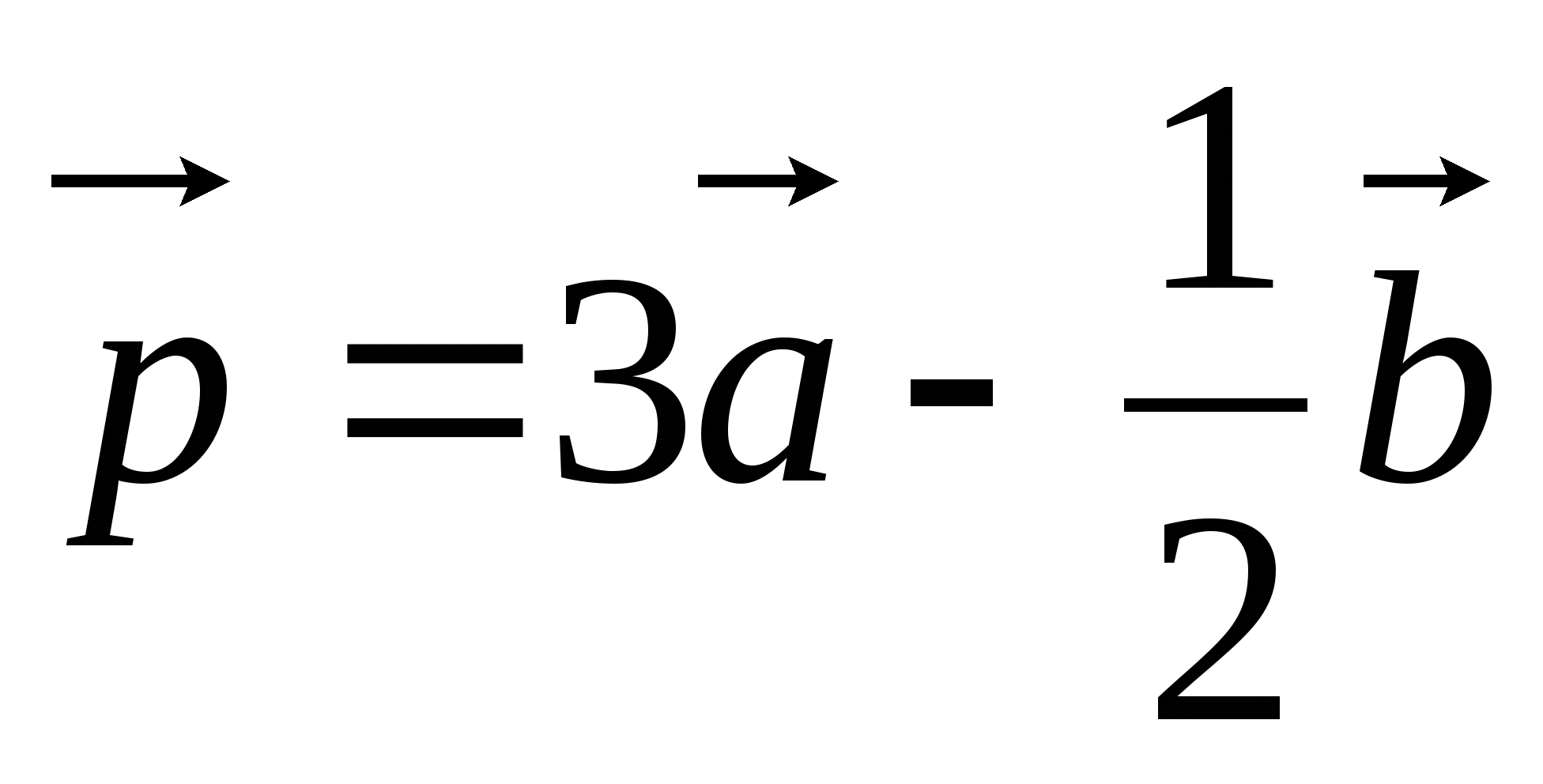
-
KMNP - параллелограмм. Выразите через векторы
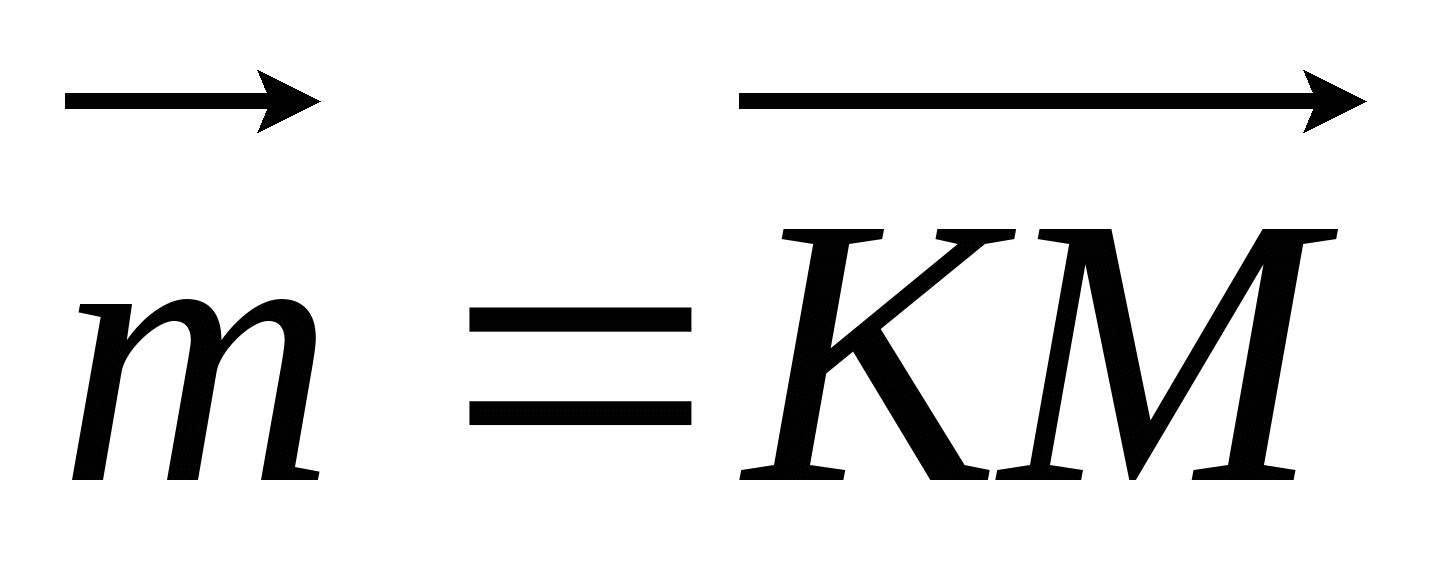 и
и 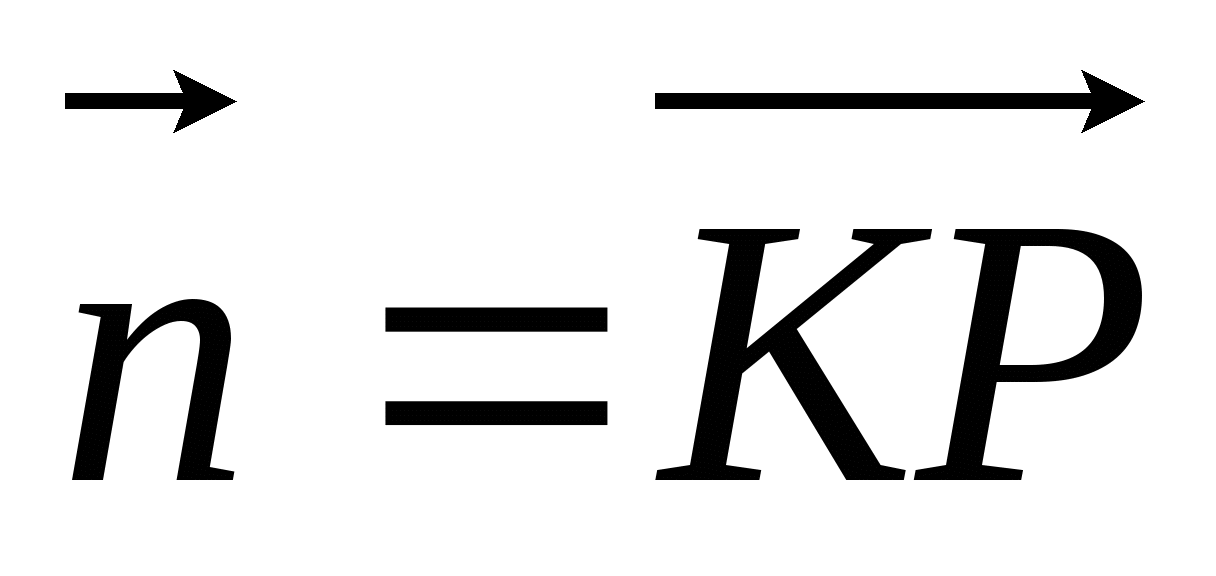 векторы
векторы
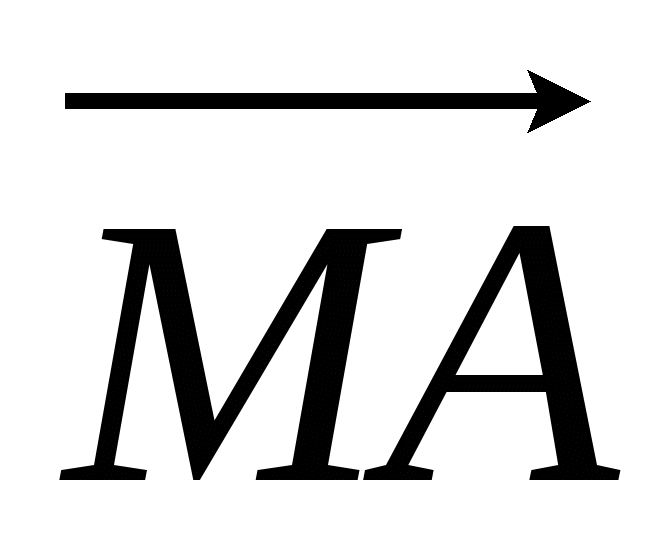 и
и 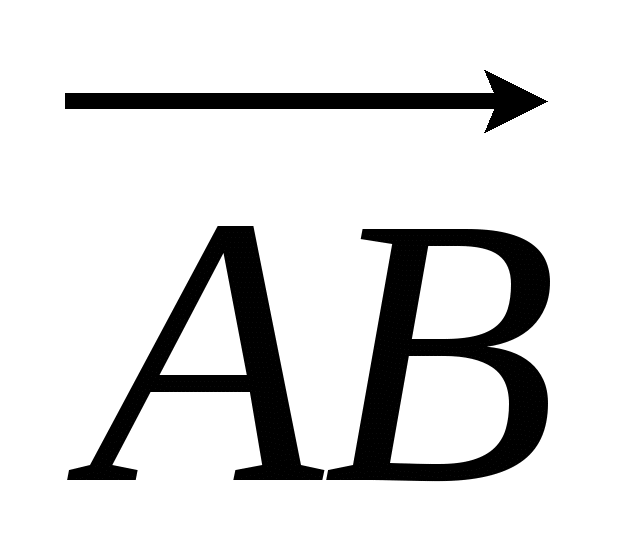 , где А - точка
на отрезке PN такая, что PA : AN = 2 : 1, B - середина отрезка
MN.
, где А - точка
на отрезке PN такая, что PA : AN = 2 : 1, B - середина отрезка
MN.
2 вариант
-
Начертите два неколлинеарных вектора
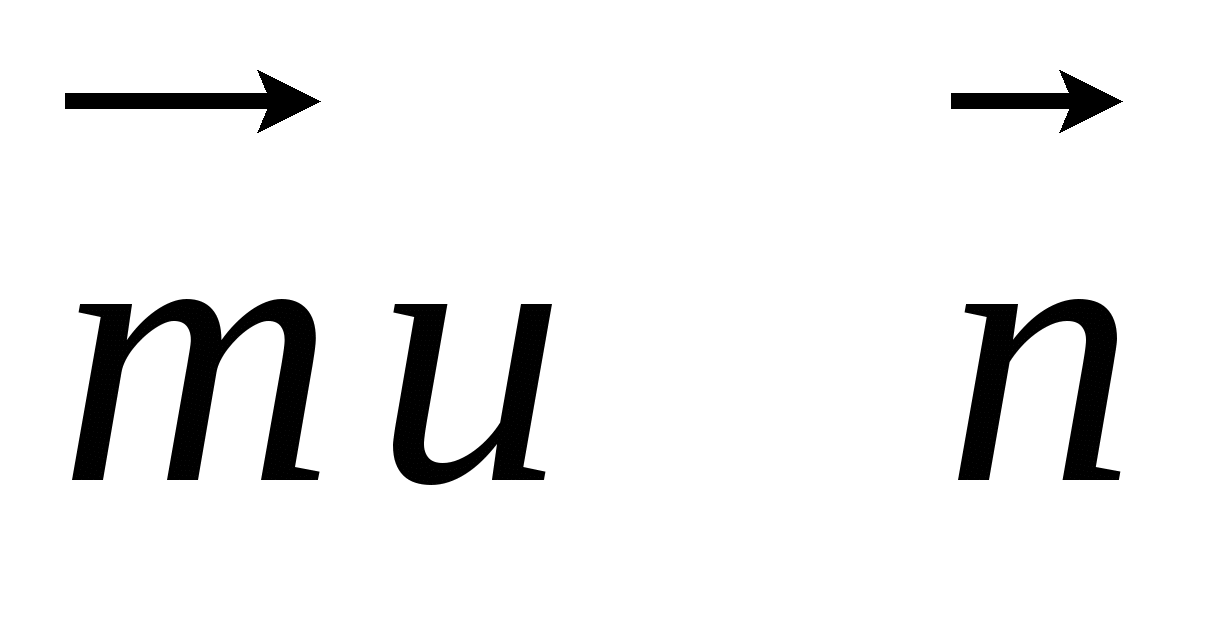 так, что
так, что
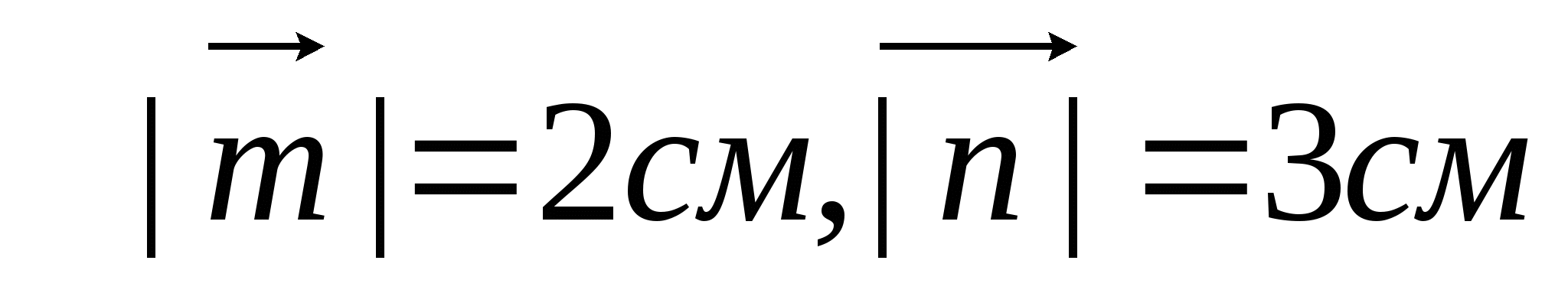 . Постройте
вектор
. Постройте
вектор 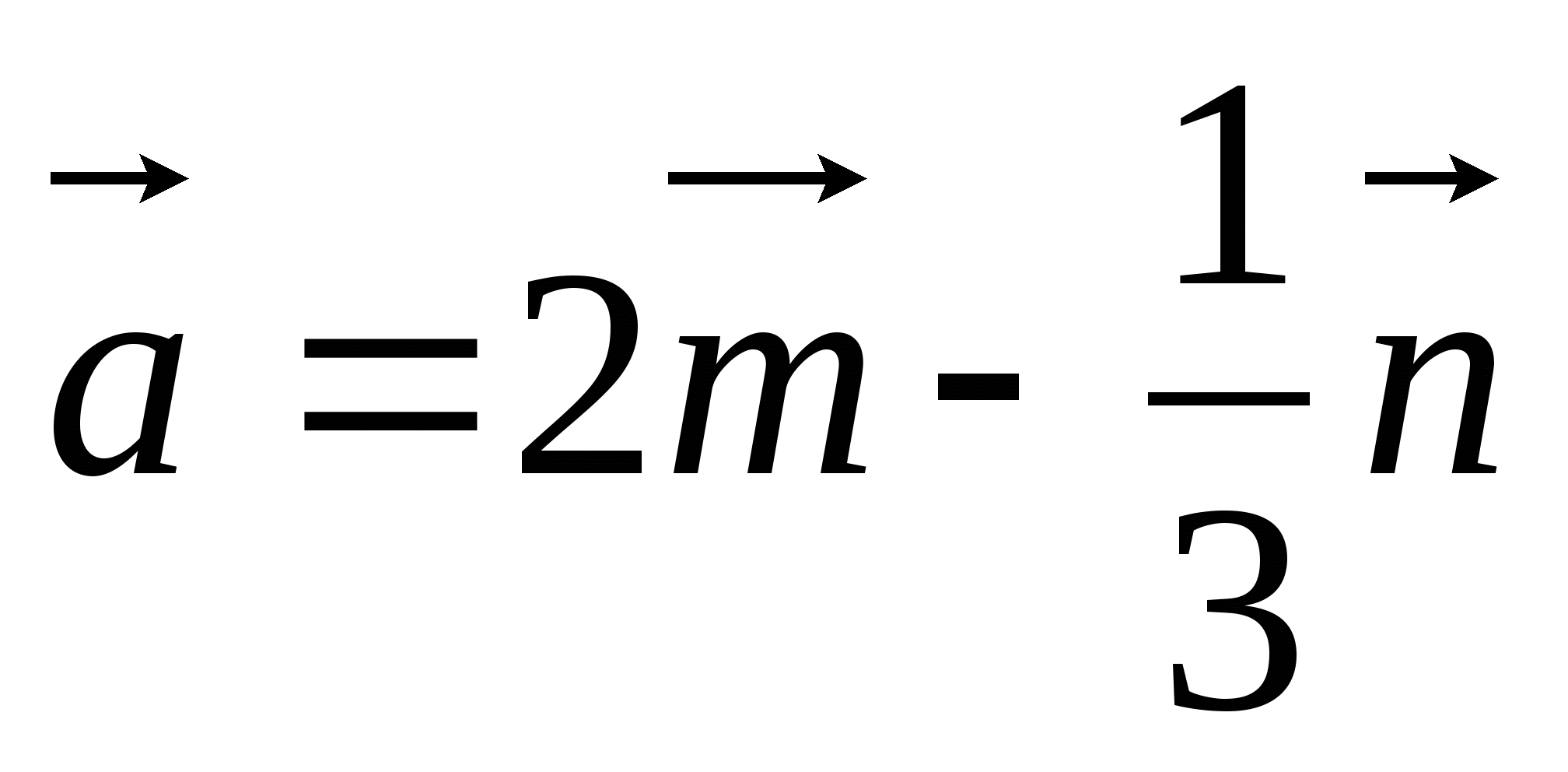
-
ABCD - параллелограмм. Точка М - середина стороны CD, N - точка на стороне AD такая, что AN : ND = 1 : 2. Выразите через векторы
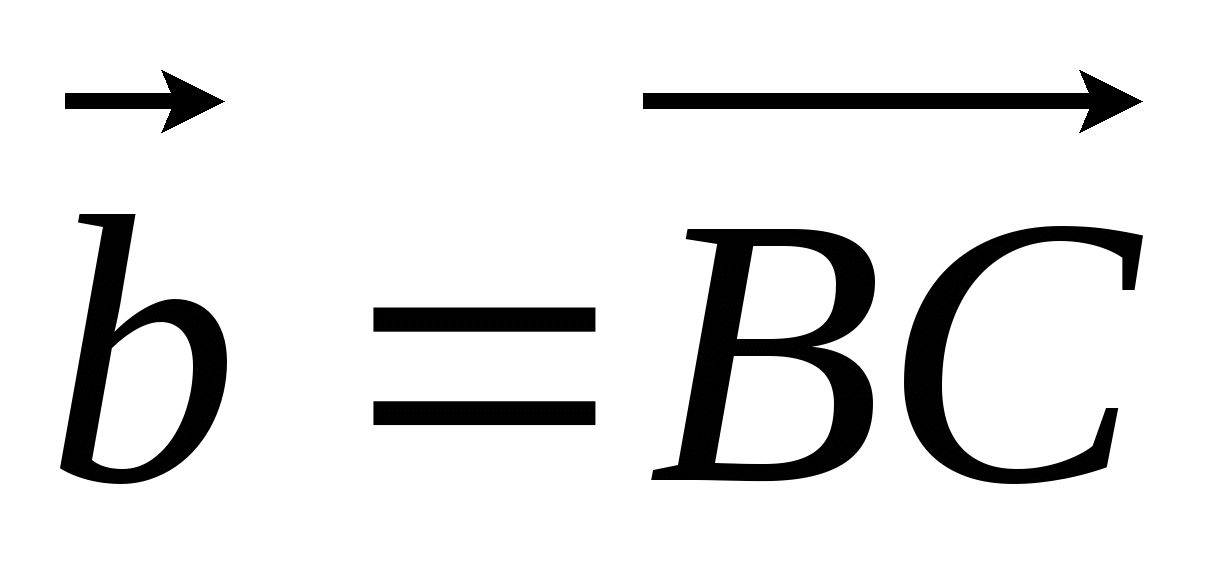 и
и 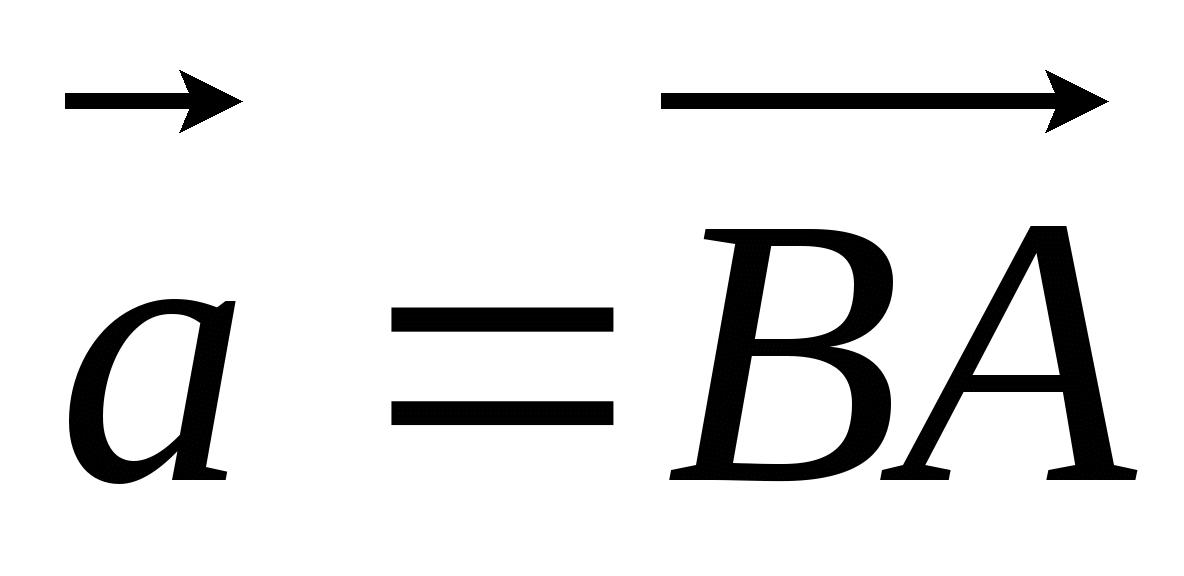 векторы
векторы
 и
и 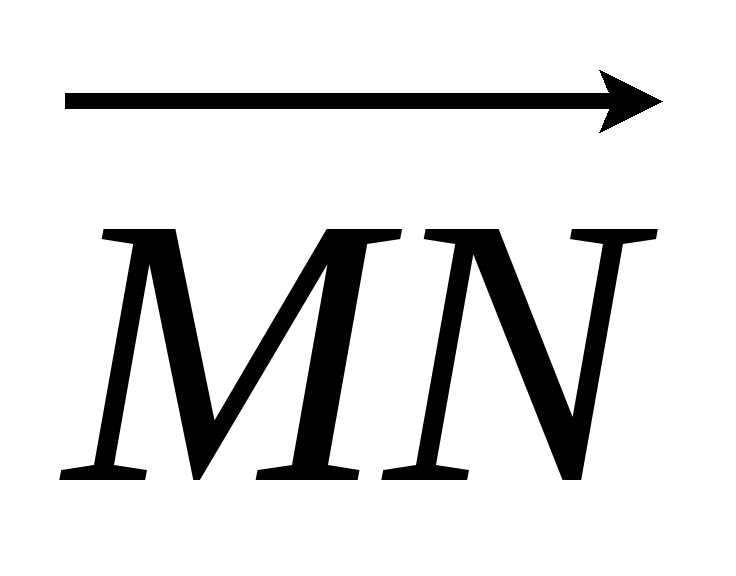 .
.
Проверочная самостоятельная работа № 27.
1 вариант
-
Точка К делит отрезок MN в отношении MK : KN = 3 : 4. Выразите через векторы
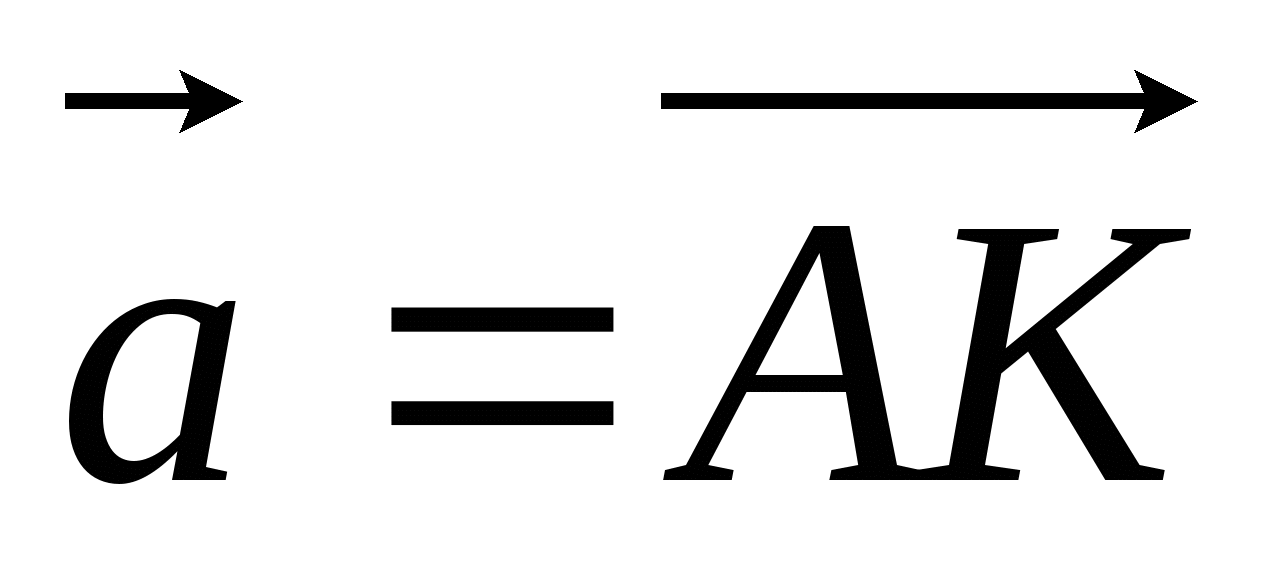 и
и 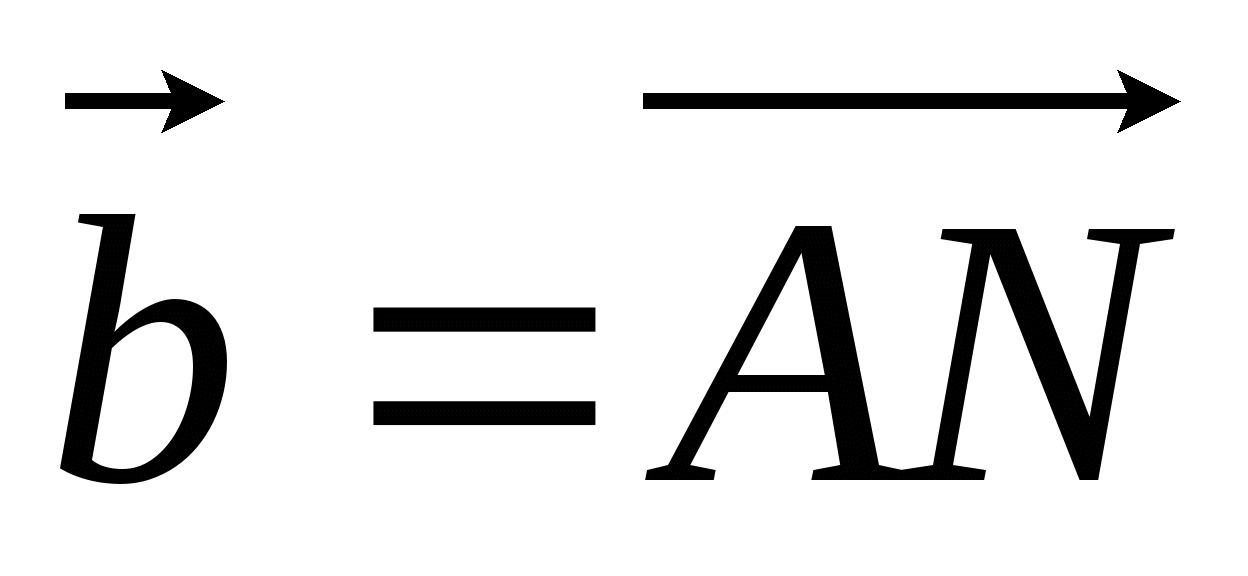 вектор
вектор
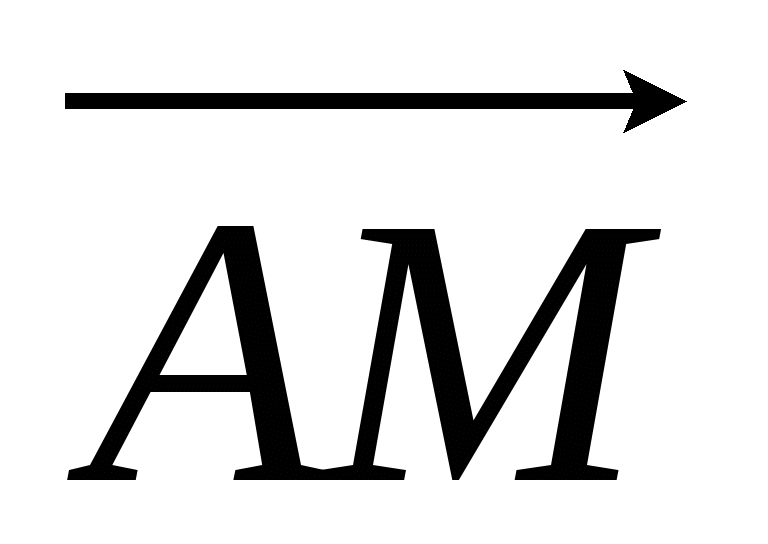 , где А -
произвольная точка
, где А -
произвольная точка
2 вариант
1. Точка А делит отрезок EF в отношении ЕА : АF = 2 : 5.
Выразите через векторы ![]() и
и
![]() вектор
вектор ![]() , где К -
произвольная точка
, где К -
произвольная точка
Проверочная самостоятельная работа № 28.
1 вариант
-
Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит большее основание трапеции на два отрезка, меньший из которых равен 2 см. Найти большее основание трапеции, если ее средняя линия равна 8 см.
2 вариант
-
Высота, проведенная из вершины тупого угла равнобедренной трапеции, делит среднюю линию трапеции на отрезки, равные 2 см и 6 см. Найти основания трапеции.
15