Система подготовки обучающихся к итоговой аттестации по математике по теме Трапеция (9 класс)

Система подготовки к ОГЭ.

Тема «Трапеция»

СПРАВОЧНЫЙ МАТЕРИАЛ

Трапеция. Свойства трапеции

Трапеция - четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две -боковые стороны.

Если боковые стороны равны, трапеция называется равнобедренной.

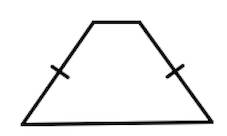
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.

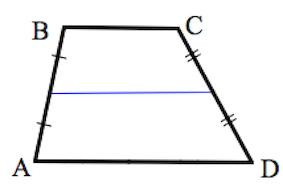
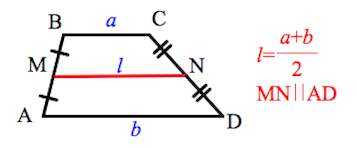
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

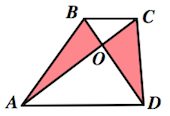
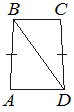
3. Треугольники AOD и COB , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия - Отношение площадей этих треугольников есть .

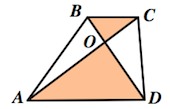
4. Треугольники ABO и DCO , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

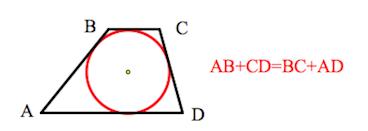
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

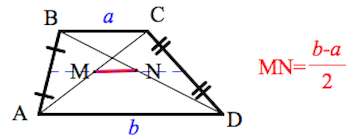
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

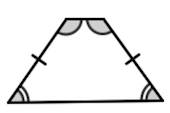
Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция - равнобедренная.

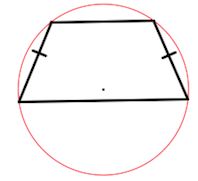
4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

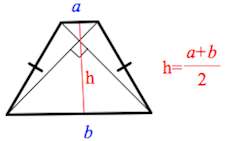
Площадь трапеции

1. Формула площади трапеции через основания и высоту

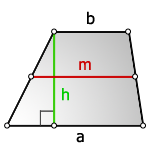
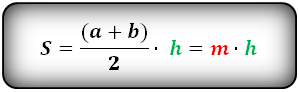
a - нижнее основание

b - верхнее основание

m - средняя линия

h - высота трапеции

2. Формула площади трапеции через диагонали и угол между ними

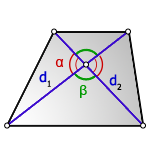
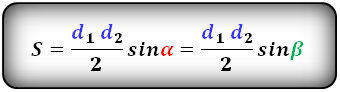
Дополнительные построения в задачах о трапециях

1. Проведение диагоналей.

2. Проведение высот.

3. Проведение через вершину трапеции прямой, параллельной одной из боковых сторон.

4. Проведение через вершину трапеции прямой, параллельной одной из диагоналей.

5. Продолжение боковых сторон трапеции до пересечения.

Используемые ресурсы:

1. egemaximum.ru/trapeciya-svojstva-trapecii/

2. www-formula.ru/

3. Ершова А.П., Голобородько В.В., Крижановский А.Ф. Тетрадь-конспект по геометрии для 8 класса. - М.: Илекса. - 2015

Часть 1.

УПРАЖНЕНИЯ

1. Тренинг.1. Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.

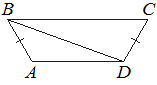
2. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.

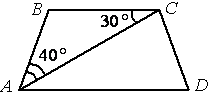
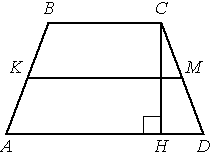
3. В трапеции АВСD боковые стороны AB и CD равны, СН - высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.

4. Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные 30° и 105° соответственно. Ответ дайте в градусах.

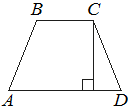
5. В равнобедренной трапеции известна высота, большее основание и угол при основании (см. рисунок). Найдите меньшее основание.

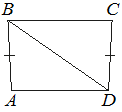
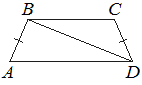
6. В трапеции ABCD известно, что AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.

7.

8. Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 8 и 15. Найдите длину основания BC.

9. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 12° и 13° соответственно. Ответ дайте в градусах.

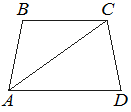
10. Основания трапеции равны 1 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

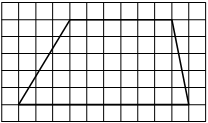
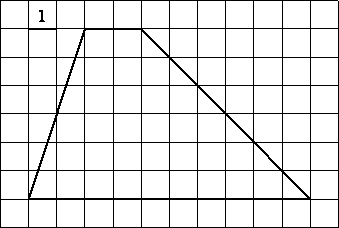
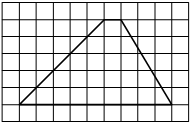
11. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

12. В трапеции ABCD известно, что AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.

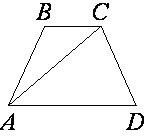
13. В трапеции ABCD известно, что AD=3, BC=1, а её площадь равна 12. Найдите площадь треугольника ABC.

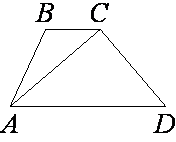
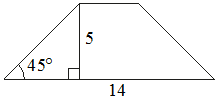
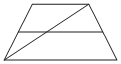
14. Найдите площадь трапеции, изображённой на рисунке.

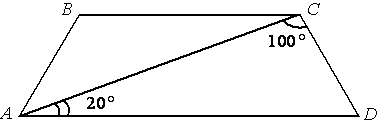
2.Задания для самостоятельного решения.1. Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно

2. Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.

3. Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.

4. В трапеции АВСD боковые стороны AB и CD равны, СН - высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 10, а меньшее основание BC равно 4.

5. В равнобедренной трапеции известны высота, меньшее основание и угол при основании (см. рисунок). Найдите большее основание.

6. В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.

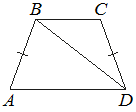
7. Сумма двух углов равнобедренной трапеции равна 102°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

8. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 17° и 23° соответственно. Ответ дайте в градусах.

9. Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 11. Найдите длину основания BC.

10.Основания трапеции равны 10 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

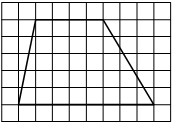
11. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

12. В трапеции ABCD известно, что AB=CD, AC=AD и ∠ABC=93°. Найдите угол CAD. Ответ дайте в градусах.

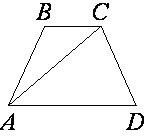
13. В трапеции ABCD известно, что AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.

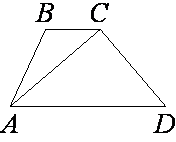
14. Найдите площадь трапеции, изображённой на рисунке.

.

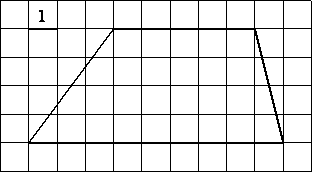
3. Контроль знаний.

Вариант 1.4. Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно. Ответ дайте в градусах.

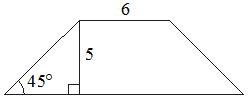
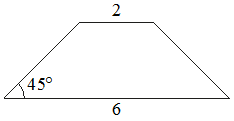
5. В равнобедренной трапеции основания равны 2 и 6, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.

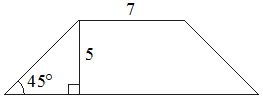
6. В равнобедренной трапеции известна высота, меньшее основание и угол

при основании (см. рисунок). Найдите большее основание.

Вариант 2.3. В трапеции АВСD боковые стороны AB и CD равны, CH - высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 4.

4.В равнобедренной трапеции основания равны 3 и 7, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.

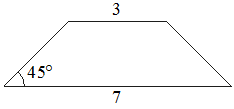
5. В равнобедренной трапеции известна высота, большее основание и угол при основании (см. рисунок). Найдите меньшее основание.

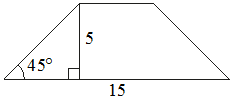
6. В трапеции ABCD известно, что AB=CD, ∠BDA=30° и ∠BDC=110°. Найдите угол ABD. Ответ дайте в градусах.

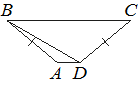
Вариант 3.1. Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 1 и 7.

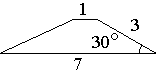
2. В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.

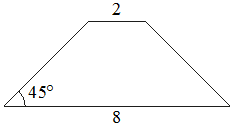
3. В равнобедренной трапеции известна высота, меньшее основание и угол при основании (см. рисунок). Найдите большее основание.

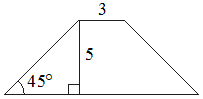
4. В трапеции ABCD известно, что AB=CD, ∠BDA=14° и ∠BDC=106°. Найдите угол ABD. Ответ дайте в градусах.

5. Сумма двух углов равнобедренной трапеции равна 94°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

6. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 47° и 15° соответственно. Ответ дайте в градусах.

Вариант 4.4. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 33° и 13° соответственно. Ответ дайте в градусах.

5. Найдите площадь трапеции, изображённой на рисунке.

6. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 19° и 54° соответственно. Ответ дайте в градусах.

Вариант 5.3. В трапеции ABCD известно, что AB=CD, ∠BDA=54°

и ∠BDC=33°. Найдите угол ABD. Ответ дайте в градусах.

4. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 1° соответственно. Ответ дайте в градусах.

5.Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 4° и 68° соответственно. Ответ дайте в градусах.

6. Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 3 и 11. Найдите длину основания BC.

Вариант 6.3.В трапеции ABCD известно, что AB=CD, ∠BDA=22° и ∠BDC=45°. Найдите угол ABD. Ответ дайте в градусах.

4. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 62° и 9° соответственно. Ответ дайте в градусах.

5. Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 10 и 11. Найдите длину основания BC.

6. Найдите площадь трапеции, изображённой на рисунке.

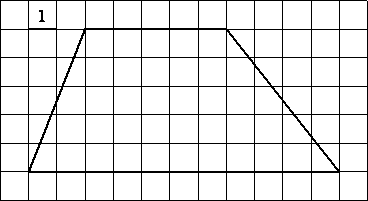
Вариант 7.2. Сумма двух углов равнобедренной трапеции равна 46°. Найдите больший угол этой трапеции. Ответ дайте в градусах.

3. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 11° и 60° соответственно. Ответ дайте в градусах.

4. Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 8 и 18. Найдите длину основания BC.

5. Основания трапеции равны 3 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

6. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии

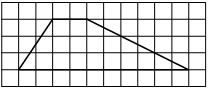
Вариант 8.

Вариант 95.Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 17 и 19. Найдите длину основания BC.

6. Найдите площадь трапеции, изображённой на рисунке.

Вариант 10

Вариант 116.Найдите площадь трапеции, изображённой на рисунке.

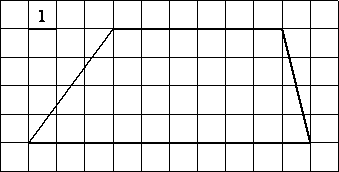
Вариант 121. Основания трапеции равны 14 и 19. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

2. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

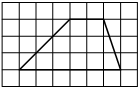
3. В трапеции ABCD известно, что AB=CD, AC=AD и ∠ABC=109°. Найдите угол CAD. Ответ дайте в градусах.

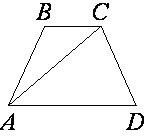
4. В трапеции ABCD известно, что AD=7, BC=1, а её площадь равна 96. Найдите площадь треугольника ABC.

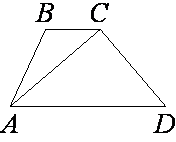
5. Основания трапеции равны 1 и 17. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.

6. На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Критерии оценивания

«5» - 6 заданий

«4» - 5 заданий

«3» - 3-4 задания

«2» - 0 - 2 задания

Используемые ресурсы

www.fipi.ru/</ Открытый банк заданий ОГЭ