Конспект открытого урока математики,

проведенного в 8 «А» классе

по теме «Решение задач с помощью

рациональных уравнений».

Учитель: З.Н.Алёхина

.

Тема урока: "Решение задач с помощью рациональных уравнений".

Цели урока: Закрепить: 1) умения составлять рациональные, дробно - рациональные уравнения по условию задачи; 2) умения определять соответствуют ли найденные корни уравнения условию задачи; 3) умения выбора способа решения текстовой задачи.

Познакомить учащихся с методом подобия при решении текстовых задач, который так же приводит к составлению дробного рационального уравнения, применением формулы среднего гармонического при решении задач на движение.

Расширять межпредметные связи посредством решения текстовых задач (физика, химия, география, геометрия).

Оборудование географическая карта Белгородской области, колбы с растворами кислоты разной концентрации, таблица «Время, скорость, расстояние», ГИА - 2014 «Типовые тестовые задания» под редакцией В.И.Ященко, ГИА Математика - 2014 под редакцией А.В.Семёнова.

Ход урока.

Ребята перед вами пословицы и поговорки, которые могут стать девизом сегодняшнего урока математики по теме: «Решение задач с помощью рациональных уравнений». В конце урока вам необходимо объяснить значение выбранной пословицы или поговорки.

1. Фронтальная работа. Ответить на вопросы:

1. Какие уравнения называют рациональными уравнениями?

2. Что называют корнем уравнения с неизвестным х?

3. Что значит решить уравнение?

4. Какие уравнения называют равносильными?

5. По какому правилу решают рациональные уравнения? Что может произойти при отклонении от этого правила?

2. Решение уравнений. Взаимопроверка - 4 варианта. Работа выполняется в тетрадях. Ответы записаны на обратной стороне доски. В ходе выполнения работы учащиеся определяют для себя алгоритм решения дробных рациональных уравнений. На каждой парте - таблица - напоминание "Алгоритм решения дробных рациональных уравнений".

О т в е т ы I вариант: , (; ).

II вариант: (; )

III вариант: () IV вариант: , (; ).

3. Устная работа. Составить уравнение для решения задачи:

Расстояние между городами Новый Оскол и Валуйки скорый поезд, идущий со скоростью 90 км/ч, проходит на 0,5 ч быстрее товарного, который идет со скоростью 60 км/ч. Каково расстояние между городами?

1. Ученику и мастеру дано задание изготовить одинаковое количество деталей. Мастер, изготовляя 18 деталей в час, затратил на выполнение задания на 3 ч меньше, чем ученик, который изготавливал лишь 12 деталей в час. Сколько деталей было заказано?

(Записать условие и решение задач по вариантам). Проверка ответов:

1 вариант - 90 км; 2 вариант - 108 деталей.

2. Решение задачи № 5.1.81 «на смеси» из сборника ГИА - 2012 под редакцией И. В. Ященко. При смешивании первого раствора кислоты, концентрация которого 20 %, и второго раствора этой же кислоты, концентрация которого 50 %, получился раствор, содержащий 30 % кислоты. В каком отношении были взяты первый и второй растворы?

Решение задачи из учебника «Алгебра - 8» под редакцией С.А.Теляковского

№ 634:* Велосипедист проехал от посёлка до станции с некоторой постоянной скоростью, а возвращался со скоростью на 5 км/ч большей. Какова была первоначальная скорость велосипедиста, если известно, что средняя скорость на всём пути следования составляла 12 км/ч?

Скорость

Время

Расстояние

I ?

?

?

II ? на 5 км/ч больше

?

?

Средняя скорость - 12 км/ч

а) анализ условия задачи; б) ход решения задачи; в) составление уравнения к решению.

Применение формулы среднего гармонического: v _{среднее} =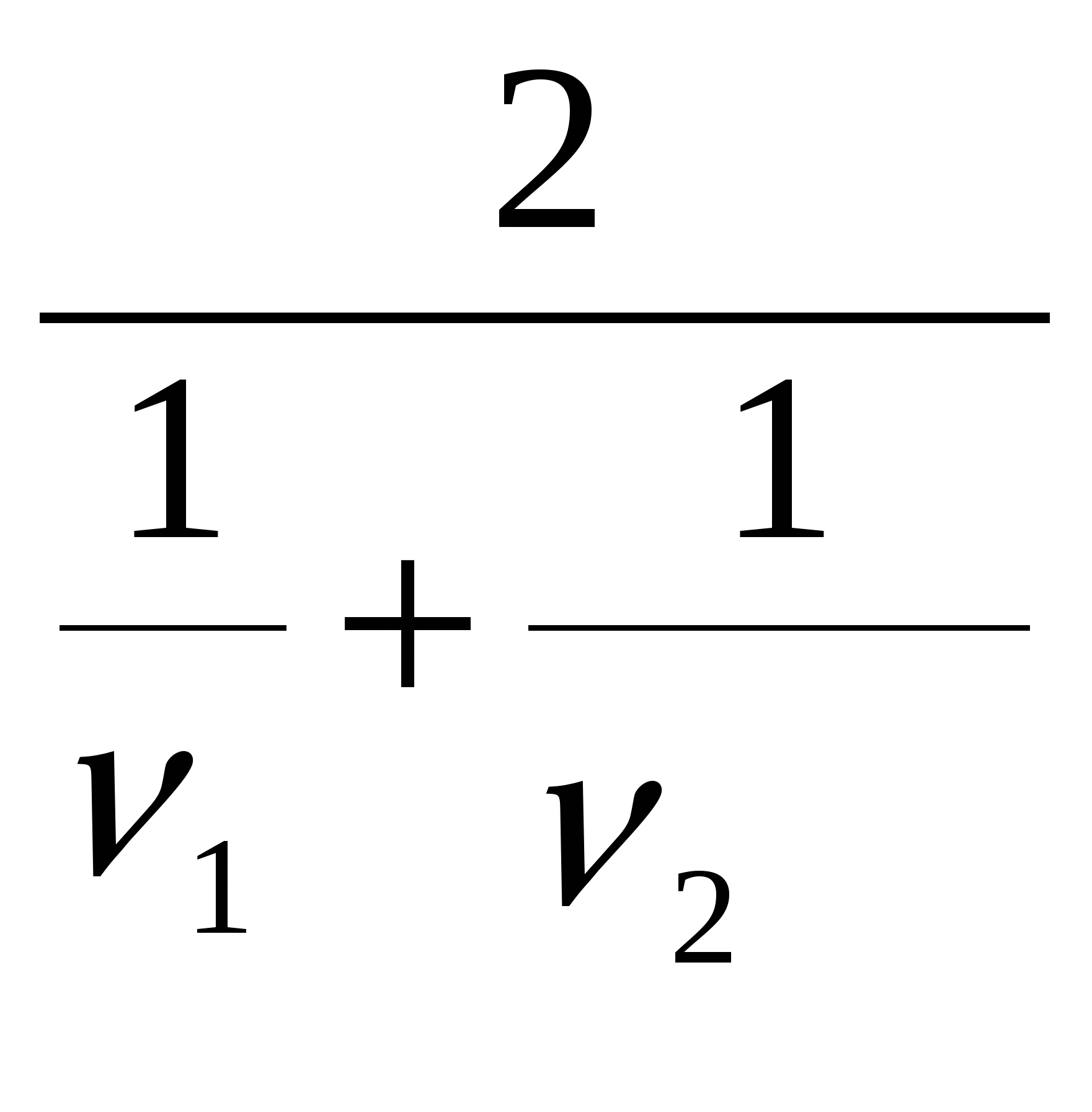

Решение задачи с использованием данных. ( Ответ: 10 км/ч).

4. (1) Решение задач. При решении задач составлением уравнения за х можно принять любое неизвестное.

Решаем задачу № 607 из учебника.

К доске вызываются четыре ученика, чтобы записать условие задачи и составить уравнение четырьмя способами:

I - ученик за х принимает скорость мотоциклиста,

II - ученик принимает за х скорость велосипедиста,

III - ученик за х принимает время велосипедиста,

IV - ученик принимает за х время мотоциклиста.

Учащиеся записывают в тетрадь условия четырьмя способами, а решают одним, в соответствии со своим вариантом.

I с п о с о б.

II с п о с о б.

III c п о с о б.

IV с п о с о б.

5) Решить задачу самостоятельно:

Бригада намечала засеять 120 га за определенный срок. Однако, перевыполняя запланированную ежедневную норму на 10 га в день, она сумела закончить сев на 2 дня раньше. Сколько гектаров засевала бригада ежедневно?

Задание: прочитать задачу, ответить на вопросы и заполнить таблицу:

1) О каких процессах идет речь в задаче?

2) Сколько процессов описано в условии задачи?

3) Какими величинами характеризуется каждый процесс, описанный в условии?

4) заполнить таблицу, составить уравнение и решить его.

Проверить решение по готовому образцу

По условию

По смыслу задачи , этому условию удовлетворяет значение

Тогда x +10 = 20 + 10 = 30

Ответ: 30 га засевала бригада ежедневно.

2) Задача № 125 из учебного пособия по математике А.В. Шевкина "Текстовые задачи. 7 - 9 классы".

Два пешехода вышли одновременно навстречу друг другу из двух городов. Они встретились в полдень и достигли чужого города: первый в 4 ч по полудни, а второй - в 9 ч. Нужно узнать, когда они вышли из своих городов.

(Пояснение. Данную задачу заранее предлагаю учащимся решить дома. В перемену, до урока, прошу учащегося, правильно решившего задачу, написать решение на обратной стороне доски.)

1) Заслушиваем комментарии по решению задачи учащимися. Задача решена составлением дробного рационального уравнения. 2) Объясняю решение данной задачи методом подобия, построив графики движения пешеходов.

• Р е ш е н и е:

• Изобразим график движения пешеходов и применим метод подобия. Пусть пешеходы до встречи шли х ч.

АD - промежуток времени движения первого пешехода, СВ - промежуток времени движения второго пешехода. КL - отсекает промежутки времени движения пешеходов до встречи. На рисунке АL - промежуток времени движения до встречи.

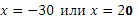
1) Рассмотрим и ∆NLA: подобен ∆NLA по двум углам.

2) Рассмотрим и , они подобны по двум углам.

3) Из подобия двух пар треугольников следует, что и , т.е.

4) Составим и решим уравнение: ()

Это уравнение имеет единственный положительный корень, удовлетворяющий условию задачи. - это время движения пешеходов до встречи.

5) Выясним, в какое время пешеходы вышли из своих городов: .

Ответ: пешеходы из своих городов вышли в 6 ч утра.

Как мы видим, метод подобия приводит к более простому решению.

6. Итоги урока. На сегодняшнем уроке мы попытались несколько задач решить с помощью рациональных уравнений. Видов таких задач гораздо больше, но все они подчиняются алгоритму решения задач с помощью рациональных уравнений.. Какие же задачи решаются данным способом?

7. Вначале урока перед вами стоял вопрос: какую выбрать пословицу или поговорку, соответствующую сегодняшнему уроку. Пришло время объяснить, что выбрано вами.

Домашнее задание п.25 - 26 повторить, № 635 решить разными способами.