- Учителю
- Контрольная работа № 6 по теме «Определение производной и ее вычисление»
Контрольная работа № 6 по теме «Определение производной и ее вычисление»
Контрольная работа № 6 (1 час)
Цели: выявление знаний учащихся, проверка степени усвоения ими изученного материала; развитие навыков самостоятельной работы.
Вариант 1
1. Вычислите 1, 5 и 100-й члены
последовательности, если ее п-й член задается формулой 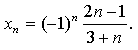
2. Представьте бесконечную периодическую десятичную дробь 1,(18) в виде обыкновенной дроби.
3. Найдите производную функции.
а) ![]() б)
б) 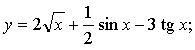
в) ![]() г)
г) ![]()
4. Найдите угловой коэффициент касательной к
графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]()
5. Докажите, что функция ![]() удовлетворяет соотношению
удовлетворяет соотношению 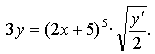
6. Найдите знаменатель бесконечно убывающей геометрической прогрессии, у которой каждый член в 6 раз больше суммы всех её последующих членов.
Вариант 2
1. Вычислите 1, 7 и 200-й члены
последовательности, если ее п-й член задается формулой ![]()
2. Представьте бесконечную периодическую десятичную дробь 2,(27) в виде обыкновенной дроби.
3. Найдите производную функции.
а) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()
4. Найдите угловой коэффициент касательной к
графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]()
5. Докажите, что функция ![]() удовлетворяет соотношению
удовлетворяет соотношению ![]()
6. Сумма бесконечной убывающей геометрической прогрессии равна 4, а сумма квадратов её членов равна 48. Найдите первый член и знаменатель прогрессии.
Вариант 3
1. Вычислите 1, 5 и 8-й члены
последовательности, если ее п-й член задается формулой ![]()
2. Представьте бесконечную периодическую десятичную дробь 0,(13) в виде обыкновенной дроби.
3. Найдите производную функции.
а) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()
4. Найдите угловой коэффициент касательной к
графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]()
5. Докажите, что функция 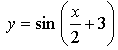 удовлетворяет соотношению
удовлетворяет соотношению ![]()
6. Найдите знаменатель бесконечно убывающей геометрической прогрессии, у которой второй член в 8 раз больше суммы всех её последующих членов.
Вариант 4
1. Вычислите 1, 3 и 6-й члены
последовательности, если ее п-й член задается формулой 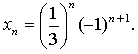
2. Представьте бесконечную периодическую десятичную дробь 0,(23) в виде обыкновенной дроби.
3. Найдите производную функции.
а) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()
4. Найдите угловой коэффициент касательной к
графику функции ![]() в точке с абсциссой
в точке с абсциссой ![]()
5. Докажите, что функция ![]() удовлетворяет соотношению
удовлетворяет соотношению ![]()
6. Сумма бесконечной убывающей геометрической прогрессии равна 2, а сумма кубов её членов равна 24. Найдите первый член и знаменатель прогрессии.
Решение вариантов контрольной работы
Вариант 1
1. ![]()
![]()
![]()
![]()
Ответ: ![]()
2. 1,(18) = 0,18 18 18 18… = ![]()
Найдем сумму бесконечной геометрической
прогрессии, у которой ![]()
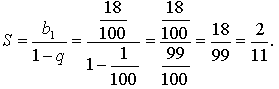
Значит, 1(18) = ![]()
Ответ: ![]()
3. а) ![]()
![]()
б) ![]()
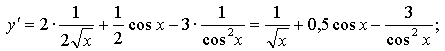
в) ![]()
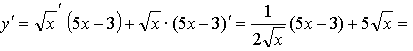
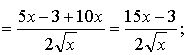
г) ![]()
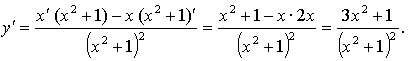
4. ![]() ,
, ![]()
![]()
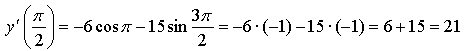
Ответ: 21.
5. ![]()
Найдем у' и подставим во второе равенство:
![]()
Имеем:
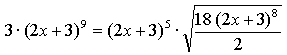
![]()
![]() Доказано.
Доказано.
6. Пусть ап - произвольный член геометрической прогрессии, q - знаменатель этой прогрессии.
Тогда ап + 1, ап + 2, ап + 3,… - последующие члены этой прогрессии. Найдем их сумму:
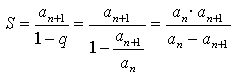
По условию ап в 6 раз больше этой суммы. Получим уравнение:
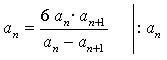
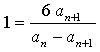
![]()
![]()
![]() .
.
Значит, знаменатель ![]()
Ответ: ![]()
Вариант 2
1. ![]()
![]()
![]()
![]()
Ответ: 5, 23, -602.
2. 0,27 = 0,27 27 27 27… = 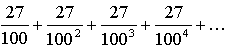
Найдем сумму бесконечной геометрической
прогрессии, у которой ![]()
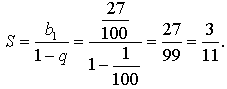
Значит, 2(27) = ![]()
Ответ: ![]()
3. а) ![]()
![]()
б) ![]()
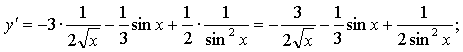
в) ![]()
![]()
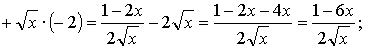
г) ![]()
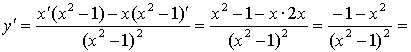
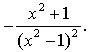
4. ![]() ,
, ![]()
![]()
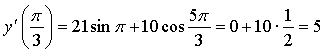
Ответ: 5.
5. ![]()
![]()
Найдем у' и подставим во второе равенство:
![]()
Имеем:
![]()
![]()
![]()
0 = 0. Доказано.
6. Пусть дана геометрическая прогрессия
![]() и пусть q - знаменатель этой прогрессии. Найдем её сумму, которая
по условию равна 4:
и пусть q - знаменатель этой прогрессии. Найдем её сумму, которая
по условию равна 4:
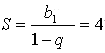
Тогда получим, что b1 = 4(1 - q).
Последовательность, состоящая из квадратов членов данной геометрической прогрессии, в свою очередь также является геометрической прогрессией, у которой первый член равен b12, а знаменатель равен q2. Найдём сумму этой прогрессии:
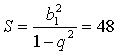
Тогда получим, что ![]()
Составим и решим уравнение:
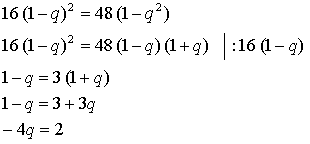
![]()
Найдем 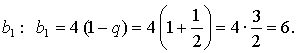
Ответ: ![]()
Вариант 3
1. ![]()
![]()
![]()
![]()
Ответ: ![]()
2. 0,(13) = 0, 13 13 13 13… = 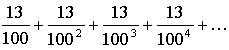
Найдем сумму бесконечной геометрической
прогрессии, у которой ![]()
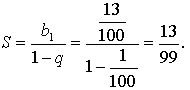
Значит, ![]()
Ответ: ![]()
3. а) ![]()
![]()
б) ![]()
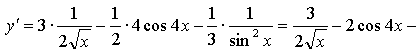
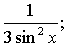
в) ![]()
![]()
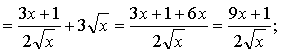
г) 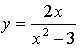
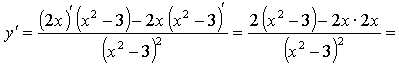
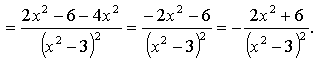
4. ![]() ,
, ![]()
![]()
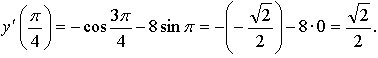
Ответ: ![]()
5. ![]()
![]()
Найдем у' и подставим во второе равенство:
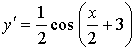
Имеем:
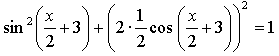
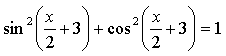
1 = 1 . Доказано.
6. Пусть дана геометрическая прогрессия
![]() и пусть q - знаменатель этой прогрессии. Найдем сумму всех её
членов, начиная с третьего:
и пусть q - знаменатель этой прогрессии. Найдем сумму всех её
членов, начиная с третьего:
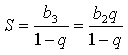
По условию b2 в 8 раз больше этой суммы. Получим уравнение:
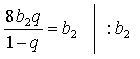
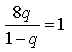
![]()
![]()
![]()
Ответ: ![]()
Вариант 4
1. 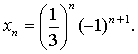
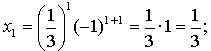
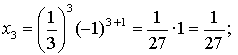
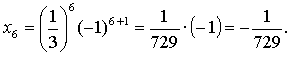
Ответ: ![]()
2. 0,(23) = 0,23 23 23 23… = 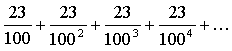
Найдем сумму бесконечной геометрической
прогрессии, у которой ![]()
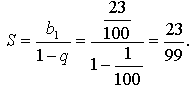
Значит, ![]()
Ответ: ![]()
3. а) 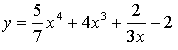
![]()
б) ![]()
![]()
![]()
в) ![]()
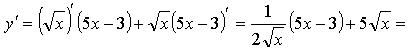
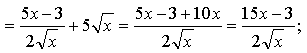
г) ![]()
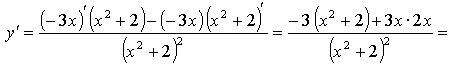
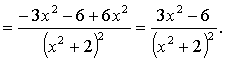
4. ![]()
![]()
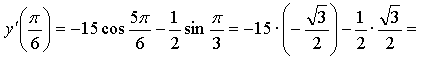
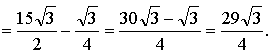
Ответ: 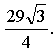
5. ![]()
![]()
Найдем у' и подставим во второе равенство:
![]()
Имеем:
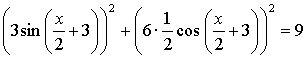
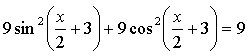
9 = 9 . Доказано.
6. Пусть дана геометрическая прогрессия
![]() и пусть q - знаменатель этой прогрессии. Найдем её сумму, которая
по условию равна 2:
и пусть q - знаменатель этой прогрессии. Найдем её сумму, которая
по условию равна 2:
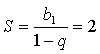
Тогда получим, что ![]()
Последовательность, состоящая из кубов членов данной геометрической прогрессии, в свою очередь также является геометрической прогрессией, у которой первый член равен b13, а знаменатель равен q3. Найдем сумму этой прогрессии:
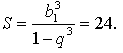
Тогда получим, что ![]()
Составим и решим уравнение:
![]()
![]()
![]()
![]()
![]()
![]()
![]() (не
подходит по смыслу задачи).
(не
подходит по смыслу задачи).
Найдем 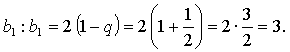
Ответ: ![]()