СтатьяМетод декомпозиции при решении логарифмических и показательных неравенств

Грищенко Т.М.,

МАОУ СОШ № 37

с углубленным изучением

искусств и английского языка

г. Таганрог

МЕТОД ДЕКОМПОЗИЦИИ ПРИ РЕШЕНИИ ПОКАЗАТЕЛЬНЫХ И ЛОГАРИФМИЧЕСКИХ НЕРАВЕНСТВ

Показательные и логарифмические неравенства часто встречаются в заданиях единого государственного экзамена (ЕГЭ). Эффективным методом решения неравенств подобного типа является метод декомпозиции. Суть метода состоит в следующем:

1) если Ф - композиция элементарных функций, которая монотонно возрастает на ОДЗ или на некотором ее подмножестве М, то

2) если Ф - монотонно убывает, то

Метод декомпозиции очень эффективен для решения показательно-степенных неравенств и логарифмических неравенств с переменной в основании.

Теорема 1. При всех допустимых , , справедливы следующие утверждения:

1)

2)

3)

4)

Доказательство.

Рассмотрим первое утверждение (остальные доказываются аналогично).

Покажем, что на ОДЗ неравенства из неравенства следует неравенство .

Если , то из неравенства следует, что , то есть , а значит, .

Если , то из неравенства следует, что , т.е. , значит, .

Теперь докажем, что на ОДЗ неравенства из неравенства следует неравенство .

Поскольку то либо либо

Если то и из неравенства следует, что и и ввиду того, что показательная функция с основанием, большим 1, возрастающая, то .

Если то и из неравенства следует, что , , и ввиду того, что показательная функция с основанием, меньшим 1, убывающая, то .

Равносильность неравенств доказана.

Пример 1. Решите неравенство

.

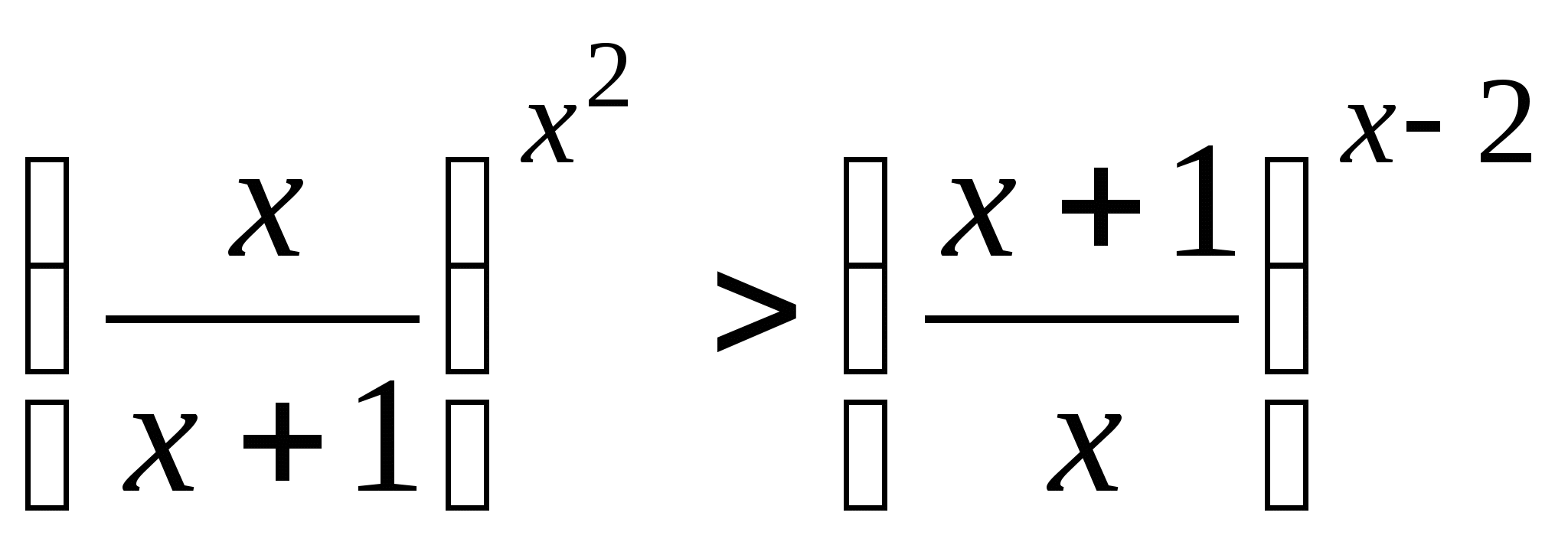Решение.

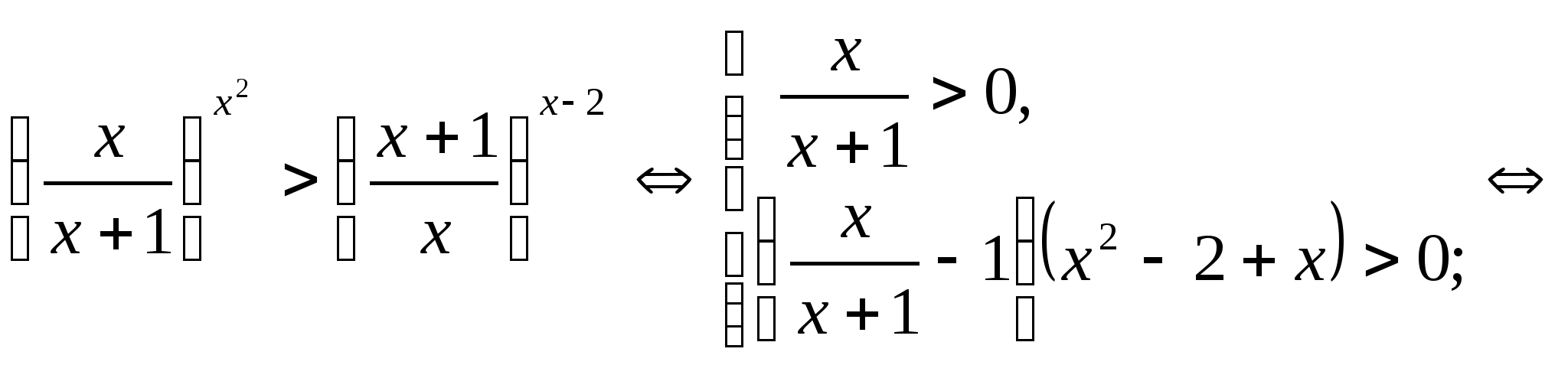
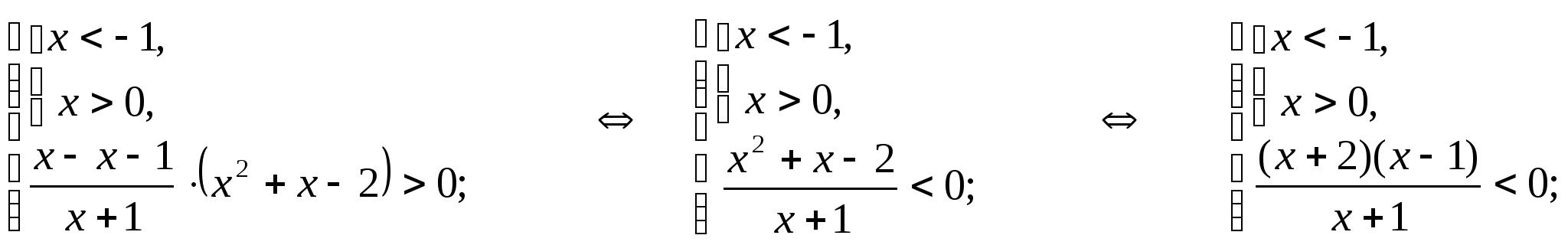
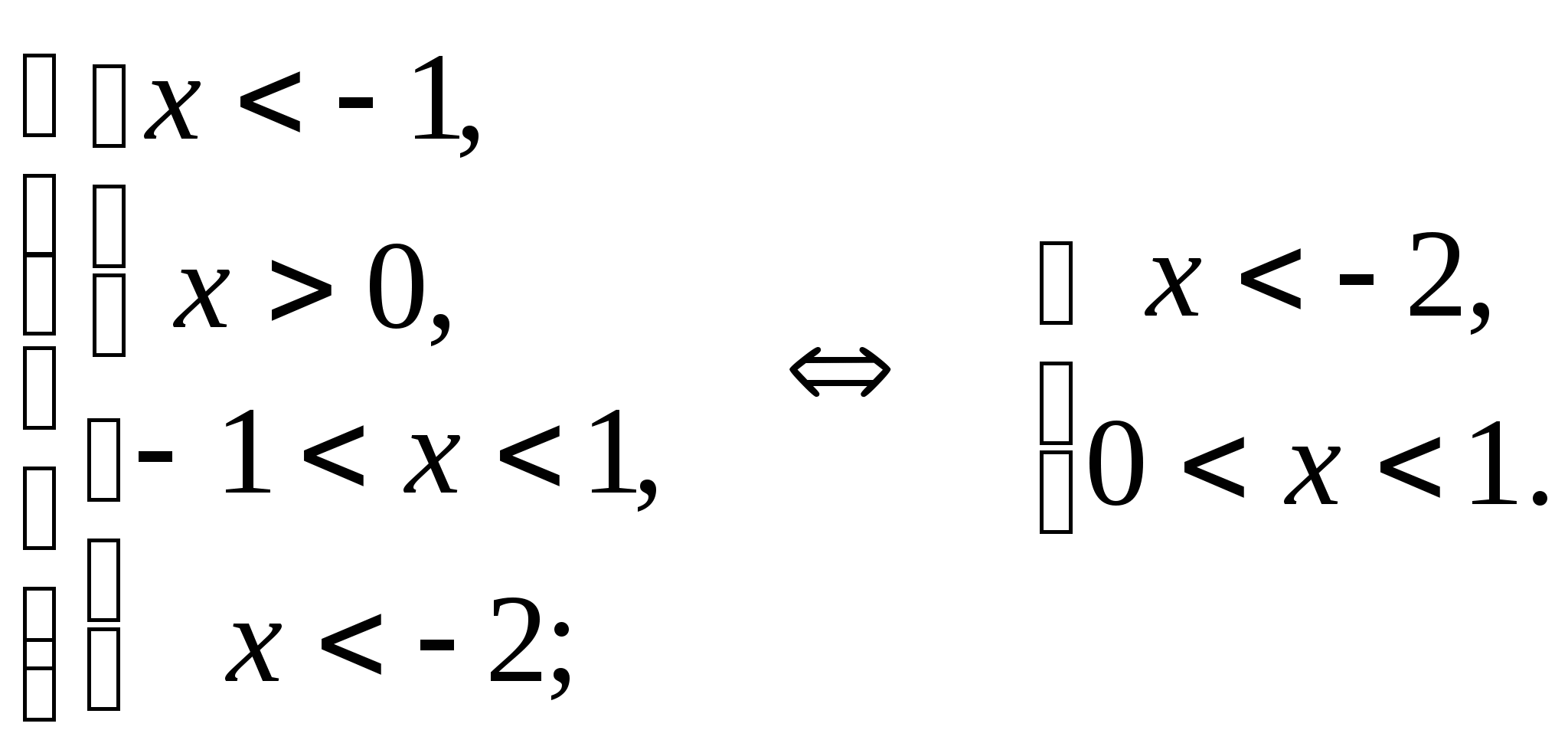
Ответ.

Теорема 2. При всех , и всех допустимых значениях и верны следующие утверждения:

1)

2)

3)

4)

Доказательство.

Докажем первое утверждение, остальные доказываются аналогично.

Докажем, что из неравенства следует неравенство .

Если , то из неравенства следует , значит, , следовательно, .

Если , то и из неравенства следует , и, следовательно, .

Докажем теперь, что из неравенства следует неравенство .

Так как то или

Если то и, значит, из неравенства следует, что и , и так как логарифмическая функция с основанием, меньшим 1, убывающая, то .

Если , то , тогда произведение , если , то есть и, учитывая, возрастание логарифмической функции с основанием, большим единицы, получим неравенство .

Следовательно, данные неравенства равносильны.

Пример 2. Решите неравенство

Решение.

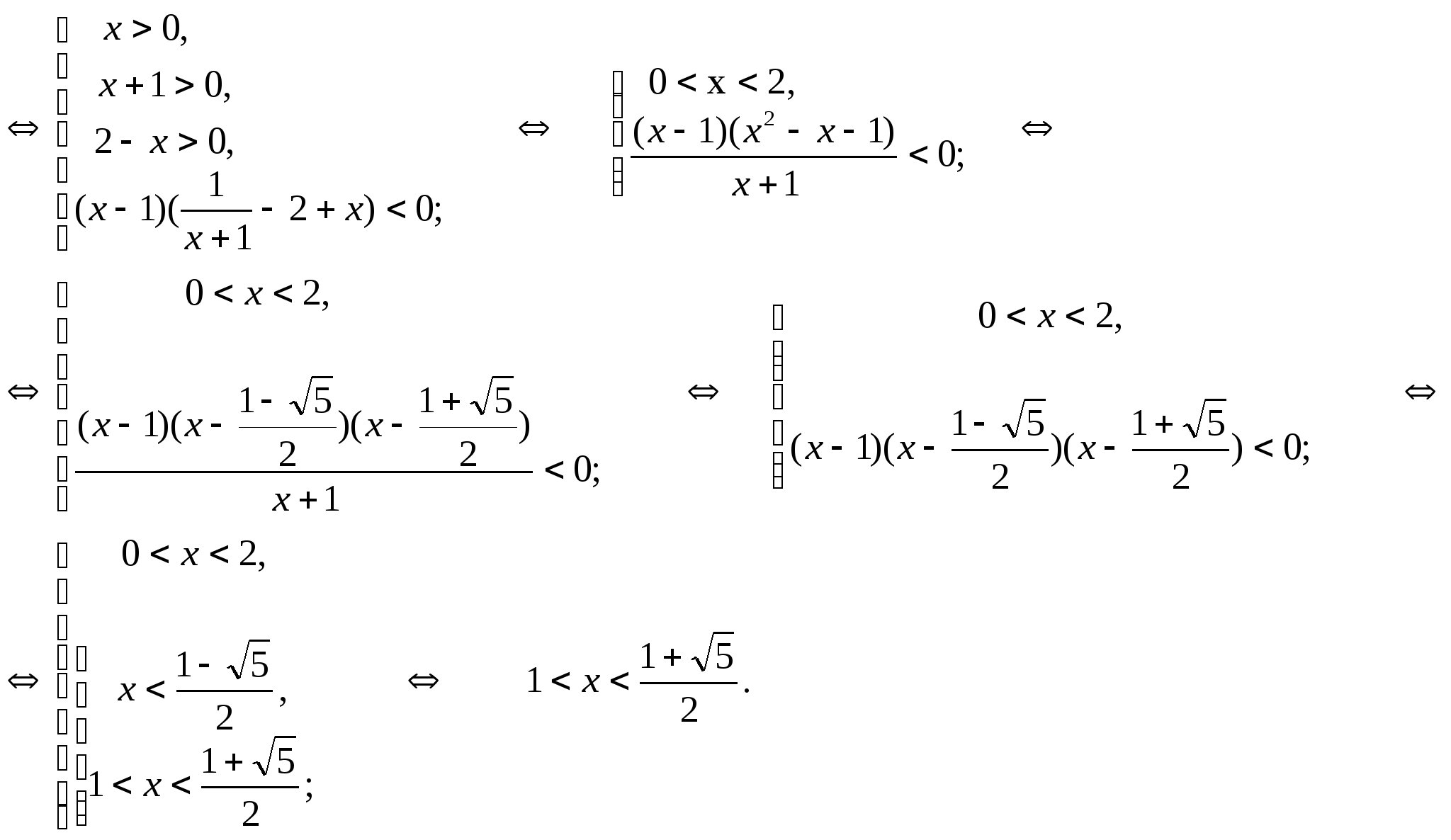
Ответ: (1; ).

Декомпозиция простейших показательных и логарифмических неравенств приведена в таблице.
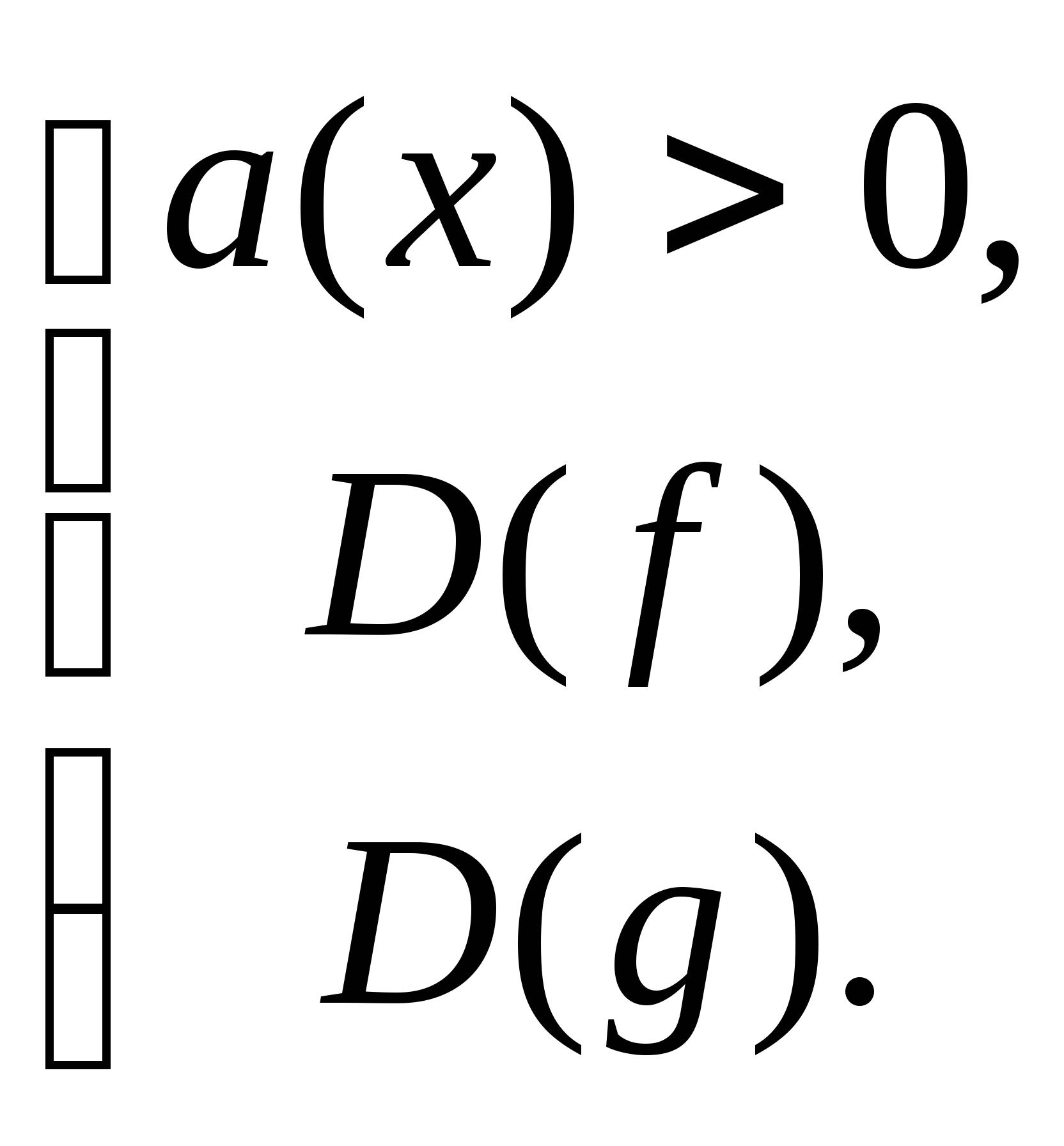
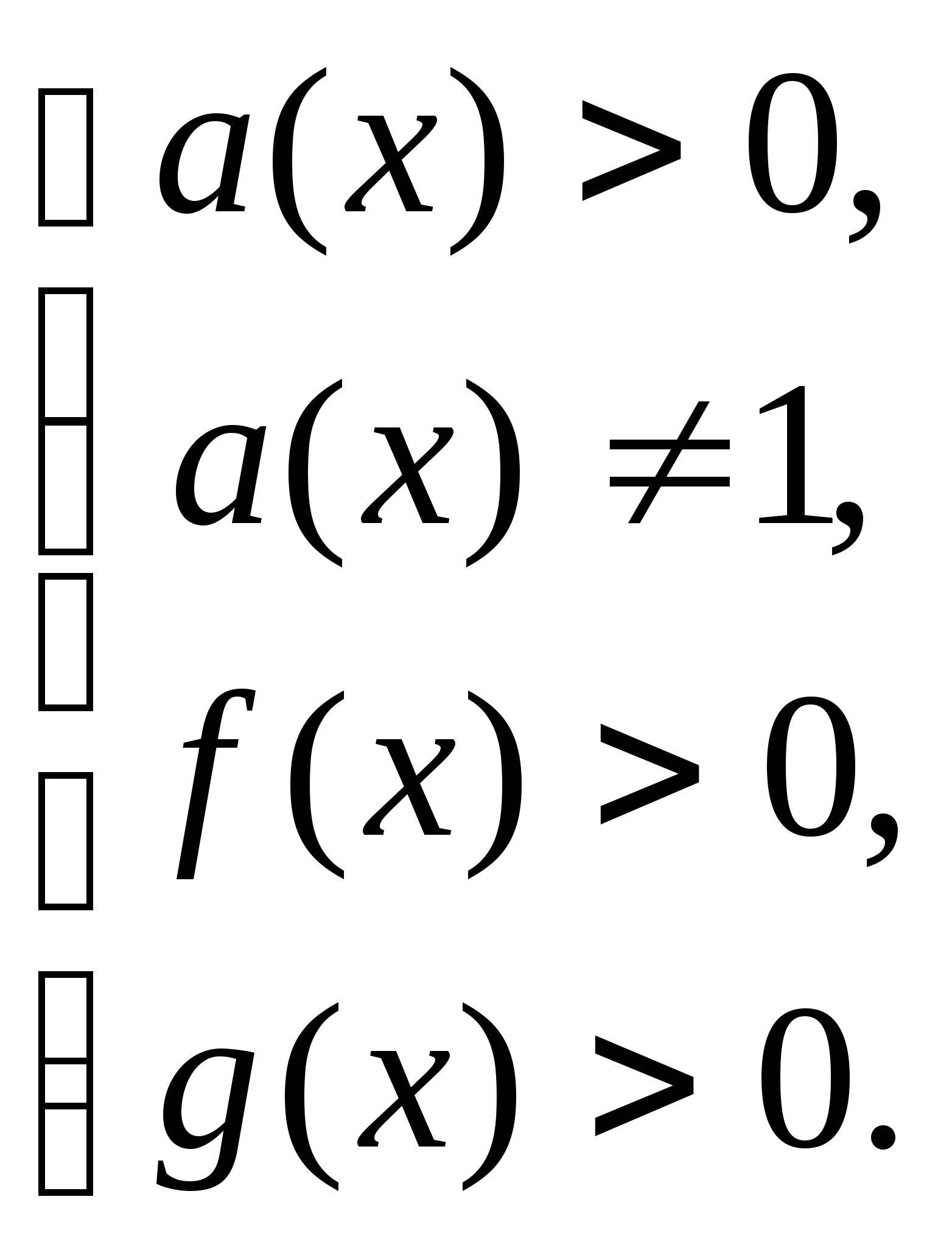
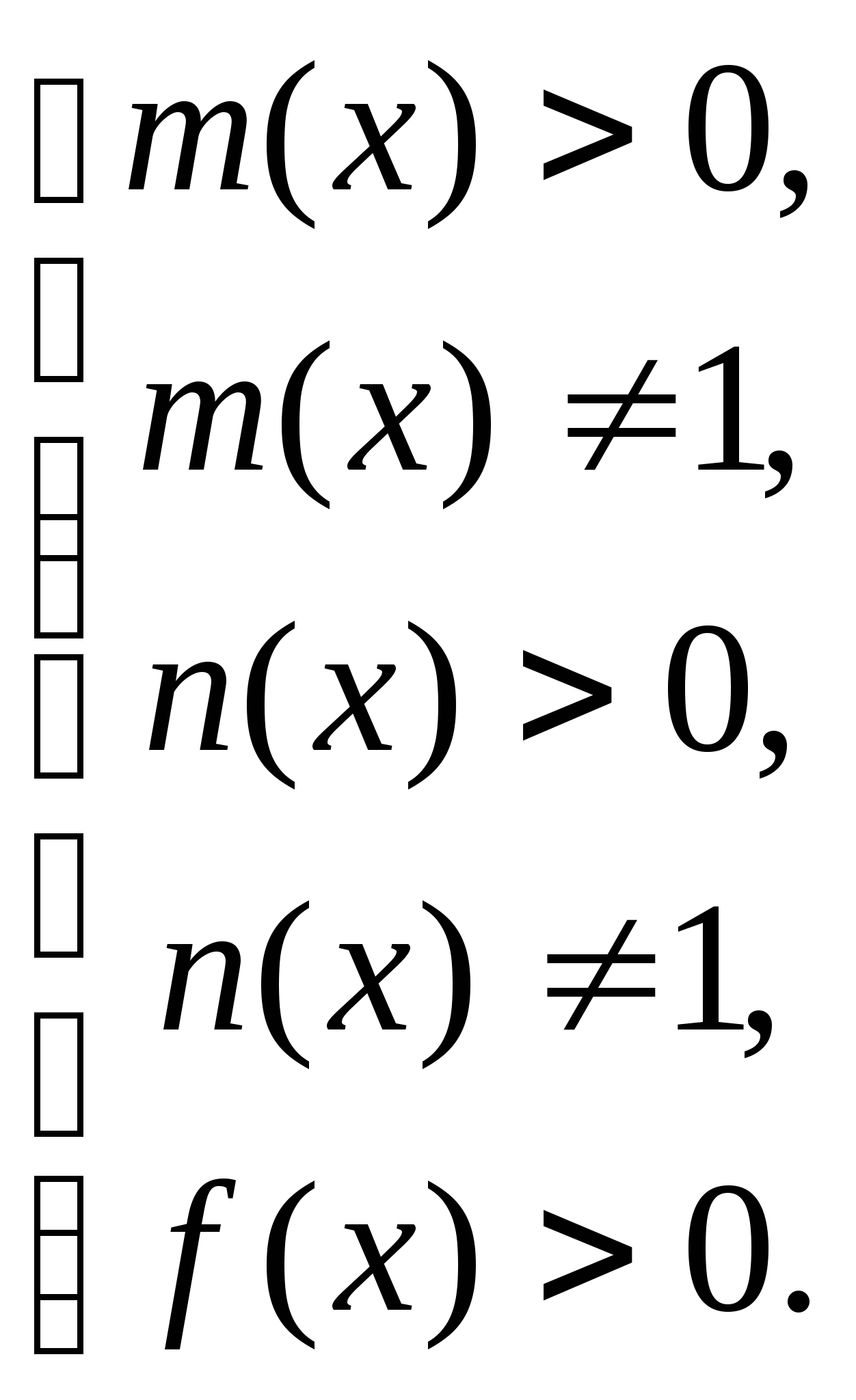