Урок по теме Исследование функции с помощью производной и построение графика

Тема: «Исследование функции с помощью производной и построение графика».

Цели урока:

1. Образовательная - отработать умения систематизировать, обобщать при исследовании функции ее свойства, применять знания производной при построении графиков функции;

2. Развивающая - развитие мыслительных операций посредством наблюдений, сравнений, сопоставлений, обобщений, развитие зрительной памяти, математической речи учащихся.

3. Воспитательные - воспитание познавательной активности, чувства ответственности, уважения друг другу, взаимопонимания, воспитание культуры общения.

Оборудование: презентация, карточки - математическое лото.

Тип урока: урок обобщения и систематизации знаний.

Ход урока.

Здравствуйте ребята! Сегодня на уроке мы продолжим изучение применения производной функции для построения графиков различных функций.

Так как урок сегодня необычный, то начать я хочу его с необыкновенных слов.

«Музыка может возвышать или умиротворять душу,

живопись - радовать глаз,

поэзия - пробуждать чувства,

философия - удовлетворять потребности разума, инженерное дело - совершенствовать материальную сторону жизни людей, а математика способна достичь всех этих целей!»

Морис Клайн

А работать мы будем под девизом: « Знания имей отличные, исследуя функции различные».

Оценочный лист:

1. Проверка домашнего задания.

Учащиеся оценивают выполненную ими домашнюю работу.

«Кто смолоду делает и думает сам, тот становиться потом, надежнее, крепче, умнее»

В. Шукшин.

Учащиеся оценивают выполнение ими домашнее задание.

2. У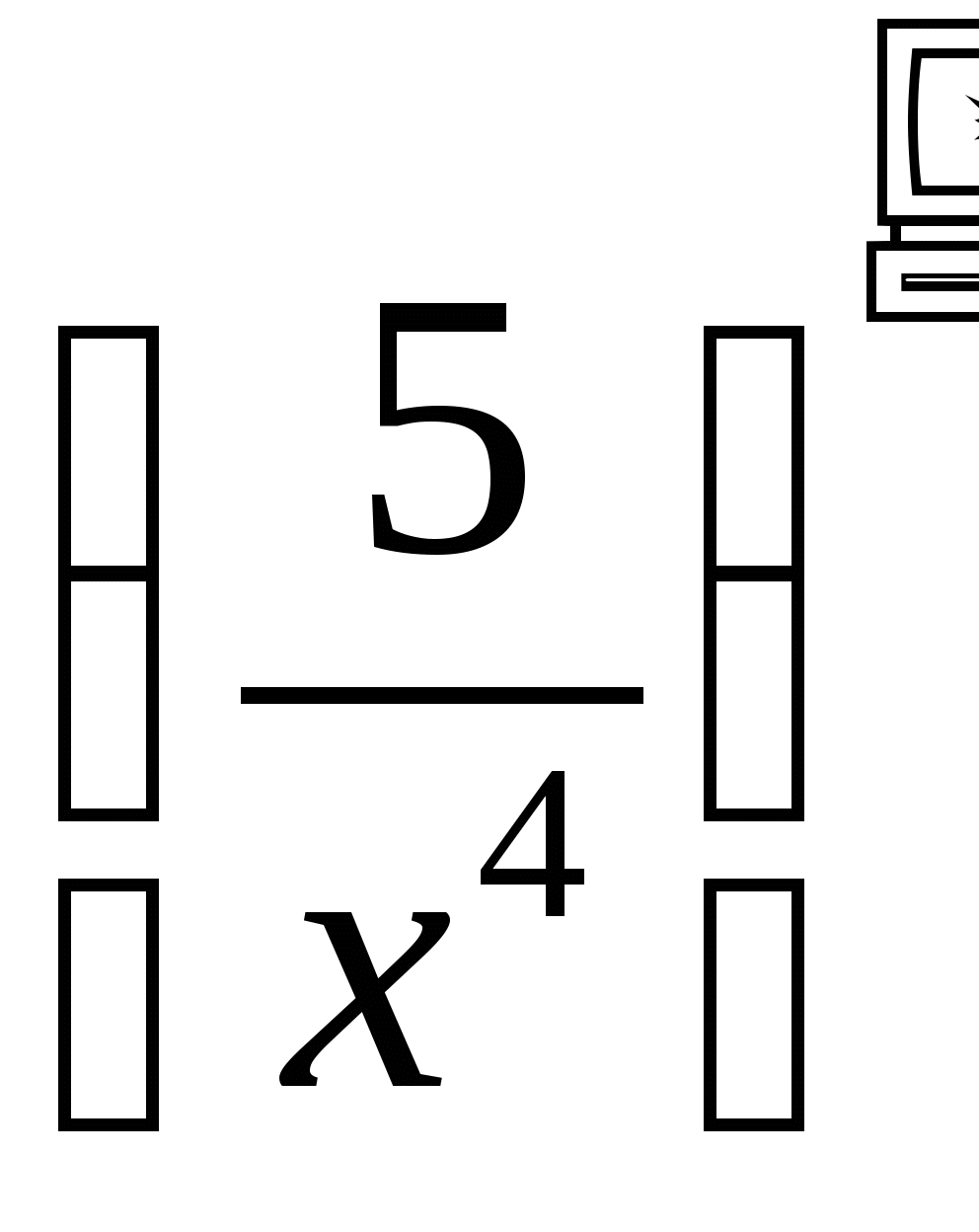стная работа - разминка.

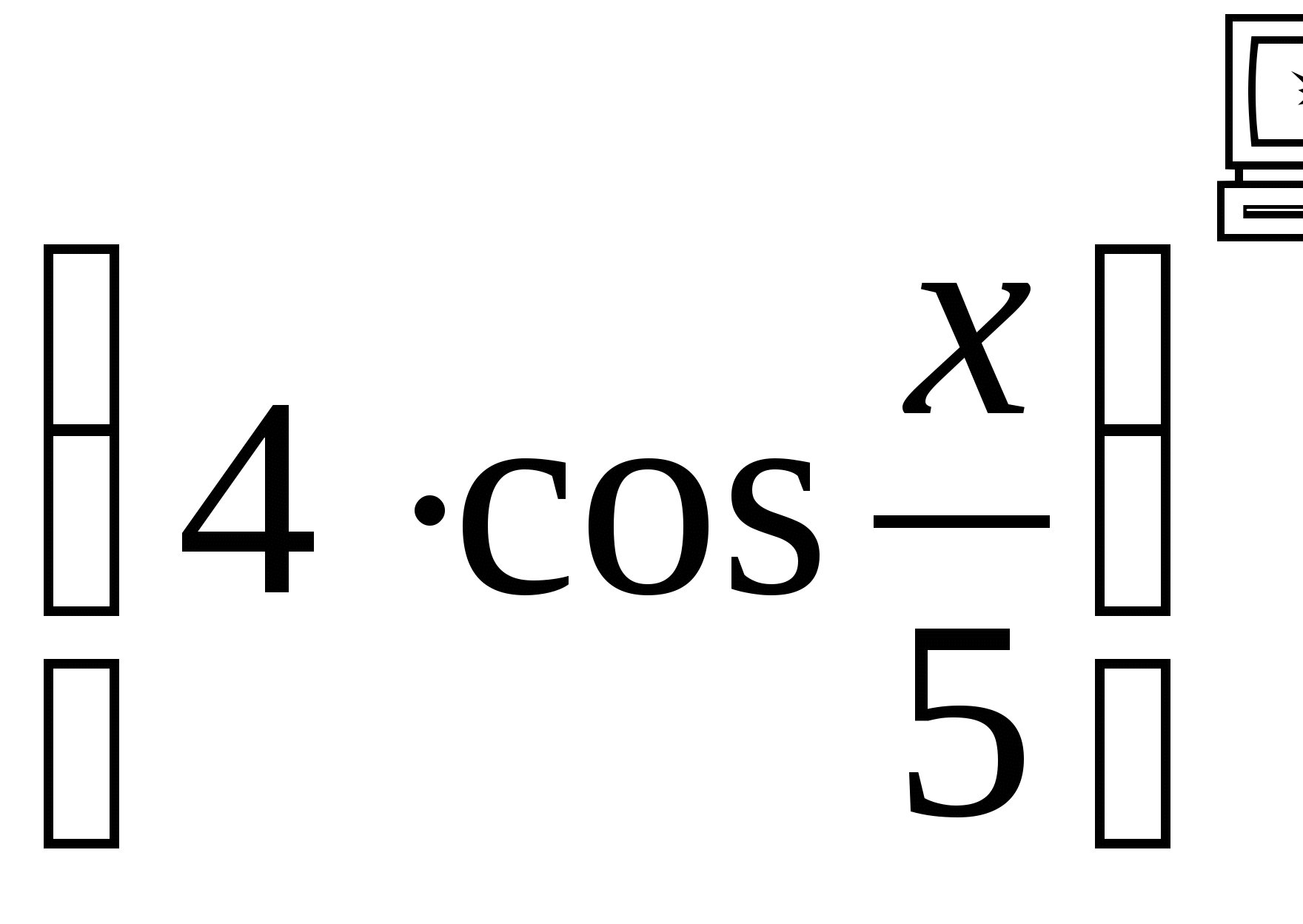
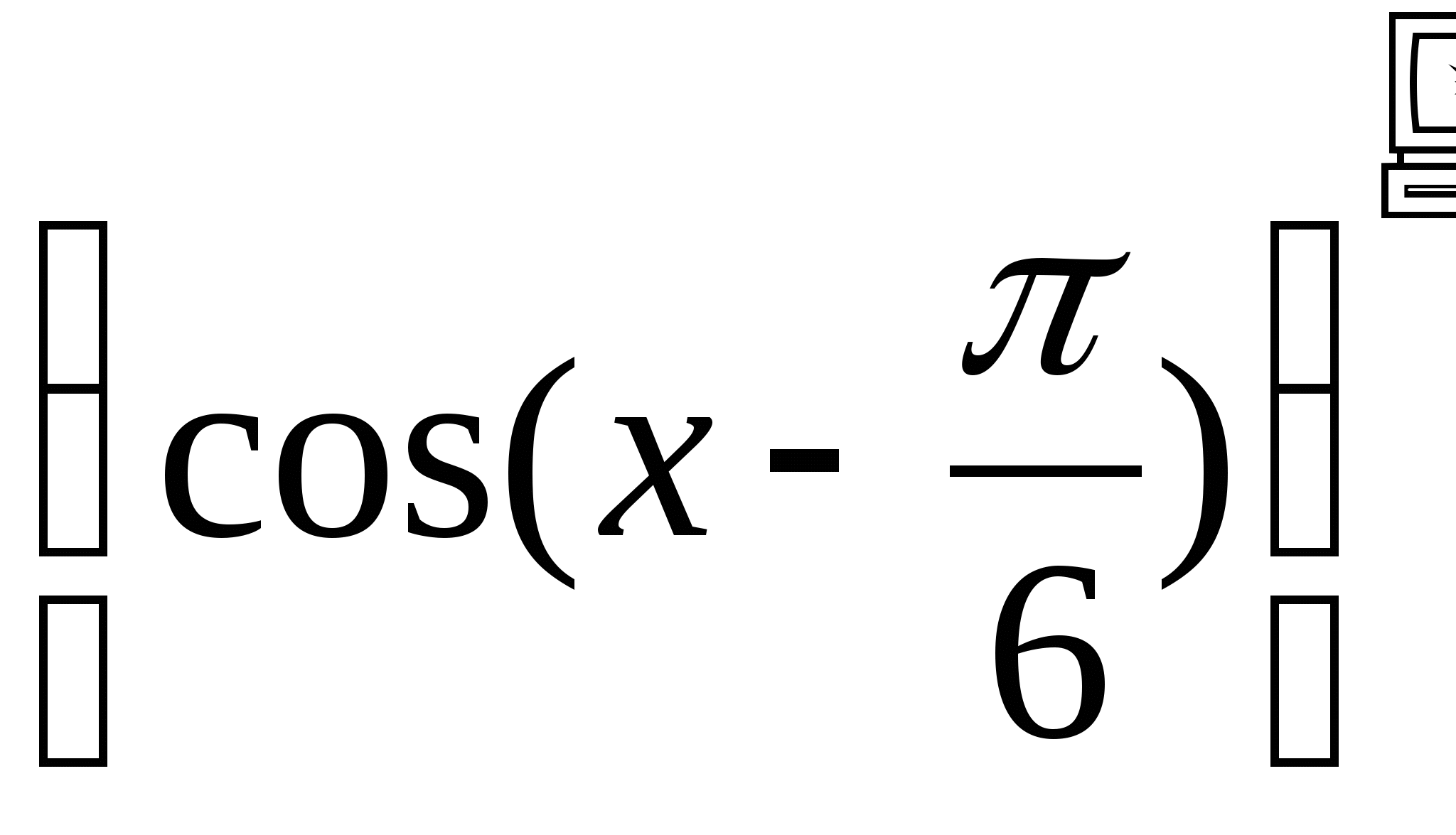
Оцените, пожалуйста, ребята долю своего участия в устной работе. Активно поднимали руку, и вам удалось ответить правильно оценка «5», ваши ответы были правильными, но вы сомневались и стеснялись «4», были неточности «3», вы были пассивны «2».

3. Найти ошибку. Проверка теоретического материала. Отвечать должны только да или нет. _^ - верно, ^_ - неверно, есть ошибка.

1. Функция возрастает на [-7; 2) и (2; 8], значит, она возрастает на [-7; 8]. Верно ли?

2. Производная функции в точке х₀ равна 0, значит х₀ - критическая точка. Верно ли?

3. Производная функции не существует в точке х₀, значит х₀ - критическая точка. Верно ли?

4. Критическая точка является точкой экстремума. Верно ли?

5. Точка экстремума является критической точкой. Верно ли?

Проверка;

Проверка, 5 правильных ответов оценка «5», 4-«4», 3-«3», 2-0 оценка «2».

4. На следующем этапе урока учащиеся группируются по 4 человека. Применяется раздаточный материал - математическое лото. Необходимо решить 9 примеров на нахождение производной функции. Результатом в каждой группе должен получиться график функции. Каждый график проверяется, и учащиеся называют свойства изображенного графика. По окончании выставляется оценка в оценочный лист.

Карточка №1.

y′(x)-?

y=(5x+23)⁷

y′(x)-?

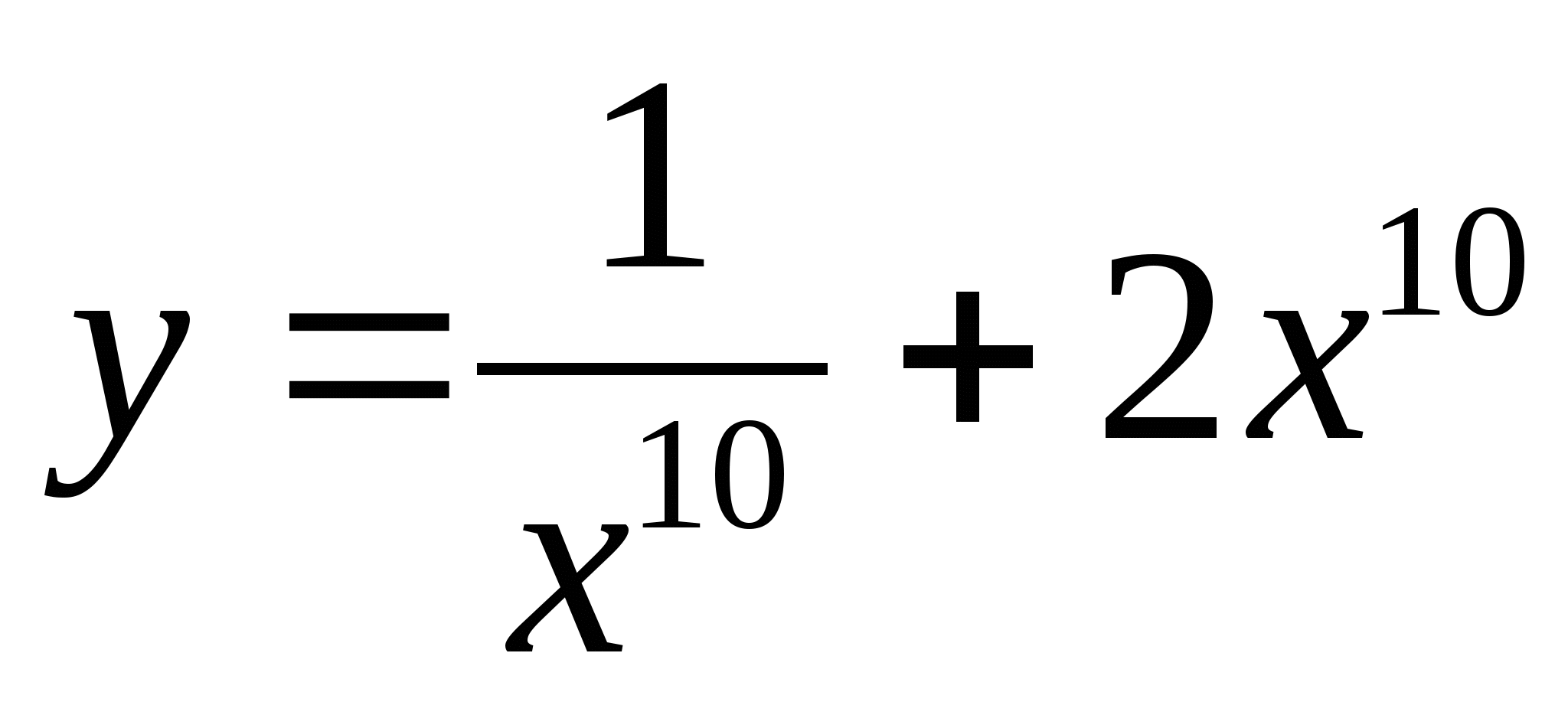
y′(x)-?

y′(x)-?

y′(x)-?

y=tg x+x²

y′(x)-?

y=sin 5x+cos3x

y′(x)-?

y=(4x+0.5)³

y′(x)-?

Правильные ответы.

y′(x)=35(5x+23)⁶

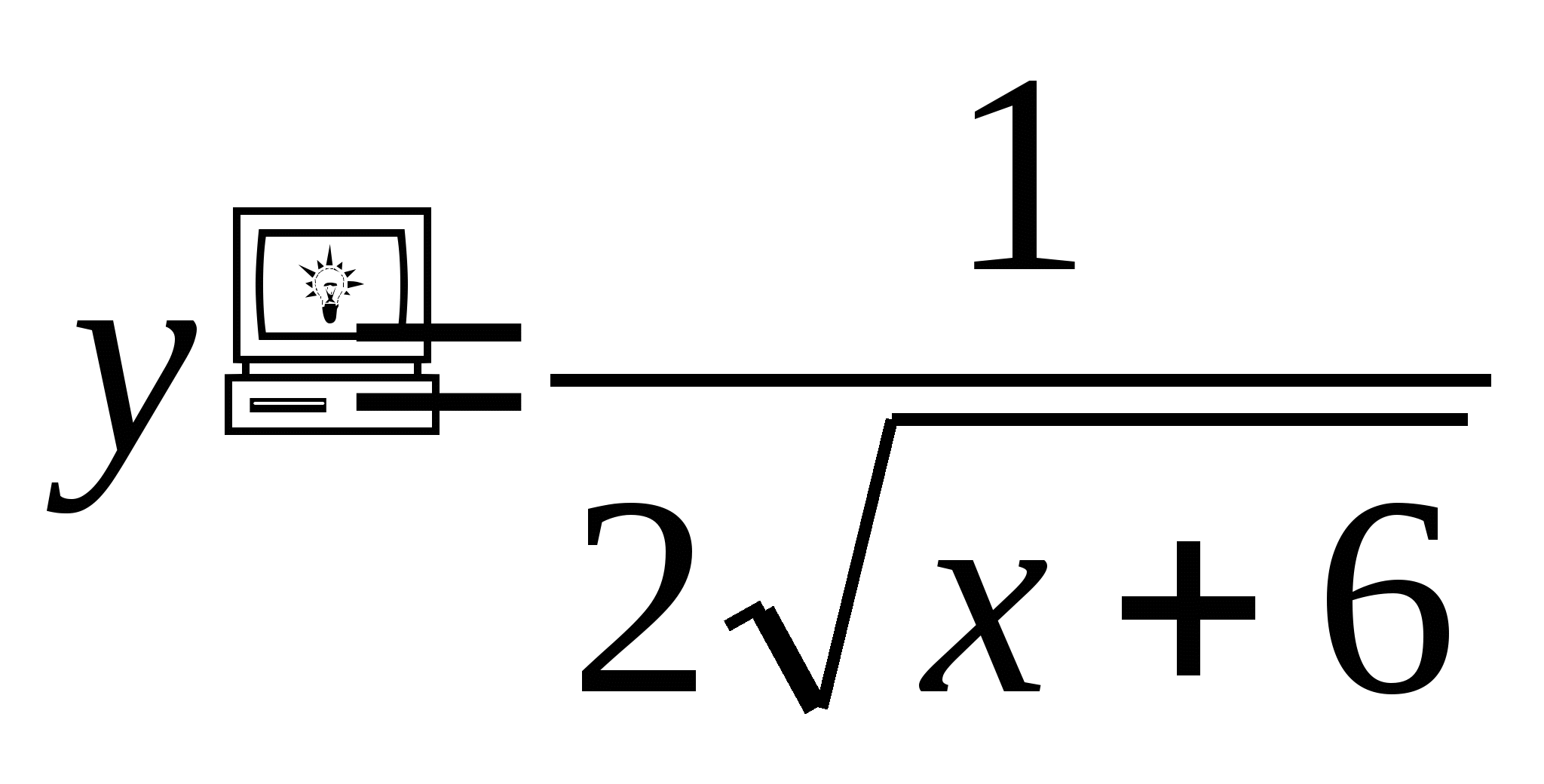
y′(x)=4x³+4x

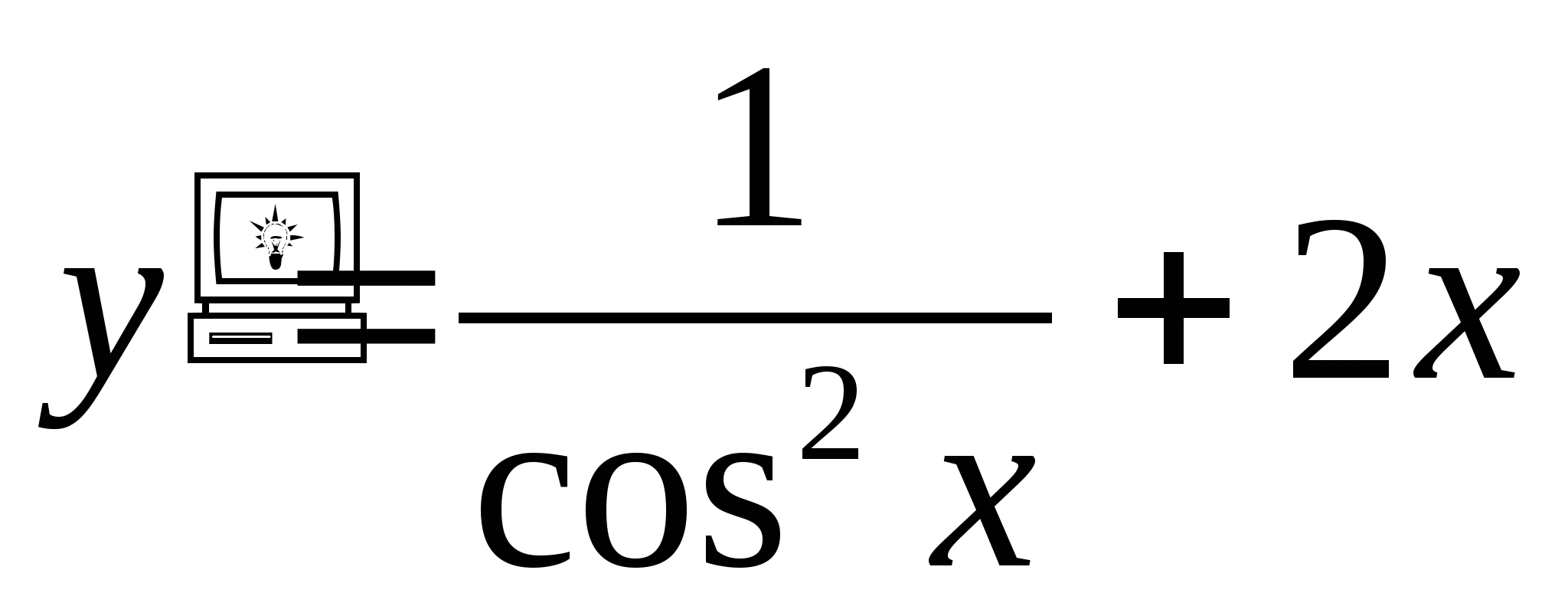
y′(x)=5cos5x-3sin3x

y′(x)=12(4x+0.5)²

Неправильные ответы.

y′(x)=6(5x+23)⁶

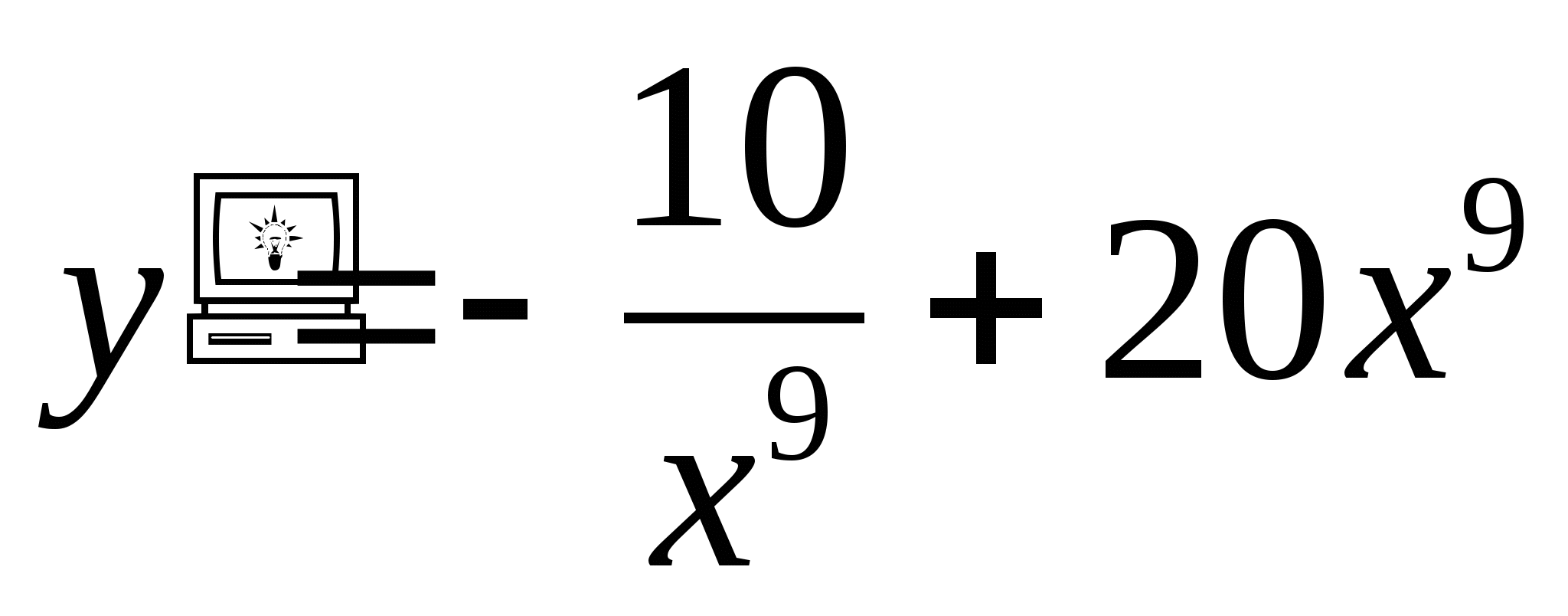
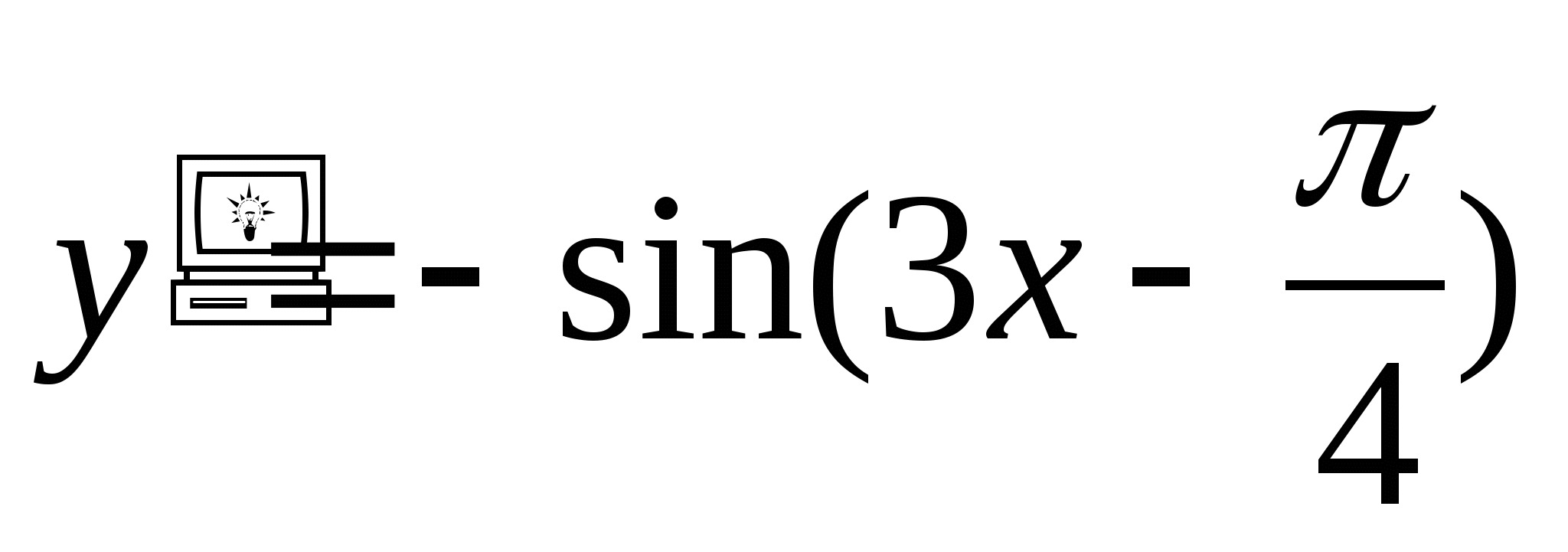
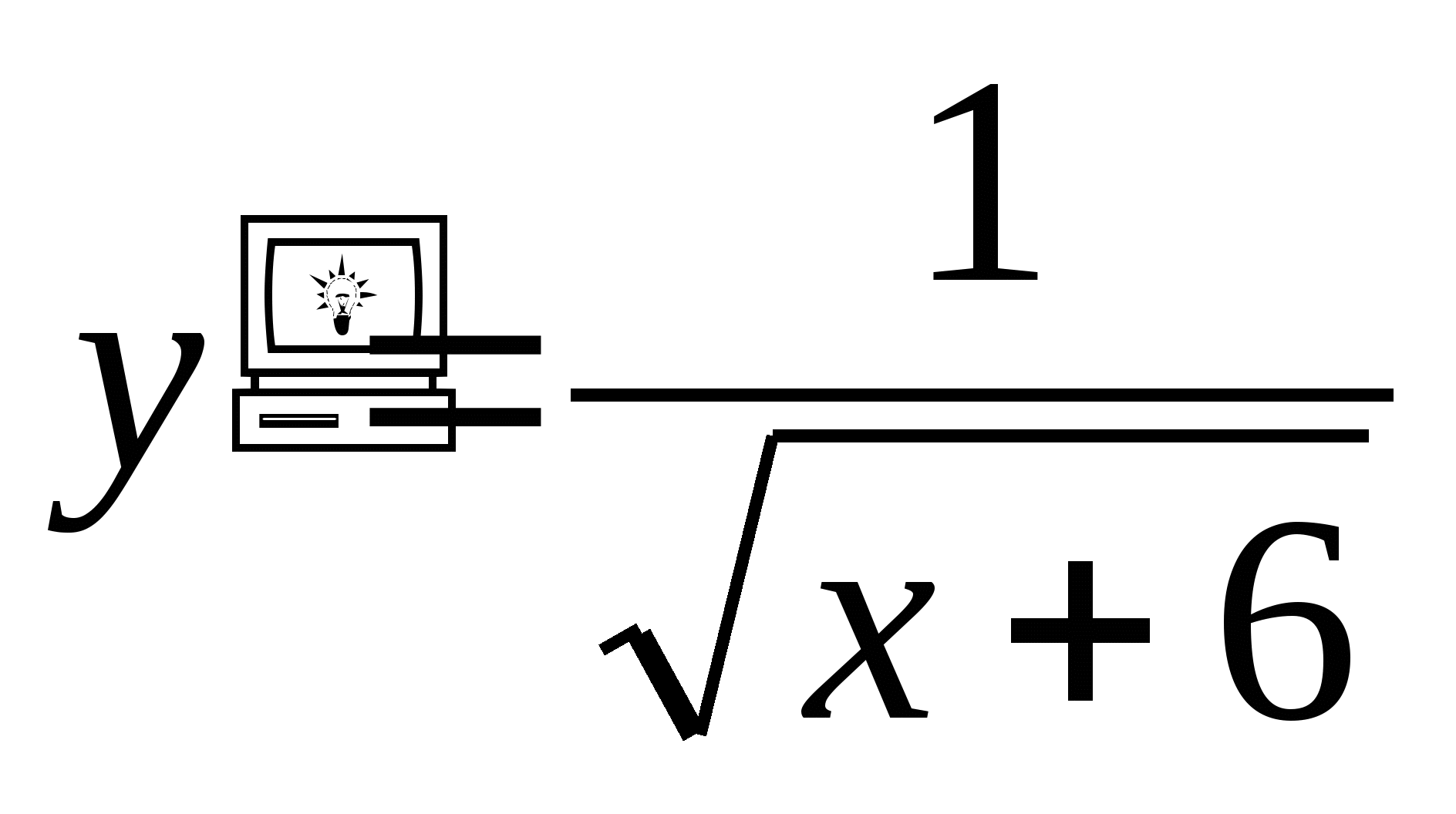
y′(x)=3x²+2

y′(x)=cos5x-sin3x

y′(x)=4(4x+0.5)²

К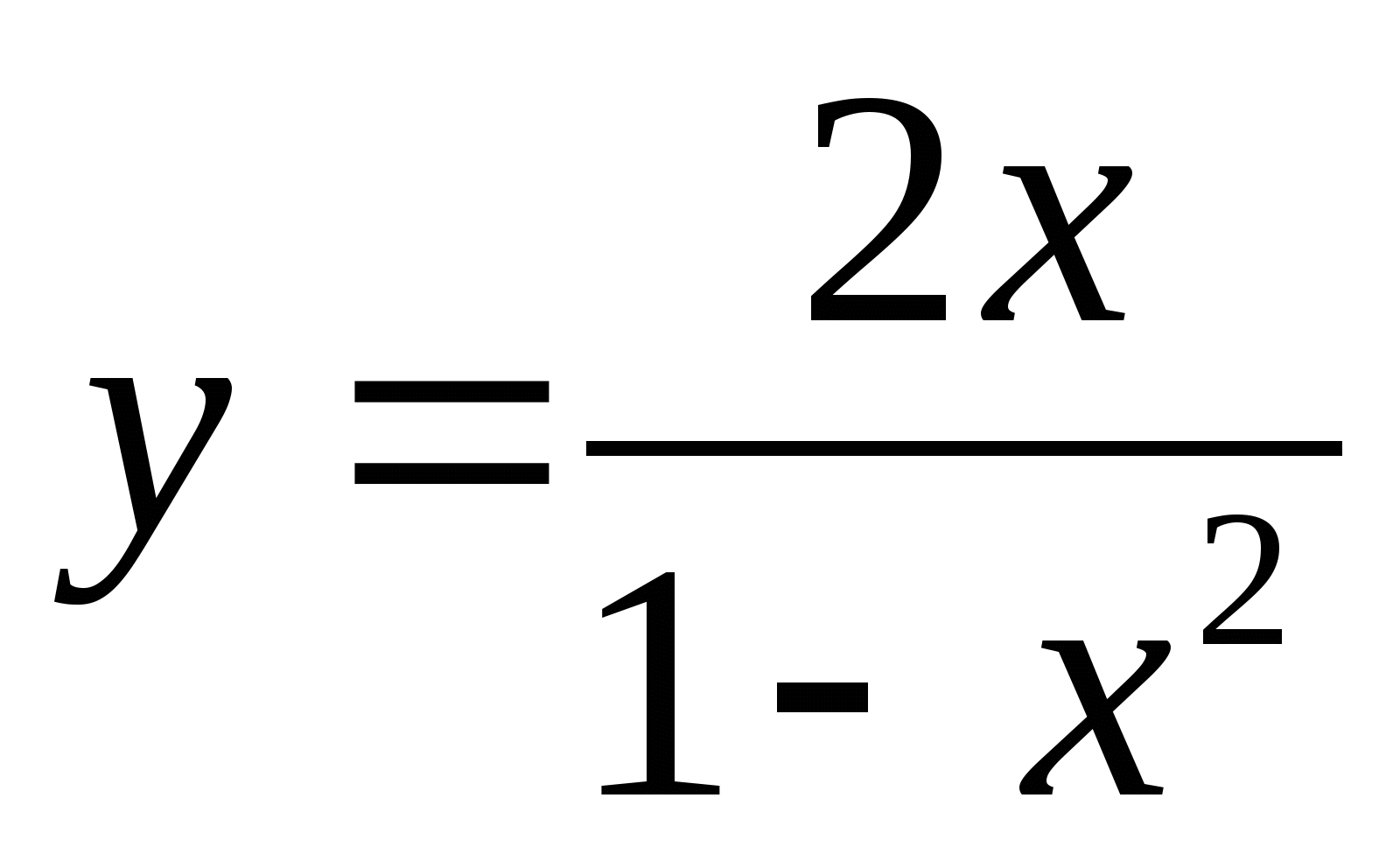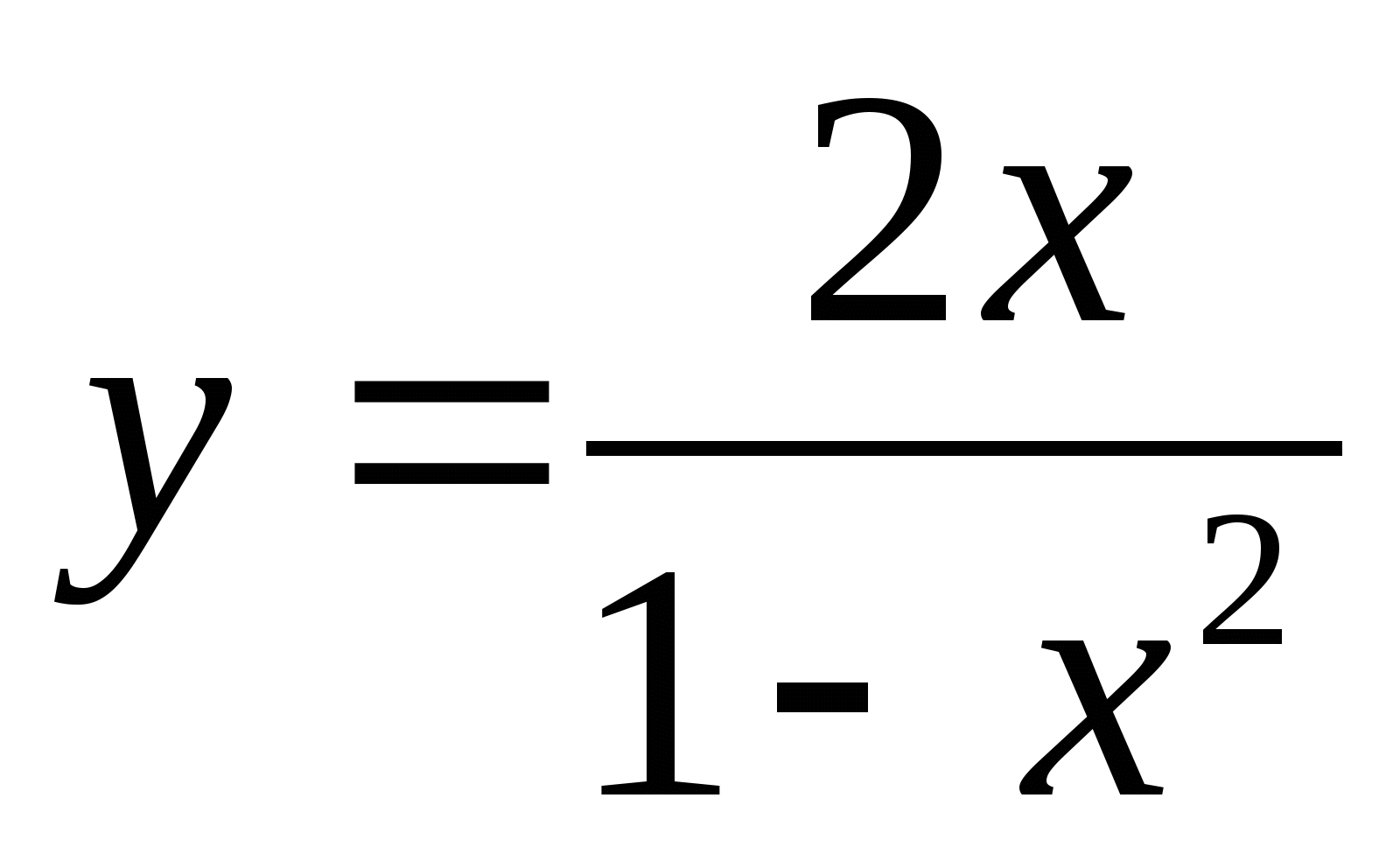арточка №2.

y′(x)-?

y=(0.4x+25)⁸

y′(x)-?

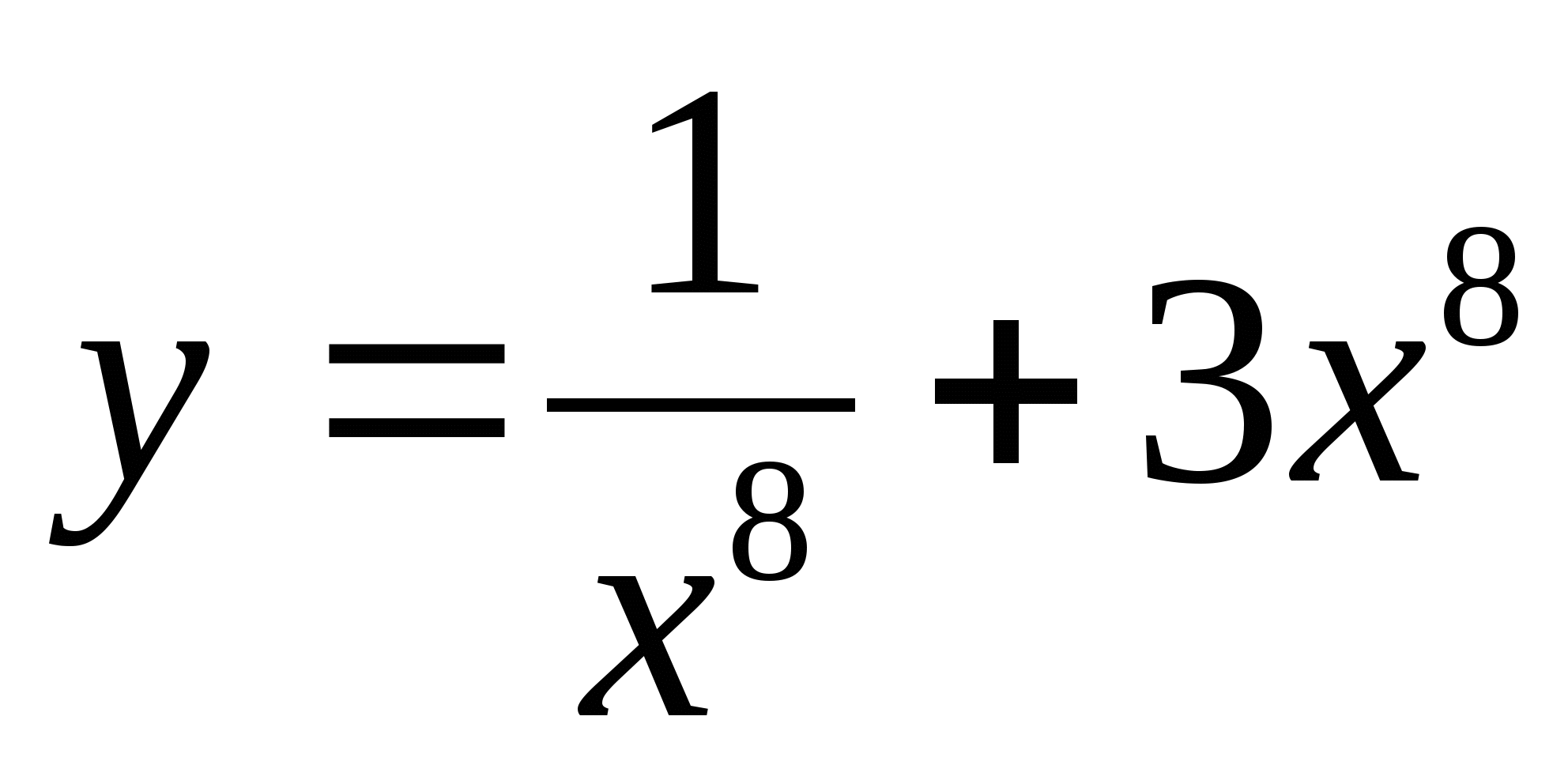
y′(x)-?

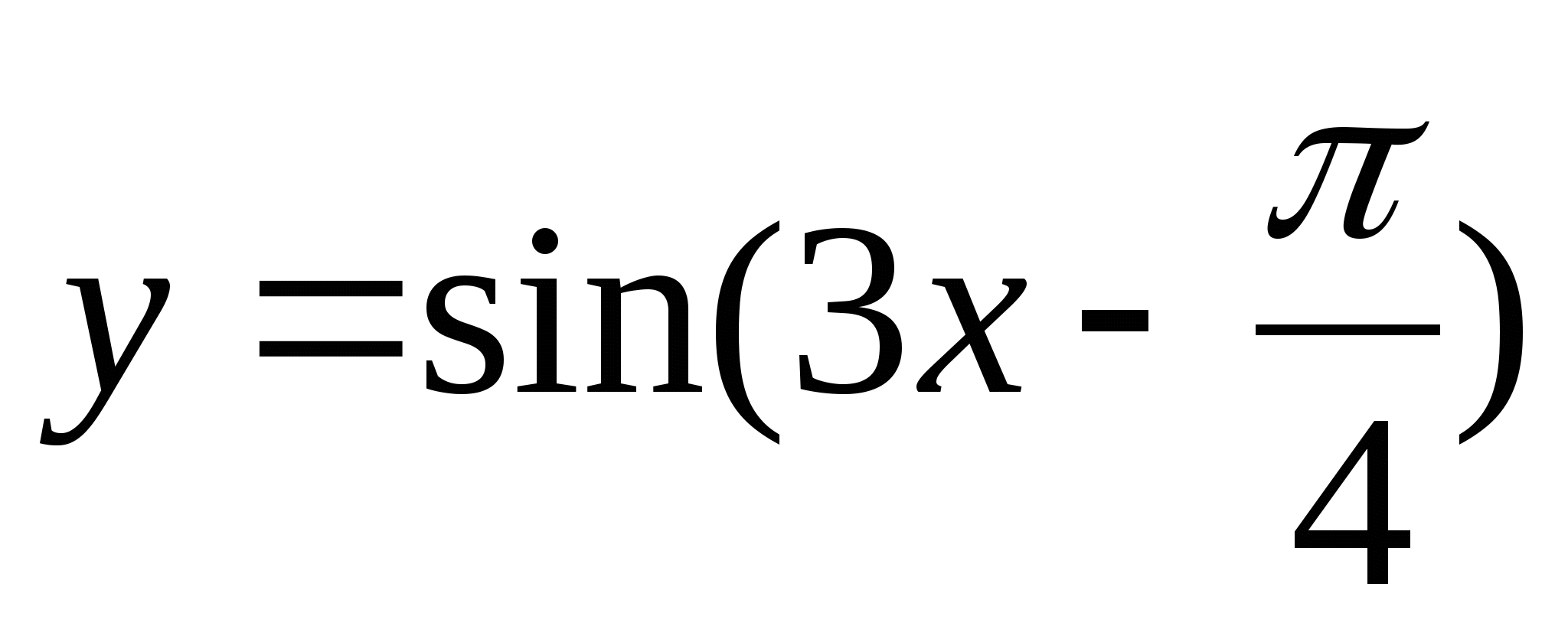
y′(x)-?

y′(x)-?

y=-2tg x+x³

y′(x)-?

y=sin 3x+cos5x

y′(x)-?

y=(6x-9.5)⁵

y′(x)-?

Правильные ответы.

y′(x)=3.2(0.4x+25)⁷

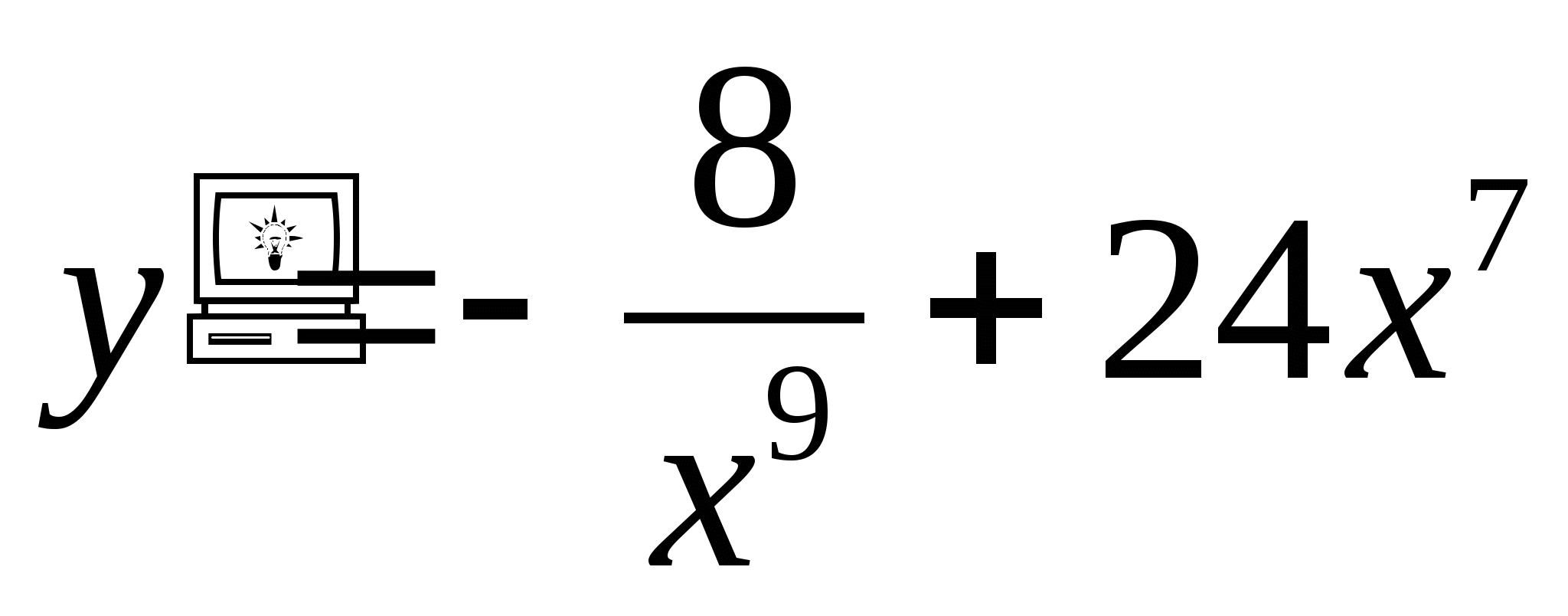
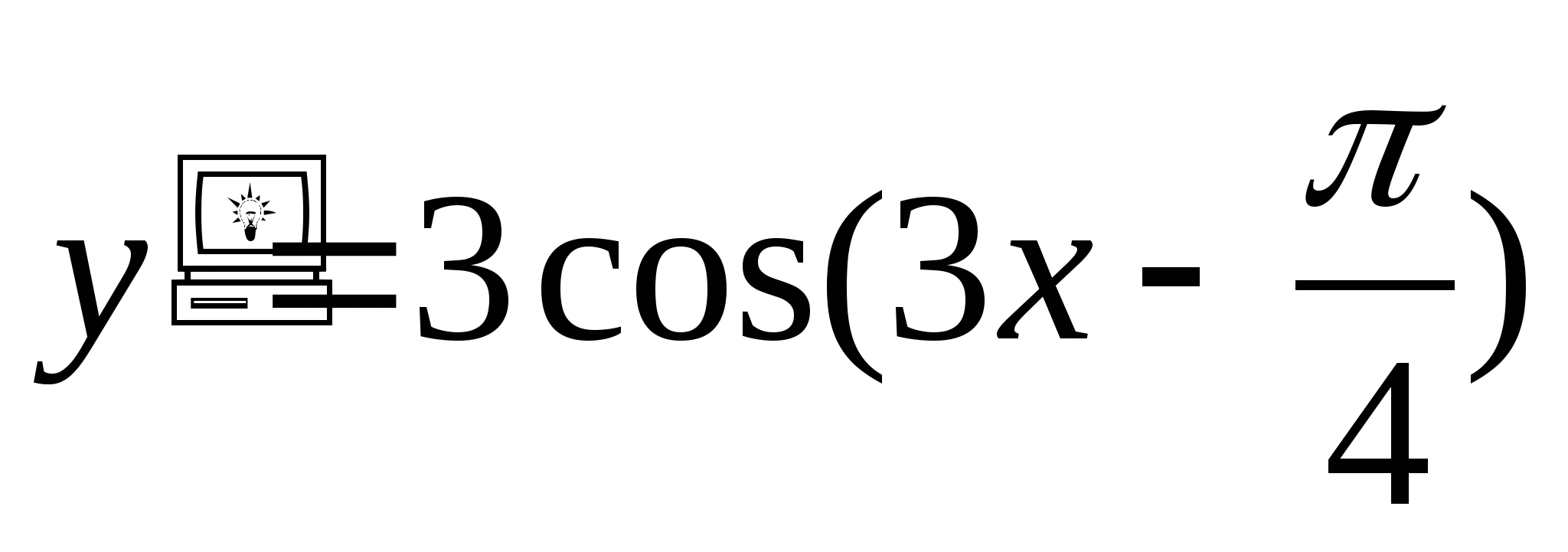
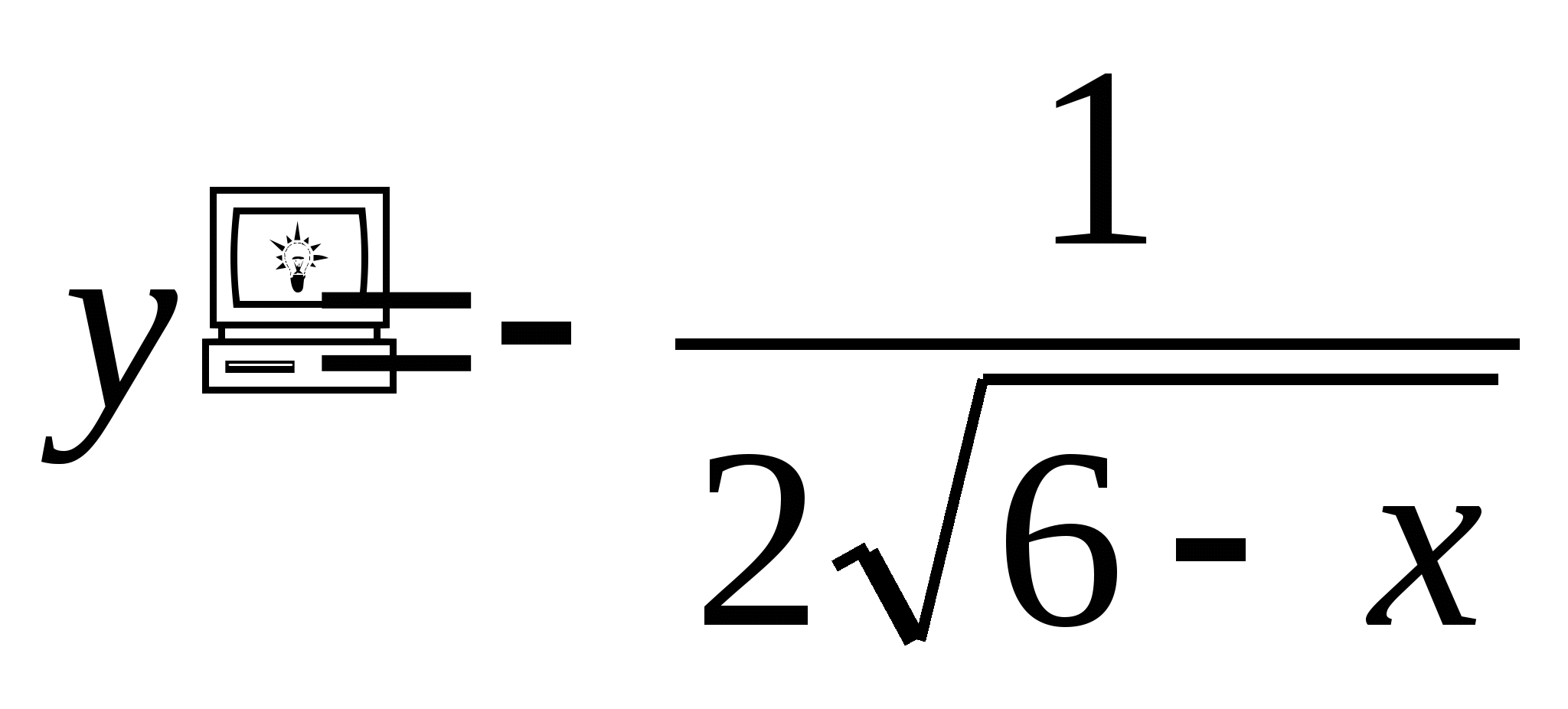
y′(x)=6x⁵-6x

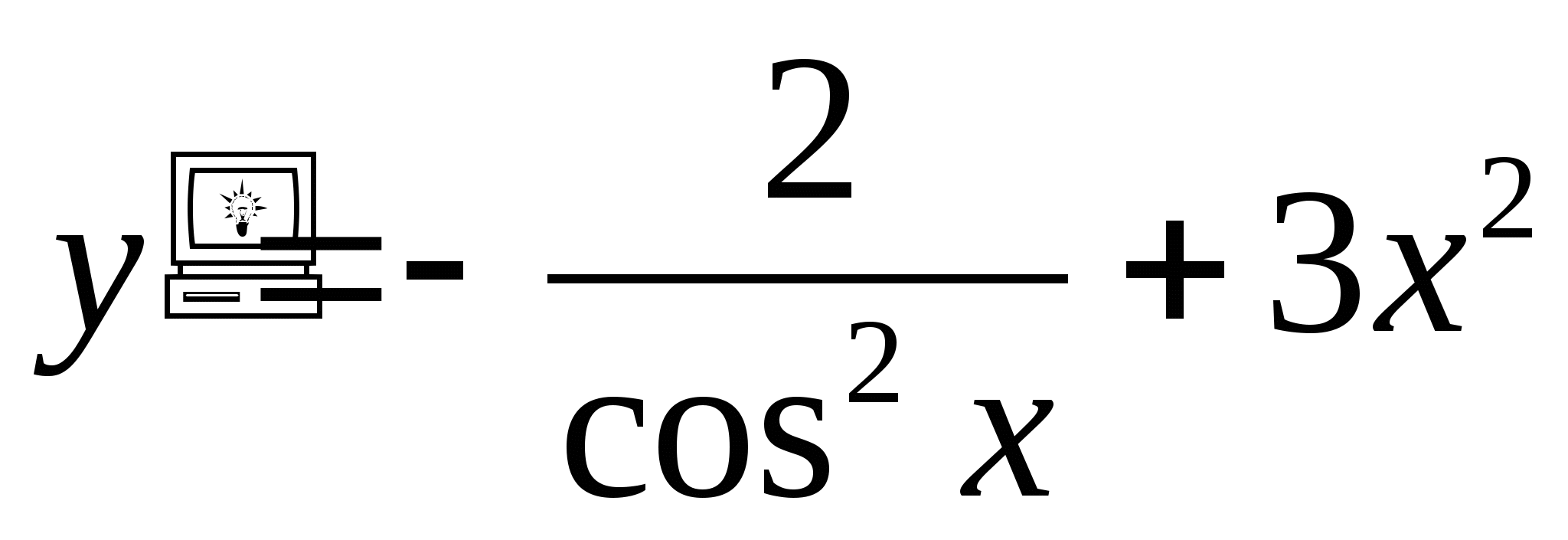
y′(x)=3cos3x-5sin5x

y′(x)=30(6x-9.5)⁴

Неправильные ответы.

y′(x)=7(0.4x+25)⁷

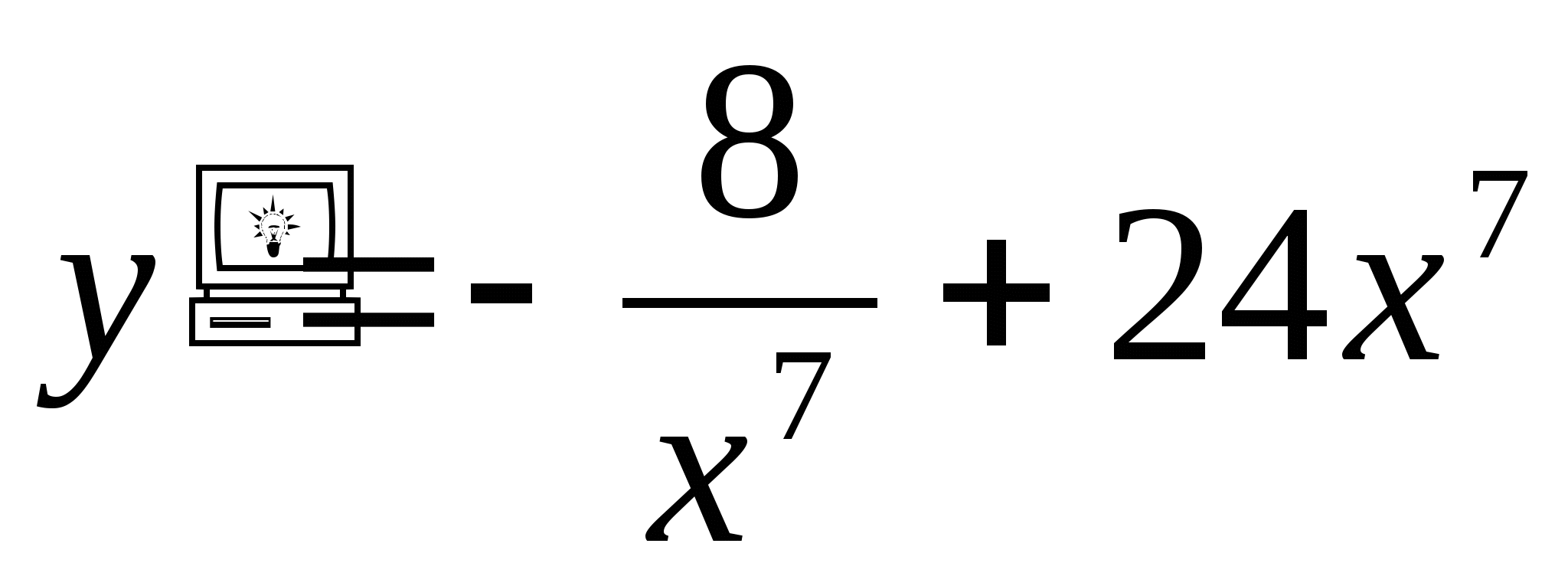
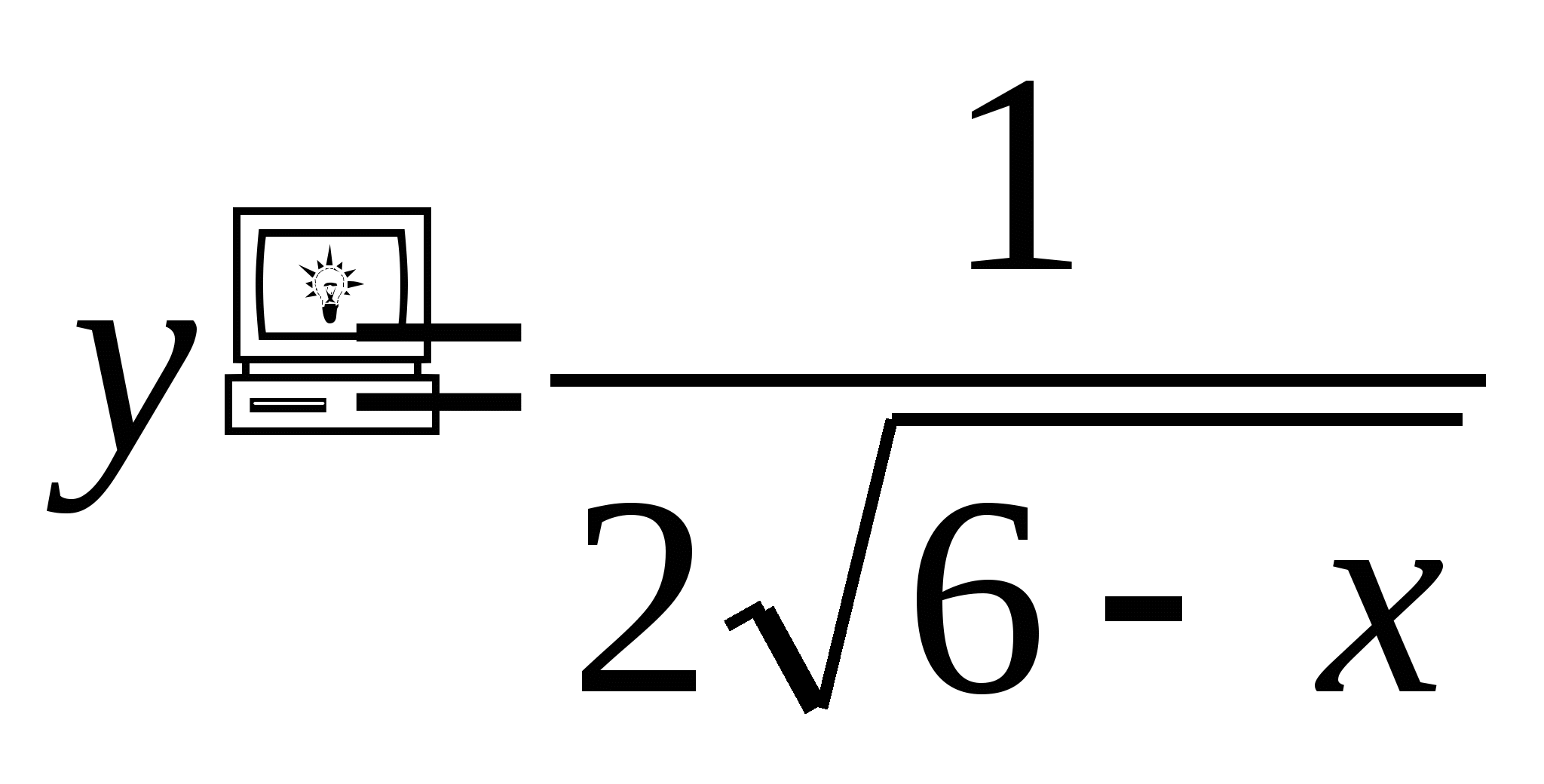
y′(x)=5x⁴-3

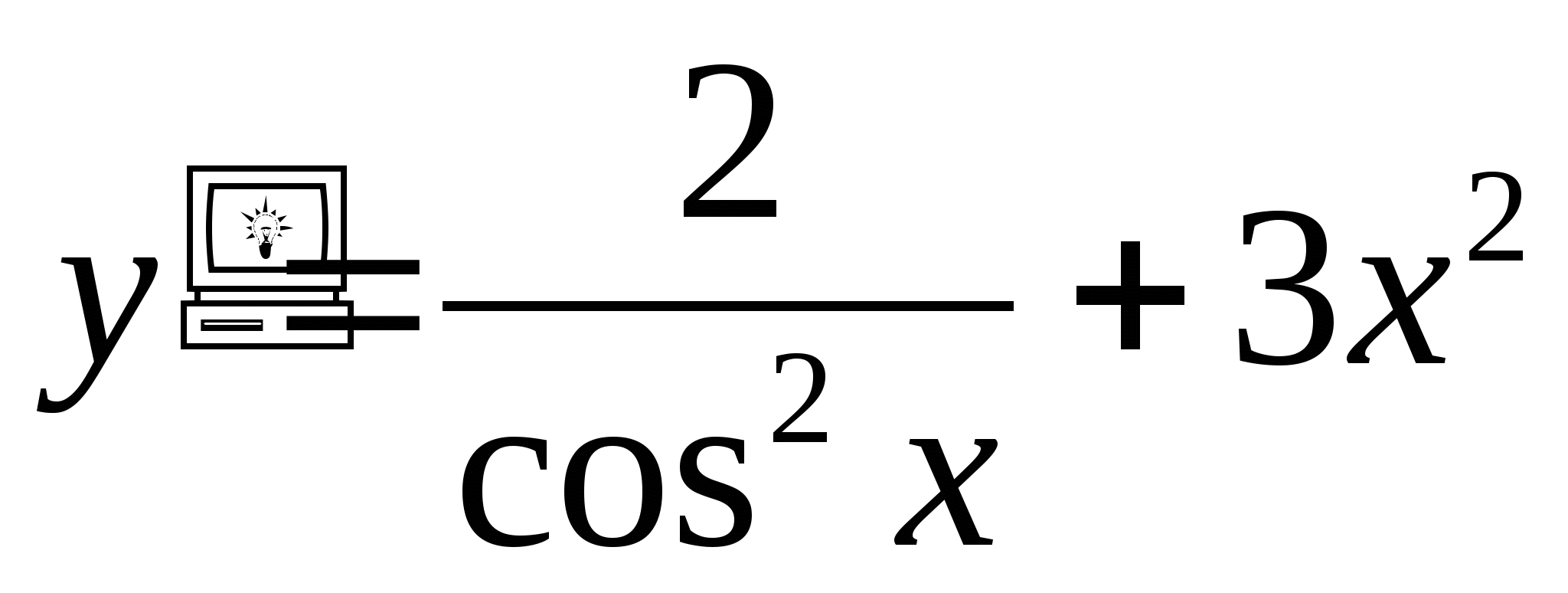
y′(x)=cos3x-sin5x

y′(x)=5(6x-9.5)²

Обратная сторона карточек.

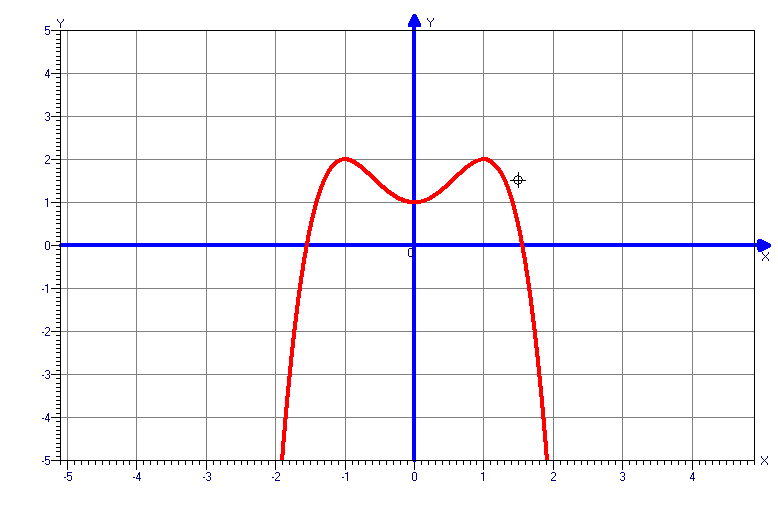
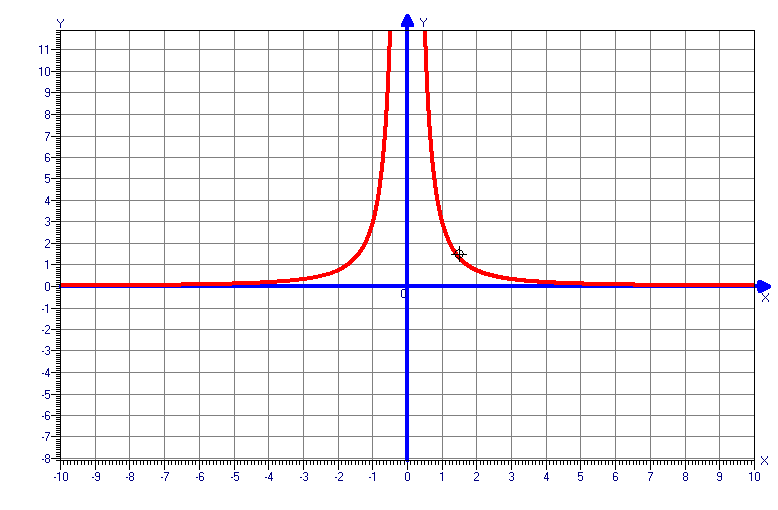
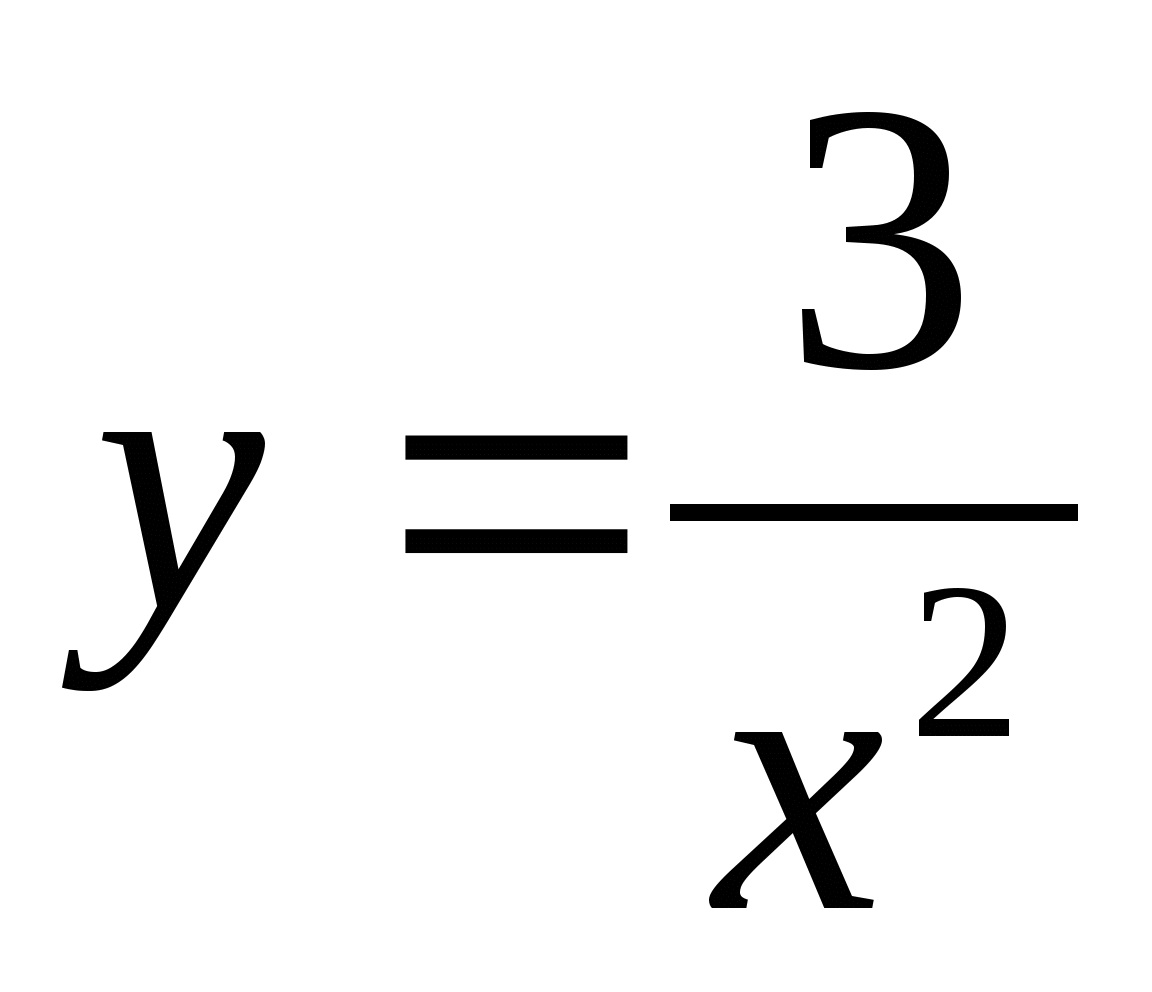
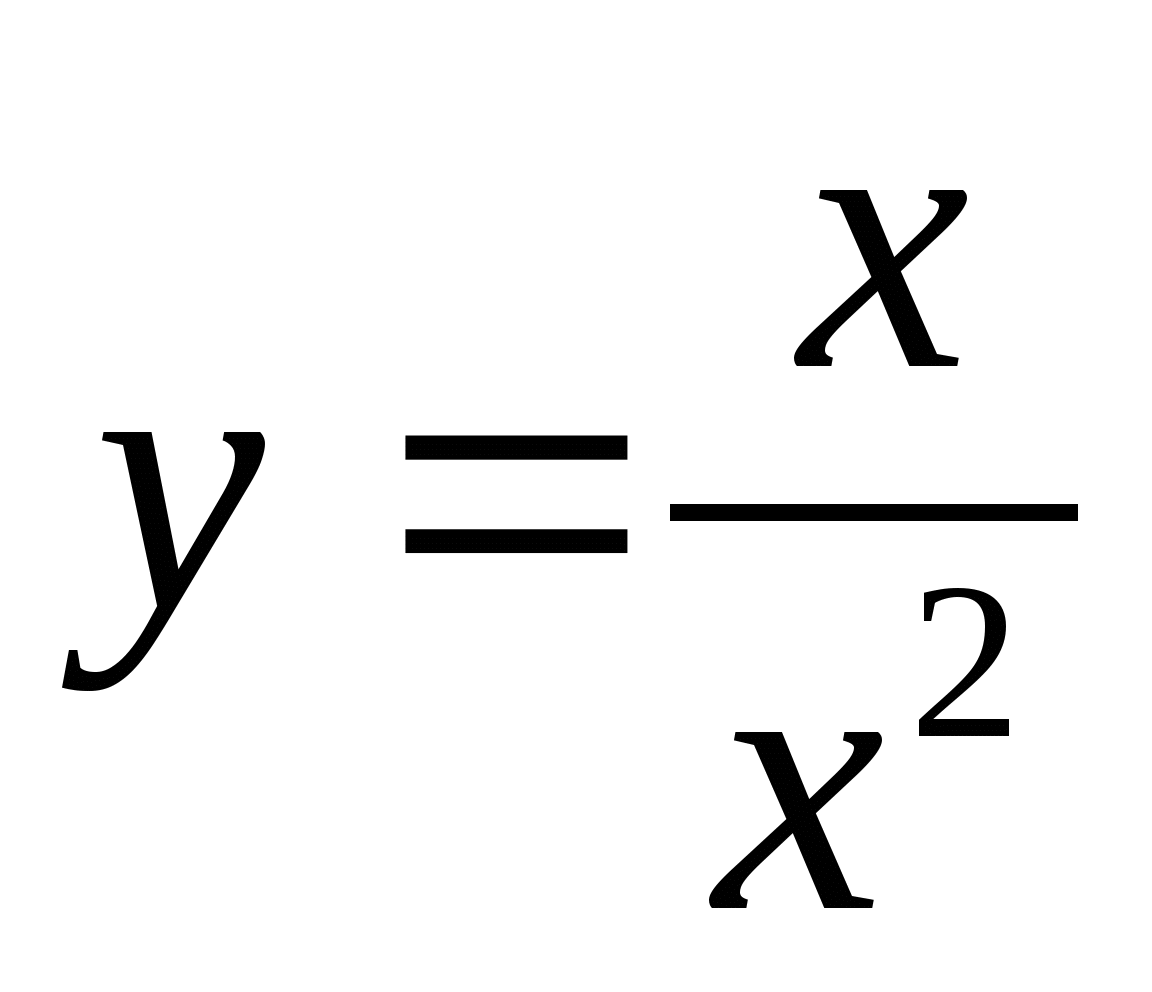
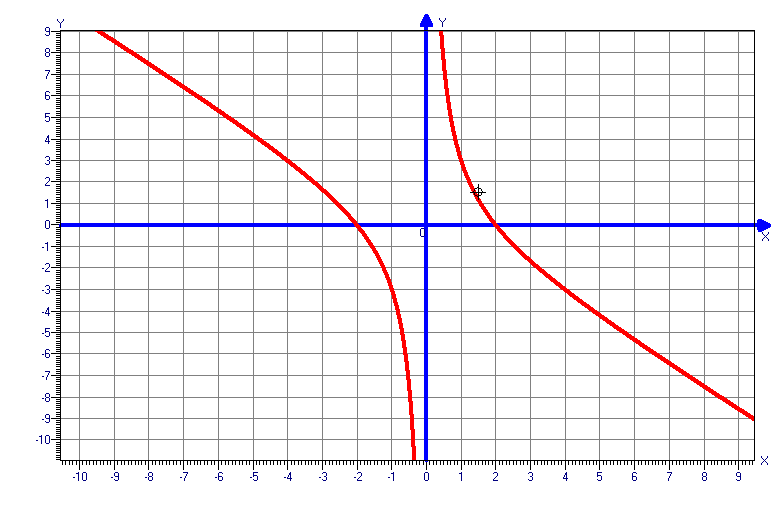
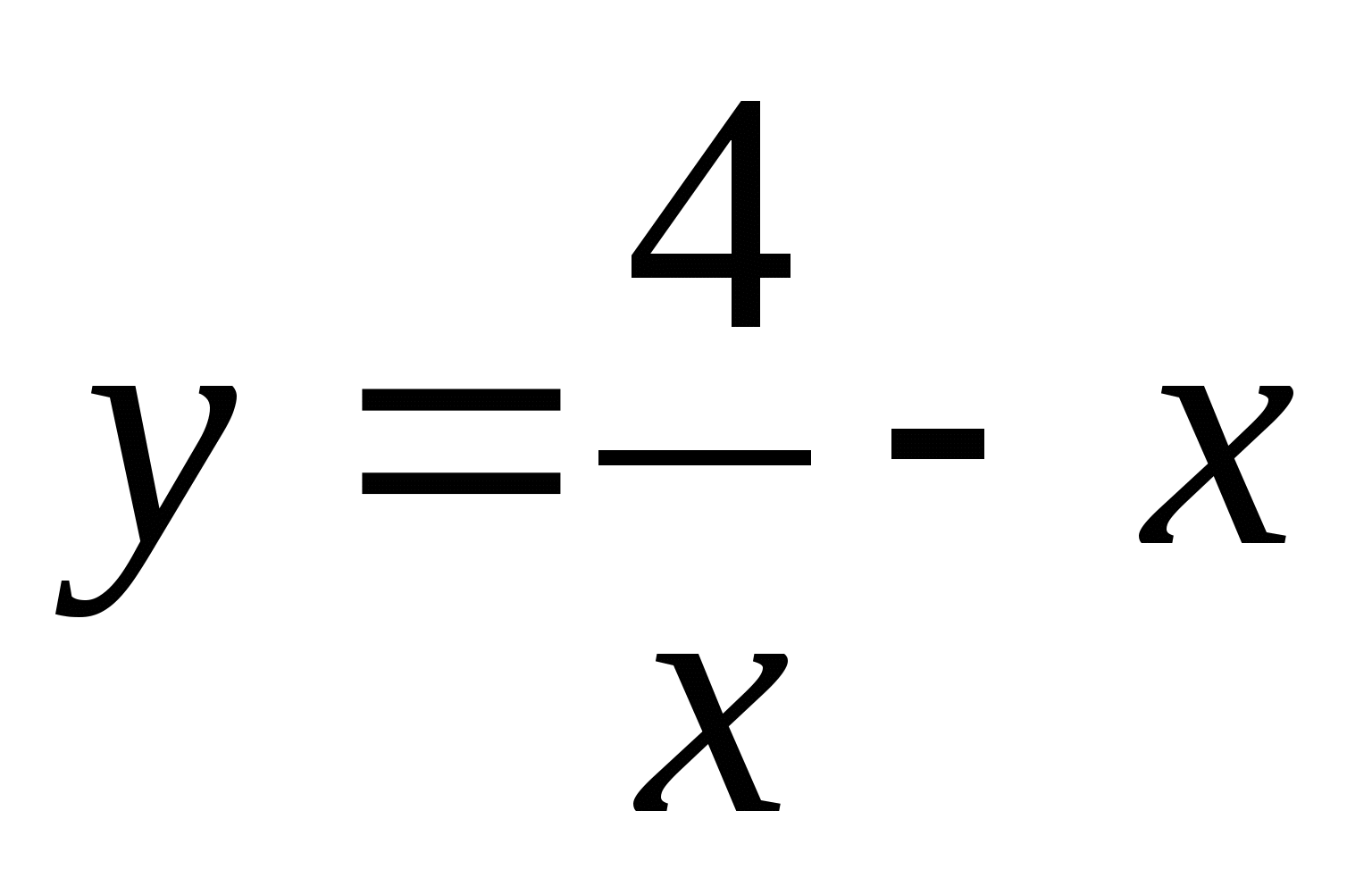
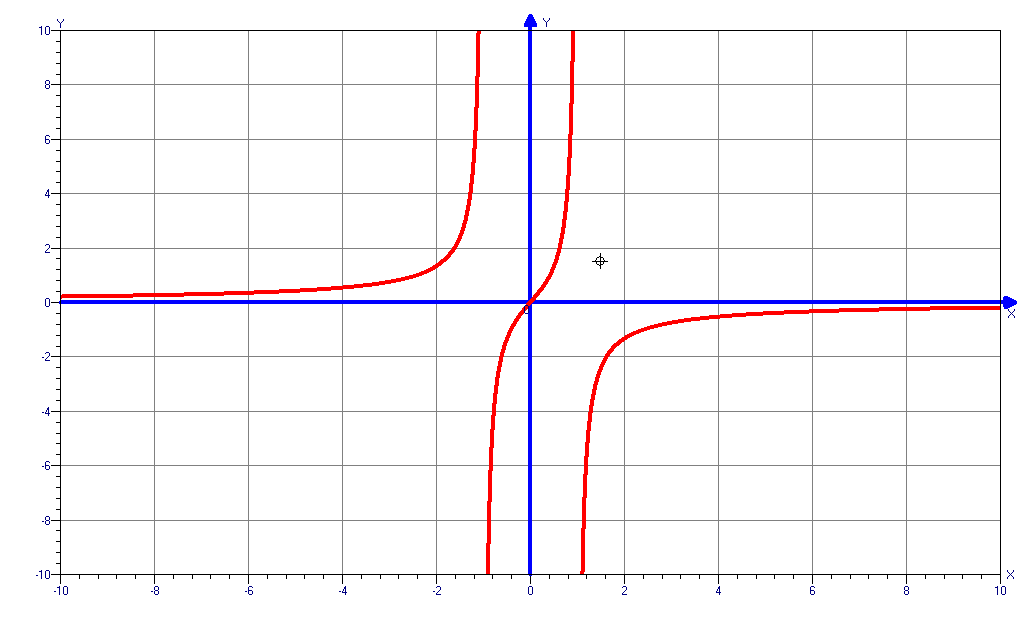
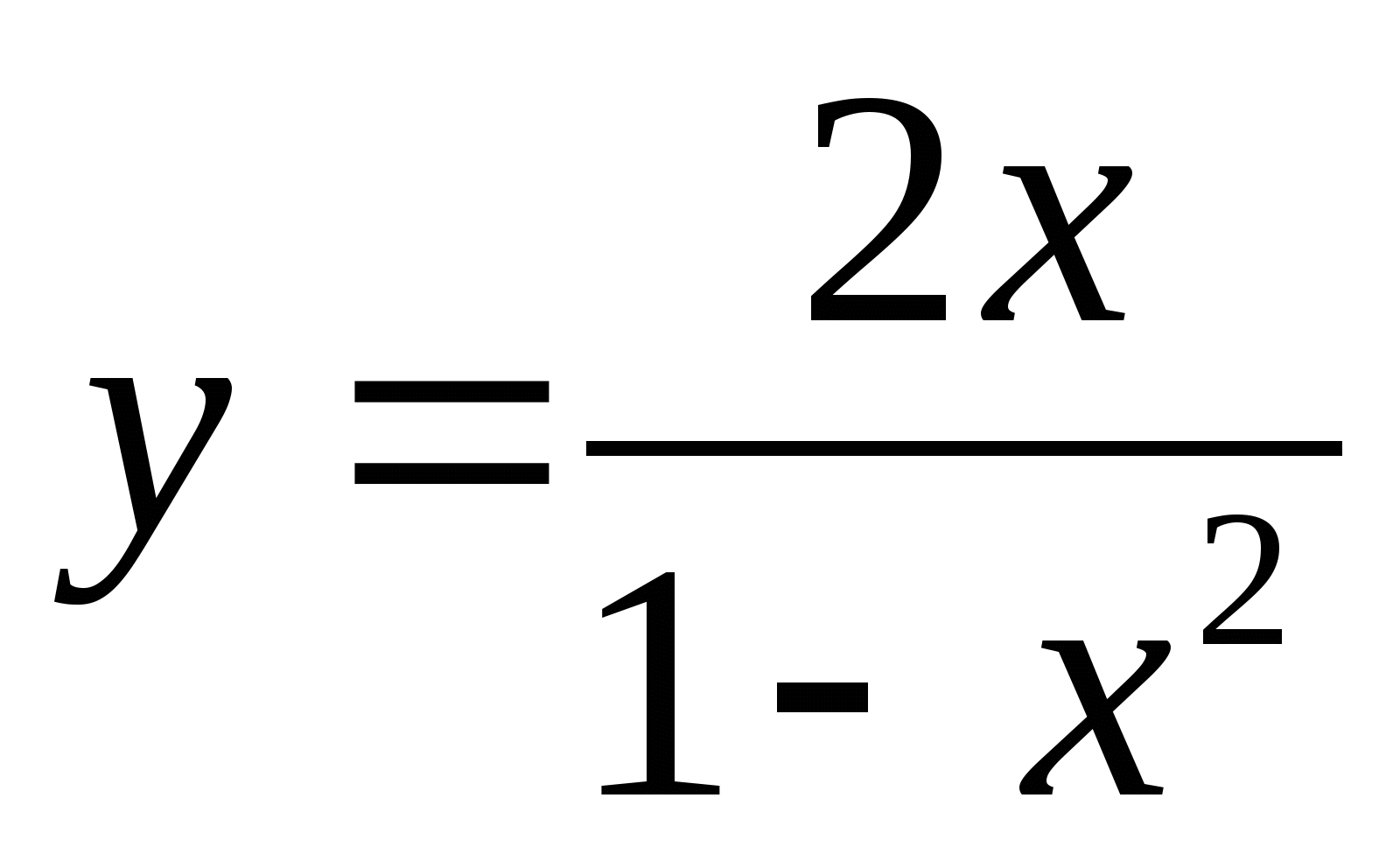
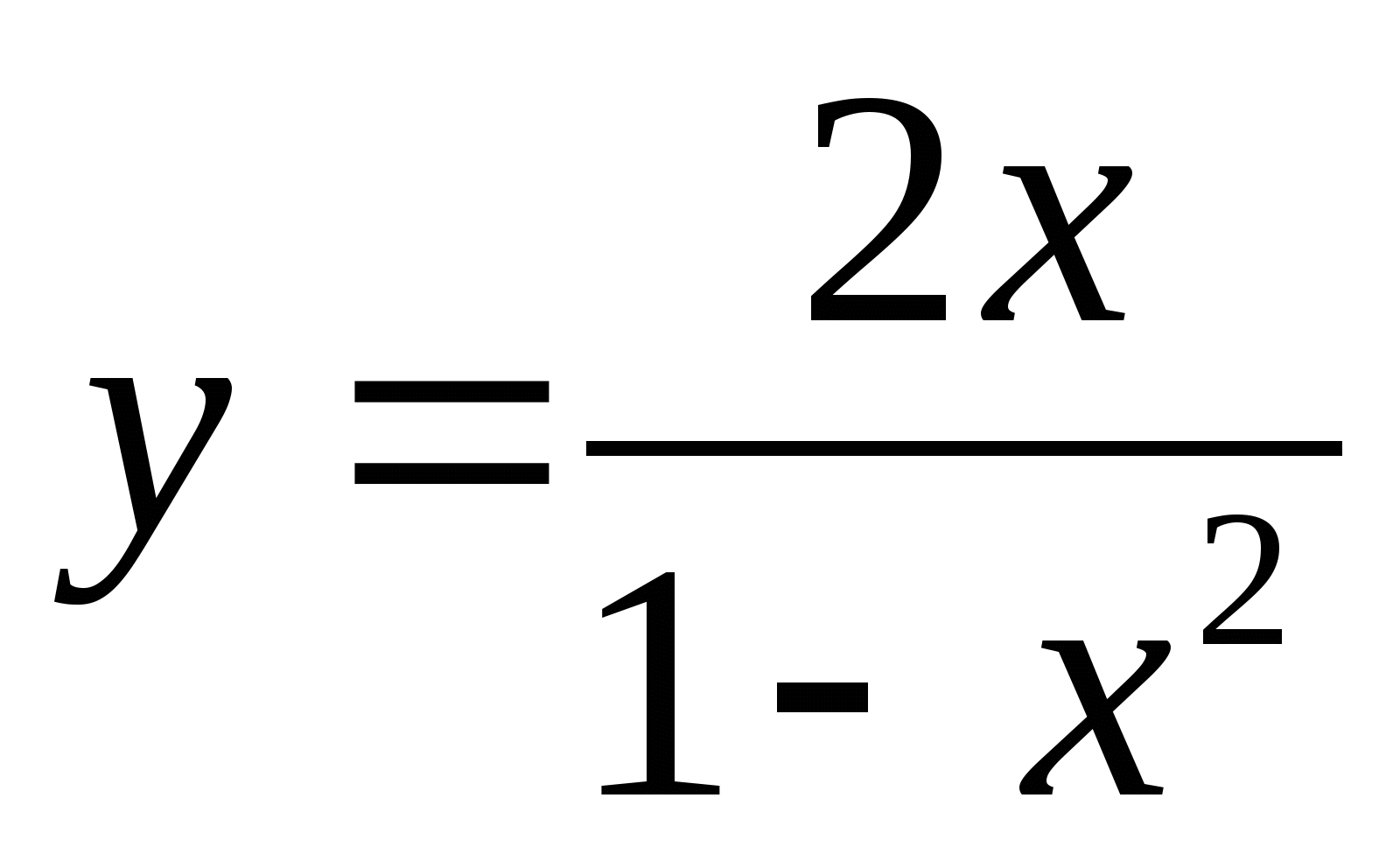
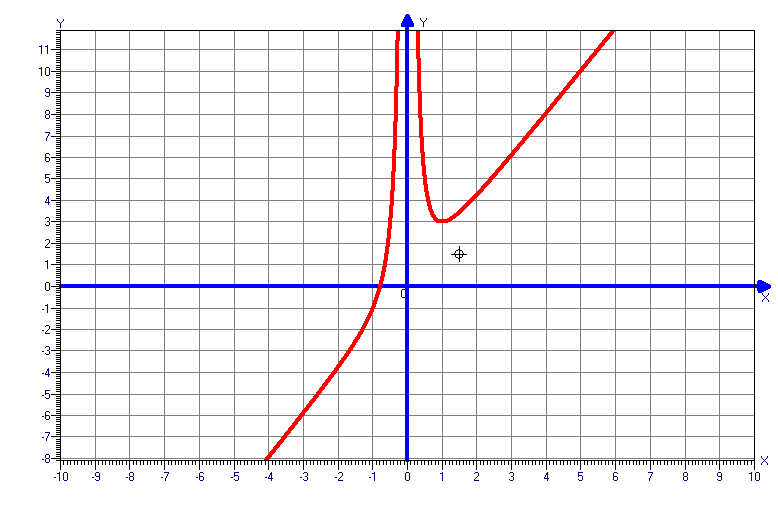
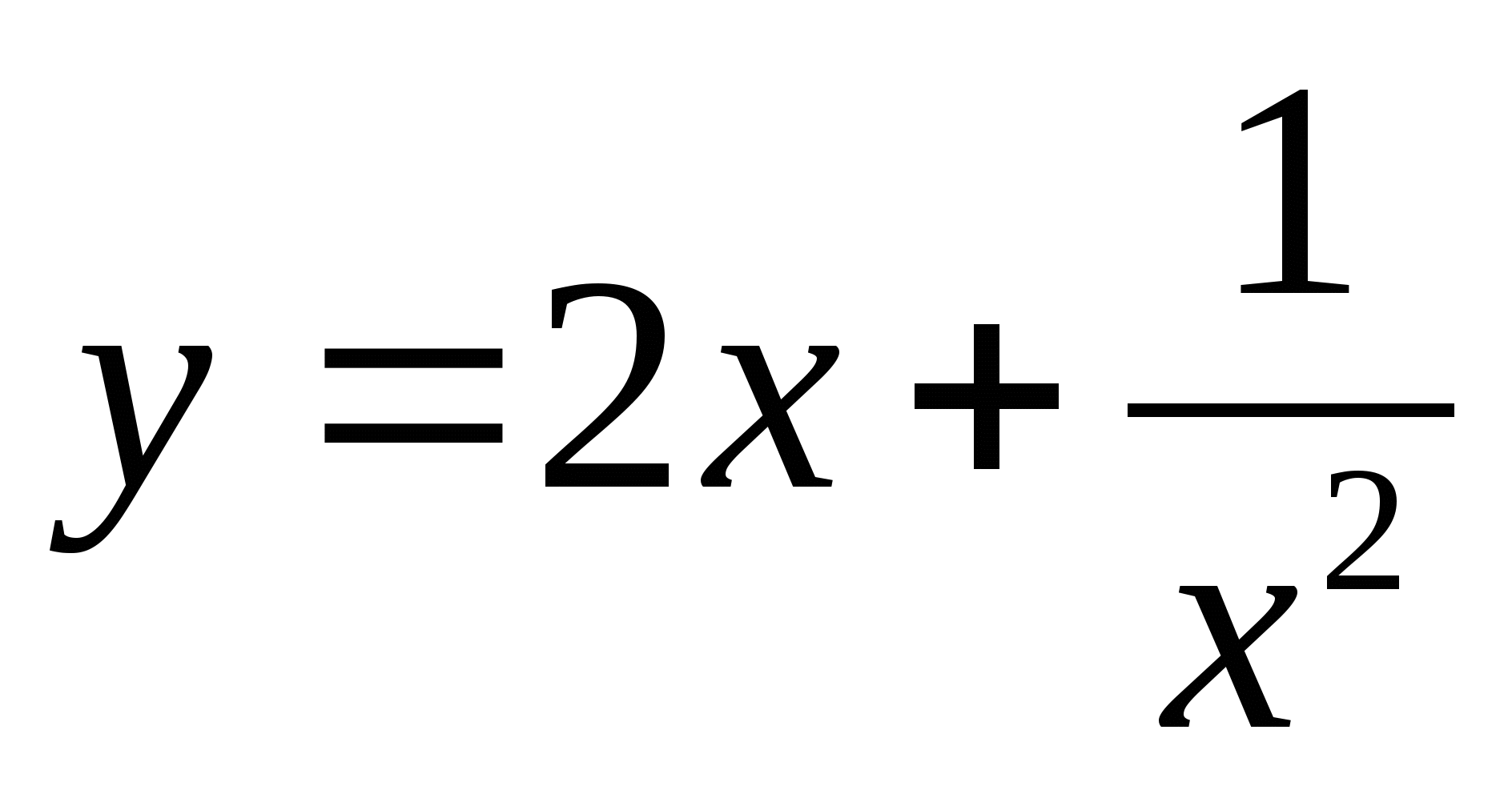
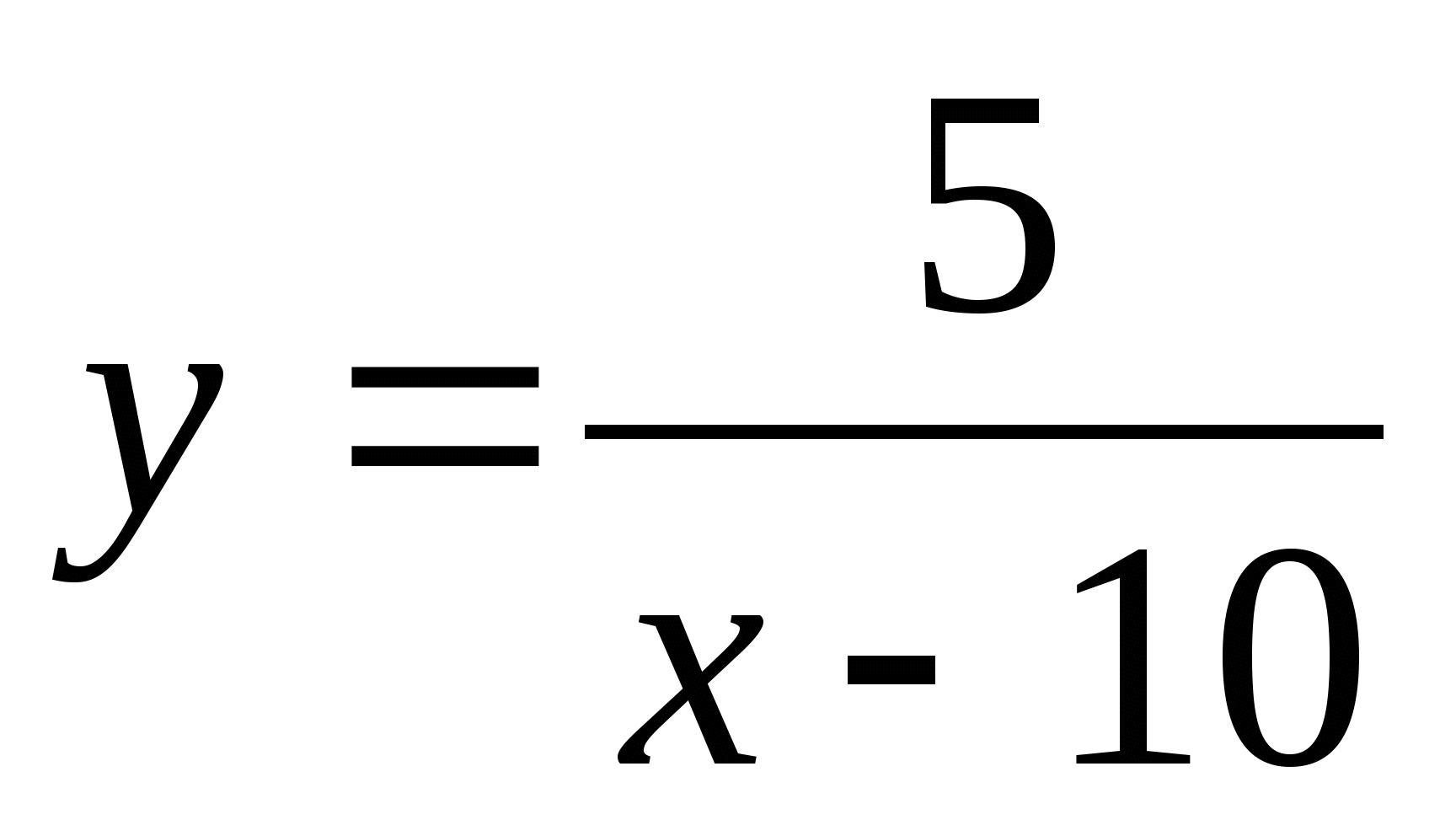
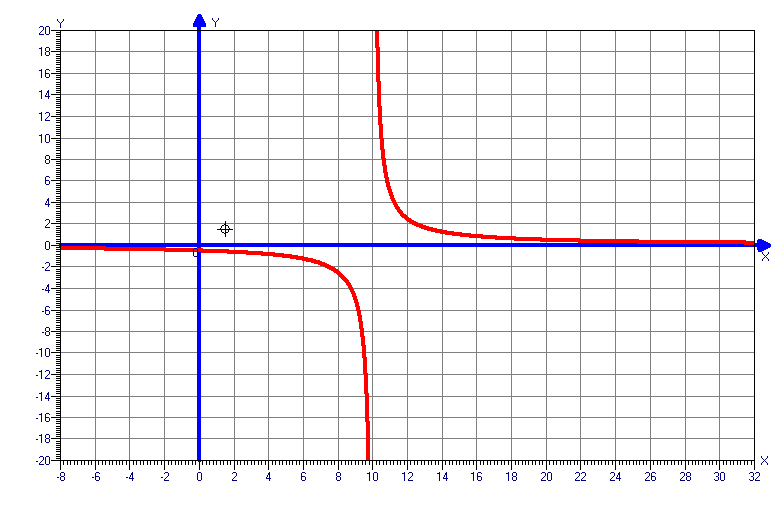
5. Необходимо каждой группе самостоятельно исследовать и построить график функции.

«Примеры учат больше, чем теория».

М.В. Ломоносов

При оценки учитывается скорость, самостоятельность и правильность выполнения.

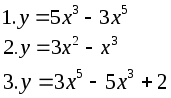
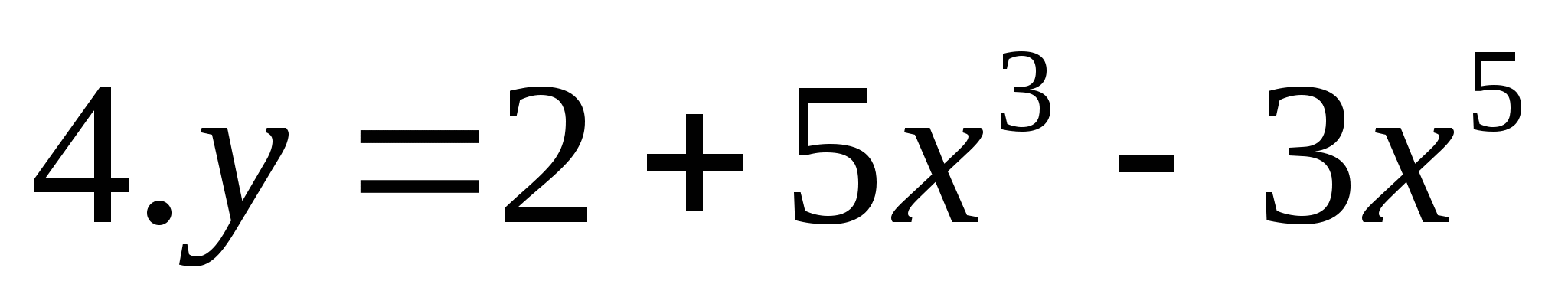
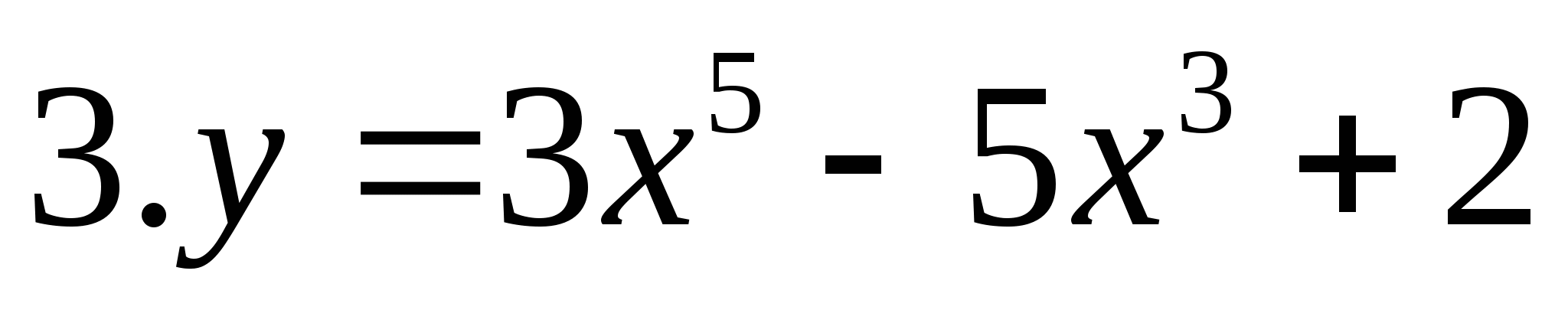
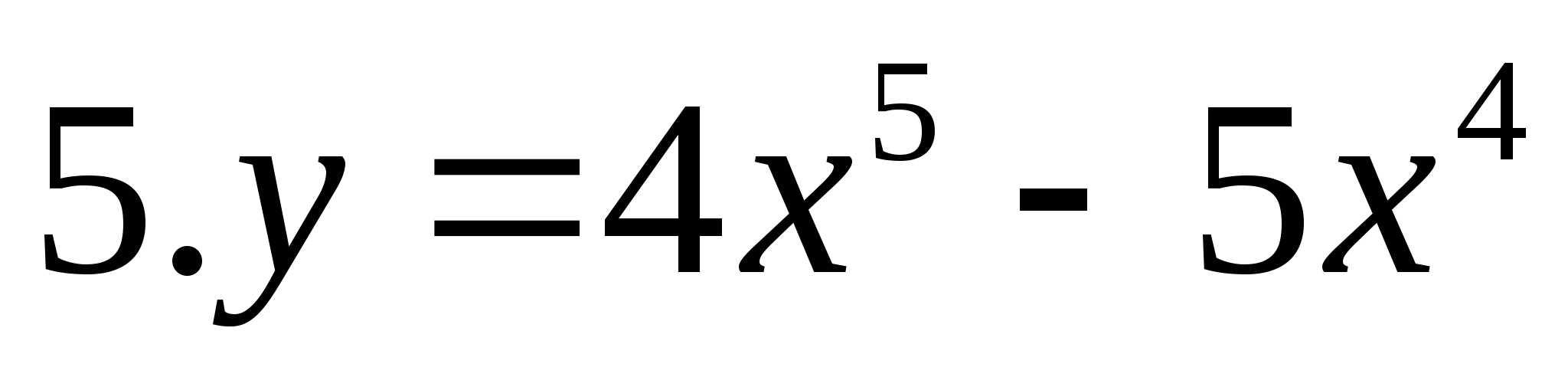
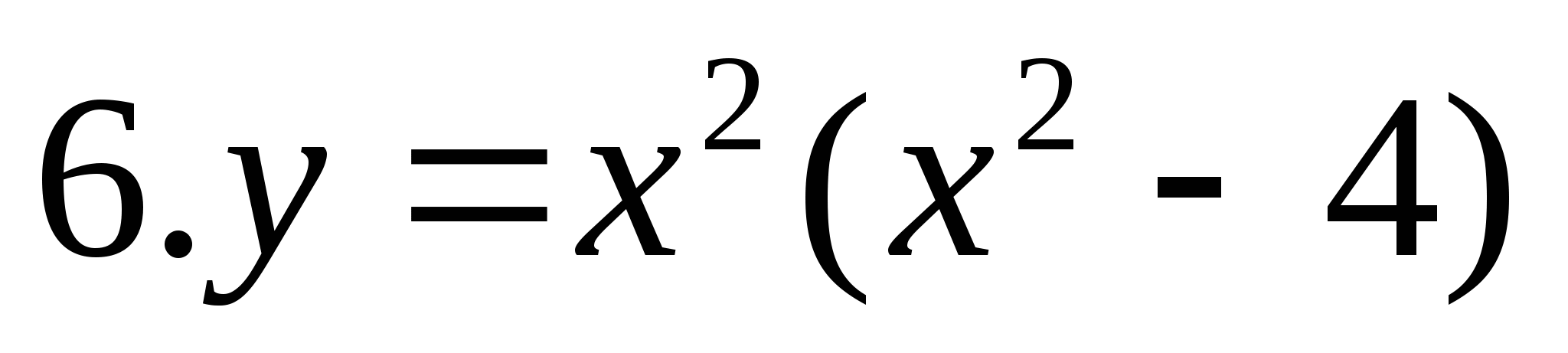
y=5x³-3x⁵

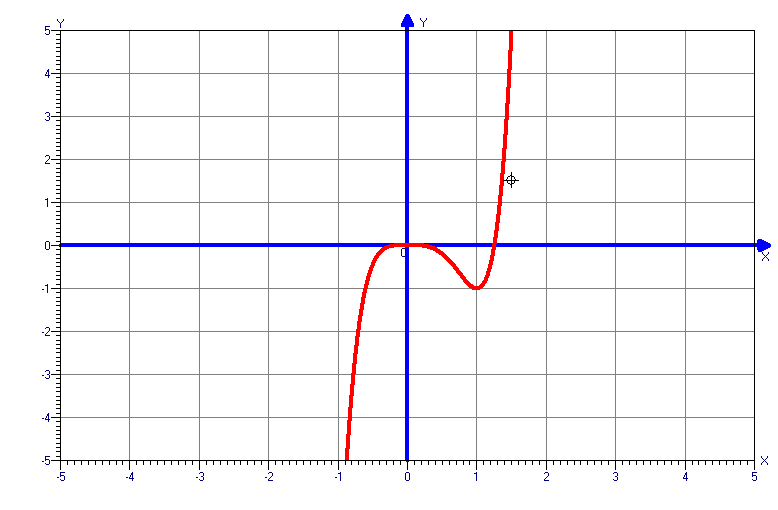
y=3x²-x³

y=3x⁵-5x³+2

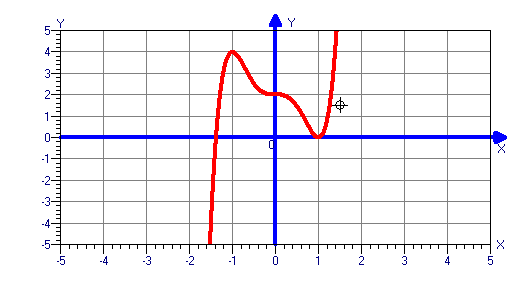
y=2+5x³-3x⁵

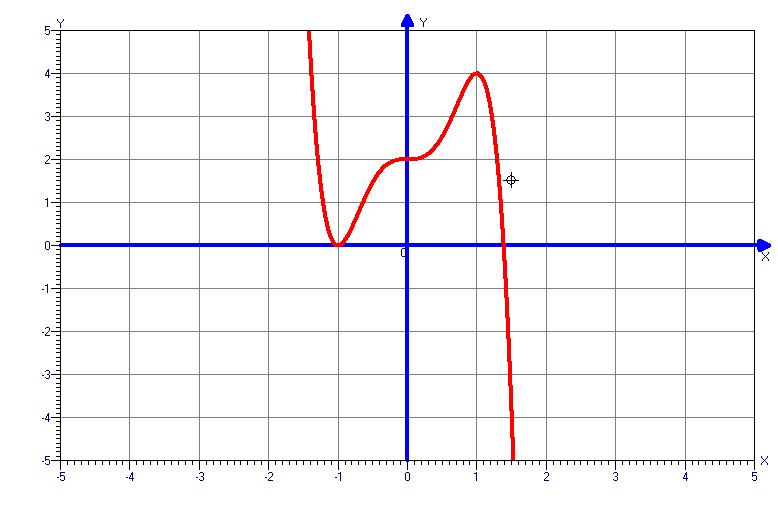
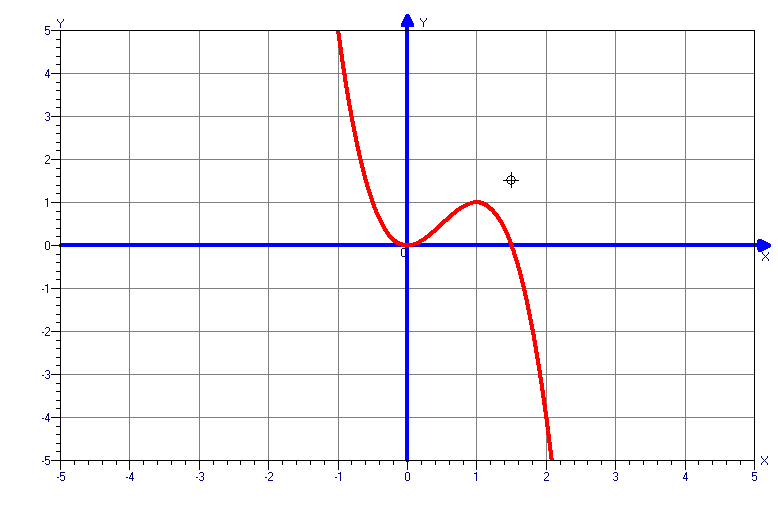
y=x²(x²-4)

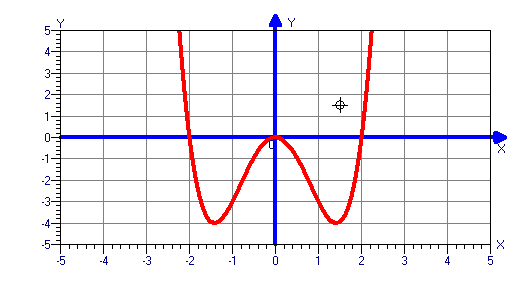
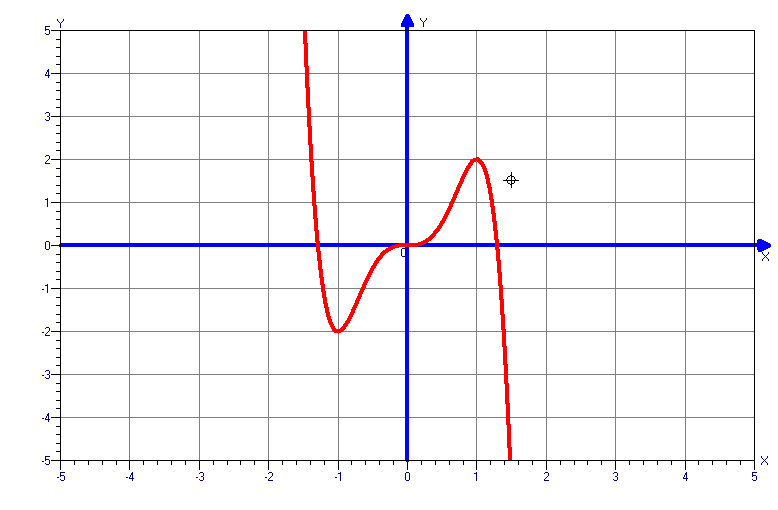
y=4x⁵-5x⁴

6. Психологическая разгрузка. Учащиеся внимательно смотрят на экран и водят по часовой стрелке за появляющимися фигурами.

7. Проверочная работа - тест.

Проверочный тест.1

Дано: f(x) = (1 + 2x)(2x -1). Найдите (0,5)

A) -4

B) 3

C) 0

D) 4

E) 2

1

Найдите производную функции

f(x) = (3 + 4x)(4x - 3)

A) 16x

B) 32x

C) 8x²

D) 16

E) 32x²

2

Дана функция f(x) = . Найдите

A) 5

B) -3

C) 1

D) 6

E) 0

2

Дана функция: f(x) = 2x² + 20. Найдите:

A)

B)

C)

D)

E)

3

Найдите производную функции

f(x) =

A)

B) 0

C)

D)

E)

3

Дана функция f(x) = 4sin3x.

Найдите (x).

A) 6cos3x

B) -4cos3x

C) 12cosx

D) -4cosx

E) 12cos3x

4

Для функции Y = определите:

а) нули;

б) промежутки возрастания;

в) промежутки убывания

A) а) -4; 0; б) (-; -4), (0; ); в) нет

B) а) -4; 4; б) (-; 0), (0; ); в) нет

C) а) -4; 0; 4; б) [-4; 0], [4; ); в) (-; -4], [0; 4]

D) а) -4; 4; б) (-; ); в) нет

E) а) -4; 4; б) (-; -4], [4; ); в) [-4; 4]

4

Найдите точки максимума и минимума функции

у = х³ + 6х² - 15х - 3

A) x = -5 точка max; x = 1 точка min

B) x = 5 точка max; x = -1 точка min

C) x = 5 точка max; x = -5 точка min

D) x = 1 точка max; x = -5 точка min

E) x = -1 точка max; x = -5 точка min

5

Найдите производную функции f(x) = (2х - 6)⁸

A) -7(2x - 6)⁷

B) 16(2x - 6)⁷

C) -7(2x + 6)⁷

D) 4(2x - 6)⁷

E) 8(2x - 6)⁷

5

Дано f(x) = (5 + 6x)¹⁰. Найдите (-1)

A) -10

B) 10

C) -60

D) 6

E) 60

Ответы:

Вариант 1 Вариант 2

1 - С 1 - B

2 - A 2 - D

3 - E 3 - E

4 - D 4 - A

5 - B 5 - C

5 баллов - «5»

4 балла - «4»

З балла - «3»

0-2 балла - «2».

8. Итоги урока. Заслушиваются оценки учеников.

Рефлексия.

Как вы считаете, кто из вас работал в полную силу своих возможностей, чувствовал себя уверенно?

А кто из вас работал хорошо, но не полную силу, испытывал чувство неуверенности, боязни, что отвечу неправильно?

А у кого из вас не было желания работать, то есть сегодня не ваш день?

Я хочу вам пожелать, чтобы у вас была только положительная производная, чтобы знания ваши только возрастали. Спасибо за урок.

9. Домашнее задание: стр.155, №346( а, в, д, ж), №348(б, г)

12