Теорема Чевы и Менелая

ТЕОРЕМЫ ЧЕВЫ И МЕНЕЛАЯ

Теорема Чевы

Большинство замечательных точек треугольника могут быть по­лучены при помощи следующей процедуры. Пусть имеется некоторое правило, согласно которому мы сможем выбрать определенную точку A₁, на стороне BC (или её про­должении) треугольника ABC (например, выберем середину этой стороны). Затем построим аналогичные точки B₁, C₁ на двух других сторонах треугольника (в нашем примере еще две середи­ны сторон). Если правило выбора удачное, то прямые AA₁, BB₁, CC₁ пересекутся в некоторой точке Z (выбор середин сторон в этом смысле, конечно, удачный, так как медианы треугольника пересекаются в одной точке).

Хотелось бы иметь какой-нибудь общий метод, позво­ляющий по положению точек на сторонах треугольника определять, пересекается ли соответствующая тройка прямых в одной точке или нет.

Универсальное условие, «закрывшее» эту проблему, нашёл в 1678 г. итальянский инженер Джованни Чева.

Определение. Отрезки, соеди­няющие вершины треугольника с точками на противолежащих сторонах (или их продолжениях), называют чевианами, если они пересекаются в одной точке.

Возможны два варианта расположения чевиан. В одном варианте точка

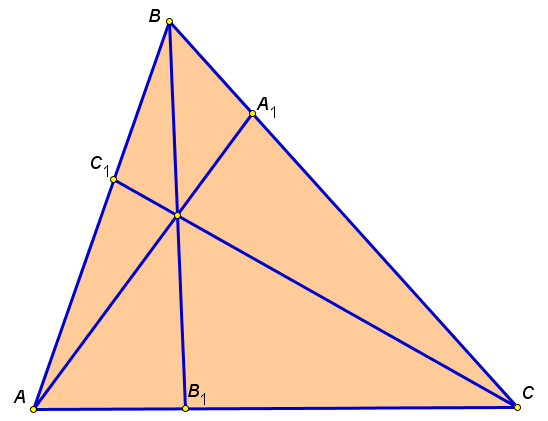
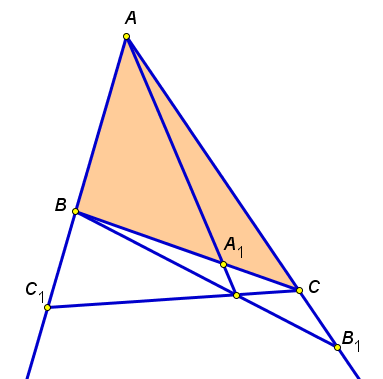
пересечения - внутренняя, а концы чевиан лежат на сторонах треугольника. Во втором варианте точка пересечения внешняя, конец одного чевиана лежит на стороне, а у двух других чевиан концы лежат на продолжениях сторон (смотри чертежи).

Теорема 3. (Прямая теорема Чевы) В произвольном треугольнике АВС на сторонах ВС, СА, АВ или их продолжениях взяты соответственно точки А₁, В₁, С₁, такие, что прямые АА₁, ВВ₁, СС₁ пересекаются в некоторой общей точке, тогда

.

Доказательство: известно несколько оригинальных доказательств теоремы Чевы, мы рассмотрим доказательство, основанное на двукратном применении теоремы Менелая. Запишем соотношение теоремы Менелая первый раз для треугольника ABB₁ и секущей CC₁ (точку пересечения чевиан обозначим Z):

,

а второй раз для треугольника B₁BC и секущей AA₁:

.

Перемножив два этих отношения, проведя необходимые сокращения получим соотношение, содержащееся в утверждении теоремы.

Теорема 4. (Обратная теорема Чевы). Если для выбранных на сторонах треугольника ABC или их продолжениях точек A₁, В₁ и C₁ выполняется условие Чевы:

,

то прямые AA₁, BB₁ и CC₁ пересекаются в одной точке.

Доказательство этой теоремы проводится методом от противного, также, как доказательство теоремы Менелая.

Рассмотрим примеры применения прямой и обратной теорем Чевы.

Пример 3. Докажите, что медианы треугольника пересекаются в одной точке.

Решение. Рассмотрим соотношение

для вершин треугольника и середин его сторон. Очевидно, что в каждой дроби в числителе и знаменателе стоят равные отрезки, поэтому все эти дроби равны единице. Следовательно, выполнено соотношение Чевы, поэтому, по обратной теореме, медианы пересекаются в одной точке.

Теорема (теорема Чевы). Пусть точки лежат на сторонах и треугольника соответственно. Пусть отрезки и пересекаются в одной точке. Тогда

(обходим треугольник по часовой стрелке).

Доказательство. Обозначим через точку пересечения отрезков и . Опустим из точек и перпендикуляры на прямую до пересечения с ней в точках и соответственно (см. рисунок).

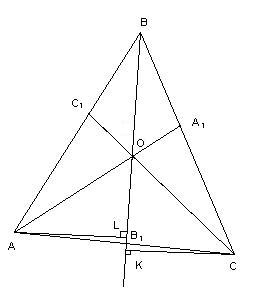
Поскольку треугольники и имеют общую сторону , то их площади относятся как высоты, проведенные на эту сторону, т.е. и :

Последнее равенство справедливо, так как прямоугольные треугольники и подобны по острому углу.

Аналогично получаем

и

Перемножим эти три равенства:

что и требовалось доказать.

Про медианы:



1. Разместим в вершинах треугольника ABC единичные массы.

2. Центр масс точек A и B находится посередине AB. Центр масс всей системы должен находиться на медиане к стороне AB, так как центр масс треугольника ABC - это центр масса центра масс точек A и B, и точки C.

(запутанно получилось)

3. Аналогично - ЦМ должен лежать на медиане к сторонам AC и BC

4. Так как ЦМ - единственная точка, то, следовательно все эти три медианы должны пересекаться в ней.



Кстати, сразу же следует, что пересечением они делятся в отношении 2:1. Так как масса центра масс точек A и B равна 2, а масса точки C равна 1, следовательно, общий центр масс согласно теореме о пропорции будет делить медиану в отношении 2/1.

Спасибо большое, доступно изложено, думаю, будет не лишним представить док-во и при помощи методов геометрии масс, например:

Прямые AA1 и CC1 пересекаются в точке O; AC1 : C1B = p и BA1 : A1C = q. Нужно доказать, что прямая BB1 проходит через точку O тогда и только тогда, когда CB1 : B1A = 1 : pq.

Поместим в точки A, B и C массы 1, p и pq соответственно. Тогда точка C1 является центром масс точек A и B, а точка A1 - центром масс точек B и C. Поэтому центр масс точек A, B и C с данными массами является точкой O пересечения прямых CC1 и AA1. С другой стороны, точка O лежит на отрезке, соединяющем точку B с центром масс точек A и C. Если B1 - центр масс точек A и C с массами 1 и pq, то AB1 : B1C = pq : 1. Остается заметить, что на отрезке AC существует единственная точка, делящая его в данном отношении AB1 : B1C.

2. Теорема Чевы

Отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне, называется чевианой. Таким образом, если в треугольнике ABC X, Y и Z - точки, лежащие на сторонах BC, CA, AB соответственно, то отрезки AX, BY, CZ являются чевианами. Этот термин происходит от имени итальянского математика Джованни Чевы, который в 1678 году опубликовал следующую очень полезную теорему:

Теорема 1.21. Если три чевианы AX, BY, CZ (по одной из каждой вершины) треугольника ABC конкурентны, то

|BX| |XC| · |CY| |YA| · |AZ| |ZB| =1 .

Когда мы говорим, что три прямые (или отрезка) конкурентны, то мы имеем в виду, что все они проходят через одну точку, которую обозначим через P. Для доказательства теоремы Чевы вспомним, что площади треугольников с равными высотами пропорциональны основаниям треугольников. Ссылаясь на рисунок 3, мы имеем:

|BX| |XC| = SABX SAXC = SPBX SPXC = SABX− SPBX SAXC− SPXC = SABP SCAP .

Аналогично,

|CY| |YA| = SBCP SABP , |AZ| |ZB| = SCAP SBCP .

Теперь, если мы перемножим их, то получим

|BX| |XC| · |CY| |YA| · |AZ| |ZB| = SABP SCAP · SBCP SABP · SCAP SBCP =1 .

Теорема, обратная к этой теореме, также верна:

Теорема 1.22. Если три чевианы AX, BY, CZ удовлетворяют соотношению

|BX| |XC| · |CY| |YA| · |AZ| |ZB| =1 ,

то они конкурентны.

Чтобы это показать, предположим, что две первые чевианы пересекаются в точке P, как и прежде, а третья чевиана, проходящая через точку P, будет CZ′. Тогда, по теореме 1.21,

|BX| |XC| · |CY| |YA| · |AZ′| |Z′B| =1 .

Но по предположению

|BX| |XC| · |CY| |YA| · |AZ| |ZB| =1 .

Следовательно,

|AZ| |ZB| = |AZ′| |Z′B| ,

точка Z′ совпадает с точкой Z, и мы доказали, что отрезки AX, BY и CZ конкурентны ([13], стр. 54 и [42], стр, 48, 317).

</