- Учителю
- Преобразование выражений, содержащих квадратные корни
Преобразование выражений, содержащих квадратные корни
Конспект урока по теме:
"ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ, СОДЕРЖАЩИХ КВАДРАТНЫЕ КОРНИ"
ФИО (полностью)
Николаева Лариса Петровна
Место работы
МАОУ средняя общеобразовательная школа №85
Должность
учитель математики
Предмет
алгебра
Класс
8
Базовый учебник Алгебра 8. / А.Г.Мордкович. / М.: Мнемозина, 2009.
Пояснительная записка.
Важным моментом в подготовке к итоговой аттестации является правильная организация обобщающего контроля. Большинство ошибок, связано с формальным и поверхностным усвоением учащимися изучаемого материала. Чтобы такого не случалось, я учу своих учеников проводить при рассмотрении любой темы самоконтроль полученных знаний и умений.
Для этого в начале изучения темы даю список основных типов заданий, которые будут изучаться по данной теме, а затем обязательно провожу урок актуализации, обобщения и контроля знаний, умений и навыков. После обобщающего урока каждый учащийся заполняет карточку самооценки. Такие уроки нужны для того, чтобы каждый ученик мог оценить уровень своих знаний на фоне одноклассников, почувствовать необходимость к усовершенствованию, и не выполнив требования учителя однажды, стремился выполнять их в следующий раз. Предлагаю конспект одного из таких уроков в 8-ом классе по теме: «Преобразование выражений, содержащих квадратные корни». Здесь в игровой форме обобщаются и контролируются знания учащихся, и сразу будут выявляются пробелы по всей теме, которые ликвидируются на следующем уроке и во внеурочное время, лично каждым учеником, который осознал свои ошибки и недоработки.
Цели урока:
-
Систематизация, обобщение и расширение знаний о квадратных корнях. Выявление у учащихся пробелов в изучении данной темы.
-
Развитие у учащихся вычислительных навыков, логического мышления, различных видов памяти.
-
Воспитание в детях сознательного отношения к учебе, чувства взаимной поддержки, заинтересованности математикой.
План урока:
-
Организационный момент.
-
Проверка реакции участников розыска (устный счет).
-
Проверка строевой подготовки бригад знатоков (решение задания со взаимопроверкой).
-
Проверка умения проводить экспертизу (решение заданий у доски).
-
Проверка умения работать со словарем правовой терминологии (самостоятельная работа).
-
Проверка логического мышления (дополнительное устное задание).
-
Подведение итогов соревнования за право работать по следу.
-
Работа по следу (решение заданий повышенной сложности).
-
Итог урока (заполнение карточки самооценки).
Ученикам 8 «А» класса
Школы №85
От профессора Игрек-са.
заявление.
15.12. сего года у меня из натурального ряда пропало число: очень ценное и нужное на каждом уроке. Прошу принять меры для розыска этого числа.
С уважением профессор Игрек-с.
P.S. Преступник оставил «след», и его я передаю одной из следственных групп, которая лучше приготовится к розыску.
Ход урока
Учитель сообщает классу о том, что на протяжении времени изучения темы «Арифметический квадратный корень, его свойства» класс готовился к заключительному уроку-игре «Следствие ведут знатоки».
Учащиеся получили список тематических заданий, умение решать которые они должны были довести до автоматизма.
Сегодня в процессе соревнований будет выяснено, какие ещё задания вызывают затруднения, и кто из учащихся подготовился недостаточно.
Учитель зачитывает заявление министра Игрек-са о том, что из ряда натуральных чисел пропало число, и просит следственные бригады, на которые поделён класс (таким образом, что сидящие на первом варианте- это первая бригада, а на втором варианте - вторая бригада) разыскать похищенное число.
Та из команд, которая по результатам соревнований получит большее число баллов, станет обладателем следа - более сложного задания, решив которое, найдёт исчезнувшее число.
Итак, следствие ведут знатоки!
-
Конкурс: «Проверка быстроты реакции»:
На доске вывешены две таблицы.

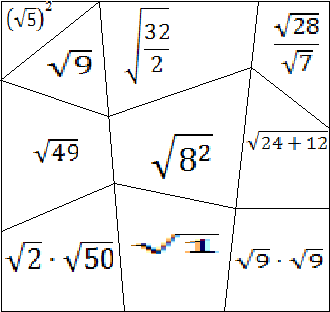
От каждой команды приглашаются по три участника. С помощью указки они должны просчитать по таблице до десяти. Та тройка, которая закончит счёт быстрее получит 5 баллов, другая - 4 балла. Команды следят за тем, чтобы те, кто считает по таблице, не ошибались и называли все числа правильно.
-
Конкурс: «Смотр строевой подготовки следственных бригад».
С помощью проектора на экран проецируется ряд чисел. Нужно расположить их первому варианту(а) в порядке возрастания, второму варианту(б) в порядке убывания:
а) ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
б) ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;![]() ;
; ![]() .
.
Учитель вместе с детьми повторяет правила сравнения выражений, содержащих квадратные корни.
В результате работы с рядом чисел учащиеся должны внести число, стоящее перед знаком арифметического квадратного корня под корень и получить следующее решение:
а) б)
![]()
![]()
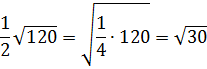
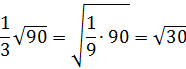
![]()
![]()
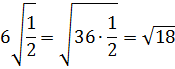
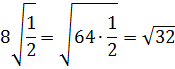
Ответ:
Ответ:
![]() ;
;![]() ;
; ![]() ;
;![]() ;
;![]() .
.
![]() ;
;![]() ;
; ![]() ;
;![]() ;
;![]() .
.
![]() ;
;![]() ;
; ![]() ;
;![]() ;
;![]() .
.
![]() ;
;![]() ;
; ![]() ;
;![]() ;
;![]() .
.
После выполнения задания учитель с помощью проектора выводит на экран правильные решения. Учащиеся, сидящие за одной партой, обмениваются тетрадями и выставляют оценки за задание друг другу. Без ошибок - 5 баллов, 1 ошибка - 4 балла, 2 ошибки - 3 балла, 3 ошибки - 2 балла, более трёх ошибок - 1 балл. Затем быстро учащиеся поднимают заготовленную табличку с количеством баллов. Учитель суммирует и записывает в графу каждой команды.
3.Конкурс: «Умение проводить экспертизу».
1 Вариант:
Проверить, является ли число (4 + ![]() корнем уравнения х2 - 8х + 13 = 0.
корнем уравнения х2 - 8х + 13 = 0.
Решение:
( 4 + ![]() )2 -
)2 - ![]() + 13 =0;
+ 13 =0;
16 + ![]() + 3 - 8
+ 3 - 8![]() 4 - 8
4 - 8![]() + 13 = 0
+ 13 = 0
0=0.
Ответ: число ![]() является корнем уравнения.
является корнем уравнения.
2 Вариант:
Проверить, является ли число ( 4 - ![]() корнем уравнения х2 - 8х + 13 = 0
корнем уравнения х2 - 8х + 13 = 0
Решение:
(4- ![]() )2 -
)2 - ![]() + 13 =0;
+ 13 =0;
16 - ![]() + 3 - 32 + 8
+ 3 - 32 + 8![]() + 13 = 0.
+ 13 = 0.
0=0.
Ответ: число (4 - ![]() является корнем уравнения.
является корнем уравнения.
Это задание решается у доски. От каждой команды приглашается для решения один учащийся, который решает уравнение. Весь класс работает в тетрадях и проверяет решение. Оценка учащимся, работающим у доски, идет в зачет команде.
4.Конкурс «Проверка умения работать со словарем правовой терминологии»
Самостоятельная работа (Приложение 1).
На столе у каждого учащегося лежит лист с текстом самостоятельной работы. Всего представлено 4 варианта двух уровней сложности. Если вы решаете самостоятельную работу 1 уровня, то за верное решение всех заданий получаете 4 балла, если вы решаете самостоятельную работу 2 уровня, то за правильно решенную работу получаете 5 баллов. Выполняя самостоятельную работу, участники следственных групп, расшифровывают правовые понятия. Получив ответ в задании №1, вы ищите такой же в 1-ой строке таблицы, и букву, соответствующую этому ответу выписываете. Таким образом, поступаете до конца самостоятельной работы. Решив все задания, вы получаете слово. Если вам не удалось его получить, значит, вы не достаточно усвоили решение предложенных типов заданий, и вам нужно продолжить работу по их изучению. Для команды вы приносите 0 баллов.
После того, как время самостоятельной работы закончилось, учитель подводит итоги работы по вариантам. На экран с помощью проектора выводятся слова, которые учащиеся должны расшифровать, решая задания. Если ученики не до конца справились с самостоятельной работой или сделали ошибки, то дома нужно будет выполнить анализ ошибок, а так же придумать и решить задания подобные нерешенным.
5. Проверка логического мышления.
Задания для устной работы записаны на дополнительной доске. Те учащиеся, которые первыми справятся с самостоятельной работой, думают над данными устными заданиями, а после проверки самостоятельной работы участвуют в обсуждении решения данных задач и получают для своей команды дополнительные баллы.
1.Задание для первой команды.
Что больше - А или В, если
А = ![]()
В = ![]()
Ответ: А![]() В, т.к. А =
В, т.к. А = ![]() ; В =
; В = ![]()
2.Задание для второй команды.
Сколько множителей должно быть в знаменателе дроби, чтобы равенство было верным? 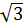 = 1.
= 1.
Ответ: 10 множителей.
Эти задания тоже оцениваются в 5 баллов.
Та из команд, которая после шестого конкурса получает большее количество баллов, побеждает и получает след (конверт с заданиями). По заданиям следа работают учащиеся победившей команды у доски. Весь класс работает в тетради.
Работа по следу:
Решив первое задание, знатоки узнают номер ряда парт, в котором находится похищенное число:
Упростите выражение: ![]()
Решение: ![]()
![]()
Ответ: 2.
Решив второе задание, знатоки узнают номер парты в ряду, где спрятано похищенное число.
Упростите выражение
![]() , если b>5.
, если b>5.
Решение:
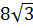
Ответ: 5.
Итак, искомое число лежит во втором ряду, в ящике пятой парты.
Учитель вместе с учащимися подводит итог урока. Выясняет, что понравилось на уроке, какие задания ещё вызывают затруднения, выставляет оценки и задает задание на дом.
Домашнее задание дифференцированное. Те учащиеся, которые допустили ошибки в самостоятельной работе, выполняют их анализ, а также придумывают и решают задания, подобные тем, в которых были допущены ошибки.
Кто выполнил все верно, решает дополнительное задание.
Сократите дроби и сравните их значения:
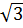 и
и 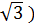 .
.
Решение.
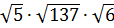 =
= 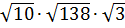 =
=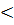 =
=![]() =
= ![]() ;
;
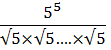 =
=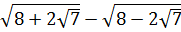 =
= 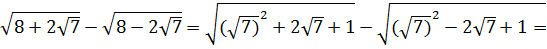 = 2
= 2![]() =
= ![]() .
.
Ответ: ![]() .
.
После урока каждый учащийся заполняет карточку самооценки, это позволит учителю узнать эмоциональный настрой учащихся, их успехи и неудачи.
Литература.
1.А.Г.Мордкович « Алгебра » учебник для 8 класса общеобразовательных учреждений.
2.Л.И. Звавич, Л.В.Кузнецова «Дидактические материалы» Алгебра 8.
3.М.Ю.Шуба « Занимательные задания в обучении математике».
4.Издательский дом Первое сентября. Учебно- методическая газета « Математика» №12,1999 год.