- Учителю
- ҰБТ-да кездесетін векторларға есептер
ҰБТ-да кездесетін векторларға есептер
Ұлттық Бірыңғай Тесттерде математика пәнінен кездесетін векторларға байланысты есептерді шығару жолдары.
Ұлттық Біріңғай Тестте математика пәнінен берілетін тест тапсырмаларының жоспары бойынша әр нұсқада кемінде бір тапсырма координаттық әдіс пен векторға берілген есеп болатындығы туралы айтылған. Алайда жоғары сыныптарда оқитын мектеп оқушыларының басым көпшілігі мұндай есептерге келгенде (әсіресе вектор тақырыбымен байланысты есептерде) қиналатындығын жиы байқауға болады. Шынында да, бұндай есептер оқушылар үшін соншалықты қиын ба? Әрине, есептің шартын түсінбеген, шығару жолын білмейтін оқушы үшін қандай есеп болмасын қиын болып көрінеді. Бірнеше жылдан бері жоғары сынып оқушыларымен ҰБТ-ға дайындық сабақтарында вектор тақырыбын қайталау барысында біз оқушылардың бірнеше сабақ ішінде мұндай есептерді шығарып кете алатындығын байқадық. Ол үшін оқушыларға вектордың анықтамасын қайталап, негізгі формулаларды беріп, бірнеше мысалдар арқылы оған байланысты есептердің шығару әдістерін көрсетіп шығу қажет.
Бұл баяндамада біз математика пәнінен тесттерде кездесетін векторларға байланысты кейбір есептердің шығару жолдарын қарастырып өтуді жөн көріп отырмыз.
Өзіміздің тәжірибемізден біз есептер шығару барысында қажет болатын формулаларды жинақтап оқушыларға ұсынып отырамыз. Бұл формулалар төменде келтірілген.
Сонымен қатар, оқушылардың осы тақырыптар бойынша білімін тереңдетіп, есептер шығару ептілігін арттыру мақсатында біз 2006 жылы жаратылыстану бағыты бойынша оқитын 10-11 сыныптарға арналған «Сызықтық алгебра және аналитикалық геометрия» тақырыбымен авторлық бағдарлама құрастырып, оны қолданбалы курстарда өтіп жатырмыз. Бұл курстың аналитикалық геометрия бөлімінде мектеп бағдарламасында қамтылмаған векторларға берілген кейбір есептердің түрлерін шығарудың жаңа тәсілдерін қарастырамыз. Мысалы, екі вектор арқылы салынған параллелограммның ауданын табу, төбелерінің координаттары берілген үшбұрыштың ауданын табу, векторлар үшін параллелограмм ережесін қолдануға берілген есептер және т. б. Бұл қолданбалы курс бағдарламасына келесі тақырыптар енгізілген: Вектор. Векторларды қосу, санға көбейту. Кеңістіктегі тікбұрышты координаталар жүйесі. Кеңістіктегі векторлар. Векторлардың скаляр көбейтіндісі. Векторлардың арасындағы бұрыш. Екі вектордың векторлық көбейтіндісі. Үш вектордың аралас көбейтіндісі. Оларды оқып-үйренуде жалпы орта білім беретін курстарға қарағанда барынша жоғары деңгейдегі міндеттер жүзеге асырылады. Бұл тараудың тақырыптарын өту барысында оқушылар жалпы мектеп бағдарламасымен қамтылмайтын (алайда Ұлттық Біріңғай Тестте кездесетін кейбір есептерді шығаруға септігін тигізетін) жоғары математиканың көптеген негізгі (мысалы матрицалар және олармен амалдар орындау, анықтауыштар, жазықтықтың теңдеуі, кеңістіктегі түзудің теңдеуі сияқты) ұғымдарымен, кейбір есептерді шығарудың жаңадан әдіс-тәсілдерімен (мысалы сызықтық теңдеулер жүйесін түрлендірулер арқылы немесе анықтауыштар көмегімен шешуді, үшбұрыш пен көпбұрыштардың аудандарын координаттар көмегімен табуды, үшбұрыш пен параллелограмның ауданын табудың векторлық әдістерімен) танысады.
Осы бағдарлама бойынша біз «Екі векторды векторлық көбейту» сабақ презентациясын дайындап, оны www.sabak.adamzat.kz</</u> сайтында орналастырдық.. Сабақта векторға байланысты барлық негізгі формулалар және Ұлттық Бірыңғай Тестте кездесетін векторларға берілген кейбір күрделі есептердің шығару жолдары қарастырылған. Сабақта берілген тест сұрақтары 2005-2008 жылдар аралығындағы тесттер жинағынан алынған.
Ал енді бізге векторларға берілген Ұлттық Бірыңғай Тестте кездесетін есептерді шығару үшін қажет формулаларды қарастырайық.
-
В
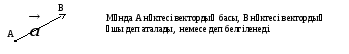ектордың негізгі
элементтері, белгіленуі.
-
Вектордың координаттары.
болса, онда 
векторының координаттары
мына формуламен аныкталады: 
-
Вектордың абсолют шамасы (ұзындығы):
болса, онда 
-
Векторларды қосу:
,
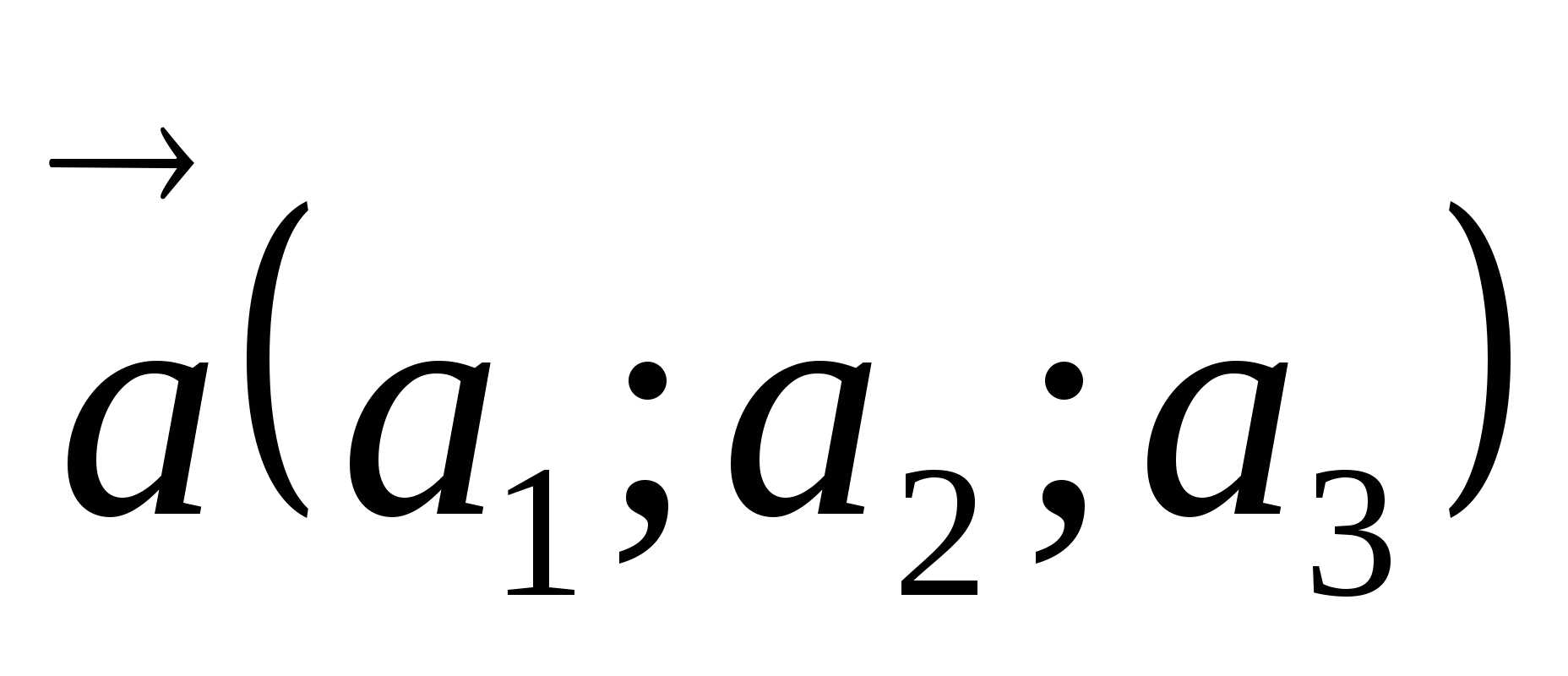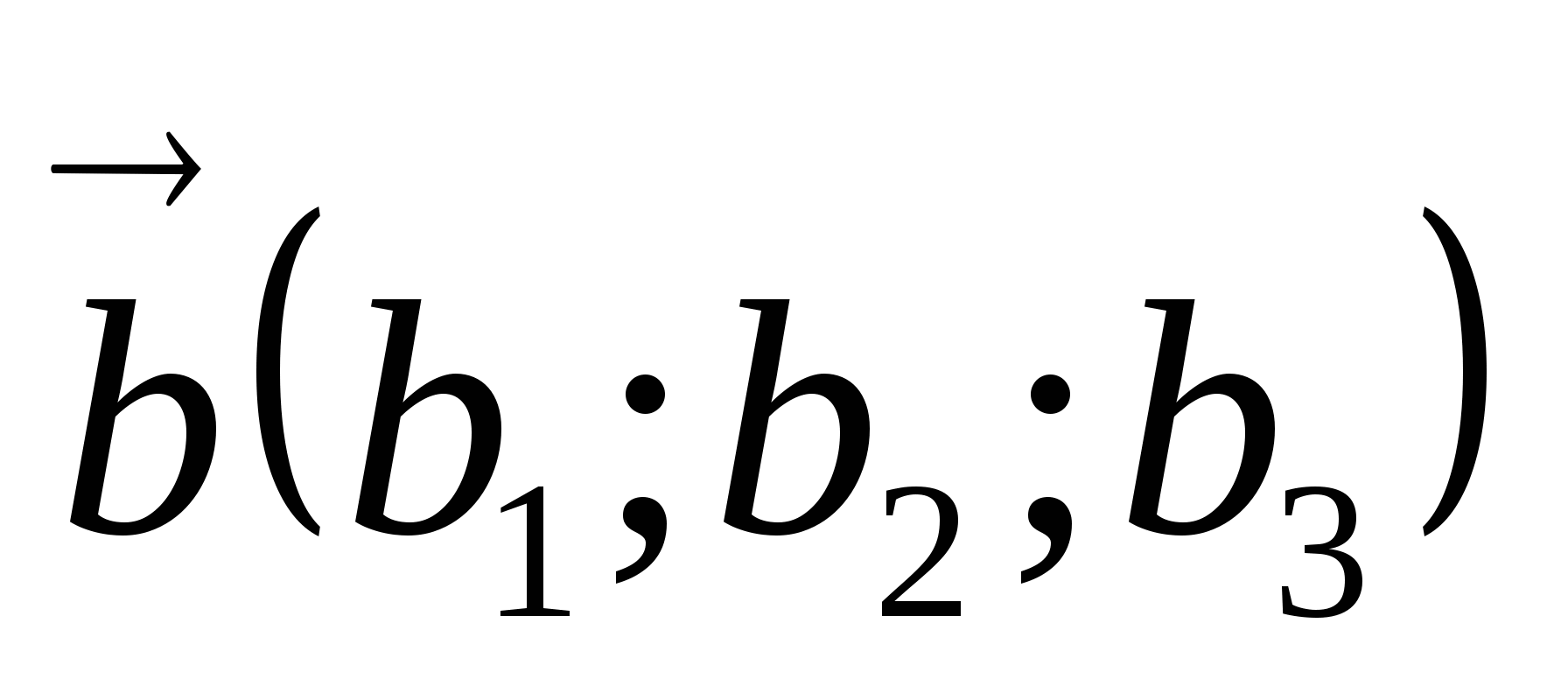векторларының
қосындысы вектор болады және оның координатасы былай
анықталады: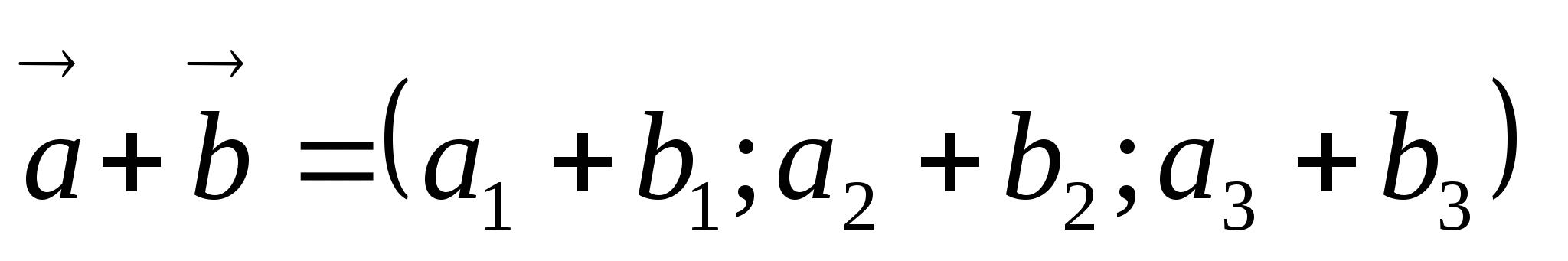 
-
Векторды санға көбейту:
-
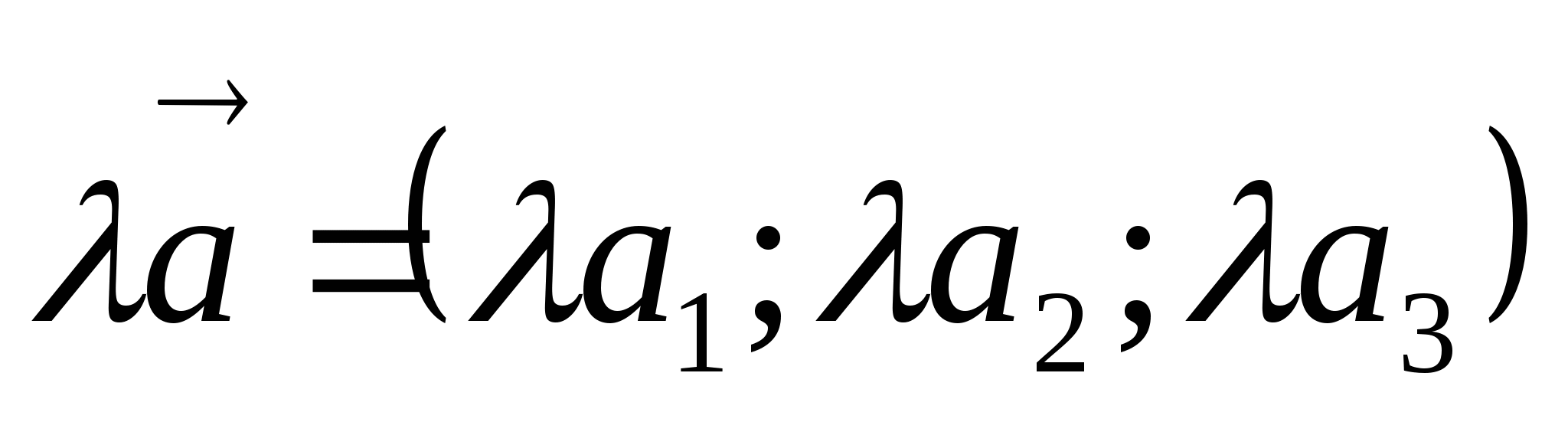
Коллинеар векторлардың координаталары үшін келесі теңдік орындалады:
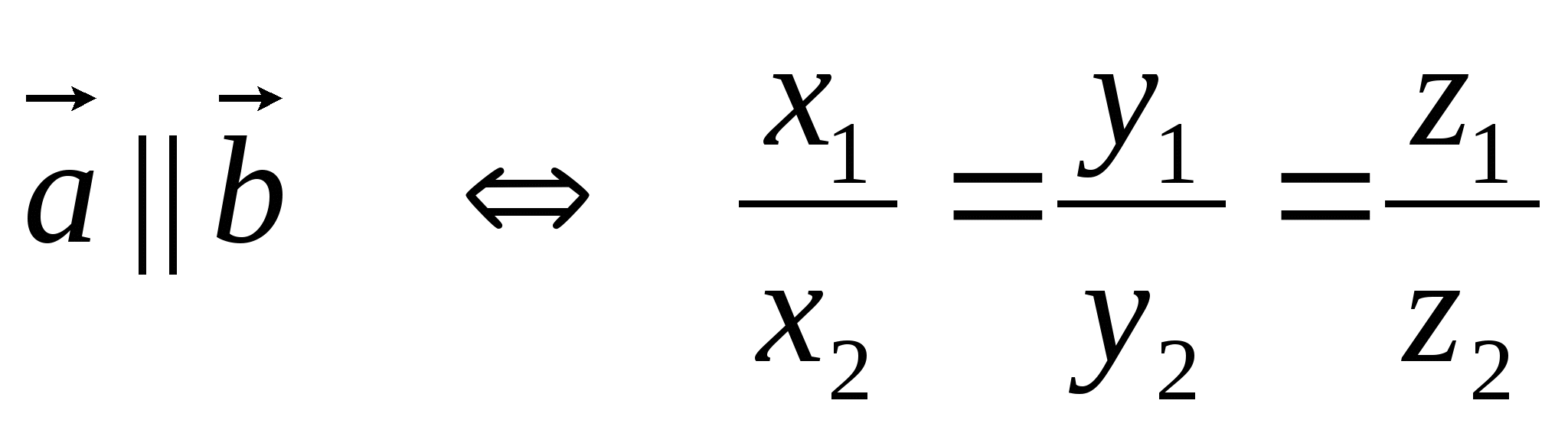, мұнда
векторлардың координаталарының ешқайсысы нөлге тең болмау
керек. Егер екі вектордың біреуінің қандай да бір координатасы
нөлге тең болған жағдайда екінші вектордың да оған сәйкес
координатасы нөлге тең болуы керек.
-
Векторлардың скаляр көбейтіндісі:
.
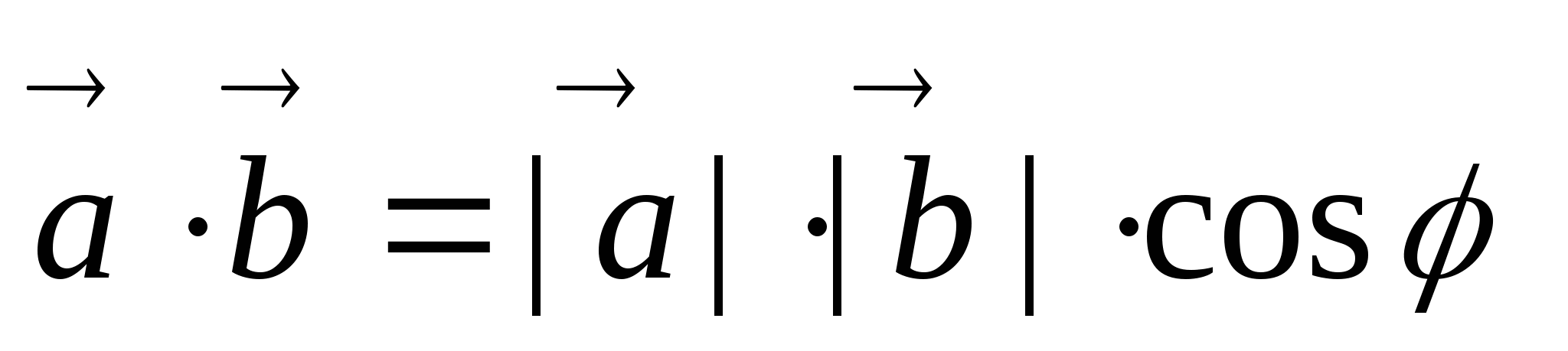Егер , болса, онда 
болады.
-
Векторлар арасындағы бұрыш.
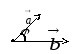
- сүйір 
.
- доғал 
.
.
.
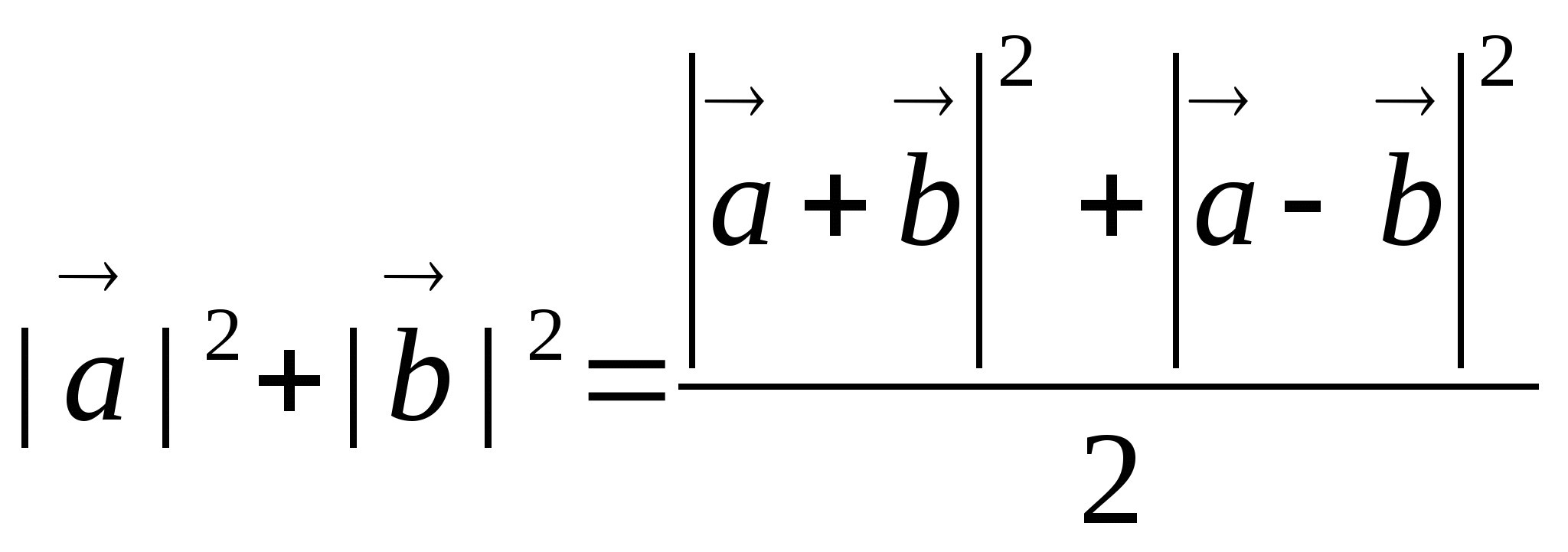9. Параллелограмның қасиеті бойынша:
-
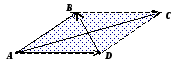
Ұзындығы бірге тең векторды бірлік вектор немесе орт дейміз. Кез келген векторды бірлік векторлар арқылы жіктеуге болады.
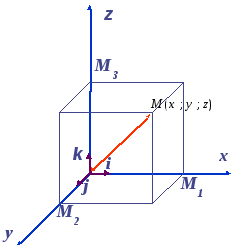
Енді векторларға берілген есептерді қарастырайық.
1-есеп. [1] m векторының қандай мәнінде 
және 
векторлары перпендикуляр
болады?
Шешуі: 
, 
, бұл теңдеудің
шешімдері
болады. Жауабы: -3; 1.
2-есеп. [1]
және 
векторларының арасындағы
бұрыштың косинусын табыңдар, егер 
және 
.
Шешуі: 
=(3; 1; 1), =(-1; 3; 1), 
, |
,
. Жауабы: 
.
3-есеп. 
және 
коллинеар векторлар. Осы
векторлардың белгісіз координаталары
p және q -дің сан мәндерін табыңдар, егер 
және 
Шешуі: ||болса, онда 
теңдігі орындалады, мұнда
векторлардың координаталарының ешқайсысы нөлге тең емес.
, бұдан p=-0,3; q=0,25
шығады. Жауабы: p=-0,3; q=0,25.
4-есеп. Егер 
және 
болса, онда 
табыңыз.
Шешуі: 
формуласын қолданамыз.
, бұдан 
, онда 
.
Жауабы: 18.
5-есеп. 
=(1; 0; 
) векторы мен аппликат осі
арасындағы бұрышты тап.
Шешуі: апликат осі деп Оz осі аталады, онда Оz осінде жатқан
векторды 
деп белгілеп аламыз және
оның координаталары (0; 0; z) болады. 
, 
, 
, 
.
Жауабы: 
.
Әдебиеттер тізімі:
-
Математика бойынша тест жинағы. Оқу-әдістемелік құрал. Астана-2008.
-
Математика бойынша тест жинағы. Оқу-әдістемелік құрал. Астана-2005.