Аттестационный материал по математике для 6 класса.

Пояснительная записка

к аттестационному материалу по математике

для проведения промежуточной аттестации

</ учащихся 6 класса в 201..-201.. учебном году .

Аттестационный материал по математике для проведения промежуточной аттестации учащихся 6 класса составлен в соответствии с требованиями федерального государственного образовательного стандарта основного общего образования (утв. приказом Минобрнауки РФ от 17.12.2010 года № 1897).

Предлагаемый комплект основан на документах, определяющих содержание современного школьного образования по математике в основной школе. В него вошли вопросы содержания, включенные в рабочую программу по математике для 6 класса и освещаемые в учебнике по математике для 6 класса (Математика: 6 класс. Учебник для общеобразоват. организаций./Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков и др./ -32-е изд. - М.: «Мнемозина», 2014), т.е. инвариантное ядро, не выходящее за рамки стандарта.

Комплект заданий состоит из 4-х вариантов, в каждом из которых по 12 заданий. Каждый вариант состоит из двух частей.

Часть 1 содержит 8 заданий. В каждом задании полученный ответ надо записать в отведенном для этого месте.

Часть 2 содержит 4 задания, требующих развернутого ответа. При этом для каждого задания надо указать его номер и записать полностью его решение (ответ).

Такое количество заданий достаточно, чтобы обеспечить проверку всего значимого содержания школьного курса математики за 6 класс и нормализовать нагрузку школьников в период проведения промежуточной аттестации.

В аттестационный материал включены вопросы, проверяющие усвоение содержания следующих дидактических единиц по математике за курс 6 класса:

1.Обыкновенные дроби.

1.1. Делимость чисел.

1.2.Сложение и вычитание обыкновенных дробей с разными знаменателями.

1.3. Умножение и деление обыкновенных дробей.

1.4. Дробные выражения.

2. Пропорции.

2.1. Отношения и пропорции.

2.2. Прямая и обратная пропорциональная зависимость.

3.Рациональные числа.

3.1. Модуль числа. Целые числа.

3.2. Сложение и вычитание положительных чисел и отрицательных чисел, чисел с разными знаками.

3.3. Умножение и деление рациональных чисел. Свойства действий с рациональными числами.

4.Решение уравнений и задач.

4.1. Подобные слагаемые.

4.2. Решение уравнений.

4.3. Решение задач (нахождение дроби от числа, нахождение числа по дроби, задачи на составление уравнения)..

5.Координаты на плоскости.

5.1. Координатная плоскость и координаты точки на плоскости.

5.2 Диаграммы.

В целом аттестационный материал позволяет проверить усвоение наиболее важных элементов содержания образования по математике за 6 класс и умение практического применения знаний.

За выполнение каждого задания ученик получает определенное количество баллов.

Исправления и зачеркивания, если они сделаны аккуратно, в каждой части теста, не являются поводом для снижения оценки.

Время, отведенное для проведения промежуточной аттестации, - 40 минут.

Система оценки выполненной работы

Промежуточная работа оценивается по пятибалльной шкале. При выставлении отметки необходимо руководствоваться следующими критериями:

Критерии оценивания.

Таблица количества баллов за выполнение задания

Количество баллов за работу в целом

Часть 1

Часть 2

задания 1-8

задания 9-11

задания 12

1 балл

2 балла

3 балла

17 баллов

Таблица перевода тестовых баллов в школьные оценки

Школьная оценка

1-5

6-9

10-14

15-17

«2»

«3»

«4»

«5»

Ответы.

Рено - 6 м.

Форд - 4 м.

Вариант 2

2

4

2

1

3

3

1

2

10

1,68

48 лет

36 км

Вариант 3

2

2

3

4

3

1

2

4

- 11

1,8

36 чел.

Первого сорта - 22,5 т.

Второго сорта - 50т.

Третьего сорта -12,5т

Вариант 4

2

2

4

2

1

4

3

2

2

2,64

21 модель

8 км

ВАРИАНТ №1

Часть 1.

При выполнении заданий 1-8 в строке ответов выберите номер правильного ответа.

1. Выполните действия: 1,763 : 0,086 - 0,34 16.

1) 1506; 2) 150,6; 3) 1,506; 4) 15,06.

2. 2. Выполните действия: 1 ( 7 - 2).

1) ; 2) 5; 3) 6 ; 4) 6.

3. Вкладчик снял в банке 2340 рублей, что составило 36% вклада. Определите первоначальную сумму вклада.

1) 6500 руб.; 2) 842.4 руб.; 3) 8424 руб. ; 4) 65000 руб.

4. Найдите неизвестный член пропорции = .

1) 1,6; 2) 1,8; 3) 18; 4) 3,2.

5. Найдите m, если m : = .

1) - 3; 2) 3; 3) 9; 4) - .

6. Найдите значение выражения ( - 4 + 3) ∙ ( - 14)

1) - 0,5 ; 2) - 30 ; 3) 15; 4) - 15.

7. По рисунку определите координаты точки пересечения прямых АВ и СК

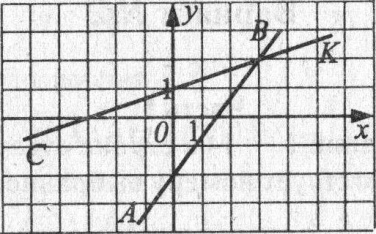
1) ( 3 ; 2 ) ; 2) ( - 3 ; 2 ) ; 3) ( 2 ; 3 ); 4) ( 3 ; - 2 )

8. Сколько целых чисел расположено между числами -3 и 8 ?

1) 10; 2) 12; 3) 11; 4) 9.

Часть 2.

При выполнении заданий 9-12 запишите номер выполняемого задания,

подробное решение с ответом.

9. Упростите выражение - 3х + 7у + 13х - 7у - 3 и найдите его значение,

если х = 3,1; у = - 15,01.

10. Решите уравнение х - 0,2 = х + 0,85.

11. Число учащихся школы, обучающихся в 6 классах, представлено в виде диаграммы на рисунке. Сколько учащихся обучается в 6 а классе, если всего в шестых классах 60 учащихся?

12. Решите задачу с помощью уравнения.

В автосалоне находилось 25 автомашин трех видов: «Тойота», «Рено» и «Форд». Автомашины «Рено» составляли 40% от числа машин «Тойота», а число автомашин «Форд» составляло от числа машин «Рено». Сколько машин каждого вида находилось в автосалоне?

ВАРИАНТ №2

Часть 1.

При выполнении заданий 1-8 в строке ответов выберите номер правильного ответа.

1. Выполните действия: 2,867 : 0,094 + 0,31 15.

1) 3,515; 2) 35,15; 3) 3515; 4) 0,3515.

2. Выполните действия: 1 ( 6 - 3).

1) ; 2) - 3; 3) 3,64; 4) 3.

3.Засеяли 195 га поля, что составило 65% всего поля. Какова площадь всего поля?

1) 3000 га; 2) 300 га; 3) 126,75 га; 4) 1267,5 га.

4. Найдите неизвестный член пропорции = .

1) 45; 2) 4,5; 3) 450; 4) 0,4.

5. Найдите k, если k - = .

1) 4,8 ; 2) -2,72; 3) 4 ; 4) - 2 .

6. Найдите значение выражения ( 5 - 7) :.

1) 2; 2) -15 ; 3) - 2; 4) 1,5.

7. По рисунку определите координаты точки пересечения прямых PQ и EF

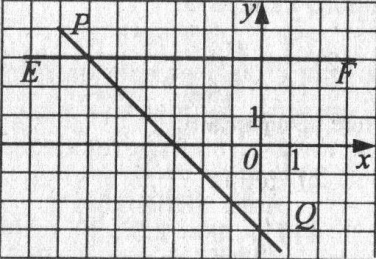
1) (- 6 ; 3); 2) (6 ; 3); 3) (3 ; - 6) ; 4) (- 6 ; -3)

8. Сколько целых чисел расположено между числами -4 и 7 ?

1) 11; 2) 10; 3) 9 ; 4) 7.

Часть 2.

При выполнении заданий 9 -12 запишите номер выполняемого задания,

подробное решение с ответом.

9. Упростите выражение 7m + 3n - 7m - 8n + 11 и найдите его значение, если m = 3,

n = .

9. Решите уравнение х + 1,3 = 0,53 + х.

10. Продолжительность жизни белого медведя, носорога и льва вместе составляет 120 лет. Соотношения продолжительности их жизни указано на диаграмме (рис.1). Сколько лет живет носорог?

лев носорог

медведь

Рис.1

12. Решите задачу с помощью уравнения.

Лыжники за три дня прошли 78 км. В первый день они прошли 40% того расстояния, которое было пройдено во второй день, а в третий - в 1,2 раза больше, чем во второй день. Сколько километров было пройдено лыжниками в третий день?

ВАРИАНТ №3

Часть 1.

При выполнении заданий 1-8 в строке ответов выберите номер правильного ответа.

1. Выполните действия: 1,029 : 0,098 - 0,28 24.

1)3,078; 2) 3,78; 3) 37,8; 4) 17,22.

2. Выполните действия: 1 ( 9 - 2).

1) 8; 2) 9; 3) 3,64; 4) .

3. Диаметр Земли 12750 метров, что составляет 75% диаметра Марса. Сколько метров составляет диаметр Марса?

1) 1700 м ; 2) 170 м ; 3) 17000 м; 4) 9562,5м

4. Найдите неизвестный член пропорции = .

1) 2; 2) 4; 3) 2,7; 4) 3.

5. Найдите z, если z · = 10.

1) 54,08; 2) - 2; 3) 2 ; 4) 15,6.

6. Найдите значение выражения (5 - 7) ∙ (-10)

1) 21; 2) - 21; 3) 19 ; 4) - 19.

7. По рисунку определите координаты точки пересечения прямых АВ и МN

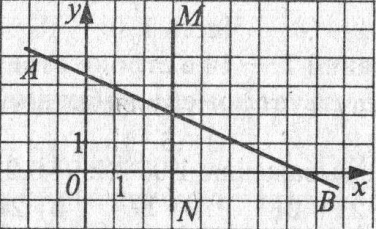
1) ( 2 ; 3); 2) ( 3 ; 2); 3) (- 3 ; 2) ; 4) ( 3 ;- 2).

8. Сколько натуральных чисел расположено между числами -2 и 5 ?

1) 8; 2) 5; 3) 6; 4) 4.

Часть 2.

При выполнении заданий 9 - 12 запишите номер выполняемого задания,

подробное решение с ответом.

9. Упростите выражение - 5а - 8b + 13a + 8b - 7 и найдите его значение,

если a = - 0,5; b = 1,01.

9. Решите уравнение 1,2 + y = у + 0,78.

10. Одна из групп, покорявшая горную вершину Эверест, состояла из спортсменов, проводников и носильщиков. Их соотношение представлено в виде диаграммы (рис.1). Сколько было носильщиков, если вся группа насчитывала 60 человек?

носильщики спортсмены

проводники

Рис.1

12. Решите задачу с помощью уравнения.

Садоводы собрали 85 тонн яблок трех сортов. Масса яблок первого сорта составляет 45% массы яблок второго сорта, а масса яблок третьего сорта составляет массы яблок первого сорта. Сколько тонн яблок каждого сорта собрали садоводы?

ВАРИАНТ №4

Часть 1.

При выполнении заданий 1-8 в строке ответов выберите номер правильного ответа.

1. Выполните действия: 2,592 : 0,064 + 0,26 23.

1) 4,698; 2) 46,48; 3) 4698; 4) 34,52.

2. Найдите действия: 1 ( 7 - 5).

1) 0,5; 2) ; 3) 2,5; 4) .

3. Фермер взял кредит в банке. На закупку семян пшеницы он потратил 4900 рублей, что составило 35% всех денег. Определите, какую сумму денег взял фермер в банке?

1) 1400 руб.; 2) 140 руб.; 3) 1715 руб.; 4) 14000руб.

4. Найдите неизвестный член пропорции = .

1) 2; 2) 0,2; 3) 8,45; 4) 0,02.

5. Найдите х, если х = · .

1) 3; 2) - 3; 3) - ; 4) .

6. Найдите значение выражения - 6 ( 2 - 3) .

1) - 7; 2) 14 ; 3) -14 ; 4) 7.

7. По рисунку определите координаты точки пересечения прямых MN и KE:

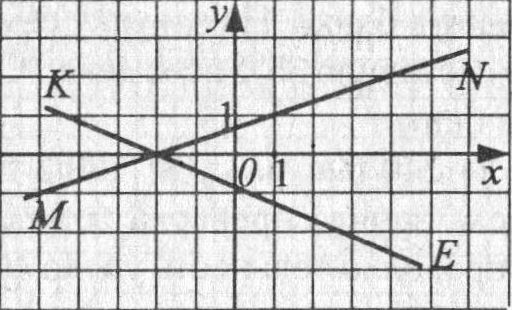
1) ( 0 ; - 2); 2) ( 2 ; 0) ; 3) ( - 2 ; 0) ; 4) ( 0 ; 2) .

8. Сколько натуральных чисел расположено между числами -3 и 4 ?

1) 8 ; 2) 3; 3) 5; 4) 4.

Часть 2.

При выполнении заданий 9 - 12 запишите номер выполняемого задания и

подробное решение с ответом.

9. Упростите выражение 10a + b - 10a - 3b + 7 и найдите его значение, если a = 2,5;

b = .

9. Решите уравнение х - 0,82 = х - 1,37.

10. Коллекция моделей одежды разной цветовой гаммы представлена в виде диаграммы

( рис.1). Сколько моделей красного цвета, если всего в коллекции 70 моделей?

красные белые

желтые зеленые

Рис.1

9. Решите задачу с помощью уравнения.

Школьники совершили трехдневный поход. В первый день было пройдено 80% того расстояния, которое прошли во второй день, а в третий - в 1,5 раза больше, чем во второй день. Сколько километров пути было пройдено в первый день, если за три дня школьники прошли 33 км?