- Учителю
- НПК Задачи на дополнительные построения
НПК Задачи на дополнительные построения
Муниципальное общеобразовательное бюджетное учреждение
средняя общеобразовательная школа № 9 городского округа г. Нефтекамск
Республики Башкортостан
Задачи на дополнительное построение
Исследовательская работа по математике
Выполнил: Абдюшев Никита ученик 8а класса
Руководитель: Кабирова Любовь Федоровна
г.Нефтекамск 2014
Оглавление
-
Введение 3
-
Основная часть 4
Виды дополнительных построений -
Глава 1: Продолжить медиану -
Глава 2: Провести прямую параллельную данной 6
Глава 3: Провести прямую перпендикулярную данной 8
Глава 4: Построить окружность 10
-
Заключение 12
-
4.Литературв 13
Введение
Приступая к решению геометрической задачи, нужно иметь в виду, что обычно геометрическая задача может быть решена несколькими способами. Поэтому, если появилась идея решения задачи, но путь к решению довольно длинный, то следует помнить, что существенную помощь могут оказать дополнительные построения. В одних случаях эти построения напрашиваются сами собой, в других они не так очевидны и требуют изобретательности, геометрической интуиции. Сейчас в школьном курсе учебников знакомят с разнообразными понятиями и средствами решения задач, но именно их разнообразие оставляет мало времени на приобретение навыков, и вкус к такого рода задачам, которые развивают геометрическое воображение. Цель работы: выделить основные виды дополнительных построений, к каждому виду подобрать и решить задачи. Изучив статью «Научим школьников выполнять дополнительные построения» в газете «Математика» приложение к газете «Первое сентября» и статью «Учимся делать дополнительные построения» в научно-популярном физико - математическом журнале «Квант», меня заинтересовала эта тема и я начал подбирать задачи, которые «красиво» решаются с помощью дополнительных построений. Изучив задачники Просолова В.В «Задачи по планиметрии» и Шарыгина И.Ф «Задачи по геометрии», я выделил четыре основных вида дополнительных построений: продолжить медиану, построить прямую параллельную данной, построить прямую перпендикулярную данной, построить окружность. В данную работу включено 10 наиболее интересных задач. Среди них задачи на вычисление, на доказательство, на построение.
Продолжить медиану
№1
Две стороны треугольника равны 27 и 29, а медиана, проведенная к
третьей
стороне равна 26. Найти высоту, проведенную к стороне 27.
Дано:
∆ABC
AB=27,BC=29,BO=26
CD − высота
BO − медиана
Найти CD.
B
D
A O C
E
B
D
A O C

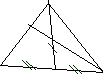

Решение
1. Дополнительное построение: строю OE=BO; ABCE - параллелограмм (по признаку), BC=AE=29; AB=EC=27
2. S∆ABC= S∆ABE (т.к составлены из равных треугольников)
3. S∆ABE= ![]() (по формуле Герона)
(по формуле Герона)
S∆ABE= ![]()
S∆ABC= ![]()
270= ![]()
![]() CD=20
CD=20
Ответ: 20
№2.
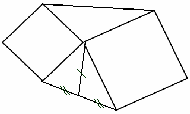
На сторонах AB и BC построены вне его квадраты ABDE и BCKF. Доказать, что отрезок DF в 2 раза больше медианы BP треугольника ABC.
Дано:
∆ABC
ABDE и BCKF - квадраты
Доказать, что DF=2BP.


B
A P
C
D
B
A P
C
Решение
-
Дополнительное построение: строю PQ=BP ABCD-параллелограмм (по признаку)
-
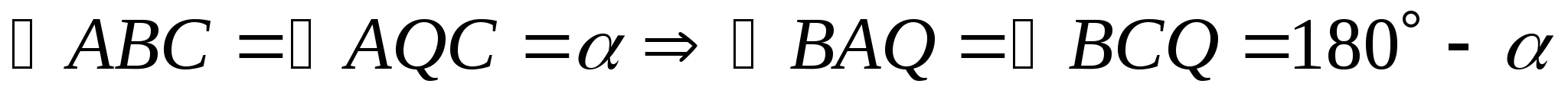
-
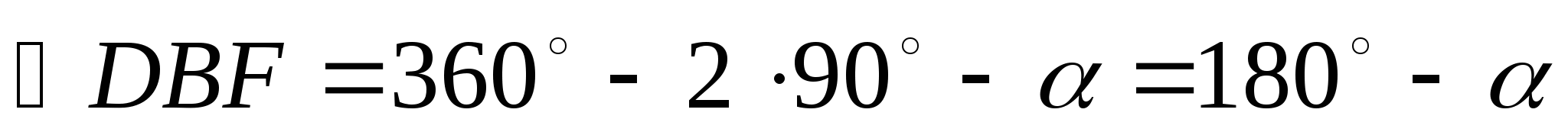
![]()
![]()
![]() - по II признаку
(
- по II признаку
(![]() DBF=BCQ, BF=BC, DB=CQ)
DBF=BCQ, BF=BC, DB=CQ)
![]()
DF=BQ=2BP
№3
Доказать, что медиана треугольника меньше полусуммы двух сторон,
имеющих с этой медианой общую вершину.
Дано:
∆ABC
BP − медиана
Д
D F
E B
A P K
Cоказать, что BP< ![]() (AB+BC)
(AB+BC)
D F
E B
A P K
C
Q
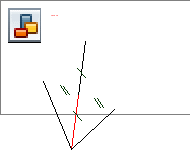
Решение
-
Дополнительное построение: строю PD=BPABCD - параллелограмм (по признаку) AB = CD, BC = AD
-
BD<BC+CD (по неравенству треугольника)
BD<BA+AD (по неравенству треугольника)
2BD
2BD<2BC+2AB
BD<BC+AB
Так как BD=2BP (по построению), то BP< ![]() (AB+BC).
(AB+BC).
Провести прямую параллельную данной
№1
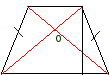
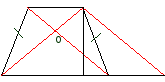
Найти высоту равнобедренной трапеции, если её диагонали взаимно перпендикулярны, а площадь трапеции равна S.
Дано:
ABCD− равнобедренная трапеция
AC и BD − диагонали
AC BD
S − площадь трапеции
Найти h − высоту трапеции
B C
A F D E
B C
A F D
Решение
-
Дополнительное построение: строю CE||BD
-
∆АСЕ - равнобедренный (т.к AC=BD, BD=CE, AC=CE)
-
∆АСЕ -прямоугольный (т.к CO
 BD, BD||CE
BD, BD||CE  CE
CE  CO)
CO)
-
Проведу высоту CF - она является медианой и биссектрисой

 ACF =
ACF =  FCE = 45O
FCE = 45O
![]()
AE=2AF=2h
Sтр.= ![]()
BC+AD=AE (т.к BC=ED)
Sтр.= ![]()
h =![]()
№2
Через середину M стороны BC параллелограмма ABCD, площадь которого
равна 1, и вершину A проведена прямая, пересекающая диагональ BD в
точке O. Найти площадь четырехугольника OMCD.
Дано:
ABCD−параллелограмм
SABCD=1
B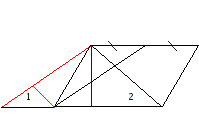 M=MC
M=MC
Найти площадь OMCD.
B M C
O
A D
B M C
O
F
E A D
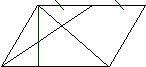
РешениеДополнительное построение: стою BE||AM, AF||BO
-
S ∆ABD =
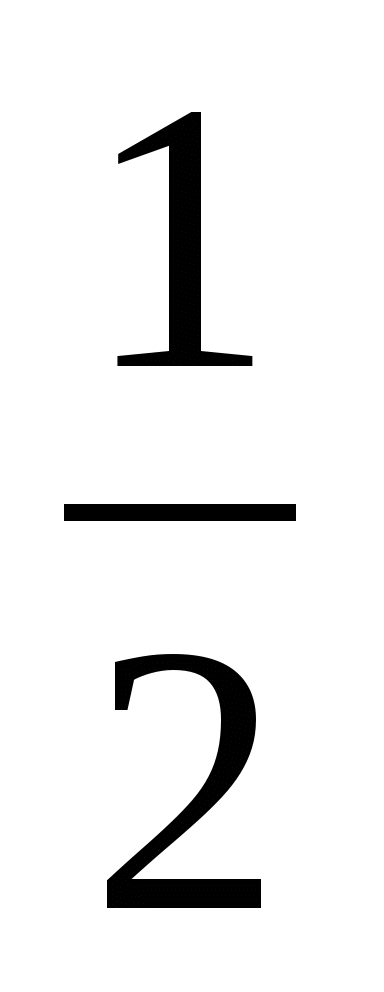 SABCD =
SABCD =
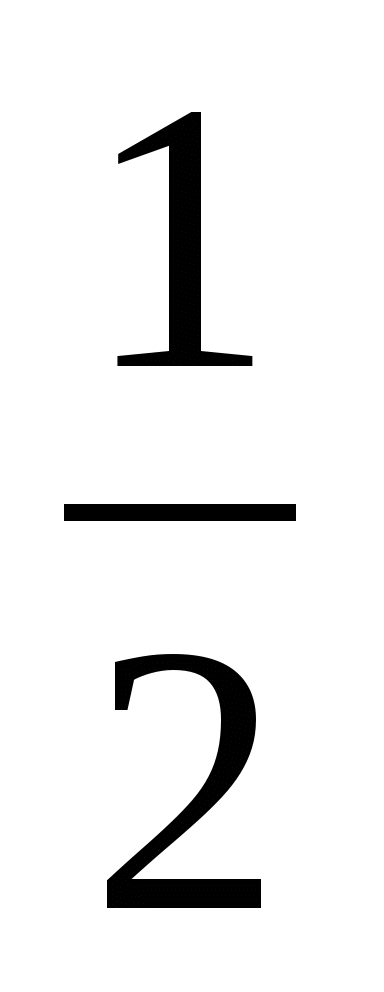
-
∆EBA и ∆ABD - они имеют общую высоту

 =
= 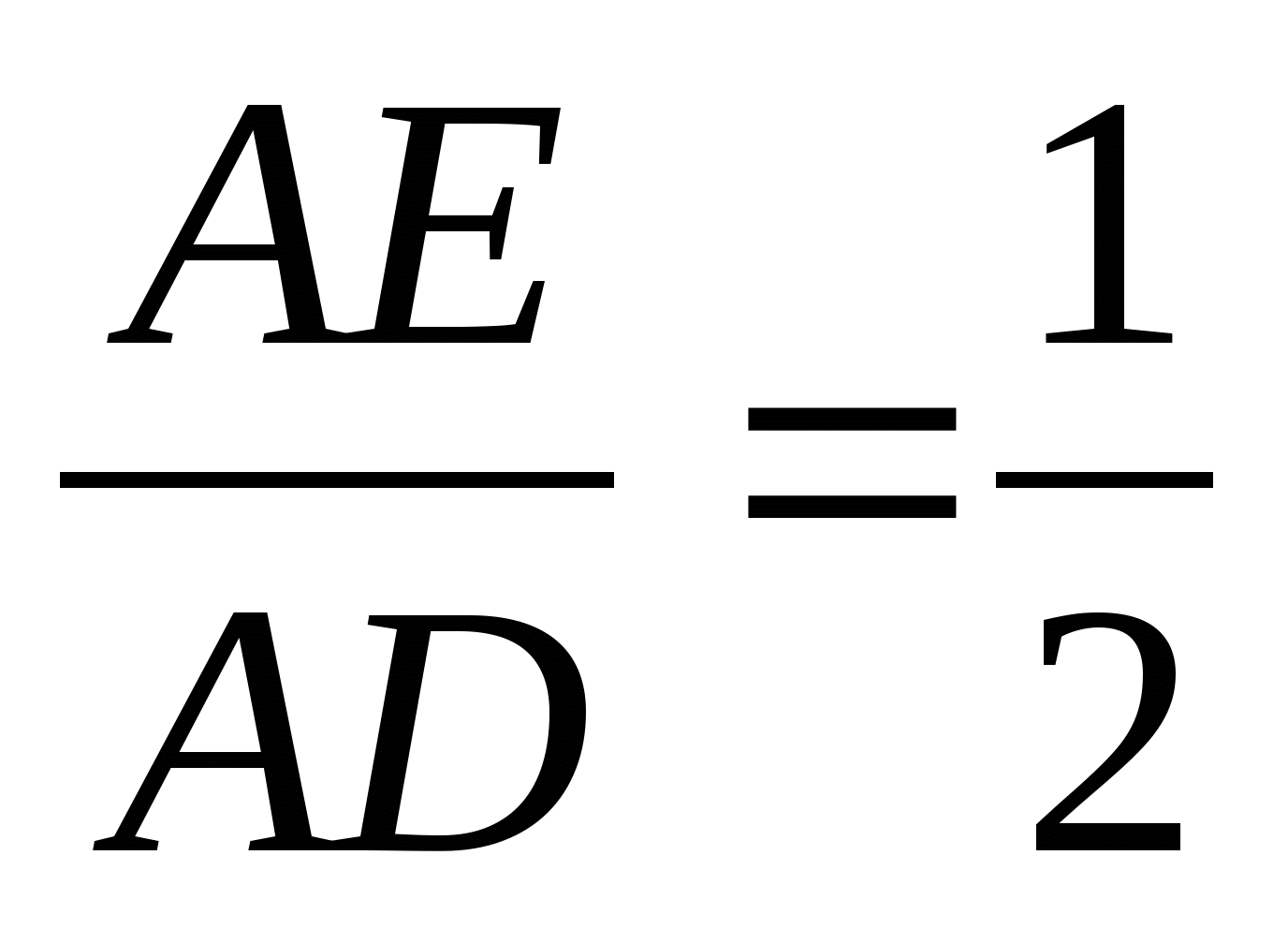
S ![]()
-
S
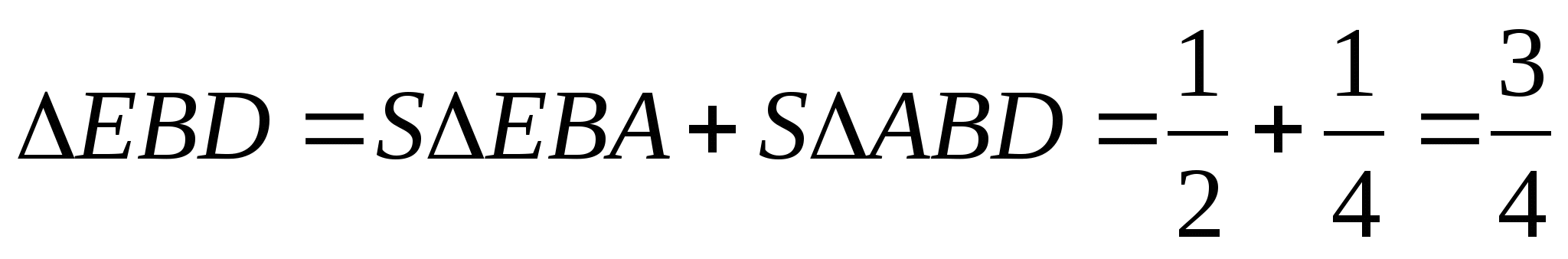
-
 ~
~  (т.к.
(т.к. 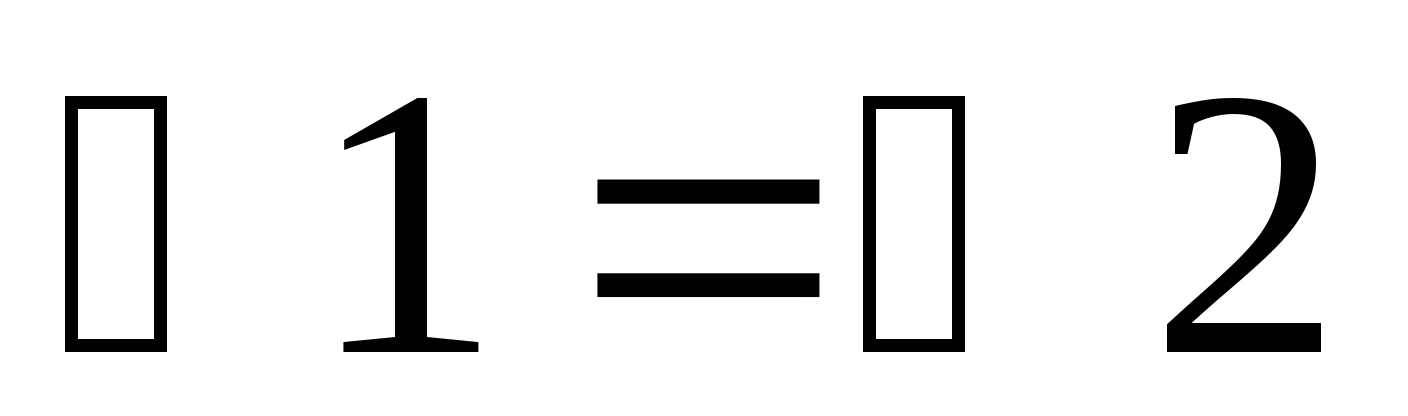 ,
, 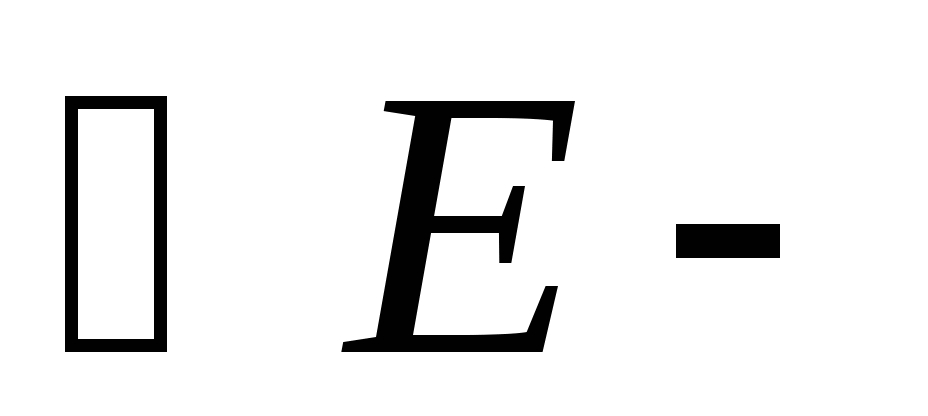 общий)
общий) 
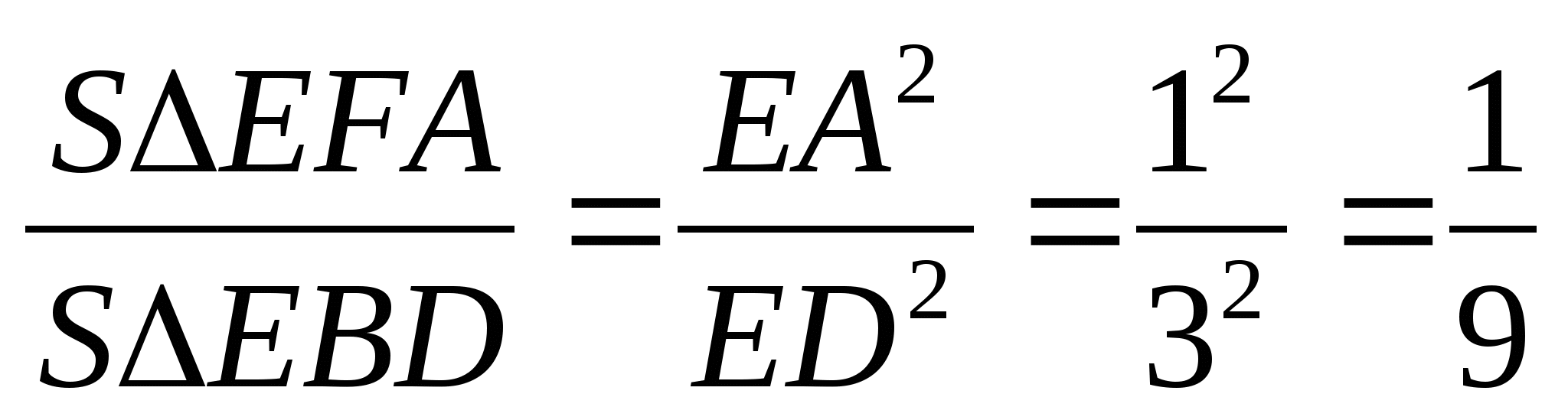

-
Рассмотрим
 и
и 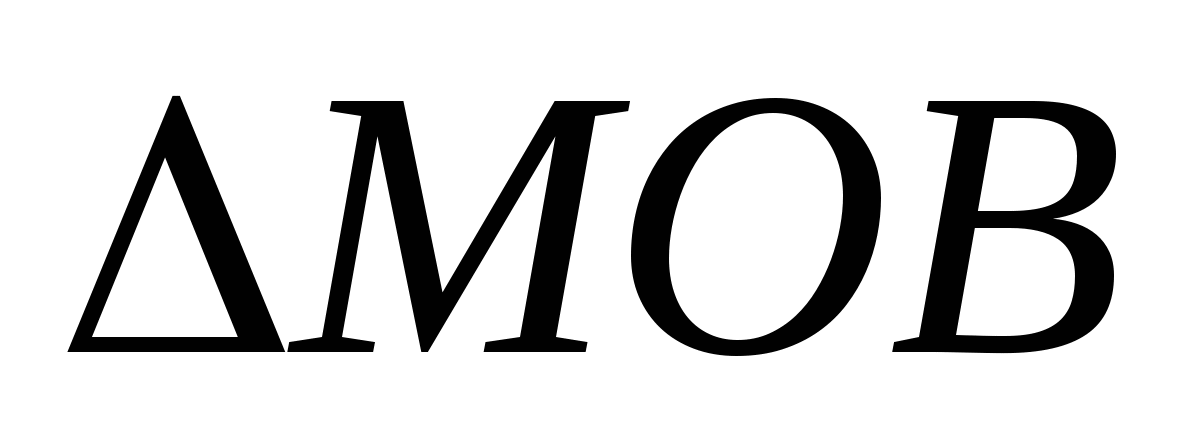
-
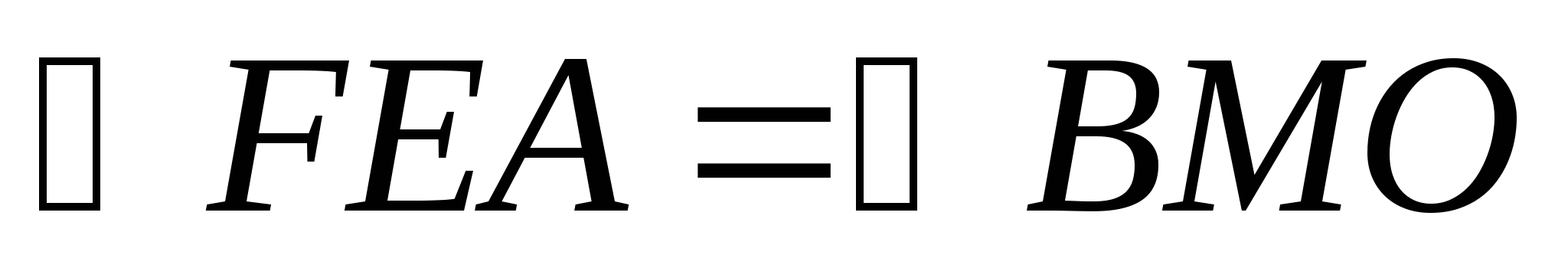 (т.к EBMA -
параллелограмм) ,
(т.к EBMA -
параллелограмм) ,
-
EA=BM
-
EF=OM (EF=EB-FB, OM=AM-AO, EB=AM, FB=AO)
![]() (по двум сторонам и углу
между ними)
(по двум сторонам и углу
между ними) ![]()
![]()
-
SOMCD=S
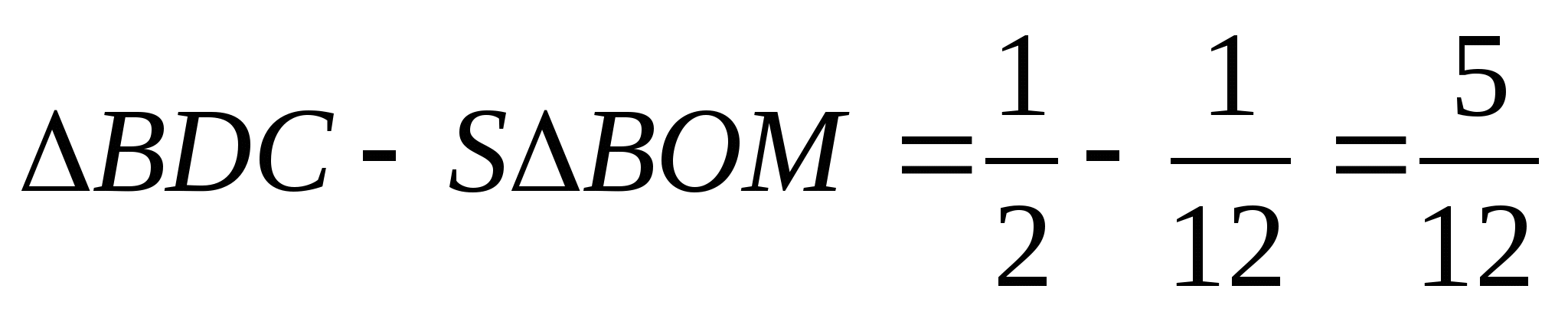
№3
Построить трапецию по четырем сторонам.
Дано:
AB=c,
BC=a,
CD=d,
AD=b
Построить трапецию ABCD
Дополнительное построение: строю BP||CD. Задача сводится к построению ABP по трем сторонам AB=c, BP=d, AP=b-a
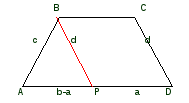
Построение:
1.СтроюABP по трем сторонам так, что AB=c, BP=d, AP=b-a.
2.Строю PD=a
3. Строю BC||PD, BC=a. AD=b
4. ABCD - искомая трапеция.
Доказательство:
1. BC||AD (по построению)
AB не параллельно CD, т.к BP||CD
ABCD - трапеция (по построению)
2. BC=a, AB=c, AD=b, CD=BP= (по построению)
3. ABCD - с данными сторонами.
Исследование: Задача имеет единственное решение, если можно построить ABP, т.е выполняется неравенство треугольника: c<d+(b-a), d<c+(b-a), b-a<c+d.
Провести прямую перпендикулярную данной
№1
На катетах AC и BC прямоугольного треугольника вне его построены квадраты ACDE и BCKF. Из точек E и F на продолжение гипотенузы опущены перпендикуляры EM и FN. Доказать, что EM+FN=AB.
Дано:
∆ABC−прямоугольный
ACDE и BCKF− квадраты
EM PA, FN BQ
Доказать, чтоEM+FN=AB.
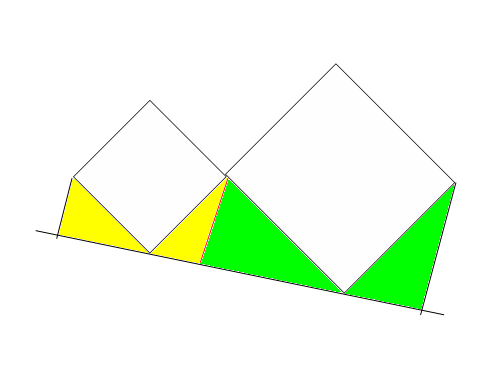
K
D
C
E F
P
M
A
L
B N Q
Решение
-
Дополнительное построение: строю CL
-
Пусть
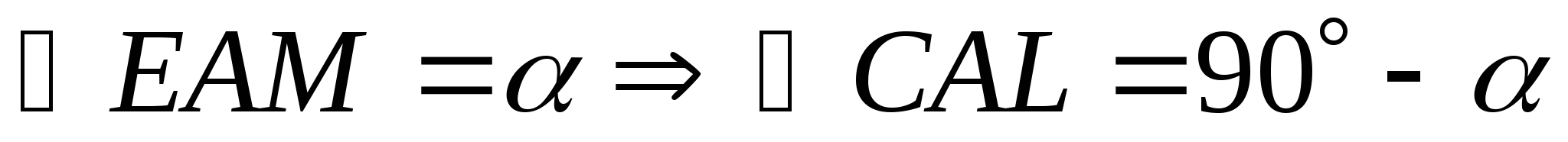 и
и 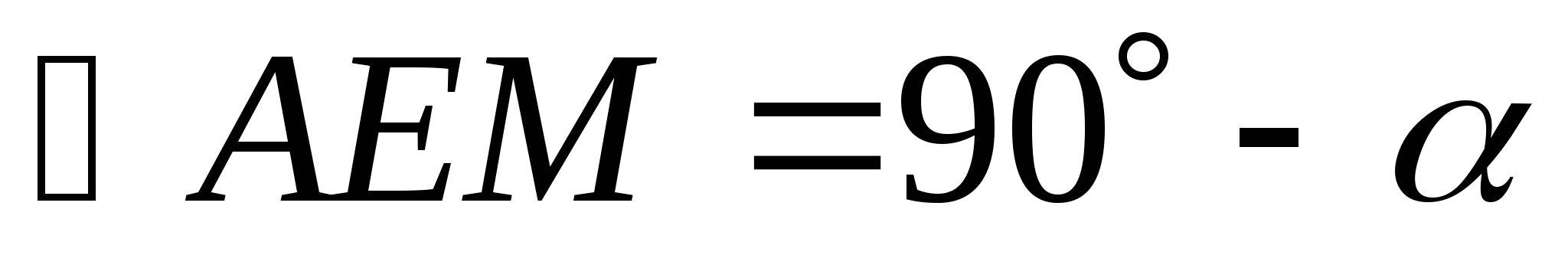
-
Аналогично
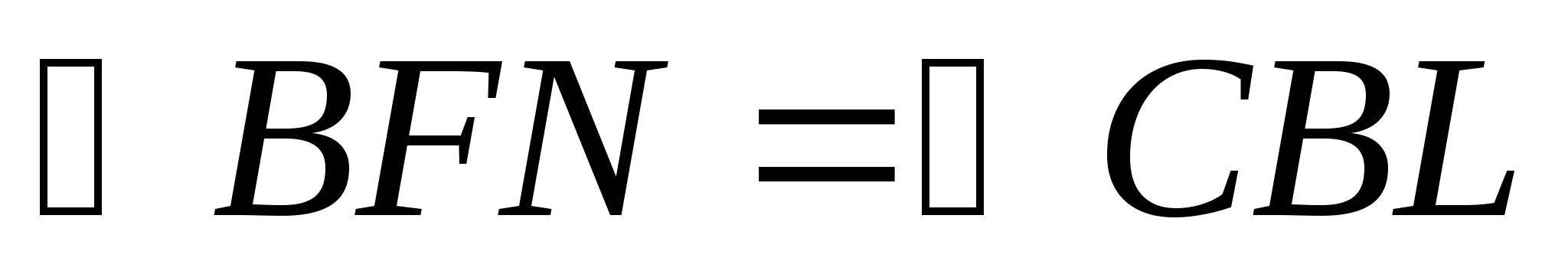
![]()
![]() (по катету и острому
углу) EM=AL, FN=LB
(по катету и острому
углу) EM=AL, FN=LB ![]() EM+FN=AL+LB=AB.
EM+FN=AL+LB=AB.
№2
Пусть AC − большая из диагоналей параллелограмма ABCD, Из точки C
на продолжения сторон AB и AD опущены перпендикуляры CE и CF
соответственно. Докажите, что AB∙AE+AD∙AF=AC ∙ AC.
Дано:
ABCD-параллелограмм
CE BN, CF DM
Доказать, что AB∙AE+AD∙AF=AC ∙ AC
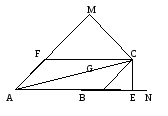
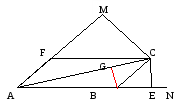
Решение
-
Дополнительное построение: строю BG
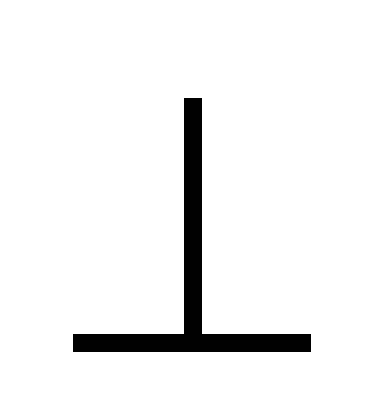 AC
AC
-
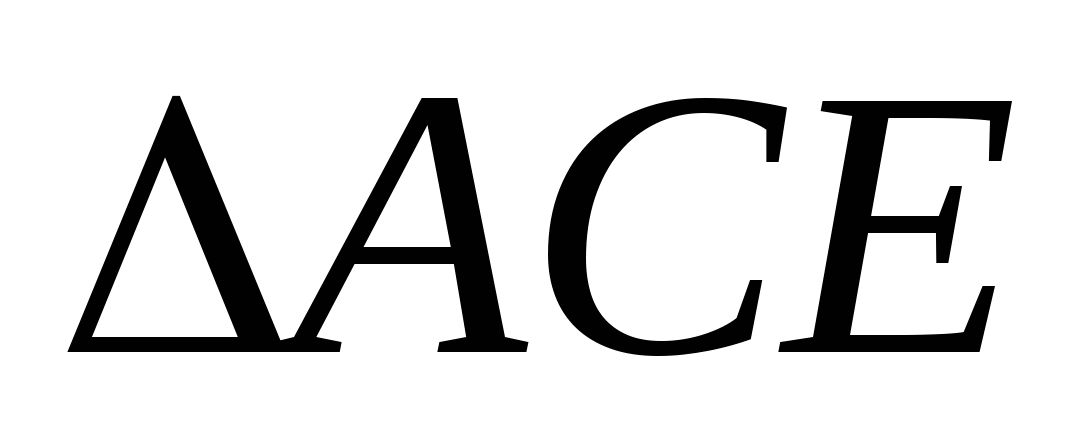 ~
~ 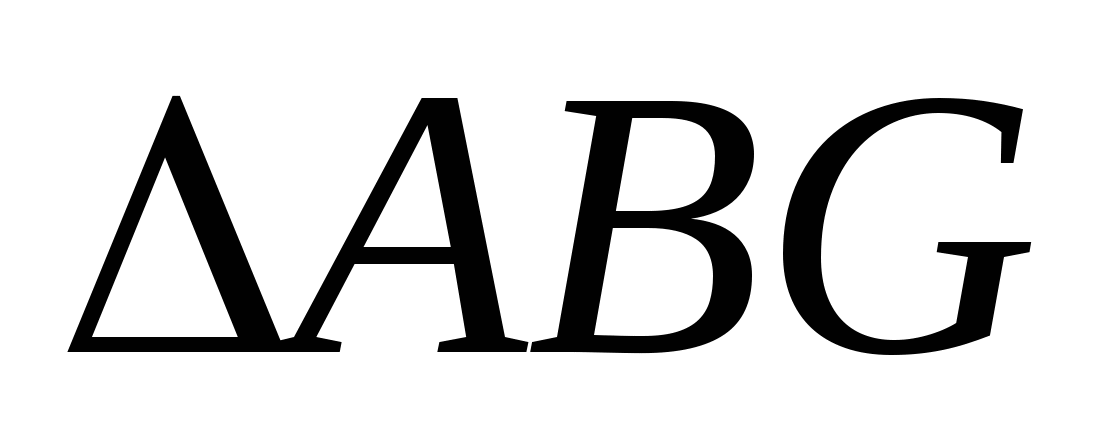 (
(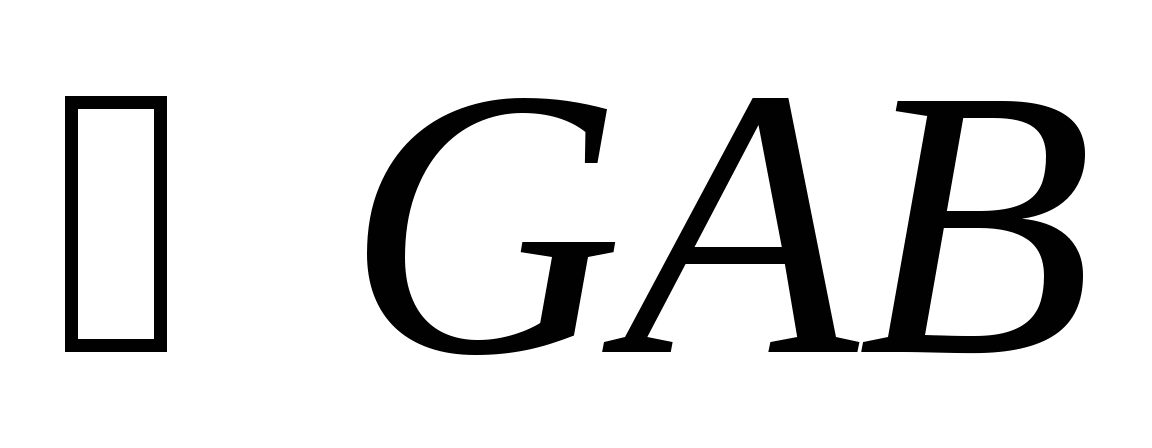 - общий,
- общий, 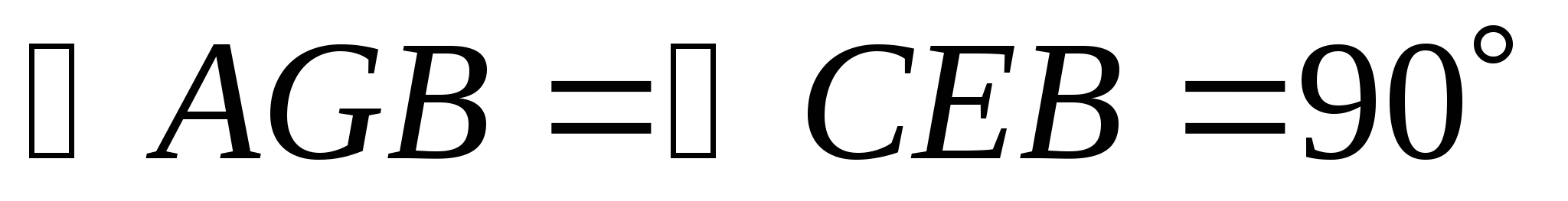 )
) 
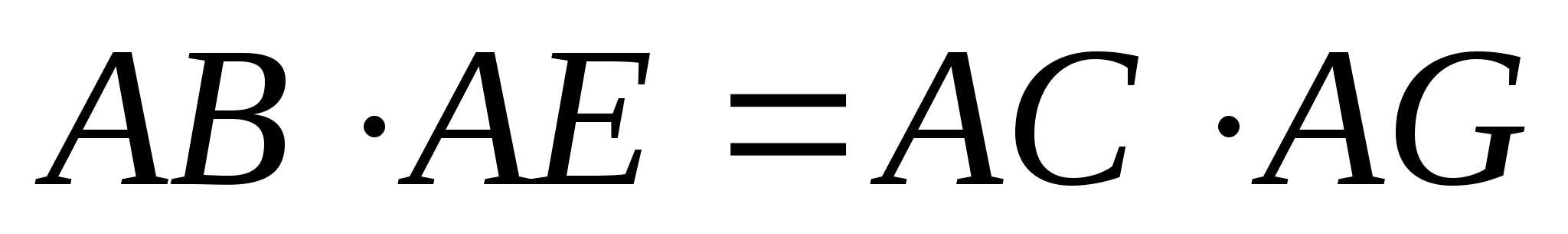
-
AF||CB


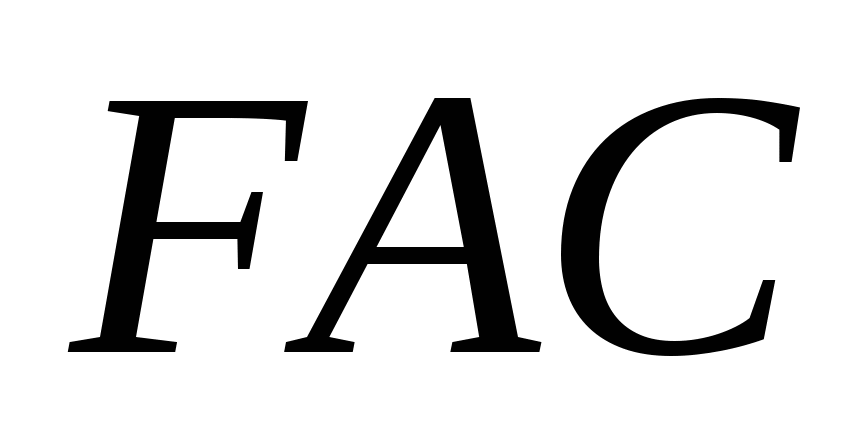 =
= 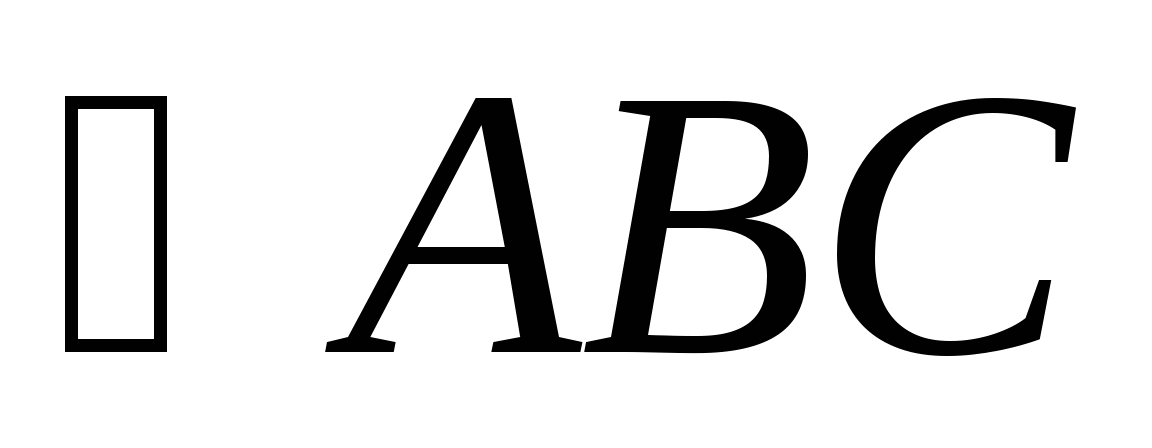 (как накрест лежащие
при прямых AF||CB b секущей AC)
(как накрест лежащие
при прямых AF||CB b секущей AC)
-
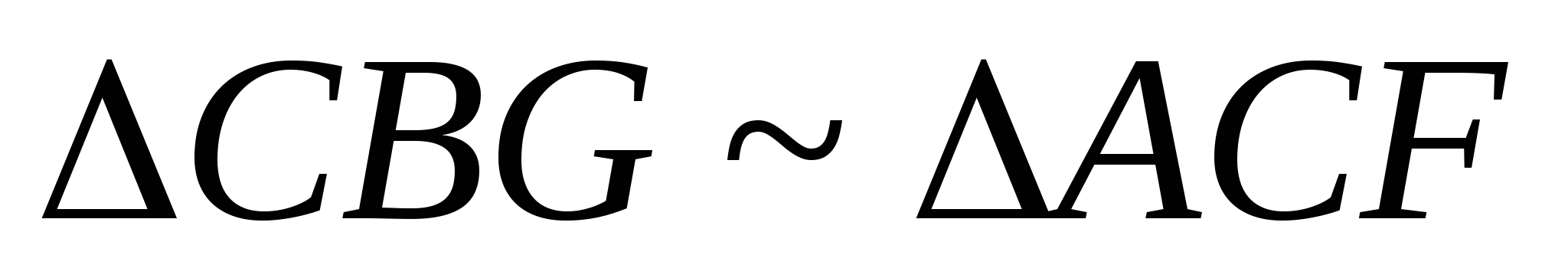 (
( FAC =
FAC =  ACB,
ACB, 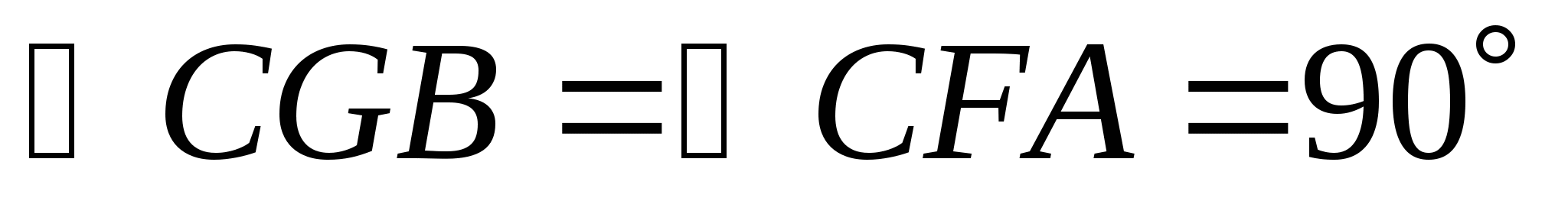 )
)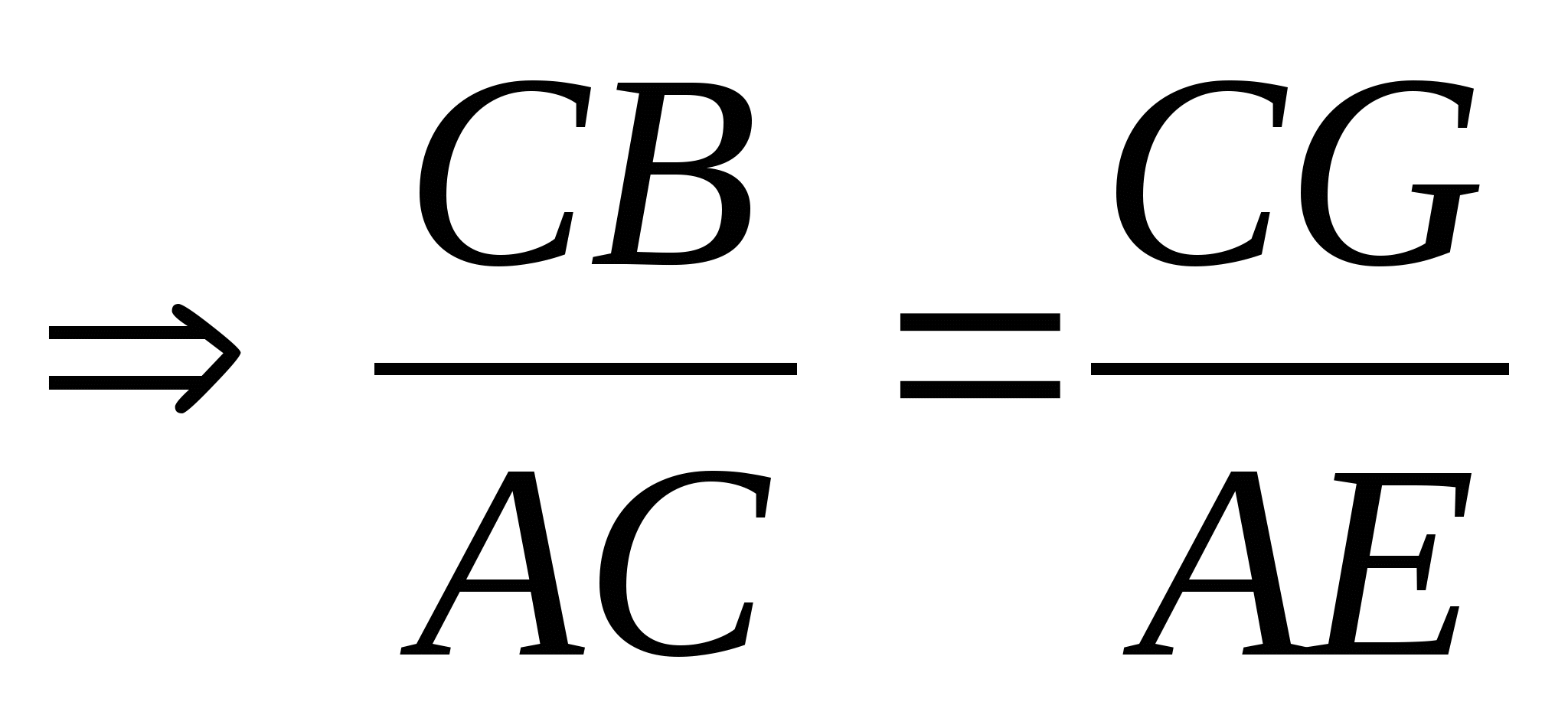
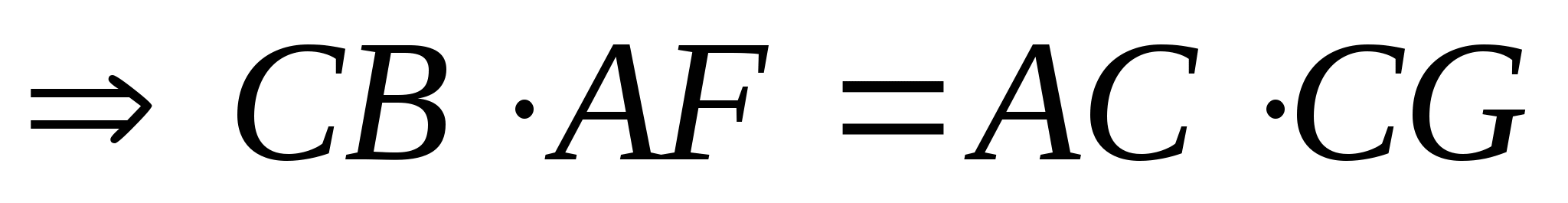
-
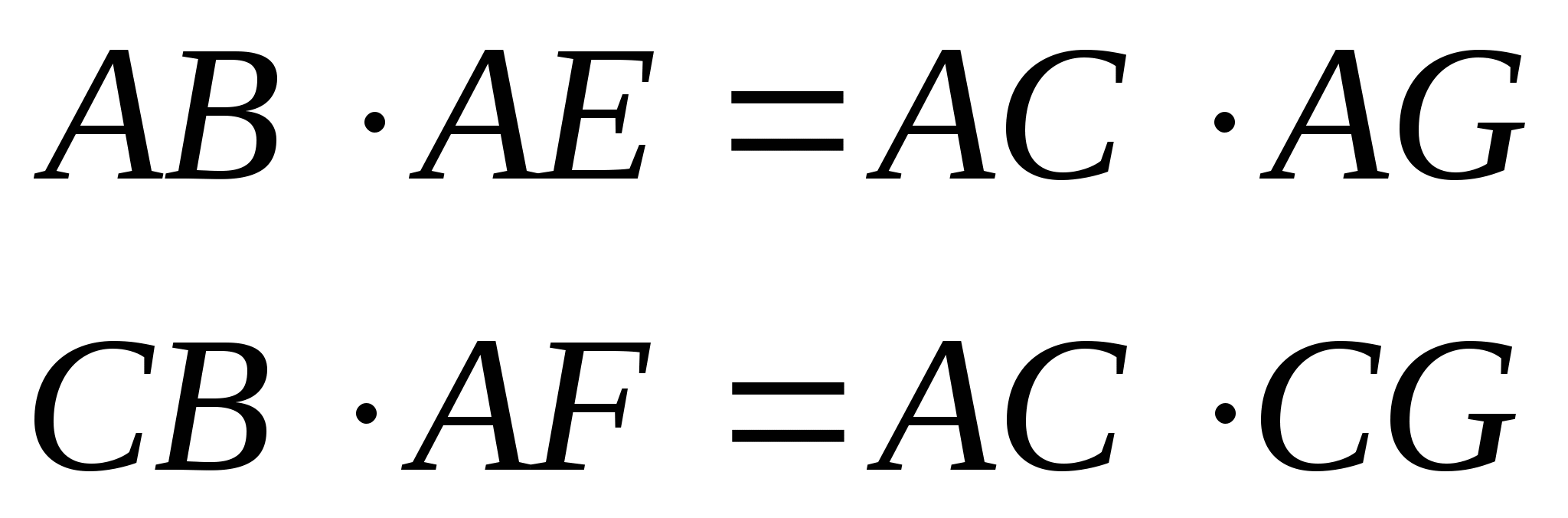
![]()
![]()
AB∙AE+AD∙AF=AC2
Построить окружность
№1
Найти сумму внутренних углов пятиконечной звезды
Дано
пятиконечная звезда
Н![]() айти:
айти:
C
B D
A E


P R
C
N S
B D
M T
A E
K Y
L X
Решение
Дополнительное построение: описываю около звезды окружность.
Угол между двумя пересекающимися хордами измеряется полусуммой заключенных между ними дуг
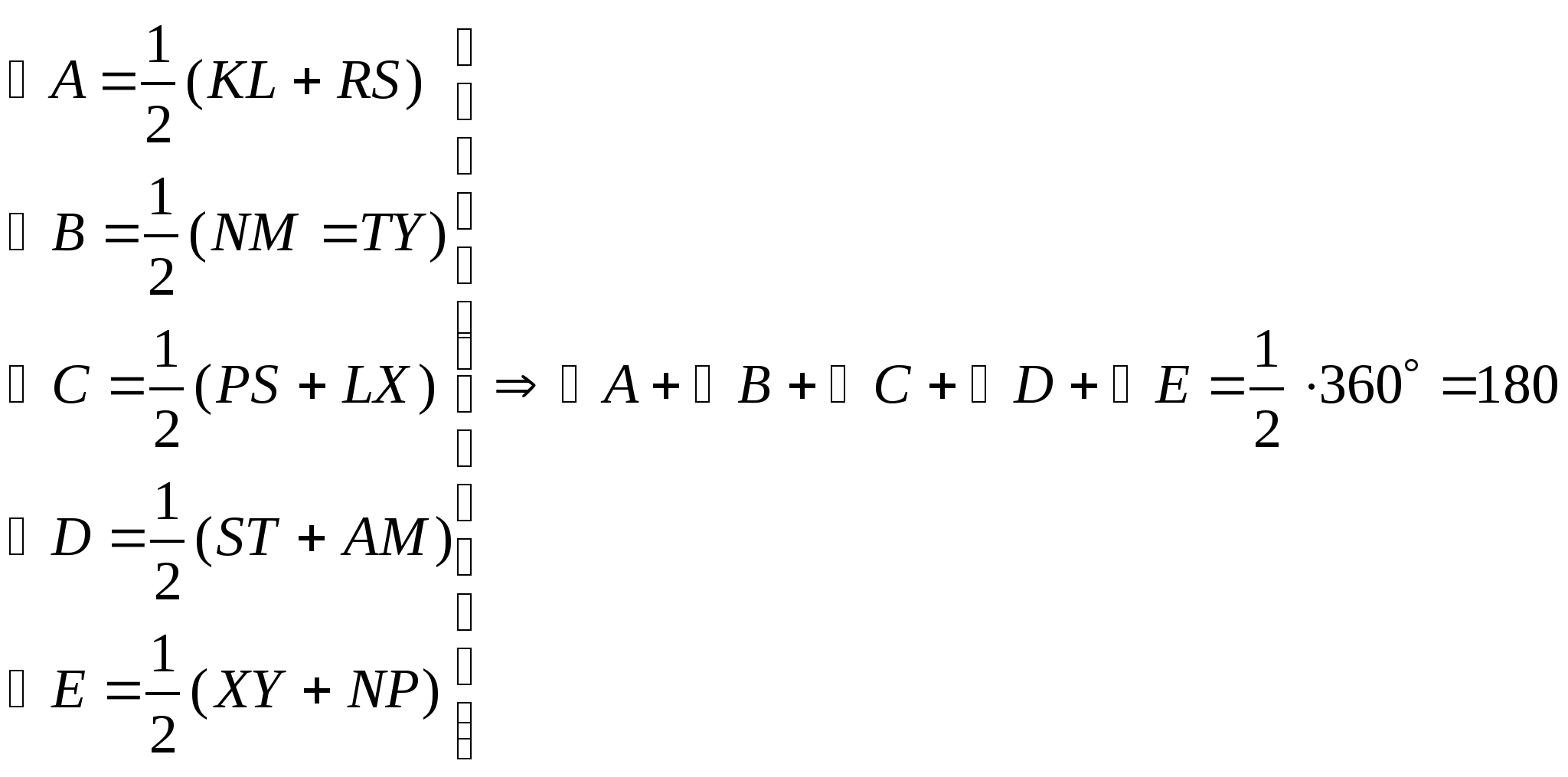
№2
В трапеции ABCD (AB и CD основания) меньшее основание равно
a, углы, прилежащие к этому основанию, равны 105 , а диагонали
взаимно перпендикулярны. Найти площадь трапеции.
Дано:
ABCD - трапеция
AB и CD -основания
Найти S трапеции.
Решение
-
Дополнительное построение: строю описанную окружность (т.к трапеция равнобедренная, то можно описать окружность)
-
Sтр. =
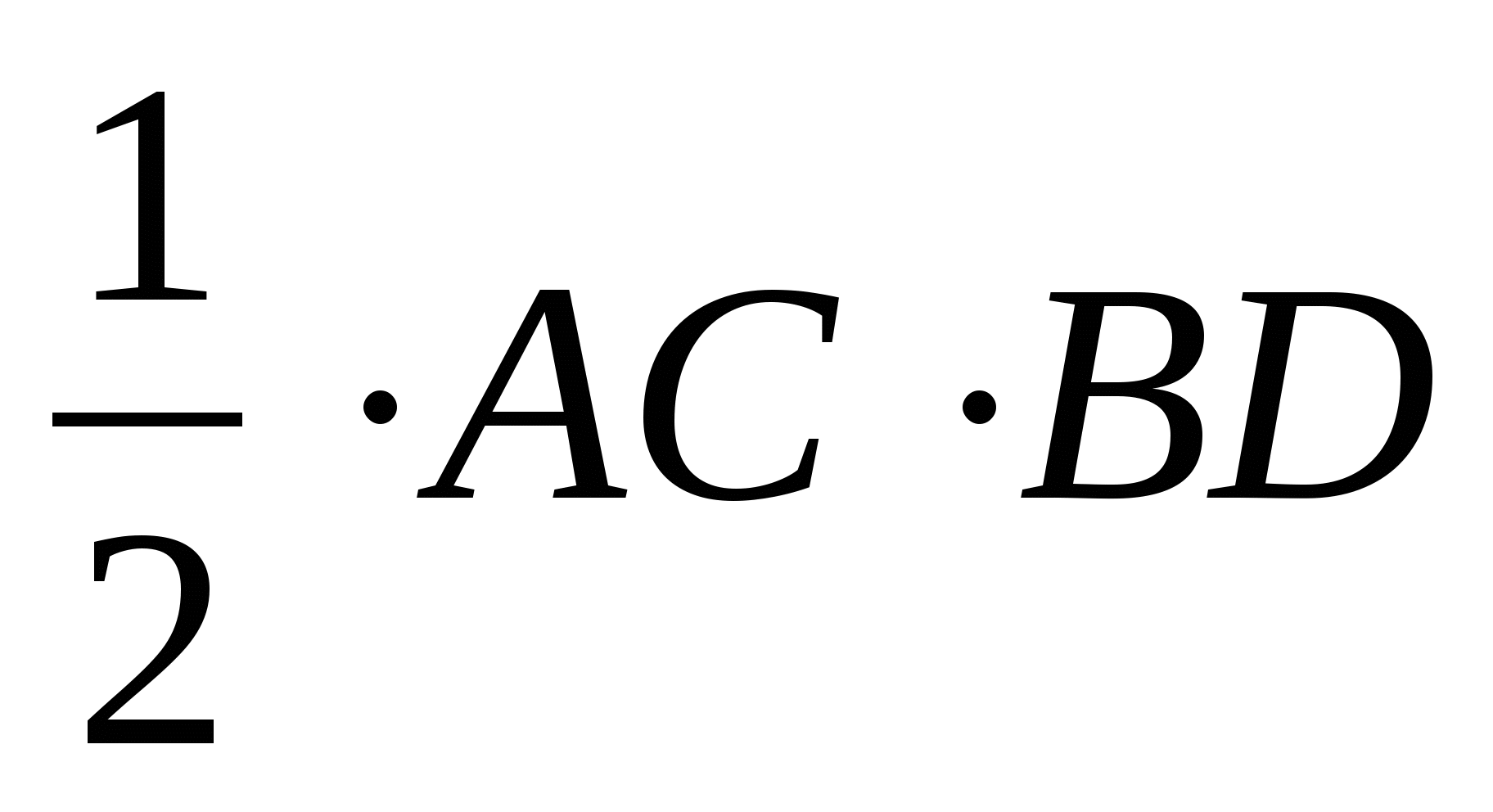
-
Пусть QB=x, AB=2x (т.к
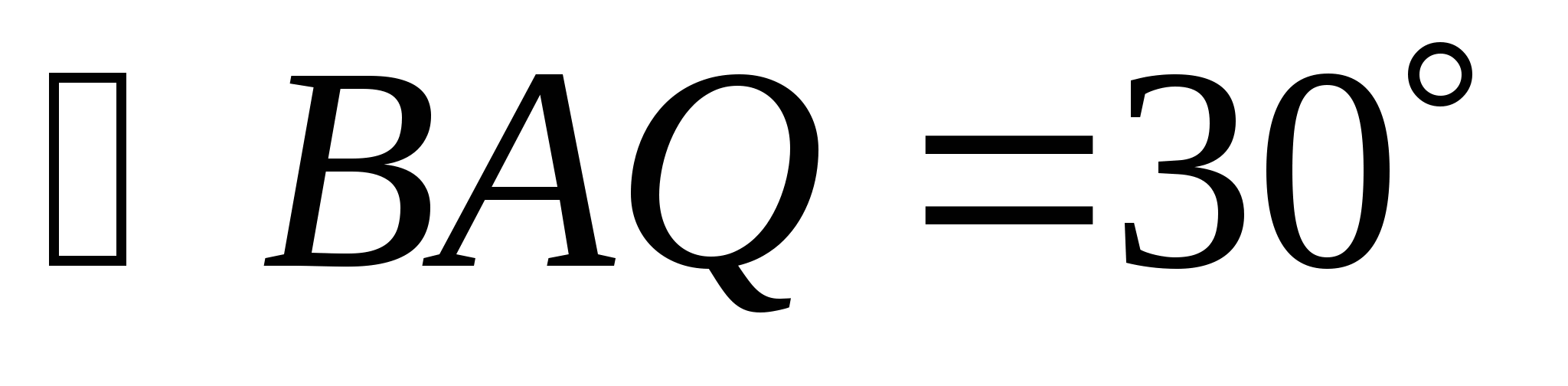 ), AQ=y по теореме
Пифагора:
), AQ=y по теореме
Пифагора:
![]()
![]()
![]()
-
BQ = QC = x
По теореме Пифагора из ∆BQC: ![]()
![]()
-
AQ=QD=y По теореме Пифагора из ∆AQD:
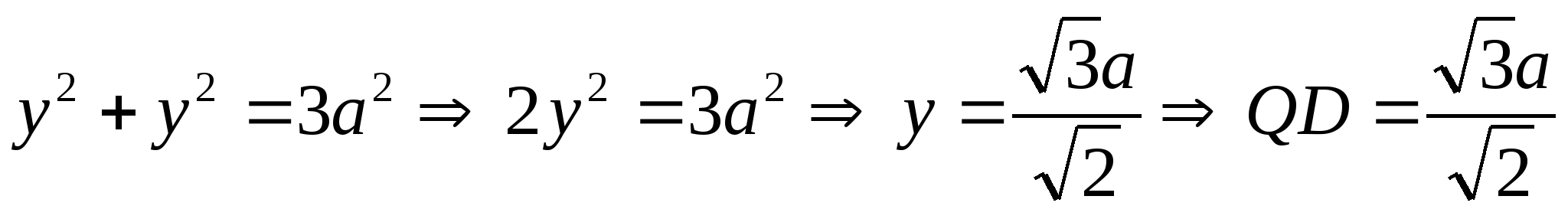
-
BD = BQ+QD =
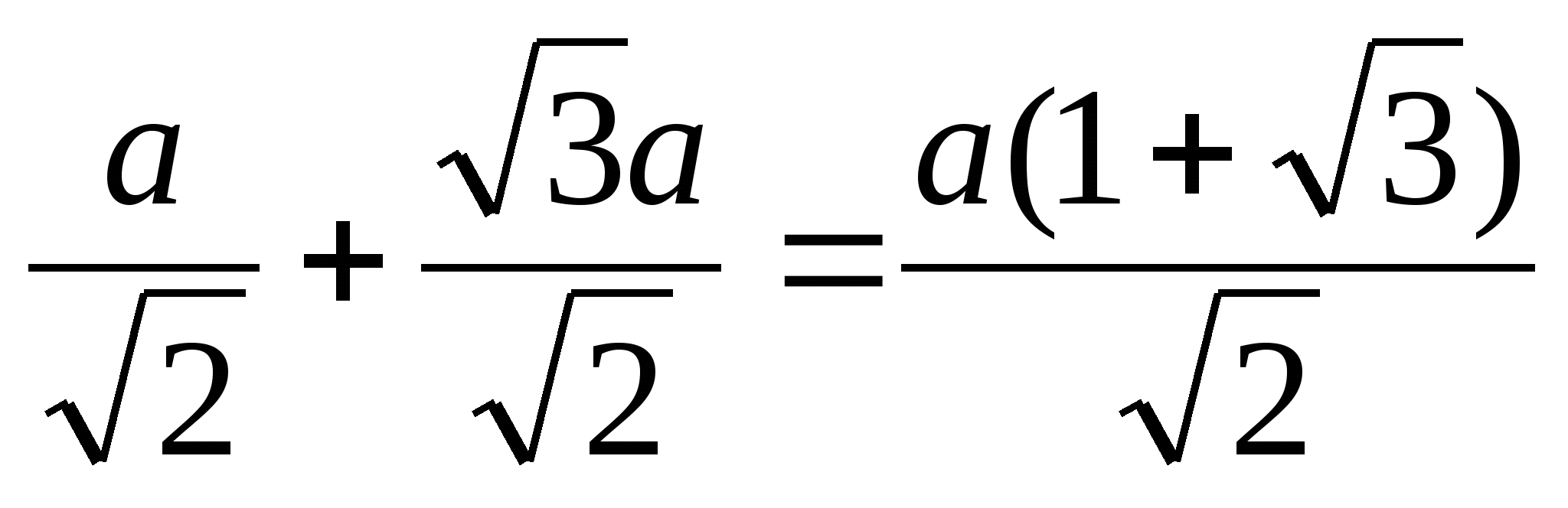
-
S
 =
= 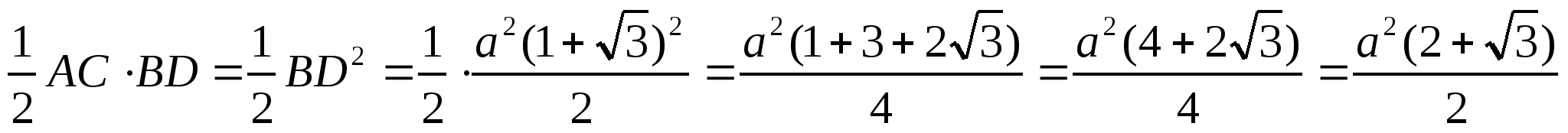
B C
Q
O
A D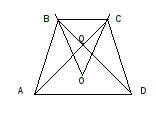
Заключение
Рассмотрев конкретные случаи, мы убедились, что решение задач с помощью дополнительных построений не только быстрей и проще, но и намного интересней, чем решение привычными способами.
Решая задачи на дополнительное построение, мы не только углубляем знания, но и развиваем изобретательность и геометрическую интуицию.
Хотелось бы продолжить работу по этой теме, добавив другие построения, например, преобразование на плоскости. Данный материал можно использовать при повторении курса планиметрии и при подготовке к ЕГЭ.
Литература
-
Математика. Приложение к газете «Первое сентября», - 1999.
-
Научно-популярный физико-математический журнал «Квант» №10,
1975.
-
Петраков И.С. Математические кружки в 8-10 классах. -
м.;Просвещение.1987.
-
Просолов В.В. задачи по планиметрии, 1часть-м.;Наука, 1986.
-
Просолов В.в. Задачи по планиметрии 2 часть - м .;Наука, 1986
-
Шарыгин И.Ф. решение задач. - м.;Просвещение, 1994.
-
Шарыгин И.Ф. Задачи по геометрии. - м;Наука , 1982.
Тезисы
-
Задачи решаемые продолжением медианы
-
Задачи решаемые проведением прямой параллельной данной
-
Задачи решаемые проведением прямой параллельной данной
-
Задачи решаемые построением окружности
Рецензия
На работу ученика 8а класса МОБУ СОШ №9 городского округа город
Нефтекамск Ярулина Булата
В работе Рассмотрены основные виды дополнительных построений при
решений задач:
-
Продолжить медиану
-
Провести прямую параллельную данной
-
Провести прямую перпендикулярную данной
-
Построить окружность
К каждому виду дополнительных построений подобранны и решены задачи,
которые
углубляют знания, развивают изобретательность и геометрическую
интуицию