- Учителю
- Урок по алгебре для 8 класса «Арифметический квадратный корень»
Урок по алгебре для 8 класса «Арифметический квадратный корень»
Тема урока. Арифметичний квадратний корінь.
Мета. Сформувати поняття квадратного кореня, арифметичного квадратного кореня, первинні навички добуваня арифметичного квадратного кореня з числа; удосконалювати вміння користуватися таблицею квадратів двоцифрових чисел.
Розвивати логічне мислення, пам'ять, навички самостійної роботи, вміння аналізувати, порівнювати, робити висновки.
Виховувати охайність, культуру математичних записів та обчислень, відповідальність, наполегливість, інтерес до вивчення математики.
Тип уроку. Урок засвоєння і первинне закріплення нових знань.
Форми роботи учнів: фронтальна, індивідуальна, парна.
Обладнання: роздавальний матеріал, презентація, проектор (телевізор),
комп`ютер.
ХІД УРОКУ
-
Організаційний момент.
Вчитель перевіряє готовність учнів до уроку. Повідомляє тему і мету уроку.
Наприкінці уроку необхідно буде
ЗНАТИ:
-що називають квадратним коренем з числа а;
-що називають арифметичним квадратним коренем з числа а;
- яким має бути число а;
ВМІТИ:
- добувати арифметичний квадратний корінь з числа;
- користуватися таблицею квадратів двоцифрових чисел;
II. Перевірка домашнього завдання.(Взаємоперевірка, коментар)
№351 ( Слайд 4, коментар учня), №355 (ілюстрація на дошці).
( Підручник алгебри для 8 класу. А.Г. Мерзляк)
-
Мотивація.
-Якому рівнянню рівносильна система з №355 (1)? (2)?
-Скільки розв'язків може мати рівняння вигляду
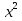 =а?
=а?
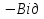 чого це залежить?
чого це залежить?
 . (Слайд 5).
. (Слайд 5).
Рівняння 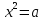
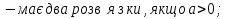
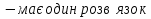 , якщо а=0;
, якщо а=0;
- не має 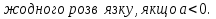
Отже, рівняння 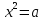 можна розв`язувати графічно. Які недоліки має графічний спосіб?
можна розв`язувати графічно. Які недоліки має графічний спосіб?
-
Пригадаємо, як ще можна розв`язувати рівняння
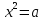 ? (Слайд 6)
? (Слайд 6)
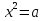
2)Знайдіть наближені значення коренів рівняння 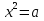 ілюстрацією до № 355 із домашнього завдання.
ілюстрацією до № 355 із домашнього завдання.
х₁ ≈ 1,4;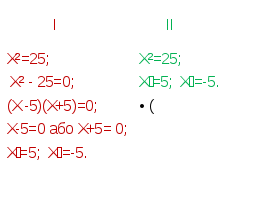 х₂ ≈ -1,4.
х₂ ≈ -1,4.
Як записати точні значення коренів такого рівняння, дізнаємося на уроці.
IV. Актуалізація знань.
1)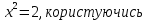

(Слайд 7)
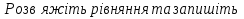
Самоперевірка(Слайд8).
V.Сприйняття нового матеріалу.
З давніх-давен поряд із
знаходженням площі квадрата за відомою довжиною його сторони, доводилося розв`язувати обернену задачу: "Якою повинна бути сторона квадрата, щоб його площа дорівнювала а?" 
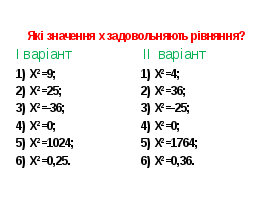
(Слайди 9,10)
Такі задачі вміли розв`язувати ще 4 тис. років тому вавілонські вчені. Вони складали таблиці квадратів чисел. Фрагмент такої таблиці знаходиться на форзаці ваших підручників.
Корені рівняння х₁ = 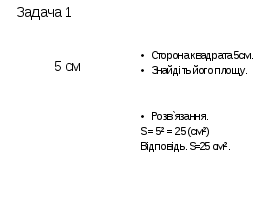 х₂ =
х₂ =  називають квадратними коренями з числа 49. Взагалі, корені рівняння
називають квадратними коренями з числа 49. Взагалі, корені рівняння 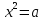 називають квадратними коренями з числа а..
називають квадратними коренями з числа а..
Знайдіть у підручнику означення квадратного кореня з числа а. Запишіть його.
Квадратним коренем з невід`ємного числа а називають число, квадрат якого дорівнює а.
-
Чому розглядають квадратний корінь саме з невід`ємного числа?
Повернемося до задачі 2. З двох протилежних коренів умові задачі задовольняє лише додатне число. Чому? (Бо довжина сторони квадрата - додатне число).
Невід`ємнє число називають арифметичним квадратним коренем з числа а.
Знайти у підручнику і записати означення арифметичного квадратного кореня.
Арифметичним квадратним коренем з невід`ємного числа а називається таке невід`ємне число х, квадрат якого дорівнює а.
Арифметичний квадратний корінь позначається √‾. Вираз, який записано під знаком кореня , називають підкореневим виразом. Зазвичай слово «арифметичний» при читанні опускають.
Наприклад: 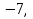 =16.
=16. 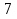 :
:
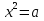 = ½.
= ½.
Процес знаходження квадратного кореня з числа називають ще добуванням квадратного кореня.
Висновок. Рівність 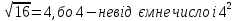 буде правильною, якщо виконуватимуться умови: (Слайд 11)
буде правильною, якщо виконуватимуться умови: (Слайд 11)
-
а
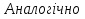 2) х
2) х 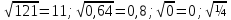 =а.
=а.
Тепер розв`язки рівняння 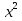 =а будемо записувати так:
=а будемо записувати так:
х₁ = 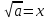 х₂ =
х₂ = 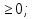
Наприклад: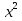 =5;
=5;
х₁ =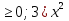 х₂=
х₂= 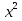 .
.
Хвилинка фізкультури
Історія виникнення знака арифметичного квадратного кореня. Повідомлення учня:
« У стародавній Індії невідоме називали «мула», що означає «початок», «основа», «корінь» (дерева). Араби для цього використовували слово «джизр» з тим самим значенням. Європейці переклали його як «radix» -
«корінь». Звідси виник математичний термін «радикал». З цією назвою пов`язано знак арифметичного квадратного кореня ![]() . Впродовж кількох століть математики вслід за Леонардо Пізанським квадратний корінь позначали знаком Rx (скорочено від radix). Поступово Rx перетворилося на букву r. У підручнику з алгебри Кристофа Рудольфа, написаному німецькою мовою (1525 р), замість r використовувався знак √. Цей символ вже схожий на той, яким ми користуємося. А горизонтальну риску запровадив у 1637 році Рене Декарт».
. Впродовж кількох століть математики вслід за Леонардо Пізанським квадратний корінь позначали знаком Rx (скорочено від radix). Поступово Rx перетворилося на букву r. У підручнику з алгебри Кристофа Рудольфа, написаному німецькою мовою (1525 р), замість r використовувався знак √. Цей символ вже схожий на той, яким ми користуємося. А горизонтальну риску запровадив у 1637 році Рене Декарт».
VI. Первинне закріплення.
№379(1,5,9,13) - учень біля дошки; №381 (усно); №383 (1,5,7) - з коментарем.
VII. Навчальна самостійна робота (у парах)
Кожен учень одержує аркуш з навчальною самостійною роботою, де необхідно
заповнити пропуски.
-
Знайдіть значення арифметичного квадратного кореня:
а)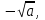 …
…
б )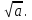 …
…
в)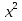 …
…
г) 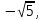 …
…
д) 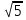 …
…
є) 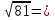 …
…
2) Розв`яжіть рівняння:
а) х² = 64;
х₁= 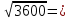 х₂ = -
х₂ = - 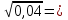 ;
;
х₁= …, х₂ = - …
Відповідь. х₁= …, х₂ = - …
б) х² = 11;
х₁= 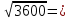 х₂ = -
х₂ = - 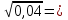 ;
;
х₁= …, х₂ = - …
Відповідь. х₁= …, х₂ = - …
в) х² = - 0,144;
VIII.Підсумки уроку. 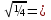
IX. Рефлексія.
ПРОАНАЛІЗУЙТЕ СВОЮ РОБОТУ НА УРОЦІ. ПОЗНАЧТЕ ЗНАКОМ «+» ТІ ВИСЛОВЛЮВАННЯ, З ЯКИМИ ВИ ЗГОДНІ:
1.У мене сьогодні все вийшло. Я не припускався помилок.
2.Всі правила я пам`ятаю, але не все вийшло при виконанні завдань.
3. Я знаю, що необхідно повторити.
X. Домашнє завдання.
1) Прочитати п.12. Вивчити означення квадратного кореня і арифметичного квадратного кореня.
2) Виконати № 380 (1,4,7,10), № 384 (1,3,5), № 396.
Навчальна самостійна робота.
8-__ клас___________________________________________________
Знайдіть значення арифметичного квадратного кореня:
а)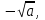
б )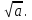
в)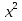
г) 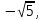
д) 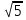
є) 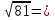
2) Розв`яжіть рівняння:
а) х² = 64; в) х² = - 0,144;
х₁= 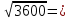 х₂ = -
х₂ = - 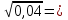 ; Відповідь………………………………
; Відповідь………………………………
х₁= …, х₂ = - …
Відповідь. х₁= …, х₂ = - …
б) х² = 11;
х₁= 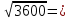 х₂ = -
х₂ = - 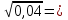 ;
;
х₁= …, х₂ = - …
Відповідь. х₁= …, х₂ = - …
РЕФЛЕКСІЯ. Проаналізуйте свою роботу на уроці та позначте знаком «+» ті висловлювання, з якими ви згодні:
1.У мене сьогодні все вийшло. Я не припускався помилок. 2.Всі правила я пам`ятаю, але не все вийшло при виконанні завдань.
3.Я знаю, що необхідно повторити.