Учителю
КОНТРОЛЬНО-ОЦЕНОЧНЫЕ СРЕДСТВА ПО УЧЕБНОЙ ДИСЦИПЛИНЕ ЕН. 01 Элементы высшей математики 230115 Программирование в компьютерных системах (базовой подготовки)

КОНТРОЛЬНО-ОЦЕНОЧНЫЕ СРЕДСТВА ПО УЧЕБНОЙ ДИСЦИПЛИНЕ ЕН. 01 Элементы высшей математики 230115 Программирование в компьютерных системах (базовой подготовки)

Автор публикации: Саттарова Г.Ф.

Дата публикации: 23.08.2016

Краткое описание:

предварительный просмотр материала

Министерство образования и науки РТ

ГАОУ СПО

«Арский агропромышленный профессиональный колледж»

КОНТРОЛЬНО-ОЦЕНОЧНЫЕ СРЕДСТВА

ПО УЧЕБНОЙ ДИСЦИПЛИНЕ

ЕН. 01 Элементы высшей математики

230115 Программирование в компьютерных системах

(базовой подготовки)

Урняк 2014 г.

Разработчик:

ГАОУ СПО ААПК преподаватель математики Г.Ф. Саттарова

(место работы) (занимаемая должность) (инициалы, фамилия)

Одобрено на заседании методической комиссии (общеобразовательных дисциплин) _________________________________________________________

Протокол №_______ от «_____» _________ 20____г.

Председатель МК ____________________ /____________/

Одобрено Методическим советом колледжа

Протокол №_______ от «_____» _________ 20____г.

Содержание.

Общие положения.
1. Освоенные знания и умения
2. Общие компетенции
1. Профессиональные компетенции

Результаты освоения учебной дисциплины, подлежащие проверке.
Контроль и оценка освоения учебной дисциплины по темам (разделам), видам контроля.
Шкала оценки образовательных достижений.
Комплект оценочных средств.
1. Задания текущего контроля.
2. Вопросы и задания для зачета.
3. Пакет экзаменатора.
Информационное обеспечение обучения.

Общие положения

Контрольно - оценочные материалы (КОС) предназначены для контроля и оценки образовательных достижений обучающихся, освоивших программу учебной дисциплины Элементы высшей математики.

КОС включают контрольные материалы для проведения текущего контроля и промежуточной аттестации в форме дифференцированного зачета.

КОС разработаны на основании положений:

основной профессиональной образовательной программы по направлению подготовки специальности СПО 230115 Программирование в компьютерных системах;

программы учебной дисциплины Элементы высшей математики.

В результате освоения учебной дисциплины Элементы высшей математики обучающийся должен обладать предусмотренными ФГОС по специальности СПО230115 Программирование в компьютерных системах следующими умениями, знаниями, которые формируют профессиональную компетенцию, и общими компетенциями:

1. Освоенные знания и умения:

У1 - выполнять операции над матрицами и решать системы линейных уравнений;

У2 - решать задачи, используя уравнения прямых и кривых второго порядка на плоскости;

У3 - применять методы дифференциального и интегрального исчисления;

У4 - решать дифференциальные уравнения,

У5 - пользоваться понятиями теории комплексных чисел;

З1 - основы математического анализа, линейной алгебры и аналитической геометрии

З2 - основы дифференциального и интегрального исчисления

З3 - основы теории комплексных чисел.

1.2. Общие компетенции:

ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.

ОК 6. Работать в коллективе и в команде, эффективно общаться с коллегами, руководством, потребителями.

ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), за результат выполнения заданий.

ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.

ОК 10. Исполнять воинскую обязанность, в том числе с применением полученных профессиональных знаний (для юношей).

1.3. Профессиональные компетенции:

ПК 1.1. Выполнять разработку спецификаций отдельных компонент.

ПК 1.2. Осуществлять разработку кода программного продукта на основе готовых спецификаций на уровне модуля.

ПК 2.4. Реализовывать методы и технологии защиты информации в базах данных.

ПК 3.4. Осуществлять разработку тестовых наборов и тестовых сценариев.

Результаты освоения дисциплины, подлежащие проверке.

2.1. В результате аттестации по учебной дисциплине осуществляется комплексная проверка следующих умений и знаний, а также динамика формирования общих и профессиональных компетенций, если предусмотрено ФГОС:

Результаты обучения: умения, знания и общие компетенции

Показатели оценки результата

Форма контроля и оценивания

Уметь:

У1 - выполнять операции над матрицами и решать системы линейных уравнений;

ОК 1, ОК 2, ОК 3, ОК 5, ОК 6

Выполнение действий над матрицами

Вычисление определителей

Нахождение обратной матрицы

Решение систем линейных уравнений по формулам Крамера

Решение систем линейных уравнений методом Гаусса.

Анализ и оценка результатов выполнения

практических работ.

Оценка результатов выполнения

контрольных работ.

Оценка выполнения

расчетных работ.

Зачет.

Экзамен

У2 - решать задачи, используя уравнения прямых и кривых второго порядка на плоскости;

ОК 1,ОК 2, ОК 3, ОК , ОК 8, ОК 9

Составлять различные виды уравнений прямой.

Составлять уравнения кривых второго порядка, находить их характерные точки, строить кривые.

У3 - применять методы дифференциального и интегрального исчисления;

ОК 1, ОК 2, ОК 3, ОК 6, ОК 9

Нахождение производной функции.

Нахождение производных высших порядков.

Исследование функций и построение ее графика.

Нахождение неопределенных

интегралов.

Вычислениеопределенных

интегралов.

Вычисление площадей плоских фигур, объемов тел вращения.

Нахождение частных производных первого и второго порядков.

Вычисление кратных интегралов

У4 - решать дифференциальные уравнения,

ОК 1, ОК 2, ОК 3, ОК 4

Решение дифференциальных уравнений первого и второго порядка.

У5 - пользоваться понятиями теории комплексных чисел;

ОК 1, ОК 2, ОК 3, ОК 6, ОК 7, ОК 9

Записывать комплексные числа в алгебраической и тригонометрической формах.

Выполнять действия над комплексными числами.

Знать:

З1 - основы математического анализа, линейной алгебры и аналитической геометрии;

Перечисление последовательности действий при нахождении суммы и произведения матриц, вычисления определителя, нахождении обратной матрицы, при решении систем линейных уравнений по правилу Крамера, методом Гаусса.

Выполнение действийнад векторами Нахождениескалярного, векторного и смешанного произведения векторов

Знание различных видов уравнений прямой.

Знание уравнений кривых второго порядка, их характерных точек.

Вычисление предела функции в точке и в бесконечности.

Перечисление признаков сходимости рядов.

Исследование рядов на сходимость.

Нахождение области сходимости степенных рядов

Оценка устных ответов

Анализ и оценка результатов выполнения

практических работ.

Оценка результатов выполнения

контрольных работ.

Оценка выполнения

расчетных работ.

Зачет.

Экзамен.

З2 - основы дифференциального и интегрального исчисления;

Формулировка определения производной.

Формулировка геометрического и механического смысла производной.

Знание таблицы производных.

Знание правил дифференцирования.

Знание правил нахождения производной от сложной функции.

Знание определения и свойств интегралов.

Знание основных табличных интегралов.

Приложение определенного интеграла к вычислению площадей плоских фигур, объемов тел вращения.

Знание правил нахождения частных производных первого и второго порядков.

Знание правил вычисления кратных интегралов

З3 - основы теории комплексных чисел.

Знание определения и различных форм записи комплексных чисел.

Правила выполнения операций над комплексными числами.

3 Контроль и оценка освоения учебной дисциплины по темам (разделам), видам контроля

Текущий контроль

Промежуточная аттестация

Форма контроля

Проверяемые ОК, ПК (или ее части), У, З

Форма контроля

Проверяемые ОК, ПК (или ее части), У, З

Раздел 1. Линейная и векторная алгебра

Зачет
Экзамен

З1
У1
ОК 1, ОК 2, ОК 4

Тема 1.1.Матрицы и действия над ними.Определители, свойства и вычисление.

Практическая работа
Расчетное задание №1
Контрольная работа №1

З1
У1
ОК 1, ОК 2, ОК 4

Тема 1.2.Системы линейных уравнений.

Практическая работа
Расчетное задание №1
Контрольная работа №1

З1
У1
ОК 1, ОК 2, ОК 4

Тема 1.3.Векторная алгебра. Нелинейные операции над векторами

Устный опрос №1
Практическая работа Расчетное задание №2
Контрольная работа №1

З1
ОК 1, ОК 2, ОК 4

Раздел 2. Аналитическая геометрия на плоскости

Зачет
Экзамен

Тема 2.1.Метод координат на плоскости. Прямая линия.

Практическая работа
Расчетное задание №3
Контрольная работа №2

З1
У2
ОК 1, ОК 2, ОК 4, ОК5

З1
У2
ОК 1, ОК 2, ОК 4, ОК5

Тема 2.2.Взаимное расположение прямых. Кривые второго порядка.

Практическая работа
Контрольная работа№2

З1
У2
ОК 1, ОК 2, ОК 4, ОК5

Раздел 3.Дифференциальное исчисление функции одной переменной

Зачет
Экзамен

Тема 3.1.Введение в математический анализ

Практическая работа
Контрольная работа№3

У3
ОК 1, ОК 2, ОК 4, ОК5

З1, З2
У3
ОК 1, ОК 2, ОК 4, ОК5

Тема 3.2.Предел и непрерывность функции

Практическая работа
Расчетное задание №4,5
Контрольная работа№3

З1
У3
ОК 1, ОК 2, ОК 4, ОК5

Тема 3.3.Понятие производной и ее геометрический смысл. Дифференциал функции.

Устный опрос№2
Практическая работа
Расчетное задание №6 Контрольная работа№3

З2
У3
ОК 1, ОК 2, ОК 4, ОК5

Тема 3.4. Производные и дифференциалы высших порядков.

Расчетное задание №6
Контрольная работа№3

З2
У3
ОК 1, ОК 2, ОК 4, ОК5

Тема 3.5.Свойства дифференцируемых функций.

Практическая работа
Расчетное задание №7
Контрольная работа №3

У3
ОК 1, ОК 2, ОК 4, ОК5

Раздел 4.Интегральное исчисление функции одной переменной

Зачет
Экзамен

Тема 4.1.Интегральное исчисление функции одной переменной

Устный опрос№3
Расчетное задание №8
Контрольная работа №4

З2
У3
ОК 1, ОК 2, ОК 4, ОК5

З2
У3
ОК 1, ОК 2, ОК 4, ОК5

Тема 4.2.Методы вычисления неопределенного интеграла.

Практическая работа
Расчетное задание №8 Контрольная работа №4

З2
У3
ОК 1, ОК 2, ОК 4, ОК5

Тема 4.3.Определенный интеграл. Приложение определенного интеграла

Практическая работа
Расчетное задание №9 Контрольная работа№4

З2
У3
ОК 1, ОК 2, ОК 4, ОК5

Раздел 5. Дифференциальное и интегральное исчисления функции нескольких переменных

Экзамен

З2
У3
ОК 1, ОК 2,ОК 4, ОК 8

Тема 5.1.Дифференциальное исчисление функции многих переменных

Практическая работа
Расчетное задание №10 Контрольная работа№5

У3
ОК 1, ОК 2,ОК 4, ОК8

Тема 5.2.Приложение дифференциального исчисления функции многих переменных

Практическая работа
Контрольная работа№5

У3
ОК 1, ОК 2,ОК4, ОК 8

Тема 5.3.Интегральное исчисление функции многих переменных.

Практическая работа
Контрольная работа№5

У3
ОК 1, ОК 2,ОК4, ОК 8

Раздел 6.Ряды

Экзамен

З1
ОК 1, ОК 2,ОК4, ОК 8

Тема 6.1. Числовые ряды

Практическая работа
Расчетное задание №11
Контрольная работа№6

З1
ОК 1, ОК 2,ОК4, ОК 8

Тема 6.2.Функциональные ряды.

Практическая работа
Расчетное задание №11 Контрольная работа№6

З1
ОК 1, ОК 2,ОК4, ОК 8

Раздел 7.Дифференциальные уравнения

Экзамен

У4
ОК 1, ОК 2,ОК 3, ОК5, ОК 8

Тема 7.1.Дифференциальные уравнения.

Практическая работа
Расчетное задание №12
Контрольная работа№7

У4
ОК 1, ОК 2,ОК 3, ОК5, ОК 8

Тема 7.2.Дифференциальные уравнения первого порядка.

Практическая работа
Расчетное задание №16
Контрольная работа№7

У4
ОК 1, ОК 2,ОК 3, ОК5, ОК 8

Тема 7.3.Дифференциальные уравнения второго и высших порядков

Устный опрос№4
Практическая работа
Расчетное задание №12
Контрольная работа№7

У4
ОК 1, ОК 2,ОК 3, ОК5, ОК 8

Тема 7.4.Линейные уравнения второго порядка с постоянными коэффициентами

Устный опрос№4
Практическая работа
Расчетное задание №12
Контрольная работа№7

У4
ОК 1, ОК 2,ОК 3, ОК5, ОК 8

Раздел 8.Основы теории комплексных чисел

Экзамен

З3
У5
ОК 1, ОК 2,ОК 3,
ОК 4, ОК 5

Тема 8.1.Основы теории комплексных чисел

Практическая работа
Расчетное задание №13 Контрольная работа№8

З3
У5
ОК 1, ОК 2,ОК 3,
ОК 4, ОК 5

Шкала оценки образовательных достижений.

1. Комплект оценочных средств.
1. 1. Задания текущего контроля.
2. Контрольная работа № 1. Линейная и векторная алгебра.
4. Вариант -1
6. 1. Найти сумму матриц А и В
7. ,
9. 2. Найти произведение матриц А и В
10. ,
12. 3. Вычислить определитель
13. 4. Найти обратную матрицу А^-1 для матрицы АA =
15. 5. Решить систему уравнений по правилу Крамера.
1. Даны векторы a(9;2;1) и b(4;3;0).
1. Найти
2. Найти[]
3. Найти
4. Найти
5. Найти координаты векторов =,.
3. Вариант- 2
5. 1. Найти сумму матриц А и В
7. ,
9. 2. Найти произведение матриц А и В
11. A= ,
14. 3. Вычислить определитель
17. 4. Найти обратную матрицу А^-1 для матрицы А
19. 5. Решить систему уравнений методом Гаусса
22. 6. Даны векторы a(-3;2;1) и b(3;0;4).
1. Найти
2. Найти[]
3. Найти
4. Найти
5. Найти координаты векторов =, .
2. Время на выполнение: 90 мин.
3. Перечень объектов контроля и оценки
4. Перечисление последовательности действий при нахождении суммы и произведения матриц, вычисления определителя, нахождении обратной матрицы, при решении систем линейных уравнений по правилу Крамера, методом Гаусса.
5. Выполнение действийнад векторами Нахождениескалярного, векторного и смешанного произведения векторов
  1. У1. выполнять операции над матрицами и решать системы линейных уравнений;
  1. Выполнение действий над матрицами
  2. Вычисление определителей
  3. Нахождение обратной матрицы
  4. Решение систем линейных уравнений по формулам Крамера
  5. Решение систем линейных уравнений методом Гаусса
Контрольная работа № 2. Аналитическая геометрия на плоскости
Вариант - 1

Общее, каноническое, параметрическое уравнения прямой впространстве.
Угол между двумя прямыми. Взаимное расположение прямых.
Расстояние от точки до прямой.
Уравнение окружности. Каноническое уравнение эллипса, гиперболы, параболы.
Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).

Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением: Схематично построить кривую.

Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Составить уравнение эллипса, если его фокусы F₁(0; 0), F₂(1; 1), большая ось равна 3. Схематично построить кривую.

Вариант - 2

Общее уравнение прямой. Уравнение прямой с угловым коэффициентом.
Уравнение прямой с данным угловым коэффициентом и проходящей через данную точку.
Уравнение прямой в отрезках, уравнение прямой проходящей через две точки.
Уравнение окружности. Каноническое уравнение эллипса, гиперболы, параболы.
Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).
На параболе у² = 8х найти точку, расстояние которой от директрисы равно 4.Схематично построить кривую.
Задано общее уравнение прямой х - у + 1 = 0. Найти уравнение этой прямой в отрезках.
Составить уравнение гиперболы, если ее эксцентриситет равен 2, а фокусы совпадают с фокусами эллипса с уравнением Схематично построить кривую.

Время на выполнение: 90 мин.
Перечень объектов контроля и оценки
Знание различных видов уравнений прямой.
Знание уравнений кривых второго порядка, их характерных точек.
1. У2. решать задачи, используя уравнения прямых и кривых второго порядка на плоскости
1. Составлять различные виды уравнений прямой.
2. Составлять уравнения кривых второго порядка, находить их характерные точки, строить кривые.
Контрольная работа № 3. Дифференциальное исчисление функции одной переменной.
Вариант - 1
1. Вычислить предел: .
2. Вычислить предел: .
3. Вычислить предел: .
4. Вычислить предел: .
5. Вычислить предел: .
6.Найти производную функции у = sin⁶(4х³ -2).
7. Найти производную второго порядка: .
8. Найти дифференциал функции: .
9. Материальная точка движется по закону х(:) = t⁴ + 2t. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
10. Найти предел, используя правило Лопиталя: .
Вариант - 2
1. Вычислить предел: .
2. Вычислить предел: .
3. Вычислить предел: .
4. Вычислить предел: .

Вычислить предел: .
Найти производную функции у = ctg⁴ (5х³ +6).
Найти производную второго порядка: .
Найти дифференциал функции: .
Написать уравнение касательной к графику функции f (х) = х3 - 1 в точке с абсциссой х0 = - 1, х0 = 2.
Найти предел, используя правило Лопиталя: .

Время на выполнение: 90 мин.
Перечень объектов контроля и оценкиНахождение производной функции.
Нахождение производных высших порядков.
Контрольная работа №4 . Интегральное исчисление функции одной переменной.
Вариант - 1
Найти неопределенные интегралы методом непосредственного интегрирования.

Найти неопределенные интегралы методом подстановки.

.
.
Найти неопределенный интеграл методом интегрирования по частям: .
Вычислить определенный интеграл: .
Вычислить определенный интеграл методом подстановки: .
Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями: .
Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями: .

Вариант - 2
Найти неопределенные интегралы методом непосредственного интегрирования.

Найти неопределенные интегралы методом подстановки.

.
.
Найти неопределенный интеграл методом интегрирования по частям: .
Вычислить определенный интеграл: .
Вычислить определенный интеграл методом подстановки: .
Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями: .
Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:

Время на выполнение: 90 мин.
Перечень объектов контроля и оценкиЗнание основных табличных интегралов.
Приложение определенного интеграла к вычислению площадей плоских фигур, объемов тел вращения.
1. У3. применять методы дифференциального и интегрального исчисления;
1. Нахождениенеопределенных
2. интегралов.
3. Вычислениеопределенных
4. интегралов.
5. Вычисление площадей плоских фигур, объемов тел вращения.
Контрольная работа №5 . Дифференциальное и интегральное исчисления функции нескольких переменных
Вариант - 1

Найти частные производные первого порядка от функции: .
Найти частные производные первого порядка от функции: .
Найти частные производные второго порядка от функции: .
Найти частные производные второго порядка от функции.
Найти дифференциал функции: .
Найти дифференциал функции: .
Вычислить двойной интеграл по прямоугольнику D: .
Вычислить двойной интеграл по области G: .

Вариант - 2

Найти частные производные первого порядка от функции: .
Найти частные производные первого порядка от функции: .
Найти частные производные второго порядка от функции: .
Найти частные производные второго порядка от функции .
Найти дифференциал функции: .
Найти дифференциал функции: .
Вычислить двойной интеграл по прямоугольнику D: .
Вычислить двойной интеграл по области G:

Время на выполнение: 90 мин.
Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. У3. применять методы дифференциального и интегрального исчисления
1. Нахождение частных производных первого и второго порядков.
2. Вычисление кратных интегралов.
1. З2. основы дифференциального и интегрального исчисления;
1. Знание таблицы производных.
2. Знание табличных интегралов.
3. Знание правил нахождения частных производных первого и второго порядков.
4. Знание правил вычисления кратных интегралов.
Контрольная работа № 6 . Ряды
Вариант - 1

Числовой ряд. Сходимость числовых рядов. Признаки сходимости числовых рядов. Абсолютная, условная сходимость.
Пользуясь необходимым признаком сходимости, показать, что ряд

расходится.

С помощью признака Даламбера решить вопрос о сходимости ряда

4. Исследовать сходимость числового ряда. а) 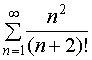б)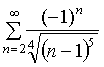

Найти область сходимости степенного ряда

а) 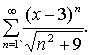б)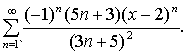
Вариант - 2

Функциональный ряд. Степенной ряд. Радиус и область сходимости. Разложение функций в степенной ряд.

Пользуясь признаком Лейбница, исследовать на сходимость знакочередующийся ряд

Пользуясь признаком сходимости знакопеременного ряда, исследовать на сходимость ряд

4. Исследовать сходимость числового ряда. а) 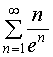б) .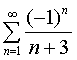
5. Найти область сходимости степенного ряда. а)
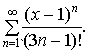
б)
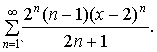
Время на выполнение: 90 мин.
Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. З1. основы математического анализа.
1. Перечисление признаков сходимости рядов.
2. Исследование рядов на сходимость.
3. Нахождение области сходимости степенных рядов.
Контрольная работа № 7 . Дифференциальные уравнения
Вариант - 1
Являются ли данные функции решениями данных дифференциальных уравнений (для № 1-4).

.
.
.
.
Решить задачу Коши: .

Решить следующие дифференциальные уравнения первого и второго порядка (для № 6-12).

Вариант - 2
Являются ли данные функции решениями данных дифференциальных уравнений (для № 1-4).

.
.
.
.
Решить задачу Коши: .

Решить следующие дифференциальные уравнения первого и второго порядка (для № 6-12).

Время на выполнение: 90 мин.
Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. У4. решать дифференциальные уравнения;
1. Решение дифференциальных уравнений первого и второго порядка
Контрольная работа № 8 . Комплексные числа.
Вариант - 1

Записать алгебраическую форму записи комплексного числа.
Перевести число из алгебраической формы записи в тригонометрическую:

Z= - -i

Дано комплексное число Z = 5 - 4i. Записать число противоположное и сопряженное к исходному.

Выполнить сложениеZ =(- 6 + 2 i)+ (- 6 - 2 i )
Выполнить умножение Z = (3 + 4 i)(3 - 4 i)
Выполнить деление Z = ( 3 - 2 i ) : ( 1 + 3 i )
Выполнить действияZ = ( 5 + 2 i ) : ( 2 - 5 i ) - ( 3 - 4 i ) : ( 4 + 3 i )

Найти z₁-z₂, z₁+z₃, z_2*z₃, z₃/z_4, если: z₁=3-5i,z₂=0.3+0.2i, z₃=, z₄=-0.4+3i.
Выполнить в тригонометрической форме записи следующие операции: z_4*z₃, z₄/z₂, , , если: z₁=2√3+2i; z₂=6-6i; z₃=-√3/2-1,5i; z₄=3.

Решить уравнение: z²-10z+34=0

Вариант - 2
1. Записать тригонометрическую форму записи комплексного числа.
2. Перевести число из алгебраической формы записи в показательную форму:
Z= -1 + i
3.Дано комплексное число Z =7 + 9 i. Записать число противоположное и сопряженное к исходному.
4.Выполнить сложениеZ =(5 + 3 i)+ (- 2 - 5 i)
5.Выполнить умножение Z =(-2 + 3 i)(-1 - 6i)
6.Выполнить деление Z =(4 +- 3i):(-2 - 5 i)
7.Выполнить действияZ = ( -1 + 3 i ) : ( 5 + i ) + (7 + 3 i ) : ( 1 - 2 i )
8. Найти z₂-z₁, z₂+z₃, z_1*z₃, z₂/z_4, если: z₁=-3-5i,z₂=0.3+0.2i, z₃=, z₄=-0.4+3i.
9. Выполнить в тригонометрической форме записи следующие операции: z_1*z₃, z₃/z₂, , , если: z₁=2√3+2i; z₂=6-6i; z₃=-√3/2-1,5i;z₄=3.
10.Решить уравнение: z²-10z+26=0
Время на выполнение: 90 мин.
Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. У5. пользоваться понятиями теории комплексных чисел.
1. Записывать комплексные числа в алгебраической и тригонометрической формах.
2. Выполнять действия над комплексными числами.
1. З3. основы теории комплексных чисел.
1. Различные формы записи комплексных чисел.
2. Правила выполнения операций над комплексными числами.
Расчетные задания.
Расчетное задание №1.
Вариант - 1

Найти матрицу C=A+3B, если , .
Решить систему линейных уравнений методом обратной матрицы.
Решить систему линейных уравнений по формулам Крамера.
Решить систему линейных уравнений методом Гаусса.

Вариант - 2

1. Найти матрицу C=2A-B, если , .
2. Решить систему линейных уравнений методом обратной матрицы.
3. Решить систему линейных уравнений по формулам Крамера.
4. Решить систему линейных уравнений методом Гаусса.

Вариант - 3

Найти матрицу C=3A+B, если , .
Решить систему линейных уравнений методом обратной матрицы.
Решить систему линейных уравнений по формулам Крамера.
Решить систему линейных уравнений методом Гаусса.

Вариант - 4

Найти матрицу C=A-4B, если , .
Решить систему линейных уравнений методом обратной матрицы.
Решить систему линейных уравнений по формулам Крамера.
Решить систему линейных уравнений методом Гаусса.

Вариант - 5

Найти матрицу C=4A-B, если , .
Решить систему линейных уравнений методом обратной матрицы.
Решить систему линейных уравнений по формулам Крамера.
Решить систему линейных уравнений методом Гаусса.

Вариант- 6

Найти матрицу C=A+2B, если , .
Решить систему линейных уравнений методом обратной матрицы.
Решить систему линейных уравнений по формулам Крамера.
Решить систему линейных уравнений методом Гаусса.

Перечень объектов контроля и оценкиНаименование объектов контроля и оценки
1. Основные показатели оценки результата
1. У 1. выполнять операции над матрицами и решать системы линейных уравнений;
1. - Выполнение действий над матрицами
2. - Вычисление определителей
3. - Решение систем линейных уравнений методом обратной матрицы
4. - Решение систем линейных уравнений по формулам Крамера
5. - Решение систем линейных уравнений методом Гаусса
1. З 1. основы математического анализа, линейной алгебры и аналитической геометрии
1. - Перечисление последовательности действий при решении систем линейных уравнений методом обратной матрицы, по формулам Крамера, методом Гаусса
Устный опрос №1
Дать определение вектора.

Дать определение проекции вектора на ось и перечислить ее свойства.
Дать определение скалярного произведения векторов и перечислить его свойства.
Дать определение векторного произведения векторов и перечислить его свойства.
Дать определение смешанного произведения векторов и перечислить его свойства.

Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. З 1. основы математического анализа, линейной алгебры и аналитической геометрии
1. - Формулировка определений и перечисление свойств скалярного, векторного и смешанного произведения векторов
Расчетное задание №2.
Вариант - 1
Даны векторы и (для № 1-5).

Найти .
Найти .
Найти .
Найти .
Найти координаты векторов , , .
В прямоугольной декартовой системе координат построить точки A (0; 0),

B (3; -4), C (-3; 4). Определить расстояние между точками A и B, B и C, A и C.
Построить точки, заданные полярными координатами: A (2; /2), B (3; /4),

C (3; 3/4).
Даны точки в полярной системе координат A (2; /4), B (4; /2). Найти их прямоугольные координаты.

Вариант - 2
Даны векторы и (для № 1-5).

Найти .
Найти .
Найти .
Найти .
Найти координаты векторов , , .
В прямоугольной декартовой системе координат построить точки A (0; 0),

C (-3; 4), D (-2; 2) E (10; -3). Определить расстояние между точками C и D, A и D, D и E.
Построить точки, заданные полярными координатами: A (4; 0), B (2; 3/2),

C (3; ).
Даны точки в прямоугольной системе координат A (0; 5), B (-3; 0),C (; 1). Найти их полярные координаты.

Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. З1 - основы математического анализа, линейной алгебры и аналитической геометрии
1. - Выполнение действий над векторами
2. - Нахождение скалярного, векторного и смешанного произведения векторов
3. - Построение точек и нахождение их координат в прямоугольной декартовой и полярной системах координат
Расчетное задание №4.
Вариант - 1
Исследовать функцию на непрерывность в точке .
Вариант - 2
Исследовать функцию на непрерывность в точке .
Вариант - 3
Исследовать функцию на непрерывность в точке .
Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. У3 - применять методы дифференциального и интегрального исчисления
1. - Исследование функции на непрерывность в точке
1. З1 - основы математического анализа, линейной алгебры и аналитической геометрии
1. - Классификация точек разрыва
Расчетное задание №5.
Вариант - 1

Вычислить предел функции:

Вычислить предел функции:

Вычислить предел функции:

Вычислить предел функции:

.
Вариант - 2

Вычислить предел функции:

Вычислить предел функции:

Вычислить предел функции:

Вычислить предел функции:

.
Вариант - 3

Вычислить предел функции:

Вычислить предел функции:

Вычислить предел функции:

Вычислить предел функции:

.
Вариант - 4

Вычислить предел функции:

Вычислить предел функции:

Вычислить предел функции:

Вычислить предел функции:

.
Вариант - 5

Вычислить предел функции:

Вычислить предел функции:

Вычислить предел функции:

Вычислить предел функции:

.
Вариант - 6

Вычислить предел функции:

Вычислить предел функции:

Вычислить предел функции:

Вычислить предел функции:

.
Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. У3 - применять методы дифференциального и интегрального исчисления
1. - Вычисление предела функции в точке и в бесконечности
Расчетное задание №6.
Вариант - 1

Найти производную функции .
Найти производную третьего порядка функции .
Написать уравнение касательной к графику функции в точке с абсциссой , .
Материальная точка движется по закону . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)

Вариант - 2

Найти производную функции .
Найти производную третьего порядка функции .
Написать уравнение касательной к графику функции в точке с абсциссой , .
Материальная точка движется по закону . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)

Вариант - 3

Найти производную функции .
Найти производную третьего порядка функции .
Написать уравнение касательной к графику функции в точке с абсциссой , .
Материальная точка движется по закону . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)

Вариант - 4

Найти производную функции .
Найти производную третьего порядка функции .
Написать уравнение касательной к графику функции в точке с абсциссой , .
Материальная точка движется по закону . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)

Вариант - 5

Найти производную функции .
Найти производную третьего порядка функции .
Написать уравнение касательной к графику функции в точке с абсциссой , .
Материальная точка движется по закону . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)

Вариант - 6

Найти производную функции .
Найти производную третьего порядка функции .
Написать уравнение касательной к графику функции в точке с абсциссой , .
Материальная точка движется по закону . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)

Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. У3 - применять методы дифференциального и интегрального исчисления;
1. - Нахождение производной функции
2. - Нахождение производных высших порядков
1. З2 - основы дифференциального и интегрального исчисления
1. - Формулировка геометрического и механического смысла производной
Устный опрос №2
Сформулировать правила дифференцирования и записать производные основных элементарных функций:
В частности,
1. 9^о.
1. 10^о.
1. 11^о.
1. 12^о.
1. 13^о.
1. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
1. 14^о.
1. 3^о.
1. 15^о.
1. 4^о.
2. В частности,
1. 16^о.
1. 17^о.
1. 5^о.
2. В частности,
1. 18^о.
2. В частности,
1. 6^о.
1. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
1. 7^о.
1. 19^о.
Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. З2 - основы дифференциального и интегрального исчисления
1. - Формулировка правил дифференцирования и перечисление производных основных элементарных функций
Расчетное задание №7.
Исследовать функцию и построить ее график.
Вариант - 1
.
Вариант - 2
.
Вариант - 3
Вариант - 4
y=
Вариант - 5
y=
Вариант - 6
y=.
Вариант - 7
y=
Вариант - 8
y=
Вариант - 9
y=
Вариант - 10
y=
Вариант - 11
y=
Вариант - 12
y=
Вариант - 13
y=
Вариант - 14
y=
Перечень объектов контроля и оценкиНаименование объектов контроля и оценки
1. Основные показатели оценки результата
1. У3 - применять методы дифференциального и интегрального исчисления;
1. - Исследование функции и построение графика
Расчетное задание №8.
Вариант - 1
Найти неопределенные интегралы методом непосредственного интегрирования (для № 1-5).

.
.
.
.
.
1. Найти неопределенные интегралы методом подстановки (для № 6-8).
.
.
.
Найти неопределенный интеграл методом интегрирования по частям: .

Вариант - 2

Найти неопределенные интегралы методом непосредственного интегрирования (для № 1-5).
.
.
.
.
.
1. Найти неопределенные интегралы методом подстановки (для № 6-8).
.
.
.
Найти неопределенный интеграл методом интегрирования по частям: .

Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. У3 - применять методы дифференциального и интегрального исчисления;
1. - Нахождение неопределенных интегралов
Устный опрос №3
Записать табличные интегралы:
1^о.
2^о.
В частности,
3^о.
4^о.
В частности,
5^о.
6^о.
7^о.
8^о.
9^о.
В частности,
10^о.
В частности,
Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. З2 - основы дифференциального и интегрального исчисления
1. - Перечисление табличных интегралов
Расчетное задание №9.
Вариант - 1

Вычислить определенный интеграл: .
Вычислить определенный интеграл методом подстановки: .
Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями: .
Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:
Скорость движения точки изменяется по закону (м/с). Найти путь S, пройденный точкой за 10 сек начала движения.

Вариант - 2

Вычислить определенный интеграл: .
Вычислить определенный интеграл методом подстановки: .
Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями: .
Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:.
Скорость движения точки изменяется по закону (м/с). Найти путь S, пройденный точкой за четвертую секунду.

Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. У3 - применять методы дифференциального и интегрального исчисления
1. - Вычисление определенных интегралов
1. З2 - основы дифференциального и интегрального исчисления
1. - Приложение определенного интеграла к вычислению площадей плоских фигур, объемов тел вращения, пути, пройденного точкой
Расчетное задание №10.
Вариант - 1
Найти частные производные функций.

Вариант - 2
Найти частные производные функций.

Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. У3 - применять методы дифференциального и интегрального исчисления
1. - Нахождение частных производных
Расчетное задание №11.

Пользуясь необходимым признаком сходимости, показать, что ряд

расходится.

С помощью признака Даламбера решить вопрос о сходимости ряда

Пользуясь признаком Лейбница, исследовать на сходимость знакочередующийся ряд

Пользуясь признаком сходимости знакопеременного ряда, исследовать на сходимость ряд

Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. З1 - основы математического анализа, линейной алгебры и аналитической геометрии
1. - Исследование рядов на сходимость
Расчетное задание №12.
Вариант - 1
Являются ли данные функции решениями данных дифференциальных уравнений (для № 1-4).

.
.
.
.
Решить задачу Коши: .

Решить следующие дифференциальные уравнения первого и второго порядка (для № 6-12).

Вариант - 2
Являются ли данные функции решениями данных дифференциальных уравнений (для № 1-4).

.
.
.
.
Решить задачу Коши: .
1. Решить следующие дифференциальные уравнения первого и второго порядка (для № 6-12).
.
.
.
.
.
.
.

Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. У4 - решать дифференциальные уравнения,
1. - Решение дифференциальных уравнений первого и второго порядка
Устный опрос №4.

Сформулировать общие положения при составлении дифференциального уравнения по условию задачи.
Записать дифференциальное уравнение показательного роста и показательного убывания и получить его решение. Привести примеры прикладных задач, решаемых с его помощью.
Сформулировать задачу о радиоактивном распаде, записать для нее дифференциальное уравнение.
Сформулировать задачу о гармонических колебаниях, записать дифференциальное уравнение гармонических колебаний.
Сформулировать задачу о падении тел в атмосферной среде, записать для нее дифференциальное уравнение.

Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. З2 - основы дифференциального и интегрального исчисления
1. - Описание процессов в естествознании и технике с помощью дифференциальных уравнений
Расчетное задание №13.
Вариант - 1

Вычислите: ( 5 + i)( -2 +3i);

( 5 + i) + ( -2 +3i).

Запишите комплексное число в стандартной тригонометрической форме: 6 - 6 i; - 4 -3 i.
Решите уравнение: х² - 2х + 2 =0
Вычислите ()².
Решите уравнение z² + 3 + 4i = 0.

Вариант - 2

Вычислите ( + 5i)(5 - ).

(3 + 5i) +(5 - ).

Запишите комплексное число в стандартной тригонометрической форме: 2 - 3i; 12i - 5.
Решите уравнение x² + 5x + 9 = 0.
Вычислите (2 + i)².
Решите уравнение z² - (4 + 3i)z + 1 + 5i = 0.

Вариант - 3

Вычислите (7 - 2i)(3,5 - i);

(7 - 2i) + (3,5 - i).

Запишите комплексное число в стандартной тригонометрической форме: 2 + 2 i; -3 - 2i.
Решите уравнение 4x² + 4x + 5 = 0.
Вычислите (1 + i)².
Решите уравнение х² + iх + 1- 3i = 0.

Вариант - 4

Вычислите ( + 5i)(5 - ).

( + 5i) +(5 - ).

Запишите комплексное число в стандартной тригонометрической форме: 3 - 3i; 12i - 6.
Решите уравнение x² + 5x + 10 = 0.
Вычислите (2 + i)².
Решите уравнение z² + 1 + 5i = 0.

Вариант - 5

Вычислите: ( 5 +4 i)( -2 +3i);

( 5 + i) + ( -2 +3i).

Запишите комплексное число в стандартной тригонометрической форме: 6 - 6 i; - 4 -3 i.
Решите уравнение: х² - 2х + 2 =0
Вычислите ()².
Решите уравнение z² + 3 + 4i = 0.

Вариант - 6

Вычислите ( + 4i)(5 - ).

(3 + 5i) +(5 - ).

Запишите комплексное число в стандартной тригонометрической форме: 2 - 3i; 12i - 5.
Решите уравнение x² + 5x + 9 = 0.
Вычислите (2 + i)².
Решите уравнение z² - (4 + 3i)z + 1 + 5i = 0.

Перечень объектов контроля и оценки
Наименование объектов контроля и оценки
1. Основные показатели оценки результата
1. У5 - пользоваться понятиями теории комплексных чисел;
1. Записывать комплексные числа в алгебраической и тригонометрической формах.
2. Выполнять действия над комплексными числами.
1. З3 - основы теории комплексных чисел.
1. Различные формы записи комплексных чисел.
2. Правила выполнения операций над комплексными числами.

1. Вопросы и задания для зачета.

Теоретические вопросы.
1. Определители второго порядка. Определители третьего порядка. Свойства определителей.
2. Минор матрицы. Алгебраическое дополнение матрицы.
3. Матрицы. Сложение матриц.
4. Матрицы. Умножение матрицы на действительное число. Умножение матриц.
5. Правило Крамера.
6. Обратная матрица.
7. Уравнение прямой с угловым коэффициентом. Уравнение прямой, проходящей через две данные точки.
8. Уравнение прямой в отрезках. Общее уравнение прямой.
9. Понятие вектора. Линейные операции над векторами.
10. Скалярное произведение векторов. Выражение скалярного произведения через координаты векторов.
11. Определение векторного произведения. Выражение векторного произведения через координаты векторов.
12. Определение и геометрический смысл смешанного произведения векторов.
13. Линии второго порядка.
14. Определение числовой последовательности. Ограниченные и неограниченные последовательности.
15. Бесконечно большие и бесконечно малые последовательности.
16. Определение предела последовательности. Основные свойства сходящихся последовательностей.
17. Определение монотонных последовательностей. Признак сходимости монотонных последовательностей.
18. Определение предела функции. Свойства пределов.
19. Понятие производной. Правила дифференцирования.
20.Правило вычисления производной сложной функции.
21. Понятие дифференциала.
22. Производные и дифференциалы высших порядков.
23. Теорема Ферма.
24. Правила Лопиталя.
25. Признак монотонности функции.
26. Точки экстремума. Необходимое условие локального экстремума. Достаточное условие экстремума.
27. Направление выпуклости графика функции. Достаточное условие выпуклости функции.
28. Необходимое и достаточное условие точки перегиба.
29. Асимптоты графика функции.
30. Понятие первообразной.
31. Понятие неопределенного интеграла. Свойства неопределенного интеграла.
32. Определение определенного интеграла. Основные свойства.
33. Формула Ньютона - Лейбница.
34. Метод интегрирования по частям.
Практические задания.

1. 1. 1. Даны матрицы А, B. 1) Найти матрицу 2А-В.

2. Найти определитель матрицы А.
3. 1) Найти матрицу А∙В.
4. Найти матрицу D∙C.
5. Решить систему уравнений методом Гаусса:
6. Решить систему уравнений по правилу Крамера:
7. Составить уравнение прямой, отсекающей на оси Oy отрезок b = 3 и образующий с осью Ox угол равный 45^o.
8. Написать каноническое уравнение эллипса, если известно, что расстояние между фокусами равно 8, а малая полуось b = 3.
9. Вычислить предел: .
10. Вычислить предел: .
11. Вычислить предел: .
12. Вычислить предел: .
13. Найти производную функции: .
14. Найти производную функции: .
15. Найти производную функции: .
16. Найти производную функции: .
17. Найти производную второго от функции:
18. Найти производную второго порядка от функции: .
19. Найти дифференциал функции: .
20. Найти дифференциал функции: .
21. Найти максимумы и минимумы функции: .
22. Найти максимумы и минимумы функции: .
23. Найти интервалы выпуклости и точки перегиба графика функции: .
24. Найти интервалы выпуклости и точки перегиба графика функции:
25. Найти неопределенный интеграл: .
26. Найти неопределенный интеграл: .
27. Найти неопределенный интеграл: .
28. Найти неопределенный интеграл: .
29. Вычислить определенный интеграл: .
30. Вычислить определенный интеграл: .
31. Вычислить определенный интеграл: .
32. Вычислить определенный интеграл: .
33. Вычислить определенный интеграл: .
34. Найти площадь фигуры, ограниченной линиями: .
35. Представьте в тригонометрической и показательной форме число: .
36. Представьте в алгебраической форме число:.
37.Извлеките корни:.

1. Пакет экзаменатора.
  1. Экзаменационные вопросы

Матрицы, действия над матрицами.
Определители 1-го, 2-го, 3-го порядков. Правило треугольников.
Определители n-го порядка. Теорема Лапласа.
Обратная матрица. Алгоритм нахождения обратной матрицы.
Ранг матрицы. Алгоритм вычисления ранга матрицы с помощью элементарных преобразований.
Система линейных уравнений. Метод обратной матрицы. Формулы Крамера. Метод Гаусса.
Векторы и операции над ними.
Проекция вектора на ось и ее свойства.
Декартова прямоугольная система координат. Полярная система координат.
Скалярное, векторное и смешанное произведения векторов.
Предел функции в точке. Основные теоремы о пределах.
Предел функции при x, стремящемся к бесконечности. Замечательные пределы. Число е.
Непрерывность функции в точке и на промежутке. Точка непрерывности функции. Точка разрыва функции. Свойства непрерывных функций. Приращение аргумента. Приращение функции.
Производная функции. Дифференциал функции. Геометрический смысл производной. Механический смысл производной.
Таблица производных. Понятие сложной функции. Производная сложной функции.
Схема исследования функции. Область определения функции. Множество значений функции. Четность и нечетность функции. Нули функции. Промежутки знакопостоянства функции. Возрастание и убывание функции, правило нахождения промежутков монотонности.Точки экстремума функции, правило нахождения экстремумов функции.
Производные высших порядков. Физический смысл второй производной. Исследование функции с помощью второй производной.
Первообразная. Неопределенный интеграл. Основные свойства неопределенного интеграла.
Таблица неопределенных интегралов.
Методы интегрирования: метод непосредственного интегрирования; метод замены переменной (метод подстановки); метод интегрирования по частям.
Определенный интеграл. Понятие интегральной суммы. Достаточное условие существования определенного интеграла (интегрируемости функции).
Основные свойства определенного интеграла. Геометрический смысл определенного интеграла.
Методы вычисления определенных интегралов. Формула Ньютона-Лейбница.
Геометрические и физические приложения определенного интеграла.
Функции нескольких переменных. Частные производные.
Понятие дифференциального уравнения. Общее и частное решение дифференциального уравнения. Интегральные кривые. Задача Коши.
Задачи, приводящие к дифференциальным уравнениям.
Методы решения дифференциальных уравнений.
Понятие числового ряда. Сходимость и расходимость числовых рядов.
Необходимый признак сходимости ряда. Признак сравнения. Признак Даламбера.
Понятие знакочередующегося ряда. Признак сходимости Лейбница.
Абсолютная и условная сходимость знакопеременного ряда.
Функциональные ряды. Степенные ряды. Область сходимости степенного ряда. Числовые ряды и свойства числовых рядов.
Функциональные ряды и свойства функциональных рядов.
Комплексные числа и операции над ними.
Геометрическая, тригонометрическая форма комплексного числа. Основные понятия. Область определения.

5.3.2. Экзаменационные задания

Вычислить предел .
Вычислить пределы:

а) ; б) ; в) .

Вычислить предел .
Вычислить предел .
Вычислить предел .
Вычислить предел .
Исследовать функцию на непрерывность в точке .
Исследовать функцию и построить ее график.
Вычислить значение производной следующих функций в точке :

а) ; б) .

Найти производную функции .
Найти производную функции .
Найти производную функции .
Найти производную функции .
Найти неопределенный интеграл .
Найти неопределенный интеграл методом замены переменной .
Найти неопределенный интеграл методом замены переменной .
Найти неопределенный интеграл методом замены переменной .
Найти неопределенный интеграл методом замены переменной .
Вычислить определенный интеграл .
Вычислить определенный интеграл .
Вычислить определенный интеграл .
Скорость движения точки изменяется по закону (м/с). Найти путь s, пройденный точкой за 4 сот начала движения.
Вычислить объем тела, полученного от вращения фигуры, ограниченной линиями , , , , вокруг оси Ox.
Вычислить площадь фигуры, ограниченной линиями , , , .
Решить дифференциальное уравнение .
Решить задачу Коши: , .
Решить дифференциальное уравнение .
Представьте в тригонометрической и показательной форме число: .
Представьте в алгебраической форме число:.
Извлеките корни:.

Информационное обеспечение обучения.

Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы
Основные источники:

Элементы высшей математики: учебник для студ. учреждений сред.проф. образования/В.П.Григорьев, Ю.А.Дубинский. - 10-е изд. стер. - М.: Издательский центр «Академия», 2014 - 320с.
Сборник задач по высшей математике: учебное пособие для студ. учреждений сред.проф. образования/В.П.Григорьев, Т.И. Сабурская. - 4-е изд. стер. - М.: Издательский центр «Академия», 2014 - 160с.
Баврин И.И. Высшая математика: Учебник для студентов естественно-научных специальностей педагогических вузов / И.И. Баврин. - М.: Издательский центр «Академия». - 2004. - 616 с.
Богомолов Н.В. Сборник задач по математике / Н.В. Богомолов. - М.: Дрофа. - 2007. - 320 с.
Богомолов Н.В. Практические занятия по математике / Н.В. Богомолов. - М.: Дрофа. - 2007. - 150 с.
Богомолов Н.В. Математика / Н.В. Богомолов. - М.: Дрофа. - 2006. - 300 с.
Минорский В.П. Сборник задач по высшей математике: Учебное пособие для втузов

/ В.П. Минорский. - М.: Издательство Физико-математич. Литературы. - 2003. -336 с.
8. Кострикин А. И. Введение в алгебру. Ч. 1. Основы алгебры / А. И. Кострикин. М.: Издательство Физико-математической литературы. - 2000. - 136 с.
9. Кострикин А. И. Введение в алгебру. Ч. 2. Линейная алгебра / А. И. Кострикин. М.: Издательство Физико-математической литературы. - 2000. - 164 с.
10. Кострикин А. И. Введение в алгебру. Ч. 3. Основные структуры алгебры / А. И. Кострикин. М.: Издательство Физико-математической литературы, 2000. - 148 с.
Дополнительные источники:
1. Баврин И.И. Общий курс высшей математики / И.И. Баврин, В.Л. Матросов. - М.: Просвещение. - 1995. - 608 с.
2. Данко П.Е. Высшая математика в упражнениях и задачах. Ч.1: Учеб.пособие для студентов втузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - М.: Высш. школа. - 1980. - 320 с.
3. Данко П.Е. Высшая математика в упражнениях и задачах. Ч.2: Учеб.пособие для студентов втузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - М.: Высш. школа. - 1980. -- 365 с.
4. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики / В.А. Кудрявцев, Б.П. Демидович. - М.: Наука. - 1975. - 624 с.
Программное обеспечение и Интернет-ресурсы:
- электронная библиотека механико-математического факультета МГУ;
www.newlibrary.ru - новая электронная библиотека;
www.edu.ru - федеральный портал российского образования;
www.mathnet.ru - общероссийский математический портал;
www.library.kemsu.ru - электронный каталог НБ КемГУ;
www.elibrary.ru - научная электронная библиотека;
www.matburo.ru - матбюро: решения задач по высшей математике;
www.nehudlit.ru - злектронная библиотека учебных материалов
mech.math.msu.su/department/algebra</ - официальный сайт механико-математического факультета МГУ.

⇧

⇩

скачать материал